Forest of Stochastic Trees: A Method for Valuing Multiple Exercise Options
Abstract
1. Introduction
- The Forest of Trees method of Lari et al. (2001) and Jaillet et al. (2004) for valuing multiple exercise options on a single asset to allow for high-dimensional underlying assets and processes; and
- The Stochastic Tree method of Broadie and Glasserman (1997) for valuing high-dimensional American-style options (single exercise right) to options having multiple exercise rights and additional controls (e.g., volume control).
- The high FOST estimator has positive bias.
- The low FOST estimator has negative bias.
- On any given realization the high FOST estimator is at least as big as the low FOST estimator.
- The high and low FOST estimators are asymptotically unbiased.
Literature Review
2. Results
- Exercising u units plus continuing with an option having remaining exercise rights and usage level ; and
- Continuing with an option having exercise rights and usage level U (i.e., no exercise).
2.1. Forest of Stochastic Trees
2.2. Estimator Bias
2.3. Estimator Convergence
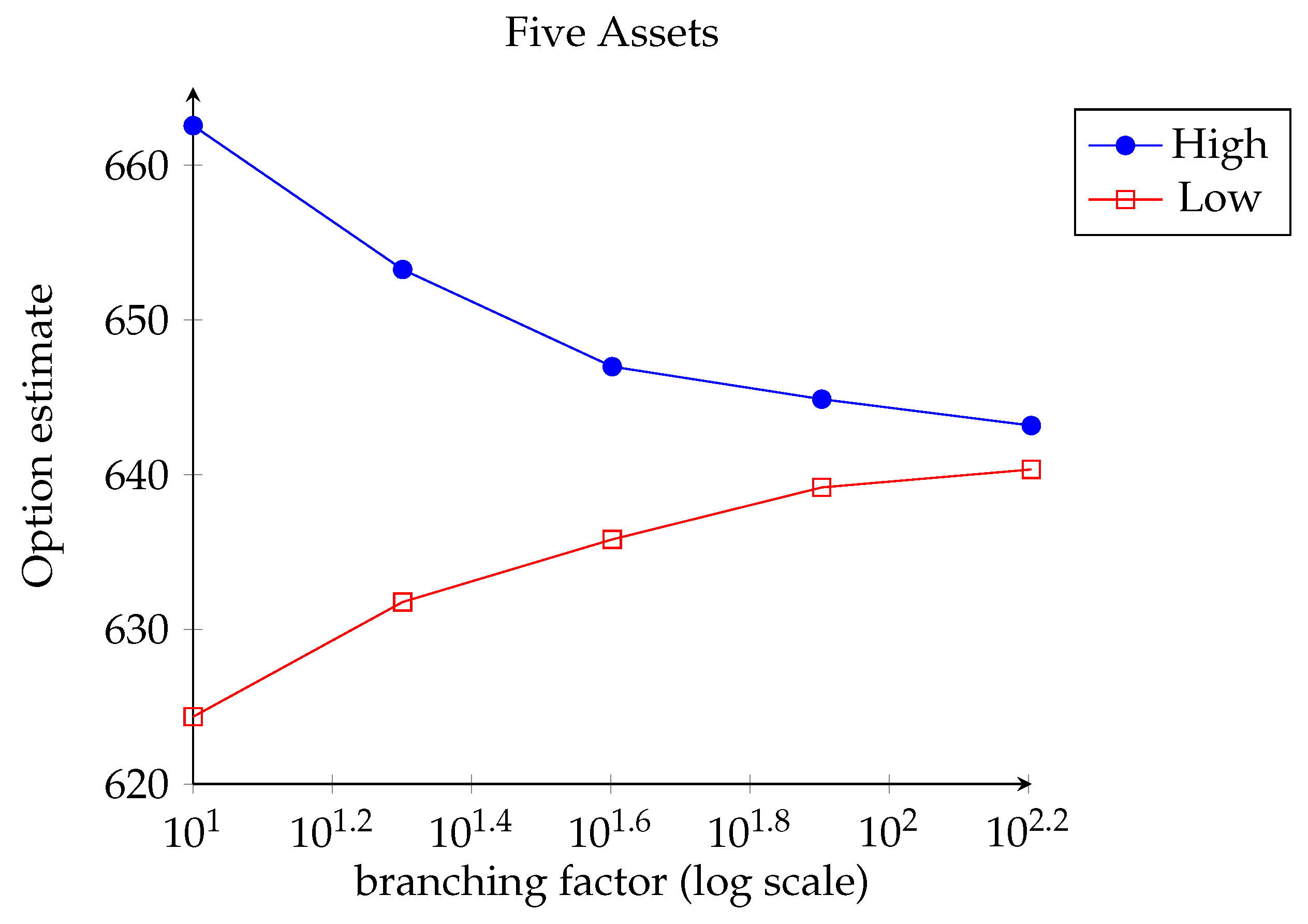
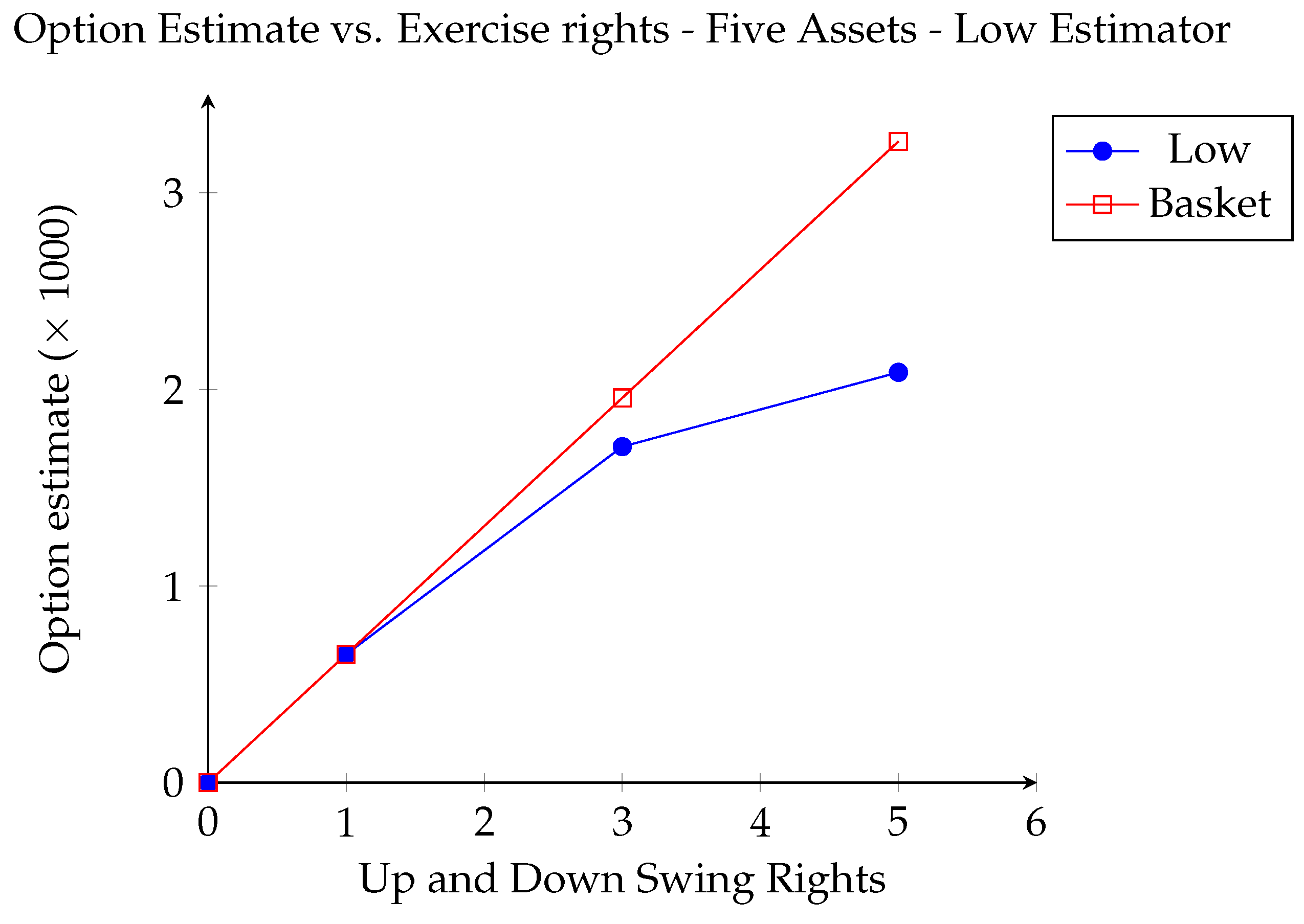
2.4. Numerical Results
2.4.1. Single Dimension
2.4.2. Calibrated Forward Curve
2.4.3. Five Dimensions
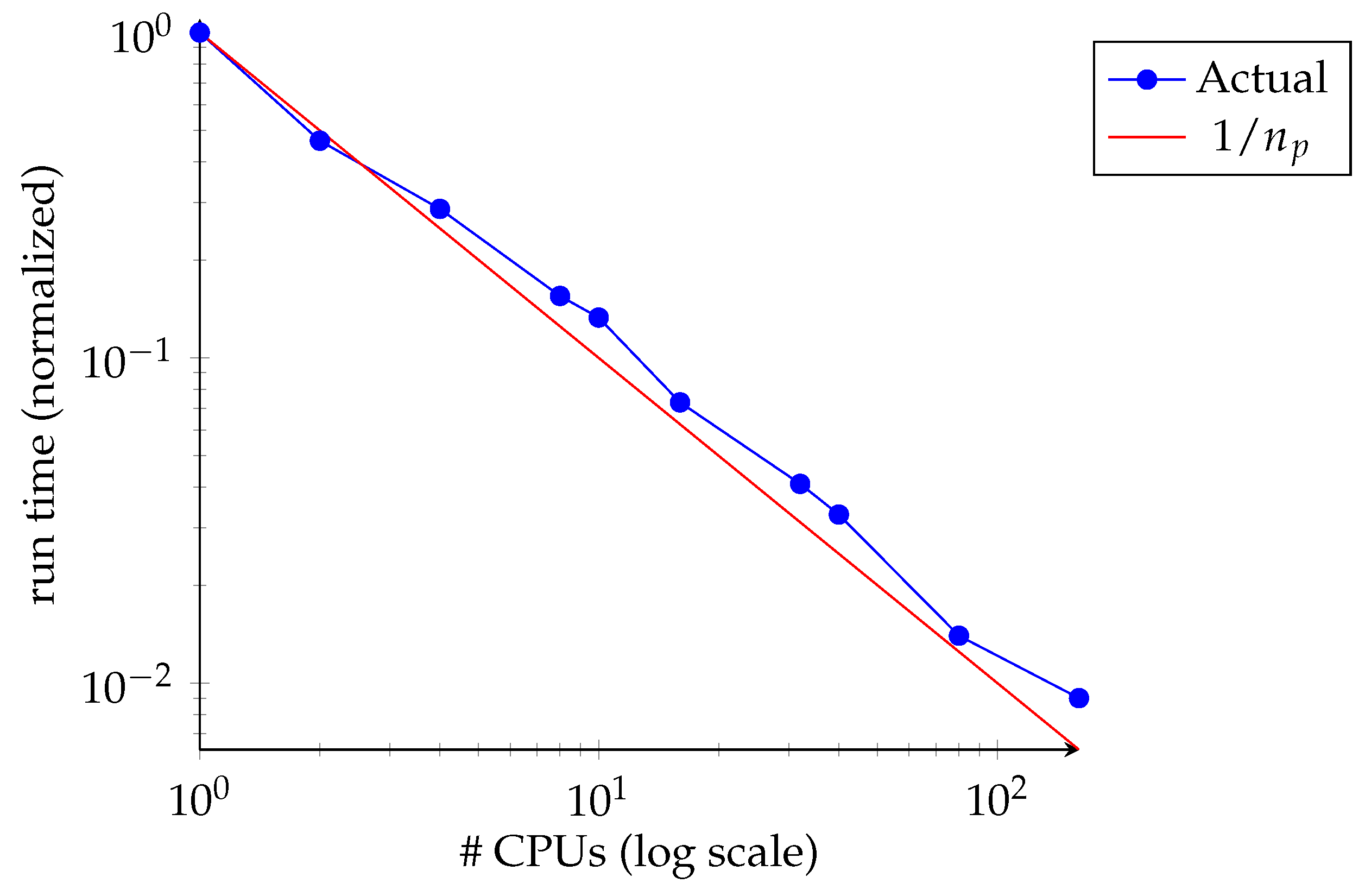
2.5. Algorithmic Enhancement via Parallel Processing
3. Discussion and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MEO | Multiple Exercise Option |
| PDE | Partial Differential Equation |
| FOST | Forest of Stochastic Trees |
| FOSM | Forest of Stochastic Meshes |
| MC | Monte Carlo |
Appendix A. Nomenclature
- Time is indexed by i for , .
- R is the number of repeated valuations of the forest.
- b is the branching factor.
- is the spot price vector at time for branch . For convenience we may suppress the bold superscript if there is no ambiguity in doing so, in these cases refers to the time- price along the branch path .
- represents the time- history of the set of state variables , where we suppress the branching history index.
- is the time-, state- high estimator.
- is the time-, state-leave one out low biased estimator which does not include node l at time-.
- is the time-, state-leave one out hold value estimator for exercising u units which does not include node l at time-,
- is the time-, state- low estimator
- is the time- number of exercise rights remaining.
- is the time- cumulative volume.
- is the time- discretized set of available volume choices,where .
- u is the time- volume exercised. Here .
- is the discount factor from to .
- is the time-, state- payoff from exercising u units with .
- is the time-, state- true hold value,
- is the time-, state- true option value,where is the indicator function for set A.
Appendix B. Proofs of Main Results and Lemmas
Appendix B.1. Proofs of Main Results
- for all and where
Appendix B.2. Lemma Proofs
- (a)
- Then
- (b)
- Note that conditions (i) and (b) imply thatand we havewhere the first inequality comes from the triangle inequality, the second comes from Inequality (A11) and the third inequality comes from another application of the triangle inequality.
- (a)
- Then
- (b)
- Note that conditions (ii) and (b) imply thatand we havewhere again the first inequality comes from the triangle inequality, the second comes from Inequality (A12) and the third inequality comes from another application of the triangle inequality.
- (a)
- where the first inequality comes from the inductive hypothesis.
- (b)
- By the definitions of and and (b) we haveThis combined with (i) givesThenwhere again the first inequality comes from the triangle inequality, the second comes from Inequality (A13) and the third inequality comes from another application of the triangle inequality.
- (a)
- (b)
- By the definitions of and and (ii) we haveThis combined with (b) givesThenwhere again the first inequality comes from the triangle inequality, the second comes from Inequality (A14) and the third inequality comes from another application of the triangle inequality.
References
- Andersen, Leif, and Mark Broadie. 2004. Primal-Dual Simulation Algorithm for Pricing Multidimensional American Options. Management Science 50: 1222–34. [Google Scholar] [CrossRef]
- Bally, Vlad, Gilles Pagés, and Jacques Printems. 2005. A Quantization Tree Method for Pricing and Hedging Multidimensional American Options. Mathematical Finance 15: 119–68. [Google Scholar] [CrossRef]
- Barraquand, Jerome, and Didier Martineau. 1995. Numerical Valuation of High Dimensional Multivariate American Securities. Journal of Financial and Quantitative Analysis 30: 383–405. [Google Scholar] [CrossRef]
- Barrera-Esteve, Christophe, Florent Bergeret, Charles Dossal, Emmanuel Gobet, Asma Meziou, Remi Munos, and Damien Reboul-Salze. 2006. Numerical Methods for the Pricing of Swing Options: A Stochastic Control Approach. Methodology and Computing in Applied Probability 8: 517–40. [Google Scholar] [CrossRef]
- Ben Latifa, Imene, Joseph Frederic Bonnans, and Mohamed Mnif. 2016. Numerical methods for an optimal multiple stopping problem. Stochastics and Dynamics 16. [Google Scholar] [CrossRef]
- Bender, Christian. 2011. Dual pricing of multi-exercise options under volume constraints. Finance and Stochastics 15: 1–26. [Google Scholar] [CrossRef]
- Bender, Christian, and John Schoenmakers. 2006. An Iterative Algorithm for Multiple Stopping: Convergence and Stability. Advances in Applied Probability 38: 729–49. [Google Scholar] [CrossRef]
- Broadie, Mark, and Paul Glasserman. 1997. Pricing American-style securities using simulation. Journal of Economic Dynamics and Control 21: 1323–52. [Google Scholar] [CrossRef]
- Broadie, Mark, and Paul Glasserman. 2004. A stochastic mesh method for pricing high-dimensional American options. The Journal of Computational Finance 7: 35–72. [Google Scholar] [CrossRef]
- Calvo-Garrido, Maria del Carmen, Matthias Ehrhardt, and Carlos Vázquez. 2017. Pricing swing options in electricity markets with two stochastic factors using a partial differential equation approach. The Journal of Computational Finance 20: 81–107. [Google Scholar] [CrossRef]
- Carriere, Jacques. 1996. Valuation of Early-Excercise Price of Options Using Simulations and Nonparametric Regression. Insurance: Mathematics and Economics 19: 19–30. [Google Scholar]
- Chandramouli, Shyam S., and Martin B. Haugh. 2012. A unified approach to multiple stopping and duality. Operations Research Letters 40: 258–64. [Google Scholar] [CrossRef]
- Chen, Zhuliang, and Peter A. Forsyth. 2007. A semi-Lagrangian approach for natural gas storage valuation and optimal operation. SIAM Journal on Scientific Computing 30: 339–68. [Google Scholar] [CrossRef]
- Clément, Emmanuelle, Damien Lamberton, and Philip Protter. 2001. An analysis of a least-squares regression algorithm for American option pricing. Finance Stochastics 6: 449–71. [Google Scholar] [CrossRef]
- Cox, John C., Stephen A. Ross, and Mark Rubinstein. 1979. Option Pricing: A Simplified Approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Deng, Shijie, and Shmuel S. Oren. 2006. Electricity derivatives and risk management. Energy 31: 940–53. [Google Scholar] [CrossRef]
- Gut, Allan. 1988. Stopped Random Walks. New York: Springer. [Google Scholar]
- Gyurkó, Lajos Gergely, Ben M. Hambly, and Jan Hendrick Witte. 2015. Monte Carlo methods via a dual approach for some discrete time stochastic control problems. Mathematical Methods of Operations Research 81: 109–35. [Google Scholar] [CrossRef][Green Version]
- Haugh, Martin B., and Leonid Kogan. 2004. Pricing American Options: A Duality Approach. Operations Research 52: 258–70. [Google Scholar] [CrossRef]
- Ibán̎ez, Alfredo. 1996. Valuation by Simulation of Contingent Claims with Multiple Early Exercise Opportunities. Mathematical Finance 19: 19–30. [Google Scholar]
- Jaillet, Patrick, Ehud I. Ronn, and Stathis Tompaidis. 2004. Valuation of Commodity-Based Swing Options. Management Science 50: 909–21. [Google Scholar] [CrossRef]
- Kim, Dong-Hyun, Eul-Bum Lee, In-Hyeo Jung, and Douglas Alleman. 2019. The Efficacy of the Tolling Model’s Ability to Improve Project Profitability on International Steel Plants. Energies 12: 1221. [Google Scholar] [CrossRef]
- Dahlgren, Martin, and Ralf Korn. 2005. The Swing Option on the Stock Market. The International Journal of Theoretical and Applied Finance 8: 123–129. [Google Scholar] [CrossRef]
- Lari-Lavassani, Ali, Mohamadreza Simchi, and Antony Ware. 2001. A Discrete Valuation of Swing Options. Canadian Applied Mathematics Quarterly 9: 35–73. [Google Scholar]
- Longstaff, Francis A., and Eduardo S. Schwartz. 2001. Valuing American Options by Simulation: A Simple Least-squares Approach. The Review of Financial Studies 14: 113–47. [Google Scholar] [CrossRef]
- Ludkovski, Michael, and Rene Carmona. 2010. Valuation of energy storage: An optimal switching approach. Quantitative Finance 10: 359–74. [Google Scholar]
- Marshall, T. James. 2012. Valuation of Multiple Exercise Options. Ph.D. thesis, Western University, London, ON, Canada. [Google Scholar]
- Marshall, T. James, and R. Mark Reesor. 2011. Forest of Stochastic Meshes: A Method for Valuing High Dimensional Swing Options. Operations Research Letters 39: 17–21. [Google Scholar] [CrossRef]
- Marshall, T. James, R. Mark Reesor, and Matthew Cox. 2011. Simulation Valuation of Multiple Exercise Options. Paper presented at the 2011 Winter Simulation Conference, Phoenix, AZ, USA, December 11–14. [Google Scholar]
- Meinshausen, Nicolai, and Ben M. Hambly. 2004. Monte Carlo Methods For the Valuation of Multiple-Exercise Options. Mathematical Finance 14: 557–83. [Google Scholar] [CrossRef]
- Stentoft, Lars. 2004. Assessing the Least-Squares Monte-Carlo Approach to American Option Valuation. Review of Derivatives Research 7: 129–68. [Google Scholar] [CrossRef]
- Thompson, Matt, Matt Davison, and Henning Rasmussen. 2009. Natural gas storage valuation and optimization: A real options application. Naval Research Logistics 56: 226–38. [Google Scholar] [CrossRef]
- Tilley, James A. 1993. Valuing American Options in a Path Simulation Model. Transactions of the Society of Actuaries 45: 83–104. [Google Scholar]
- Whitehead, Tyson, R. Mark Reesor, and Matt Davison. 2012. A bias-reduction technique for Monte Carlo pricing of early-exercise options. Journal of Computational Finance 15. [Google Scholar] [CrossRef]
- Wilhelm, Martina, and Christoph Winter. 2008. Finite element valuation of swing options. Journal of Computational Finance 11: 107–32. [Google Scholar] [CrossRef]
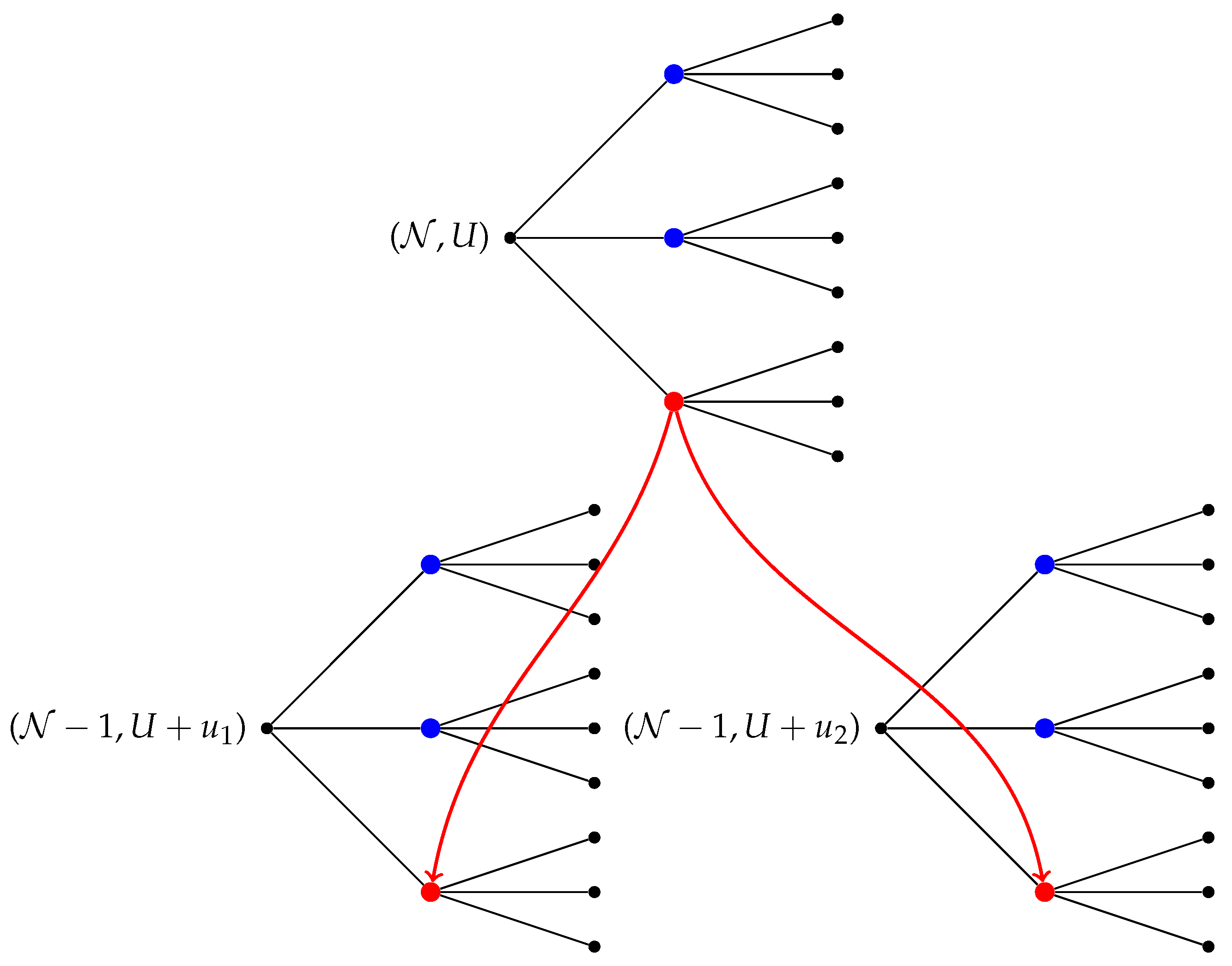
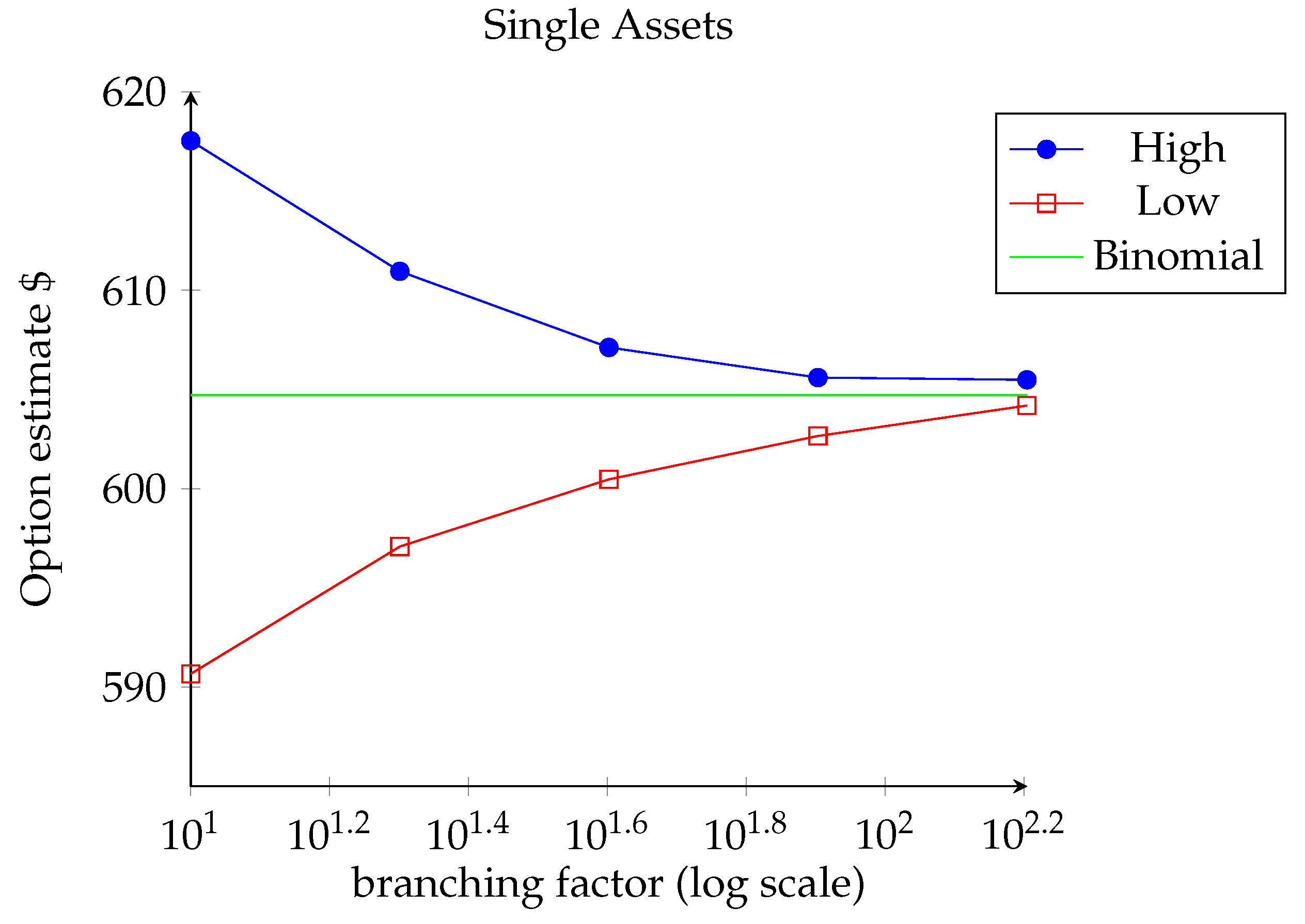
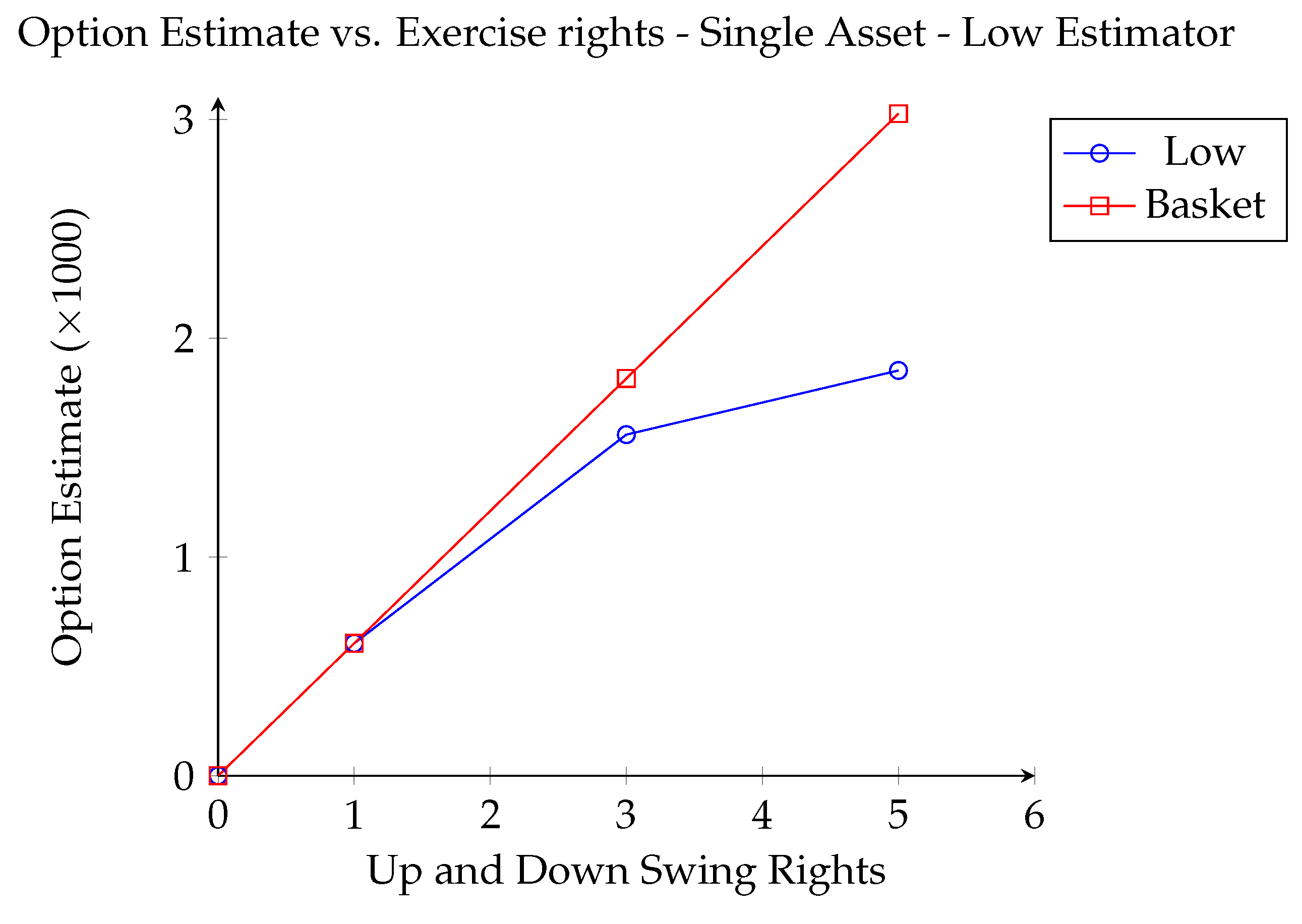
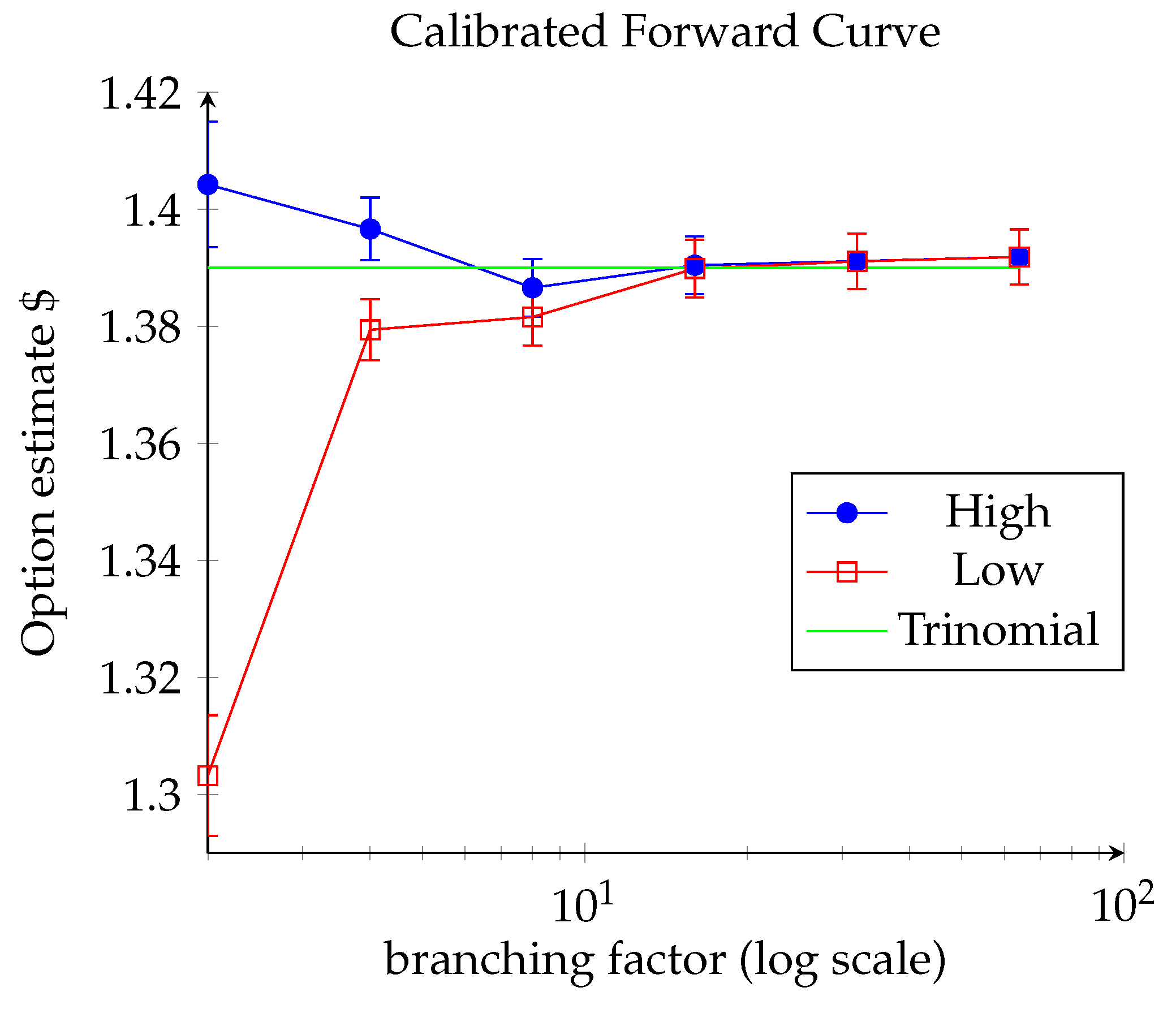
| 1-Dimensional Asset | High-Dimensional Asset | |
|---|---|---|
| Single exercise American option | Binomial Tree | Stochastic Tree |
| Cox et al. (1979) | Broadie and Glasserman (1997) | |
| Multiple exercise option | Forest of Trees | Forest of Stochastic Trees |
| Lari et al. (2001); Jaillet et al. (2004) | Marshall and Reesor |
| Penalty | High | Error | Low | Error | Binomial | |
|---|---|---|---|---|---|---|
| 60 | ON | 2271.153 | 1.418 | 2240.319 | 1.378 | 2259.845 |
| OFF | 2422.781 | 1.576 | 2392.872 | 1.523 | 2411.844 | |
| 50 | ON | 1445.468 | 0.844 | 1408.843 | 0.904 | 1429.645 |
| OFF | 1542.053 | 0.978 | 1503.963 | 0.980 | 1526.055 | |
| 40 | ON | 1018.104 | 0.859 | 968.793 | 1.044 | 989.651 |
| OFF | 1156.591 | 0.911 | 1134.093 | 0.903 | 1145.801 | |
| 30 | ON | 1345.556 | 1.205 | 1309.214 | 1.280 | 1326.266 |
| OFF | 1562.347 | 1.316 | 1532.854 | 1.343 | 1546.055 | |
| 20 | ON | 2189.531 | 0.905 | 2147.623 | 1.018 | 2157.976 |
| OFF | 2443.877 | 0.924 | 2402.192 | 1.034 | 2412.354 |
| High | Error | Low | Error | Binomial | |
|---|---|---|---|---|---|
| 1 | 630.054 | 0.449 | 605.394 | 0.453 | 617.832 |
| 3 | 1573.237 | 1.449 | 1559.517 | 1.437 | 1567.344 |
| 5 | 1852.788 | 2.128 | 1852.788 | 2.128 | 1852.627 |
| Penalty | High | Error | Low | Error | |
|---|---|---|---|---|---|
| 60 | ON | 3577.280 | 2.864 | 3517.297 | 2.845 |
| OFF | 3832.050 | 2.286 | 3772.123 | 2.856 | |
| 50 | ON | 2246.657 | 2.280 | 2197.957 | 2.259 |
| OFF | 2479.081 | 2.341 | 2431.065 | 2.318 | |
| 40 | ON | 1221.847 | 1.595 | 1189.610 | 1.564 |
| OFF | 1257.171 | 1.499 | 1226.370 | 1.467 | |
| 30 | ON | 1105.831 | 0.453 | 1087.851 | 0.447 |
| OFF | 1209.179 | 0.393 | 1196.255 | 0.391 | |
| 20 | ON | 1937.615 | 0.445 | 1930.860 | 0.472 |
| OFF | 2177.194 | 0.489 | 2177.031 | 0.513 |
| High | Error | Low | Error | |
|---|---|---|---|---|
| 1 | 683.144 | 0.741 | 652.481 | 0.721 |
| 3 | 1728.947 | 2.279 | 1709.497 | 2.248 |
| 5 | 2087.495 | 3.114 | 2087.495 | 3.114 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reesor, R.M.; Marshall, T.J. Forest of Stochastic Trees: A Method for Valuing Multiple Exercise Options. J. Risk Financial Manag. 2020, 13, 95. https://doi.org/10.3390/jrfm13050095
Reesor RM, Marshall TJ. Forest of Stochastic Trees: A Method for Valuing Multiple Exercise Options. Journal of Risk and Financial Management. 2020; 13(5):95. https://doi.org/10.3390/jrfm13050095
Chicago/Turabian StyleReesor, R. Mark, and T. James Marshall. 2020. "Forest of Stochastic Trees: A Method for Valuing Multiple Exercise Options" Journal of Risk and Financial Management 13, no. 5: 95. https://doi.org/10.3390/jrfm13050095
APA StyleReesor, R. M., & Marshall, T. J. (2020). Forest of Stochastic Trees: A Method for Valuing Multiple Exercise Options. Journal of Risk and Financial Management, 13(5), 95. https://doi.org/10.3390/jrfm13050095




