Monthly Art Market Returns
Abstract
1. Introduction
2. Model Specification and Estimation
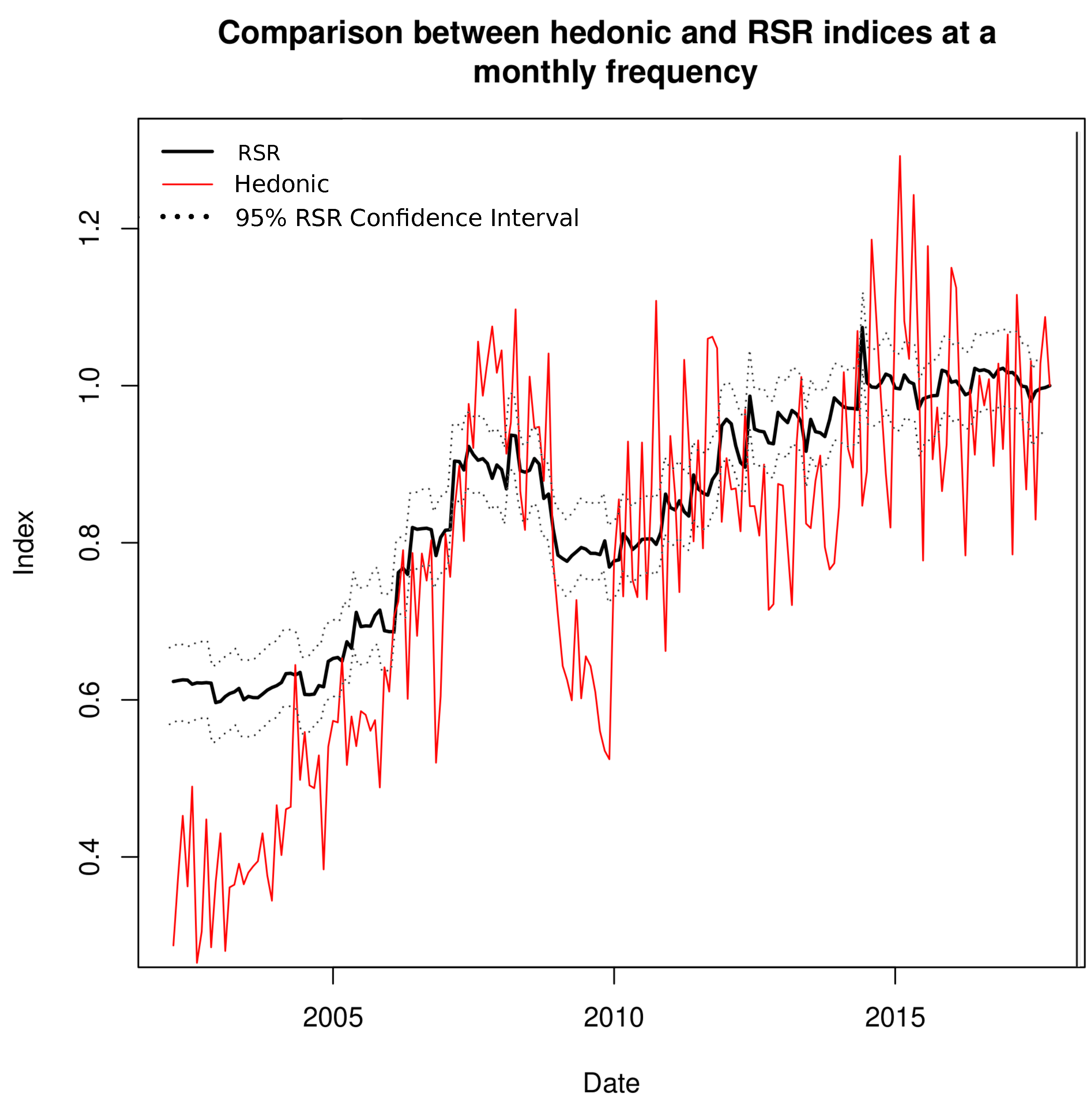
2.1. Model Specification
2.2. Estimation
- Prediction step ():
- Correction step ():
- Smoothing step ():To estimate the underlying state , one uses the full sample information ().
3. Empirical Findings
4. Art as an Asset Class
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| T/N | 60/175 | 120/688 | 240/2873 | 360/5040 |
|---|---|---|---|---|
| 60/175 | 0.00% | 3.72% | −4.08% | 1.08% |
| 120/688 | 0.00% | −4.92% | −3.24% | |
| 240/2873 | 0.00% | 3.00% | ||
| 360/5040 | 0.00% |
| Industry | Full Sample | Pre-Crisis | Post-Crisis | Industry | Full Sample | Pre-Crisis | Post-Crisis |
|---|---|---|---|---|---|---|---|
| Beer and Liquor | 0.07 | 0.06 | 0.10 | Trading | −0.05 | −0.10 | −0.01 |
| Banking | 0.05 | 0.02 | 0.08 | Electronic Equipment | −0.06 | −0.13 | 0.04 |
| Fabricated Products | 0.05 | −0.17 | 0.18 | Business Services | −0.06 | −0.16 | 0.03 |
| Other | 0.05 | 0.05 | 0.05 | Candy and Soda | −0.06 | 0.02 | −0.12 |
| Agriculture | 0.04 | −0.07 | 0.09 | Computers | −0.06 | −0.11 | −0.02 |
| Healthcare | 0.01 | −0.09 | 0.09 | Pharmaceutical Products | −0.06 | −0.09 | −0.02 |
| Printing and Publishing | 0.01 | −0.05 | 0.06 | Tobacco Products | −0.06 | −0.07 | −0.06 |
| Entertainment | 0.00 | −0.10 | 0.06 | Computer Software | −0.06 | −0.13 | 0.01 |
| Insurance | −0.01 | 0.00 | 0.00 | Transportation | −0.07 | −0.24 | 0.05 |
| Precious Metals | −0.01 | −0.24 | 0.13 | Coal | −0.07 | −0.34 | 0.09 |
| Business Supplies | −0.02 | −0.16 | 0.08 | Machinery | −0.07 | −0.25 | 0.03 |
| Chemicals | −0.02 | −0.15 | 0.05 | Aircraft | −0.08 | −0.21 | 0.03 |
| Consumer Goods | −0.02 | −0.15 | 0.06 | Textiles | −0.08 | −0.19 | −0.02 |
| Food Products | −0.02 | −0.08 | 0.03 | Retail | −0.08 | −0.16 | 0.00 |
| Real Estate | −0.02 | −0.16 | 0.04 | Measuring and Control Equipment | −0.08 | −0.21 | 0.04 |
| Automobiles and Trucks | −0.03 | −0.15 | 0.06 | Restaurants, Hotels, Motels | −0.08 | −0.15 | −0.01 |
| Personal Services | −0.03 | −0.13 | 0.03 | Non-Metallic and Industrial Metal Mining | −0.09 | −0.27 | 0.01 |
| Defense | −0.03 | −0.12 | 0.04 | Construction | −0.09 | −0.24 | 0.03 |
| Utilities | −0.04 | −0.14 | 0.05 | Electrical Equipment | −0.09 | −0.23 | −0.01 |
| Medical Equipment | −0.04 | −0.15 | 0.02 | Wholesale | −0.10 | −0.22 | −0.02 |
| Construction Materials | −0.04 | −0.18 | 0.03 | Apparel | −0.10 | −0.17 | −0.06 |
| Shipbuilding, Railroad Equipment | −0.04 | −0.29 | 0.08 | Steel Works, etc. | −0.11 | −0.30 | 0.01 |
| Petroleum and Natural Gas | −0.04 | −0.21 | 0.07 | Shipping Containers | −0.12 | −0.20 | −0.07 |
| Rubber and Plastic Products | −0.05 | −0.21 | 0.06 | Recreation | −0.12 | −0.26 | −0.02 |
| Communication | −0.05 | −0.05 | −0.03 |
| Industry | Full Sample | Pre-Crisis | Post-Crisis | Industry | Full Sample | Pre-Crisis | Post-Crisis |
|---|---|---|---|---|---|---|---|
| Beer and Liquor | 0.22 | 0.23 | 0.23 | Computer Software | 0.11 | 0.16 | 0.06 |
| Food Products | 0.22 | 0.10 | 0.32 | Banking | 0.10 | 0.14 | 0.09 |
| Personal Services | 0.21 | 0.17 | 0.23 | Shipping Containers | 0.10 | 0.17 | 0.06 |
| Rubber and Plastic Products | 0.20 | 0.18 | 0.23 | Trading | 0.10 | 0.19 | 0.04 |
| Business Supplies | 0.18 | 0.20 | 0.18 | Candy and Soda | 0.10 | 0.23 | 0.00 |
| Consumer Goods | 0.17 | 0.16 | 0.19 | Computers | 0.09 | 0.14 | 0.05 |
| Wholesale | 0.16 | 0.25 | 0.11 | Chemicals | 0.09 | 0.11 | 0.08 |
| Communication | 0.16 | 0.18 | 0.15 | Construction | 0.09 | 0.07 | 0.10 |
| Agriculture | 0.15 | 0.11 | 0.18 | Restaurants, Hotels, Motels | 0.08 | 0.10 | 0.08 |
| Retail | 0.15 | 0.21 | 0.12 | Machinery | 0.08 | 0.11 | 0.07 |
| Other | 0.15 | 0.18 | 0.14 | Steel Works, etc. | 0.08 | 0.12 | 0.05 |
| Electrical Equipment | 0.14 | 0.20 | 0.11 | Printing and Publishing | 0.08 | 0.09 | 0.10 |
| Transportation | 0.14 | 0.18 | 0.13 | Entertainment | 0.07 | 0.20 | 0.01 |
| Measuring and Control Equipment | 0.13 | 0.12 | 0.15 | Recreation | 0.07 | 0.24 | −0.03 |
| Utilities | 0.13 | 0.02 | 0.23 | Petroleum and Natural Gas | 0.07 | 0.03 | 0.09 |
| Business Services | 0.13 | 0.19 | 0.10 | Medical Equipment | 0.07 | 0.02 | 0.09 |
| Construction Materials | 0.13 | 0.19 | 0.12 | Aircraft | 0.06 | 0.04 | 0.08 |
| Real Estate | 0.12 | 0.27 | 0.08 | Tobacco Products | 0.06 | −0.02 | 0.15 |
| Automobiles and Trucks | 0.12 | 0.16 | 0.11 | Non-Metallic and Industrial Metal Mining | 0.05 | 0.05 | 0.05 |
| Electronic Equipment | 0.11 | 0.20 | 0.03 | Apparel | 0.05 | 0.27 | −0.07 |
| Healthcare | 0.11 | 0.21 | 0.06 | Defense | 0.02 | 0.03 | 0.01 |
| Fabricated Products | 0.11 | 0.09 | 0.12 | Textiles | 0.02 | 0.09 | −0.01 |
| Shipbuilding, Railroad Equipment | 0.11 | 0.07 | 0.14 | Coal | 0.01 | −0.02 | 0.02 |
| Pharmaceutical Products | 0.11 | 0.14 | 0.10 | Precious Metals | −0.08 | −0.11 | −0.06 |
| Insurance | 0.11 | 0.17 | 0.08 |
| Industry | Full Sample | Pre-Crisis | Post-Crisis | Industry | Full Sample | Pre-Crisis | Post-Crisis |
|---|---|---|---|---|---|---|---|
| Retail | 0.22 | 0.18 | 0.25 | Steel Works, etc. | 0.12 | −0.01 | 0.21 |
| Beer and Liquor | 0.21 | 0.11 | 0.30 | Automobiles and Trucks | 0.12 | 0.03 | 0.18 |
| Business Services | 0.19 | 0.05 | 0.29 | Communication | 0.12 | 0.04 | 0.19 |
| Trading | 0.19 | 0.10 | 0.25 | Shipping Containers | 0.12 | 0.00 | 0.20 |
| Candy and Soda | 0.17 | 0.15 | 0.19 | Measuring and Control Equipment | 0.12 | 0.02 | 0.21 |
| Construction | 0.17 | 0.06 | 0.24 | Computer Software | 0.12 | 0.03 | 0.21 |
| Transportation | 0.17 | 0.05 | 0.24 | Printing and Publishing | 0.12 | 0.05 | 0.16 |
| Insurance | 0.16 | 0.01 | 0.25 | Electrical Equipment | 0.10 | −0.09 | 0.22 |
| Other | 0.16 | 0.09 | 0.21 | Utilities | 0.10 | 0.06 | 0.13 |
| Banking | 0.16 | 0.05 | 0.23 | Consumer Goods | 0.10 | 0.03 | 0.14 |
| Restaurants, Hotels, Motels | 0.16 | 0.09 | 0.22 | Pharmaceutical Products | 0.10 | −0.07 | 0.21 |
| Real Estate | 0.16 | 0.14 | 0.18 | Agriculture | 0.09 | −0.01 | 0.15 |
| Construction Materials | 0.15 | 0.02 | 0.22 | Chemicals | 0.09 | −0.05 | 0.17 |
| Machinery | 0.15 | 0.02 | 0.22 | Petroleum and Natural Gas | 0.09 | 0.00 | 0.15 |
| Medical Equipment | 0.15 | −0.01 | 0.23 | Electronic Equipment | 0.09 | −0.01 | 0.20 |
| Rubber and Plastic Products | 0.15 | 0.15 | 0.16 | Non-Metallic and Industrial Metal Mining | 0.09 | −0.05 | 0.16 |
| Apparel | 0.15 | 0.11 | 0.17 | Aircraft | 0.07 | −0.06 | 0.17 |
| Business Supplies | 0.15 | 0.05 | 0.21 | Textiles | 0.07 | −0.03 | 0.13 |
| Wholesale | 0.15 | 0.09 | 0.19 | Coal | 0.07 | −0.04 | 0.14 |
| Shipbuilding, Railroad Equipment | 0.15 | 0.06 | 0.19 | Defense | 0.06 | −0.14 | 0.22 |
| Personal Services | 0.14 | 0.06 | 0.19 | Food Products | 0.06 | 0.05 | 0.07 |
| Recreation | 0.13 | 0.02 | 0.21 | Computers | 0.05 | −0.08 | 0.17 |
| Entertainment | 0.13 | 0.14 | 0.13 | Tobacco Products | 0.03 | 0.00 | 0.07 |
| Healthcare | 0.13 | 0.00 | 0.21 | Precious Metals | 0.00 | −0.04 | 0.01 |
| Fabricated Products | 0.13 | 0.03 | 0.18 |
| Industry | Full Sample | Pre-Crisis | Post-Crisis | Industry | Full Sample | Pre-Crisis | Post-Crisis |
|---|---|---|---|---|---|---|---|
| Fabricated Products | 0.13 | −0.08 | 0.20 | Retail | 0.01 | −0.06 | 0.06 |
| Personal Services | 0.10 | −0.04 | 0.16 | Business Services | 0.00 | −0.10 | 0.06 |
| Other | 0.10 | 0.26 | 0.05 | Computers | 0.00 | −0.04 | 0.02 |
| Healthcare | 0.10 | 0.05 | 0.13 | Candy and Soda | 0.00 | 0.04 | 0.00 |
| Business Supplies | 0.08 | 0.09 | 0.10 | Communication | 0.00 | −0.09 | 0.06 |
| Consumer Goods | 0.07 | 0.04 | 0.09 | Shipbuilding, Railroad Equipment | 0.00 | −0.05 | 0.02 |
| Rubber and Plastic Products | 0.07 | 0.01 | 0.11 | Electrical Equipment | −0.01 | −0.10 | 0.03 |
| Real Estate | 0.07 | 0.02 | 0.09 | Insurance | −0.01 | −0.07 | 0.04 |
| Banking | 0.06 | −0.06 | 0.12 | Chemicals | −0.01 | −0.02 | −0.01 |
| Printing and Publishing | 0.05 | −0.25 | 0.17 | Textiles | −0.01 | −0.03 | 0.01 |
| Transportation | 0.05 | −0.01 | 0.08 | Non-Metallic and Industrial Metal Mining | −0.01 | −0.13 | 0.01 |
| Measuring and Control Equipment | 0.05 | −0.11 | 0.15 | Aircraft | −0.01 | −0.01 | −0.01 |
| Apparel | 0.04 | 0.03 | 0.05 | Coal | −0.02 | −0.24 | 0.04 |
| Shipping Containers | 0.04 | 0.05 | 0.03 | Construction | −0.02 | −0.23 | 0.08 |
| Automobiles and Trucks | 0.04 | −0.06 | 0.10 | Agriculture | −0.02 | −0.07 | −0.02 |
| Restaurants, Hotels, Motels | 0.03 | −0.03 | 0.08 | Beer and Liquor | −0.02 | −0.01 | 0.00 |
| Trading | 0.03 | −0.15 | 0.11 | Computer Software | −0.02 | −0.05 | 0.00 |
| Medical Equipment | 0.03 | −0.15 | 0.08 | Electronic Equipment | −0.03 | −0.10 | 0.04 |
| Wholesale | 0.02 | −0.11 | 0.09 | Utilities | −0.03 | −0.20 | 0.06 |
| Machinery | 0.02 | −0.09 | 0.07 | Recreation | −0.03 | −0.11 | 0.01 |
| Defense | 0.02 | 0.04 | 0.03 | Food Products | −0.03 | −0.07 | 0.00 |
| Steel Works, etc. | 0.02 | −0.10 | 0.06 | Tobacco Products | −0.10 | −0.05 | −0.16 |
| Entertainment | 0.02 | 0.07 | 0.02 | Pharmaceutical Products | −0.10 | −0.23 | −0.03 |
| Petroleum and Natural Gas | 0.02 | −0.12 | 0.06 | Precious Metals | −0.12 | −0.20 | −0.10 |
| Construction Materials | 0.01 | −0.10 | 0.06 |
References
- Anderson, Robert C. 1974. Paintings as an investment. Economic Inquiry 12: 13–26. [Google Scholar] [CrossRef]
- Aruoba, S. Borağan, Francis X. Diebold, and Chiara Scotti. 2009. Real-time measurement of business conditions. Journal of Business and Economic Statistics 27: 417–27. [Google Scholar] [CrossRef]
- Bailey, Martin J., Richard F. Muth, and Hugh O. Nourse. 1963. A regression method for real estate price index construction. Journal of the American Statistical Association 58: 933–42. [Google Scholar] [CrossRef]
- Baumol, William J. 1986. Unnatural value: Or art investment as floating crap game. American Economic Review 76: 10–14. [Google Scholar] [CrossRef]
- Bocart, Fabian Y.R.P., and Christian M. Hafner. 2015. Volatility of price indices for heterogeneous goods with applications to the fine art market. Journal of Applied Econometrics 30: 291–312. [Google Scholar] [CrossRef]
- Buelens, Nathalie, and Victor Ginsburgh. 1993. Revisiting baumol’s ‘art as floating crap game’. European Economic Review 37: 1351–71. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On persistence in mutual fund performance. Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Case, Karl E., and Robert J. Shiller. 1987. Prices of Single Family Homes since 1970: New Indexes for Four Cities. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Chanel, Olivier. 1995. Is art market behavior predictable? European Economic Review 39: 519–27. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Francke, M.K. 2010. Repeat sales index for thin markets, a structural time series approach. Journal of Real Estate Finance and Economics 41: 24–52. [Google Scholar] [CrossRef]
- Ginsburgh, Victor, Jianping Mei, and Michael Moses. 2006. The computation of prices indices. In Handbook of the Economics of Art and Culture–Volume 1. Edited by V. A. Ginsburg and D. Throsby. Amsterdam: Elsevier, pp. 947–79. [Google Scholar]
- Goetzmann, William Nelson. 1992. The accuracy of real estate indices: Repeat sale estimators. Journal of Real Estate Finance and Economics 5: 5–53. [Google Scholar] [CrossRef]
- Goetzmann, William N. 1993. Accounting for taste: Art and the financial markets over three centuries. American Economic Review 83: 1370–76. [Google Scholar]
- Grant, Daniel. 2018. As Natural Disasters Loom, What You Should Know about Insuring Your Art. Available online: https://observer.com/2018/01/how-art-insurance-is-changing-with-rising-natural-disasters/ (accessed on 1 May 2020).
- Heckman, James. 1974. Shadow prices, market wages, and labor supply. Econometrica: Journal of the Econometric Society 42: 679–94. [Google Scholar] [CrossRef]
- Korteweg, Arthur, Roman Kräussl, and Patrick Verwijmeren. 2016. Does it pay to invest in art? A selection-corrected returns perspective. Review of Financial Studies 29: 1007–38. [Google Scholar] [CrossRef]
- Mandel, Benjamin. 2009. Art as an investment and conspicuous consumption good. American Economic Review 99: 1653–63. [Google Scholar] [CrossRef]
- Mei, Jianping, and Michael Moses. 2002. Art as an investment and the underperformance of masterpieces. American Economic Review 92: 1656–68. [Google Scholar] [CrossRef]
- Mei, Jianping, and Michael Moses. 2005. Vested interest and biased price estimates: Evidence from an auction market. Journal of Finance 60: 2409–35. [Google Scholar] [CrossRef]
- Oosterlinck, Kim. 2016. Art as a wartime investment: Conspicuous consumption and discretion. Economic Journal 127: 2665–701. [Google Scholar] [CrossRef]
- Pástor, L’uboš, and Robert F. Stambaugh. 2003. Liquidity risk and expected stock returns. Journal of Political Economy 111: 642–85. [Google Scholar] [CrossRef]
- Pesando, James E. 1993. Art as an investment: The market for modern prints. American Economic Review 83: 1075–89. [Google Scholar]
- Picinati di Torcello, Adriano. 2012. Art as an Investment. Why Should Art Be Considered as an Asset Class? Available online: https://www2.deloitte.com/lu/en/pages/art-finance/articles/art-as-investment.html (accessed on 1 May 2020).
- Renneboog, Luc, and Christophe Spaenjers. 2013. Buying beauty: On prices and returns in the art market. Management Science 59: 36–53. [Google Scholar] [CrossRef]
- Stein, John Picard. 1977. The monetary appreciation of paintings. Journal of Political Economy 85: 1021–35. [Google Scholar] [CrossRef]
- van de Minne, Alex, Marc Francke, David Geltner, and Robert White. 2019. Using revisions as a measure of price index quality in repeat-sales models. Journal of Real Estate Finance and Economics, 1–40. [Google Scholar] [CrossRef]
- Vermeylen, Filip, Maarten van Dijck, and Veerle de Laet. 2013. The test of time. art encyclopedia and the formation of the canon of seventeenth-century painters in the low countries. Empirical Studies of the Arts 31: 81–105. [Google Scholar] [CrossRef]
- Zanola, Roberto. 2007. The dynamics of art prices: The selection corrected repeat-sales index. In Art Markets Symposium, Maastricht. Princeton: Citeseer. [Google Scholar]
| 1. | See, e.g., Ginsburgh et al. (2006) for an extensive description of hedonic regressions and their application to the art market. |
| 2. | |
| 3. | In the vector , missing observations are discarded, so that this vector is of length . |
| 4. | In our empirical example, this occurs in only five months of a total 189 months covered by the sample. |
| 5. | These companies were Bassett Furniture Industries Inc., Stanley Furniture Co., Leggett and Platt Inc., Lazboy Inc., Haverty Furniture Companies Inc., and American Woodmark Corp. |
| 6. | Note that 10% (actually 9.6%) is the threshold beyond which correlations for our sample size were significantly different from zero at the 95 percent confidence level. |
| 7. | The bought-in rate is defined as the proportion of works that do not meet the reserve price at auction and are left unsold. |
| 8. | According to their higher bought-in rate. |
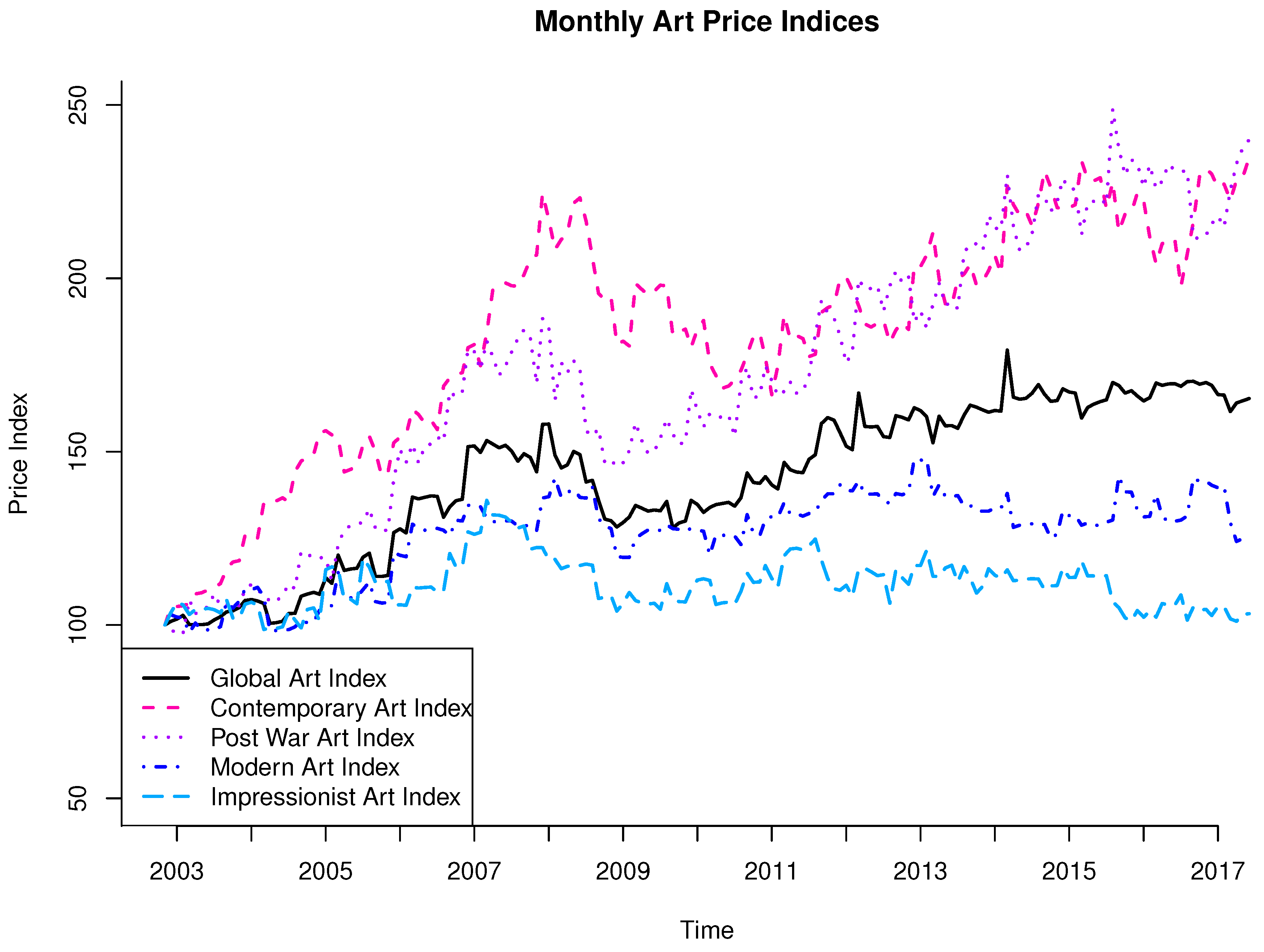
| S&P 500 | Gold | Art Co | Real Estate ETF | Luxury Co | Furniture Co | Global Art Index | Contemporary Art Index | Post-War Art Index | Modern Art Index | Impressionist Art Index | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Annualized | 0.08 | 0.10 | 0.20 | 0.10 | 0.17 | 0.09 | 0.04 | 0.06 | 0.06 | 0.02 | 0.00 |
| returns | |||||||||||
| Annualized | 0.14 | 0.18 | 0.33 | 0.23 | 0.24 | 0.26 | 0.10 | 0.11 | 0.14 | 0.10 | 0.12 |
| volatility | |||||||||||
| Sharpe ratio | 0.56 | 0.53 | 0.62 | 0.43 | 0.71 | 0.36 | 0.37 | 0.52 | 0.46 | 0.16 | 0.02 |
| Bought-in rate | 0.23 | 0.19 | 0.20 | 0.25 | 0.26 | ||||||
| Correlations | |||||||||||
| S&P 500 | 1.00 | −0.14 | 0.46 | 0.74 | 0.63 | 0.63 | 0.22 | 0.00 | 0.18 | 0.12 | −0.00 |
| Gold | 1.00 | 0.01 | −0.14 | −0.02 | −0.03 | −0.22 | 0.02 | 0.07 | −0.24 | −0.03 | |
| Art Co | 1.00 | 0.39 | 0.38 | 0.27 | 0.25 | 0.12 | 0.15 | 0.19 | 0.14 | ||
| Real Estate | 1.00 | 0.51 | 0.56 | 0.15 | −0.03 | 0.07 | 0.10 | −0.07 | |||
| Luxury Co | 1.00 | 0.44 | 0.12 | −0.14 | 0.08 | 0.07 | 0.01 | ||||
| Furniture Co | 1.00 | 0.08 | 0.07 | 0.15 | 0.07 | −0.11 | |||||
| Art Indices | |||||||||||
| Global | 1.00 | 0.34 | 0.62 | 0.61 | 0.34 | ||||||
| Contemporary | 1.00 | 0.13 | 0.27 | 0.15 | |||||||
| Post-War | 1.00 | 0.09 | 0.07 | ||||||||
| Modern | 1.00 | 0.21 | |||||||||
| Industry | Full Sample | Pre-Crisis | Post-Crisis | Industry | Full Sample | Pre-Crisis | Post-Crisis |
|---|---|---|---|---|---|---|---|
| Beer and Liquor | 0.27 | 0.19 | 0.35 | Electronic Equipment | 0.15 | 0.13 | 0.19 |
| Other | 0.25 | 0.22 | 0.29 | Computer Software | 0.15 | 0.11 | 0.21 |
| Banking | 0.23 | 0.18 | 0.27 | Construction | 0.15 | −0.01 | 0.27 |
| Rubber and Plastic Products | 0.22 | 0.17 | 0.27 | Medical Equipment | 0.15 | 0.01 | 0.24 |
| Trading | 0.21 | 0.18 | 0.24 | Utilities | 0.15 | 0.00 | 0.28 |
| Personal Services | 0.21 | 0.09 | 0.29 | Electrical Equipment | 0.15 | 0.02 | 0.23 |
| Candy and Soda | 0.21 | 0.28 | 0.16 | Restaurants, Hotels, Motels | 0.14 | 0.08 | 0.21 |
| Retail | 0.20 | 0.21 | 0.22 | Shipbuilding, Railroad Equipment | 0.14 | −0.01 | 0.23 |
| Business Supplies | 0.20 | 0.08 | 0.30 | Chemicals | 0.14 | 0.00 | 0.22 |
| Business Services | 0.20 | 0.09 | 0.29 | Agriculture | 0.14 | −0.01 | 0.22 |
| Insurance | 0.19 | 0.11 | 0.26 | Shipping Containers | 0.13 | 0.06 | 0.19 |
| Communication | 0.19 | 0.15 | 0.24 | Steel Works, etc. | 0.13 | 0.02 | 0.21 |
| Real Estate | 0.19 | 0.23 | 0.19 | Petroleum and Natural Gas | 0.13 | −0.03 | 0.25 |
| Construction Materials | 0.19 | 0.08 | 0.26 | Pharmaceutical Products | 0.13 | 0.02 | 0.22 |
| Transportation | 0.19 | 0.09 | 0.26 | Recreation | 0.12 | 0.14 | 0.12 |
| Food Products | 0.19 | 0.13 | 0.24 | Non-Metallic and Industrial Metal Mining | 0.12 | −0.05 | 0.22 |
| Wholesale | 0.18 | 0.13 | 0.22 | Apparel | 0.11 | 0.20 | 0.07 |
| Automobiles and Trucks | 0.18 | 0.13 | 0.22 | Computers | 0.11 | 0.06 | 0.16 |
| Entertainment | 0.17 | 0.18 | 0.19 | Aircraft | 0.11 | −0.01 | 0.20 |
| Printing and Publishing | 0.17 | 0.06 | 0.25 | Textiles | 0.09 | 0.04 | 0.12 |
| Measuring and Control Equipment | 0.17 | 0.09 | 0.25 | Defense | 0.06 | −0.13 | 0.22 |
| Machinery | 0.16 | 0.04 | 0.25 | Coal | 0.06 | −0.19 | 0.21 |
| Fabricated Products | 0.16 | 0.06 | 0.23 | Tobacco Products | 0.03 | −0.03 | 0.10 |
| Consumer Goods | 0.16 | 0.08 | 0.21 | Precious Metals | −0.01 | −0.25 | 0.14 |
| Healthcare | 0.16 | 0.10 | 0.20 |
| Art Index | |||
|---|---|---|---|
| Full sample: 2002:04 to 2017:09 | |||
| Global | 0.064 | 0.145 | 0.048 |
| (0.322) | (3.042) | ||
| Impressionist | 0.034 | −0.034 | 0.002 |
| (0.135) | (−0.580) | ||
| Modern | −0.102 | 0.105 | 0.022 |
| (−0.469) | (2.034) | ||
| Post-War | 0.199 | 0.158 | 0.029 |
| (0.702) | (2.339) | ||
| Contemporary | 0.377 | 0.003 | 0.000 |
| (1.545) | (0.058) | ||
| Pre-crisis: 2002:04 to 2008:08 | |||
| Global | 0.243 | 0.103 | 0.016 |
| (0.716) | (1.090) | ||
| Impressionist | 0.246 | −0.160 | 0.025 |
| (0.594) | (−1.387) | ||
| Modern | 0.030 | 0.172 | 0.038 |
| (0.084) | (1.716) | ||
| Post-War | 0.326 | 0.043 | 0.002 |
| (0.708) | (0.340) | ||
| Contemporary | 0.914 | −0.088 | 0.012 |
| (2.783) | (−0.939) | ||
| Post-crisis: 2008:09 to 2017:09 | |||
| Global | −0.076 | 0.168 | 0.085 |
| (−0.312) | (3.147) | ||
| Impressionist | −0.152 | 0.027 | 0.002 |
| (−0.499) | (0.402) | ||
| Modern | −0.182 | 0.079 | 0.016 |
| (−0.668) | (1.328) | ||
| Post-War | 0.078 | 0.211 | 0.064 |
| (0.217) | (2.699) | ||
| Contemporary | −0.004 | 0.049 | 0.004 |
| (−0.012) | (0.659) | ||
| Art Index | |||||
|---|---|---|---|---|---|
| Full sample: 2002:04 to 2017:09 | |||||
| Global | 0.059 | 0.131 | 0.056 | 0.029 | 0.051 |
| (0.293) | (2.563) | (0.633) | (0.352) | ||
| Impressionist | 0.052 | −0.011 | −0.162 | 0.043 | 0.014 |
| (0.210) | (−0.175) | (−1.473) | (0.427) | ||
| Modern | −0.109 | 0.099 | 0.054 | −0.029 | 0.024 |
| (−0.497) | (1.788) | (0.563) | (−0.329) | ||
| Post-War | 0.179 | 0.127 | 0.177 | −0.006 | 0.040 |
| (0.633) | (1.758) | (1.418) | (−0.053) | ||
| Contemporary | 0.382 | −0.051 | 0.155 | 0.161 | 0.027 |
| (1.578) | (−0.810) | (1.399) | (1.629) | ||
| Pre-crisis: 2002:04 to 2008:08 | |||||
| Global | 0.202 | 0.101 | 0.053 | 0.078 | 0.020 |
| (0.576) | (1.018) | (0.358) | (0.423) | ||
| Impressionist | 0.385 | −0.116 | −0.350 | −0.083 | 0.081 |
| (0.925) | (−0.989) | (−1.997) | (−0.378) | ||
| Modern | 0.001 | 0.155 | 0.111 | −0.022 | 0.044 |
| (0.004) | (1.480) | (0.709) | (−0.112) | ||
| Post-War | 0.228 | 0.038 | 0.124 | 0.185 | 0.016 |
| (0.483) | (0.285) | (0.623) | (0.747) | ||
| Contemporary | 0.892 | −0.103 | 0.076 | 0.033 | 0.016 |
| (2.654) | (−1.018) | (0.494) | (0.183) | ||
| Post-crisis: 2008:09 to 2017:09 | |||||
| Global | −0.077 | 0.161 | 0.045 | −0.009 | 0.086 |
| (−0.309) | (2.622) | (0.405) | (−0.099) | ||
| Impressionist | −0.143 | 0.022 | −0.017 | 0.034 | 0.002 |
| (−0.460) | (0.293) | (−0.121) | (0.298) | ||
| Modern | −0.187 | 0.082 | 0.005 | −0.017 | 0.017 |
| (−0.676) | (1.198) | (0.039) | (−0.171) | ||
| Post-War | 0.052 | 0.198 | 0.197 | −0.117 | 0.082 |
| (0.145) | (2.222) | (1.204) | (−0.877) | ||
| Contemporary | 0.059 | −0.029 | 0.202 | 0.166 | 0.038 |
| (0.174) | (−0.345) | (1.315) | (1.320) | ||
| Art Index | |||||||
|---|---|---|---|---|---|---|---|
| Full sample: 2002:04 to 2017:09 | |||||||
| Global | 0.116 | 0.152 | 0.079 | 0.026 | 0.039 | −0.053 | 0.062 |
| (0.511) | (2.534) | (0.769) | (0.252) | (0.749) | (−0.837) | ||
| Impressionist | 0.073 | −0.043 | −0.135 | 0.103 | −0.021 | 0.015 | 0.016 |
| (0.267) | (−0.590) | (−1.091) | (0.823) | (−0.328) | (0.195) | ||
| Modern | −0.051 | 0.147 | 0.060 | −0.025 | 0.081 | −0.017 | 0.048 |
| (−0.222) | (2.418) | (0.579) | (−0.238) | (1.540) | (−0.270) | ||
| Post-War | 0.193 | 0.189 | 0.153 | 0.088 | 0.142 | −0.036 | 0.066 |
| (0.620) | (2.302) | (1.100) | (0.622) | (2.006) | (−0.416) | ||
| Contemporary | 0.383 | −0.050 | 0.128 | 0.204 | 0.047 | 0.002 | 0.031 |
| (1.462) | (−0.708) | (1.049) | (1.683) | (0.788) | (0.026) | ||
| Pre-crisis: 2002:04 to 2008:08 | |||||||
| Global | 0.301 | 0.121 | 0.057 | 0.081 | 0.007 | −0.096 | 0.028 |
| (0.791) | (0.991) | (0.372) | (0.430) | (0.073) | (−0.753) | ||
| Impressionist | 0.571 | −0.123 | −0.319 | −0.095 | −0.047 | −0.148 | 0.098 |
| (1.274) | (−0.854) | (−1.750) | (−0.428) | (−0.417) | (−0.984) | ||
| Modern | 0.041 | 0.170 | 0.109 | −0.018 | 0.013 | −0.044 | 0.046 |
| (0.101) | (1.316) | (0.665) | (−0.088) | (0.124) | (−0.324) | ||
| Post-War | 0.204 | 0.144 | 0.068 | 0.229 | 0.146 | −0.059 | 0.034 |
| (0.402) | (0.879) | (0.327) | (0.909) | (1.135) | (−0.346) | ||
| Contemporary | 0.984 | −0.107 | 0.093 | 0.018 | −0.028 | −0.077 | 0.024 |
| (2.717) | (−0.877) | (0.581) | (0.096) | (−0.307) | (−0.624) | ||
| Post-crisis: 2008:09 to 2017:09 | |||||||
| Global | −0.024 | 0.180 | 0.100 | −0.022 | 0.051 | −0.056 | 0.106 |
| (−0.078) | (2.448) | (0.698) | (−0.156) | (0.798) | (−0.708) | ||
| Impressionist | −0.062 | −0.031 | 0.038 | 0.226 | 0.008 | 0.089 | 0.028 |
| (−0.172) | (−0.360) | (0.223) | (1.357) | (0.106) | (0.944) | ||
| Modern | −0.063 | 0.130 | 0.032 | 0.026 | 0.127 | −0.007 | 0.079 |
| (−0.216) | (1.854) | (0.232) | (0.196) | (2.085) | (−0.094) | ||
| Post-War | 0.132 | 0.231 | 0.234 | −0.038 | 0.130 | −0.060 | 0.111 |
| (0.311) | (2.266) | (1.168) | (−0.191) | (1.469) | (−0.539) | ||
| Contemporary | 0.039 | −0.037 | 0.169 | 0.282 | 0.088 | 0.025 | 0.050 |
| (0.100) | (−0.388) | (0.908) | (1.549) | (1.077) | (0.246) | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bocart, F.Y.R.P.; Ghysels, E.; Hafner, C.M. Monthly Art Market Returns. J. Risk Financial Manag. 2020, 13, 100. https://doi.org/10.3390/jrfm13050100
Bocart FYRP, Ghysels E, Hafner CM. Monthly Art Market Returns. Journal of Risk and Financial Management. 2020; 13(5):100. https://doi.org/10.3390/jrfm13050100
Chicago/Turabian StyleBocart, Fabian Y.R.P., Eric Ghysels, and Christian M. Hafner. 2020. "Monthly Art Market Returns" Journal of Risk and Financial Management 13, no. 5: 100. https://doi.org/10.3390/jrfm13050100
APA StyleBocart, F. Y. R. P., Ghysels, E., & Hafner, C. M. (2020). Monthly Art Market Returns. Journal of Risk and Financial Management, 13(5), 100. https://doi.org/10.3390/jrfm13050100






