A Principal Component-Guided Sparse Regression Approach for the Determination of Bitcoin Returns
Abstract
1. Introduction
2. Methods and Data
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The PC-LASSO Methodology
Appendix B. Data Description and Supplementary Results
| Variable | Market/Factor Type | Region | Eikon Code |
|---|---|---|---|
| Crude Oil-WTI Spot Cushing (in USD/BBL) | Commodities market returns | World | CRUDOIL |
| MLCX - Gas oil Spot Index - price index | Commodities market returns | World | MLCXQSS |
| S&P GSCI Gold Total Return | Commodities market returns | World | GSGCTOT |
| DJGL World - price index | Equity market returns | World | DJWRLD$ |
| Dow Jones 65 Composite Average - price index | Equity market returns | US | DJCMP65 |
| MSCI Europe - price index | Equity market returns | Europe | MSEROP$ |
| Nasdaq Composite - price index | Equity market returns | US | NASCOMP |
| Nikkei 225 Psychological - price index | Equity market returns | Asia | JAPDOWP |
| Nikkei 225 Stock Average - price index | Equity market returns | Asia | JAPDOWA |
| S&P 500 Composite - price index | Equity market returns | US | S&PCOMP |
| Shangai SE Composite - price index | Equity market returns | Asia | CHSCOMP |
| CBOE SPX Volatility VIX - price index | Equity market volatility | US | CBOEVIX |
| Euro Stoxx 50 Volatility Index - price index | Equity market volatility | Europe | VST1MEI |
| MSCI Europe Minimum Volatility (in USD) - price index | Equity market volatility | Europe | MSURMV$ |
| Nikkei Stock Average Volatility Index - price index | Equity market volatility | Asia | VXJINDX |
| Chinese Yuan to USD (WMR) – exchange rate | FX market returns | US/Asia | CHIYUA$ |
| Japanese Yen to USD (WMR) – exchange rate | FX market returns | US/Asia | JAPAYE$ |
| USD to Euro (WMR&DS) – exchange rate | FX market returns | US/Europe | USEURSP |
| USD to UK pound (WMR) – exchange rate | FX market returns | US/Europe | USDOLLR |
| China Government Benchmark Bid Yield - 10 Years | Government bond yields | Asia | TRCH10T |
| Japan Government Benchmark Bid Yield - 10 Years | Government bond yields | Asia | TRJP10T |
| US Government Benchmark Bid Yield - 10 Years | Government bond yields | US | TRUS10T |
| Google Trend for the term ‘’bitcoin’’ | Investor attention | World | - |
| Wikipedia trend for the article on bitcoin | Investor attention | World | - |
| Euro Overnight Deposit (ECB) – middle rate | Monetary policy | Europe | EURODEP |
| Japan Uncollateralized Overnight – middle rate | Monetary policy | Asia | JPCALLO |
| Chinese Renminbi 1D Notice Deposit – middle rate | Monetary Policy | Asia | CHDEPCL |
| US Fed Funds Effective Rate – middle rate | Monetary policy | US | FRFEDFD |
| Australia Economic Policy Uncertainty Index (news based) | Policy uncertainty | Australia | AUEPUNEWR |
| China Economic Policy Uncertainty Index (news based) | Policy uncertainty | Asia | CHEPUNEWR |
| EU Economic Policy Uncertainty Index (news based) | Policy uncertainty | Europe | EUEPUNEWR |
| India Economic Policy Uncertainty Index (news based) | Policy uncertainty | Asia | INEPUNEWR |
| Japan Economic Policy Uncertainty Index (news based) | Policy uncertainty | Asia | JPEPUOVAR |
| Russia Economic Policy Uncertainty Index (news based) | Policy uncertainty | Europe/Asia | RSEPUNEWR |
| Singapore Economic Policy Uncertainty Index (news based) | Policy uncertainty | Asia | SPEPUTWAR |
| South Korea Economic Policy Uncertainty Index (news based) | Policy uncertainty | Asia | KOEPUOVAR |
| UK Economic Policy Uncertainty Index | Policy uncertainty | Europe | UKEPUPO |
| US Economic Policy Uncertainty Index (news based) | Policy uncertainty | US | USEPUNEWR |
| US Economic Policy Uncertainty Index | Policy uncertainty | US | USEPUPO |
| US Equity-related Economic Policy Uncertainty Index | Policy uncertainty | US | USEPUEQ |
| World Economic Policy Uncertainty Index – PPP-adj | Policy uncertainty | World | WDEPUPPPR |
References
- Aalborg, Halvor Aarhus, Peter Molnár, and Jon Erik de Vries. 2019. What can explain the price, volatility and trading volume of bitcoin? Finance Research Letters 29: 255–65. [Google Scholar] [CrossRef]
- Biais, Bruno, Christophe Bisière, Matthieu Bouvard, Catherine Casamatta, and Albert J. Menkveld. 2018. Equilibrium Bitcoin Pricing. Available online: https://ssrn.com/abstract=3261063 (accessed on 7 February 2020). [CrossRef]
- Caspi, Itamar. 2017. Rtadf: Testing for bubbles with eviews. Journal of Statistical Software, Code Snippets 81: 1–16. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018. Datestamping the Bitcoin and Ethereum bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Goczek, Ł, and I. Skliarov. 2019. What drives the bitcoin price? A factor augmented error correction mechanism investigation. Applied Economics 51: 6393–410. [Google Scholar] [CrossRef]
- Hotz-Behofsits, Christian, Florian Huber, and Thomas Otto Zörner. 2018. Predicting crypto-currencies using sparse non-Gaussian state space models. Journal of Forecasting 37: 627–40. [Google Scholar] [CrossRef]
- Jin, J., J. Yu, Y. Hu, and Y. Shang. 2019. Which one is more informative in determining price movements of hedging assets? Evidence from bitcoin, gold and crude oil markets. Physica A: Statistical Mechanics and its Applications 527: 121121. [Google Scholar] [CrossRef]
- Kalaba, R., and L. Tesfatsion. 1989. Time-varying linear regression via flexible least squares. Computers & Mathematics with Applications 17: 1215–45. [Google Scholar] [CrossRef]
- Kapetanios, George, and Filip Zikes. 2018. Time-varying Lasso. Economics Letters 169: 1–6. [Google Scholar] [CrossRef]
- Kjærland, Frode, Aras Khazal, Erlend A. Krogstad, Frans B. G. Nordstrøm, and Are Oust. 2018. An analysis of bitcoin’s price dynamics. Journal of Risk and Financial Management 11: 63. [Google Scholar] [CrossRef]
- Li, Jiahan, and Weiye Chen. 2014. Forecasting macroeconomic time series: LASSO-based approaches and their forecast combinations with dynamic factor models. International Journal of Forecasting 30: 996–1015. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 7 February 2020).
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2018a. On the determinants of bitcoin returns: A LASSO approach. Finance Research Letters 27: 235–40. [Google Scholar] [CrossRef]
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2018b. The effects of markets, uncertainty and search intensity on bitcoin returns. International Review of Financial Analysis 63: 220–42. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., Shuping Shi, and Jun Yu. 2015. Testing for multiple bubbles: Limit theory of real-time detectors. International Economic Review 56: 1079–134. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., Yangru Wu, and Jun Yu. 2011. Explosive Behavior In The 1990s Nasdaq: When Did Exuberance Escalate Asset Values?*. International Economic Review 52: 201–26. [Google Scholar] [CrossRef]
- Schilling, Linda, and Harald Uhlig. 2019. Some simple bitcoin economics. Journal of Monetary Economics 106: 16–26. [Google Scholar] [CrossRef]
- Tay, J. Kenneth, Jerome Friedman, and Robert Tibshirani. 2018. Principal component-guided sparse regression. arXiv arXiv:1810.04651. [Google Scholar]
- Tibshirani, Robert. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological) 58: 267–88. [Google Scholar] [CrossRef]
| 1. | |
| 2. | There is a large literature testing for the importance of different variables for bitcoin. See for example (Kjærland et al. 2018; Aalborg et al. 2019; Goczek and Skliarov 2019; Jin et al. 2019). For a review of such literature see (Panagiotidis et al. 2018a). |
| 3. | While standard LASSO has been around for more than two decades since it was introduced by (Tibshirani 1996), PC-LASSO was not available at the time of (Panagiotidis et al. 2018a’s) work. |
| 4. | Due to discrepancies in the data and different scales of the two sources, a simple linear regression was estimated for the time period for which data from both sources was available, and Wikipedia trend values from 21 January and on were estimated using the values from tools.wmflabs.org. |
| 5. | Google does not provide trend data in daily frequency for large time periods. Thus, for higher precision, daily Google trend data were obtained in nine-month intervals; then, log differences were computed and the values for the missing observations every nine months were interpolated. |
| 6. | All variables were found to be I(0). Unit root tests are available upon request. |
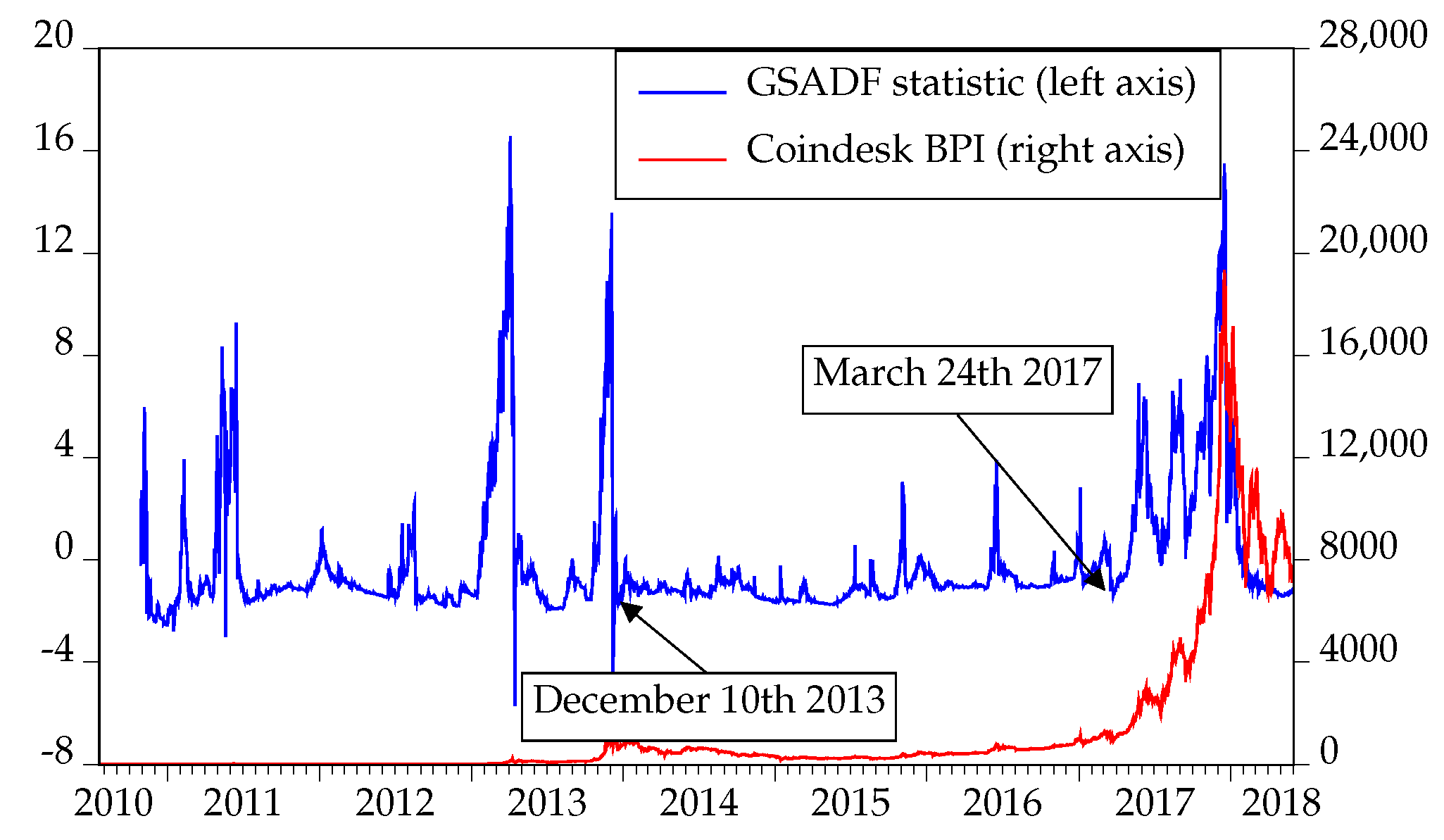
| 7. | GSADF is implemented in Eviews (Caspi 2017). Although in their empirical application (Phillips et al. 2015) used the S&P 500 stock price index and the real S&P 500 stock price index dividend data to implement the test on the price–dividend ratio, in our case it is hard to argue for any (measure of) fundamental value of bitcoin, so we implemented the test on bitcoin alone. This approach is most valid if the fundamental value of bitcoin is constant across time. For example, following a standard approach of the macroeconomic literature, (Schilling and Uhlig 2019) developed a model of an endowment economy with infinitely-lived agents and two intrinsically worthless currencies, a currency supplied by a central bank trying to achieve its inflation target, and bitcoin, whose supply grows deterministically. On the other hand, in the overlapping generations model with investors, miners and hackers (Biais et al. 2018) of the fundamental value of the cryptocurrency is the stream of net transactional benefits it will provide, which depend on its future prices. Looking into the fundamental drivers of the Bitcoin and Ethereum price, (Corbet et al. 2018) tested for the existence and dates of pricing bubbles employing the earlier methodology introduced in (Phillips et al. 2011). |
| 8. | |
| 9. | We implement PC-LASSO using the R package “pcLasso”. (Hotz-Behofsits et al. 2018) test the forecasting performance of sparse state space models using a limited number of predictors. |
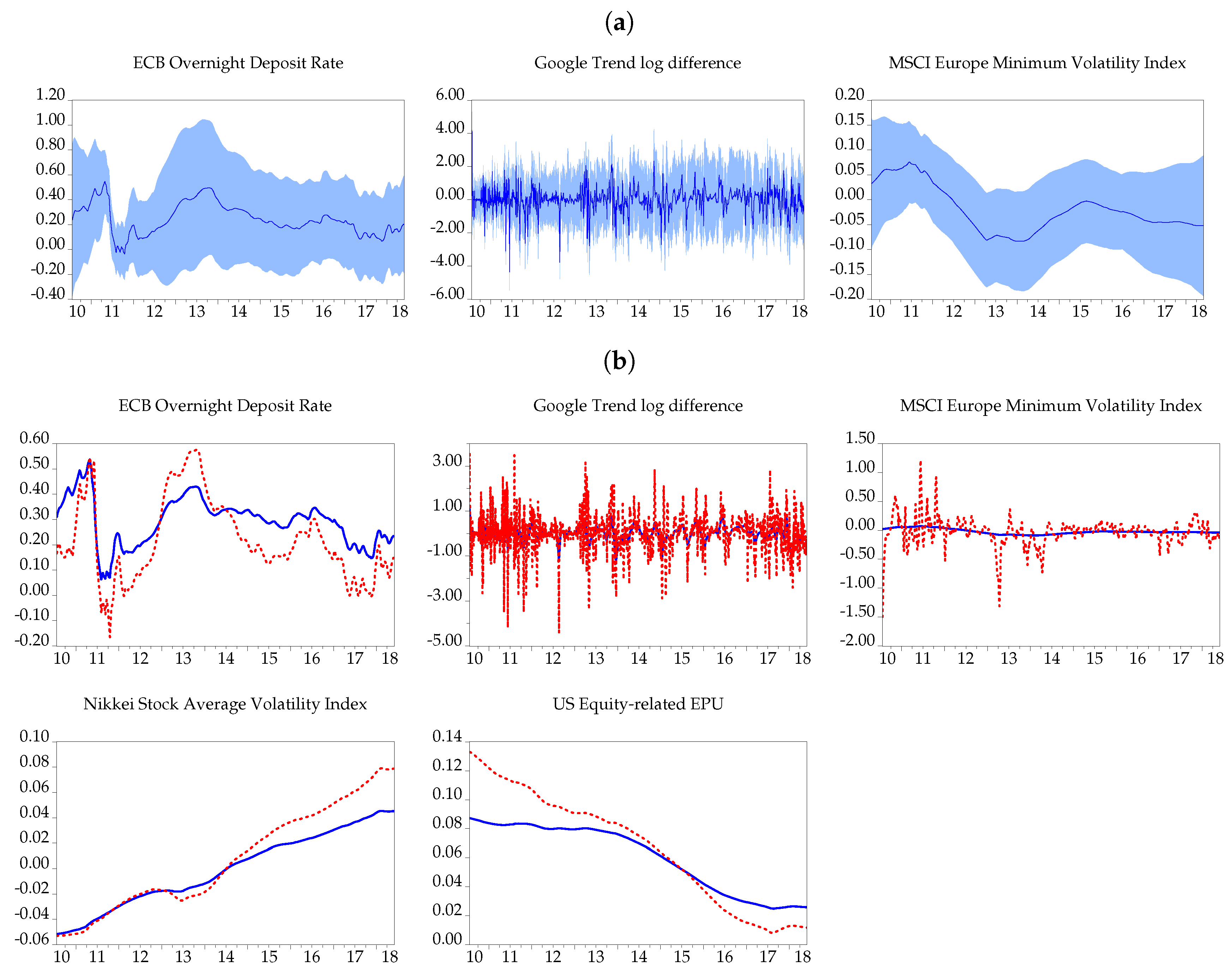
| 10. | The FLS and state-space methods are implemented using the add-in "tvpuni" in Eviews. For the results, see Appendix B. |
| 11. | Rolling window LASSO estimation has been employed by (Li and Chen 2014), while (Kapetanios and Zikes 2018) present an alternative methodology for time-varying Lasso estimation. Both of these are based on standard LASSO methods not exploiting the correlation and group structure of the independent variables through principal component guidance. |
| 12. |
| Method | Details—Specifications |
|---|---|
| GSADF | Initial window size: 100 obs; intercept and trend included in the equation; number of lags in the test equation selected based on the Schwarz information criterion (with maximum allowed 7) |
| PC-LASSO | Dependent variable distribution: Gaussian; ; principal component groups as given in the market/factor type column (Table 2 results) or in the region column (Table 3 results) of Table A1; selected through 30-fold cross validation (that is, by repeated estimations of the model in subsamples of the total sample and making out-of-sample predictions, we find which value of leads to better predictions on average); standardized variables; convergence threshold for coordinate descent algorithm: |
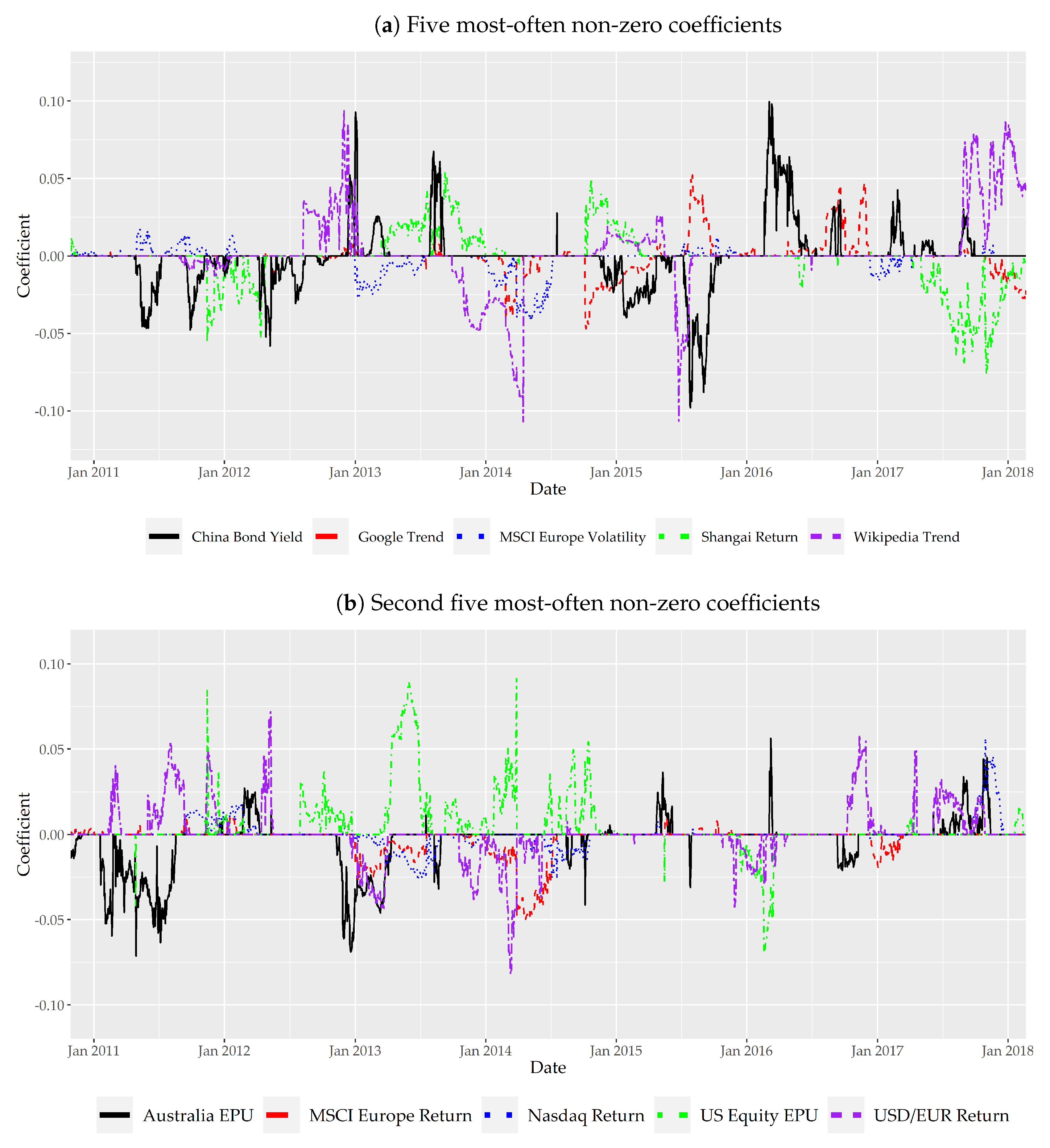
| Rolling window PC-LASSO | Dependent variable distribution: Gaussian; ; ; window size: 200obs.; principal component groups as given in the market/factor type column of Table A1; variables standardized in each window separately so that they are comparable within each time window; convergence threshold for coordinate descent algorithm: |
| FLS | Flexible Least Squares (Kalaba and Tesfatsion 1989) and state-space models with Kalman filtering; smoothing parameter set equal to 1/0.1 |
| Variable | Full Sample | 1st Period | 2nd Period | 3rd Period |
|---|---|---|---|---|
| CBOE SPX Volatility VIX | −0.0358 | −0.0290 | 0.0000 | 0.0000 |
| US Equity-related EPU | 0.0242 | 0.0010 | 0.0000 | 0.0000 |
| Russia EPU | −0.0228 | −0.0062 | 0.0000 | 0.0000 |
| Australia EPU | −0.0215 | −0.0488 | 0.0000 | 0.0000 |
| Japan Government Benchmark Bid Yield | 0.0170 | 0.0000 | 0.0000 | 0.0000 |
| S&P 500 Composite 2-day return | 0.0114 | 0.0098 | 0.0000 | 0.0000 |
| US Government Benchmark Bid Yield | 0.0026 | 0.0000 | 0.0000 | 0.0000 |
| South Korea EPU | 0.0020 | 0.0000 | 0.0000 | 0.0000 |
| ECB Overnight Deposit Rate | 0.0019 | 0.0000 | 0.0000 | - |
| MSCI Europe Minimum Volatility Index | 0.0015 | 0.0000 | 0.0000 | 0.0000 |
| Google Trend log difference | 0.0010 | 0.0000 | −0.0102 | 0.0000 |
| Euro Stoxx 50 Volatility Index | 0.0008 | 0.0000 | 0.0000 | 0.0000 |
| Nikkei Stock Average Volatility Index | −0.0004 | −0.0026 | 0.0000 | 0.0000 |
| Dow Jones 65 Composite 2-day return | 0.0000 | 0.0002 | 0.0000 | 0.0000 |
| US FFER | 0.0000 | 0.0000 | 0.0000 | −0.0074 |
| India EPU | 0.0000 | −0.0023 | 0.0000 | 0.0000 |
| Nikkei 225 Psychological Index | 0.0000 | −0.0071 | 0.0032 | 0.0000 |
| China Government Benchmark Bid Yield | 0.0000 | 0.0015 | −0.0263 | 0.0000 |
| US EPU | 0.0000 | −0.0046 | 0.0000 | 0.0000 |
| USD/UK pound return | 0.0000 | 0.0000 | −0.0049 | 0.0000 |
| Wikipedia trend log difference | 0.0000 | 0.0000 | −0.0026 | 0.0000 |
| Cross-validation | 39 | 21.06 | 56.42 | 53.87 |
| Variable | Full Sample | 1st Period | 2nd Period | 3rd Period |
|---|---|---|---|---|
| Russia EPU | −0.0032 | −0.0075 | 0.0000 | 0.0000 |
| CBOE SPX Volatility VIX | −0.0024 | −0.0097 | 0.0000 | 0.0000 |
| S&P 500 Composite 2-day return | 0.0001 | 0.0040 | 0.0000 | 0.0000 |
| Australia EPU | 0.0000 | −0.0164 | 0.0000 | 0.0000 |
| Dow Jones 65 Composite 2-day return | 0.0000 | 0.0025 | 0.0000 | 0.0000 |
| US FFER | 0.0000 | 0.0000 | 0.0000 | −0.0010 |
| Google Trend log difference | 0.0000 | 0.0000 | −0.0094 | 0.0000 |
| India EPU | 0.0000 | −0.0099 | 0.0000 | 0.0000 |
| Japan Uncollateralized Overnight Rate | 0.0000 | 0.0000 | −0.0003 | 0.0000 |
| Japan EPU | 0.0000 | −0.0095 | 0.0000 | 0.0000 |
| Nikkei Stock Average Volatility Index | 0.0000 | −0.0043 | 0.0000 | 0.0000 |
| Singapore EPU | 0.0000 | −0.0042 | 0.0000 | 0.0000 |
| China Government Benchmark Bid Yield | 0.0000 | 0.0005 | −0.0025 | 0.0000 |
| Japan Government Benchmark Bid Yield | 0.0000 | 0.0000 | −0.0006 | 0.0000 |
| US EPU | 0.0000 | −0.0050 | 0.0000 | 0.0000 |
| USD/UK pound return | 0.0000 | 0.0000 | −0.0002 | 0.0000 |
| Cross-validation | 98.89 | 21.06 | 81.86 | 53.87 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotidis, T.; Stengos, T.; Vravosinos, O. A Principal Component-Guided Sparse Regression Approach for the Determination of Bitcoin Returns. J. Risk Financial Manag. 2020, 13, 33. https://doi.org/10.3390/jrfm13020033
Panagiotidis T, Stengos T, Vravosinos O. A Principal Component-Guided Sparse Regression Approach for the Determination of Bitcoin Returns. Journal of Risk and Financial Management. 2020; 13(2):33. https://doi.org/10.3390/jrfm13020033
Chicago/Turabian StylePanagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2020. "A Principal Component-Guided Sparse Regression Approach for the Determination of Bitcoin Returns" Journal of Risk and Financial Management 13, no. 2: 33. https://doi.org/10.3390/jrfm13020033
APA StylePanagiotidis, T., Stengos, T., & Vravosinos, O. (2020). A Principal Component-Guided Sparse Regression Approach for the Determination of Bitcoin Returns. Journal of Risk and Financial Management, 13(2), 33. https://doi.org/10.3390/jrfm13020033







