A Gated Recurrent Unit Approach to Bitcoin Price Prediction
Abstract
1. Introduction
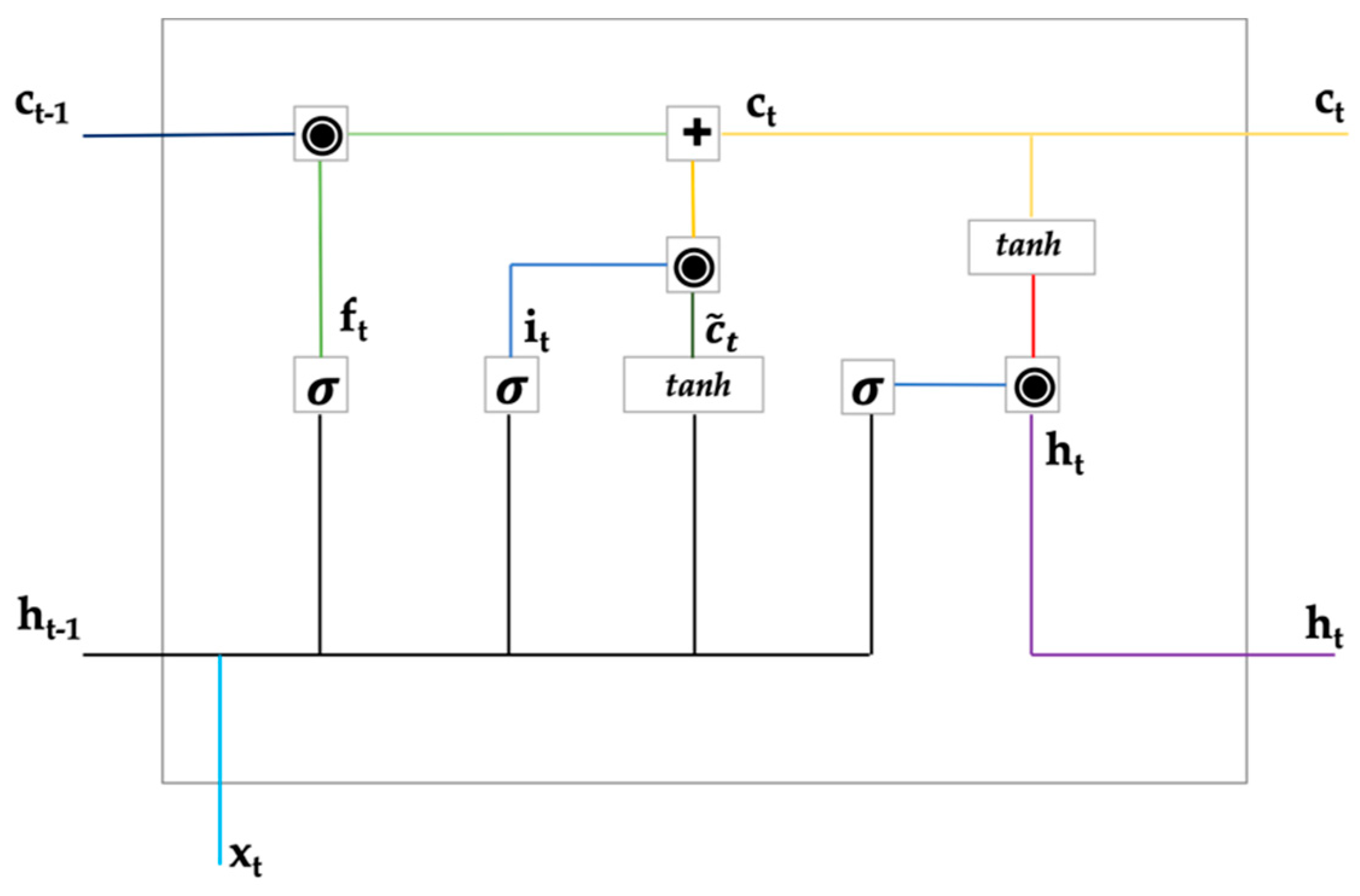
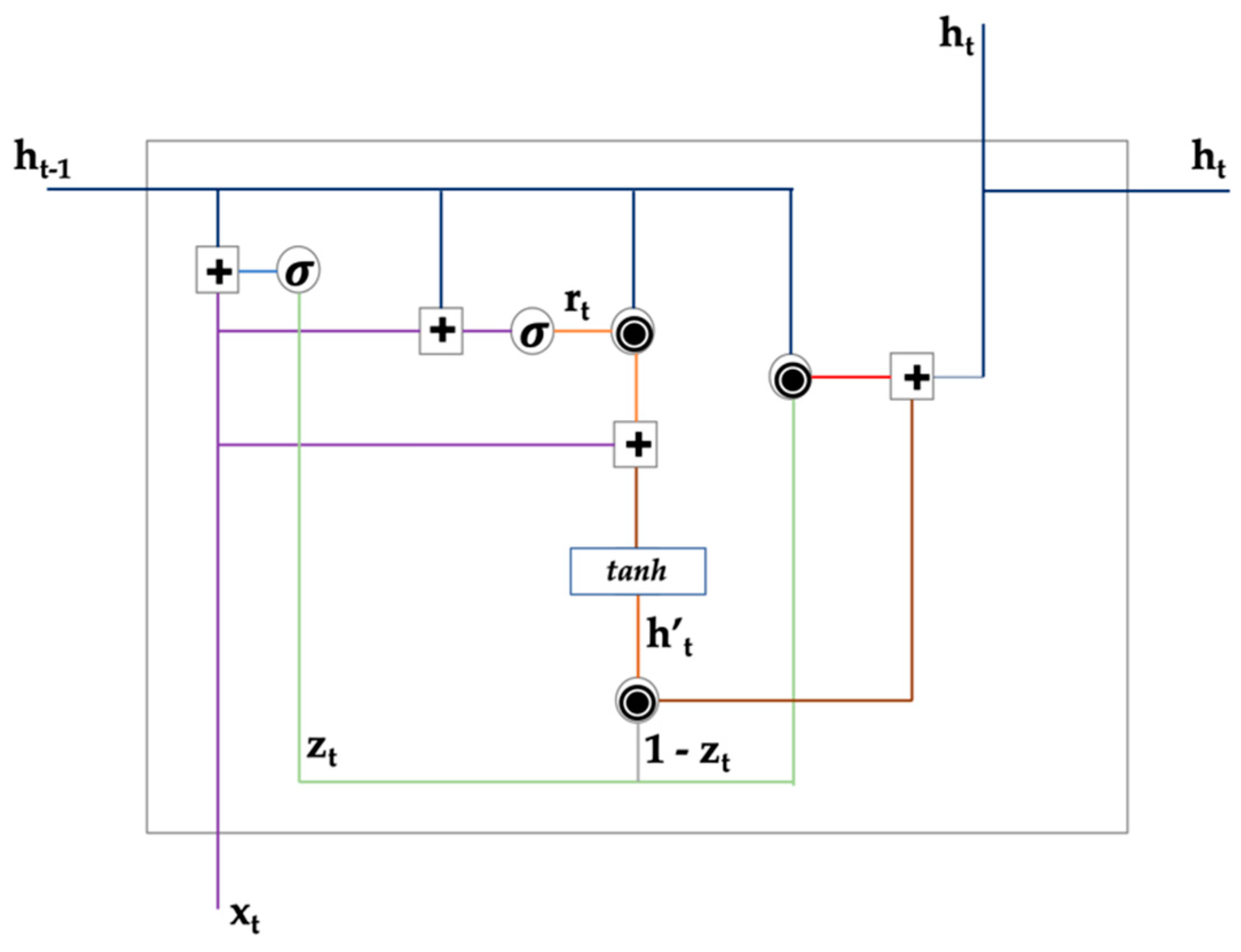
2. Methodology
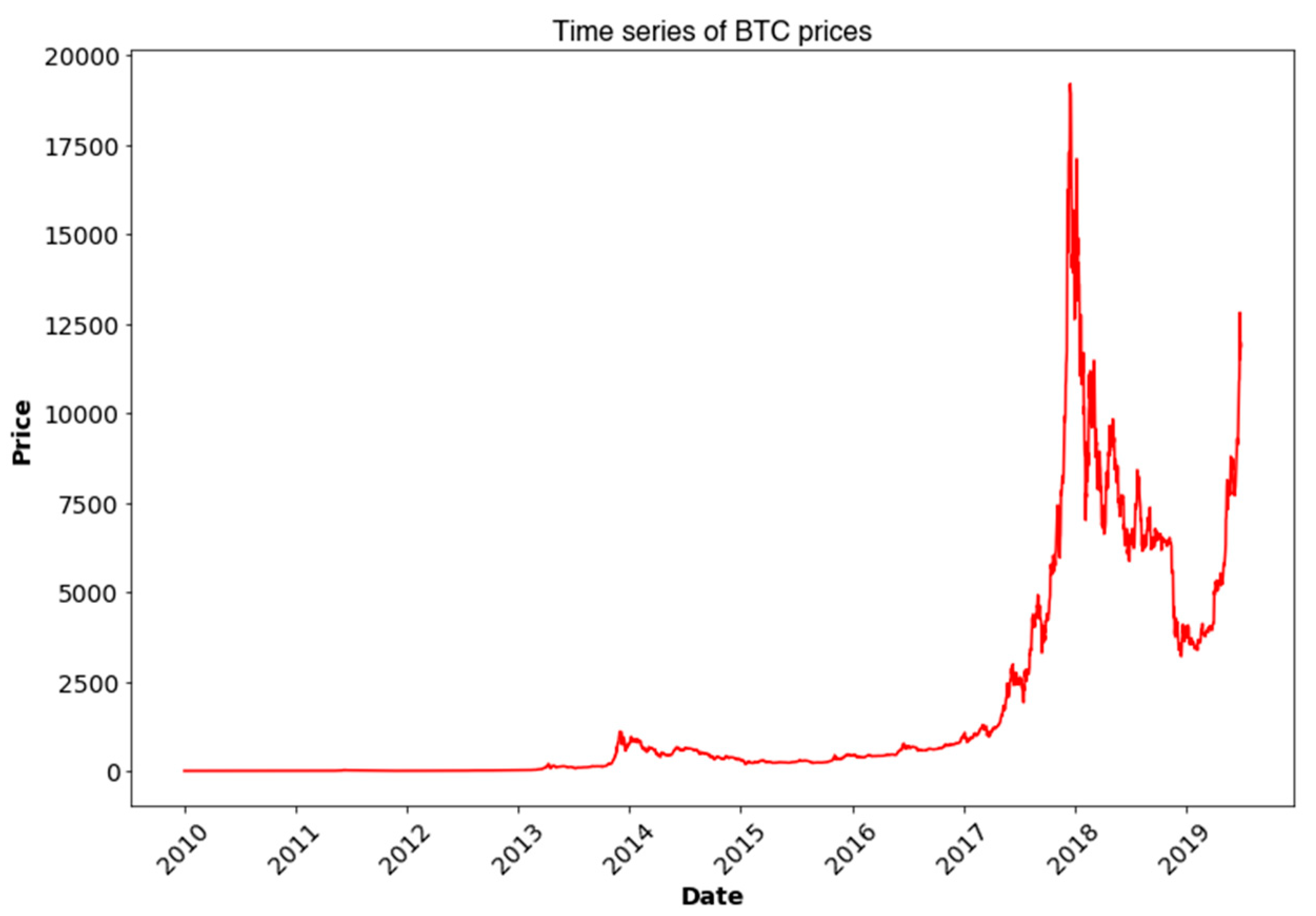
3. Data Collection and Feature Engineering
3.1. Data Pre-Processing
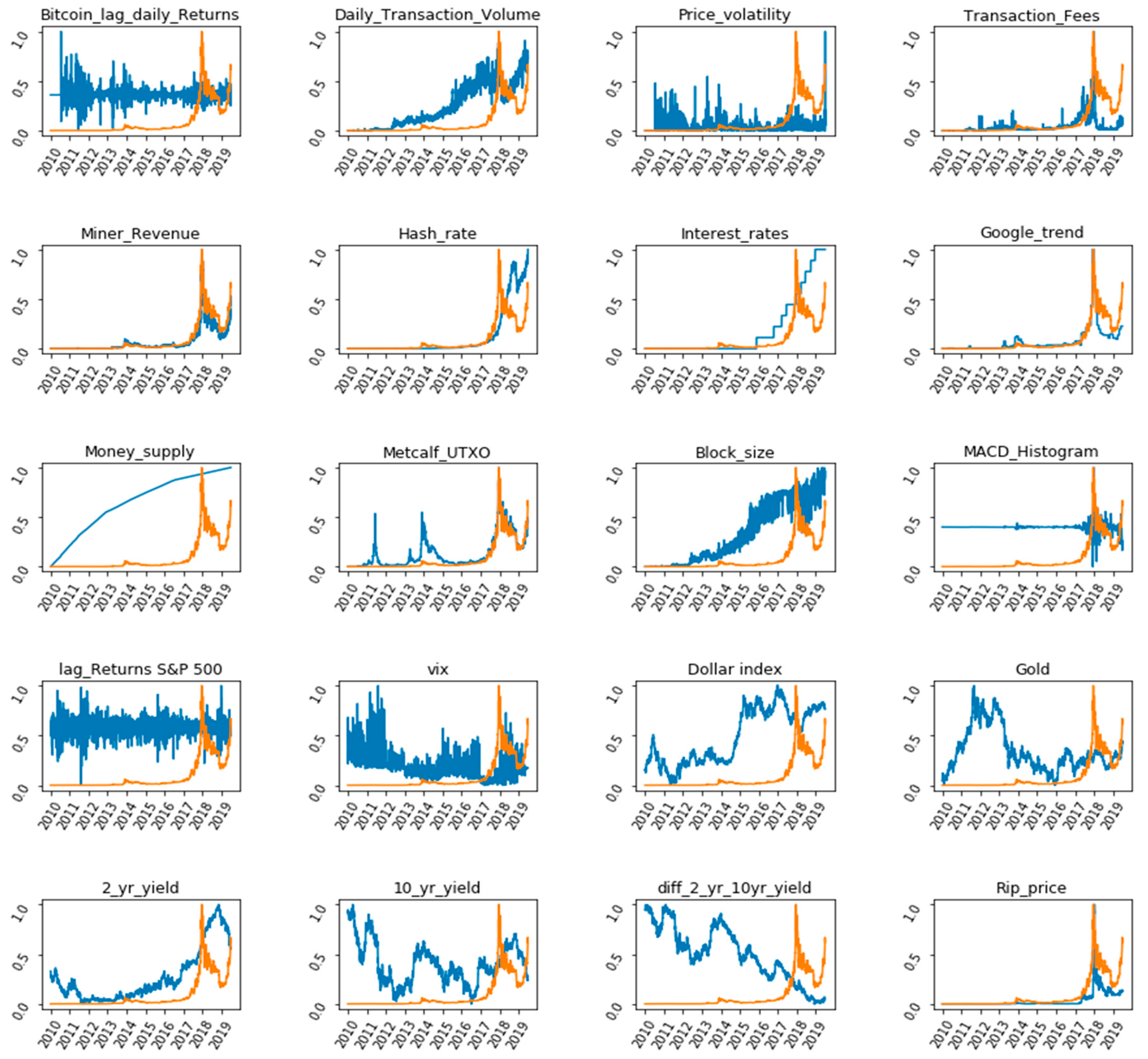
3.2. Feature Selection
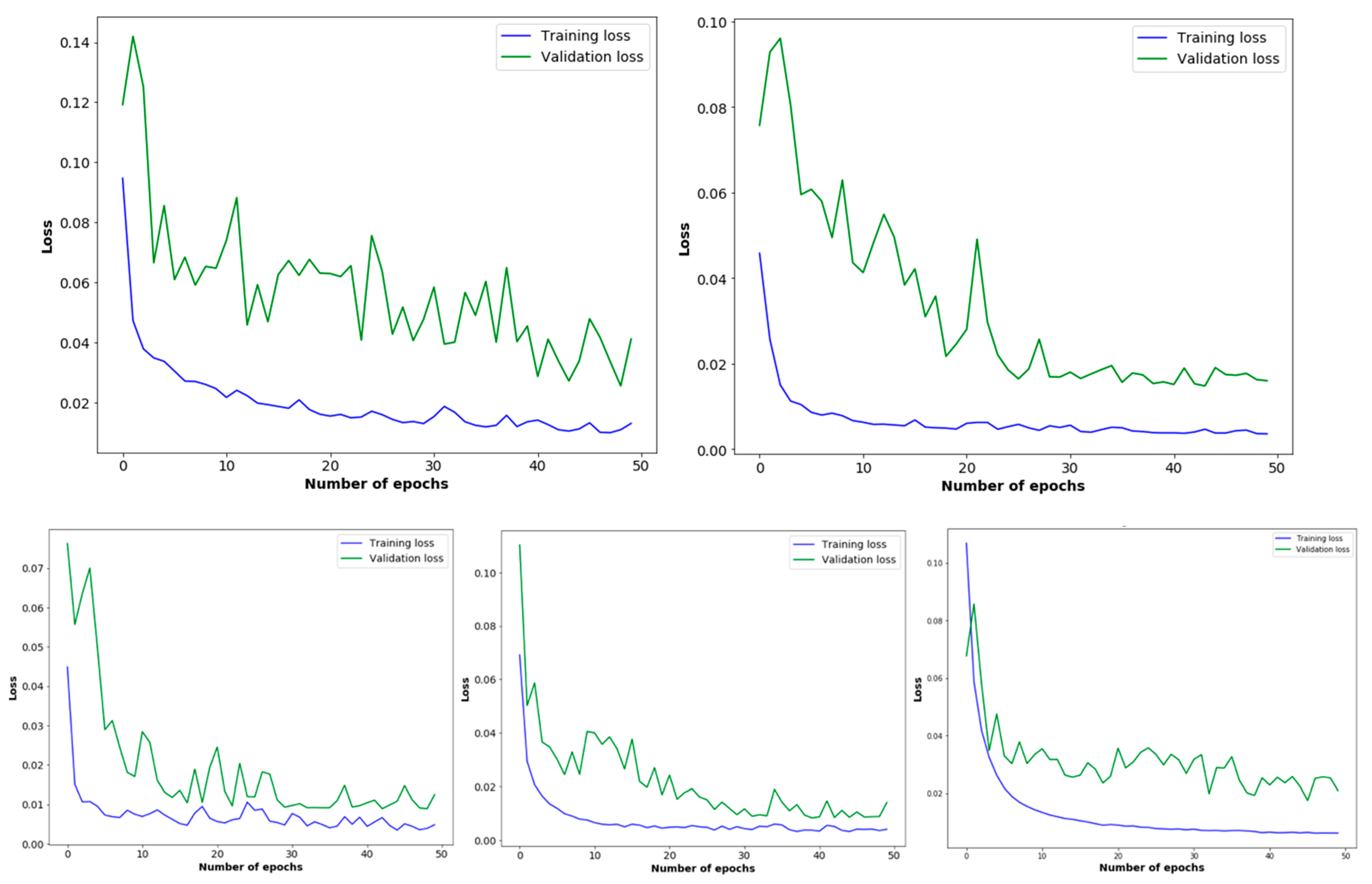
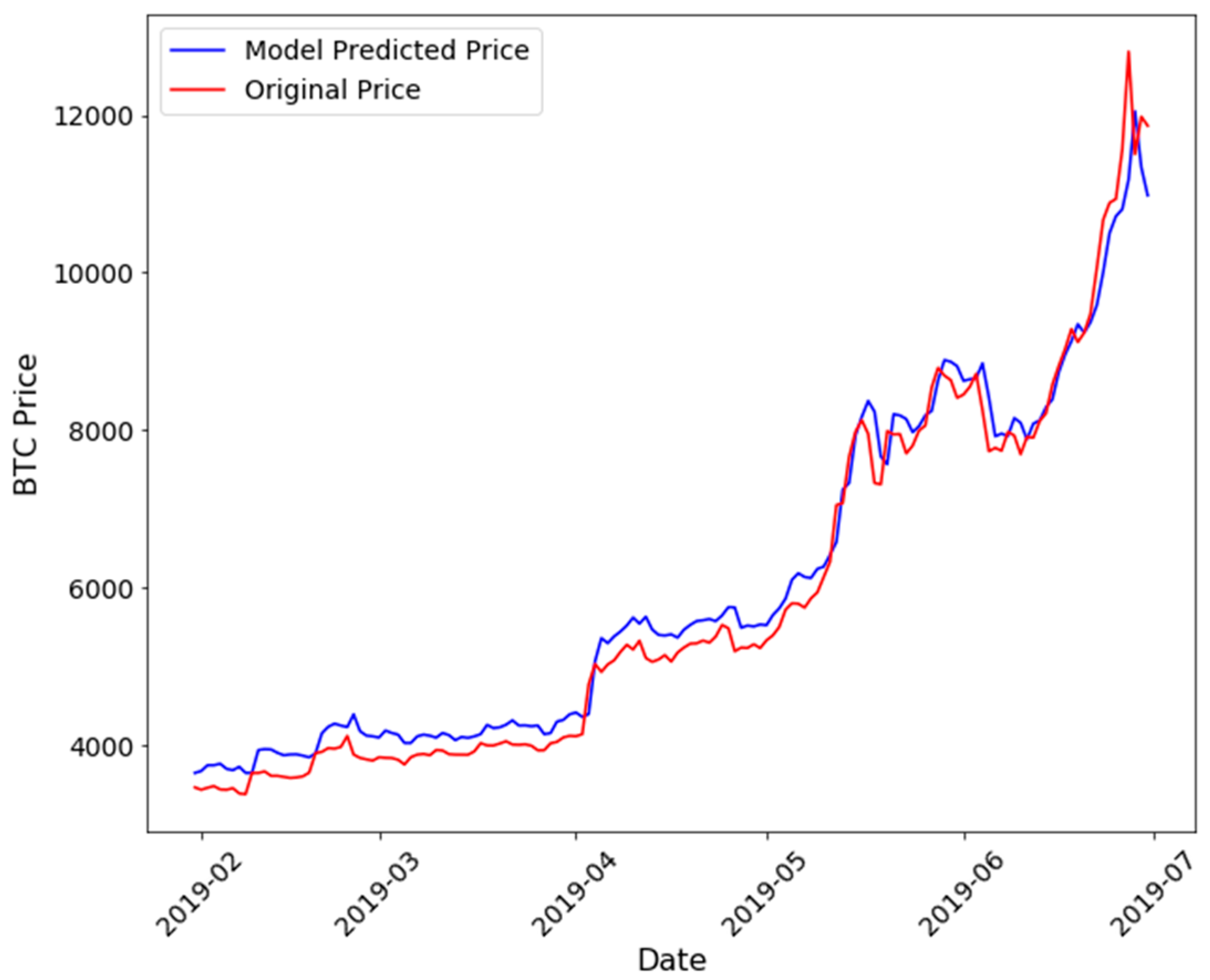
4. Model Implementation and Results
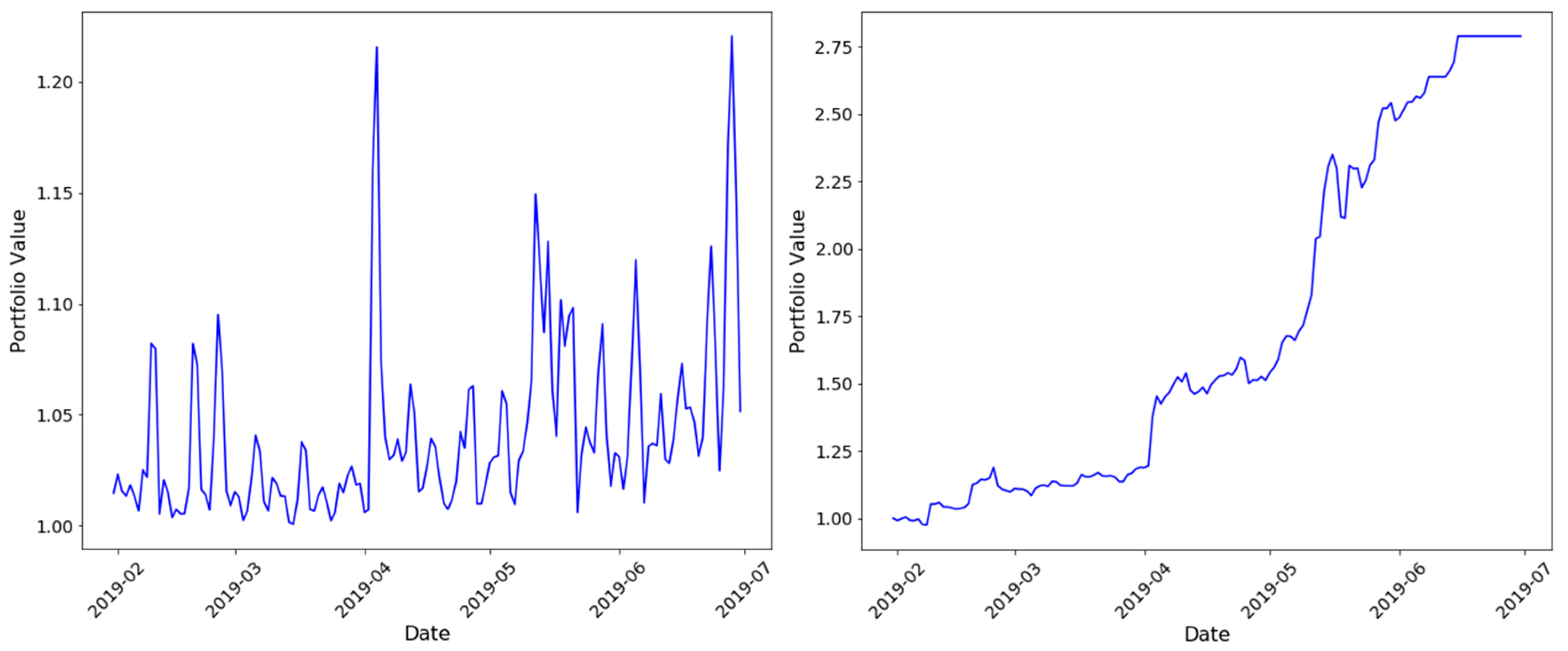
5. Portfolio Strategy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Features | Definition | Source |
|---|---|---|
| Bitcoin Price | Bitcoin prices. | https://charts.bitcoin.com/btc/ |
| BTC Price Volatility | The annualized daily volatility of price changes. Price volatility is computed as the standard deviation of daily returns, scaled by the square root of 365 to annualize, and expressed as a decimal. | https://charts.bitcoin.com/btc/ |
| BTC Miner Revenue | Total value of Coinbase block rewards and transaction fees paid to miners. Historical data showing (number of bitcoins mined per day + transaction fees) * market price. | https://www.quandl.com/data/BCHAIN/MIREV-Bitcoin-Miners-Revenue |
| BTC Transaction Volume | The number of transactions included in the blockchain each day. | https://charts.bitcoin.com/btc/ |
| Transaction Fees | Total amount of Bitcoin Core (BTC) fees earned by all miners in 24-hour period, measured in Bitcoin Core (BTC). | https://charts.bitcoin.com/btc/ |
| Hash Rate | The number of block solutions computed per second by all miners on the network. | https://charts.bitcoin.com/btc/ |
| Money Supply | The amount of Bitcoin Core (BTC) in circulation. | https://charts.bitcoin.com/btc/ |
| Metcalfe-UTXO | Metcalfe’s Law states that the value of a network is proportional to the square of the number of participants in the network. | https://charts.bitcoin.com/btc/ |
| Block Size | Miners collect Bitcoin Core (BTC) transactions into distinct packets of data called blocks. Each block is cryptographically linked to the preceding block, forming a "blockchain." As more people use the Bitcoin Core (BTC) network for Bitcoin Core (BTC) transactions, the block size increases. | https://charts.bitcoin.com/btc/ |
| Google Trends | This is the month-wise Google search results for the Bitcoins. | https://trends.google.com |
| Volatility (VIX) | VIX is a real-time market index that represents the market’s expectation of 30-day forward-looking volatility. | http://www.cboe.com/products/vix-index-volatility/vix-options-and-futures/vix-index/vix-historical-data |
| Gold price Level | Gold price level. | https://www.quandl.com/data/WGC/GOLD_DAILY_USD-Gold-Prices-Daily-Currency-USD |
| US Dollar Index | The U.S. dollar index (USDX) is a measure of the value of the U.S. dollar relative to the value of a basket of currencies of the majority of the U.S.’ most significant trading partners. | https://finance.yahoo.com/quote/DX-Y.NYB/history?period1=1262332800&period2=1561878000&interval=1d&filter=history&frequency=1d |
| US Bond Yields | 2-year / short-term yields. | https://www.quandl.com/data/USTREASURY/YIELD-Treasury-Yield-Curve-Rates |
| US Bond Yields | 10-year/ long term yields. | https://www.quandl.com/data/USTREASURY/YIELD-Treasury-Yield-Curve-Rates |
| US Bond Yields | Difference between 2 year and 10 year/ synonymous with yield inversion and recession prediction | https://www.quandl.com/data/USTREASURY/YIELD-Treasury-Yield-Curve-Rates |
| MACD | MACD=12-Period EMA −26-Period EMA. We have taken the data of the MACD with the signal line. MACD line = 12-day EMA Minus 26-day EMA Signal line = 9-day EMA of MACD line MACD Histogram = MACD line Minus Signal line | |
| Ripple Price | The price of an alternative cryptocurrency. | https://coinmarketcap.com/currencies/ripple/historical-data/?start=20130428&end=20190924 |
| One Day Lagged S&P 500 Market Returns | Stock market returns. | https://finance.yahoo.com/quote/%5EGSPC/history?period1=1230796800&period2=1568012400&interval=1d&filter=history&frequency=1d |
| Interest Rates | The federal funds rate decide the shape of the future interest rates in the economy. | http://www.fedprimerate.com/fedfundsrate/federal_funds_rate_history.htm#current |
References
- Baek, Chung, and Matt Elbeck. 2015. Bitcoin as an Investment or Speculative Vehicle? A First Look. Applied Economics Letters 22: 30–34. [Google Scholar] [CrossRef]
- Barrdear, John, and Michael Kumhof. 2016. The Macroeconomics of Central Bank Issued Digital Currencies. SSRN Electronic Journal. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2811208 (accessed on 2 February 2020).
- Baronchelli, Andrea. 2018. The emergence of consensus: A primer. Royal Society Open Science 5: 172189. [Google Scholar] [CrossRef]
- Bech, Morten L., and Rodney Garratt. 2017. Central Bank Cryptocurrencies. BIS Quarterly Review 2017: 5–70. [Google Scholar]
- Blau, Benjamin M. 2017. Price Dynamics and Speculative Trading in Bitcoin. Research in Internatonal Business and Finance 41: 493–99. [Google Scholar] [CrossRef]
- Blundell-Wignall, Adrian. 2014. The Bitcoin Question: Currency versus Trust-less Transfer Technology. OECD Working Papers on Finance, Insurance and Private Pensions 37: 1. [Google Scholar]
- Bohme, Rainer, Nicolas Christin, Benjamin Edelman, and Tyler Moore. 2015. Bitcoin: Economics, technology, and governance. Journal of Economic Perspectives (JEP) 29: 213–38. [Google Scholar] [CrossRef]
- Bouri, Elie, Peter Molnár, Georges Azzi, and David Roubaud. 2017. On the hedge and safe haven properties of Bitcoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Briere, Marie, Kim Oosterlinck, and Ariane Szafarz. 2015. Virtual currency, tangible return: Portfolio diversification with bitcoin. Journal Asset Management 16: 365–73. [Google Scholar] [CrossRef]
- Cagli, Efe C. 2019. Explosive behavior in the prices of Bitcoin and altcoins. Finance Research Letters 29: 398–403. [Google Scholar] [CrossRef]
- Casey, Michael J., and Paul Vigna. 2015. Bitcoin and the digital-currency revolution. The Wall Street Journal. Available online: https://www.wsj.com/articles/the-revolutionary-power-of-digital-currency-1422035061 (accessed on 2 February 2020).
- Chang, Pei-Chann, Chen-Hao Liu, Chin-Yuan Fan, Jun-Lin Lin, and Chih-Ming Lai. 2009. An Ensemble of Neural Networks for Stock Trading Decision Making. In Emerging Intelligent Computing Technology and Applications. With Aspects of Artificial Intelligence 5755 of Lecture Notes in Computer Science. Berlin/Heidelberg: Springer, pp. 1–10. Available online: https://doi.org/10.1007/978-3-642-04020-7_1 (accessed on 2 February 2020).
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative bubbles in Bitcoin markets? An empirical investigation into the fundamental value of Bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef]
- Chen, Zheshi, Chunhong Li, and Wenjun Sun. 2020. Bitcoin price prediction using machine learning: An approach to sample dimension engineering. Journal of Computational and Applied Mathematics 365: 112395. [Google Scholar] [CrossRef]
- Cho, Kyunghyun, Bart van Merrienboer, Caglar Gulcehre, Dzmitry Bahdanau, Bougares Fethi, Schwenk Holger, and Yoshua Bengio. 2014. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. Available online: https://arxiv.org/abs/1406.1078.pdf (accessed on 2 February 2020).
- Chollet, Francois. 2015. Keras: Deep Learning for humans. Available online: https://github.com/keras-team/keras (accessed on 2 February 2020).
- Chong, Eunsuk, Chulwoo Han, and Frank C. Park. 2017. Deep learning networks for stock market analysis and prediction: methodology, data representations, and case studies. Expert System with Applications 83: 187–205. [Google Scholar] [CrossRef]
- Chung, Junyoung, Caglar Gulcehre, Kyung H. Cho, and Yoshua Bengio. 2014. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. Available online: https://arxiv.org/pdf/1412.3555.pdf (accessed on 2 February 2020).
- Ciaian, Pavel, Miroslava Rajcaniova, and d’Artis Kancs. 2016. The economics of Bitcoin price formation. Applied Economics 48: 1799–815. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, Maurice Peat, and Samuel Vigne. 2018. Bitcoin Futures—What use are they? Economics Letters 172: 23–27. [Google Scholar] [CrossRef]
- Cusumano, Michael A. 2014. The Bitcoin ecosystem. Communications of the ACM 57: 22–24. [Google Scholar] [CrossRef]
- Cybenko, George. 1989. Approximation by superpositions of a sigmoidal function. Math. Control Signals Systems 2: 303–14. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Mariano Roberto S. 1995. Comparing Predictive Accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Dow, Sheila. 2019. Monetary Reform, Central Banks and Digital Currencies. International Journal of Political Economy 48: 153–73. [Google Scholar] [CrossRef]
- Dyhrberg, Anne H. 2016. Bitcoin, gold and the dollar-A Garch volatility. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Dwyer, Gerald P. 2015. The economics of Bitcoin and similar private digital currencies. Journal of Financial Stability 17: 81–91. [Google Scholar] [CrossRef]
- ElBahrawy, Abeer, Laura Alessandretti, Anne Kandler, Romualdo Pastor-Satorras, and Andrea Baronchelli. 2017. Evolutionary dynamics of the cryptocurrency market. Royal Society Open Science 4: 170623. [Google Scholar] [CrossRef] [PubMed]
- Enke, David, and Suraphan Thawornwong. 2005. The use of data mining and neural networks for forecasting stock market returns. Expert Systems with Applications 29: 927–40. [Google Scholar] [CrossRef]
- Fama, Marco, Andrea Fumagalli, and Stefano Lucarelli. 2019. Cryptocurrencies, Monetary Policy, and New Forms of Monetary Sovereignty. International Journal of Political Economy 48: 174–94. [Google Scholar] [CrossRef]
- Fantacci, Luca. 2019. Cryptocurrencies and the Denationalization of Money. International Journal of Political Economy 48: 105–26. [Google Scholar] [CrossRef]
- Filippi, Primavera De. 2014. Bitcoin: A Regulatory Nightmare to a Libertarian Dream. Internet Policy Review 3. [Google Scholar] [CrossRef]
- Gajardo, Gabriel, Werner D. Kristjanpoller, and Marcel Minutolo. 2018. Does Bitcoin exhibit the same asymmetric multifractal cross-correlations with crude oil, gold and DJIA as the Euro, Great British Pound and Yen? Chaos, Solitons & Fractals 109: 195–205. [Google Scholar]
- Gal, Yarin, and Zoubin Ghahramani. 2016. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. Available online: https://arxiv.org/pdf/1506.02142.pdf (accessed on 2 February 2020).
- Gal, Yarin, and Zoubin Ghahramani. 2016. A theoretically grounded application of dropout in recurrent neural networks. Advances in Neural Information Processing Systems 2016: 1019–27. [Google Scholar]
- Gandal, Neil, and Hanna Halaburda. 2016. Can we predict the winner in a market with network effects? Competition in cryptocurrency market. Games 7: 16. [Google Scholar] [CrossRef]
- Guo, Tian, Albert Bifet, and Nino Antulov-Fantulin. 2018. Bitcoin volatility forecasting with a glimpse into buy and sell orders. Paper presented at 2018 IEEE International Conference on Data Mining (ICDM), Singapore, November 17–20. [Google Scholar]
- Guo, Tian, and Nino Antulov-Fantulin. 2018. Predicting Short-Term Bitcoin Price Fluctuations from Buy and Sell Orders. Available online: https://arxiv.org/pdf/1802.04065v1.pdf (accessed on 2 February 2020).
- Hair, Joseph F., Rolph E. Anderson, and Ronald L. Tatham. 1992. Multivariate Data Analysis, 3rd ed. New York: Macmillan. [Google Scholar]
- Hileman, G, and M. Rauchs. 2017. Global Cryptocurrency Bench- marking Study. Cambridge Centre for Alternative Finance. Available online: https://www.jbs.cam.ac.uk/fileadmin/user_upload/research/centres/alternative-finance/downloads/2017-04-20-global-cryptocurrency-benchmarking-study.pdf (accessed on 2 February 2020).
- Hinton, Geoffrey E., Simon Osindero, and Yee-Whye The. 2006. A fast learning algorithm for deep belief nets. Neural Computation 18: 1527–54. [Google Scholar] [CrossRef]
- Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. Long Short-Term Memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef]
- Hochreiter, Sepp. 1998. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 6: 107–16. [Google Scholar] [CrossRef]
- Huang, Wei, Yoshiteru Nakamori, and Shou-Yang Wang. 2005. Forecasting stock market movement direction with support vector machine. Computers & Operations Research 32: 2513–22. [Google Scholar]
- Huck, Nicolas. 2010. Pairs trading and outranking: The multi-step-ahead forecasting case. European Journal of Operational Research 207: 1702–16. [Google Scholar] [CrossRef]
- Jang, Huisu, and Jaewook Lee. 2017. An Empirical Study on Modeling and Prediction of Bitcoin Prices with Bayesian Neural Networks Based on Blockchain Information. IEEE Access 6: 5427–37. [Google Scholar] [CrossRef]
- Kaiser, Lukasz, and Ilya Sutskever. 2016. Neural GPUS Learn Algorithms. Available online: https://arxiv.org/pdf/1511.08228.pdf (accessed on 2 February 2020).
- Kaiser, Lars. 2019. Seasonality in cryptocurrencies. Finance Research Letters 31: 232–38. [Google Scholar] [CrossRef]
- Karakoyun, Ebru Şeyma, and Ali Osman Çıbıkdiken. 2018. Comparison of ARIMA Time Series Model and LSTM Deep Learning Algorithm for Bitcoin Price Forecasting. Paper presented at the 13th Multidisciplinary Academic Conference in Prague 2018 (The 13th MAC 2018), Prague, Czech Republic, May 25–27. [Google Scholar]
- Karasu, Seçkin, Aytaç Altan, Zehra Saraç, and Rifat Hacioğlu. 2018. Prediction of Bitcoin prices with machine learning methods using time series data. Paper presented at 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, May 2–5. [Google Scholar]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Kennedy, Peter E. 1992. A Guide to Econometrics. Oxford: Blackwell. [Google Scholar]
- Kim, Young B., Jun G. Kim, Wook Kim, Jae H. Im, Tae H. Kim, Shin J. Kang, and Chang H. Kim. 2016. Predicting Fluctuations in Cryptocurrency Transactions Based on User Comments and Replies. PLoS ONE 11: e0161197. [Google Scholar] [CrossRef]
- Kingma, Diederik P., and Jimmy Ba. 2015. Adam: A method for stochastic optimization. arXiv 2015: 9. [Google Scholar]
- Krafft, Peter M., Nicolas D. Penna, and Alex S. Pentland. 2018. An Experimental Study of Cryptocurrency Market Dynamics. Paper presented at CHI Conference, Montreal, QC, Canada, April 21–26. [Google Scholar]
- Kristoufek, Ladoslav. 2015. What Are the Main Drivers of the Bitcoin Price? Evidence from Wavelet Coherence Analysis. PLoS ONE 10: e0123923. [Google Scholar] [CrossRef]
- Lawrence, Steve, Giles C. Lee, and Ah C. Tsoi. 1997. Lessons in Neural Network Training: Overfitting May be Harder than Expected. In Proceedings of the Fourteenth National Conference on Artificial Intelligence. Menlo Park: AAAI Press, pp. 540–45. [Google Scholar]
- Lo, Stephanie, and J. Christina Wang. 2014. Bitcoin as Money? Working Paper 14. Boston, MA, USA: Federal Reserve Bank of Boston. [Google Scholar]
- Luo, Zhaojie, Xiaojing Cai, Katsuyuki Tanaka, Tetsuya Takiguchi, Takuji Kinkyo, and Shigeyuki Hamori. 2019. Can we forecast daily oil futures prices? Experimental evidence from convolutional neural networks. Journal of Risk and Financial Management 12: 9. [Google Scholar] [CrossRef]
- Madan, Issax, Saluja Shaurya, and Zhao Aojja. 2015. Automated Bitcoin Trading via Machine Learning Algorithms. Available online: https://pdfs.semanticscholar.org/e065/3631b4a476abf5276a264f6bbff40b132061.pdf (accessed on 2 February 2020).
- Malherbe, Leo, Matthieu Montalban, Nicolas Bedu, and Caroline Granier. 2019. Cryptocurrencies and Blockchain: Opportunities and Limits of a New Monetary Regime. International Journal of Political Economy 48: 127–52. [Google Scholar] [CrossRef]
- Marquardt, Donald W. 1970. Generalized inverses, ridge regression, biased linear estimation, and nonlinear estimation. Technometrics 12: 591–612. [Google Scholar] [CrossRef]
- McNally, Sean, Jason Roche, and Simon Caton. 2018. Predicting the Price of Bitcoin Using Machine Learning. Paper presented at 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, March 21–23. [Google Scholar]
- Merity, Stephen, Nitish S. Keskar, and Richard Socher. 2017. Regularizing and Optimizing LSTM Language Models. Available online: https://arxiv.org/abs/1708.02182 (accessed on 2 February 2020).
- Muzammal, Muhammad, Qiang Qu, and Bulat Nasrulin. 2019. Renovating blockchain with distributed databases: An open source system. Future Generation Computer Systems 90: 105–17. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 2 February 2020).
- Nawata, Kazumitsu, and Nobuko Nagase. Estimation of sample selection bias models. Econometric Reviews 15: 4. [CrossRef]
- Neter, John, William Wasserman, and Michael H. Kutner. 1989. Applied Linear Regression Models. Homewood: Irwin. [Google Scholar]
- Pichl, Lukas, and Taisei Kaizoji. 2017. Volatility Analysis of Bitcoin Price Time Series. Quantitative Finance and Economics 1: 474–85. [Google Scholar] [CrossRef]
- Poyser, Obryan. 2017. Exploring the Determinants of Bitcoin’s Price: An Application of Bayesian Structural Time Series. Available online: https://arxiv.org/abs/1706.01437 (accessed on 2 February 2020).
- Pascanu, Razvan, Tomas Mikolov, and Yochus Bengio. 2013. On the Difficulty of Training Recurrent Neural Networks. Available online: https://arxiv.org/pdf/1211.5063.pdf (accessed on 2 February 2020).
- Rogojanu, Angel, and Liana Badeaetal. 2014. The issue of competing currencies. Case study bitcoin. Theoretical and Applied Economics 21: 103–14. [Google Scholar]
- Selmi, Refk, Walid Mensi, Shawkat Hammoudeh, and Jamal Boioiyour. 2018. Is Bitcoin a hedge, a safe haven or a diversifier for oil price movements? A comparison with gold. Energy Economics 74: 787–801. [Google Scholar] [CrossRef]
- Sheta, Alaa F., Sara Elsir M. Ahmed, and Hossam Faris. 2015. A comparison between regression, artificial neural networks and support vector machines for predicting stock market index. Soft Computing 7: 8. [Google Scholar]
- Siami-Namini, Sima, and Akbar S. Namin. 2018. Forecasting Economics and Financial Time Series: ARIMA vs. LSTM. Available online: https://arxiv.org/abs/1803.06386v1 (accessed on 2 February 2020).
- Sovbetov, Yhlas. 2018. Factors influencing cryptocurrency prices: Evidence from bitcoin, ethereum, dash, litcoin, and monero. Available online: https://mpra.ub.uni-muenchen.de/85036/1/MPRA_paper_85036.pdf (accessed on 2 February 2020).
- Srivastava, Nitish, Geoffrey Hinton, Alex Krizhesvsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research 15: 1929–58. [Google Scholar]
- Wang, Lin, Yi Zeng, and Tao Chen. 2015. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Systems with Applications 42: 855–63. [Google Scholar] [CrossRef]
- White, Lawrence H. 2015. The market for cryptocurrencies. The Cato Journal 35: 383–402. [Google Scholar] [CrossRef][Green Version]
- Yin, Wenpeng, Katharina Kann, Mo Yu, and Hinrich Schutze. 2017. Comparative Study of CNN and RNN for Natural Language Processing. Available online: https://arxiv.org/pdf/1702.01923.pdf (accessed on 2 February 2020).
- Yelowitz, Aaron, and Matthew Wilson. 2015. Characteristics of Bitcoin users: an analysis of Google search data. Applied Economics Letters 22: 1030–36. [Google Scholar] [CrossRef]
- Yu, Lean, Kin K. Lai, Shouyang Wang, and Wei Huang. 2006. A Bias-Variance-Complexity Trade-Off Framework for Complex System Modeling. In Computational Science and Its Applications-ICCSA 2006. Lecture Notes in Computer Science. Berlin/Heidelberg: Springer, Volume 3980. [Google Scholar]
| Predictor Variables | VIF | Predictor Variables | VIF |
|---|---|---|---|
| Bitcoin daily lag returns | 1.023 | Block size | 30.208 |
| Daily transaction volume | 2.823 | MACD histogram | 1.27 |
| Price volatility | 1.13 | S&P lag returns | 1.005 |
| Transaction fees | 4.671 | VIX | 1.671 |
| Miner revenue | 28.664 | Dollar index | 6.327 |
| Hash rate | 2.694 | Gold | 5.267 |
| Interest rates | 49.718 | 2 Yr yield | 3.074 |
| Google trend | 9.847 | 10 Yr yield | 8.101 |
| Money supply | 8.462 | Ripple price | 5.866 |
| Metcalf UTXO | 12.003 | Diff 2 yr–10 yr diff | 11.283 |
| Models | RMSE Train | RMSE Test | p-Value |
|---|---|---|---|
| Neural Network | 0.020 | 0.031 | |
| LSTM | 0.010 | 0.024 | 0.0000 |
| GRU | 0.010 | 0.019 | 0.0000 |
| GRU-Dropout | 0.014 | 0.017 | 0.0012 |
| GRU-Dropout-GRU | 0.012 | 0.034 | 0.0000 |
| Lookback Period (Days) | RMSE Train | RMSE Test | p-Value |
|---|---|---|---|
| 15 | 0.012 | 0.016 | |
| 45 | 0.011 | 0.019 | 0.0010 |
| 60 | 0.011 | 0.017 | 0.0006 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, A.; Kumar, S.; Basu, M. A Gated Recurrent Unit Approach to Bitcoin Price Prediction. J. Risk Financial Manag. 2020, 13, 23. https://doi.org/10.3390/jrfm13020023
Dutta A, Kumar S, Basu M. A Gated Recurrent Unit Approach to Bitcoin Price Prediction. Journal of Risk and Financial Management. 2020; 13(2):23. https://doi.org/10.3390/jrfm13020023
Chicago/Turabian StyleDutta, Aniruddha, Saket Kumar, and Meheli Basu. 2020. "A Gated Recurrent Unit Approach to Bitcoin Price Prediction" Journal of Risk and Financial Management 13, no. 2: 23. https://doi.org/10.3390/jrfm13020023
APA StyleDutta, A., Kumar, S., & Basu, M. (2020). A Gated Recurrent Unit Approach to Bitcoin Price Prediction. Journal of Risk and Financial Management, 13(2), 23. https://doi.org/10.3390/jrfm13020023




