Regime-Switching Factor Investing with Hidden Markov Models
Abstract
1. Introduction
2. Literature Review
2.1. Factor Investing
2.2. Hidden Markov Models
2.3. Market Regimes
2.4. Regime Classification
3. Model Specification
3.1. Data Source and Processing
3.2. Hidden Markov Model
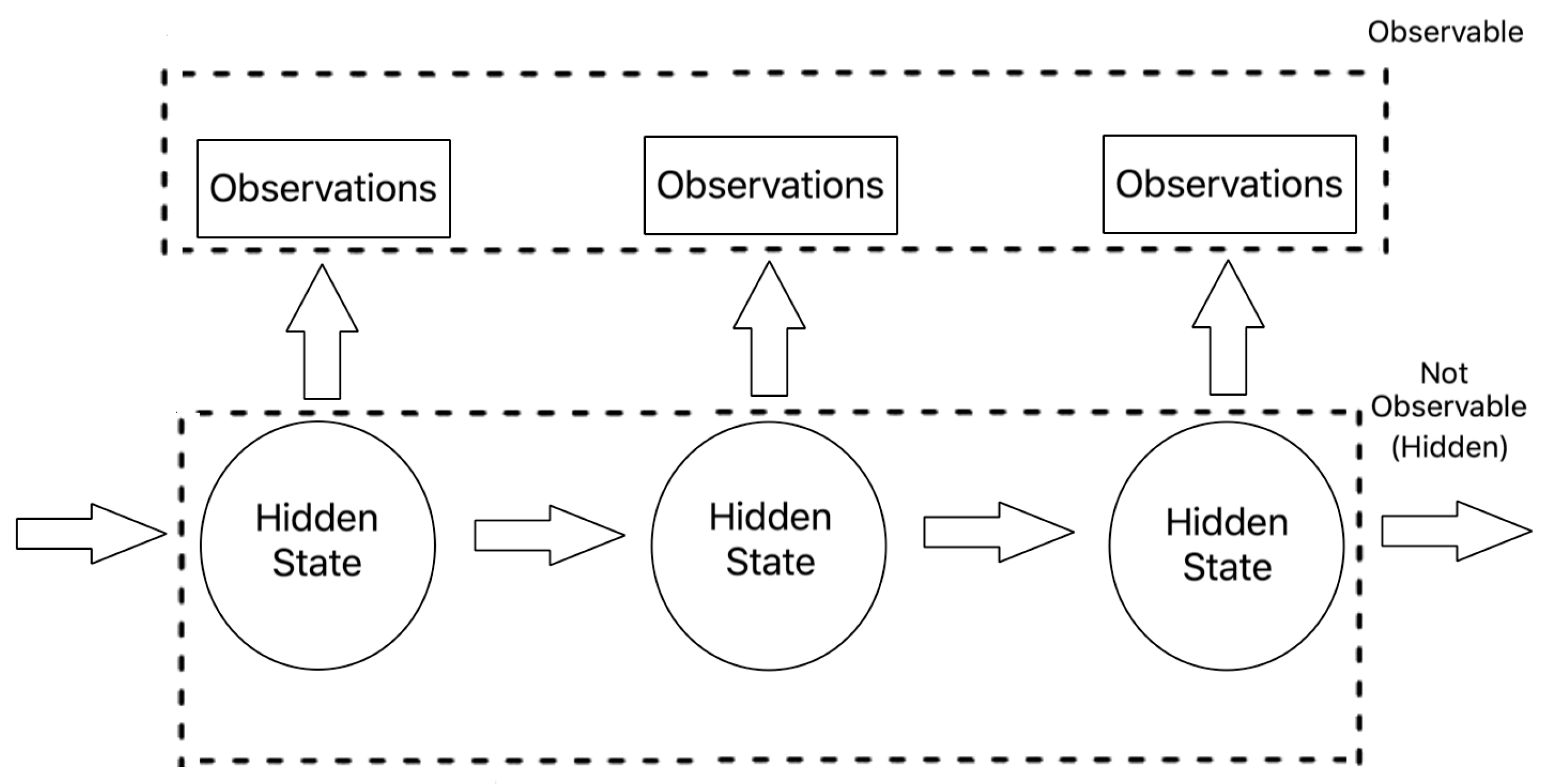
3.2.1. Model Description
3.2.2. Model Application
- Estimate the probability of occurrence for the set of observations
- Determining the most optimal sequence of hidden states for the HMM given the set of observations
- Finding the optimal parameters A, , , and of the HMM.
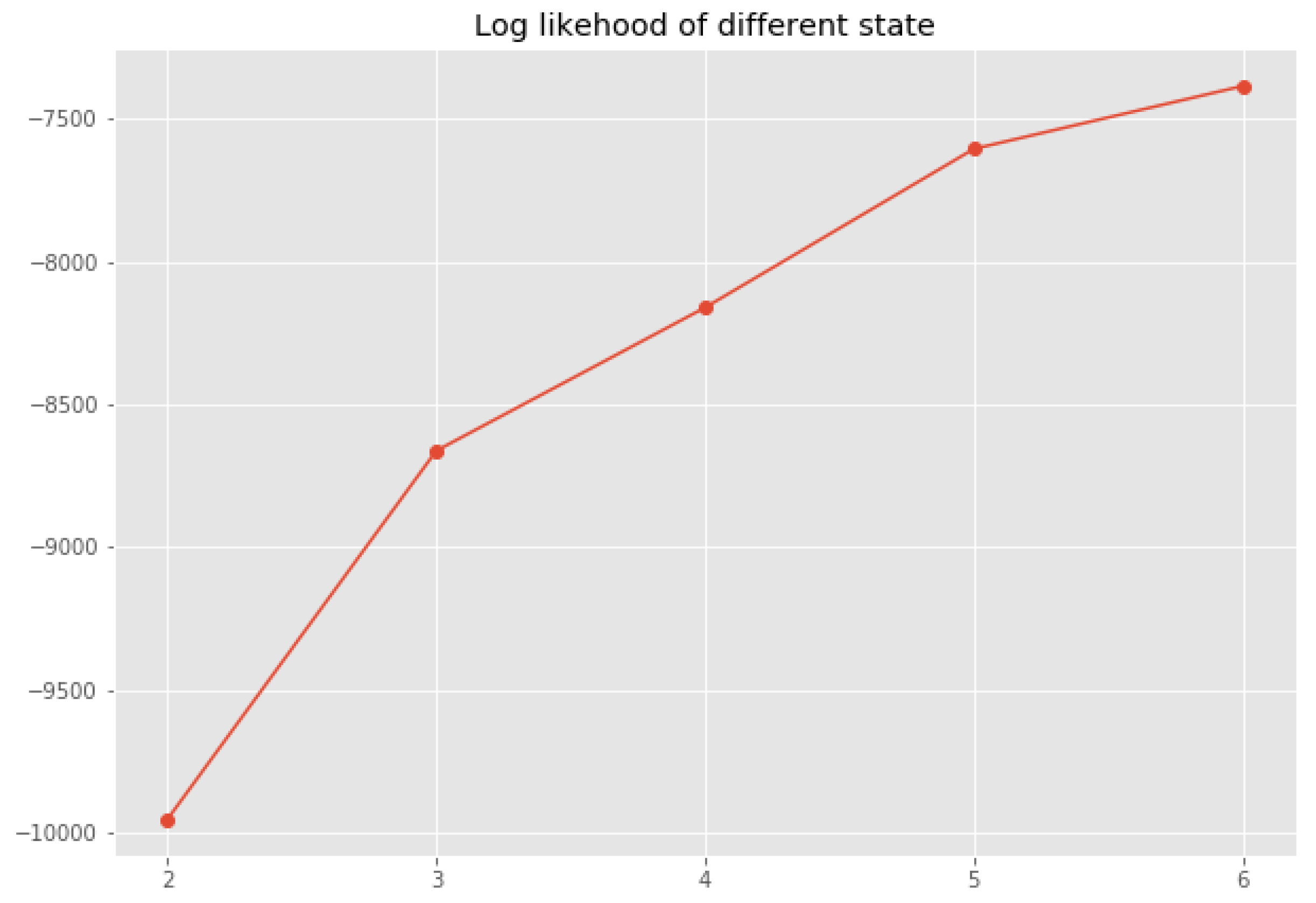
3.2.3. Model Configuration
3.3. Regime Classification
3.4. Factor Models
3.4.1. Fama-French Three-Factor Model
3.4.2. Modified Fama–French Model
3.4.3. Carhart Four-Factor Model
3.4.4. Value
3.4.5. AQR Factor Model
3.4.6. S&P500 ETF
3.5. Trading Model Implementation
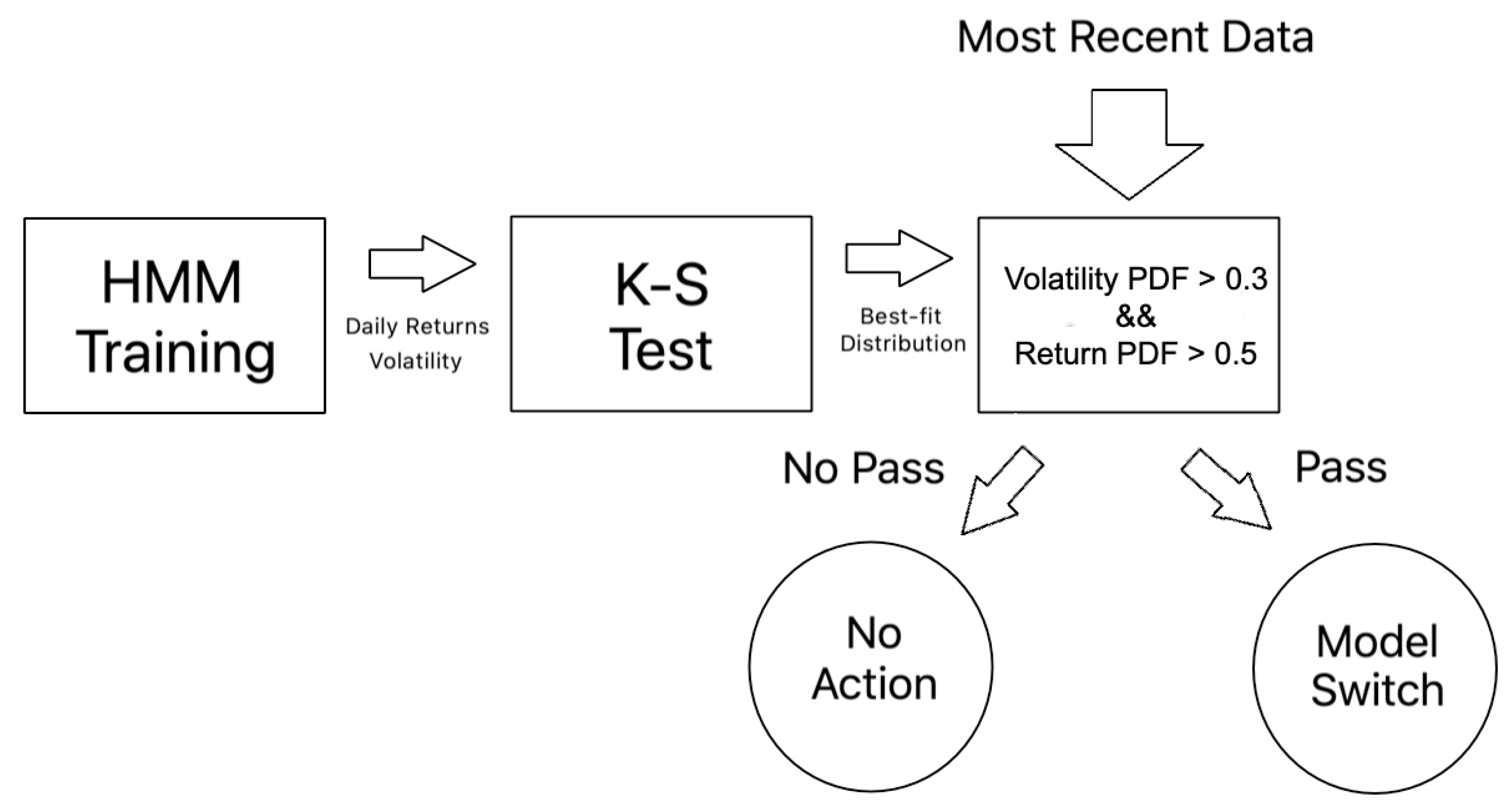
3.5.1. Model Training
3.5.2. Regime Detection
4. Empirical Analysis
4.1. Sharpe Ratio
4.2. Information Ratio
4.3. Treynor Ratio
4.4. Treynor-Mazuy Measurement
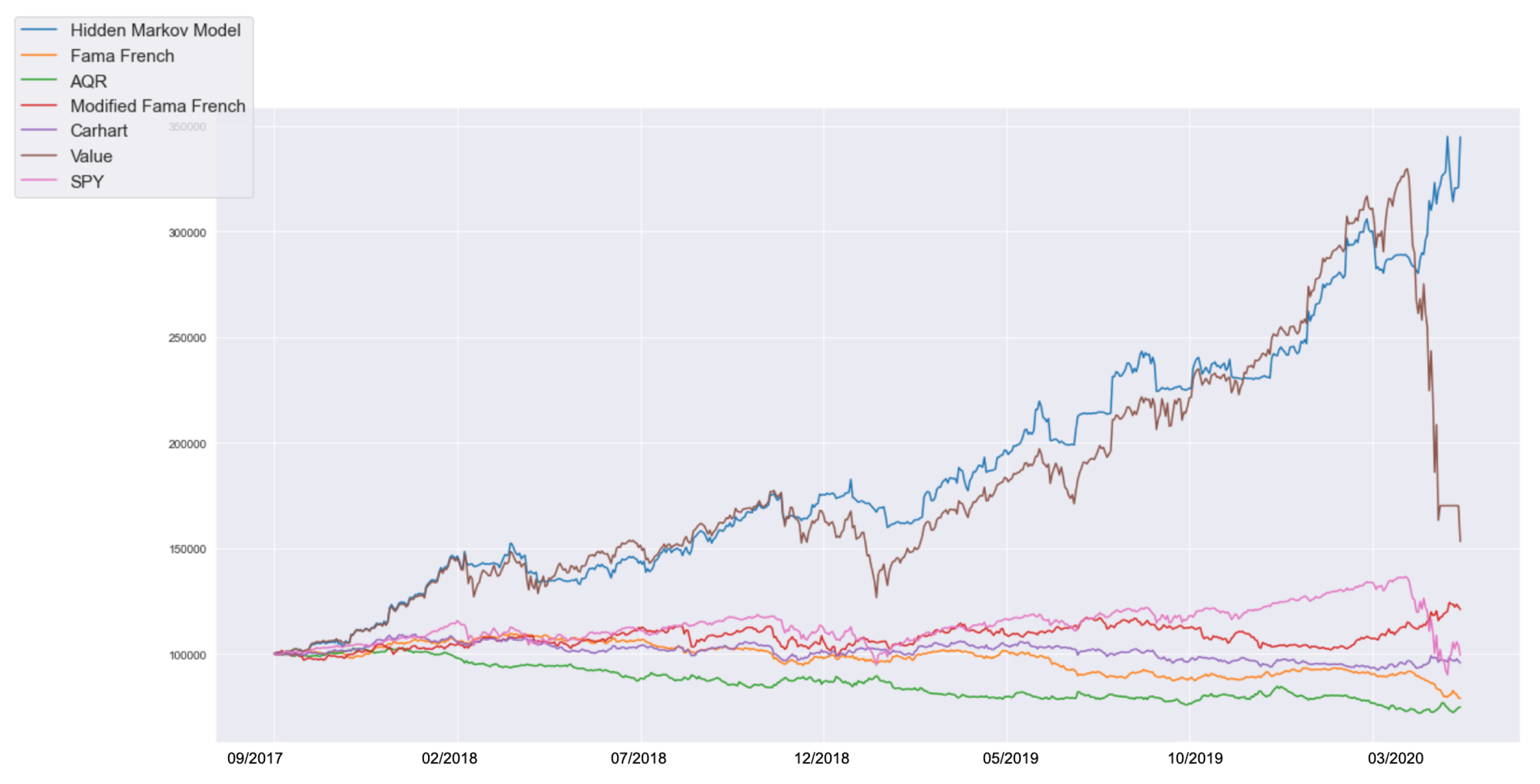
4.5. Evaluations
4.6. Qualitative Considerations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asness, Clifford S., Andrea Frazzini, and Lasse H. Pedersen. 2014. Quality minus junk. SSRN Electronic Journal 24: 34–112. [Google Scholar]
- Ammann, Manuel, and Michael Verhofen. 2006. The Effect of Market Regimes on Style Allocation. Financial Markets and Portfolio Management 20: 309–37. [Google Scholar] [CrossRef]
- Ang, Andrew, Geert Bekaert, and Min Wei. 2008. The Term Structure of Real Rates and Expected Inflation. Journal of Finance 63: 797–849. [Google Scholar] [CrossRef]
- Ang, Andrew, and Geert Bekaert. 2004. How Do Regimes Affect Asset Allocation. Financial Analysts Journal 60: 86–99. [Google Scholar] [CrossRef]
- Asness, Clifford S. 2016. The Siren Song of Factor Timing. Journal of Portfolio Management. [Google Scholar] [CrossRef]
- Baum, Leonard E., and John Alonzo Eagon. 1967. An Inequality with Applications to Statistical Estimation for Probabilistic Functions of a Markov Process and to a Model for Ecology. Bulletin of the American Mathematical Society 73: 360–63. [Google Scholar] [CrossRef]
- Baum, Leonard E., Ted Petrie, George Soules, and Norman Weiss. 1970. A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains. The Annals of Mathemtatical Statistics 41: 164–71. [Google Scholar] [CrossRef]
- Bender, Jennifer, Remy Briand, Dimitris Melas, and Raman Aylur Subramanian. 2013. Foundations of Factor Investing. MSCI Research Insight. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Chen, Jun, and Edward Tsang. 2018. Classification of Normal and Abnormal Regimes in Financial Markets. Algorithms 11: 202. [Google Scholar] [CrossRef]
- Clarke, Roger, Harindra de Silva, and Steven Thorley. 2001. Portfolio Constraints and The Fundamental Law of Active Management. SSRN Electronic Journal 58: 48–66. [Google Scholar] [CrossRef]
- Cont, Rama. 2005. Volatility Clustering in Financial Markets: Empirical Facts and Agent-Based Models. In Long Memory in Economics. Berlin: Springer. [Google Scholar]
- Dapena, José P., Juan Andrés Serur, and Julián R. Siri. 2019. Risk On-Risk Off: A Regime Switching Model for Active Portfolio Management. Buenos Aires: Universidad del CEMA. [Google Scholar]
- Daniel, Kent, and Tobias Moskowitz. 2014. Momentum Crashes. SSRN Electronic Journal 122: 221–47. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 1993. Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2004. The Capital Asset Pricing Model: Theory and Evidence. Journal of Economic Perspectives 18: 25–46. [Google Scholar] [CrossRef]
- Frazzini, Andrea, and Lasse Heje Pedersen. 2014. Betting against Beta. Journal of Financial Economics 111: 1–25. [Google Scholar] [CrossRef]
- Frazzini, Andrea, Ronen Israel, Tobias J. Moskowitz, and Robert Novy-Marx. 2013. A New Core Equity Paradigm. AQR Research White Papers. Greenwich: AQR Capital Management. [Google Scholar]
- Gibbons, Joel Clarke. 2010. The S&P500 Universe: Trend and Volatility Regimes. The Journal of Index Investing 1: 85–91. [Google Scholar]
- Hamilton, James D. 1989. A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Hwang, Soosung, and Mark Salmon. 2001. An Analysis of Performance Measures Using Copulae. Oxford: Butterworth-Heinemann. [Google Scholar]
- Ilmanen, Antti S., Ronen Israel, Tobias J. Moskowitz, Ashwin K. Thapar, and Franklin Wang. 2019. Factor Premia and Factor Timing: A Century of Evidence. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Kim, Chang-Jin, and Charles R. Nelson. 2017. State-Space Models with Regime Switching. Cambridge: MIT Press. [Google Scholar]
- Kim, Eun-Chong, Han-Wook Jeong, and Nak-Young Lee. 2019. Global Asset Allocation Strategy Using a Hidden Markov Model. Journal of Risk and Financial Management 12: 168. [Google Scholar] [CrossRef]
- Kritzman, Mark, Sébastien Page, and David Turkington. 2012. Regime Shifts: Implications for Dynamic Strategies. Financial Analysts Journal 68: 22–39. [Google Scholar] [CrossRef]
- Gales, Mark J. F. 1999. Semi-tied Covariance Matrices for Hidden Markov Models. IEEE Transactions on Speech and Audio Processing 7: 272–81. [Google Scholar] [CrossRef]
- Hassan, Md Rafiul, and Baikunth Nath. 2005. Stock market forecasting using hidden Markov model: A new approach. Paper presented at 5th International Conference on Intelligent Systems Design and Applications, Auburn, WA, USA, December 3–5; pp. 192–196. [Google Scholar]
- Nguyen, Nguyet, and Dung Nguyen. 2015. Hidden Markov Model for Stock Selection. Risks 3: 455–73. [Google Scholar] [CrossRef]
- Paramita, V. Santi. 2015. Testing Treynor-Mazuy Conditional Model in Bull and Bear Market. Society of Interdisciplinary Business Research 4: 208–19. [Google Scholar]
- Rabiner, Lawrence R. 1989. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE 77: 257–86. [Google Scholar] [CrossRef]
- Raffinot, Thomas. 2007. Hidden Markov Models Fundamentals. CS229 Section Notes 1. Available online: http://cs229.stanford.edu/section/cs229-hmm.pdf (accessed on 7 September 2020).
- Ramage, Daniel. 2007. Time-Varying Risk Premiums and Economic Cycles. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Ross, Stephen A. 1976. The Arbitrage Theory of Capital Asset Pricing. Journal of Economic Theory 13: 341–60. [Google Scholar] [CrossRef]
- Sharpe, William F. 1966. Mutual Fund Performance. Journal of Business 34: 119–38. [Google Scholar] [CrossRef]
- Treynor, Jack, and Kay Mazuy. 1966. Can Mutual Funds Outguess the Market? Harvard Business Review 44: 131–6. [Google Scholar]
- Treynor, Jack. 1965. How to Rate Management of Investment Funds. Harvard Business Review 41: 63–75. [Google Scholar]
- Viterbi, Andrew. 1967. Error Bounds for Convolutional Codes and An Asymptotically Optimum Decoding Algorithm. IEEE Transactions on Information Theory 13: 260–69. [Google Scholar] [CrossRef]
- Vo, Huyh Thanh, and Raimond Maurer. 2013. Dynamic Asset Allocation with Regime Shifts and Long Horizon CVaR-Constraints. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Yuan, Yuan, and Mitra Gautam. 2019. Market Regime Identification Using Hidden Markov Models. SSRN Electronic Journal. [Google Scholar] [CrossRef]
| 1. | Open-sourced HMM library https://hmmlearn.readthedocs.io/. |
| 2. | Free algorithmic backtesting and trading tool https://www.quantconnect.com/. |
| 3. | We obtain MKT, SMB, HML, MOM from Ken French’s data library: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html; QMJ data comes from Andrea Frazzin’s library: http://www.econ.yale.edu/~af227/data_library.htm. |


| Regime | Probability |
|---|---|
| 0 | 1.22182739 × |
| 1 | 1.00000000 |
| 2 | 5.05164158 × |
| Source Regime | Destination Regime | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 0 | 9.019 × | 6.472 × | 3.32960344 × |
| 1 | 6.144 × | 9.385 × | 1.91529674 × |
| 2 | 1.085 × | 5.466 × | 8.914 × |
| Regime | Distribution | Average | Average |
|---|---|---|---|
| of Occurrence | Daily Return | Volatility | |
| 0 | 0.4237 | 0.0398 | 3.4739 |
| 1 | 0.4463 | 0.04635 | 0.9438 |
| 2 | 0.13 | −0.066 | 13.63465 |
| S&P500 | Fama-French | Modified | Carhart | Value | AQR | HMM | |
|---|---|---|---|---|---|---|---|
| Three-Factor | Three-factor | Four-Factor | Factor | Factor | |||
| Model | Model | Model | Model | Model | |||
| Sharpe | −0.174 | −1.418 | 0.208 | −0.668 | 0.463 | −1.423 | 2.017 |
| IR | None | −0.481 | 0.249 | −0.668 | 0.989 | −0.53 | 1.64 |
| Treynor | −0.03 | −0.0059 | 0.0003 | −0.015 | 0.02 | 0.123 | 0.264 |
| Treynor- Mazuy | None | −0.3688 | 0.1763 | 0.1548 | −3.687 | 0.1993 | 0.3698 |
| Returns | −0.0068 | −0.2115 | 0.2097 | 0.0442 | 0.5318 | −0.2535 | 2.4491 |
| Max Drawdown | 0.341 | 0.2803 | 0.131 | 0.1557 | 0.5356 | 0.30 | 0.1283 |
| S&P500 | Fama-French | Modified | Carhart | Value | AQR | |
|---|---|---|---|---|---|---|
| Three-Factor | Fama-French | Four-Factor | Factor | Factor | ||
| Model | Model | Model | Model | Model | ||
| Regime 0 | 0.03956 | −0.01687 | 0.00061 | −0.01331 | 0.07997 | −0.01403 |
| Regime 1 | 0.04517 | 0.03162 | 0.01647 | 0.01015 | 0.08538 | −0.03338 |
| Regime 2 | −0.06607 | 0.03127 | 0.03338 | −0.04775 | −0.02835 | −0.01136 |
| S&P500 | Fama-French | Modified | Carhart | Value | AQR | |
|---|---|---|---|---|---|---|
| Three-Factor | Fama-French | Four-Factor | Factor | Factor | ||
| Model | Model | Model | Model | Model | ||
| Regime 0 | 1.13402 | 0.65923 | 0.66564 | 0.81728 | 2.03671 | 0.74407 |
| Regime 1 | 0.65726 | 0.53003 | 0.49889 | 0.62230 | 1.25162 | 0.58465 |
| Regime 2 | 2.63856 | 0.93578 | 0.89436 | 1.13175 | 3.33736 | 0.79118 |
| S&P500 | Fama-French | Modified | Carhart | Value | AQR | |
|---|---|---|---|---|---|---|
| Three-Factor | Fama-French | Four-Factor | Factor | Factor | ||
| Model | Model | Model | Model | Model | ||
| Regime 0 | 0.03488 | −0.02559 | 0.00092 | −0.01629 | 0.03926 | −0.01885 |
| Regime 1 | 0.06872 | 0.05966 | 0.03301 | 0.01631 | 0.06821 | −0.05710 |
| Regime 2 | −0.02504 | 0.03342 | 0.03732 | −0.04219 | −0.00849 | −0.01435 |
| alpha | MKT | SMB | HML | MOM | QMJ | |
|---|---|---|---|---|---|---|
| coef | 0.1723 | 0.1511 | 0.0279 | −0.5879 | −0.1774 | −0.1144 |
| t(coef) | 3.308 | 3.910 | 0.294 | −6.301 | −2.075 | −0.828 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Lin, Y.-H.; Mikhelson, I. Regime-Switching Factor Investing with Hidden Markov Models. J. Risk Financial Manag. 2020, 13, 311. https://doi.org/10.3390/jrfm13120311
Wang M, Lin Y-H, Mikhelson I. Regime-Switching Factor Investing with Hidden Markov Models. Journal of Risk and Financial Management. 2020; 13(12):311. https://doi.org/10.3390/jrfm13120311
Chicago/Turabian StyleWang, Matthew, Yi-Hong Lin, and Ilya Mikhelson. 2020. "Regime-Switching Factor Investing with Hidden Markov Models" Journal of Risk and Financial Management 13, no. 12: 311. https://doi.org/10.3390/jrfm13120311
APA StyleWang, M., Lin, Y.-H., & Mikhelson, I. (2020). Regime-Switching Factor Investing with Hidden Markov Models. Journal of Risk and Financial Management, 13(12), 311. https://doi.org/10.3390/jrfm13120311







