Equity Option Pricing with Systematic and Idiosyncratic Volatility and Jump Risks
Abstract
1. Introduction
2. Equity Option Valuation
2.1. Model Description
2.2. Characteristic Function
2.3. Valuation of the European Index and Equity Options
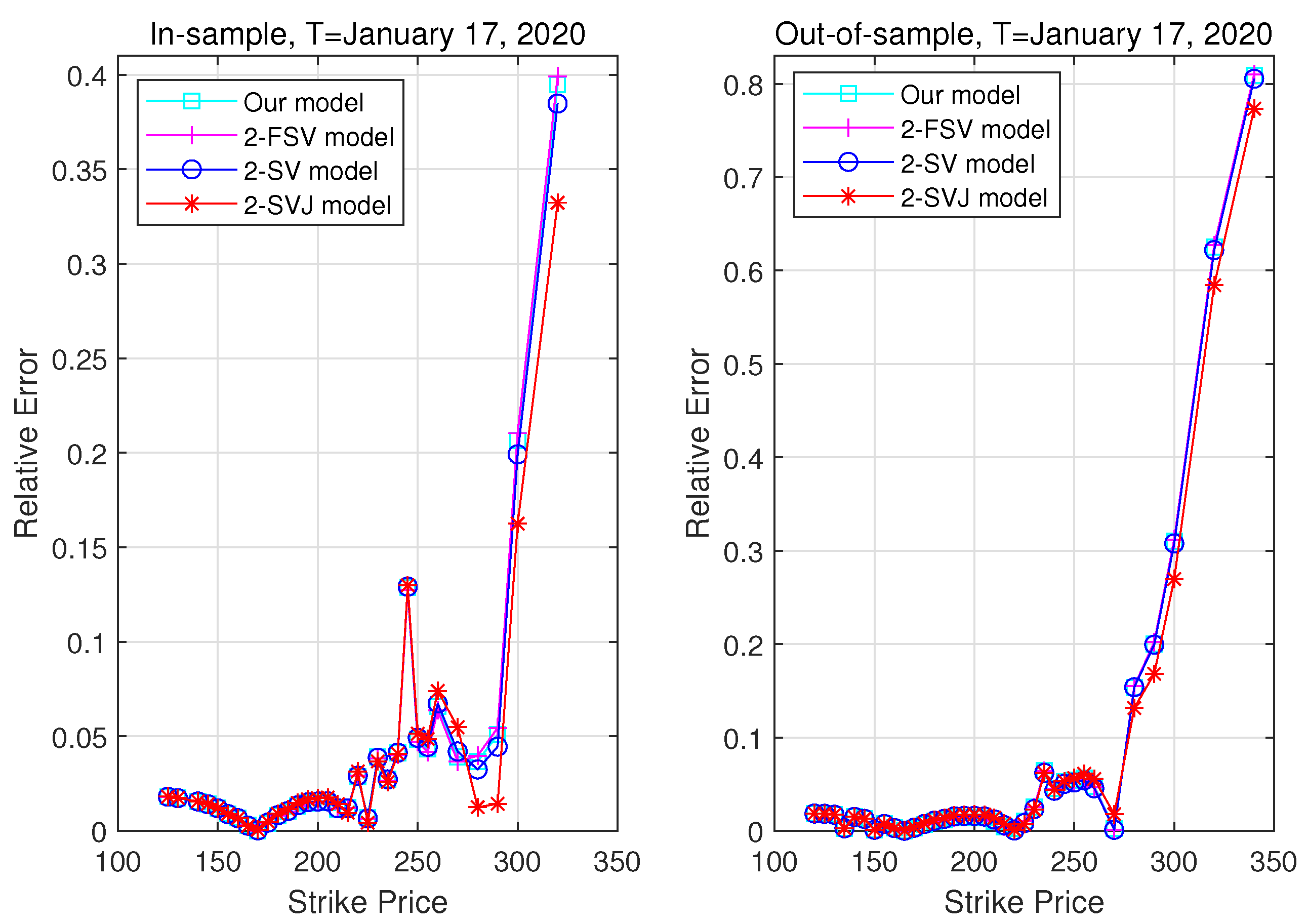
3. Empirical Studies
3.1. Data Description
3.2. Parameter Estimation
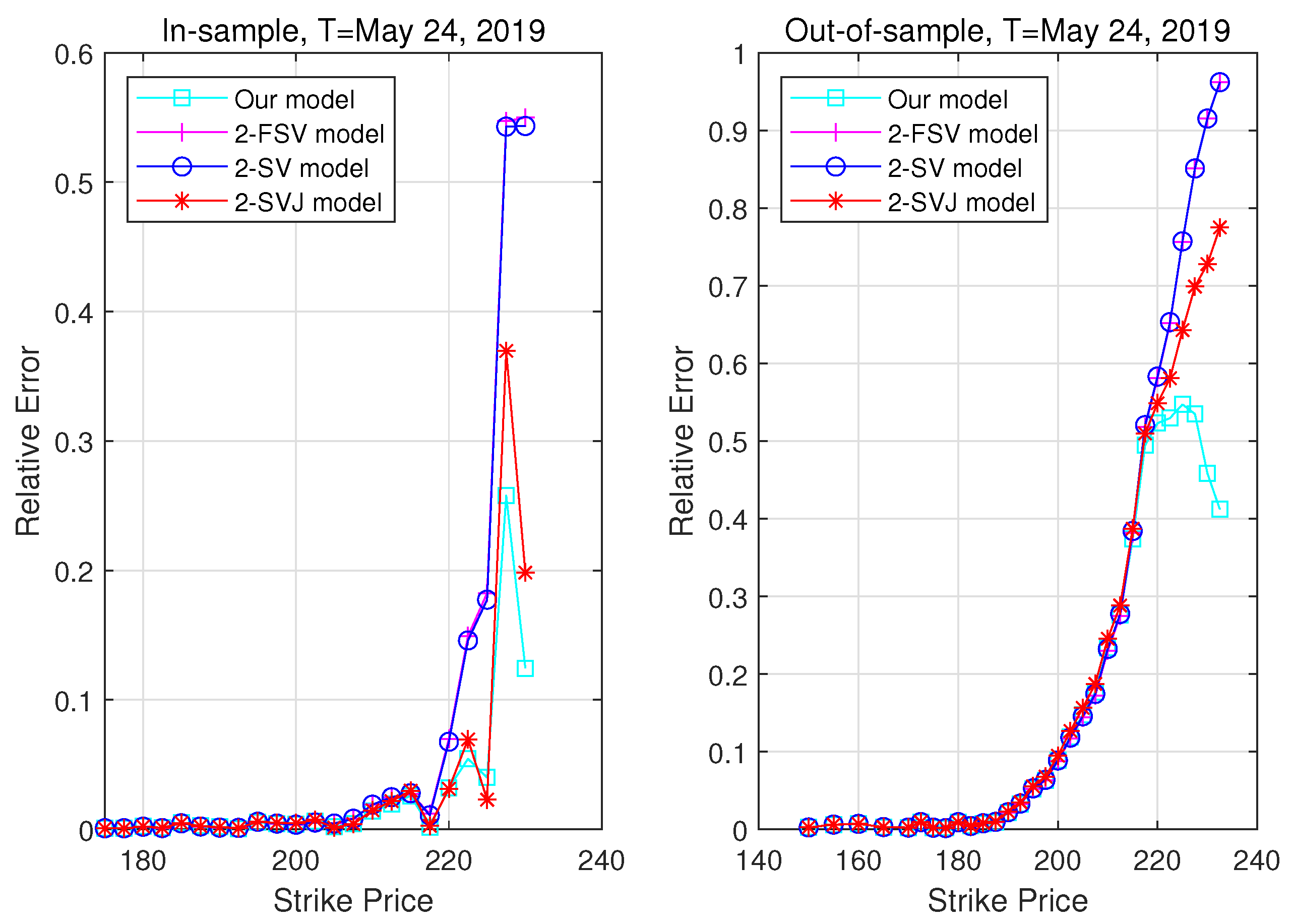
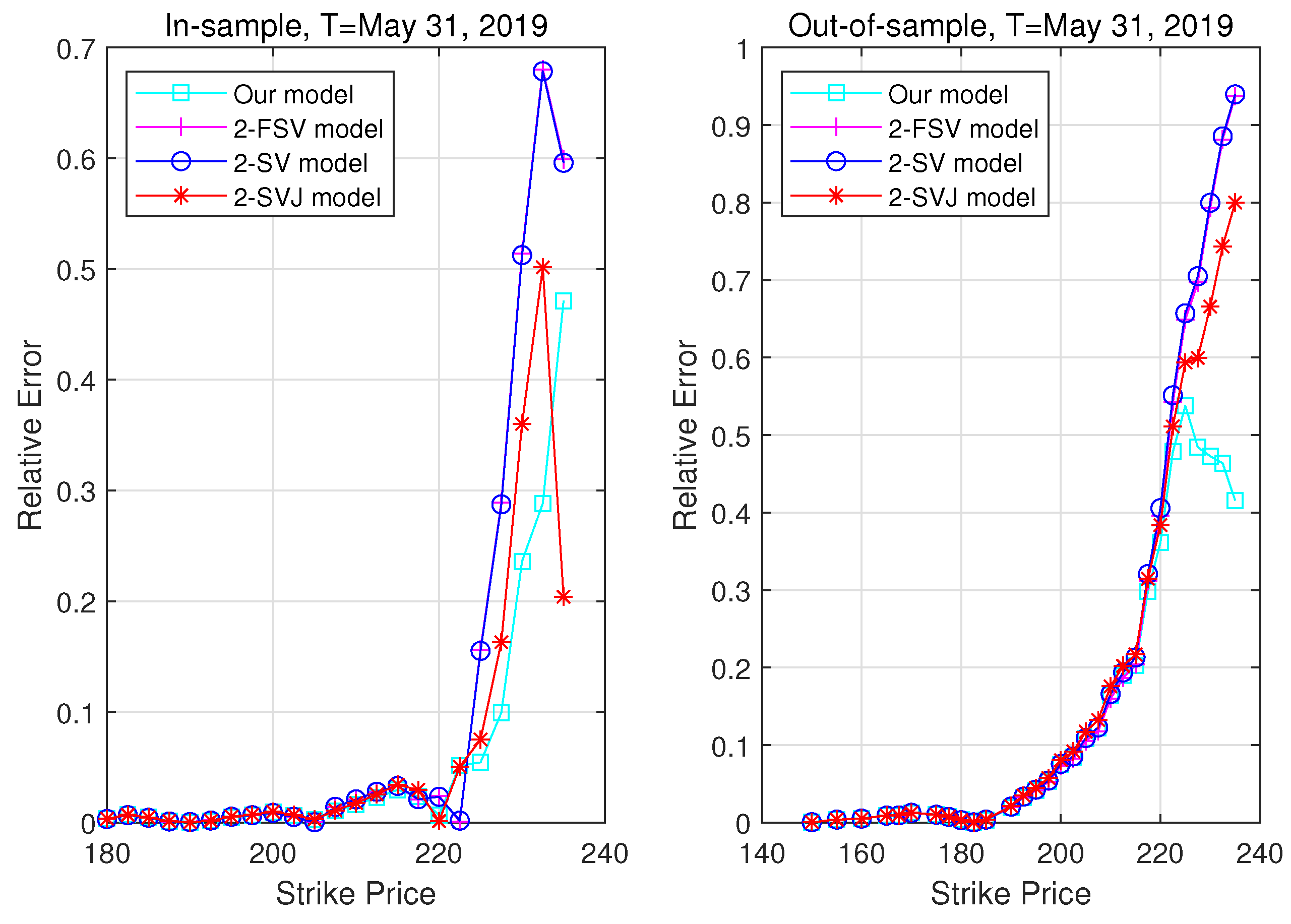
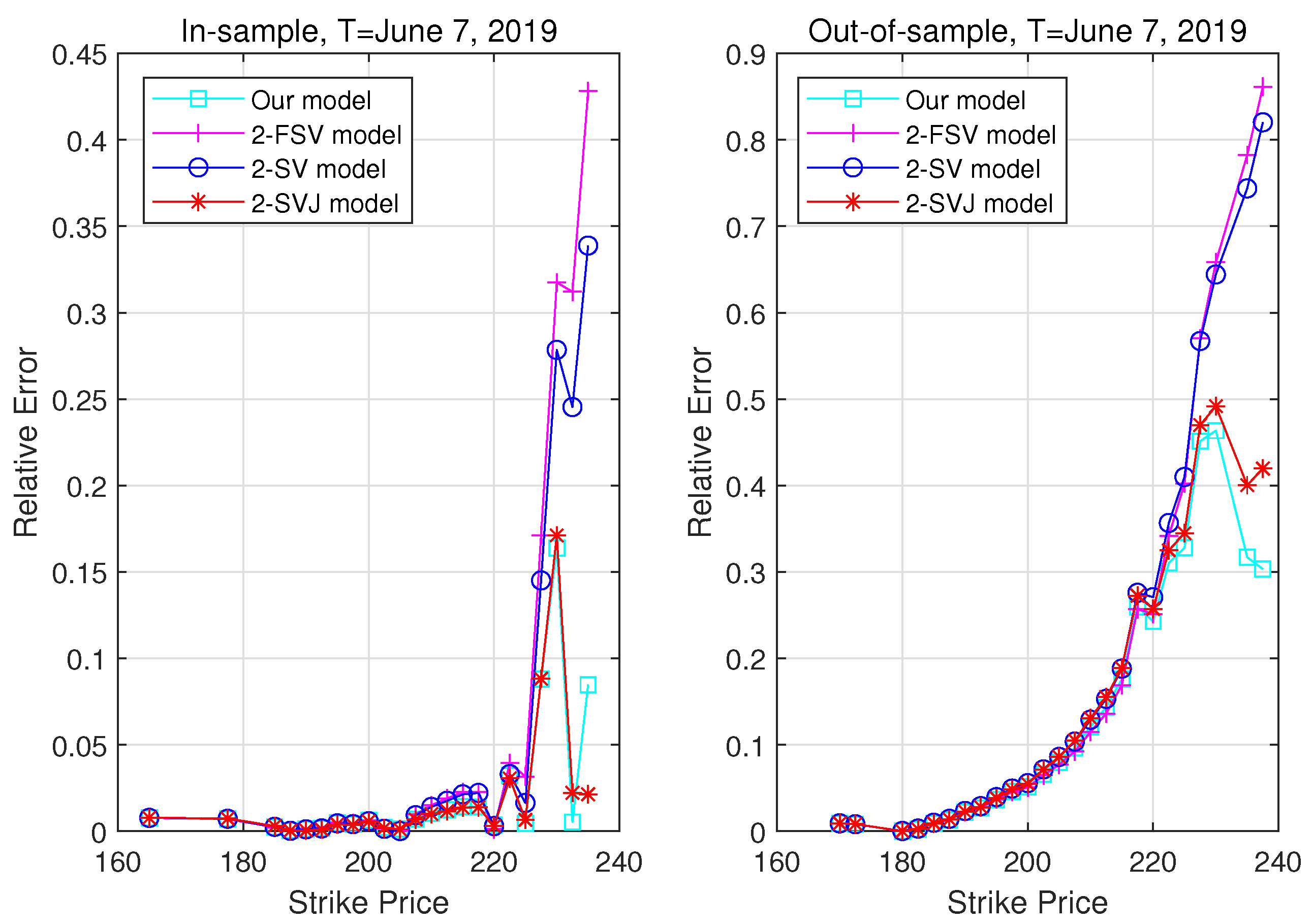
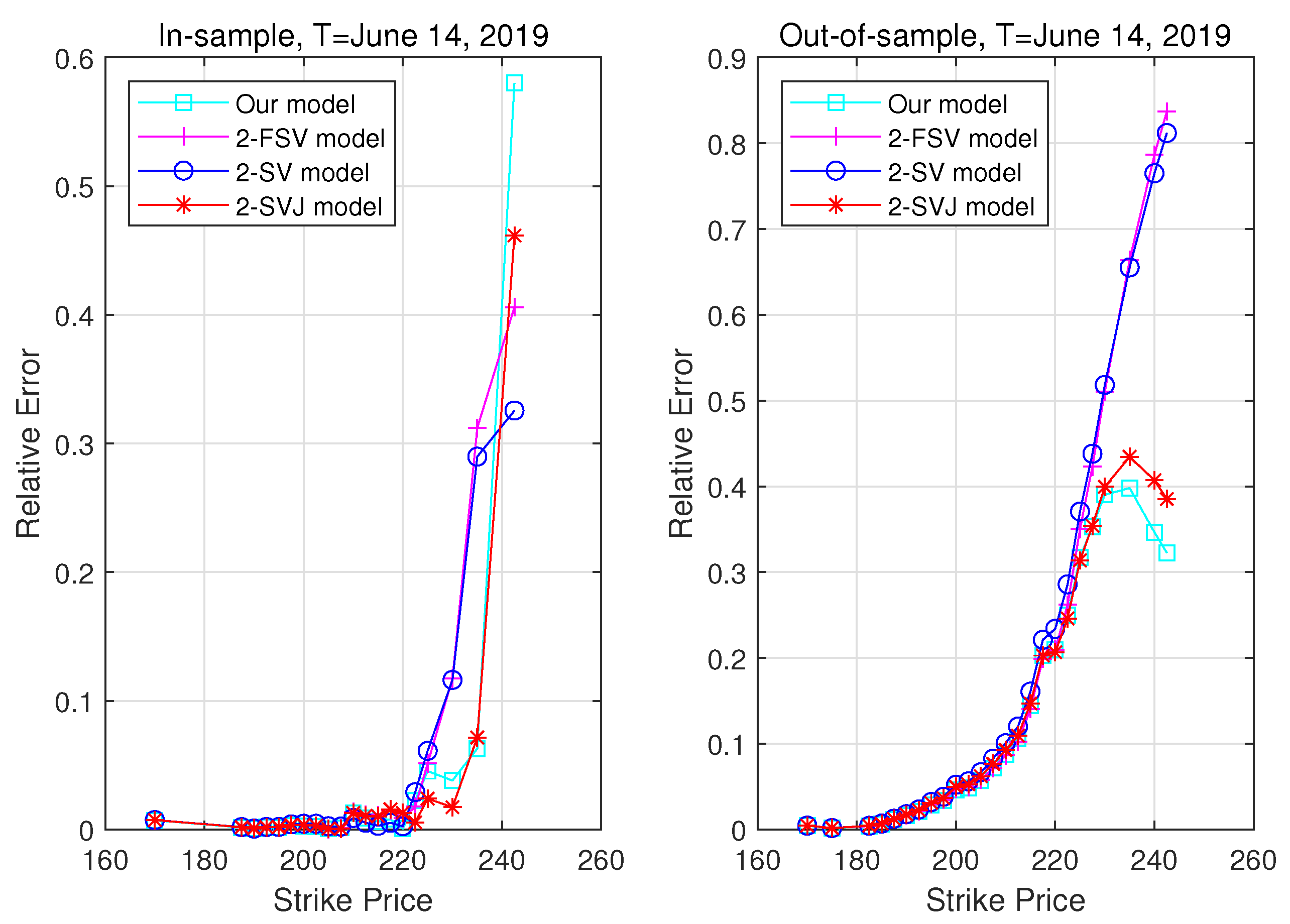
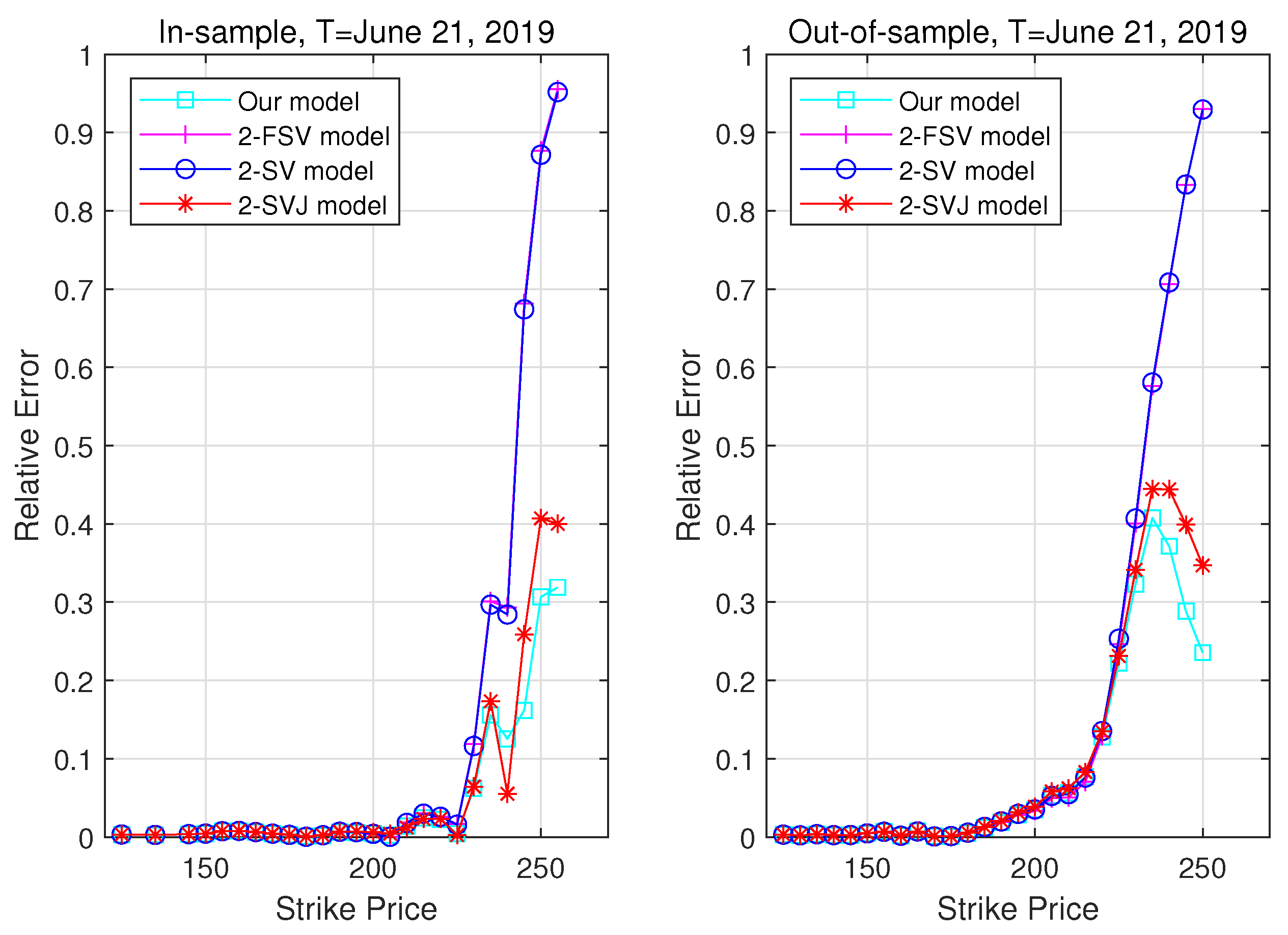
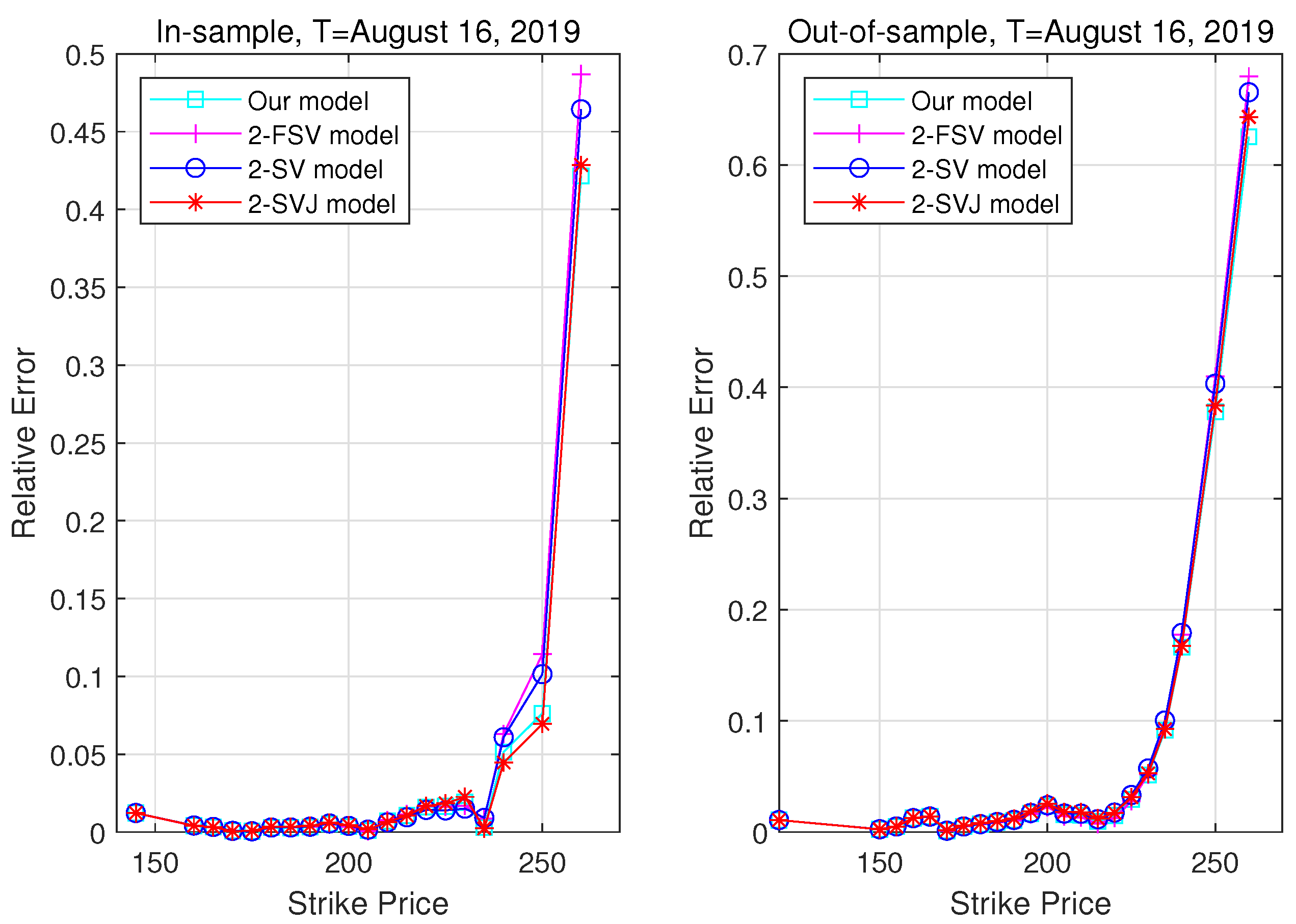
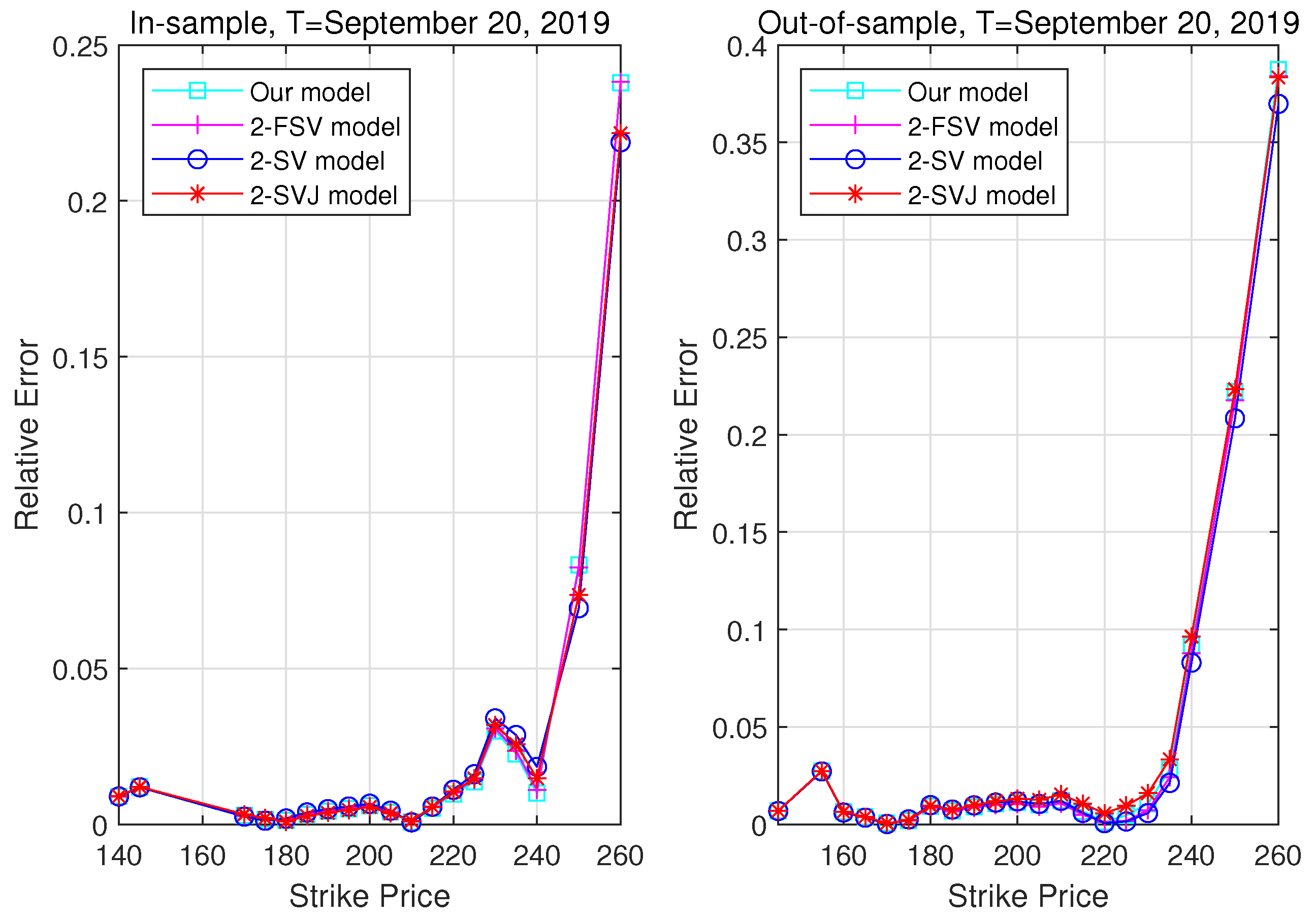
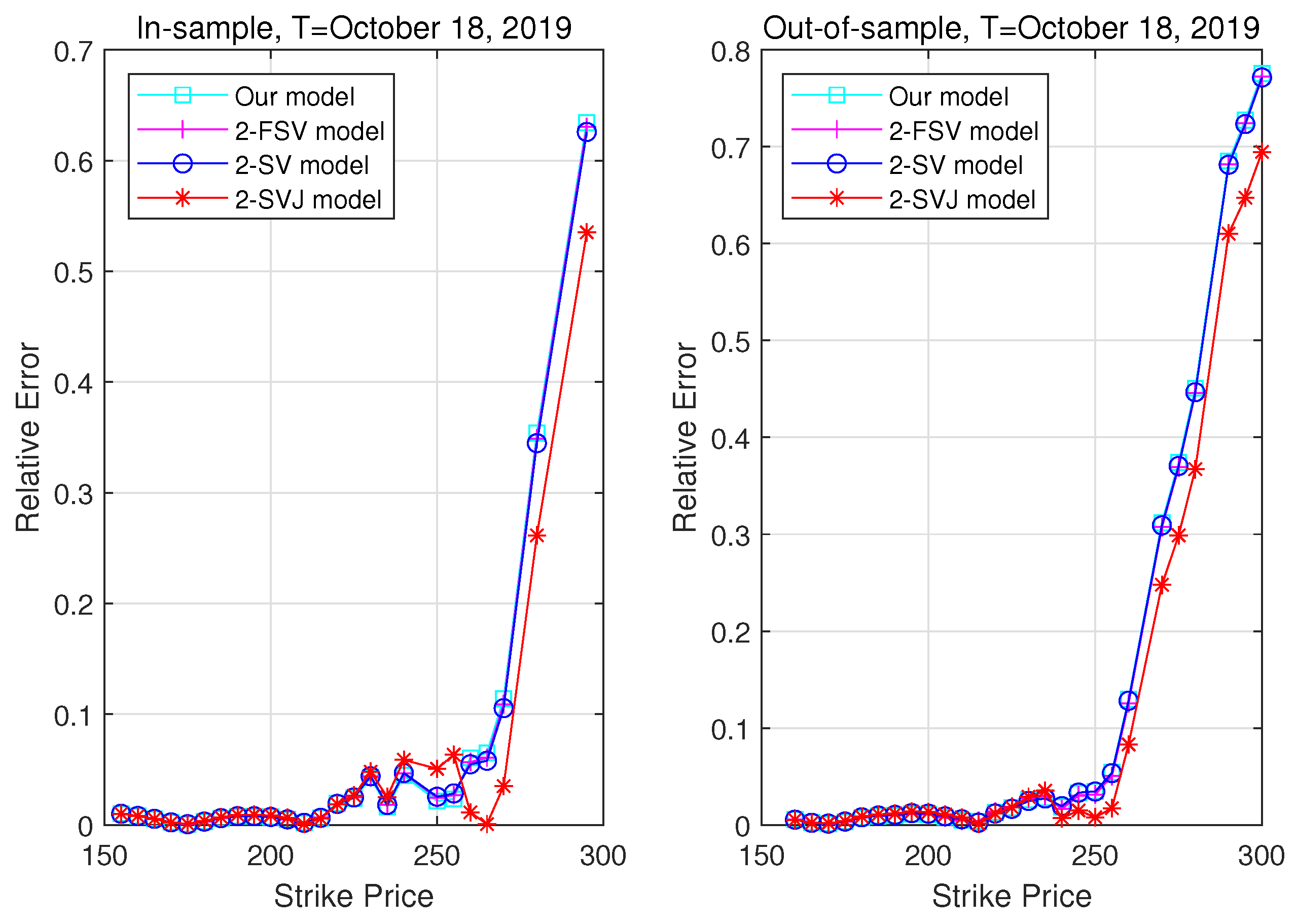
3.3. Pricing Performance
4. Conclusions
Funding
Conflicts of Interest
References
- Andersen, Torben G., Nicola Fusari, and Viktor Todorov. 2015. The risk premia embedded in index options. Journal of Financial Economics 117: 558–84. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 1997. Empirical performance of alternative option pricing models. Journal of Finance 52: 2003–49. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Nikunj Kapadia, and Dilip Madan. 2003. Stock return characteristics, skew laws, and the differential pricing of individual equity options. Review of Financial Studies 16: 101–43. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, and Nikunj Kapadia. 2003a. Delta-hedged gains and the negative market volatility risk premium. Review of Financial Studies 16: 527–66. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, and Nikunj Kapadia. 2003b. Volatility risk premiums embedded in individual equity options: Some new insights. Journal of Derivatives 11: 45–54. [Google Scholar] [CrossRef]
- Bardgett, Chris, Elise Gourier, and Markus Leippold. 2019. Inferring volatility dynamics and risk premia from the S&P 500 and VIX markets. Journal of Financial Economics 131: 593–618. [Google Scholar]
- Bates, David S. 1996. Jumps and stochastic volatility: Exchange rate processes implicit in Deutsche mark options. Review of Financial Studies 9: 69–107. [Google Scholar] [CrossRef]
- Bates, David S. 2000. Post-’87 crash fears in the S&P 500 futures option market. Journal of Econometrics 94: 181–238. [Google Scholar]
- Broadie, Mark, Mikhail Chernov, and Michael Johannes. 2007. Model specification and risk premia: Evidence from futures options. Journal of Finance 62: 1453–90. [Google Scholar] [CrossRef]
- Bégin, Jean-François, Christian Dorion, and Geneviève Gauthier. 2020. Idiosyncratic jump risk matters: Evidence from equity returns and options. Review of Financial Studies 33: 155–211. [Google Scholar] [CrossRef]
- Carr, Peter, and Dilip B. Madan. 2012. Factor models for option pricing. Asia-Pacific Financial Markets 19: 319–29. [Google Scholar] [CrossRef]
- Cheang, Gerald H. L., Carl Chiarella, and Andrew Ziogas. 2013. The representation of American options prices under stochastic volatility and jump-diffusion dynamics. Quantitative Finance 13: 241–53. [Google Scholar] [CrossRef]
- Cheang, Gerald H. L., and Len Patrick Dominic M. Garces. 2019. Representation of exchange option prices under stochastic volatility jump-diffusion dynamics. Quantitative Finance. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Kris Jacobs, and Chayawat Ornthanalai. 2012. Dynamic jump intensities and risk premiums: Evidence from S&P 500 returns and options. Journal of Financial Economics 106: 447–72. [Google Scholar]
- Christoffersen, Peter, Mathieu Fournier, and Kris Jacobs. 2018. The factor structure in equity options. Review of Financial Studies 31: 595–637. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Steven Heston, and Kris Jacobs. 2009. The shape and term structure of the index option smirk: Why multifactor stochastic volatility models work so well. Management Science 55: 1914–32. [Google Scholar] [CrossRef]
- Duffie, Darrell, Jun Pan, and Kenneth Singleton. 2000. Transform analysis and asset pricing for affine jump diffusions. Econometrica 68: 1343–76. [Google Scholar] [CrossRef]
- Eraker, Biørn, Miichael Johannes, and Nicholas Polson. 2003. The Impact of Jumps in Volatility and Returns. Journal of Finance 58: 1269–1300. [Google Scholar] [CrossRef]
- Fouque, Jean-Pierre, and Adam P. Tashman. 2012. Option pricing under a stressed-beta model. Annals of Finance 8: 183–203. [Google Scholar] [CrossRef]
- Fouque, Jean-Pierre, and Eli Kollman. 2011. Calibration of stock betas from skews of implied volatilities. Applied Mathematical Finance 18: 119–37. [Google Scholar] [CrossRef]
- Kapadia, Nishad, and Morad Zekhnini. 2019. Do idiosyncratic jumps matter? Journal of Financial Economics 131: 666–92. [Google Scholar] [CrossRef]
- Kou, Steven G. 2002. A jump-diffusion model for option pricing. Management Science 48: 1086–101. [Google Scholar] [CrossRef]
- Merton, Robert C. 1976. Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics 3: 125–44. [Google Scholar] [CrossRef]
- Wong, Hoi Ying, Edwin Kwan Hung Cheung, and Shiu Fung Wong. 2012. Lévy betas: Static hedging with index futures. Journal of Futures Markets 32: 1034–59. [Google Scholar] [CrossRef]
- Xiao, Xiao, and Chen Zhou. 2018. The decomposition of jump risks in individual stock returns. Journal of Empirical Finance 47: 207–28. [Google Scholar] [CrossRef]
| 1. | In fact, the work of Xiao and Zhou (2018) is a complement to the recent studies that disentangle the four types of risks in equity premiums, such as Bégin et al. (2020), who developed a GARCH-jump model in which an individual firm’s systematic and idiosyncratic risk have both a Gaussian diffusive and a jump component. Their empirical results showed that normal diffusive and jump risks have drastically different effects on the expected return of individual stocks by using 20 years of returns and options on the S&P 500 and 260 stocks. |
| 2. | One can refer to Assumption 2.1 of Cheang et al. (2013) and Cheang and Garces (2019) for a more detailed explanation. |
| 3. | Obviously, our proposed model for the dynamics of the market factor and individual equity prices is an extension of Christoffersen et al. (2018). In fact, our model also can be regarded as a further generalization of Cheang et al. (2013) and Cheang and Garces (2019) by taking into account the factor structure. |
| 4. | One can refer to the Assumption 2.1 of Cheang et al. (2013) and Cheang and Garces (2019) for a more detailed explanation. |
| 5. | The relative error is defined by , where and denote the theoretical model option prices and the real market prices, respectively. |

| Parameters | Our | 2-FSV | 2-SV | 2-SVJ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPX | AAPL | SPX | AAPL | AAPL | AAPL | |||||||
| / | 0.0133 | 0.0119 | 0.0239 | 0.0181 | ||||||||
| (0.0000) | (0.0000) | (0.0002) | (0.0001) | |||||||||
| / | 0.0470 | 0.0514 | 0.0197 | 0.0176 | ||||||||
| (0.0000) | (0.0000) | (0.0002) | (0.0002) | |||||||||
| / | 0.2496 | 0.2929 | 0.3489 | 0.4064 | ||||||||
| (0.0212) | (0.0148) | (0.0118) | (0.0311) | |||||||||
| / | 0.2454 | 0.1504 | 0.4131 | 0.4108 | ||||||||
| (0.0288) | (0.0797) | (0.0729) | (0.0171) | |||||||||
| / | 0.2820 | 0.3066 | 0.3314 | 0.2817 | ||||||||
| (0.0181) | (0.0317) | (0.0534) | (0.0348) | |||||||||
| / | 0.2303 | 0.3683 | 0.2447 | 0.3415 | ||||||||
| (0.0190) | (0.0590) | (0.0365) | (0.0423) | |||||||||
| / | 0.3472 | 0.3932 | 0.1615 | 0.1898 | ||||||||
| (0.0127) | (0.0137) | (0.0081) | (0.0106) | |||||||||
| / | 0.1496 | 0.1640 | 0.2206 | 0.1970 | ||||||||
| (0.0056) | (0.0135) | (0.0386) | (0.0059) | |||||||||
| 0.0450 | ||||||||||||
| (0.0017) | ||||||||||||
| 0.3413 | 0.3065 | |||||||||||
| (0.2463) | (0.1194) | |||||||||||
| 0.1657 | ||||||||||||
| (0.0599) | ||||||||||||
| 0.0889 | 0.0333 | |||||||||||
| (0.0391) | (0.0042) | |||||||||||
| 0.0850 | ||||||||||||
| (0.0113) | ||||||||||||
| 0.0679 | 0.0534 | |||||||||||
| (0.0078) | (0.0013) | |||||||||||
| 0.3891 | 0.2457 | |||||||||||
| (0.0381) | (0.0983) | |||||||||||
| 0.8429 | ||||||||||||
| (0.8091) | ||||||||||||
| / | −0.9290 | −0.8498 | −0.9222 | −0.7445 | ||||||||
| (0.0063) | (0.0080) | (0.0096) | (0.0297) | |||||||||
| / | −0.9926 | −0.8938 | −0.7673 | −0.7817 | ||||||||
| (0.0001) | (0.0469) | (0.1632) | (0.0549) | |||||||||
| RMSE | Our | 2-FSV | 2-SV | 2-SVJ | Improvement Rate | ||
|---|---|---|---|---|---|---|---|
| Maturity | Our vs. 2-FSV | Our vs. 2-SV | Our vs. 2-SVJ | ||||
| 24 May 2019 | 0.2573 | 0.2574 | 0.2596 | 0.2707 | 0.0373% | 0.8803% | 4.9568% |
| 31 May 2019 | 0.2507 | 0.2508 | 0.2564 | 0.2652 | 0.0392% | 2.2499% | 5.4846% |
| 7 June 2019 | 0.2343 | 0.2347 | 0.2527 | 0.2474 | 0.1764% | 7.2947% | 5.3044% |
| 14 June 2019 | 0.1992 | 0.2041 | 0.2261 | 0.2099 | 2.4278% | 11.9155% | 5.0858% |
| 21 June 2019 | 0.1824 | 0.1827 | 0.1873 | 0.1916 | 0.1399% | 2.5963% | 4.7934% |
| 19 July 2019 | 0.3256 | 0.3301 | 0.3326 | 0.3383 | 1.3434% | 2.0948% | 3.7368% |
| 16 August 2019 | 0.2856 | 0.2835 | 0.2879 | 0.2922 | −0.7573% | 0.7946% | 2.2384% |
| 20 September 2019 | 0.3177 | 0.3159 | 0.3162 | 0.3222 | −0.5932% | -0.4851% | 1.4002% |
| 18 October 2019 | 0.1185 | 0.1180 | 0.1215 | 0.1272 | −0.4458% | 2.4886% | 6.8593% |
| 17 January 2020 | 0.4882 | 0.4882 | 0.4893 | 0.4943 | −0.0071% | 0.2182% | 1.2201% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z. Equity Option Pricing with Systematic and Idiosyncratic Volatility and Jump Risks. J. Risk Financial Manag. 2020, 13, 16. https://doi.org/10.3390/jrfm13010016
Li Z. Equity Option Pricing with Systematic and Idiosyncratic Volatility and Jump Risks. Journal of Risk and Financial Management. 2020; 13(1):16. https://doi.org/10.3390/jrfm13010016
Chicago/Turabian StyleLi, Zhe. 2020. "Equity Option Pricing with Systematic and Idiosyncratic Volatility and Jump Risks" Journal of Risk and Financial Management 13, no. 1: 16. https://doi.org/10.3390/jrfm13010016
APA StyleLi, Z. (2020). Equity Option Pricing with Systematic and Idiosyncratic Volatility and Jump Risks. Journal of Risk and Financial Management, 13(1), 16. https://doi.org/10.3390/jrfm13010016





