Abstract
Machine learning research has gained momentum—also in finance. Consequently, initial machine-learning-based statistical arbitrage strategies have emerged in the U.S. equities markets in the academic literature, see e.g., Takeuchi and Lee (2013); Moritz and Zimmermann (2014); Krauss et al. (2017). With our paper, we pose the question how such a statistical arbitrage approach would fare in the cryptocurrency space on minute-binned data. Specifically, we train a random forest on lagged returns of 40 cryptocurrency coins, with the objective to predict whether a coin outperforms the cross-sectional median of all 40 coins over the subsequent 120 min. We buy the coins with the top-3 predictions and short-sell the coins with the flop-3 predictions, only to reverse the positions after 120 min. During the out-of-sample period of our backtest, ranging from 18 June 2018 to 17 September 2018, and after more than 100,000 trades, we find statistically and economically significant returns of 7.1 bps per day, after transaction costs of 15 bps per half-turn. While this finding poses a challenge to the semi-strong from of market efficiency, we critically discuss it in light of limits to arbitrage, focusing on total volume constraints of the presented intraday-strategy.
1. Introduction
The cryptocurrency markets are a phenomenon. During the year of 2017, Bitcoin has reached a total market capitalization of more than USD 300 bn—next to more than one thousand smaller cryptoassets with less significant capitalization (coinmarketcap.com 2018). Despite these heights, the market has remained fairly unregulated by governmental institutions (Dyhrberg 2016). We hypothesize that this unique, early-stage environment may exhibit pricing inefficiencies that can potentially be detected and exploited by statistical arbitrage strategies. So far, only few academic studies have touched upon this question, and most of them only focus on a few selected cryptocurrencies.
One of the first works addressing this question is Shah and Zhang (2014). Specifically, the authors aim for predicting price changes of Bitcoin during a six month period in 2014 with a Bayesian regression model. The results are astonishing, with a return of 89 percent and a Sharpe ratio of 4.10 during a period of merely 50 trading days. However, no transaction costs are taken into account, perfect liquidity is assumed, and only one cryptocurrency is considered. Utilizing some of the ideas proposed by Shah and Zhang (2014), Madan et al. (2015) deploy several classification models to predict the sign of Bitcoin price changes, leveraging information on prices, transaction volume, and data about the underlying blockchain. A binomial generalized linear model and a random forest perform exceptionally well with percent and percent accuracy for the daily sign, respectively. However, the authors note that these results may very well be due to, in general, rising long-term prices in the market—a naive buy-and-hold strategy would have achieved similar results in ever-rising crypto markets at that time. Lintilhac and Tourin (2017) develop a pairs trading strategy for Bitcoin, following ideas of Tourin and Yan (2013), and other representatives of the stochastic control approach—for an overview see Krauss (2017). Balcilar et al. (2017) find that volume can help in predicting returns, based on a Granger-causal relationship between these two variables. Another innovative idea for constructing explanatory variables is to include social signals. Garcia and Schweitzer (2015) build a vector autoregressive (VAR) model to predict the sign of future returns of Bitcoin on a daily basis. The model is provided with market information, such as returns, transaction volumes, as well as social signals. These signals include relative search popularity based on Google trends data, the volume of tweets containing the term “bitcoin”, and the emotional valence and sentiment expressed in these tweets1. Daily returns above percent and a Sharpe ratio of over 1.75, prior to transaction costs, are generated. Up to transaction costs of 25 bps, the results remain profitable. Also related to social signals and the “fear of missing out” (FOMO) of uniformed investors is the recent work by Baur and Dimpfl (2018). The authors analyze asymmetric volatility effects for 20 cryptocurrencies and find, as opposed to equities markets, that positive shocks lead to a stronger increase of volatility compared to negative shocks. In a similar spirit, Koutmos (2018) observes an increase in the frequency of return and volatility spillovers in recent times, especially during major news events and oftentimes driven by Bitcoin. Beneki et al. (2019) dive deeper into this topic and test for volatility spillovers and hedging abilities between Bitcoin and Ethereum using impulse response analysis and a multivariate BEKK-GARCH model. In their study, the authors find a significant reduction of the diversification potential due to a delayed positive response and large changes in time-varying correlation among the two cryptocurrencies. Colianni et al. (2015) explore the predictive information potentially comprised in Twitter data. With the use of text-processing, the authors analyze the negativity, positivity, and neutrality of words contained in tweets relating to Bitcoin. Based on these data, features are generated. These features are processed with several classification models that manage to accomplish astonishingly high accuracy values when predicting the hour-to-hour and day-to-day sign change of Bitcoin. Instead of utilizing Twitter data, Kim et al. (2016) base their model on sentiment expressed in user forums relating to cryptocurrencies. The authors’ framework consists of three steps. First, they crawl text data from the relevant forums where participants express opinions about the coin. Second, a sentiment for each comment is derived with the VADER algorithm2. Third, an averaged one-dependence-estimator is applied as a predictive model for future price fluctuations. With a simple trading strategy, profits of over 35 percent are accumulated. As of the day of writing, very few studies have introduced deep learning to predictive tasks in the cryptocurrency market. McNally et al. (2018) investigate the performance of state-of-the-art deep learning models, such as a long short-term memory (LSTM) network, in predicting future price changes of Bitcoin. Using a rolling window of 100 days of input data, this model achieves a predictive accuracy of percent in forecasting the price change of the next day. Jiang and Liang (2017) follow a different approach based on deep reinforcement learning. Recently, Ha and Moon (2018) use genetic programming to detect profitable technical trading patterns for cryptocurrencies, and find that their system performs better than a buy-and-hold strategy.
However, to our knowledge, none of these studies have systematically transferred a well-established statistical arbitrage approach from more mature markets to the cryptocurrency space. With the present paper, we aim to fill this void and make the following contributions to the literature:
- Development of an advanced, machine-learning-based statistical arbitrage approach for the cryptocurrency space: we build our approach on the ideas of Fischer and Krauss (2018); Huck (2009, 2010); Krauss et al. (2017); Moritz and Zimmermann (2014); Takeuchi and Lee (2013), who have developed similar methods for U.S. cash equities, but on much lower frequencies (days to months). With the present manuscript, we successfully show that relative-value arbitrage opportunities exist in this young and aspiring market, given that a random forest is able to produce daily returns of 7.1 bps after transaction costs.
- Consideration of microstructural effects: advancing to higher frequencies, e.g., minute-binned data, brings along substantial challenges. First, trading volume needs to be taken into account. In cash equities, many strategies are backtested on the closing price, which captures 7 percent of daily liquidity for NYSE listed stocks—see Intercontinental Exchange (2018). In stark contrast, liquidity needs to be carefully assessed for every minute bar in the cryptocurrency space, especially in case of smaller coins. We incorporate this effect in our study and only execute trades in case liquidity is present. Second, micro-structural effects, and especially the bid-ask bounce, need to be considered. We therefore introduce a lag between the price on which the prediction is generated, and the subsequent price on which execution is taking place. Hence, we eliminate the bid-ask bounce see, e.g., (Gatev et al. 2006) and we render the strategy realistic in the digital age, given that there is sufficient time for signal generation, order routing, and order execution.
- Shining light into the black box: machine learning models often have the downside of being intransparent and opaque. Hence, we analyze feature importances, and we compare the random forest to the transparent logistic regression. We find that both methods capture short-term characteristics in the data, with past returns over the past 60 min contributing most when explaining future returns over the subsequent 120 min.
2. Data and Software
2.1. Data
In this paper, we use minute-binned price and volume data from 5 January 2018 to 7 September 2018, collected from www.cryptocompare.com via their official application programming interface (cryptocompare.com 2018). For each minute, we collect Open, High, Low, Close, , , and Timestamp data. Open, High, Low, and Close denote the first, highest, lowest, and last price paid for a coin c in minute t, respectively. and quantify the volume of coins being traded during that period of time and the equivalent value in USD. Timestamp is the UNIX-timestamp, i.e., is the number of seconds that have passed since 1 January 1970 (IEEE and The Open Group 2018).
The initial collection of coins and possible exchanges consist of the 100 coins with the highest market capitalization according to coinmarketcap.com (2018) and all 78 exchanges available with respect to the API, both as of 27 December 2017. To this large database, we apply several filters, ensuring minimum liquidity requirements and data quality, and rigorously drop many of the coin-exchange combinations. Going forward, we work with 40 coins and the data from their most liquid exchange—the combinations are listed in Appendix A.
2.2. Software
The code for this study is written in Python 3.5 (Python Software Foundation 2016). It involves the preprocessing and formatting of the data, the training of the models and the backtesting engine, as well as the evaluation of the performance, i.e., the calculation of risk and return metrics. Data preparation mostly relies on the packages numpy (van der Walt et al. 2011) and pandas (McKinney 2010), which are powerful tools for handling large amounts of data. Furthermore, the package sci-kit learn (Pedregosa et al. 2011) is used for the random forest and logistic regression model and the packages SciPy (Jones et al. 2014) and Empyrical (Quantopian Inc. 2016) are deployed for the calculation of the statistical properties and performance analysis of the results.
3. Methodology
Following Krauss et al. (2017), the methodology of this paper consists of four steps. First, the entire data set is split into a training set and a trading set. Second, the features (explanatory variables) and targets (dependent variables) are created. Third, a random forest, and a simpler logistic regression model are trained in the training period (in-sample data). Fourth, with each trained model, out-of-sample predictions are made on the respective trading set to test the effectiveness of the model and its trading performance. The rest of this section follows the outlined structure.
3.1. Generation of Training and Trading Set
Of the data available for each coin, the first two thirds of the time-series are used as training data (in-sample) while the remaining third makes up the trading period (out-of-sample). The training and trading sets are strictly non-overlapping to ensure that no look-ahead bias is introduced. As minute-binned data since the beginning of January 2018 up to the beginning of September 2018 are used, one complete time-series consists of close to data points.3 Taking into account the coins, this results in approximately million training examples and million trading examples for the models.
3.2. Feature and Target Generation
3.2.1. Features—Multiperiod Returns
Loosely following the logic of Takeuchi and Lee (2013), each feature sequence (input) is generated in the following way: Let denote the price process of coin c, with , and the simple return for a coin c over the last m periods, i.e.,
where the periods are in minutes. Each feature sequence then consists of the set with . Hence, the model first puts emphasis on the returns of the last 120 min and then switches to a less granular resolution to focus on the returns of the last , with , points in time. With this approach, we follow the logic of Takeuchi and Lee (2013) and transfer it to minute-binned data with the aim of forecasting the return of the next two hours or 120 min, while using information of the returns of the last 24 h.
3.2.2. Targets
As in Krauss et al. (2017), a binary response variable is introduced. All target values of the cross-section are classified as class “1” if the return over the 120 min after the predict time t (including a one minute gap), i.e., , is at or above the cross-sectional median of all coins, and “0” otherwise. Therefore, instead of predicting the actual value of the future 120 min returns, the probability of the coin outperforming the cross-sectional median is predicted. This approach is promising, as classification problems have found to work better than regression problems in the context of financial market predictions (Enke and Thawornwong 2005; Leung et al. 2000).
3.3. Models
3.3.1. Logistic regression
As a baseline model, we include a transparent (we can interpret the regression coefficients to better understand what leads to a prediction) logistic regression (LR). The model’s name “logistic regression” stems from the logistic function which is used to model the binary response variable. As our classification problem comprises two classes (hence, binary), i.e., “the coin outperforms the cross-sectional median of all coins over the following 120 min” (class 1) and “the coin does not outperform” (class 0), our model is a linear function of the form
with denoting the intercept and coefficients, y the dependent and x the independent variable/feature vector (Berkson 1953; Kleinbaum and Klein 2010). The coefficients can be estimated by maximum likelihood using the observations from the training set—further details are available in Hastie et al. (2008).
For this paper, we rely on the implementation of Pedregosa et al. (2011) for the logistic regression and follow the parameters outlined in Fischer and Krauss (2018), i.e., the optimal L2-regularization is determined among 100 values on a logarithmic scale from 0.0001 to 10,000 via 5-fold cross-validation on the respective training set and L-BFGS is deployed to find an optimum. Further, we restrict the maximum number of iterations to 100.
3.3.2. Random forest
Following Krauss et al. (2017), who find the random forest (RF) to yield the best trading performance in their empirical study for the S&P 500 constitutents, we opt for this model as our machine learning benchmark. Random forests Breiman (1996, 2001); Ho (1995, 1998) are ensemble learners consisting of many decorrelated decision trees which can be understood as their building blocks. During the learning phase, the decision trees are trained individually on random subsets of the training samples. Hereby, each tree is “grown” with the objective of separating the training samples as pure as possible with respect to their class (the target value “0” or “1”). At each split (node of the tree), the samples are divided into two buckets depending on whether or not the respective sample fulfills the learned split criterion, e.g., whether or not the value of the feature “return over the past 60 min” exceeds 3 percent. This process is repeated recursively until all buckets are pure or another stop criterion, e.g., max depth J of the tree, is reached. Once all trees are trained, the random forest model can be applied to make predictions for the unseen data. Hereby, each tree of the forest predicts the class of the new sample based on its learned split criterions—simply speaking, if the new sample is sorted into a “0” bucket, the tree predicts “0”, otherwise “1”. In the last step, the predictions of all B trees of the forest are averaged to compute the final prediction—a value between 0 and 1 which can be interpreted as the probability that the sample belongs to class “1”. Further details and a comprehensive description of the algorithm are available in Raschka (2015).
As random forest implementation, we use Pedregosa et al. (2011) and largely follow Fischer and Krauss (2018) and Krauss et al. (2017) with respect to the parameters of random forest model. Specifically, we set the number of trees B to 1000 and the maximum tree depth J to 15. For the random feature selection, we follow the default value for classification, whereby p denotes the number of features—see (Pedregosa et al. 2011).
3.4. Forecasting, Ranking and Trading
Once the two models are trained using the features and targets of the training set (Note: we train universal models, i.e., each of the two models is trained using the samples of all coins), the learned parameters are fixed and the two models are transferred to the trading phase. In this phase, only the features are used (which are limited to the information an investor would have known at the respective point in time) and out of sample predictions are made. Specifically, at the end of each minute t of the trading period, each model forecasts the price development of all individual coins over the next two hours, i.e., the probability to outperform the cross-sectional median. We hence obtain two lists (one list per model) with 40 probabilities (one for each coin) which we sort in descending order. At the top of the lists, we find the coins that are most likely to outperform the cross-section of coins, whereas at the bottom, we find those coins most likely to underperform. Based on that ranking, we enter a long position for the top-3 coins, and a short position for the flop-3 coins. Finally, we reverse all positions at the end of the two hours holding period. To simulate the whole trading period from 18 June 2018 to 7 September 2018, the above procedure is repeated for each minute of the trading set resulting in 120 parallel portfolios active at each point in time (each portfolio is funded with th of the overall capital and comprises three long and three short positions at leverage 1). To render the backtest more realistic, we incorporate several execution constraints and transaction cost assumptions:
- Execution gap: We create the trading signal at the end of minute t and place the order for execution at the closing price of the following minute . In other words, we introduce a one period gap between signal generation and execution to account for the time frame required for data processing, prediction making, and order management.
- Volume constraint (opening of position): A position is only opened when at least one unit of the currency pair is traded at the respective point in time—otherwise, the order is canceled and the amount of capital foreseen for the position is kept in cash for the two hours period.
- Volume constraint (closing of position): Once the position has reached its two hours lifetime, a closing order is triggered and executed at the first bar with sufficient volume.
- Elimination of starting point bias: To avoid any bias related to the starting point (point in time at which the first portfolio is opened), we open a new portfolio at every minute and average the results across the 120 portfolios that are opened at each time t.
- Transaction costs: We assume 15 bps per half turn, based on analyses on transaction costs and liquidity costs provided in Schnaubelt et al. (2019) on cryptocurrency limit order book data.
Finally, at the end of the backtesting period, we analyze the financial performance for each of the two models based on the logged trades.
4. Results
In this section, we evaluate the financial performance of the RF and the LR model (when investing in the top-3 and flop-3 coins), and contrast them to a simple buy-and-hold strategy in Bitcoin (BTC) as well as the general market (MKT). The latter shall be defined as an equally-weighted investment in all coins at the beginning of the trading period. We proceed in three steps. First, we analyze the performance on trade level. Next, we aggregate the individual trades to daily returns and explore the development of the financial performance over time. Finally, we move beyond financial results and shed light on the patterns the employed predictive models exploit to select coins for trading.
4.1. Trade-Level Results
First, we evaluate the predictive performance of the logistic regression (LR) and the random forest (RF) model on the level of individual round trip trades.
Table 1 depicts the results of the more than 100,000 round trip trades over the full out-of-sample period from 18 June 2018 until 7 September 2018 after transaction costs of 30 bps. We make the following observations:

Table 1.
Key return characteristics on the level of individual round trip trades for the logistic regression (LR) and the random forest model (RF) when investing in the top-3 and flop-3 coins, after transaction costs of 30 bps for the round trip trade.
- Positive mean returns: Both models yield positive and statistically significant mean returns with the RF (3.8 bps) clearly outperforming the LR (2.0 bps) by a factor of almost two. Looking at the contribution from long trades and short trades, we find that the latter are more profitable (−2.1 bps. vs. 5.6 bps (LR) and 0.2 bps. vs. 6.4 bps. (RF))—a finding that is likely driven by the overall decline of the cryptocurrency market during this period.
- Extreme price movements: Looking at the minimum (−42.8 percent) and maximum returns (34.4 percent), we find astonishingly high values given the two hour holding period. However, these observations can be attributed to the extreme price movements in cryptocurrency markets—see Osterrieder and Lorenz (2017). The 25 percent and 75 percent quartiles are less extreme with values between −1.2 and 1.3 percent for both models.
- Negative median: We further notice that both, the RF and the LR model, have negative median returns. In other words, more trades lead to a loss than to a profit. However, taking into account the magnitude of the profits and losses, we find that the profits surpass the losses by approximately 5 bps (LR) and 10 bps (RF) on average (simply speaking, more money is made when the model is right than lost when it is wrong). In result, the mean trade of the RF is positive, i.e., .
- Skewness and Kurtosis: Both, LR and RF exhibit positive skewness, which is a favorable property for investors, given that the right tail tends to be more pronounced than the left tail. By contrast, kurtosis values above 9 indicate leptokurtic behavior, and that significant risk lies in the extremes—see Osterrieder and Lorenz (2017).
- Differing number of trades: Finally, we observe that the number of executed trades differs between the two models as well as the long and short leg. As described in the previous section, our backtesting engine cancels orders in case no volume is available to execute the respective trade. We may therefore cautiously conclude that the RF model selects a larger share of less liquid coins (119,829 executed trades) compared to the LR model (158,408 trades). Note: the overall high number of trades results from the backtesting logic in which we open a new portfolio with three long orders and three short orders by the end of each minute to avoid starting point bias.
4.2. Return Development over Time
Next, we aggregate the individual trades to daily returns and further explore the financial performance. Table 2 depicts daily and annualized risk-return metrics for the logistic regression (LR) and the random forest (RF) compared to Bitcoin (BTC) as well as the general market (MKT), i.e., an equal investment in all coins at the beginning of the trading period.

Table 2.
Daily and annualized risk-return metrics for the logistic regression (LR) and the random forest model (RF) model when investing in the top-3 and flop-3 coins, versus Bitcoin (BTC) and the general market (MKT), i.e., an equal investment in all coins at the beginning of the trading period. Panel A depicts daily return characteristics, panel B depicts risk and panel C annualized risk-return metrics.
We make the following findings:
- Panel A—daily return characteristics: With regard to mean return, the random forest surpasses the logistic regression by 2.2 bps per day (7.1 bps vs. 4.9 bps). We further observe that both, the maximum and minimum daily returns, are within reasonable levels of −2.6 percent (LR) and +2.1 percent (RF), respectively. The underlying reason is the large number of active positions at each point in time (see Section 3.4) which also explains the low standard deviation of 66 bps (LR) and 53 bps (RF). Looking at Bitcoin (BTC) and the general market (MKT), we find mean returns of −0.5 bps per day and −28.1 bps, respectively.
- Panel B—risk metrics: Panel B reveals favorable risk metrics for the random forest with a 1-percent value at risk of −1.0 percent compared to −1.5 percent for the logistic regression. Moreover, we find a significantly lower maximum drawdown of −2.4 percent for the RF and -5.9 percent for the LR compared to −26.7 percent for Bitcoin and −32.9 percent for the general market. The difference is caused by the short leg of the portfolio, i.e., the investment in the flop-3 coins which helps in eliminating market risk.
- Panel C—annualized risk-return metrics: Finally, panel C depicts annualized risk-return metrics. We observe annualized returns of 29.0 percent for the random forest and 18.8 percent for the logistic regression, compared to vastly negative results for the buy-and-hold benchmarks. Given the low volatility, these results translate into a Sharpe ratio of 1.4 (LR) and 2.5 (RF) respectively—hereby outperforming both Bitcoin and the general market by a clear margin.
Finally, Figure 1 depicts the cumulative profits for the random forest model (RF), and compares it to the development of Bitcoin (BTC) and the general market (MKT) over the duration of the out-of-sample trading period from 18 June 2018 to 7 September 2018:
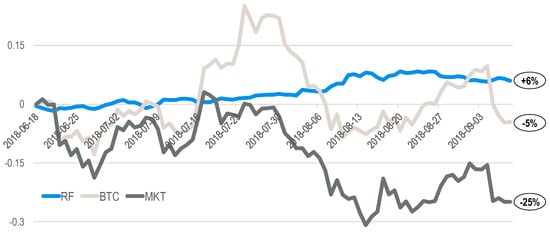
Figure 1.
Development of financial performance of random forest model (RF) when investing in the top-3 and flop-3 coins vs. Bitcoin (BTC) and general market (MKT), i.e., an equal investment in all coins at the beginning of the trading period.
We observe that the RF model shows fairly steady growth at low volatility levels—which is in stark contrast to the rugged nature and wild swings of Bitcoin and the general market. By the end of the trading period, the random forest has accumulated profits of +6 percent, whereas Bitcoin (BTC) and the general market (MKT) yield negative profits of −5 percent and −25 percent respectively.
4.3. Beyond Returns—Shedding Light Into the Patterns Exploited for Trading
In the following paragraphs, we move beyond the financial results and shed light into specific aspects of our predictive models. Specifically, we extract the feature importance of the random forest and contrast it with the regression coefficients of the logistic regression. We hereby aim to gain insights into the patterns our models exploit in order to select coins for trading. Figure 2 depicts the feature importance (RF) and regression coefficients (LR) respectively:
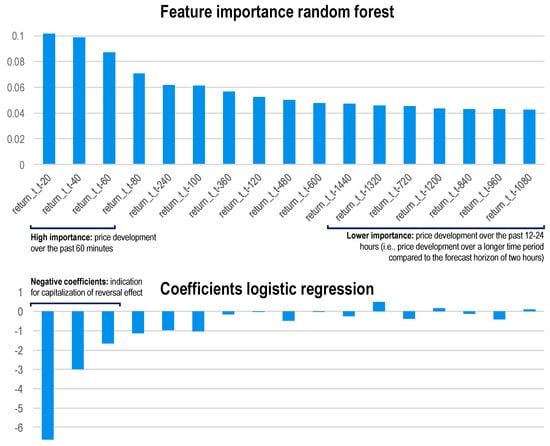
Figure 2.
Feature importance extracted from the random forest and regression coefficients for the logistic regression model. The features (explanatory variables) are sorted in descending order based on their importance extracted from the random forest model. The coefficients of the logistic regression model are plotted following the same order.
We make the following observations:
- Feature importance analysis: The upper half of the figure shows the features (explanatory variables) used by the random forest, sorted by feature importance in descending order. The most important features are the returns over the past 20, 40 and 60 min. In other words, the random forest pays most attention to the price development over the past hour. By contrast, the longer term price development (past 12–24 h) does not seem to have a substantial contribution to predicting the price change over the next two hours.
- Coefficient analysis: Looking at the lower part of the figure, we take advantage of the high transparency and explanatory value of the logistic regression model. The highest regression coefficient of approximately −6.5 belongs to the return over the past 20 min, followed by the coefficients for the 40 and 60 min returns. Moreover, we find that almost all regression coefficients exhibit a negative sign—in other words, the model likely produces a positive forecast (long), in case the respective coin has experienced a decline in the recent past (negative feature values which are multiplied with negative regression coefficients) and vice versa. We may therefore cautiously conclude that the model capitalizes on short-term mean-reversion—see Jegadeesh (1990); Lehmann (1990).
5. Discussion—Limits to Arbitrage
We would like to discuss our findings in light of limits to arbitrage. The most prominent effect that may adversely affect returns, is market microstructure. Inadvertently trading the bid-ask bounce in a backtest leads to high and statistically significant returns that may yet not be captured in reality. Hence, we have followed Gatev et al. (2006) and representatives of the high-frequency pairs trading literature—see Bowen and Hutchinson (2016); Liu et al. (2017), and only trade (i) when volume is present for a coin and (ii) with a one period gap after signal generation. In other words, when the signal is generated at the end of minute t, we only enter the market at the closing price of minute , as long as volume is present. To corroborate our findings, and to take into account potential liquidity issues, we further delay execution by additional periods—see Table 3 for our findings. We see that executing without gap—as is often the baseline in the literature—would lead to returns of 20.5 bps per round trip4. This value drops drastically to 3.8 bps when delaying execution to minute —our base case used throughout this study. A delay to minute leads to returns of 2.4 bps and a delay to minute to 1.6 bps—both of them still statistically significant. When delaying execution to minute , returns are still positive at 0.9 bps, albeit not statistically significant. As of minute , the alpha has vanished. Hence, we may conclude that fast execution after signal generation is paramount to the success of such a strategy. The latter is technically possible, but still a challenge. A second limit to arbitrage are short-selling constraints—which are commonly known in equity markets, see Gregoriou (2012). For cryptocurrencies, at the time of writing, several exchanges offer short selling (e.g., Poloniex, Bitfinex, etc.), but it is questionable whether the desired coin is always available at reasonable costs and in reasonable quantities. Given that the majority of the RF profits stem from the short leg in a downward market environment, this limit poses a challenge to any investor implementing such a strategy. The third major limit to arbitrage is capacity. An intraday strategy for cryptocurrencies may offer high Sharpe ratios. By contrast, costs for productionizing and operating such a strategy would be significant, when taking into account human capital and technical infrastructure. The reward may be fairly thin. The average trading volume per coin and minute is 7000 USD for the considered coin-exchange combinations (see Appendix A). Assuming a participation rate of 5 percent and a six-positions portfolio (top-3 long, flop-3 short) would lead to an estimated capacity of [USD] per minute—a fairly low value, compared to more mature markets.

Table 3.
Key return characteristics on the level of individual round trip trades for the random forest (RF) model when investing in the top-3 and flop-3 coins, after transaction costs of 30 bps. Each column represents the gap between signal generation and signal execution, i.e., gap 0 refers to signal generation at the closing price of bar t and execution at the opening price of bar . Gap 1 refers to a delayed execution at the closing price of bar , gap 2 to a delayed execution at the closing price of bar , and so forth.
6. Conclusions
With our paper, we have successfully transferred an advanced machine-learning-based statistical arbitrage approach from the U.S. equities markets to a large universe of 40 cryptocurrency coins on minute-binned data. Using returns over the past 1440 min (24 hours) and a random forest classifier, we aim to forecast the development of each coin for the subsequent 120 min. When going long the top-3 and short the flop-3 predictions, we find statistically and economically significant excess returns of 3.8 bps per round-trip trade—even after delaying order execution by one period, incorporating volume constraints for the opening and closing of the position, and transaction costs of 15 bps per half-turn. These results outperform a naive buy-and-hold strategy of Bitcoin, and of all 40 participating coins, equally-weighted by far—thereby indicating that this young and aspiring market may not (yet) follow the semi-strong form of market efficiency (Fama 1970). By analyzing the feature importances of the random forest and by comparing it to the coefficients of a logistic regression model, we observe that both methods capture short-term characteristics in the data, with returns over the past 60 min contributing most when explaining future returns over the subsequent 120 min. Moreover, the regression coefficients of the logistic regression model suggest the capitalization on short-term mean reversion—a well-documented phenomena in the finance literature (see Jegadeesh 1990; Lehmann 1990). Finally, we critically discuss these findings in light of potential limits to arbitrage. Hereby, we find the returns to remain positive and statistically significant when waiting up to three minutes after signal generation—so timely execution is paramount. Furthermore, potential short-selling constraints and overall market liquidity, which limits the capacity of the strategy, pose additional challenges on the implementation of statistical arbitrage strategies in the yet developing cryptocurrency markets.
Author Contributions
Conceptualization, T.G.F. and C.K.; Data curation, A.D.; Investigation, T.G.F., C.K. and A.D.; Methodology, T.G.F. and C.K.; Software, T.G.F. and A.D.; Validation, T.G.F., C.K. and A.D.; Visualization, T.G.F. and C.K.; Writing—original draft, T.G.F., C.K. and A.D.; Writing—review & editing, T.G.F. and C.K.
Funding
This research received no external funding.
Acknowledgments
The authors have benefited from many helpful discussions with Ingo Klein. We are further grateful to the “Open Access Publikationsfonds”, which has covered 75 percent of the publication fees.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BTC | Bitcoin |
| LR | logistic regression |
| MKT | market, i.e., an equal investment in all coins at the beginning of the trading period |
| RF | random forest |
| VaR | value at risk |
Appendix A

Table A1.
Overview of coins and corresponding exchanges used throughout this study. Note: All coins are denominated in USD prices as provided by www.cryptocompare.com.
Table A1.
Overview of coins and corresponding exchanges used throughout this study. Note: All coins are denominated in USD prices as provided by www.cryptocompare.com.
| No | Coin | Exchange | No | Coin | Exchange | |
|---|---|---|---|---|---|---|
| 1 | ADA | BitTrex | 21 | QTUM | Bitfinex | |
| 2 | BCH | Bitfinex | 22 | RDD | Yobit | |
| 3 | BCN | HitBTC | 23 | SAN | Bitfinex | |
| 4 | BTC | Bitfinex | 24 | SNT | Bitfinex | |
| 5 | BTG | Bitfinex | 25 | STRAT | HitBTC | |
| 6 | CND | HitBTC | 26 | TNB | Bitfinex | |
| 7 | CVC | HitBTC | 27 | TNT | HitBTC | |
| 8 | DASH | Bitfinex | 28 | TRX | Bitfinex | |
| 9 | DATA | Bitfinex | 29 | USDT | Kraken | |
| 10 | EOS | Bitfinex | 30 | VIB | HitBTC | |
| 11 | ETC | Bitfinex | 31 | WAVES | Yobit | |
| 12 | ETH | Bitfinex | 32 | XDN | HitBTC | |
| 13 | ETP | Bitfinex | 33 | XEM | Yobit | |
| 14 | GNT | Bitfinex | 34 | XLM | Poloniex | |
| 15 | LTC | Bitfinex | 35 | XMR | Bitfinex | |
| 16 | MANA | Bitfinex | 36 | XRP | Bitfinex | |
| 17 | NEO | Bitfinex | 37 | XVG | BitTrex | |
| 18 | NXT | Poloniex | 38 | YOYOW | Bitfinex | |
| 19 | OMG | Bitfinex | 39 | ZEC | Bitfinex | |
| 20 | QASH | Bitfinex | 40 | ZRX | Bitfinex |
References
- Balcilar, Mehmet, Elie Bouri, Rangan Gupta, and David Roubaud. 2017. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Economic Modelling 64: 74–81. [Google Scholar]
- Baur, Dirk G., and Thomas Dimpfl. 2018. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Beneki, Christina, Alexandros Koulis, Nikolaos A. Kyriazis, and Stephanos Papadamou. 2019. Investigating volatility transmission and hedging properties between Bitcoin and Ethereum. Research in International Business and Finance 48: 219–27. [Google Scholar] [CrossRef]
- Berkson, Joseph. 1953. A statistically precise and relatively simple method of estimating the bio-assay with quantal response, based on the logistic function. Journal of the American Statistical Association 48: 565–99. [Google Scholar] [CrossRef]
- Bowen, David A., and Mark C. Hutchinson. 2016. Pairs trading in the UK equity market: Risk and return. The European Journal of Finance 22: 1363–87. [Google Scholar] [CrossRef]
- Breiman, Leo. 1996. Bagging predictors. Machine Learning 24: 123–40. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- coinmarketcap.com. 2018. Overview of available cryptocurrencies. Available online: coinmarketcap.com (accessed on 27 July 2018).
- Colianni, Stuart, Stephanie Rosales, and Michael Signorotti. 2015. Algorithmic Trading of Cryptocurrency Based on Twitter Sentiment Analysis. Working Paper. Stanford, CA, USA: Stanford University. [Google Scholar]
- cryptocompare.com. 2018. Overview of CryptoCompare API. Available online: cryptocompare.com (accessed on 6 September 2018).
- Dyhrberg, Anne Haubo. 2016. Bitcoin, gold and the dollar—A GARCH volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Enke, David, and Suraphan Thawornwong. 2005. The use of data mining and neural networks for forecasting stock market returns. Expert Systems with Applications 29: 927–40. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fischer, Thomas, and Christopher Krauss. 2018. Deep learning with long short-term memory networks for financial market predictions. European Journal of Operational Research 270: 654–69. [Google Scholar] [CrossRef]
- Garcia, David, and Frank Schweitzer. 2015. Social signals and algorithmic trading of Bitcoin. Royal Society Open Science 2: 150288. [Google Scholar] [CrossRef] [PubMed]
- Gatev, Evan, William N. Goetzmann, and K. Geert Rouwenhorst. 2006. Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies 19: 797–827. [Google Scholar] [CrossRef]
- Gilbert, Clayton J. Hutto Eric. 2014. Vader: A parsimonious rule-based model for sentiment analysis of social media text. Paper presented at Eights International Conference on Weblogs and Social Media, Ann Arbor, MI, USA, June 1–4. [Google Scholar]
- Gregoriou, Greg N. 2012. Handbook of Short Selling. Amsterdam and Boston: Academic Press. [Google Scholar]
- Ha, Sungjoo, and Byung-Ro Moon. 2018. Finding attractive technical patterns in cryptocurrency markets. Memetic Computing 10: 301–6. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2008. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed. Series in Statistics; New York: Springer. [Google Scholar]
- Ho, Tin Kam. 1995. Random decision forests. Paper presented at the third International Conference on Document Analysis and Recognition, Montreal, QC, Canada, August 14–16, vol. 1, pp. 278–82. [Google Scholar]
- Ho, Tin Kam. 1998. The random subspace method for constructing decision forests. IEEE Transactions on Pattern Analysis and Machine Intelligence 20: 832–44. [Google Scholar]
- Huck, Nicolas. 2009. Pairs selection and outranking: An application to the S&P 100 index. European Journal of Operational Research 196: 819–25. [Google Scholar]
- Huck, Nicolas. 2010. Pairs trading and outranking: The multi-step-ahead forecasting case. European Journal of Operational Research 207: 1702–16. [Google Scholar] [CrossRef]
- IEEE, and The Open Group. 2018. The open group base specifications. 7. Available online: http://pubs.opengroup.org/onlinepubs/9699919799/basedefs/V1_chap04.html#tag_04_16 (accessed on 6 September 2018).
- Intercontinental Exchange. 2018. Behind the Scenes—An insider’s guide to the NYSE closing auction. Available online: https://www.nyse.com/article/nyse-closing-auction-insiders-guide (accessed on 30 December 2018).
- Jegadeesh, Narasimhan. 1990. Evidence of predictable behavior of security returns. The Journal of Finance 45: 881. [Google Scholar] [CrossRef]
- Jiang, Zhengyao, and Jinjun Liang. 2017. Cryptocurrency portfolio management with deep reinforcement learning. arXiv, arXiv:1612.01277v5. [Google Scholar]
- Jones, Eric, Travis Oliphant, and Pearu Peterson. 2014. SciPy: open source scientific tools for Python. Available online: http://www.scipy.org/ (accessed on 30 December 2018).
- Kim, Y. Bin, Jun G. Kim, Wook Kim, Jae H. Im, Tae H. Kim, Shin J. Kang, and Chang H. Kim. 2016. Predicting fluctuations in cryptocurrency transactions based on user comments and replies. PLoS ONE 11: e0161197. [Google Scholar] [CrossRef] [PubMed]
- Kleinbaum, David G., and Mitchel Klein. 2010. Logistic Regression: A Self-Learning Text. New York: Springer. [Google Scholar]
- Koutmos, Dimitrios. 2018. Return and volatility spillovers among cryptocurrencies. Economics Letters 173: 122–27. [Google Scholar] [CrossRef]
- Krauss, Christopher. 2017. Statistical arbitrage pairs trading strategies: Review and outlook. Journal of Economic Surveys 31: 513–45. [Google Scholar] [CrossRef]
- Krauss, Christopher, Xuan Anh Do, and Nicolas Huck. 2017. Deep neural networks, gradient-boosted trees, random forests: Statistical arbitrage on the S&P 500. European Journal of Operational Research 259: 689–702. [Google Scholar]
- Lehmann, Bruce N. 1990. Fads, martingales, and market efficiency. The Quarterly Journal of Economics 105: 1. [Google Scholar] [CrossRef]
- Leung, Mark T., Hazem Daouk, and An-Sing Chen. 2000. Forecasting stock indices: A comparison of classification and level estimation models. International Journal of Forecasting 16: 173–90. [Google Scholar] [CrossRef]
- Lintilhac, Paul S., and Agnes Tourin. 2017. Model-based pairs trading in the Bitcoin markets. Quantitative Finance 17: 703–16. [Google Scholar] [CrossRef]
- Liu, Bo, Lo-Bin Chang, and Hélyette Geman. 2017. Intraday pairs trading strategies on high frequency data: The case of oil companies. Quantitative Finance 17: 87–100. [Google Scholar] [CrossRef]
- Madan, Isaac, Shaurya Saluja, and Aojia Zhao. 2015. Automated Bitcoin Trading via Machine Learning Algorithms. Working Paper. Stanford, CA, USA: Stanford University. [Google Scholar]
- McKinney, Wes. 2010. Data structures for statistical computing in python. Paper presented at the 9th Python in Science Conference, Austin, TX, USA, June 28–July 3, vol. 445, pp. 51–56. [Google Scholar]
- McNally, Sean, Jason Roche, and Simon Caton. 2018. Predicting the price of Bitcoin using machine learning. Paper presented at the 26th International Conference on Parallel, Distributed and Network-Based Processing, Cambridge, UK, March 21–23; pp. 339–43. [Google Scholar]
- Moritz, Benjamin, and Tom Zimmermann. 2014. Deep Conditional Portfolio Sorts: The Relation between Past and Future Stock Returns. Working Paper. Munich, Germany: LMU Munich. Cambridge, MA, USA: Harvard University. [Google Scholar]
- Osterrieder, Joerg, and Julian Lorenz. 2017. A statistical risk assessment of Bitcoin and its extreme tail behavior. Annals of Financial Economics 12: 1750003. [Google Scholar] [CrossRef]
- Pedregosa, F., G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, and et al. 2011. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 12: 2825–30. [Google Scholar]
- Python Software Foundation. 2016. Python 3.5.2 Documentation. Available online: https://docs.python.org/3.5/ (accessed on 15 December 2018).
- Quantopian Inc. 2016. Empyrical: Common Financial Risk Metrics. Available online: https://github.com/quantopian/empyrical (accessed on 15 December 2018).
- Raschka, Sebastian. 2015. Python Machine Learning. Birmingham: Packt Publishing. [Google Scholar]
- Schnaubelt, Matthias, Jonas Rende, and Christopher Krauss. 2019. Testing Stylized Facts of Bitcoin Limit Order Books. Journal of Risk and Financial Management 12: 25. [Google Scholar] [CrossRef]
- Shah, Devavrat, and Kang Zhang. 2014. Bayesian regression and Bitcoin. Paper presented at the 52nd Conference on Communication, Control, and Computing, Monticello, IL, USA, October 1–3; pp. 409–14. [Google Scholar]
- Takeuchi, Lawrence, and Yu-Ying Lee. 2013. Applying Deep Learning to Enhance Momentum Trading Strategies in Stocks. Working Paper. Stanford, CA, USA: Stanford University. [Google Scholar]
- Tourin, Agnès, and Raphael Yan. 2013. Dynamic pairs trading using the stochastic control approach. Journal of Economic Dynamics and Control 37: 1972–81. [Google Scholar] [CrossRef]
- Van der Walt, S., S. C. Colbert, and G. Varoquaux. 2011. The NumPy array: A structure for efficient numerical computation. Computing in Science & Engineering 13: 22–30. [Google Scholar] [CrossRef]
- Warriner, Amy Beth, Victor Kuperman, and Marc Brysbaert. 2013. Norms of valence, arousal, and dominance for 13,915 English lemmas. Behavior Research Methods 45: 1191–207. [Google Scholar] [CrossRef] [PubMed]
| 1 | The emotional valence and opinion polarization are computed on a daily basis as proposed by Warriner et al. (2013). |
| 2 | Vader = Valence Aware Dictionary for sEntiment Reasoning. This algorithm allows to interpret slang, neologisms, and emoticons, which are oftentimes found on social media platforms. Further information on this algorithm can be found in Gilbert (2014). |
| 3 | Not all time-series examined are complete in the sense that they cover the whole period from January to September 2018. This could be due to several reasons such as the delisting of a coin. It is noteworthy that such time-series are not eliminated but traded according to the available data. |
| 4 | More precisely, by executing at the opening price of minute , we still leave a small gap compared to an execution at the closing price of minute t (which is used to make the prediction). |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).