U.K. House Prices: Bubbles or Market Efficiency? Evidence from Regional Analysis
Abstract
1. Introduction
2. Literature Review
3. Methods and Materials
3.1. Basic Modelling of House Price Growth
3.2. Data Sources and Sample
4. Results
4.1. Panel Unit Root Test
4.2. Cointegration Test
4.3. Test Results
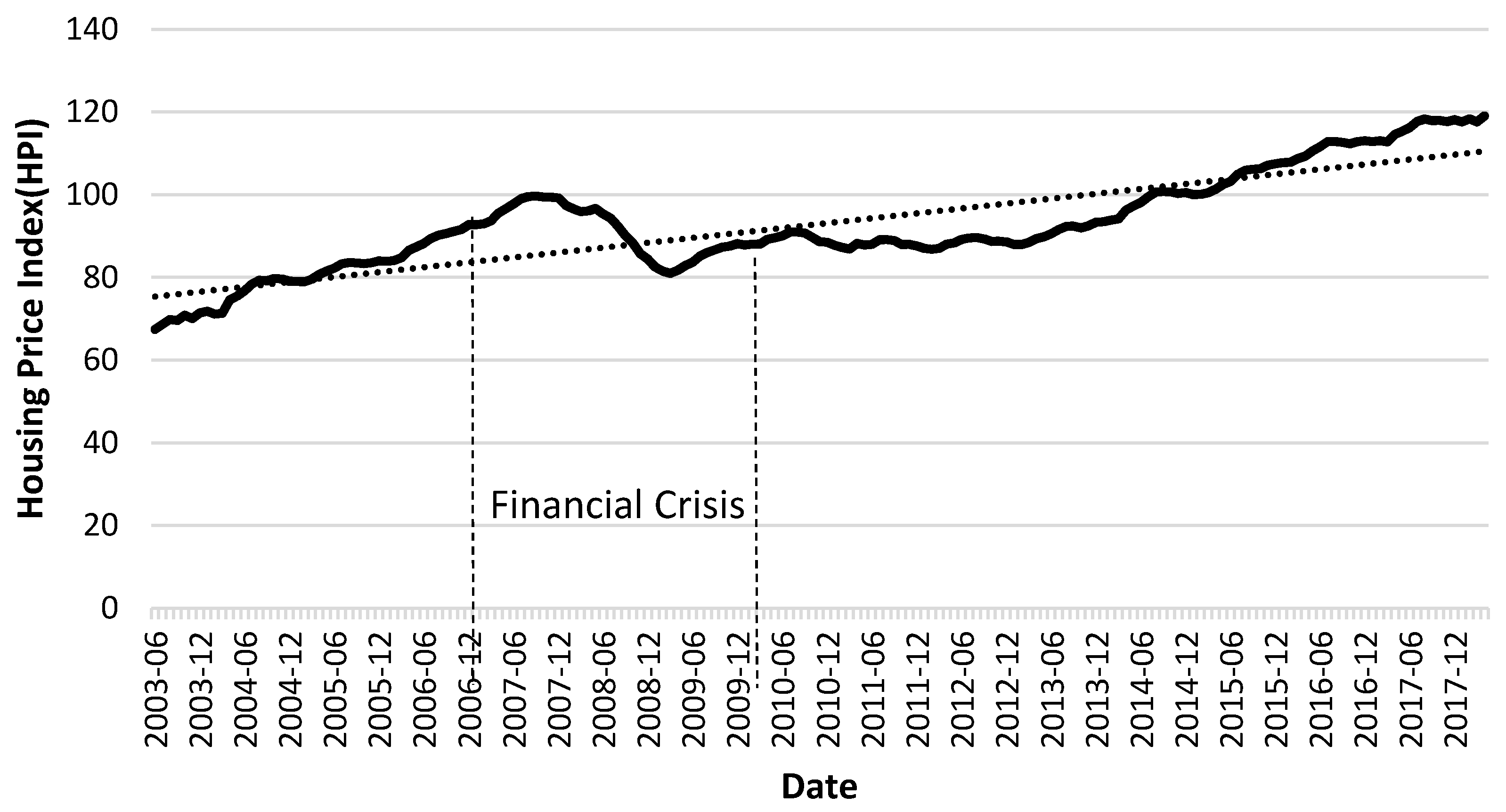
4.4. Financial Crisis Test
5. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Abraham, Jesse M., and Patric H. Hendershott. 1993. Patterns and Determinants of Metropolitan House Prices, 1977–91 (October 1992). NBER Working Paper No. w4196. Available online: https://ssrn.com/abstract=879241 (accessed on 12 September 2018).
- Abraham, Jesse M., and Patric H. Hendershott. 1996. Bubbles in metropolitan housing markets. Journal of Housing Research 7: 191–207. [Google Scholar] [CrossRef]
- Barrell, Ray, Simon Kirby, and Rebecca Riley. 2004. The Current Position of UK House Prices. National Institute Economic Review 189: 57–60. [Google Scholar] [CrossRef]
- Black, Angela, Patricia Fraser, and Martin Hoesli. 2006. House Prices, Fundamental and Bubbles. Journal of Business Finance and Accounting 33: 1535–55. [Google Scholar] [CrossRef]
- Chan, Hing Lin, Shu Kam Lee, and Kai Yin Woo. 2001. Detecting Rational Bubbles in the Residential Housing Markets in Hong Kong. Economic Modelling 18: 61–73. [Google Scholar] [CrossRef]
- Cutler, David M., James M. Poterba, and Lawrence H. Summers. 1991. Speculative dynamics. The Review of Economic Studies 58: 529–46. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1988. Dividend yields and expected stock returns. Journal of financial economics 22: 3–25. [Google Scholar] [CrossRef]
- Favilukis, Jack, Sydney C. Ludvigson, and Stijn Van Nieuwerburgh. 2017. The macroeconomic effects of housing wealth, housing finance, and limited risk-sharing in general equilibrium. Journal of Political Economy 125: 140–223. [Google Scholar] [CrossRef]
- Flood, Robert P., and Robert J. Hodrick. 1990. On testing for speculative bubbles. Journal of Economic Perspectives 4: 85–101. [Google Scholar] [CrossRef]
- Gholipour, Hassan Fereidouni, Usama Al-mulali, and Abdul Hakim Mohammed. 2014. Foreign investments in real estate, economic growth and property prices: Evidence from OECD countries. Journal of Economic Policy Reform 17: 33–45. [Google Scholar] [CrossRef]
- Giglio, Stefano, Matteo Maggiori, and Johannes Stroebel. 2016. No-bubble condition: Model-free tests in housing markets. Econometrica 84: 1047–91. [Google Scholar] [CrossRef]
- Glaeser, Edward L., Joseph Gyourko, and Albert Saiz. 2008. Housing supply and housing bubbles. Journal of Urban Economics 64: 198–217. [Google Scholar] [CrossRef]
- Glaeser, Edward L., Joshua D. Gottlieb, and Joseph Gyourko. 2010. Can Cheap Credit Explain the Housing Boom? In NBER book Housing and the Financial Crisis (2013). Edited by Edward L. Glaeser and Todd Sinai. Chicago: University of Chicago Press, pp. 301–59. [Google Scholar]
- Glaeser, Edward L., and Charles G. Nathanson. 2017. An extrapolative model of house price dynamics. Journal of Financial Economics 126: 147–70. [Google Scholar] [CrossRef]
- Goodman, Allen C., and Thomas G. Thibodeau. 2008. Where are the speculative bubbles in US housing markets? Journal of Housing Research 17: 117–37. [Google Scholar] [CrossRef]
- Hadri, Kaddour. 2000. Testing for stationarity in heterogeneous panel data. The Econometrics Journal 3: 148–61. [Google Scholar] [CrossRef]
- Himmelberg, Charles, Christopher Mayer, and Todd Sinai. 2005. Assessing high house prices: Bubbles, fundamentals, and misperceptions. Journal of Economic Perspectives 19: 67–92. [Google Scholar] [CrossRef]
- Im, Kyung So, M. Hashem Pesaran, and Yongcheol Shin. 2003. Testing for unit roots in heterogeneous panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Khandani, Amir E., Andrew W. Lo, and Robert C. Merton. 2013. Systemic risk and the refinancing ratchet effect. Journal of Financial Economics 108: 29–45. [Google Scholar] [CrossRef]
- Lai, Rose N., and Robert A. Van Order. 2010. Momentum and house price growth in the United States: Anatomy of a bubble. Real Estate Economics 38: 753–73. [Google Scholar] [CrossRef]
- Lai, Rose Neng, and Robert Van Order. 2017. US House Prices over the Last 30 Years: Bubbles, Regime Shifts and Market (In) Efficiency. Real Estate Economics 45: 259–300. [Google Scholar] [CrossRef]
- Mayer, Christopher, and Todd Sinai. 2009. U.S. House Price Dynamics and Behavioral Finance. In Policy Making Insights from Behavioral Economics. Edited by Christopher L. Foote, Lorenz Goette and Stephan Meier. Boston: Federal Reserve Bank of Boston, chp. 5. [Google Scholar]
- Meese, Richard, and Nancy Wallace. 1994. Testing the present value relation for housing prices: Should I leave my house in San Francisco? Journal of Urban Economics 35: 245–66. [Google Scholar] [CrossRef]
- Mikhed, Vyacheslav, and Petr Zemčík. 2009. Testing for bubbles in housing markets: A panel data approach. The Journal of Real Estate Finance and Economics 38: 366–86. [Google Scholar] [CrossRef]
- Nickell, Steve. 2005. Practical Issues in UK Monetary Policy, 2000–2005. Keynes Lecture in Economics. London: British Academy. [Google Scholar] [CrossRef]
- Paul, Biru Paksha, Md Gazi Salah Uddin, and Abdullah M. Noman. 2011. Remittances and output in Bangladesh: An ARDL bounds testing approach to cointegration. International Review of Economics 58: 229–42. [Google Scholar] [CrossRef]
- Peláez, Rolando F. 2012. The housing bubble in real-time: The end of innocence. Journal of Economics and Finance 36: 211–25. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Ron Smith. 1995. Estimating long-run relationships from dynamic heterogeneous panels. Journal of Econometrics 68: 79–113. [Google Scholar] [CrossRef]
- Hasham, Pesaran M., Shin Yongcheol, and P. Smith Ron. 1997. Pooled Estimation of Long-Run Relationships in Dynamic Heterogeneous Panels. Cambridge Working Paper in Economics, Cambridge. August. Available online: https://EconPapers.repec.org/RePEc:cam:camdae:9721 (accessed on 12 September 2018).
- Pesaran, M. Hashem. 2007. Simple panel unit root test in the presence of cross-section dependence. Journal of Applied Econometrics 22: 265–312. [Google Scholar] [CrossRef]
- Hwang, Min, and John M. Quigley. 2006. Economic fundamentals in local housing markets: evidence from US metropolitan regions. Journal of Regional Science 46: 425–53. [Google Scholar] [CrossRef]
- Rodríguez, Carlos, and Ricardo Bustillo. 2010. Modelling Foreign Real Estate Investment: The Spanish Case. The Journal of Real Estate Finance and Economics 41: 354. [Google Scholar] [CrossRef]
- Rogers, Dallas, Chyi Lin Lee, and Ding Yan. 2015. The Politics of Foreign Investment in Australian Housing: Chinese Investors, Translocal Sales Agents and Local Resistance. Housing Studies 30: 730–48. [Google Scholar] [CrossRef]
- Stiglitz, Joseph E. 1990. Symposium on bubbles. Journal of Economic Perspectives 4: 13–18. [Google Scholar] [CrossRef]
- West, Kenneth D. 1987. A specification test for speculative bubbles. The Quarterly Journal of Economics 102: 553–80. [Google Scholar] [CrossRef]
- Taipalus, Katja. 2006. A Global House Price Bubble? Evaluation Based on a New Rent-Price Approach. Bank of Finland Research Discussion Paper No. 29/2006. Available online: https://ssrn.com/abstract=1018329 (accessed on 12 September 2018). [CrossRef]
- Westerlund, Joakim. 2007. Testing for error correction in panel data. Oxford Bulletin of Economics and Statistics 69: 709–48. [Google Scholar] [CrossRef]
| 1 | We use the cubic spline interpolation method of plugging the quarterly values for the monthly time intervals. |
| 2 | |
| 3 | We use the econometric code package “ipshin”, which estimates the t-test for unit roots in heterogeneous panels developed by Im, Pesaran, and Shin (Im et al. 2003). |
| 4 | We use the econometric code package “hadrilm” performs a test for stationarity in heterogeneous panel data (Hadri 2000). |
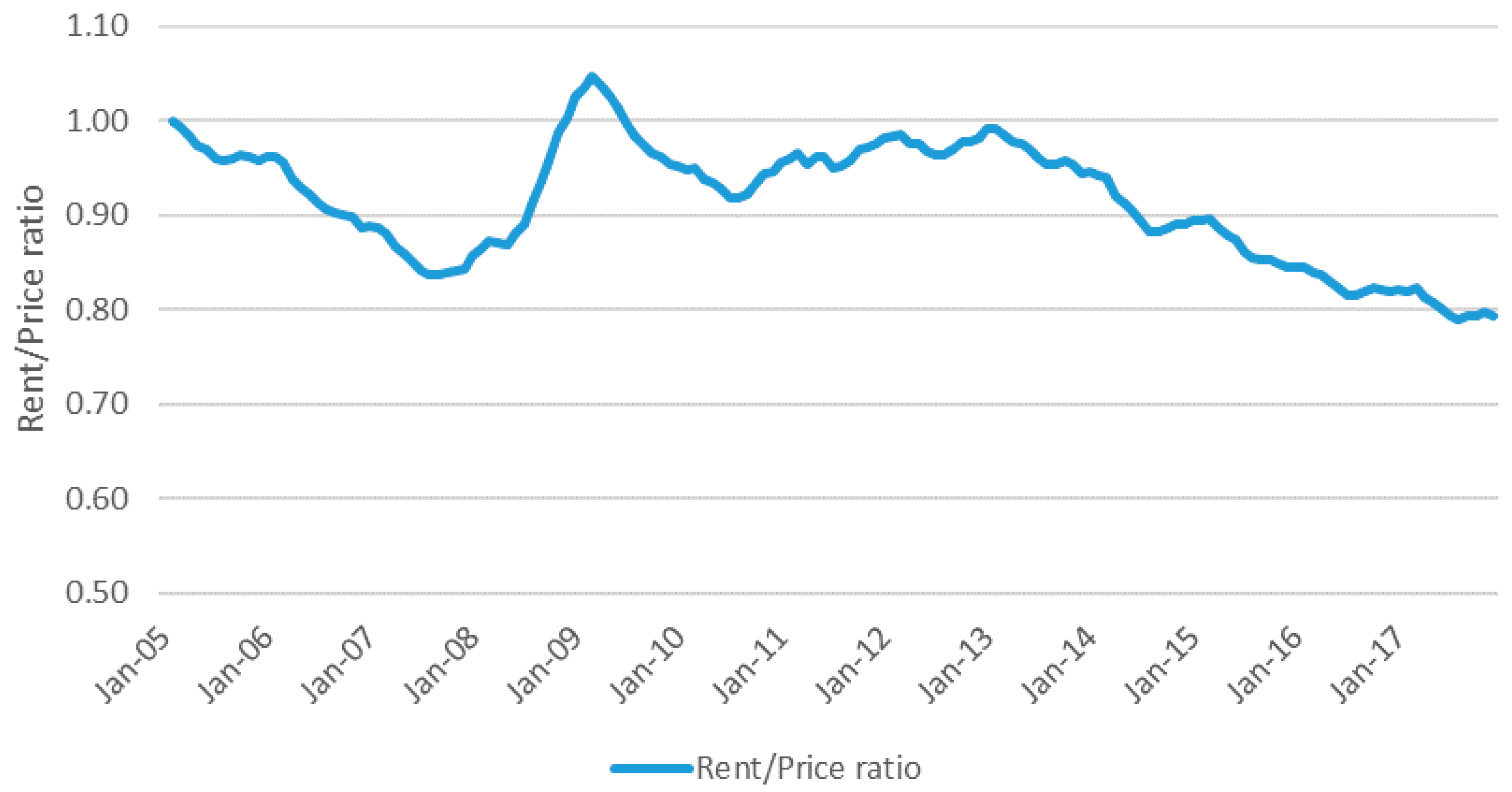
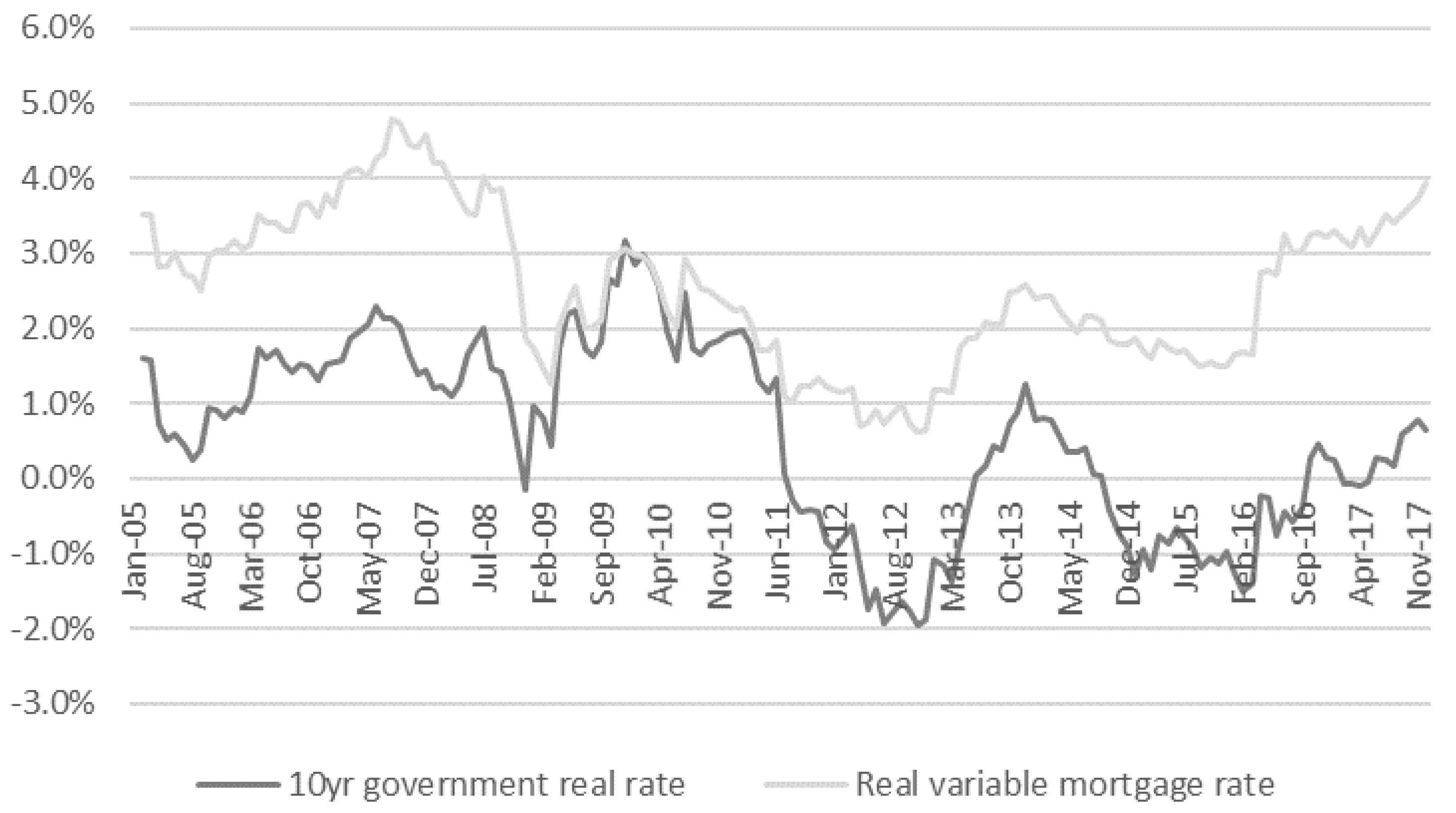
| Variables | Individual ADF Based Tests | IPS Test | Hadri Test |
|---|---|---|---|
| Rent to Price Ratio | −1.323 | −1.452 | 18.610 *** |
| Δ Rent to Price Ratio | −4.252 *** | −4.097 *** | −0.376 |
| 10-Year Government real bond rate | 15.137 *** | ||
| Δ 10-Year Government real bond rate | −2.019 | ||
| Residential Mortgage Rate | 6.705 *** | ||
| Δ Residential Mortgage Rate | −0.831 | ||
| First time buyer affordability Rate | −1.069 | −1.316 | 30.413 *** |
| Δ First time buyer affordability Rate | −4.512 *** | −4.208 *** | −1.201 |
| Disposable Household Income | −2.501 * | −1.869 * | 9.123 *** |
| Δ Disposable Household Income | −4.179 *** | −4.057 *** | 7.150 *** |
| Earnings ratio | −0.860 | −0.833 | 27.699 *** |
| Δ Earnings ratio | −4.397 *** | −4.135 *** | 0.955 |
| R/P and 10-Year Government real bond rate | −2.187 | −7.697 | −6.896 | −8.090 |
| R/P and Residential Mortgage Rate | −2.786 * | −11.761 | −7.609 * | −10.472 |
| R/P and First time buyer affordability Rate | −1.142 | −2.966 | −3.181 | −2.159 |
| R/P and Disposable Household Income | −1.760 | −5.102 | −4.145 | −3.837 |
| R/P and Earnings ratio | −3.101 *** | −21.556 *** | −9.109 *** | −19.898 *** |
| Variable | Dependent Variable: Rent to Price Ratio | |||
|---|---|---|---|---|
| Model A1 | Model A2 | Model B1 | Model B2 | |
| PMG | MG | PMG | MG | |
| Long-Run Equation | ||||
| Residential Mortgage Rate | 3.712 *** (10.265) | −0.910 (−0.083) | 5.800 *** (7.226) | 1.831 (0.223) |
| Earnings Ratio | −25.882 *** (−22.937) | −18.678 (−0.475) | −25.828 *** (−16.894) | −20.898 (−0.927) |
| 10-Year Government real bond rate | −2.388 *** (−3.931) | −0.196 (−0.054) | ||
| Short-Run Equation | ||||
| Error-correction (EC) | −0.079 *** (−5.560) | −0.007 (−1.046) | −0.054 *** (−5.451) | 0.013 (1.658) |
| Δ Rent to Price Ratiot−1 | 0.938 *** (28.668) | 0.990 *** (96.368) | 0.877 *** (27.735) | 1.005 *** (123.896) |
| Δ Rent to Price Ratiot−2 | 0.054 (1.675) | −0.310 *** (−51.879) | 0.122 *** (3.888) | −0.315 *** (−45.312) |
| Δ Residential Mortgage Ratet | −1.264 *** (−4.818) | −1.572 *** (−9.370) | −1.281 *** (−6.851) | −2.068 *** (−11.341) |
| Δ Residential Mortgage Ratet−1 | 0.843 * (2.083) | 0.339 (1.003) | 0.286 (0.537) | 1.538 *** (4.153) |
| Δ Residential Mortgage Ratet−2 | 0.817 * (2.477) | 0.218 (0.625) | −0.097 (−0.194) | −0.684 (−1.791) |
| Δ Residential Mortgage Ratet−3 | −0.359 (−1.823) | −0.102 (−0.954) | 0.115 (0.736) | 0.14 (1.203) |
| Δ Earnings ratiot | −3.709 *** (−4.829) | −7.650 *** (−7.605) | −5.783 *** (−4.713) | −6.117 *** (−7.366) |
| Δ Earnings ratiot−1 | −1.689 (−1.292) | 10.052 *** (5.935) | 7.422 *** (4.176) | 8.953 *** (6.873) |
| Δ Earnings ratiot−2 | 5.352 *** (6.911) | −4.685 *** (−7.068) | −3.711 *** (−4.058) | −4.129 *** (−7.762) |
| Δ 10-Year Government real bond ratet | −0.473 *** (−4.894) | −0.282 *** (−3.385) | ||
| Δ 10-Year Government real bond ratet−1 | 1.264 *** (7.137) | 1.041 *** (7.202) | ||
| Δ 10-Year Government real bond ratet−2 | −0.878 *** (−6.645) | −0.844 *** (−8.199) | ||
| Δ 10-Year Government real bond ratet−3 | 0.207 *** (4.656) | 0.217 *** (8.180) | ||
| Constant | 0.007 (1.329) | 0.032 ** (2.663) | 0.097 *** (5.574) | −0.012 (−0.899) |
| Observations | 1422 | 1404 | 1404 | 1404 |
| Selected Model | ARDL(2,3,2) | ARDL(2,3,2,3) chi2(2) = −5.89 | ||
| Hausman test | chi2(2) = −13.02 | |||
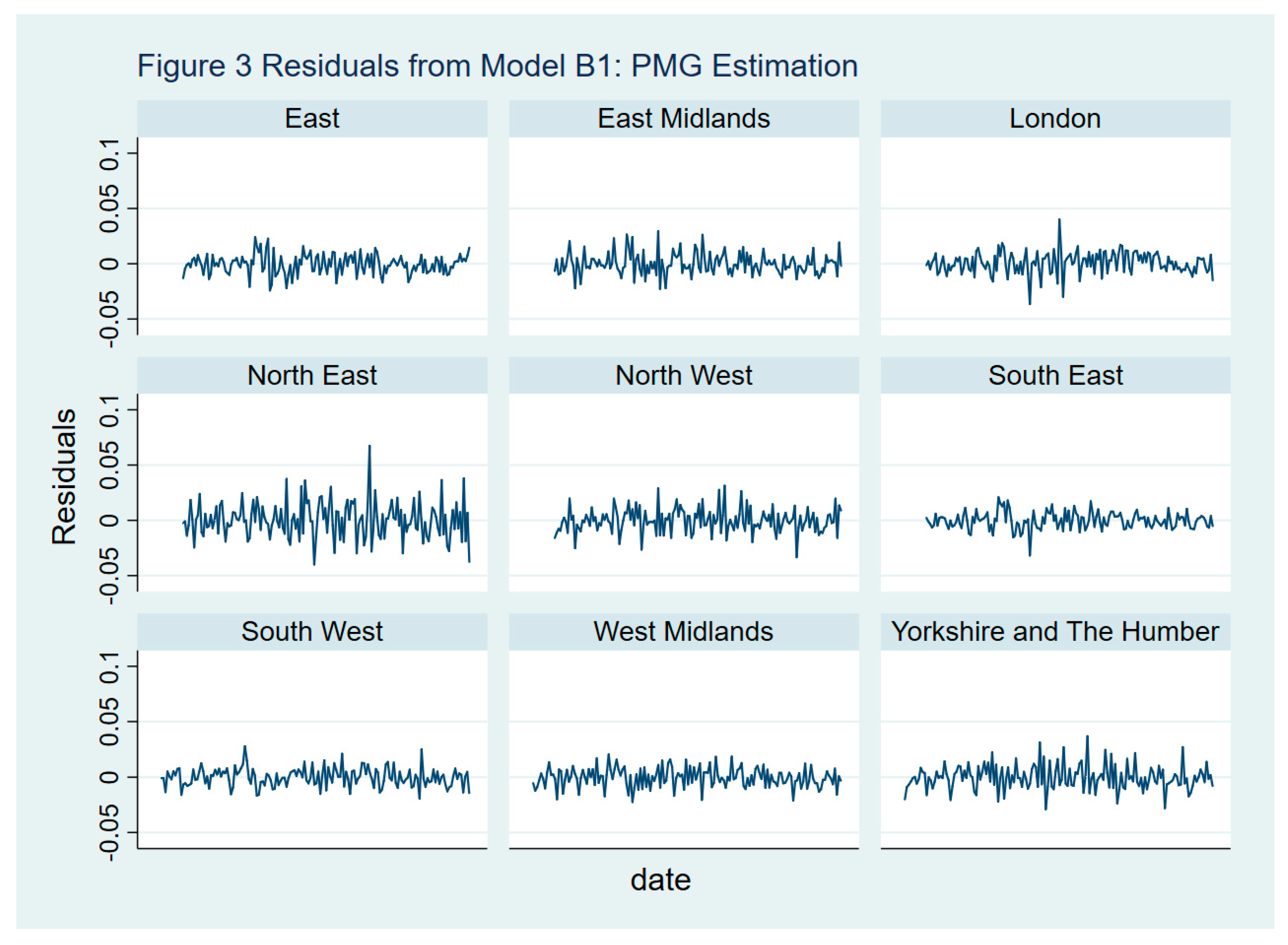
| Region | Error Correction | ΔR/P | Δ Residential Mortgage Rate | Δ Earnings Ratio | Δ 10 Year Government Real Bond Rate | Constant |
|---|---|---|---|---|---|---|
| East | −0.095 | 0.064 | −0.739 | −1.957 | 0.171 | 0.179 |
| East Midlands | −0.071 | 0.134 | −0.367 | −3.082 | 0.038 | 0.128 |
| London | −0.002 | 0.918 | −1.565 | −1.950 | 0.084 | 0.003 |
| North East | −0.087 | −0.083 | −0.861 | −1.072 | 0.282 | 0.145 |
| North West | −0.060 | 0.083 | −1.539 | −0.846 | 0.082 | 0.099 |
| South East | −0.027 | 0.340 | −0.598 | −3.200 | 0.031 | 0.053 |
| South West | −0.041 | 0.102 | −1.687 | −2.556 | −0.069 | 0.086 |
| West Midlands | −0.059 | 0.167 | −0.979 | −0.364 | 0.031 | 0.108 |
| Yorkshire and The Humber | −0.041 | 0.007 | −0.466 | −3.630 | 0.430 | 0.069 |
| Maximum | −0.002 (London) | 0.918 (London) | −0.367 (East Midlands) | −0.364 (West Midlands) | 0.171 (East) | 0.179 (East) |
| Minimum | −0.095 (East) | −0.083 (North East) | −1.687 (South West) | −3.630 (Yorkshire and The Humber) | −0.069 (South West) | 0.003 (London) |
| Variable | Dependent Variable: Rent to Price Ratio | |
|---|---|---|
| Coefficients | Standard Errors | |
| Long-Run Equation | ||
| Residential Mortgage Rate | 5.708 *** | 0.777 |
| Earnings Ratio | −26.526 *** | 1.669 |
| 10-Year Government real bond rate | −2.190 *** | 0.616 |
| CRISIS | 0.004 *** | 0.001 |
| Short-Run Equation | ||
| EC | −0.058 *** | 0.010 |
| CRISIS | −0.036 *** | 0.006 |
| Δ Rent to Price Ratiot−1 | −0.101 *** | 0.027 |
| Δ Rent to Price Ratiot−2 | 0.164 *** | 0.027 |
| Δ Residential Mortgage Ratet | −1.245 *** | 0.204 |
| Δ Residential Mortgage Ratet−1 | 0.221 *** | 0.563 |
| Δ Residential Mortgage Ratet−2 | −0.045 *** | 0.530 |
| Δ Residential Mortgage Ratet−3 | 0.099 *** | 0.169 |
| Δ Earnings ratiot | −5.247 *** | 1.275 |
| Δ Earnings ratiot−1 | 6.842 *** | 1.756 |
| Δ Earnings ratiot−2 | −3.476 *** | 0.881 |
| Δ 10-Year Government real bond ratet | −0.452 *** | 0.109 |
| Δ 10-Year Government real bond ratet−1 | 1.243 *** | 0.177 |
| Δ 10-Year Government real bond ratet−2 | −0.871 *** | 0.135 |
| Δ 10-Year Government real bond ratet−3 | 0.207 *** | 0.045 |
| Constant | 0.106 *** | 0.018 |
| Observations | 1404 | |
| Variable | Dependent Variable: Rent to Price Ratio | ||
|---|---|---|---|
| Pre-Financial Crisis | Financial Crisis | Post-Financial Crisis | |
| Long-Run Equation | |||
| Residential Mortgage Rate | 3.6212 (5.012) | 2.481 *** (7.190) | −10.330 *** (3.450) |
| Earnings Ratio | −16.493 ** (2.241) | −19.076 *** (−16.963) | −26.824 *** (4.940) |
| 10-Year Government real bond rate | −1.5992 (2.620) | −1.785 *** (−7.160) | 0.744 ** (0.288) |
| Short-Run Equation | |||
| EC | 0.013 (0.083) | −0.276 *** (−11.353) | −0.184 *** (0.033) |
| Δ Rent to Price Ratiot−1 | 0.034 (0.543) | −0.048 (0.048) | −0.214 *** (−5.510) |
| Δ Rent to Price Ratiot−2 | 0.037 (0.597) | 0.241 *** (0.048) | 0.012 (0.331) |
| Δ Residential Mortgage Ratet | −0.323 (−0.555) | −2.620 *** (−6.679) | 0.961 (1.750) |
| Δ Residential Mortgage Ratet−1 | 0.986 (1.694) | 2.848 *** (3.541) | 0.446 (0.730) |
| Δ Residential Mortgage Ratet−2 | 1.490 * (2.222) | −2.137 ** (-2.621) | 1.755 ** (2.790) |
| Δ Residential Mortgage Ratet−3 | −2.374 *** (−3.553) | 0.752 ** (2.667) | −0.233 (−0.395) |
| Δ Earnings ratiot | −5.112 ** (−2.837) | 5.323 (1.930) | −3.232 * (−2.421) |
| Δ Earnings ratiot−1 | 5.041 * (2.386) | −5.291 (−1.821) | −0.355 (−0.209) |
| Δ Earnings ratiot−2 | −6.712 *** (−3.648) | 2.585 * (1.967) | −4.319 ** (−3.223) |
| Δ 10-Year Government real bond ratet | 0.563 * (2.292) | 0.880 ** (3.265) | 0.204 (1.752) |
| Δ 10-Year Government real bond ratet−1 | −0.863 *** (−3.451) | −0.593 (−1.385) | −0.002 (−0.015) |
| Δ 10-Year Government real bond ratet−2 | 0.285 (1.225) | 0.284 (0.876) | −0.447 *** (−3.926) |
| Δ 10-Year Government real bond ratet−3 | −1.121 *** (−4.408) | −0.063 (−0.756) | −0.375 *** (−3.352) |
| Constant | −0.003 *** (−5.039) | 0.480 *** (11.263) | −0.002 *** (−4.238) |
| Observations | 243 | 441 | 684 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Lux, N. U.K. House Prices: Bubbles or Market Efficiency? Evidence from Regional Analysis. J. Risk Financial Manag. 2018, 11, 54. https://doi.org/10.3390/jrfm11030054
Wu Y, Lux N. U.K. House Prices: Bubbles or Market Efficiency? Evidence from Regional Analysis. Journal of Risk and Financial Management. 2018; 11(3):54. https://doi.org/10.3390/jrfm11030054
Chicago/Turabian StyleWu, Yi, and Nicole Lux. 2018. "U.K. House Prices: Bubbles or Market Efficiency? Evidence from Regional Analysis" Journal of Risk and Financial Management 11, no. 3: 54. https://doi.org/10.3390/jrfm11030054
APA StyleWu, Y., & Lux, N. (2018). U.K. House Prices: Bubbles or Market Efficiency? Evidence from Regional Analysis. Journal of Risk and Financial Management, 11(3), 54. https://doi.org/10.3390/jrfm11030054





