The Burr X Pareto Distribution: Properties, Applications and VaR Estimation
Abstract
:1. Introduction
2. The New Model
3. Expansions of pdf and cdf
4. Properties
4.1. Moments
4.2. Residual and Reversed Residual Life
4.3. Order Statistics
5. Estimation Methods
5.1. Maximum Likelihood Estimation
5.2. Ordinary and Weighted Least Squares
6. Simulation Study
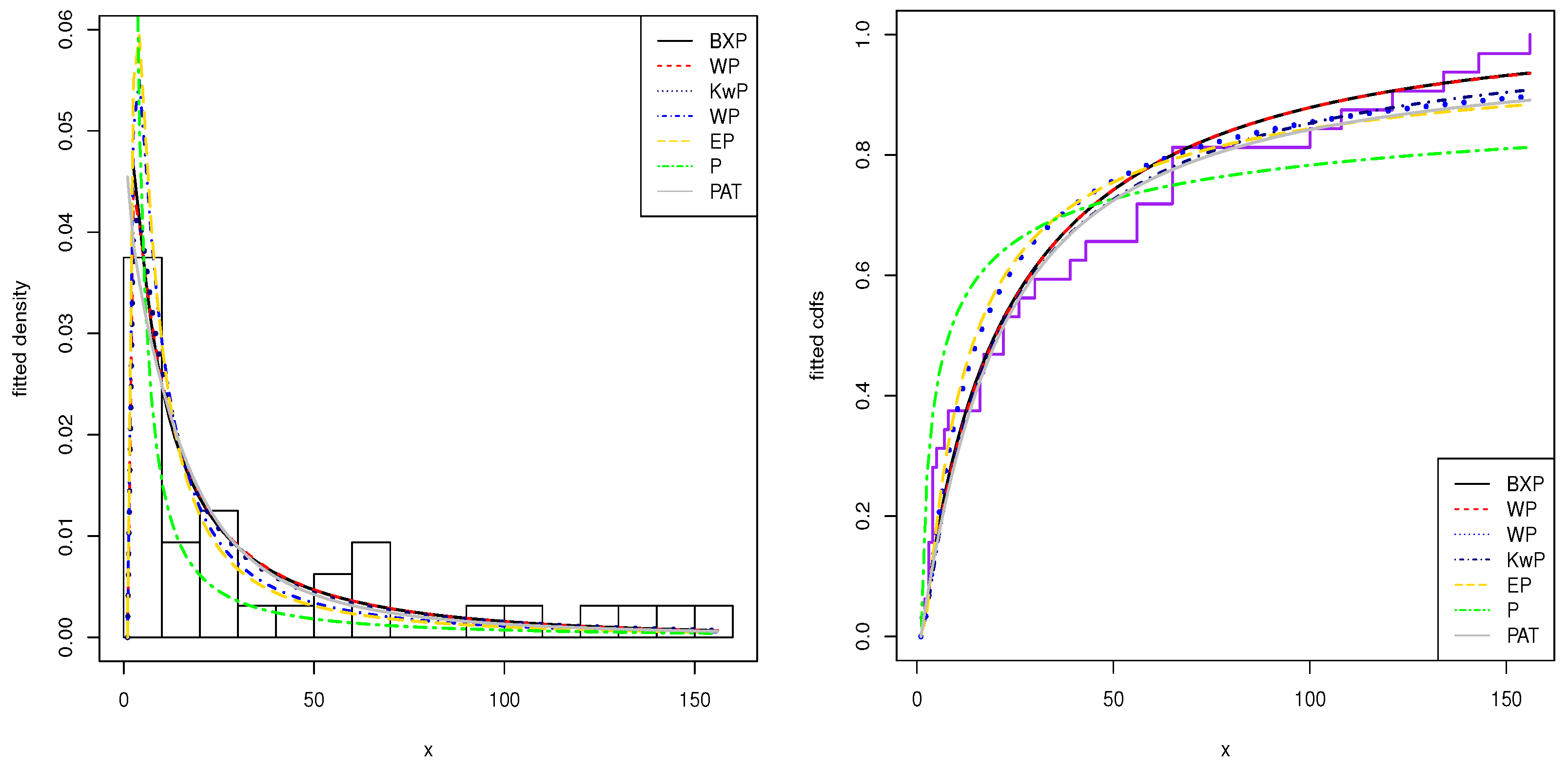
7. Real Data Modelling
8. Value-at-Risk Estimation with the BXP Distribution
8.1. S&P-500
9. Conclusions
Author Contributions
Conflicts of Interest
References
- Afify, Ahmed Z., Haitham M. Yousof, Gholamhossein Hamedani, and Gokarna Aryal. 2016. The exponentiated Weibull-Pareto distribution with Application. Journal of Statistical Theory and Applications 15: 326–44. [Google Scholar] [CrossRef]
- Akinsete, Alfred, Felix Famoye, and Carl Lee. 2008. The beta-Pareto distribution. Statistics 42: 547–63. [Google Scholar] [CrossRef]
- Balkema, August Aimé, and Laurens De Haan. 1974. Residual life time at great age. The Annals of Probability 2: 792–804. [Google Scholar] [CrossRef]
- Bourguignon, Marcelo, Rodrigo B. Silva, Luz M. Zea, and Gauss M. Cordeiro. 2013. The Kumaraswamy Pareto distribution. Journal of Statistical Theory and Applications 12: 129–44. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Feigl, Polly, and Marvin Zelen. 1965. Estimation of exponential survival probabilities with concomitant information. Biometrics 21: 826–38. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2015. Modelling insurance data with the Pareto ArcTan distribution. ASTIN Bulletin The Journal of the International Actuarial Association 45: 639–60. [Google Scholar] [CrossRef]
- Gupta, Ramesh C., Pushpa Gupta, and Rameshwar Gupta. 1998. Modeling failure time data by Lehmann alternatives. Communications in Statistics-Theory and Methods 27: 887–904. [Google Scholar] [CrossRef]
- Johnson, Norman L., Samuel Kotz, and Narayanaswamy Balakrishnan. 1994. Continuous Univariate Distributions. New York: Wiley, vol. 1. [Google Scholar]
- Kuş, Coşkun. 2007. A new lifetime distribution. Computational Statistics & Data Analysis 51: 4497–509. [Google Scholar]
- Mead, Mohamed E., Ahmed Z. Afify, Gholamhossein Hamedani, and Indranil Ghosh. 2017. The beta exponential Frechet distribution with applications. Austrian Journal of Statistics 46: 41–63. [Google Scholar] [CrossRef]
- Nadarajah, Saralees, and Sumaya Eljabri. 2013. The Kumaraswamy GP distribution. Journal of Data Science 11: 739–66. [Google Scholar]
- Pickands, James, III. 1975. Statistical inference using extreme order statistics. The Annals of Statistics 3: 119–31. [Google Scholar]
- Stoppa, Gabriele. 1990. A new model for income size distribution. In Income and Wealth Distribution, Inequality and Poverty. Berlin: Springer, pp. 33–41. [Google Scholar]
- Swain, James J., Sekhar Venkatraman, and James R. Wilson. 1988. Least squares estimation of distribution function in Johnsons translation system. Journal of Statistical Computation and Simulation 29: 271–97. [Google Scholar] [CrossRef]
- Tahir, Muhammad H., Gauss M. Cordeiro, Ayman Alzaatreh, M. Mansoor, and M. Zubair. 2016. A New Weibull-Pareto Distribution: Properties and Applications. Communications in Statistics-Simulation and Computation 45: 3548–67. [Google Scholar] [CrossRef]
- Yousof, Haitham M., Ahmed Z. Afify, Gholamhossein Hamedani, and Gokarna Aryal. 2016. The Burr X generator of distributions for lifetime data. Journal of Statistical Theory and Applications 16: 1–19. [Google Scholar] [CrossRef]





| (0.5, 0.5, 0.5) | 1.2801 | 1.1395 | 0.7311 | 4.4238 |
| (1, 1, 1) | 1.6330 | 0.9671 | −1.2539 | 3.2132 |
| (2, 2, 2) | 2.5365 | 1.7311 | −1.9644 | 4.3986 |
| (1, 2, 3) | 2.9606 | 5.9323 | −0.8355 | 1.3785 |
| (4, 2, 0.5) | 0.7411 | 0.0415 | −4.1218 | 17.7934 |
| (10, 2, 0.25) | 0.4074 | 0.0011 | −6.3710 | 97.4674 |
| (0.25, 5, 2) | 0.4962 | 1.2671 | 1.4287 | 2.6058 |
| (0.9, 5, 1.8) | 1.0633 | 1.5440 | 0.0255 | 0.7191 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3, 1.5, 2 | 3.0144 | 1.5495 | 2.0286 | 2.9995 | 1.5247 | 2.0159 | 3.0001 | 1.5125 | 2.0060 |
| (0.1831) | (0.1585) | (0.1155) | (0.0399) | (0.1059) | (0.0757) | (0.0400) | (0.0648) | (0.0485) | |
| [0.0144] | [0.0494] | [0.0286] | [−0.0005] | [0.0247] | [0.0160] | [0.0001] | [0.0125] | [0.0059] | |
| {0.0330} | {0.0270} | {0.0140} | {0.0016} | {0.0117} | {0.0060} | {0.0016} | {0.0043} | {0.0023} | |
| 3, 2, 1 | 3.0772 | 2.0550 | 1.0040 | 3.0019 | 2.0093 | 1.0021 | 3.0016 | 2.0073 | 1.0013 |
| (0.2928) | (0.2053) | (0.0443) | (0.0212) | (0.0976) | (0.0211) | (0.0203) | (0.0851) | (0.0182) | |
| [0.0772] | [0.0550] | [0.0040] | [0.0019] | [0.0093] | [0.0021] | [0.0016] | [0.0073] | [0.0013] | |
| {0.0900} | {0.0443} | {0.0020} | {0.0004} | {0.0095} | {0.0004} | {0.0004} | {0.0072} | {0.0003} | |
| 5, 0.5, 5 | 5.0863 | 0.5111 | 5.1216 | 5.0044 | 0.5012 | 5.0065 | 4.9954 | 0.4996 | 4.9970 |
| (0.2792) | (0.0290) | (0.3641) | (0.0404) | (0.0095) | (0.0490) | (0.0400) | (0.0084) | (0.0439) | |
| [0.0863] | [0.0111] | [0.1216] | [0.0044] | [0.0012] | [0.0065] | [−0.0046] | [−0.0004] | [−0.0030] | |
| {0.0838} | {0.0010} | {0.1447} | {0.0072} | {0.00008} | {0.0071} | {0.0054} | {0.00007} | {0.0070} | |
| 10, 30, 20 | 10.0407 | 30.0438 | 20.0024 | 10.0009 | 30.0013 | 19.9998 | 9.9984 | 29.9980 | 20.0001 |
| (0.2318) | (0.2809) | (0.0101) | (0.0110) | (0.0130) | (0.0086) | (0.0101) | (0.0120) | (0.0059) | |
| [0.0406] | [0.0438] | [0.0024] | [0.0009] | [0.0013] | [−0.0002] | [−0.0016] | [−0.0020] | [0.0001] | |
| {0.0543} | {0.0793} | {0.0001} | {0.0001} | {0.0001} | {0.00007} | {0.0001} | {0.0001} | {0.00004} | |
| 4, 0.5, 0.5 | 3.9077 | 0.5147 | 0.5265 | 4.0179 | 0.5121 | 0.5203 | 4.0012 | 0.5052 | 0.5079 |
| (0.1261) | (0.0532) | (0.0926) | (0.1010) | (0.0411) | (0.0711) | (0.0878) | (0.0246) | (0.0440) | |
| [−0.0923] | [0.0147] | [0.0265] | [0.0179] | [0.0121] | [0.0203] | [0.0012] | [0.0052] | [0.0079] | |
| {0.0356} | {0.0030} | {0.0100} | {0.0164} | {0.0018} | {0.0054} | {0.0076} | {0.0006} | {0.0019} | |
| Leukaemia Data | ||||
| Model | ||||
| BXP | 0.8505 | 0.1900 | 1 | |
| (0.1785) | (0.0146) | |||
| PAT | 0.8603 | 12.6124 | 1 | |
| (0.1428) | (6.6619) | |||
| KwP | 2.3992 | 0.0007 | 1,828,015 | 1 |
| (0.0291) | (0.0001) | (5.9317) | ||
| WP | 1.8274 | 0.1994 | 1 | |
| (0.2846) | (0.0145) | |||
| BP | 51.9800 | 0.0239 | 3.8540 | 1 |
| (0.1240) | (0.0048) | (0.6551) | ||
| EP | 4.3606 | 0.7089 | 1 | |
| (1.3221) | (0.1192) | |||
| P | 0.3319 | 1 | ||
| (0.0596) | ||||
| Earthquake Data | ||||
| BXP | 1.9916 | 0.1678 | 9 | |
| (0.5622) | (0.0117) | |||
| PAT | 1.1704 | 168.1574 | 9 | |
| (0.0667) | (5.9619) | |||
| WP | 2.9843 | 0.1408 | 9 | |
| (0.4949) | (0.0074) | |||
| BP | 60.8341 | 0.0428 | 12.5592 | 9 |
| (1.0981) | (0.0053) | (0.9570) | ||
| EP | 26.9837 | 0.8707 | 9 | |
| (5.7196) | (0.0770) | |||
| P | 0.2264 | 9 | ||
| (0.0472) | ||||
| Leukaemia Data | |||||
|---|---|---|---|---|---|
| Model | AIC | CAIC | BIC | HQIC | KS |
| BXP | 295.0115 | 295.4401 | 297.8795 | 295.9464 | 0.1328 |
| PAT | 301.1477 | 301.5763 | 304.0157 | 302.0826 | 0.1398 |
| KwP | 298.9148 | 299.8037 | 303.2167 | 300.3171 | 0.1486 |
| WP | 295.2830 | 295.7116 | 298.1510 | 296.2179 | 0.1418 |
| BP | 301.5970 | 302.4859 | 305.8990 | 302.9994 | 0.1494 |
| EP | 300.9643 | 301.3929 | 303.8323 | 301.8992 | 0.1630 |
| P | 319.1294 | 319.2673 | 320.5634 | 319.5968 | 0.2733 |
| Earthquake Data | |||||
| BXP | 381.9004 | 382.5004 | 384.1714 | 382.4715 | 0.0817 |
| PAT | 383.7187 | 384.3187 | 385.9897 | 384.2899 | 0.0971 |
| WP | 382.3901 | 382.9901 | 384.6610 | 382.9612 | 0.0962 |
| BP | 384.5029 | 385.7661 | 387.9094 | 385.3597 | 0.0819 |
| EP | 384.3233 | 384.9233 | 386.5943 | 384.8944 | 0.1038 |
| P | 420.6338 | 420.8243 | 421.7693 | 420.9194 | 0.4218 |
| Descriptive Statistics | S&P-500 |
|---|---|
| Number of observations | 1465 |
| Minimum | −0.0402 |
| Maximum | 0.0383 |
| Mean | 0.0004 |
| Median | 0.0004 |
| Std.Deviation | 0.007 |
| Skewness | −0.322 |
| Kurtosis | 5.403 |
| Jarque–Bera | 377.839 (<0.001) |
| Ljung–Box | 28.516 (0.098) |
| Models | Parameters | Goodness-of-Fit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| KS | |||||||||
| BXP | 3.2480 | 0.1893 | 4.89818 × 10 | −93.4016 | 0.1427 | 0.3809 | 0.0556 | ||
| 1.0266 | 0.0120 | - | |||||||
| GP | 0.0847 | 0.0057 | −88.7171 | 0.1498 | 0.4039 | 0.0661 | |||
| 0.1996 | 0.0015 | ||||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkmaz, M.Ç.; Altun, E.; Yousof, H.M.; Afify, A.Z.; Nadarajah, S. The Burr X Pareto Distribution: Properties, Applications and VaR Estimation. J. Risk Financial Manag. 2018, 11, 1. https://doi.org/10.3390/jrfm11010001
Korkmaz MÇ, Altun E, Yousof HM, Afify AZ, Nadarajah S. The Burr X Pareto Distribution: Properties, Applications and VaR Estimation. Journal of Risk and Financial Management. 2018; 11(1):1. https://doi.org/10.3390/jrfm11010001
Chicago/Turabian StyleKorkmaz, Mustafa Ç., Emrah Altun, Haitham M. Yousof, Ahmed Z. Afify, and Saralees Nadarajah. 2018. "The Burr X Pareto Distribution: Properties, Applications and VaR Estimation" Journal of Risk and Financial Management 11, no. 1: 1. https://doi.org/10.3390/jrfm11010001
APA StyleKorkmaz, M. Ç., Altun, E., Yousof, H. M., Afify, A. Z., & Nadarajah, S. (2018). The Burr X Pareto Distribution: Properties, Applications and VaR Estimation. Journal of Risk and Financial Management, 11(1), 1. https://doi.org/10.3390/jrfm11010001