Mapping the Trend, Application and Forecasting Performance of Asymmetric GARCH Models: A Review Based on Bibliometric Analysis
Abstract
:1. Introduction
- To evaluate the current trend in asymmetric GARCH models in the literature using bibliometric analysis;
- To provide thorough analysis of the use and forecasting capabilities of asymmetric GARCH models.
2. Data and Methodology
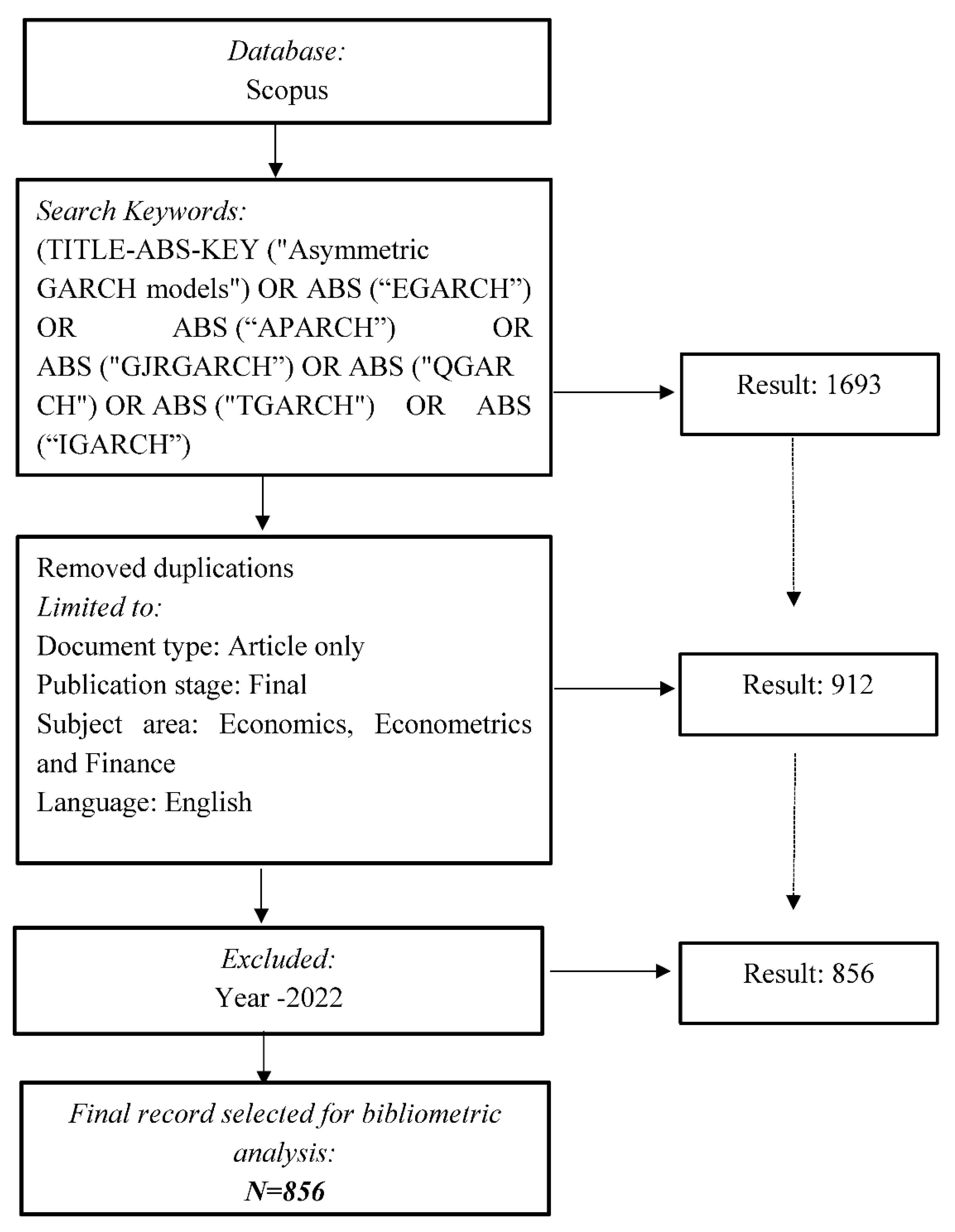
2.1. Locating Study
2.2. Selection of Relevant Research
3. Bibliometric Analysis
3.1. Descriptive Analysis
3.1.1. Annual Publication Trend
3.1.2. Leading Countries
3.1.3. Influential Authors
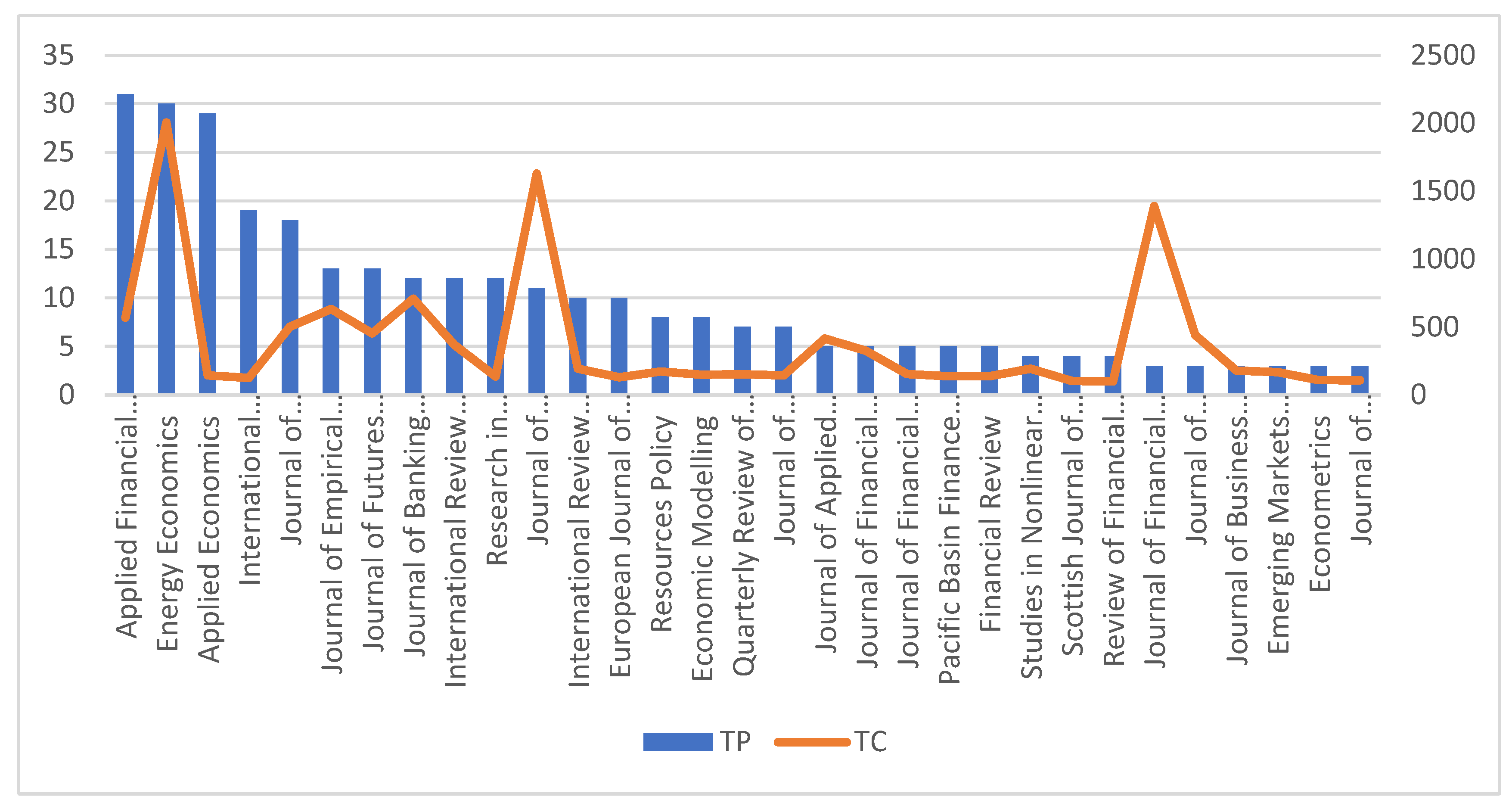
3.1.4. Impactful Journals
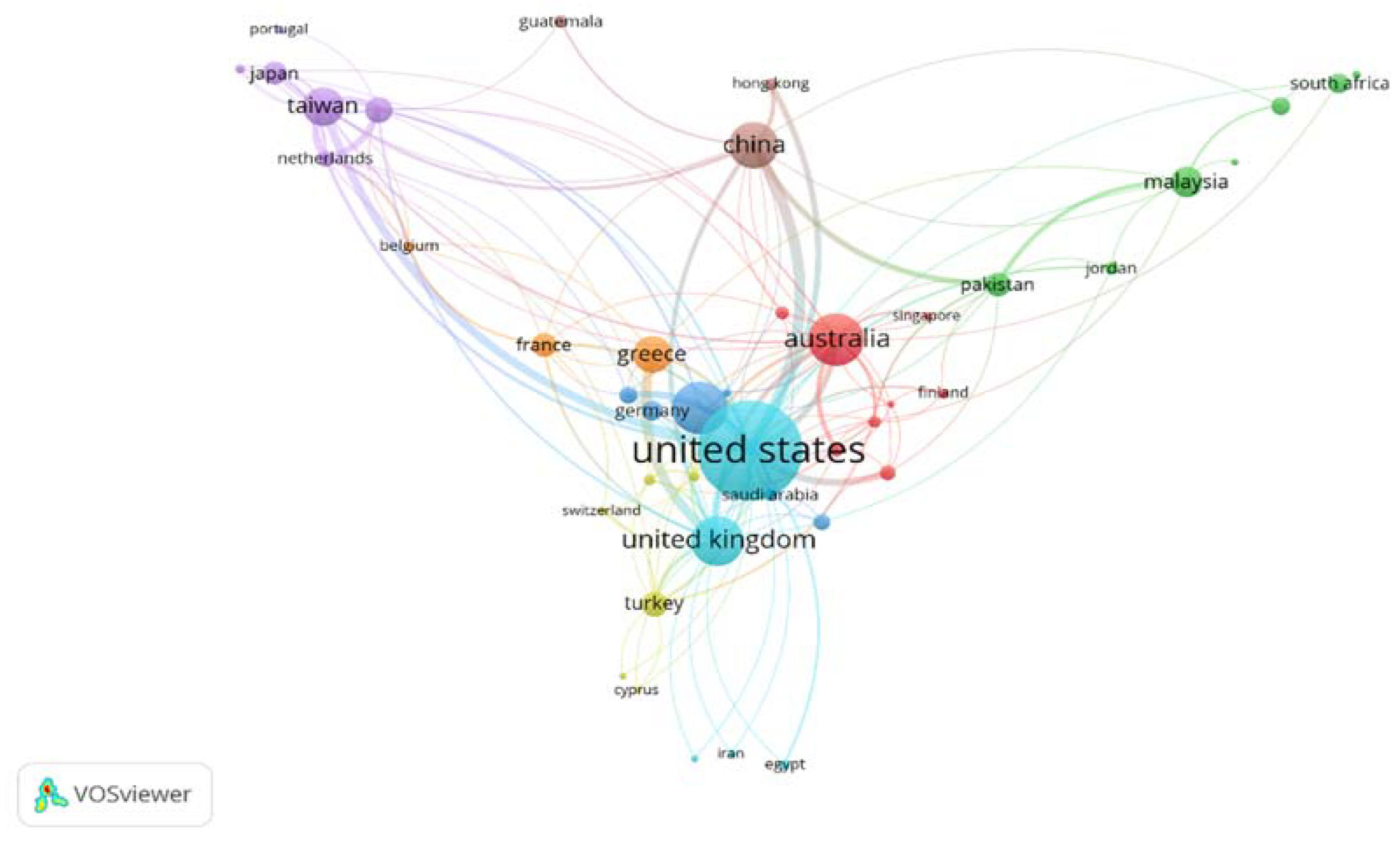
3.1.5. Country Collaborations
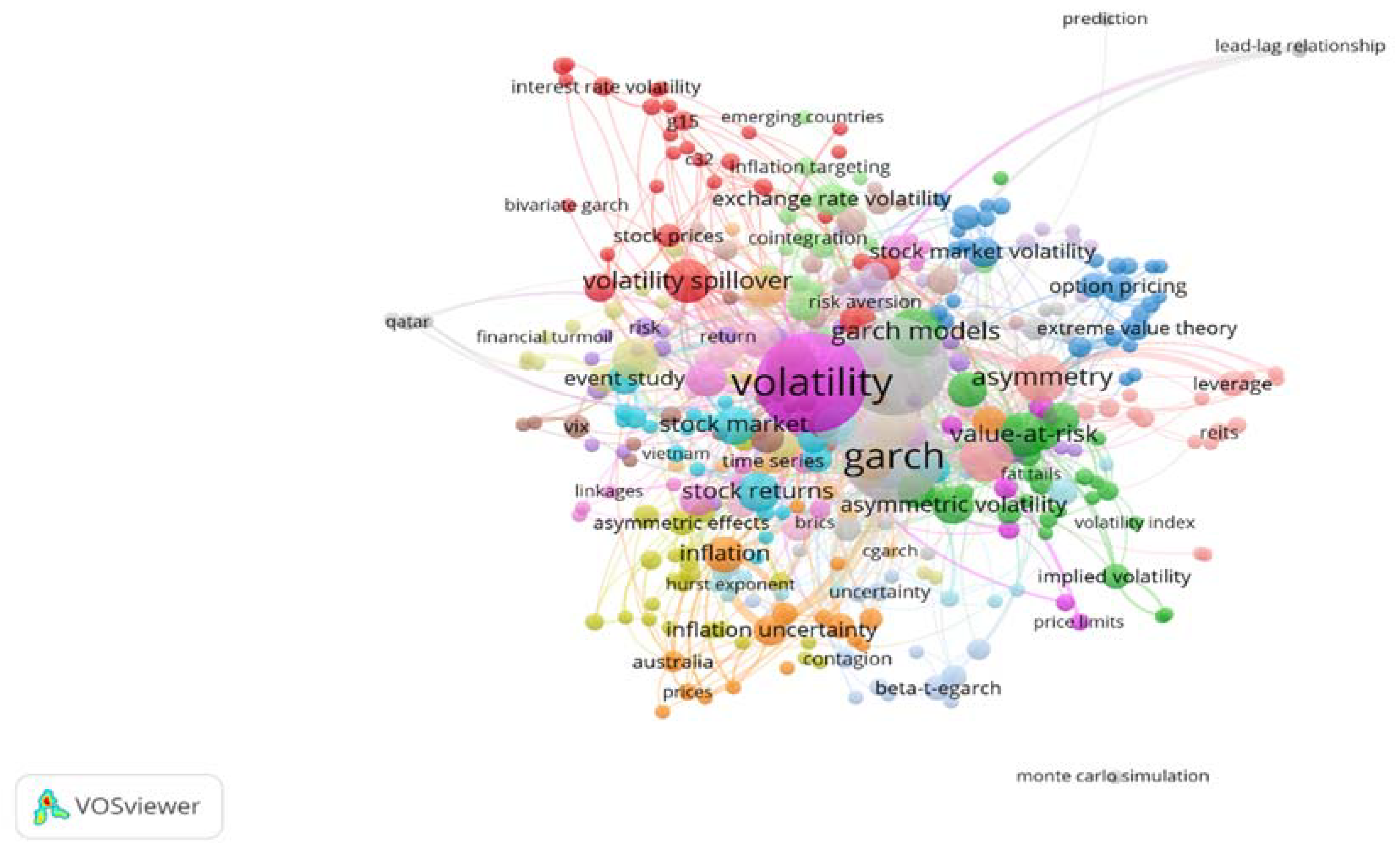
3.1.6. Co-Occurrence of Author Keywords
3.1.7. Factor Analysis Exposing the Thematic Factors of Asymmetric GARCH Models
3.1.8. Bibliographic Coupling of Countries
3.1.9. Factors Influencing Citation: Correlation and Regression
4. Systematic Review of Highly Cited Articles and Critical Evaluation
A Critical Evaluation of GARCH Models
5. Recommendations for Future Research
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alberg, Dima, Haim Shalit, and Rami Yosef. 2008. Estimating stock market volatility using asymmetric GARCH models. Applied Financial Economics 18: 1201–8. [Google Scholar] [CrossRef]
- Aliyev, Fuzuli, Richard Ajayi, and Nijat Gasim. 2020. Modelling asymmetric market volatility with univariate GARCH models: Evidence from Nasdaq-100. The Journal of Economic Asymmetries 22: e00167. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Tim Bollerslev. 1989. Common Stochastic Trends in a System of Exchange Rates. The Journal of Finance 44: 167–81. [Google Scholar] [CrossRef]
- Bauwens, Luc, Sébastien Laurent, and Jeroen VK Rombouts. 2006. Multivariate GARCH models: A survey. Journal of Applied Econometrics 21: 79–109. [Google Scholar] [CrossRef]
- Black, Fischer. 1976. Studies of Stock Market Volatility Changes. In Proceedings of the 1976 Meeting of the Business and Economic Statistics Section. Washington, DC: American Statistical Association. [Google Scholar]
- Bollerslev, Tim, and Hans Ole Mikkelsen. 1996. Modeling and pricing long memory in stock market volatility. Journal of Econometrics 73: 151–84. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics 69: 542. [Google Scholar] [CrossRef]
- Booth, G. Geoffrey, Teppo Martikainen, and Yiuman Tse. 1997. Price and volatility spillovers in Scandinavian stock markets. Journal of Banking & Finance 21: 811–23. [Google Scholar]
- Braun, Phillip A., Daniel B. Nelson, and Alain M. Sunier. 1995. Good news, bad news, volatility, and betas. The Journal of Finance 50: 1575–603. [Google Scholar] [CrossRef]
- Campbell, John Y., and Ludger Hentschel. 1992. No news is good news. An asymmetric model of changing volatility in stock returns. Journal of Financial Economics 31: 281–318. [Google Scholar] [CrossRef]
- Cao, Charles Q., and Ruey S. Tsay. 1992. Nonlinear time-series analysis of stock volatilities. Journal of Applied Econometrics 7: S165–85. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2019a. The accuracy of asymmetric GARCH model estimation. International Economics 157: 179–202. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2019b. Volatility estimation for Bitcoin: Replication and robustness. International Economics 157: 23–32. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances. Value, leverage, and interest rate effects. Journal of Financial Economics 10: 407–32. [Google Scholar] [CrossRef]
- Cochrane, John H. 1991. A critique of the application of unit root tests. Journal of Economic Dynamics and Control 15: 275–84. [Google Scholar] [CrossRef]
- Day, Theodore E., and Craig M. Lewis. 1992. Stock market volatility and the information content of stock index options. Journal of Econometrics 52: 267–87. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987. [Google Scholar] [CrossRef]
- Engle, Robert F., and Victor K. Ng. 1993. Measuring and Testing the Impact of News on Volatility. The Journal of Finance 48: 1749–78. [Google Scholar] [CrossRef]
- French, Kenneth R., G. William Schwert, and Robert F. Stambaugh. 1987. Expected stock returns and volatility. Journal of Financial Economics 19: 3–29. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Gökbulut, R. İlker, and Mehmet Pekkaya. 2014. Estimating and Forecasting Volatility of Financial Markets Using Asymmetric GARCH Models: An Application on Turkish Financial Markets. International Journal of Economics and Finance 6: 23–35. [Google Scholar] [CrossRef]
- Goodell, John W., Satish Kumar, Weng Marc Lim, and Debidutta Pattnaik. 2021. Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. Journal of Behavioral and Experimental Finance 32: 100577. [Google Scholar] [CrossRef]
- Hammoudeh, Shawkat, and Yuan Yuan. 2008. Metal volatility in presence of oil and interest rate shocks. Energy Economics 30: 606–20. [Google Scholar] [CrossRef]
- Hentschel, Ludger. 1995. All in the family Nesting symmetric and asymmetric GARCH models. Journal of Financial Economics 39: 71–104. [Google Scholar] [CrossRef]
- Heynen, Ronald, Angelien Kemna, and Ton Vorst. 2016. Analysis of the Term Structure of Implied Volatilities. The Journal of Financial and Quantitative Analysis 29: 31–56. [Google Scholar] [CrossRef]
- Huang, Wei-Chiao, and Yuanlei Zhu. 2004. Are shocks asymmetric to volatility of Chinese stock markets? Review of Pacific Basin Financial Markets and Policies 7: 379–95. [Google Scholar] [CrossRef]
- Jain, Jinesh, Nidhi Walia, Simarjeet Singh, and Esha Jain. 2021. Mapping the field of behavioural biases: A literature review using bibliometric analysis. Management Review Quarterly vol. 1: 1–33. [Google Scholar] [CrossRef]
- Kanas, Angelos. 2000. Volatility Spillovers Between Stock Returns and Exchange Rate Changes: International Evidence. Journal of Business Finance & Accounting 27: 447–67. [Google Scholar]
- Koutmos, Gregory, and G. Geoffrey Booth. 1995a. Asymmetric volatility transmission in international stock markets. Journal of International Money and Finance 14: 747–62. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar, Seema Narayan, and Arti Prasad. 2008. Understanding the oil price-exchange rate nexus for the Fiji islands. Energy Economics 30: 2686–96. [Google Scholar] [CrossRef]
- Lee, Cheng F., Gong-meng Chen, and Oliver M. Rui. 2001. Stock returns and volatility on China’s stock markets. Journal of Financial Research 24: 523–43. [Google Scholar] [CrossRef]
- Lee, Hojin. 2017. Forecasting Performance of Asymmetric GARCH Stock Market Volatility Models. SSRN Electronic Journal 13: 109–43. [Google Scholar] [CrossRef]
- Lundbergh, Stefan, and Timo Teräsvirta. 2002. Evaluating GARCH models. Journal of Econometrics 110: 417–35. [Google Scholar] [CrossRef]
- Maqsood, Arfa, Suboohi Safdar, Rafia Shafi, and Ntato Jeremiah Lelit. 2013. Modeling Stock Market Volatility Using GARCH Models: A Case Study of Nairobi Securities Exchange (NSE). Open Journal of Statistics 7: 369–81. [Google Scholar] [CrossRef]
- McAleer, Michael, Felix Chan, and Dora Marinova. 2007. An econometric analysis of asymmetric volatility: Theory and application to patents. Journal of Econometrics 139: 259–84. [Google Scholar] [CrossRef]
- Mohammadi, Hassan, and Lixian Su. 2010. International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models. Energy Economics 32: 1001–8. [Google Scholar] [CrossRef]
- Naik, Maithili S., and Y. V. Reddy. 2021. India VIX and forecasting ability of symmetric and asymmetric GARCH models. Asian Economic and Financial Review 11: 252–262. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 59: 347. [Google Scholar] [CrossRef]
- Pattnaik, Debidutta, Mohammad Kabir Hassan, Satish Kumar, and Justin Paul. 2020. Trade credit research before and after the global financial crisis of 2008—A bibliometric overview. Research in International Business and Finance 54: 101287. [Google Scholar] [CrossRef]
- Phoong, Seuk Wai, Seuk Yen Phoong, and Shi Ling Khek. 2022. Systematic Literature Review With Bibliometric Analysis on Markov Switching Model: Methods and Applications. SAGE Open 12: 21582440221093062. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2006. Modeling and forecasting petroleum futures volatility. Energy Economics 28: 467–88. [Google Scholar] [CrossRef]
- Shahateet, Mohammed. 2019. Testing the linkages of Arab stock markets: A multivariate GARCH approach. Investment Management and Financial Innovations 16: 192–204. [Google Scholar] [CrossRef]
- Srinivasan, P., and P. Ibrahim. 2010. Forecasting Stock Market Volatility of Bse-30 Index Using Garch Models. Asia Pacific Business Review 6: 47–60. [Google Scholar] [CrossRef]
- Tandon, Anushree, Puneet Kaur, Matti Mäntymäki, and Amandeep Dhir. 2021. Blockchain applications in management: A bibliometric analysis and literature review. Technological Forecasting and Social Change 166: 120649. [Google Scholar] [CrossRef]
- Teräsvirta, Timo. 2009. An Introduction to Univariate GARCH Models. In Handbook of Financial Time Series. Edited by Thomas V. Mikosch, Jens-Peter Kreiß, Richard A. Davis and Torben Gustav Andersen. Berlin and Heidelberg: Springer. [Google Scholar] [CrossRef]
- Tse, Yiuman. 1999. Price discovery and volatility spillovers in the DJIA index and futures markets. Journal of Futures Markets 19: 911–30. [Google Scholar] [CrossRef]
- Virbickaite, Audrone, M. Concepción Ausín, and Pedro Galeano. 2015. Bayesian inference methods for univariate and multivariate GARCH models: A survey. Journal of Economic Surveys 29: 76–96. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]





| Research Objective | Research Methodology | |
|---|---|---|
| Bibliometric analysis | To understand the evolution of and trend in asymmetric GARCH models | Publication trend |
| To figure out the leading countries, impactful journals, and influential authors with respect to asymmetric GARCH models | Citation analysis | |
| To assess the structure and pattern of country collaboration in this field of research | Co-authorship analysis of countries | |
| To figure out the conceptual structure of keywords in asymmetric GARCH models | Co-occurrence analysis | |
| To understand countries’ coupling structures and how often countries share similar literature in this field of research | Bibliographic coupling of countries | |
| Factor analysis exposing thematic factors in asymmetric GARCH models Factors influencing total citation in publication in asymmetric GARCH models | Principal Component Analysis Correlation and Regression | |
| Systematic review | To understand the application and forecasting performance of asymmetric GARCH models | Citation analysis of highly cited documents |
| No. | Author | TP | TC |
|---|---|---|---|
| 1 | Engle R.F. | 2 | 2796 |
| 2 | Ng V.K. | 1 | 1749 |
| 3 | Hentschel L. | 2 | 1369 |
| 4 | Campbell J.Y. | 1 | 1003 |
| 5 | Bollerslev T. | 2 | 719 |
| 6 | Mikkelsen H.O. | 2 | 719 |
| 7 | Laurent S. | 4 | 661 |
| 8 | Giot P. | 3 | 589 |
| 9 | Booth G.G. | 3 | 568 |
| 10 | Koutmos G. | 5 | 428 |
| Rank | Source | TP | P (%) | TC | C/P | ABDC | H |
|---|---|---|---|---|---|---|---|
| 1 | Energy Economics | 30 | 10.6 | 2006 | 66.86 | A* | 168 |
| 2 | Journal of Econometrics | 11 | 3.88 | 1630 | 148.18 | A* | 166 |
| 3 | Journal of Empirical Finance | 13 | 4.59 | 632 | 48.61 | A | 80 |
| 4 | Applied Financial Economics | 31 | 10.9 | 568 | 18.32 | B | 57 |
| 5 | International Review of Financial Analysis | 12 | 4.24 | 368 | 30.66 | A | 69 |
| 6 | International Review of Economics and Finance | 10 | 3.53 | 193 | 19.3 | N/A | 59 |
| 7 | Economic Modelling | 8 | 2.82 | 149 | 18.62 | A | 87 |
| 8 | Applied Economics | 29 | 10.24 | 144 | 4.96 | A | 91 |
| 9 | European Journal of Finance | 10 | 3.53 | 129 | 12.9 | A | 39 |
| 10 | International Research Journal of Finance and Economics | 19 | 6.71 | 124 | 6.52 | N/A | 27 |
| 11 | Applied Economics Letters | 19 | 6.71 | 99 | 5.21 | B | 54 |
| 12 | Journal of Economics and Finance | 9 | 3.18 | 79 | 2.11 | B | 31 |
| 13 | Finance Research Letters | 9 | 3.18 | 66 | 7.33 | A | 62 |
| 14 | International Journal of Financial Studies | 8 | 2.82 | 53 | 6.62 | B | 17 |
| 15 | Asia-Pacific Financial Markets | 12 | 4.24 | 50 | 4.16 | C | 22 |
| 16 | Cogent Economics and Finance | 11 | 3.88 | 49 | 4.45 | B | 23 |
| 17 | Journal of Asian Finance, Economics, and Business | 11 | 3.88 | 44 | 4 | N/A | 20 |
| 18 | International Journal of Energy Economics and Policy | 8 | 2.82 | 34 | 4.25 | C | 39 |
| 19 | Investment Management and Financial Innovations | 13 | 4.59 | 27 | 2.07 | B | 20 |
| 20 | Economics Bulletin | 10 | 3.53 | 17 | 1.7 | C | 34 |
| No. | Country | Documents | Citations | Total Link Strength |
|---|---|---|---|---|
| 1 | United States | 167 | 7277 | 79 |
| 2 | United Kingdom | 67 | 1072 | 46 |
| 3 | Australia | 72 | 1437 | 37 |
| 4 | China | 62 | 896 | 35 |
| 5 | Spain | 29 | 366 | 29 |
| 6 | Taiwan | 48 | 542 | 28 |
| 7 | Netherlands | 15 | 808 | 26 |
| 8 | Pakistan | 26 | 202 | 18 |
| 9 | Turkey | 28 | 239 | 18 |
| 10 | Greece | 45 | 641 | 15 |
| No | Keyword | Occurrences | TLS |
|---|---|---|---|
| 1 | Volatility | 135 | 270 |
| 2 | EGARCH | 130 | 262 |
| 3 | GARCH | 114 | 256 |
| 4 | GARCH Models | 29 | 50 |
| 5 | Asymmetry | 28 | 64 |
| 6 | EGARCH Model | 27 | 35 |
| 7 | Leverage Effect | 27 | 55 |
| 8 | Asymmetric GARCH | 23 | 55 |
| 9 | Volatility Spillover | 22 | 45 |
| 10 | Asymmetric Volatility | 16 | 38 |
| Communalities | |||||||
|---|---|---|---|---|---|---|---|
| SI | Initial | Extraction | SI | Initial | Extraction | ||
| 1 | Crisis | 1.000 | 0.719 | 21 | Exchange Rate | 1.000 | 0.864 |
| 2 | ARCH | 1.000 | 0.736 | 22 | Forecasting | 1.000 | 0.860 |
| 3 | GARCH | 1.000 | 0.818 | 23 | Risk Assessment | 1.000 | 0.991 |
| 4 | Europe | 1.000 | 0.965 | 24 | Price Dynamics | 1.000 | 0.914 |
| 5 | Uk | 1.000 | 0.636 | 25 | Financial Uncertainty | 1.000 | 0.949 |
| 6 | Asymmetry | 1.000 | 0.656 | 26 | APARCH | 1.000 | 0.969 |
| 7 | Volatility Forecasting | 1.000 | 0.973 | 27 | Oil Price | 1.000 | 0.994 |
| 8 | China | 1.000 | 0.993 | 28 | Eurasia | 1.000 | 0.997 |
| 9 | Forecasting Model | 1.000 | 0.997 | 29 | EGARCH | 1.000 | 0.983 |
| 10 | Gold | 1.000 | 0.673 | 30 | TGARCH | 1.000 | 0.994 |
| 11 | Japan | 1.000 | 0.993 | 31 | COVID-19 | 1.000 | 0.991 |
| 12 | Asymmetric Volatility | 1.000 | 0.993 | 32 | Global Pandemic | 1.000 | 0.995 |
| 13 | Econometrics | 1.000 | 0.912 | 33 | Leverage Effect | 1.000 | 0.996 |
| 14 | GARCH Models | 1.000 | 0.956 | 34 | Causality | 1.000 | 0.984 |
| 15 | United States | 1.000 | 0.969 | 35 | Regression Analysis | 1.000 | 0.969 |
| 16 | Time Series Analysis | 1.000 | 0.921 | 36 | Financial Crisis | 1.000 | 0.995 |
| 17 | Stock Returns | 1.000 | 0.993 | 37 | Interest Rate | 1.000 | 0.988 |
| 18 | Far East | 1.000 | 0.985 | 38 | Volatility Clustering | 1.000 | 0.985 |
| 19 | Asymmetric Effect | 1.000 | 0.994 | 39 | Asymmetric Volatility | 1.000 | 0.994 |
| 20 | Volatility Persistence | 1.000 | 0.997 | 40 | Volatility Spillover | 1.000 | 0.881 |
| Components | ||||
|---|---|---|---|---|
| Forecasting Models | Financial Assets | Financial Markets | Financial Crisis | |
| ARCH | 0.994 | |||
| GARCH | 0.994 | |||
| EGARCH | 0.994 | |||
| TGARCH | 0.994 | |||
| GARCH Models | 0.994 | |||
| Asymmetry | 0.994 | |||
| Leverage Effect | 0.994 | |||
| Forecasting model | 0.994 | |||
| Time Series Analysis | 0.993 | |||
| Volatility Forecasting | 0.955 | |||
| Risk Assessment | 0.954 | |||
| Econometrics | 0.954 | |||
| APARCH | 0.954 | |||
| Forecasting | 0.953 | |||
| Asymmetric Effect | 0.986 | |||
| Asymmetric Volatility | 0.984 | |||
| Causality | 0.984 | |||
| Oil Price | 0.984 | |||
| Exchange Rate | 0.983 | |||
| Gold | 0.980 | |||
| Stock Returns | 0.979 | |||
| Volatility Persistence | 0.941 | |||
| Volatility Spillover | 0.850 | |||
| Interest Rate | 0.845 | |||
| Asia | 0.956 | |||
| Europe | 0.956 | |||
| Far East | 0.955 | |||
| United States | 0.955 | |||
| Japan | 0.895 | |||
| China | 0.872 | |||
| United Kingdom | 0.812 | |||
| Eurasia | 0.771 | |||
| COVID-19 | 0.992 | |||
| Regression Analysis | 0.992 | |||
| Financial Crisis | 0.992 | |||
| Price Dynamics | 0.992 | |||
| Financial Uncertainty | 0.986 | |||
| Asymmetric Volatility | 0.979 | |||
| Global Pandemic | 0.805 | |||
| Crisis | 0.712 | |||
| Extraction Method: Principal Component Analysis. Rotation Method: Varimax With Kaiser Normalisation. | ||||
| N | Mean | Std. Deviation | |
|---|---|---|---|
| TC | 856 | 22.42 | 62.54 |
| LA | 856 | 12.00 | 5.43 |
| NA | 856 | 2.92 | 0.97 |
| AC | 856 | 2.17 | 0.33 |
| SAA | 856 | 1.08 | 0.15 |
| M1 | 856 | 0.82 | 0.21 |
| M2 | 856 | 0.83 | 0.24 |
| M3 | 856 | 0.25 | 0.25 |
| M4 | 856 | 0.47 | 0.72 |
| TC | LA | NA | AC | SAA | M1 | M2 | M3 | M4 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| TC | r | 1 | ||||||||
| LA | r | 0.22 ** | 1 | |||||||
| 0.000 | ||||||||||
| NA | r | 0.21 ** | −0.03 ** | 1 | ||||||
| 0.000 | 0.000 | |||||||||
| AC | r | 0.21 ** | −0.02 * | 0.03 ** | 1 | |||||
| 0.000 | 0.020 | 0.000 | ||||||||
| SAA | r | 0.12 ** | 0.13 * | 0.14 * | −0.05 * | 1 | ||||
| 0.030 | 0.030 | 0.020 | 0.026 | |||||||
| M1 | r | 0.15 ** | −0.03 | 0.21 | −0.06 | 0.871 ** | 1 | |||
| 0.001 | 0.211 | 0.112 | 0.062 | 0.075 | ||||||
| M2 | r | 0.020 ** | 0.255 | 0.288 | 0.350 | 0.785 ** | 0.748 ** | 1 | ||
| 0.002 | 0.425 | 0.363 | 0.265 | 0.002 | 0.005 | |||||
| M3 | r | 0.195 ** | 0.214 | 0.249 | 0.296 | 0.764 ** | 0.725 ** | 0.987 ** | 1 | |
| 0.004 | 0.504 | 0.435 | 0.351 | 0.004 | 0.008 | 0.000 | ||||
| M4 | r | 0.288 * | 0.310 | 0.337 | 0.342 | 0.737 ** | 0.741 ** | 0.870 ** | 0.925 ** | 1 |
| 0.064 | 0.327 | 0.284 | 0.277 | 0.006 | 0.006 | 0.000 | 0.000 | |||
| Variables | Beta | t Statistics | Sig. Value |
|---|---|---|---|
| (Constant) | −2.21 | 0.01 | |
| LA | 0.31 | 1.21 | 0.01 |
| NA | 0.40 | 1.02 | 0.00 |
| AC | 0.21 | 0.89 | 0.01 |
| SAA | 0.41 | 0.11 | 0.00 |
| M1 | 0.03 | 2.02 | 0.03 |
| M2 | 0.04 | 2.01 | 0.02 |
| M3 | 0.02 | 1.32 | 0.12 |
| M4 | 0.01 | 1.22 | 0.13 |
| R2 = 0.42 Adj. R2 = 0.411 | |||
| Document | Citation | Title | Journal | Major Research Focus | GARCH Models Used | Major Research Finding (s)/Contribution (s) | Forecasting Accuracy of GARCH Models |
|---|---|---|---|---|---|---|---|
| (Engle and Ng 1993) | 2012 | Measuring and Testing the Impact of News on Volatility | The Journal of Finance | Several models of predictable volatility were discussed, and the concept of a news impact curve was put forth. In order to account for asymmetry in the impact of news on volatility, they compared the GARCH (1, 1) model with a number of other volatility models. | GARCH (1,1), EGARCH, GJR-GARCH, AGARCH, VGARCH, NGARCH | The standard indicator of how news is incorporated into volatility estimates is the news impact curve. According to all models, negative shocks increase volatility more than positive ones. | The best model is the one proposed by Glosten, Jagannathan, and Runkle (GJR Model). |
| (Campbell and Hentschel 1992) | 1003 | No news is good news: An asymmetric model of changing volatility in stock returns | Journal of Financial Economics | Used QGARCH to estimate a model of volatility feedback in stock returns. | QGARCH, GARCH-M, QGARCH-M | The QGARCH model, in contrast to the simple GARCH model, produces residuals with means that are close to zero and fits the negative correlation between stock returns and the future volatility of returns. | No best model |
| (Bollerslev and Mikkelsen 1996) | 628 | Modeling and pricing long memory in stock market volatility | Journal of Econometrics | Proposed a new class of more adaptable fractionally integrated EGARCH models to describe the long-run determinants of volatility in the US stock market. | GARCH (1,1), EGARCH, IEGARCH, FIEGARCH | The Standard and Poor’s 500 composite index’s conditional variance is best modelled as a mean-reverting fractionally integrated process. | No best model |
| (Koutmos and Booth 1995) | 404 | Asymmetric volatility transmission in international stock markets | Journal of International Money and Finance | Spillovers in price and volatility across the three main stock markets, New York, Tokyo, and London, were modelled. The volatility transmission mechanism was explicitly modelled in the paper to account for any potential asymmetries. | Multivariate EGARCH | Using the benchmark EGARCH model, all linear and nonlinear dependencies in the return series are successfully taken into account. The mechanism for transmitting volatility is asymmetric. | The EGARCH model performs better than the Quadratic GARCH model because the latter tends to underpredict volatility associated with negative innovations. |
| (Hentschel 1995) | 366 | All in the family Nesting symmetric and asymmetric GARCH models | Journal of Financial Economics | The paper developed a family of models of generalised autoregressive heteroskedasticity (GARCH) that encompasses all the popular existing GARCH models. | GARCH, EGARCH, TGARCH, AGARCH, NAGARCH, GJRGARCH, NARCH, APARCH | The data prefer models in which large shocks increase volatility by more than they would in either the AGARCH or EGARCH models, but by less than they would in a GARCH model. | The EGARCH model is almost as robust to large shocks. |
| (Day and Lewis 1992) | 329 | Stock market volatility and the information content of stock index options | Journal of Econometrics | Analysed the informational value of the ex-ante market volatility estimates implicit in the call option prices on the Standard and Poor’s 100 Index. | GARCH (1,1), EGARCH | GARCH models provide better forecasts than EGARCH models. | The GARCH model is the best. |
| (Sadorsky 2006) | 320 | Modeling and forecasting petroleum futures volatility | Energy Economics | Compared the forecasting performance of various univariate and multivariate GARCH models. | GARCH, TGARCH, GARCH-M | The TGARCH and GARCH models both provide good fits for the volatility of heating oil, natural gas, and unleaded gasoline. | The TGARCH and GARCH models are the best. |
| (Hammoudeh and Yuan 2008) | 206 | Metal volatility in the presence of oil and interest rate shocks | Energy Economics | Used three GARCH family models to simulate volatility persistence and the leverage effect in the short and long runs. | GARCH, CGARCH, EGARCH | According to the EGARCH results, the leverage effect is only present and significant for copper, indicating that gold and silver can be good investments in anticipation of difficult times. | No best model. |
| (Braun et al. 1995) | 204 | Good News, Bad News, Volatility, and Betas | The Journal of Finance | Estimated time-varying conditional betas using the exponential ARCH (EGARCH) model in a bivariate setting. | EGARCH | These models enable asymmetrical responses to both positive and negative market and portfolio returns for market volatility, portfolio-specific volatility, and beta. | The EGARCH model can build better estimates of beta and volatility than rolling regressions. |
| (Mohammadi and Su 2010) | 197 | International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models | Energy Economics | The study extended the works on estimating the time series properties of crude oil price. | GARCH, EGARCH APARCH FIGARCH | The conditional variance of oil returns shows volatility that changes over time. Asymmetric effects are present in conditional variance. | The APARCH forecasts outperform those of the GARCH, EGARCH andFIGARCH models. |
| (Tse 1999) | 166 | Price Discovery and Volatility Spillovers in the DJIA Index and Futures Markets | Journal of Futures Markets | By analysing the common stochastic trend between the DJIA cash and futures prices, they investigated the intraday price discovery process and volatility spillover mechanism. | EGARCH | More than positive news, unfavourable innovations in either market will increase volatility in the stock and futures markets. | No best model. |
| (Booth et al. 1997) | 163 | Price and volatility spillovers in Scandinavian stock markets | Journal of Banking and Finance | Investigated the potential interaction between four Scandinavian stock markets. | EGARCH | The presence of volatility clustering and the leverage effect is found, except in the case of Denmark. | The four markets are well described by an EGARCH model with autoregressive returns. |
| (Kanas 2000) | 136 | Volatility spillovers between stock returns and exchange rate changes: International evidence | Journal of Business Finance and Accounting | Analysed the interdependence of stock returns and exchange rate. | EGARCH(1,1) EGARCH (2,1) | The study found evidence of symmetric volatility spillover from stock returns to exchange rate for all markets, except in the case of Germany. | EGARCH (1,1) is best for US, UK, France, and Canada, whereas EGARCH (2,1) is best for Germany and Japan. |
| (Kumar et al. 2008) | 113 | Understanding the oil price-exchange rate nexus for the Fiji islands | Energy Economics | Examined the connection between oil prices and the exchange rate between the dollars of Fiji and the US. | GARCH, EGARCH | The Fiji dollar appreciates as exchange rate volatility rises, and shocks to exchange rate volatility have asymmetries in their effects. | No best model. |
| (Heynen et al. 2016) | 111 | Analysis of the Term Structure of Implied Volatilities | Journal of Financial and Quantitative Analysis | Compared the mean-reverting, GARCH, and EGARCH model assumptions for stock return volatility behaviour. | GARCH, EGARCH | Based on Akaike’s information criterion, the EGARCH (1,1) model fits the daily stock returns better than the other two models. | The EGARCH gives the best description of asset prices and the term structure of options implied. |
| (Alberg et al. 2008) | 107 | Estimating stock market volatility using asymmetric GARCH models | Applied Financial Economics | The Tel Aviv Stock Exchange (TASE) indices’ mean return and conditional variance were empirically examined using a variety of GARCH models and the three different density functions: normal, Student’s t, and asymmetric Student’s t. | GARCH, EGARCH, GJRGARCH APARCH | An asymmetric GARCH model with fat-tailed densities for calculating conditional variance was advised as a way to enhance overall estimation. Comparing the asymmetric GARCH, GJR, and APARCH models for forecasting TASE indices, the asymmetric EGARCH model is a better predictor. | The EGARCH model using a skewed Student’s t distribution is the most successful for forecasting TASE indices. |
| (Lee et al. 2001 ) | 106 | Stock returns and volatility in China’s stock markets | Journal of Financial Research | In four of China’s stock exchanges, the time-series characteristics of stock returns, volatility, and the relationship between returns and volatility were examined. | GARCH, EGARCH | Application of GARCH andEGARCH models provides strong evidence of time-varying volatility and shows volatility is highly persistent and predictable. | The EGARCH model provides a better result. |
| (McAleer et al. 2007) | 91 | An econometric analysis of asymmetric volatility: Theory and application to patents | Journal of Econometrics | Provided an econometric analysis of the symmetric and asymmetric volatility in patent shares. | GARCH; GJRGARCH EGARCH; | For Australia, it was determined that the asymmetric GJR (1,1) model was appropriate, whereas the symmetric GARCH model was preferred for Switzerland and the Netherlands (1,1). For Canada, France, Germany, Italy, Japan, Korea, Sweden, and Taiwan, it was discovered that the alternative asymmetric model EGARCH (1,1) is appropriate. | Overall, EGARCH (1,1) is found to be suitable for most countries. |
| (Cao and Tsay 1992) | 76 | Nonlinear Time-Series Analysis of Stock Volatilities | Journal of Applied Econometrics | Compared the threshold autoregressive model’s forecasting precision to that of models from the ARCH family. | TAR, GARCH, EGARCH | In comparison to the widely used GARCH(1,l) and EGARCH(1, O) models, TAR models may be useful in providing volatility forecasts, especially for large stock returns. | The TAR models provide better forecasts than the GARCH and EGARCH models. |
| (Huang and Zhu 2004) | 63 | Are Shocks Asymmetric to Volatility of Chinese Stock Markets? | Review of Pacific Basin Financial Markets and Policies | Studied the impact of leverage and the risk associated with holding A- and B-shares in the Chinese stock market. | GARCH, EGARCH, GJR GARCH | The GJR-GARCH and EGARCH are two examples of nonlinear GARCH models that are inappropriate for estimating the volatility of the Chinese stock market. Therefore, the GARCH model would be adequate and suitable to describe Chinese stock returns. The impact of leverage is absent. | A better model to fit Chinese B-share stock returns seems to be the GARCH model, rather than the nonlinear GARCH model. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalissery, N.; Anagreh, S.; Nishad T., M.; Tabash, M.I. Mapping the Trend, Application and Forecasting Performance of Asymmetric GARCH Models: A Review Based on Bibliometric Analysis. J. Risk Financial Manag. 2022, 15, 406. https://doi.org/10.3390/jrfm15090406
Chalissery N, Anagreh S, Nishad T. M, Tabash MI. Mapping the Trend, Application and Forecasting Performance of Asymmetric GARCH Models: A Review Based on Bibliometric Analysis. Journal of Risk and Financial Management. 2022; 15(9):406. https://doi.org/10.3390/jrfm15090406
Chicago/Turabian StyleChalissery, Neenu, Suhaib Anagreh, Mohamed Nishad T., and Mosab I. Tabash. 2022. "Mapping the Trend, Application and Forecasting Performance of Asymmetric GARCH Models: A Review Based on Bibliometric Analysis" Journal of Risk and Financial Management 15, no. 9: 406. https://doi.org/10.3390/jrfm15090406
APA StyleChalissery, N., Anagreh, S., Nishad T., M., & Tabash, M. I. (2022). Mapping the Trend, Application and Forecasting Performance of Asymmetric GARCH Models: A Review Based on Bibliometric Analysis. Journal of Risk and Financial Management, 15(9), 406. https://doi.org/10.3390/jrfm15090406







