3.1. Objective Function
Optimized land-use zones can effectively improve the land-use multi-efficiency, achieve optimal allocation and guarantee sustainable utilization of land resources; therefore, each land-use patch should be assigned to a certain zone, not only considering the natural and social characteristics of each land-use patch but also the global spatial compactness, spatial harmony of the land-use zones and the ecological benefits of land use. Hence, optimal land-use zones should reach the following objectives:
(1) The attribute difference between land-use zones maxfAD
Land-use zoning needs to divide n patches xd(d = 1,2,…,m, m is the number of attributes) into C land-use zones Gj(j = 1,2,…c). The difference between all the land-use zones is greatest when the sum of the distances from each land-use patch to the center of the corresponding land-use zone is smallest. So, the problem can be formulated as:
where n is the number of land-use patches and
c is the number of land-use zones when patch
xk belongs tozone
Gj, then
ukj is equal to 1, or otherwise equal to 0.
vj is the center of zone
Gj that can be calculated by formula
![Ijerph 09 02801 i005]()
,
![Ijerph 09 02801 i006]()
is the value of attribute
i for the center of zone
Gj,
![Ijerph 09 02801 i007]()
is the value of attribute
i for patch
xN that belongs to zone
Gj,
Nj is the total number of patches that belongs to zone
Gj, and
![Ijerph 09 02801 i008]()
is the Euclidean distance between patch
xk and
vj that is given by formula
![Ijerph 09 02801 i009]()
.
(2) The spatial compactness of land-use zones maxfSC
To meet the needs of land-use control, besides the optimization of the quantity and quality of land use, the optimization of the spatial pattern is also an important component of land-use zoning. Reducing the fragmentary zones benefits the spatial control. The problem can be formulated as Equation (3):
If land-use patch
xk is assigned to spatial cluster
Gj,
bkj is the number of adjacent patches that also belong to
Gj.
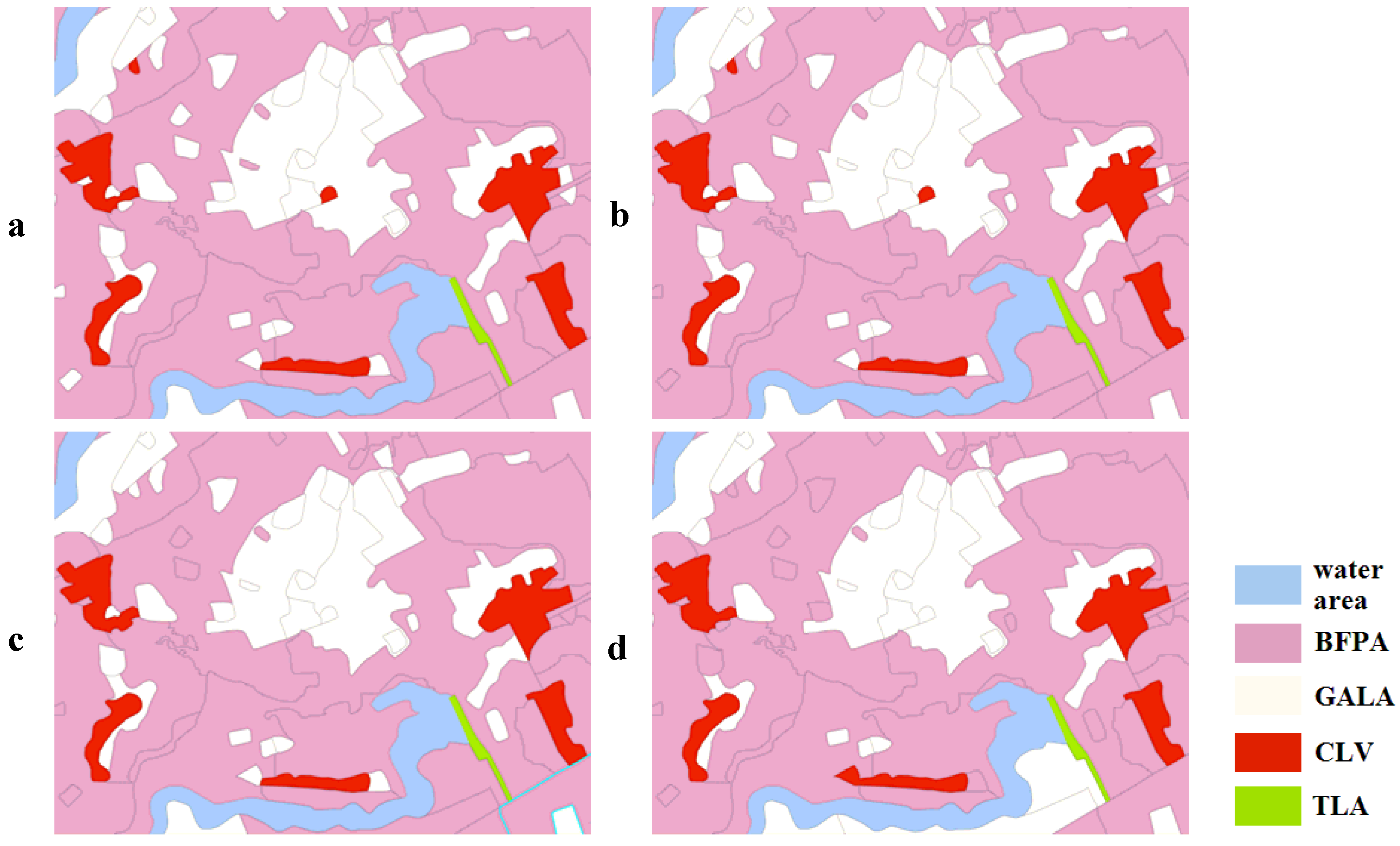
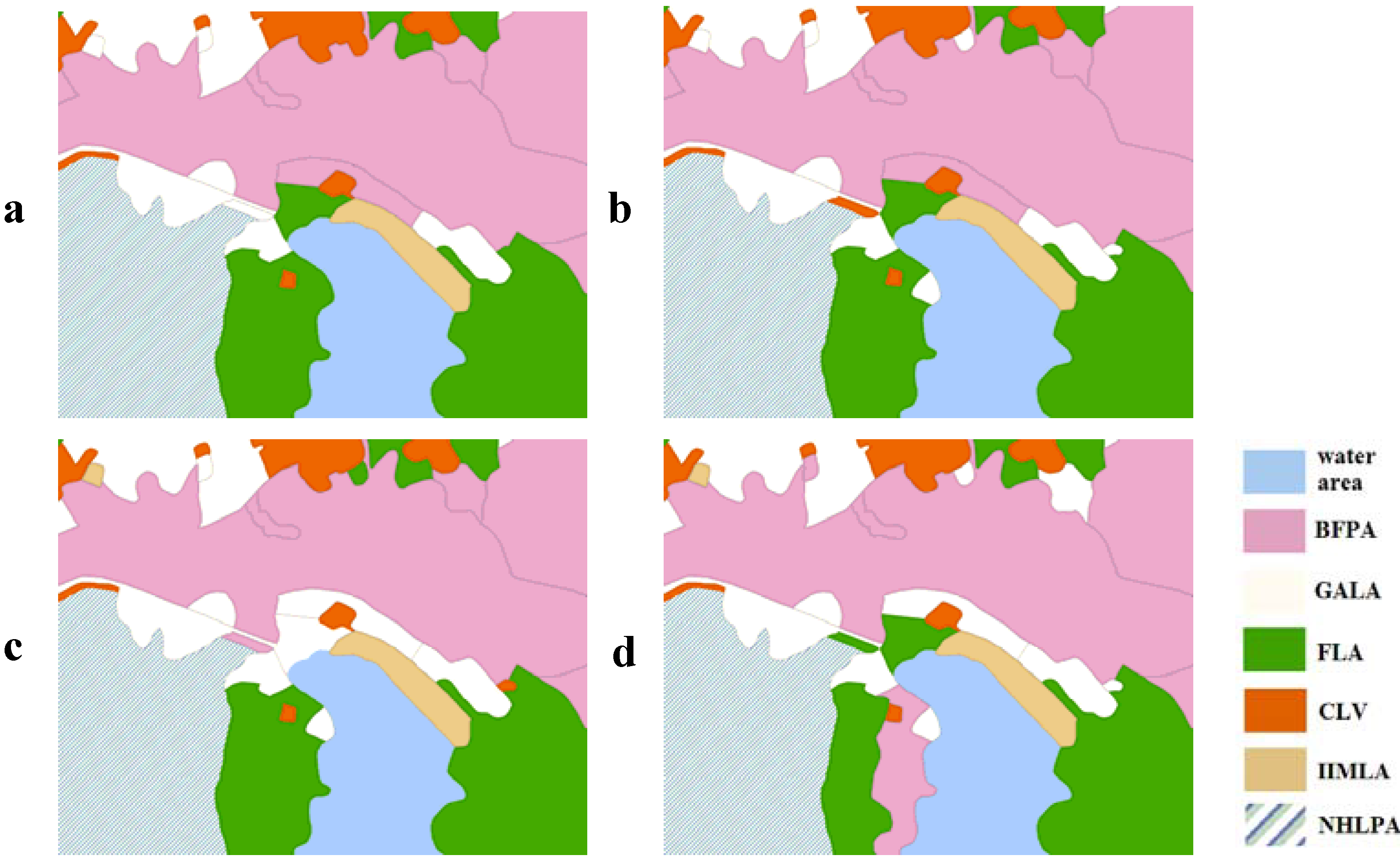
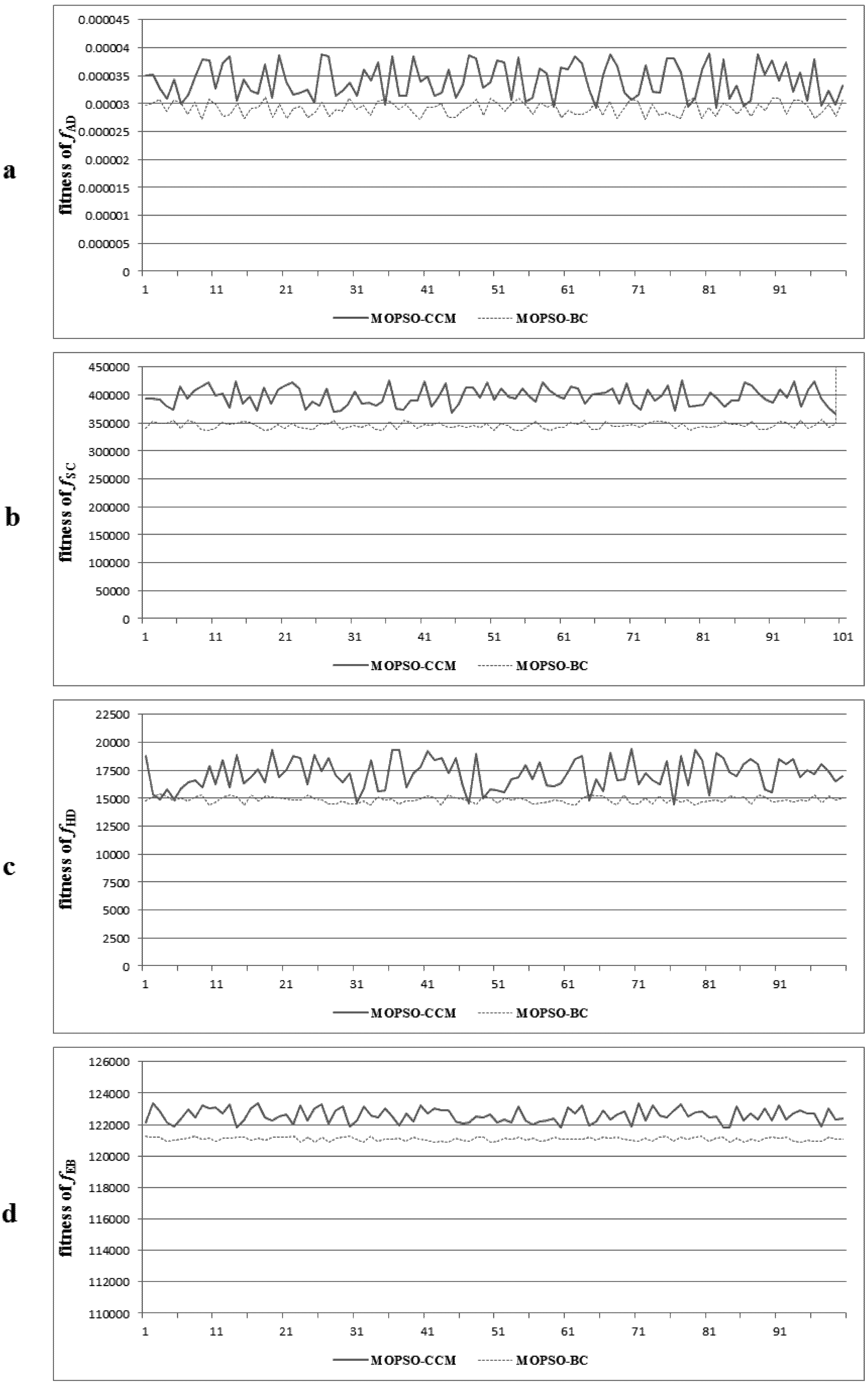
fSC achieves a maximum value when land-use patches with the same attributes are adjacent to each other, and
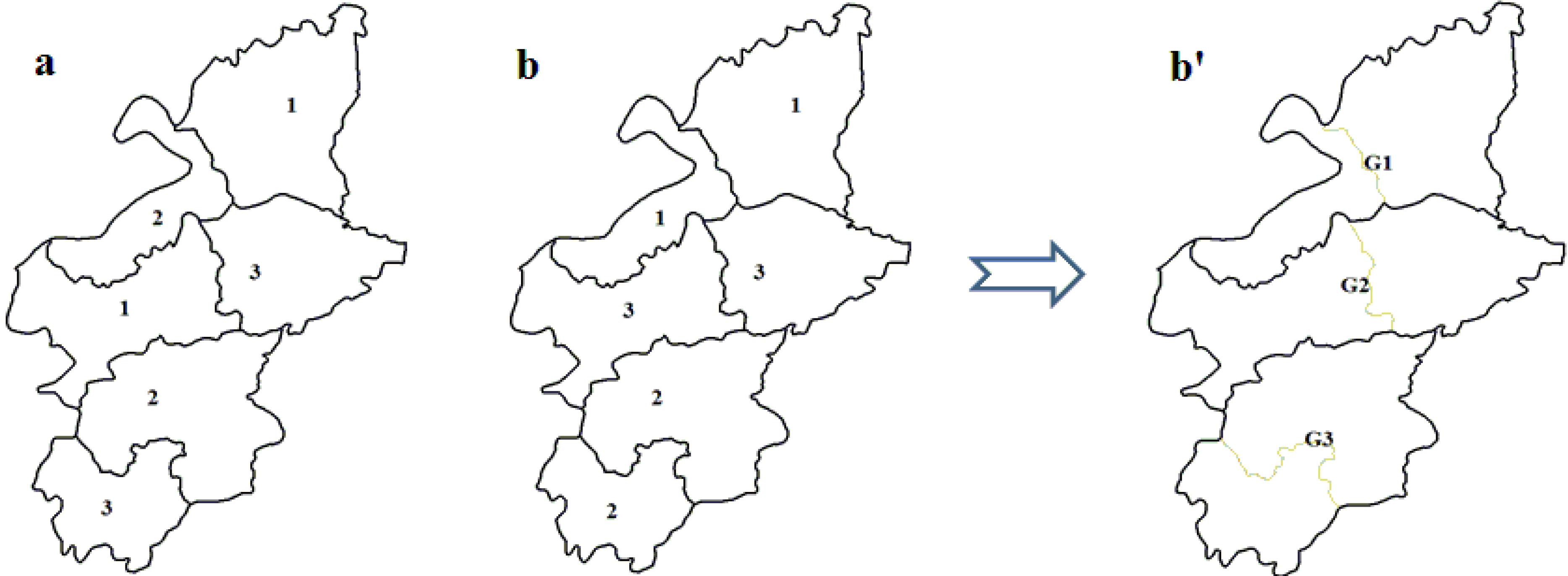
fSC achieves a minimum value when each patch has no adjacent patches that belong to the same zone, a small area with several patches in Yicheng is chosen to describe this vividly (
Figure 3).
Figure 3.
The spatial pattern of land-use zoning: the spatial compactness of b is obviously better than a; b′ represents the spatial clusters.
Figure 3.
The spatial pattern of land-use zoning: the spatial compactness of b is obviously better than a; b′ represents the spatial clusters.
(3) The degree of spatial harmony of land-use zones maxfHD
While in the process of partitioning the n patches into C land-use zones and D spatial clusters (
Figure 3b), the state and influence of the neighborhood of each zone (spatial cluster) should be considered. The proper adjacent distribution of two land-use zones will promote the convenience degree of social production activities of human. Therefore, the problem can be expressed as in Equation (4):
where
d is the number of spatial clusters,
vij is equal to 1 when cluster
i and cluster
j are adjacent to each other, otherwise
vij is equal to 0.
hpij represents the spatial harmony index between cluster
i and cluster
j, which belong to two different zones, respectively. The spatial harmony index between different land-use zones is obtained according to a combination of expert experience and the Delphi method, the results are listed in
Table 3.
The ecological benefits of land-use zones maxfEB: Different land-use patterns provide a different ESV. Objective fEB aims to improve the global ESV, based on the optimal land-use zones from an ecological point of view. So, the problem can be expressed as follows:
where
epk represents the ecological benefit coefficient (refer to
Table 2) when patch
xk is allotted to zone
j.
fEB achieves a maximum value when all the land-use patches are assigned to the zone of FLA, and
fEB achieves a minimum value when all the patches are assigned to the zone of CLTV or IIMLA.
Table 3.
The spatial harmony index between different land-use zones.
Table 3.
The spatial harmony index between different land-use zones.
| Land-use zone | BFPA | GALA | FLA | CLV | CLT | IIMLA | TLA | NHLPA |
|---|
| BFPA | 1 | 0.8 | 0.6 | 0.5 | 0.1 | 0.1 | 0.3 | 0.4 |
| GALA | | 1 | 0.8 | 0.5 | 0.2 | 0.1 | 0.3 | 0.4 |
| FLA | | | 1 | 0.3 | 0.3 | 0.3 | 0.8 | 0.8 |
| CLV | | | | 1 | 0.8 | 0.6 | 0.4 | 0.2 |
| CLT | | | | | 1 | 0.3 | 0.2 | 0.1 |
| IIMLA | | | | | | 1 | 0.1 | 0.1 |
| TLA | | | | | | | 1 | 0.6 |
| NHLPA | | | | | | | | 1 |
Since these four objective functions (Equations (2–5)) represent conflicting land use demands, the scenario of land-use zoning with the optimal spatial pattern does not promise to give the maximum ecological benefits; therefore, there does not exist a single ideal solution which simultaneously satisfies the decision makers across all criteria. So, a compromise solution is sought based on a linear weighting method, which is a simple and practical way to convert the multi-objective problem into a single-objective one by using the following expression:
where w1, w2, w3 and w4 are the weights of four objective functions, respectively, and subject to the condition w1 + w2 + w3 +w4 = 1. gnorm normalizes the values of the objectives within the range [0, 1] to eliminate the impact of different dimensions by:
3.3. The Particle Swarm Optimization Model
As an important branch of swarm intelligence, the PSO algorithm maintains a population of particles, where each particle represents a potential solution to an optimization problem. The set of particles, also known as a swarm, is flown through the D-dimensional search space of the problem. The position of each particle is changed, based on the experiences of the particle itself and those of its neighbors [
42]. The particle in the model of land-use zoning, based on the multi-objective particle swarm optimization with constriction factor, and crossover and mutation operator (MOPSO-CCM), is seen as a potential scenario of land-use zoning. The velocity and position of the particle are updated under the guidance and restriction of the aforementioned objective functions and constraints. To implement the application of MOPSO-CCM in land-use zoning, it is necessary to define the coding scheme for the particle, design the crossover and mutation operator, and set up the updating mechanism for the particle’s position and velocity, according to the particular land-use zoning problem.
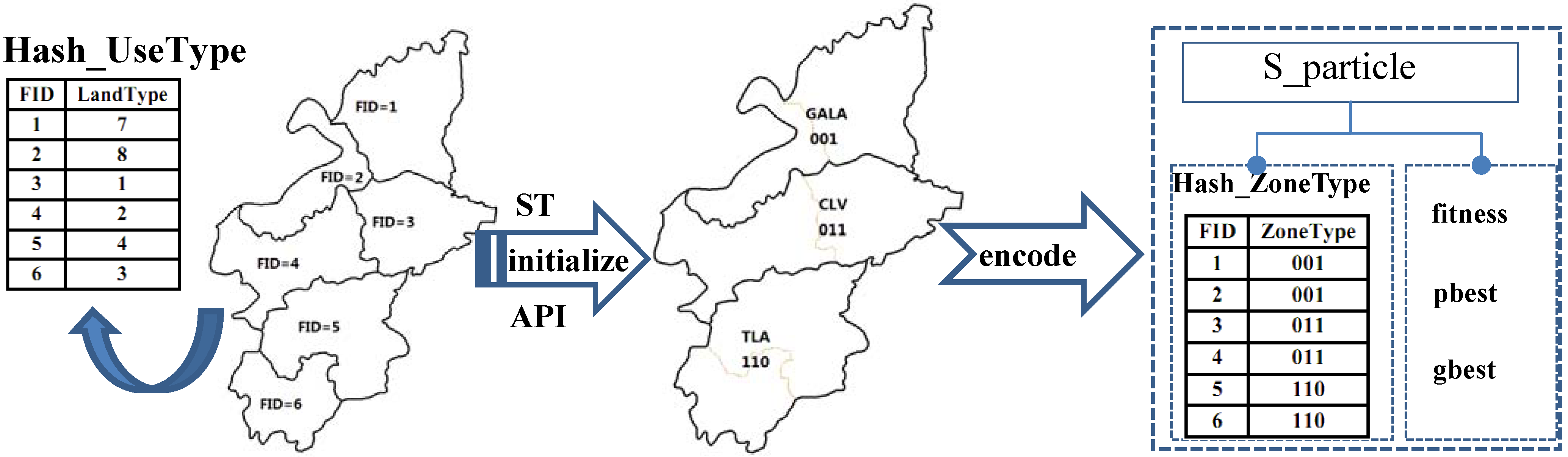
(1) Coding scheme of the particle (
Figure 5)
The eight land-use zones are encoded with a hybrid code system consisting of both decimal code and binary code (see
Table 7). Decimal code is defined for the updating of the particle’s position, and binary code is proposed for the crossover and mutation of the particle. The encoded information is stored in a relational table in the database, which is convenient for the operation of encoding and decoding.
Figure 5.
The coding scheme for a particle.
Figure 5.
The coding scheme for a particle.
Table 7.
The coding of the land-use zones.
Table 7.
The coding of the land-use zones.
| Land-use zone | BFPA | GALA | FLA | CLV | CLT | IIMLA | TLA | NHLPA |
|---|
| Decimal code | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Binary code | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
The land-use patches are encoded with a serial integer and unique numbers in ascending order. The code of each land-use patch and corresponding land-use type are stored in a hash table named as Hash-UseType.
When the initialization of a population of random particles starts, each land-use patch obtains the type of land-use zone, based on the stochastic technique (ST) integrated with assigning the probability interval (API, refer to
Table 6). The relevant information is stored in a hash table named as Hash-ZoneType.
The particle can be represented by the structure named as S_particle, which consists of a hash table (Hash-LandZoneType), the current fitness (fitness), the best fitness achieved by itself (pbest) and the best fitness obtained by any particle in the population (gbest). The array of S_particles is used to represent the swarm of particles.
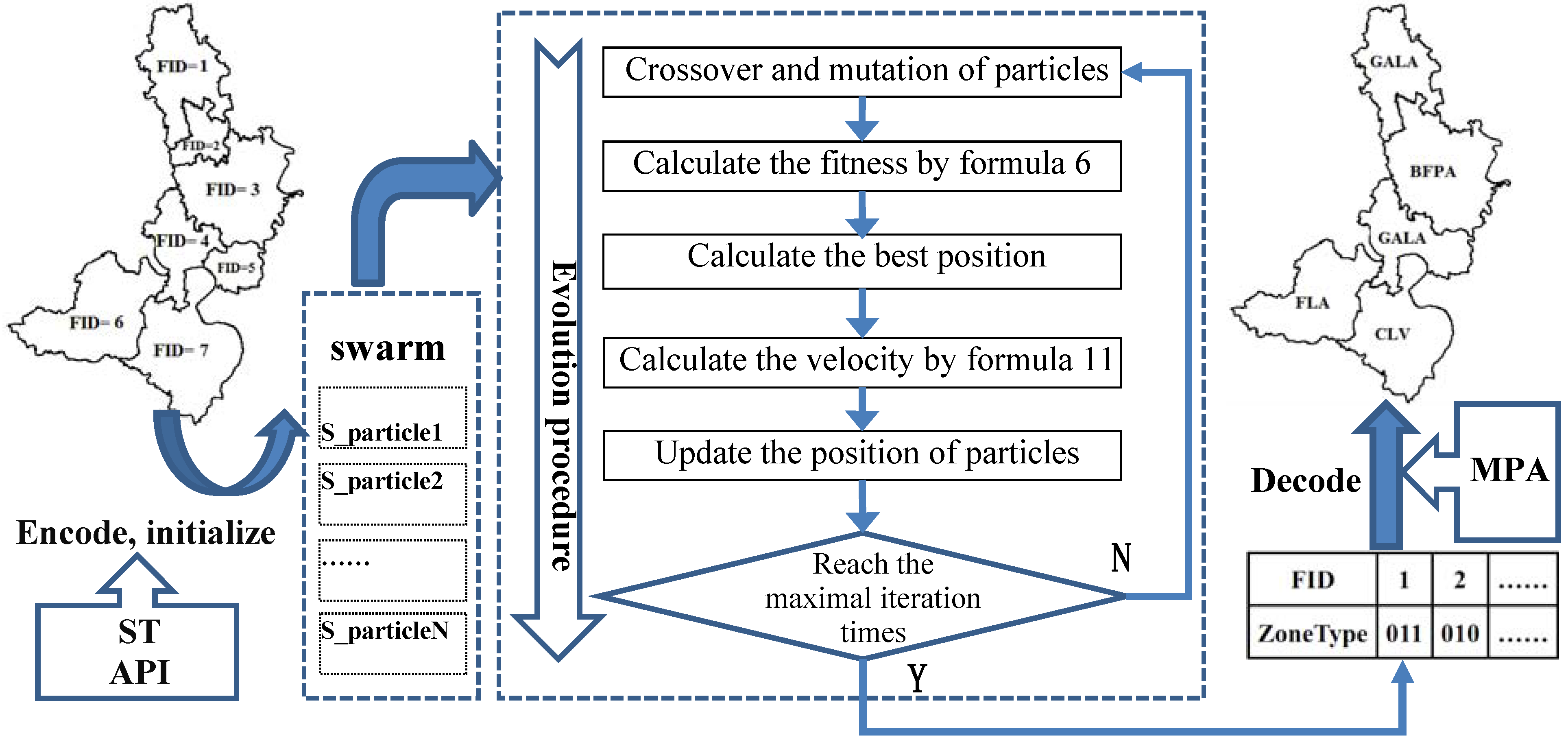
(2) Designing the crossover and mutation operator (
Figure 6)
In the process of crossover or mutation, the particle will be seen as a chromosome, and a land-use patch will be seen as a gene.
Figure 6.
The crossover and mutation operator.
Figure 6.
The crossover and mutation operator.
A single-point crossover operator is adopted to reproduce offspring. The selection of parents for performing crossover is done at a specified probability and is displayed in the mating pool. The number and FID code of genes preparing for crossover are determined randomly. For the purpose of the crossover operation, the crossover point i (i∈{1,2,3}) is also chosen randomly, then the corresponding binary bits before and after the crossover point of the parents are interchanged, leading to two new individuals.
The mutation operator is designed as follows. A chromosome is chosen for mutation at a preset probability. Some genes and the corresponding position i (i∈{1,2,3}) for mutation then need to be chosen randomly. Thanks to the gene structure of the binary code, if the value at the mutation position is 1, then reset it to 0, otherwise to 1.
When crossover or mutation is proceeding, the constraint of API should be considered. For example, cropland is prohibited in the land-use zone of TLA, so if the transition of the gene offends against the constraint of API, the operation of crossover or mutation should be repeated until the transition is acceptable or reaches a preset try-number.
(3) Updating mechanism of the particle’s position and velocity
A new position for the particle is computed by the following formula in the basic PSO with inertial weight [
43].
where xid and vid are the position and velocity of a particle, r1 and r2 are two distinct random values in [0, 1], c1 and c2 are acceleration constants, pid and pgd are the best previous position of the particle itself (pbest) and of all the particles of the swarm (gbest), respectively.
Eberhart and Shi [
44] found that constriction factor
k introduced by Clerc [
45], combined with constraints on
Vmax (equal to
xmax), significantly improved the PSO performance. The formula used to compute the velocity is then modified as:
The land-use zoning problem can be regarded as an integer programming problem, which is described as follows:
where Zn is the n-dimensional integer space, and S is an integer set. In this paper, S can be represented as {x|0≤ x≤ 7 and x∈Zn}.
When PSO is used to solve the land-use zoning problem, the new position of the particle may be changed to a real number, even though the previous location and velocity are both integers, because the parameters of k, r1, r2, c1 and c2 are all real numbers. To make sure the particles are flown through the integer number space of the problem, vid (t + 1), including the three parts of kvid (t), kc1r1 (pid-xid), and kc2r2(pgd-xid), must be an integer number in the evolutionary process. kvid (t) can be changed into an integer number by function int(). kc1r1 (pid-xid) is defined as μ1, when pid > xid, and μ1 is a random number within [0, kc1 (pid-xid)], otherwise within [-kc1(pid-xid),0], so we can also define μ1 as a random number within [a1, b1] for simplification. On the assumption that there are n integer numbers in [a1, b1], any integer number can be chosen to set to μ1, with an equivalent probability equal to 1/n. kc2r2(pgd-xid) is defined as μ2 with the same processing method. So, the formula to compute the velocity of the particle can be modified again as:
As with the crossover and mutation, it may also offend against the constraint of API when the position of the particle is updating. Simultaneously, xid(t + 1) of the particle may be outside the range of S. So, the attribute of the land-use patch will be randomly decided, subject to the API when the phenomenon mentioned above occurred.
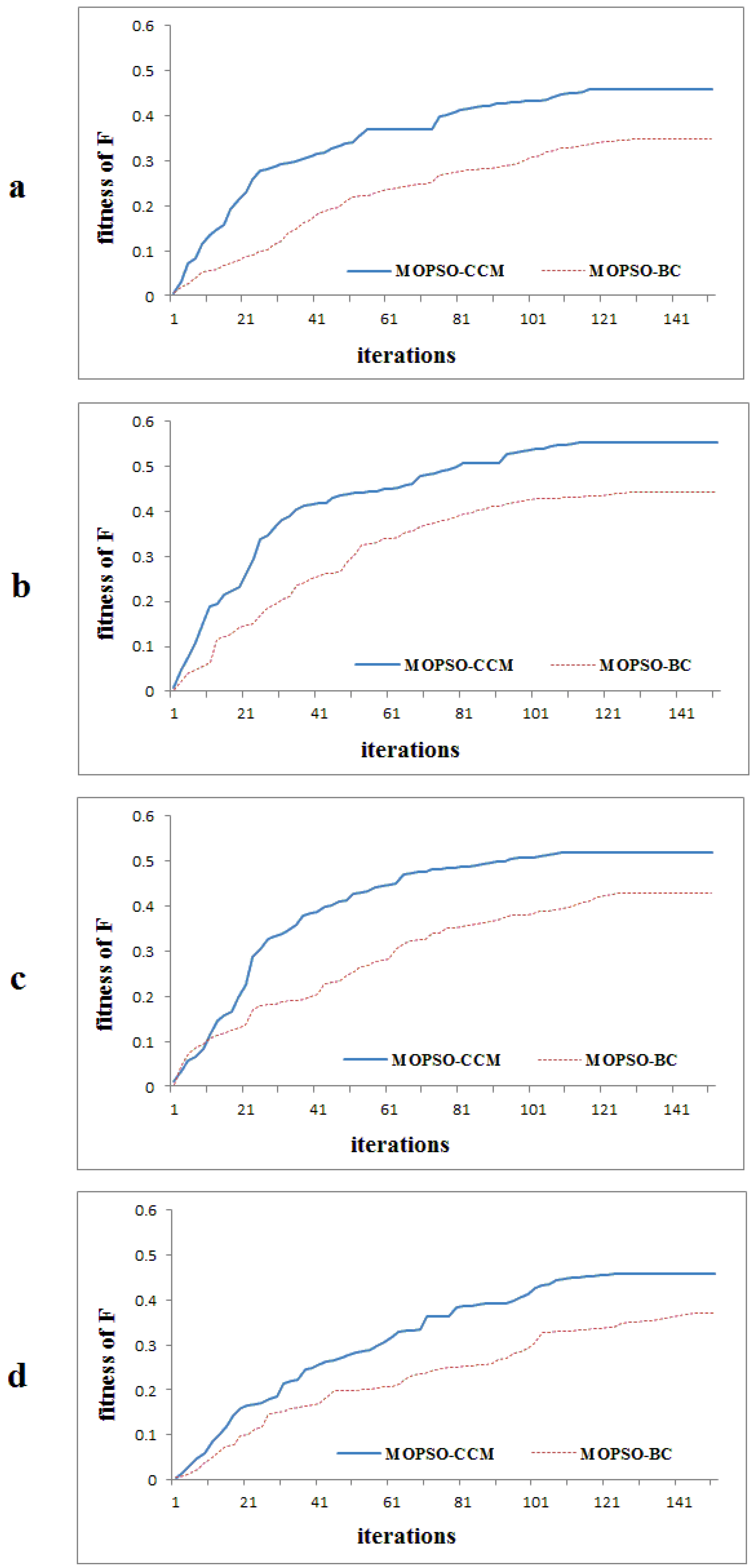
Figure 7 presents a flow diagram of the MOPSO-CCM model, which is based on the objective functions, constraint condition, encoding and decoding scheme, and updating mechanism for the swarm.
Figure 7.
The crossover and mutation operator.
Figure 7.
The crossover and mutation operator.
The performance of the model depends on several critical parameters [
46], including the population size
N, acceleration constants
c1 and
c2, constriction factor k and maximum velocity
Vmax. Carlisle and Doziert [
47] put forward a classical combination of parameters, with
N = 30,
c1 = 2.8,
c2 = 1.3 and
k = 0.7299. Additionally, we set
Vmax = 7, and the maximum number of iterations
Maxtimes = 200.


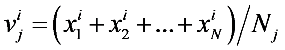 ,
, 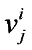 is the value of attribute i for the center of zone Gj,
is the value of attribute i for the center of zone Gj, 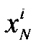 is the value of attribute i for patch xN that belongs to zone Gj, Nj is the total number of patches that belongs to zone Gj, and
is the value of attribute i for patch xN that belongs to zone Gj, Nj is the total number of patches that belongs to zone Gj, and  is the Euclidean distance between patch xk and vj that is given by formula
is the Euclidean distance between patch xk and vj that is given by formula  .
.