Abstract
Manufactured nanomaterials (MNs) are commonly considered to be commercial products possessing at least one dimension in the size range of 10−9 m to 10−7 m. As particles in this size range represent the smaller fraction of colloidal particles characterized by dimensions of 10−9 m to 10−6 m, they differ from both molecular species and bulk particulate matter in the sense that they are unlikely to exhibit significant settling under normal gravitational conditions and they are also likely to exhibit significantly diminished diffusivities (when compared to truly dissolved species) in environmental media. As air/water, air/soil, and water/soil intermedium transport is governed by diffusive processes in the absence of significant gravitational and inertial impaction processes in environmental systems, models of MN environmental intermedium transport behavior will likely require an emphasis on kinetic approaches. This review focuses on the likely environmental fate and transport of MNs in atmospheric and aquatic systems. Should significant atmospheric MNs emission occur, previous observations suggest that MNs may likely exhibit an atmospheric residence time of ten to twenty days. Moreover, while atmospheric MN aggregates in a size range of 10−7 m to 10−6 m will likely be most mobile, they are least likely to deposit in the human respiratory system. An examination of various procedures including the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory of colloidal particle suspension stability in water indicates that more sophisticated approaches may be necessary in order to develop aquatic exposure models of acceptable uncertainty. In addition, concepts such as Critical Coagulation Concentrations and Critical Zeta Potentials may prove to be quite useful in environmental aquatic exposure assessments.
1. Introduction
Manufactured nanomaterials (MNs) may be defined as a class of commercial products that possess at least one dimension in the size range of 1 nm to 100 nm. In recognition of the fact that particulate matter with these dimensions may display unique and valuable properties, the United States federal government promulgated the 2001 National Nanotechnology Initiative [1] in order to facilitate the implementation of nanotechnology into commercial production. Consequently, current and future MN applications will play an increasingly important role in such diverse areas as coatings, electronics, photovoltaics, energy, construction, pharmacology and agriculture [2,3].
With the introduction of any new commercial product, new procedures for assessing the potential environmental safety and health issues are sometimes necessary. In contrast to chemicals, insoluble MNs may possess properties that limit the applicability of existing physical/chemical characterization procedures that are designed to assess the risks associated with their environmental dispersal [4].
One to 100 nm particles represent the smaller size fraction of traditional colloidal particles (colloids can be defined as particles in the 1 nm to 1 μm size range). In turn, colloidal particles differ from more traditional (larger) bulk materials in two areas: colloidal particles are too small to exhibit significant settling under normal gravitational conditions, and colloids are too large to display significant diffusive properties [5]. In addition, nanoparticles have much larger specific surface areas than do bulk materials of the same composition. Therefore, any properties that are sensitive to exposed surface area are emphasized with nanoparticles.
Environmental exposures are traditionally apportioned into the following possible pathways: inhalation (atmospheric, gaseous and aerosol), dermal (aqueous, atmospheric and soil), and gastrointestinal (food, water and possibly soil). Therefore, in order to assess the possibility of unacceptable environmental or human health adverse effects, one must be in a position to estimate potential exposures through an understanding of the potential fate, transport and persistence of MNs in environmental media; subsequently, one may compare these potential exposures with toxicological guidelines. At present neither toxicological guidelines for MNs nor mature models for assessing potential MN exposures are available [2]. This review focuses on potentially useful approaches for addressing this latter aspect.
2. Manufactured Nanomaterial Physical/Chemical Properties Relevant to Environmental Exposures
2.1. Anecdotal Information on the Likely Transport Behavior of MNs in the Environment
Although the regulatory community focuses largely on MNs, an understanding of the reported environmental behavior of other suspended matter may lend insights into the likely environmental behavior of MNs. For example, estimated atmospheric residence times for reactive and unreactive gases range from 107 years (e.g., He) to 10−2 years (Rn, H2O) [6]. In contrast:
- * Burton and Stewart [7] estimate a mean tropospheric residence time for particles of 22 days; the authors also indicate that 1 nm diameter particles in the atmosphere may aggregate to 10 nm diameter aggregates within one hour and may further aggregate to 80 nm diameter masses in 20 hours.
- * Francis et al. [8] report a mean atmospheric particle residence time of 9.6 ± 20% days.
- * Sipin et al. ([9]; and references cited therein) discuss the atmospheric fate of ultrafine particulate matter (particles with a diameter less than 100 nm) and suggest that particles may remain suspended in the atmosphere for days to weeks (depending on their size).
- * USEPA [10] concurs with a likely rapid atmospheric particle aggregation for particles in a size range of 10 nm to 100 nm.
These observations suggest that should a significant atmospheric MN emission occur, rapid aggregation may ensue and atmospheric residence times of 10 to 20 days may be typical. Particle deposition presumably occurs through both wet and dry deposition processes, although Lerman [11] indicates that dry deposition predominates in many cases. If one assumes an average near-surface atmospheric windspeed of 2.2 m/s [6], then those emissions entrained in an atmospheric air mass could travel up to ~1,900 km in 10 days.
Modeling the transport of colloidal material in aquatic systems may be more problematic. The literature suggests that colloids may be more mobile in ground waters at ionic strengths less than 0.001 M [12]. In addition, Degueldre et al. [13] published statistical relationships documenting that the stability of colloidal suspensions in natural waters is sensitive to the chemical composition of the water; in particular, they observe that maximum rates of particle aggregation occur at total dissolved salt contents equal to or greater than 0.01 molar (M) or at alkaline earth metal concentrations in excess of 0.0001 M. Assuming that these observations are applicable to environmental aqueous MN suspensions, aquatic MN transport in a stable colloidal suspension would most likely occur in rainwater and low ionic strength freshwaters [14,15].
Another issue is whether or not the environmental introduction of MNs may lead to the formation of stable aquatic colloidal suspensions. For example, Zhang et al. [16] found that SiO2 was the only synthesized nanomaterial out of a collection of TiO2, SiO2, Fe2O3, ZnO, and NiO products that did not aggregate in pH 8.2 tap water at an ionic strength of less than 5×10−6 M. Thus, even upon their introduction into the environment, it is not clear that many of these products would necessarily experience aquatic transport as stable colloidal suspensions.
The transport of MNs associated with natural soils/sediments is a potentially significant environmental transport (and exposure) mechanism. However, as with our understanding of MN toxicological and environmental fate properties, developing procedures to understand those phenomena leading to MN solid/water partitioning is extremely challenging. For example, the filtration of water column samples may well composite suspended particulate matter that is not necessarily associated in the natural state. In addition, as will be demonstrated, MNs are likely to display relatively slow kinetics with respect to adsorption onto environmental solid phases (when compared to truly dissolved species); hence only systems of prolonged duration may begin to exhibit solid/water partitioning phenomena that are customarily attributed to thermodynamic equilibrium processes. Lastly, there are well recognized experimental difficulties associated with measuring those quantities of MNs associated with soils, sediments and sewage sludges and this represents yet another area of active research. Once reliable procedures become available for estimating MN solid/water partition coefficients, this potential exposure pathway is perhaps more amenable to simulation via a large variety of soil/sediment transport models that are and have been under development for many decades [17].
Models describing the intermedium transport behavior of contaminants with an acceptable degree of uncertainty are needed to assess the overall environmental fate and transport of potentially significant commercial products. In particular, it is necessary to adequately assess the air/water [18], air/solid [19], and solid/water [20] partitioning behavior of new products upon their introduction into environmental systems. Traditional approaches rely on air/solid partition coefficients (KSAs), air/water (Henry’s Law) partition coefficients, and solid/water partition coefficients (Kds). Theoretically these partition coefficients are based on an equilibrium partitioning concept. Specifically, given an appropriate equilibration period, the concentration ratio of a given material in any two phases in contact is presumed to approach a constant value. In systems where the assumption of equilibrium is not valid, one must resort to kinetic approaches for assessing intermedium transport. As an example, Jafvert and Kulkarni [21] measured the octanol/water partition coefficient (Kow; where Kow = Coctanol/Cwater and the subscripted C’s designate concentrations in each phase) of nanoparticulate buckminsterfullerene (a spherical cage of sixty carbon atoms [C60] that is approximately 1 nm in diameter). The authors employed a room temperature equilibration period of 4 to 13 days. A 4 to 13 day period to reach equilibration may be too long in some environmental transport scenarios. Moreover, as buckminsterfullerene particles may be among the smallest of MNs in commercial production, a 4 to 13 day equilibration period also may be too short to attain equilibrium with MNs possessing larger dimensions. In summary, kinetic models may be necessary for predicting MN fate, transport and exposures to the biosphere.
2.2. Environmental Significance of the High Specific Surface Areas Associated with MNs
There are a number of examples of the significant influence that their high specific surface areas exert on MN properties. Nanoparticles possess a much larger fraction of constituents on the surface when compared to corresponding, consolidated larger-grain bulk material [22]. As surficial constituents have fewer bonds than do those in the bulk interior, they exist in higher-energy, less stable states. Because of this phenomenon, it was demonstrated, for example, that the melting point of cadmium sulfide (CdS) decreased from ~1200 °K to ~600 °K when CdS particle radii decreased from 3.5 nm to 1.5 nm [22].
In addition, the significance of interfacial tension and particle specific surface area/radius on the aqueous solubility of the material has been discussed by numerous authors. For example, Stumm and Morgan [23] published the following expression:
where log(Ksp, SSA) is the logarithm of the solubility product of a material with a specific surface area SSA, log(Ksp, SSA=0) is the logarithm of the solubility product of the bulk material, γ is the solid water interfacial tension, R is the ideal gas constant and T is the absolute temperature. The net effect is that depending on the interfacial tension, in many cases fine nanoparticles will be far more soluble than larger-sized particles of the same composition. Specifically, even if a potentially toxic bulk material is too insoluble to lead to dissolved concentrations of toxicological concern, the same cannot necessarily be said for the same material in the nanoparticulate state.
Another phenomenon associated with high specific surface areas (and very small radii) is that the pressure inside of small spherical bubbles is much higher than in the corresponding atmosphere [11,24]. Davies and Rideal [24] published the following expression for estimating the excess pressure, Pexcess, inside of a bubble of radius r:
where γ represents the interfacial tension. This phenomenon is responsible for the common observation that surficial ocean waters are frequently supersaturated with respect to atmospheric gases (i.e., during wave activity very small bubbles are entrained in surface waters that acquire very high pressures and hence introduce dissolved gas concentrations much higher than would be expected from atmospheric equilibrium estimates). This phenomenon may be relevant to the environmental fate and persistence of nanometer sized atmospheric aerosols.
Lastly, the high specific surfaces areas associated with MNs will enhance any reactions dependent on the number of exposed sites. Concerns about dust explosions from finely ground coal, flour, sugar or other combustible products illustrate the significance of high specific surface areas associated with small particulate matter in commercial operations [25].
2.3. Relevance of Diffusive Processes to Environmental Atmosphere/Surface MN Partitioning
In quiescent fluid systems without turbulence, applications of Fick’s first law relate the one dimensional transport (flux) of a diffusing compound (F; in units of g/m2s) to an observed concentration gradient (dC/dz; in units of g/[cm3cm]) via a diffusivity coefficient D:
with this notation, Equation (3) can be rearranged to illustrate that the diffusivity coefficient D may be defined in units of cm2/s.
Equation (3) is applicable in quiescent, laminar, stagnant systems where turbulent transport of the suspending fluid is insignificant. In systems where rapid, turbulent flow exists, the consequent eddies and vortices also transport (and disperse) all dissolved and suspended materials that are contained within the fluid volume. As with atomic/molecular diffusion coefficients, the associated macroscopic coefficients that account for turbulent dispersion also may have units of cm2/s.
Table 1 compares literature-reported diffusivity values for atomic/molecular species in air and water with dispersivity coefficients in the same media. In addition, through application of the Stokes-Einstein equation, diffusivity estimates for MNs in water with radii of 0.5 nm to 50 nm are also presented. Lerman [11] suggested that the Stokes-Einstein equation is useful for providing order-of-magnitude estimates for spherical particles that do not interact with the fluid and that do not alter the fluid viscosity. As observed in Table 1, gaseous diffusivities in water are generally four orders of magnitude lower than diffusivities in air. Note also that estimates of the time required for a diffusing gas to travel a root mean square distance of 1 cm range from seconds in air to hours in water. The estimated MN diffusivities in water are one to three orders of magnitude lower than atomic/molecular species diffusivities in the same medium; consequently, liquid/surface exchange dominated by diffusion across a thin laminar layer in the interfacial region will be correspondingly slower. Although the Stokes-Einstein equation yields reasonable diffusivity estimates for spheres in water, this relationship may underestimate diffusivities under circumstances where the atmospheric mean free path of the particle (between collisions) is of the same magnitude as the particle radius [11,25,29].

Table 1.
Diffusivities and dispersivities observed in environmental media. Idealized diffusivities for MNs in water are estimated using the Stokes-Einstein equation (D = kT/6πηr; k = Boltzmann constant, T = abs. temperature, η = viscosity of water, r = particle radius). Ballpark estimates for the time to travel a root mean square 1 dimensional distance of 1 cm are estimated using the equation: <x2> = 2Dt (where x is the root mean square distance in one dimension and t is the time in seconds. Dispersivities with a “v” designate vertical values and dispersivities with an “h” represent horizontal estimates.
Therefore, atmospheric diffusivity estimates for buckminsterfullerene (C60) particles are listed in Table 1 using the Stokes-Einstein equation amended by two separate procedures for estimating a Cunningham slip factor; these two amended Stokes-Einstein estimates suggest that C60 diffusivities may approach that of gases in the atmosphere. Lastly, the dispersivity estimates in both air and water can be up to 11 orders of magnitude greater than diffusivity estimates.
Although bulk transport is typically dominated by turbulence in most atmospheric and aquatic systems, the issue of air/surface intermedium exchange is more complex. For example, a number of authors [17,30–32] have documented that three processes may potentially govern air/surface deposition: (1) gravitational settling; (2) inertial impaction; and (3) Brownian diffusion. Of the three, due to their size, nanoparticle gravitational settling is unlikely to be significant in environmental aquatic and atmospheric systems [5]. USEPA suggests that atmospheric impaction, while efficient for particles larger than 10 μm, is inefficient with particles less than 0.3 μm [17]. Hence, as MNs may have a maximum size of 0.1 μm, it is likely that Brownian diffusion will dominate air/surface MN exchange.
Figure 1 illustrates predicted average air/surface particle atmospheric deposition velocities as a function of particle diameter for particles with a net density of 10 g/cm3 [33]. As this is a fairly high density material, gravitational and impaction processes are likely to be more significant with these particles than would be observed with similarly sized materials of lesser density.
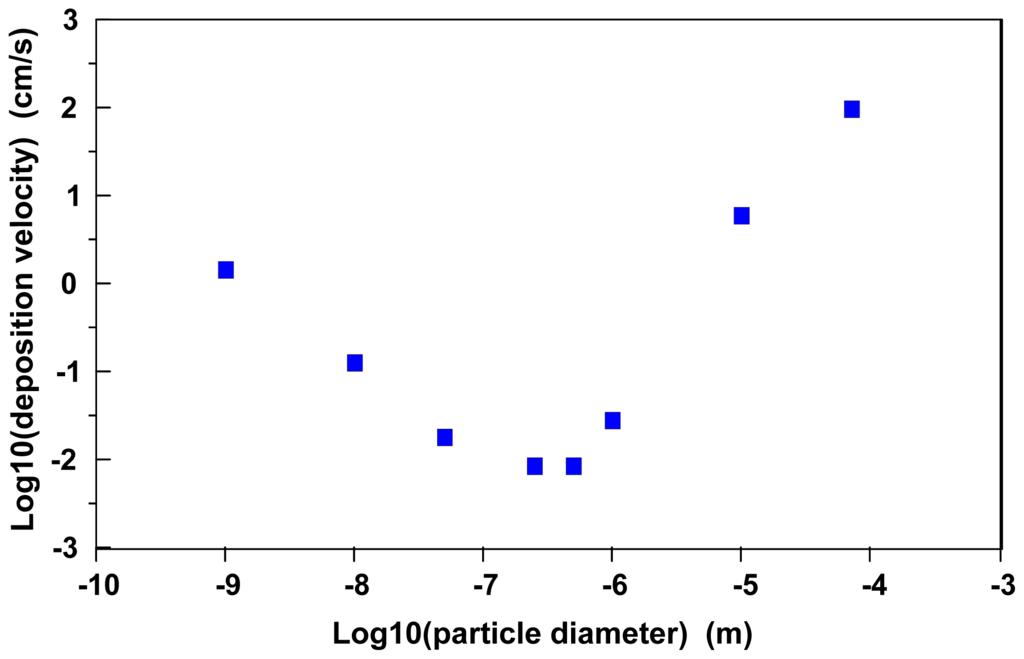
Figure 1.
Average, representative estimated atmospheric particle deposition velocities as a function of particle diameter (particle density = 10 g/cm3; windspeed friction velocities range from 2.3 to 145 cm/s; data used in calculating averages obtained from Sehmel [33]).
The rightmost portion of the curve in Figure 1 illustrates the effects of gravitational settling and impaction on predicted deposition velocities. Essentially, particles with a diameter much greater than 1 μm approach a deposition velocity equal to the terminal settling velocity for a mass in the atmosphere. The minimum predicted deposition velocities are for particles in the size range 0.1 μm to 1 μm; presumably particles in this size range would exhibit the greatest atmospheric transport. Because of this phenomenon, Hoffman [32] estimates that particles in the 0.1 μm to 1.0 μm size range also are less likely to deposit in the human respiratory system.
The descending portion of the curve on the left side of Figure 1 illustrates the transition to a particle size range where the deposition velocity is largely dominated by diffusive transport across a thin, laminar, stagnant layer in the interfacial region. Equation (3) can be rearranged to define a deposition velocity (vd) governed by diffusive processes:
If one has paired experimental measurements of the deposition flux [F; g/(cm2s)] and the concentration gradient dC (where dC = g/cm3 atm–g/cm3 srf) or the diffusivity and the thin stagnant layer thickness, one can estimate a deposition velocity (vd) in units of cm/s (e.g., [27]). In addition, if the rate of surface to air transport is insignificant or the initial concentration in the surface region is zero, then one also can simplify dC to equal the atmospheric concentration (g/cm3 atm—[30,33,34]). Given the diffusivity estimates in Table 1, one also may estimate particle diffusion-limited deposition velocities provided that one has an estimate of the thickness of the thin stagnant layer dz [30].
The leftmost portion of the curve in Figure 1 illustrates that nanoparticle diffusivities become a major variable in predicting atmospheric air/surface deposition velocities. Essentially, maximum deposition velocities will be exhibited by gases in the diffusion-limited regime and minimal deposition velocities will occur with particles in a diameter size range of 0.1 μm to 1 μm.
In the case of air/water deposition, a situation may arise whereby one may have turbulent mixing in both the overlying atmospheric air mass and the underlying water body. In this situation, two thin, diffusive layers may limit intermedium exchange [35,36]) and one therefore needs diffusivities in both media and thicknesses of the two respective diffusive thin layers. Gladyshev [37] suggests that the thin stagnant aqueous layer at the air/water interface may range from 0.01 mm to 0.15 mm for gaseous oxygen exchange.
2.4. Possible Metrics for Assessing MN Transport in Aquatic Systems
Traditional fate and transport modelers generally rely on partition coefficients (Kds; where Kd = Csolid/Cwater) to simulate potential toxicant transport and biological exposures in natural waters. For nonpolar uncharged chemicals, it is frequently assumed that partitioning occurs through binding with natural organic matter (NOM) and the associated organic carbon partition coefficients (Kocs) can be related to experimentally measured octanol-water partition coefficients (Kows) with a variety of regression relationships [36]. Ionizable toxicants are far more problematic; however, empirically derived partition coefficients for ionizable species also find utility in the fate, transport and exposure modeling community [20].
The fundamental theoretical interpretation of a partition coefficient (Kd) is that equilibrium partitioning occurs: (1) when the chemical potential of the species of interest is the same in both phases; and/or (2) when forward and backward rates of intermedium exchange are equal. As the rate for attaining equilibrium is diffusion limited, the 4 to 13 day equilibration period reported by Jafvert and Kulkarni [21] for the smallest of MNs may represent the minimum required equilibration period for MNs possessing larger dimensions.
Given the limitations of equilibrium partitioning theory for larger MNs in water, classical colloid chemistry may address the issue of colloidal suspension stability with the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory (developed in the 1940s [38]). According to DLVO theory, particles in aqueous suspension experience two opposing energies: (1) attractive energies resulting from London/Van der Waals/Keesom dipole interaction energies; and (2) repulsive electrostatic energies that occur when two electrostatically like-charged particles in water approach one another. In situations where the repulsive electrostatic energies dominate, the suspension remains stable in water. In situations where the electrostatic repulsive energies are minimized such that the attractive energies can dominate, the particles are likely to aggregate, settle out and become immobile. The two variables commonly used to quantify these opposing energies are Hamaker constants (for attractive energies; [39–41]) and zeta potentials (for repulsive energies; [42,43]).
Traditional DLVO theory can be extended through either the adoption of additional non-DLVO energies and/or describing the interaction between particles and dissimilar (environmental) surfaces. Extending DLVO theory requires incorporating one or more additional parameters with their associated uncertainties. Using DLVO theory to interpret interactions between suspended particles and chemically dissimilar environmental surfaces requires knowledge of parameters that is not commonly available (and hence limits the utility of this approach). For these reasons, an approach examining the usefulness (and associated uncertainties) of traditional DLVO theory for making predictions of the likely self-aggregation behavior of colloidal suspensions is currently under investigation [14,15, and the present work].
Hamaker constants are required in DLVO theory. Typically, Hamaker constants for colloidal particles in water range from ~10−19 J (for aluminum and iron oxides) to ~10−21 J (for some biocolloids). The comparatively large Hamaker constants associated with aluminum and iron oxides help explain why solutions of alum and ferric chloride are commonly used to clarify turbid water samples. The relatively low Hamaker constants frequently observed with biocolloids explains both why biocolloids are sometimes observed in aged natural waters and why erstwhile unstable suspensions remain in aqueous suspension as the result of natural organic matter coatings that may dominate the interfacial properties of the suspended particles.
The understanding of interfacial properties as it relates to estimating zeta potentials is an active area of research. Generally speaking, zeta potentials can be estimated from electrokinetic experimental data [24,42,43] or they can be related to diffuse layer potentials estimated with geochemical speciation models (e.g., Diffuse Layer models [44], Triple Layer models [45]). The zeta potential is understood to be the potential at the “plane of shear” that is located a distance away from the beginning of the diffuse layer and is therefore generally considered have a magnitude that either equals or is less than that of the diffuse layer potential [42,43,45,46].
Figure 2 provides mechanistic insight into the observations reported by Degueldre et al. [13] that water chemistry can play a major role in the likely stability of aqueous colloidal suspensions. This figure illustrates both simulated diffuse layer potentials and the relative site distributions of ionizable sites on the surface of colloidal amorphous iron oxide particles suspended in “world average river water” as a function of pH [15]. These simulations were conducted using an enhanced version [15] of the MIT Diffuse Layer Model [44] that is currently in the MINTEQA2 geochemical speciation model [47]. From these simulations, surficial iron oxide sites are likely to be dominated by doubly protonated sites and surface complexed sulfate ions at low pH conditions and are likely to be dominated by surface sites that are complexed with calcium and carbonate ions at high pH conditions. As illustrated in the figure, surface complexation with the ions commonly found in water also can have a significant impact on model-generated diffuse layer potential estimates. In turn, these diffuse layer potential estimates can be interpreted as representing the maximum magnitude of the possible zeta potentials for amorphous iron oxide particles under these conditions.
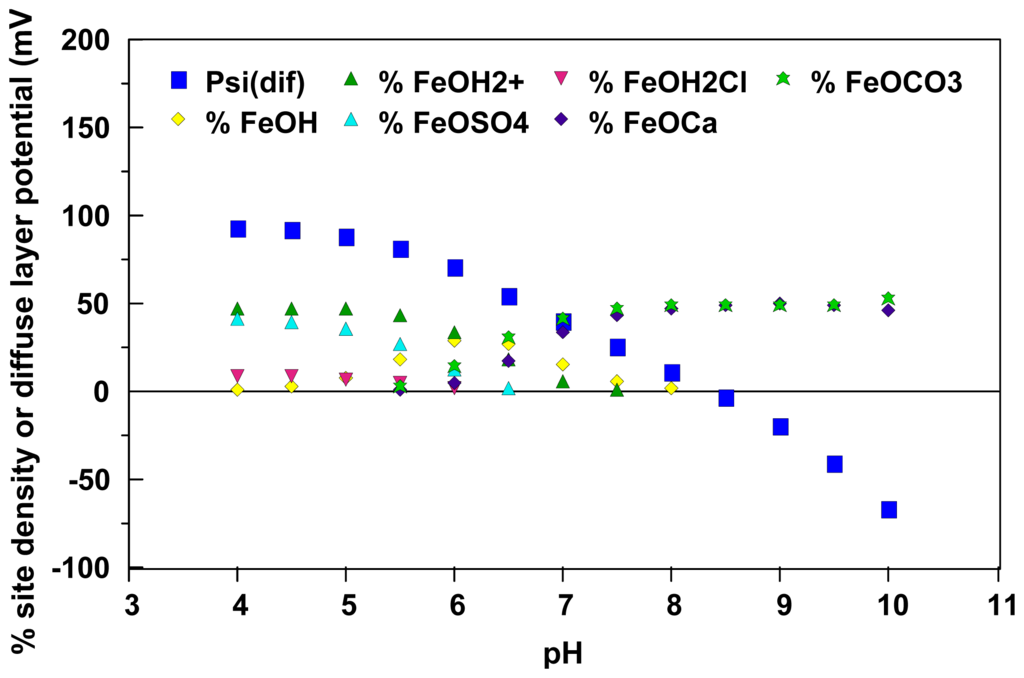
Figure 2.
Enhanced MIT Diffuse Layer Model [44,15] predicted site distributions and diffuse layer potentials for reactive ionizable sites on the surface of amorphous iron oxide particles in world average river water. Site concentrations less than one percent are not included in this figure. Temperature = 20 °C, pCO2 = 3.8×10−4 atm. Simulated conditions given in Loux [15].
If one has estimates of both Hamaker constants (from experimental data) and zeta/diffuse layer potentials (either experimentally measured or obtained from electrostatic surface complexation models) for a given colloidal suspension in water, one can make predictions as to whether or not that colloidal suspension will rapidly aggregate in natural waters. Basically, under conditions where the energies of attraction equal and counterbalance the energies of repulsion with distance from the particle surface, mathematically one can define a Critical Coagulation Concentration (CCC). The critical coagulation concentration is the minimum dissolved salt content (or ionic strength I-- I = 1/2∑cizi 2; where ci is the concentration of ions of valence zi) needed to lead to the rapid aggregation of a suspension in water. Although like-charged particles in aqueous suspension will experience electrostatic repulsion, the presence of higher dissolved salt concentrations will lead to a partial screening of these electrostatic repulsive energies when ions of opposite charge accumulate between the particles. This ionic strength sensitivity explains the observation that suspended colloidal particles in freshwater rivers may well aggregate once the river water discharges into higher ionic strength estuaries.
Three published room temperature expressions for estimating CCCs at room temperature include [48–50]:
[48]
[49]
[50]
where following traditional colloid chemistry, the variables in equations (5) through (7) are defined by: γ = (EXP(zeΨ/2kT) − 1)/(EXP(zeΨ/2kT) + 1, not to be confused with the interfacial tension given in Equations (1) and (2). Ψ is the zeta potential [V], k is the Boltzmann constant [J/K], T is the absolute temperature [K], e is the charge of the proton [C], z is the counterion valence, and A is the Hamaker constant [J]. These expressions were used to estimate the potential self-aggregation behavior of a number of metal oxide suspensions in water; additional assumptions employed in developing these expressions are discussed in refs. [14,15].
Fowkes [51] published an expression for estimating room temperature critical interfacial potentials as functions of Hamaker constants. Fowkes defined his potential as a surface potential; in this work the requisite interfacial potential in Fowkes’ expression is assumed to be a zeta potential. Using these assumptions, a critical zeta potential can be defined as the minimum magnitude of the zeta potential needed to maintain a stable colloidal suspension in water. In SI units, Fowkes’ expression is:
where Ψcrit is the magnitude of the minimum interfacial (zeta) potential required to maintain a stable suspension, A121 is the Hamaker constant describing the attractive interactions between two particles of phase one in a liquid of phase two (water in this case) and 1/κ represents the ionic-strength-dependent Debye length. Fowkes developed this expression assuming that the attractive and repulsive energies counterbalanced one another when the two particles were a distance of 1/κ apart.
Using Equation (8) one can estimate amorphous iron oxide critical zeta potential values of ±24 mV to ±33 mV for the simulated world average river water data depicted in Figure 2. When one compares the diffuse layer potentials with these critical zeta potentials, it is suggested that maximum coagulation rates are likely to occur between pH values of ~7 to ~9. Johnson and Amirtharajah [52] suggested optimum settling conditions for amorphous iron oxide suspensions in a pH range of 6 to 10. Hence, these findings are consistent with previous observations [44,53,19] that the magnitude of the MIT diffuse layer model diffuse layer potential estimates likely exceed that of the associated zeta potentials (i.e., the shear plane is distant from the beginning of the diffuse layer).
The possibility also exists that “ballpark” estimates may be useful for screening-level assessments of the potential mobility of MNs in natural waters. For example, Sprycha [54] suggests that shear plane charge densities rarely exceed an absolute value of 0.02 C/m2. Loux and Anderson [55] suggested that interfacial potentials in environmental aquatic systems are unlikely to exceed an absolute value of 25 mV (due to the ubiquity of multivalent ions in natural waters). Table 2 evaluates some of these “rule of thumb” assertions. Generally speaking, the assumption of a maximum diffuse layer charge density of 0.02 C/m2 (with associated potential) or the assumption of a maximum diffuse layer potential of 25 mV would provide useful insight only at the highest ionic strengths where colloidal particles are already considered to likely aggregate. These observations support a contention that more sophisticated approaches will likely be required to assess MN mobility in environmental waters.

Table 2.
Room temperature estimates of the Debye length thickness (1/κ; 1:1 electrolyte), planar Poisson-Boltzmann diffuse layer potential estimates assuming a charge density of 0.02 C/m2 (1:1 electrolyte; [54]), and critical zeta potential estimates [51] as functions of ionic strength and Hamaker constants.
Figure 3 represents a test of consistency between the critical zeta potential concept given by Fowkes [51] and CCC Equation (6) [49]. Essentially, critical zeta potentials were estimated using Equation (6) over a Hamaker constant range of 1×10−18 J to 1×10−22 J at ionic strengths ranging from 1×10−5 M to 1 M. The representative critical zeta potential estimates, Hamaker constants and Debye layer thicknesses were then inserted into Equation (6) to estimate the CCC values needed to reach optimum aggregation rates. Ideal agreement between the two approaches would occur when the expression log10(CCC/Ionic Strength) equals zero. It is perhaps fortuitous that MNs with the lowest Hamaker constants that are likely to be mobile at ionic strengths less than 0.01 M yield an agreement approaching 18% in these stability metrics under these conditions. If one performs a similar exercise with the averages of Equations (5)–(7), the minimum difference approaches 50%. Given that Ackler et al. [40] found that Hamaker constants may differ by as much as a factor of 7; these estimates suggest that experimental uncertainties may in some cases surpass the conceptual uncertainties in these comparisons.
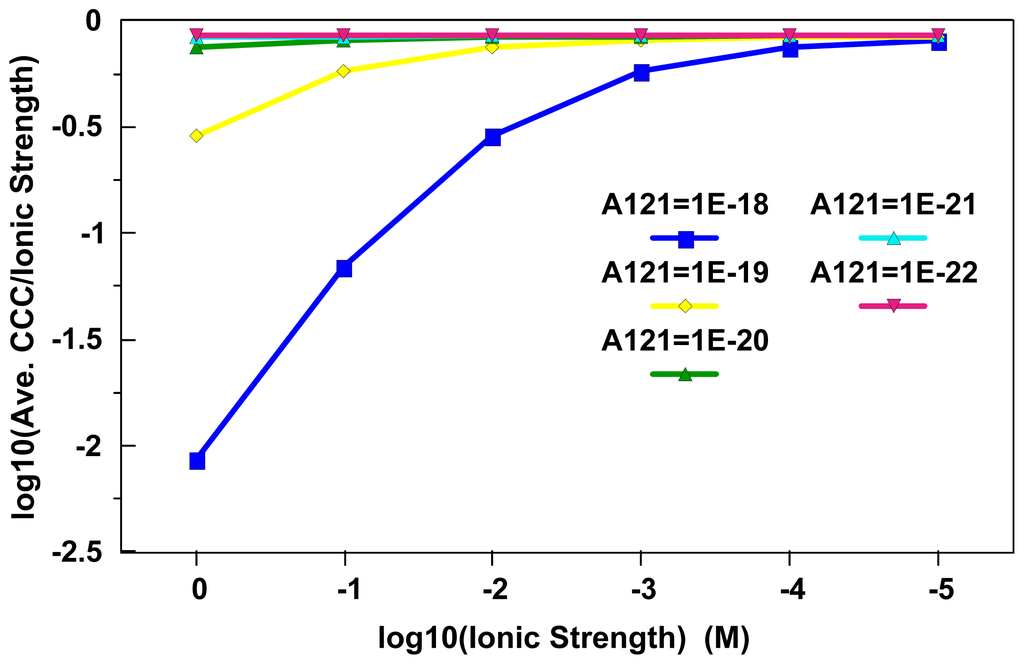
Figure 3.
Evaluation of consistency between the Ross and Morrison [49] CCC expression [Equation (6)] and the critical zeta potential expression given by Fowkes [[51]; Equation (8)]. The log10(CCC/Ionic Strength) term should equal zero with perfect agreement between the two approaches. As materials with lower Hamaker constants are most likely to be mobile at ionic strengths below 0.01 M, these two approaches do approach agreement to within 18% in systems where colloidal mobility is more likely.
Figure 4 illustrates one approach for converting the diffuse layer potentials illustrated in Figure 2 into estimated zeta potentials (employing procedures delineated in Lyklema and Overbeek [46]). These calculation results are in accord with previous observations that the zeta potential can be significantly less than the diffuse layer potential at higher charge densities. It is well known from electrokinetic studies that zeta potentials typically reach maximum values for a given ionic strength; Lyklema and Overbeek [46] interpreted this phenomenon as resulting from changes in the aqueous viscosity as a function of field strength in the interfacial region.
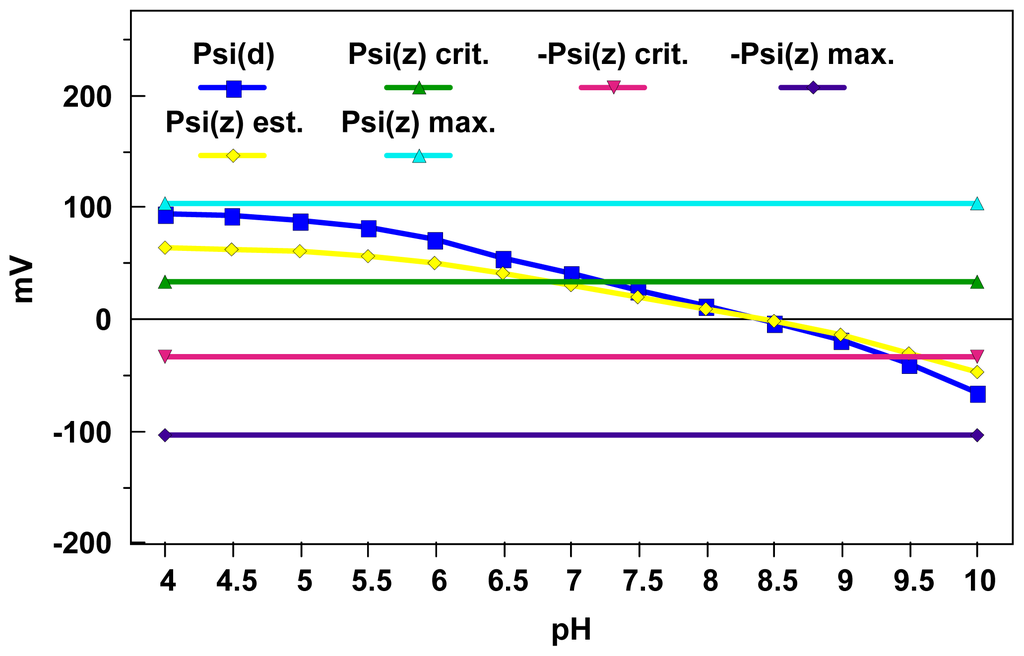
Figure 4.
Comparison of the world average river water pH-dependent amorphous iron oxide DLM diffuse layer potentials depicted in Figure 2 with zeta potential estimates obtained using “correction” procedures given by Lyklema and Overbeek [46]. An estimated maximum zeta potential for this system using a procedure from Lyklema and Overbeek [46] is ±103 mV and an estimated critical zeta potential for this system using a procedure from Fowkes [51] is ±33 mV.
Using procedures developed by these authors, one can estimate a maximum zeta potential magnitude for the world average river water simulations depicted in Figures 2 and 4 of ≈103 mV. This maximum zeta potential estimate does appear to agree reasonably well with the low pH diffuse layer potential estimates depicted in these figures. When one compares the critical zeta potential magnitude estimates of ≈33 mV obtained using Equation (8) with the zeta potential estimates in Figure 4, one can predict an optimum pH range for aggregation of 6.8 to 9.6. This represents a slight improvement over the range result of 7 to 9.5 given in ref. [15] with respect to capturing the optimum iron oxide pH aggregation range of 6 to 10 determined by Johnson and Amirthirajah [52].
3. Conclusions
One to one hundred nanometer insoluble manufactured nanomaterials represent a new class of products whose toxicity, fate, transport and exposures upon dispersal into the environment are active areas of research. As the result of their small size and high specific surface areas, chemical reactivities sensitive to exposed surface sites will likely be magnified with these products.
Upon dispersal into various environmental media, atmospheric MN emissions will likely rapidly aggregate into a size range of 0.1 μm to 1 μm and display an atmospheric residence time of 10 to 20 days. In contrast to aquatic emissions, atmospheric emissions are likely amenable to existing exposure assessment algorithms designed to describe the atmospheric behavior of ultrafine particles.
Estimating potential aquatic exposures to insoluble MN suspensions is more problematic because MNs are unlikely to display equilibrium solid/water partitioning behavior within the time frames associated with many environmental transport phenomena. Various kinetic approaches to estimating potential MN immobilization in aquatic systems that incorporate underlying DLVO theory show promise with respect to theoretical consistency and explaining generally observed phenomena. However, it is likely that defensible models incorporating a kinetic-based, self-aggregation component will require validating experimental datasets before defensible exposure assessment tools can be made available.
Acknowledgments
The authors wish to acknowledge previous discussions with the EPA OSP Nanomaterial Physical Chemical Properties workgroup, Steering Group 4 of the OECD Working Party on Manufactured Nanomaterials, the EPA Las Vegas Nanomaterial Journal Club, and the EPA Nanomeeters workgroup. The authors also wish to acknowledge the value of reviewers’ comments in both the present and previous manuscripts in this area.
- DisclaimerThe U.S. Environmental Protection agency through its Office of Research and Development partially funded the research described here and subjected it to Agency review. Although it has been approved for publication, it does not necessarily represent official agency policy. Mention of trade names or commercial products does not represent endorsement or recommendation for use.
References
- National Nanotechnology Initiative (Nano.org). 2010. Available online: www.nano.gov accessed on 6 December 2010.
- OECD, Guidance Manual for the Testing of Manufactured Nanomaterials: OECD’s Sponsorship Programme: First Revision. 2010. In OECD Working Party on Manufactured Nanomaterials, ENV/JM/MONO(2009)20/REV, 02-Jun-2010; p. JT03282410.
- Woodrow Wilson International Center for Scholars. The Project on Emerging Nanotechnologies. 2011. Available online: http://www.nanotechproject.org/inventories/consumer/ accessed on 10 January 2011.
- OECD, Preliminary Guidance Notes on Sample Preparation and Dosimetry for the Safety Testing of Manufactured Nanomaterials. 2010. In OECD Working Party on Manufactured Nanomaterials, Steering Goup 4; ENV/JM/MONO(2010)25; p. JT03284434. 31 May 2010.
- Overbeek, JThG. Colloids, a fascinating subject: Introductory lecture, Chapter 1. In Colloidal Dispersions; Goodwin, JW, Ed.; Royal Society of Chemistry: London, UK, 1982. [Google Scholar]
- Junge, CE. Residence time and variability of tropospheric trace gases. Tellus 1974, 26, 477–488. [Google Scholar]
- Burton, WM; Stewart, NG. Use of long-lived natural radioactivity as an atmospheric tracer. Nature 1960, 156, 584–589. [Google Scholar]
- Francis, CW; Chesters, G; Haskin, LA. Determination of 210Pb mean residence time in the atmosphere. Environ Sci Technol 1970, 4, 586–589. [Google Scholar]
- Sipin, MF; Guazzotti, SA; Prather, KA. Recent advances and some remaining challenges in analytical chemistry of the atmosphere. Anal Chem 2003, 75, 2929–2940. [Google Scholar]
- USEPA. Basic Concepts in Environmental Sciences: Full Table of Contents. 2010. Available online: www.epa.gov/apti/bces/toc/full_toc.htm accessed on 5 October 2010.
- Lerman, A. Geochemical Processes in Water and Sediment Environments; Robert, E, Ed.; Krieger Publishing Co: Malabar, FL, USA, 1988. [Google Scholar]
- Utsunomiya, S; Kersting, AB; Ewing, RC. Groundwater nanoparticles in the far-field at the nevada test site: Mechanism for radionuclide transport. Environ Sci Technol 2009, 43, 1293–1298. [Google Scholar]
- Degueldre, C; Triay, I; Kim, JI; Vilks, P; Laaksoharju, M; Miekeley, N. Groundwater colloid properties: A global approach. Appl Geochem 2000, 15, 1043–1051. [Google Scholar]
- Loux, NT; Savage, N. An assessment of the fate of metal oxide nanomaterials in porous media. Water Air Soil Poll 2008, 194, 227–241. [Google Scholar]
- Loux, NT. Simulating the stability of colloidal amorphous iron oxide suspensions in natural waters. Water Air Soil Poll 2011, 217, 157–172. [Google Scholar]
- Zhang, Y; Chen, Y; Westerhoff, P; Hristovski, K; Crittenden, JC. Stability of commercial metal oxide nanoparticles in water. Water Res 2008, 42, 2204–2212. [Google Scholar]
- USEPA. Council for Regulatory Environmental Modeling. 2010. Available online: www.epa.gov/crem/cremlib.html accessed on 15 October 2010.
- Schwartzenbach, RP; Gschwend, PM; Imboden, DM. Environmental Organic Chemistry, 2nd ed; Wiley Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Meijer, SN; Shoeib, M; Jones, KC; Harner, T. Air-soil exchange of organochlorine pesticides in agricultural soils. 2. Laboratory measurements of the soil/air partition coefficient (Ksa). Environ Sci Technol 2003, 37, 1300–1305. [Google Scholar]
- Allison, JD; Allison, TL. Partition Coefficients for Metals in Surface Water, Soil, and Waste; U.S. Environmental Protection Agency: Athens, GA, USA, 2005. [Google Scholar]
- Jafvert, CT; Kulkarni, PP. Buckkminsterfullerene’s (C60) Octanol-water partition coefficient (Kow) and aqueous solubility. Environ Sci Technol 2008, 42, 5945–5950. [Google Scholar]
- Goldstein, AN; Echer, CM; Alivisatas, AP. Melting in semiconductor nanocrystals. Science 1992, 256, 1425–1427. [Google Scholar]
- Stumm, W; Morgan, JJ. Aquatic Chemistry, 2nd ed; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Davies, JT; Rideal, EK. Interfacial Phenomena; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Hinds, WC. Aerosol Technology, Properties, Behavior and Measurement of Airborne Particles, 2nd ed; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- CRC, CRC Handbook of Chemistry and Physics, 83rd ed; Lide, DR (Ed.) CRC Press: Boca Raton, FL, USA, 2003.
- Pasquill, F. Atmospheric Diffusion; Van Nostrand Co: London, UK, 1962. [Google Scholar]
- Bricker, JD; Nakayama, A. Estimation of far-field horizontal and vertical turbulent diffusion coefficients from the concentration field of a wastewater plume near the Akashi Strait. Environ Fluid Mech 2007, 7, 1–22. [Google Scholar]
- Fromherz, Z. Physico-Chemical Calculations in Science and Industry; Butterworths: London, UK, 1964. [Google Scholar]
- Sehmel, GA. Particle and gas dry deposition: A review. Atmos Environ 1980, 14, 983–1011. [Google Scholar]
- Noll, KE; Jackson, MM; Oskouie, AK. Development of an atmospheric particle dry deposition model. Aerosol Sci Technol 2001, 35, 627–635. [Google Scholar]
- Hoffman, W. Modeling particle deposition in human lungs; modeling concepts and comparison with experimental data. Biomarkers 2009, 14, 59–62. [Google Scholar]
- Sehmel, GA. Particle diffusivities and deposition velocities over a horizontal smooth surface. J Coll Interface Sci 1971, 37, 891–906. [Google Scholar]
- Chamberlain, AC. Aspects of the deposition of radioactive and other gases and particles. Int J Air Poll 1960, 3, 63–88. [Google Scholar]
- Liss, PS; Slater, PG. Flux of gases across the air-sea interface. Nature 1974, 247, 181–184. [Google Scholar]
- Thomas, RG. Handbook of Chemical Property Estimation Methods; McGraw Hill Book Co: New York, NY, USA, 1982. [Google Scholar]
- Gladyshev, MI. Biophysics of the Surface Microlayer of Aquatic Ecosystems; IWA Publishing: London, UK, 2002. [Google Scholar]
- Verwey, EJW; Overbeek, JThG. Theory of the Stability of Lyophobic Colloids; Dover Publications: New York, NY, USA, 1948. [Google Scholar]
- Visser, J. On Hamaker constants: A comparison between Hamaker constants and Lifshitz-Van der Waals constants. Adv Coll Interface Sci 1972, 3, 331–363. [Google Scholar]
- Ackler, HD; French, RH; Chiang, YM. Comparison of Hamaker constants for ceramic systems with intervening vacuum or water: From force laws and physical properties. J Coll Int Sci 1996, 179, 460–469. [Google Scholar]
- Bergstrom, L. Hamaker constants of inorganic materials. Adv Coll Interface Sci 1997, 70, 125–169. [Google Scholar]
- Hunter, RJ. Zeta Potential in Colloid Science; Academic Press: London, UK, 1981. [Google Scholar]
- Delgado, AV; Gonzalez-Caballero, F; Hunter, RJ; Koopal, LK; Lyklema, J. Measurement and interpretation of electrokinetic phenomena. J Coll Int Sci 2007, 309, 194–224. [Google Scholar]
- Dzombak, DA; Morel, FMM. Surface Complexation Modeling: Hydrous Ferric Oxide; John Wiley and Sons: New York, USA, 1990. [Google Scholar]
- Hunter, RJ; Wright, HJL. The dependence of electrokinetic potential on concentration of electrolyte. J Coll Int Sci 1971, 37, 564–580. [Google Scholar]
- Lyklema, J; Overbeek, JThG. On the interpretation of electokinetic potentials. J Colloid Sci 1961, 16, 501–512. [Google Scholar]
- Allison, JD; Brown, DS; Novo-Gradac, KJ. MINTEQA2/PRODEFA2, A Geochemical Assessment Model For Environmental Systems, Version 3.0 Users Manual; U.S. Environmental Protection Agency: Athens, GA, USA, 1991. [Google Scholar]
- Shaw, DJ. Introduction to Colloid and Surface Chemistry, 4th ed; Butterworth Heinemann: Oxford, UK, 1992. [Google Scholar]
- Ross, S; Morrison, ID. Colloidal Systems and Interfaces; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Overbeek, JThG. Stability of Hydrophobic Colloids and Emulsions. Volume Chapter 8, In Colloid Science, Vol. I, Irreversible Systems; Kruyt, HR, Ed.; Elsevier Publishing Co: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Fowkes, FM. Predicting Attractive Forces at Interfaces. In Chemistry and Physics of Intefaces, II; Gushee, DE, Ed.; American Chemical Society: Washington, DC, USA, 1971. [Google Scholar]
- Johnson, PN; Amirtharajah, A. Ferric chloride and alum as single and dual coagulents. J Am Water Works Assoc 1983, 75, 232–239. [Google Scholar]
- Cromieres, L; Moulin, V; Fourest, B; Giffault, E. Physico-chemical characterization of the colloidal hematite/water interface: Experimentation and modeling. Coll Surf A 2002, 202, 101–115. [Google Scholar]
- Sprycha, R. Electrical double layer at alumina/electrolyte interface. I. Surface charge and zeta potential. J Coll Int Sci 1989, 127, 12–45. [Google Scholar]
- Loux, NT; Anderson, MA. Mobile Ion Activities at Charged Interfaces. Colloids Surf A 2001, 177, 123–131. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).