When Do Sexual Partnerships Need to Be Accounted for in Transmission Models of Human Papillomavirus?
Abstract
:1. Introduction
1.1. Human Papillomavirus
1.2. HPV Vaccination
1.3. Mathematical Models of HPV
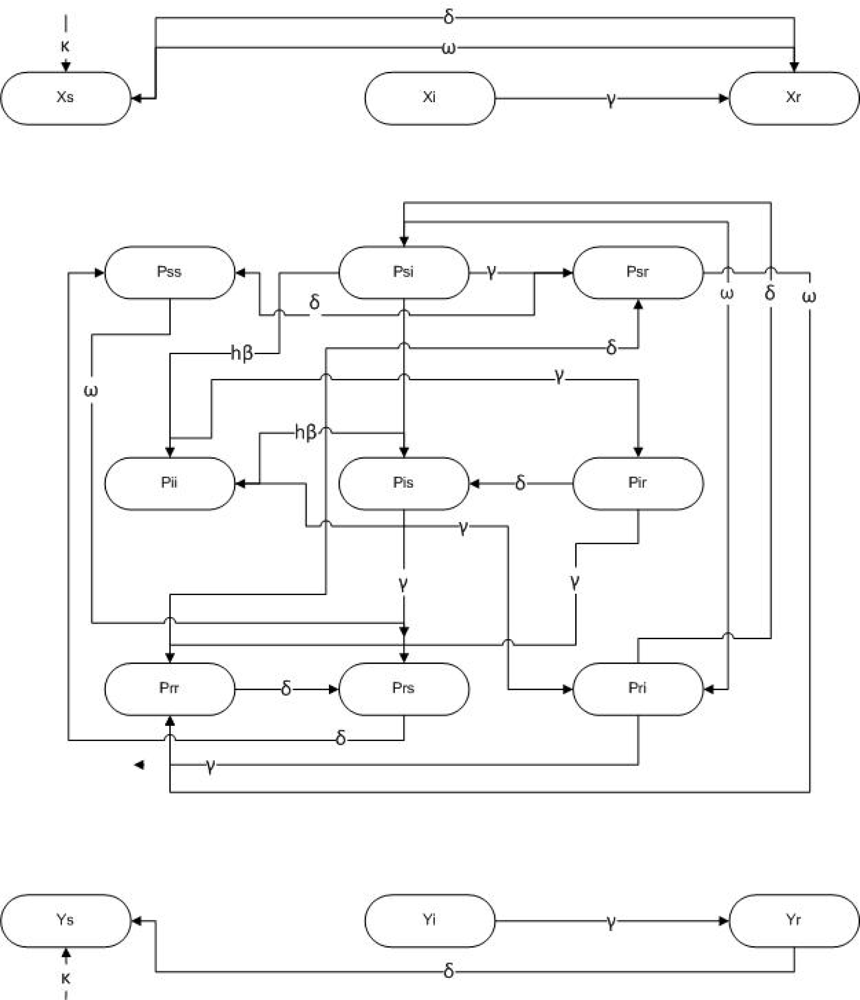
1.4. Pair Models for Sexually Transmitted Infections
1.5. Outline of Paper
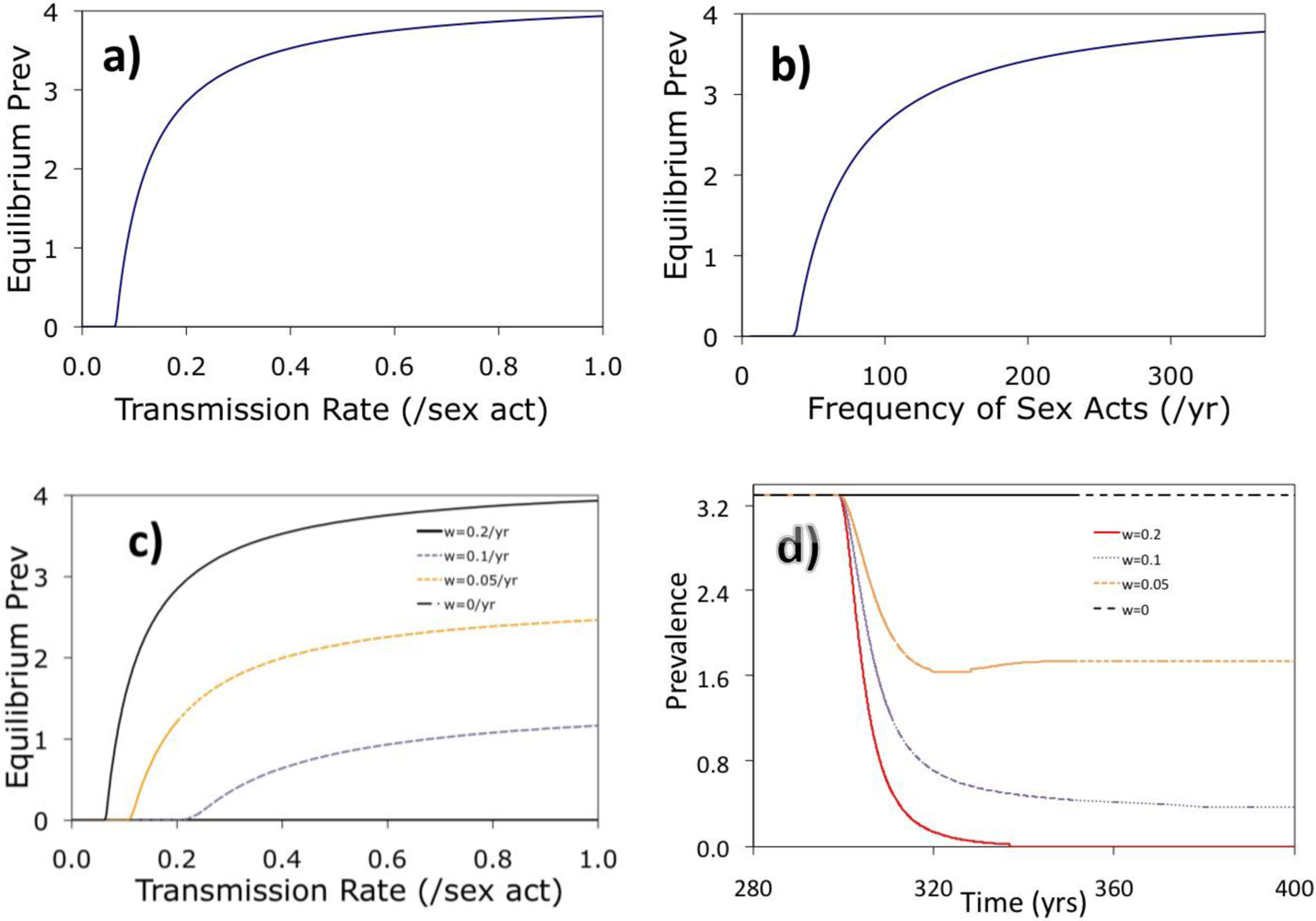
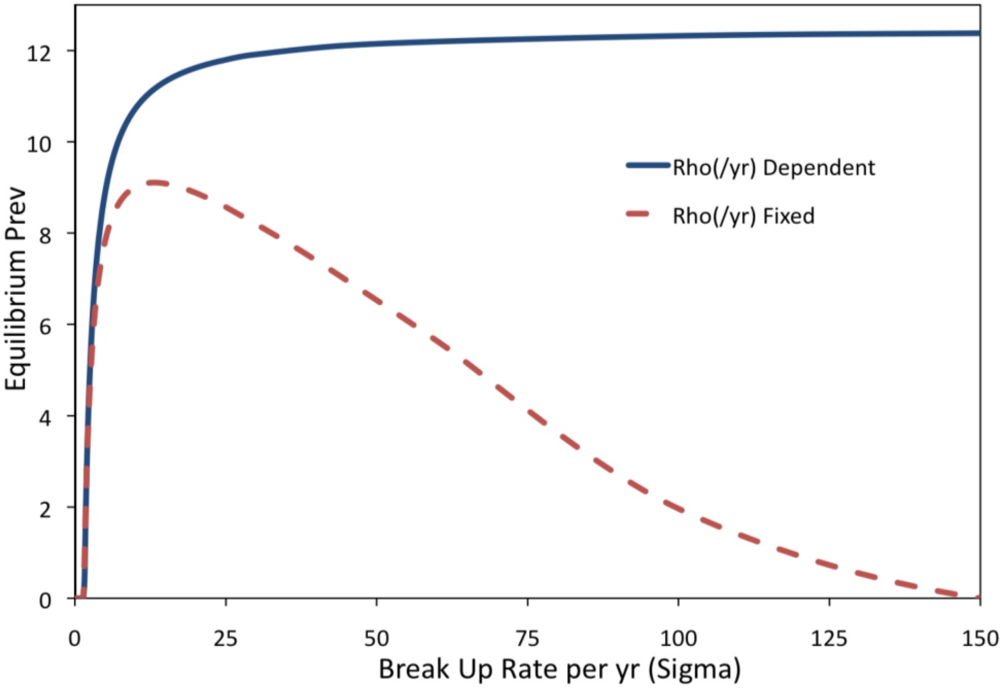
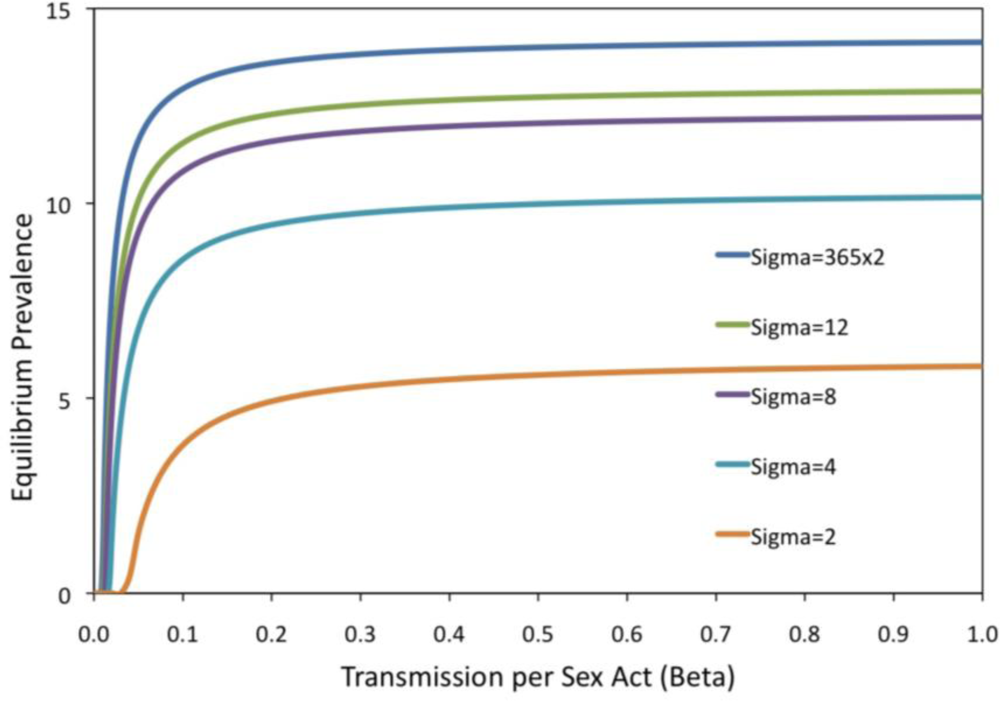
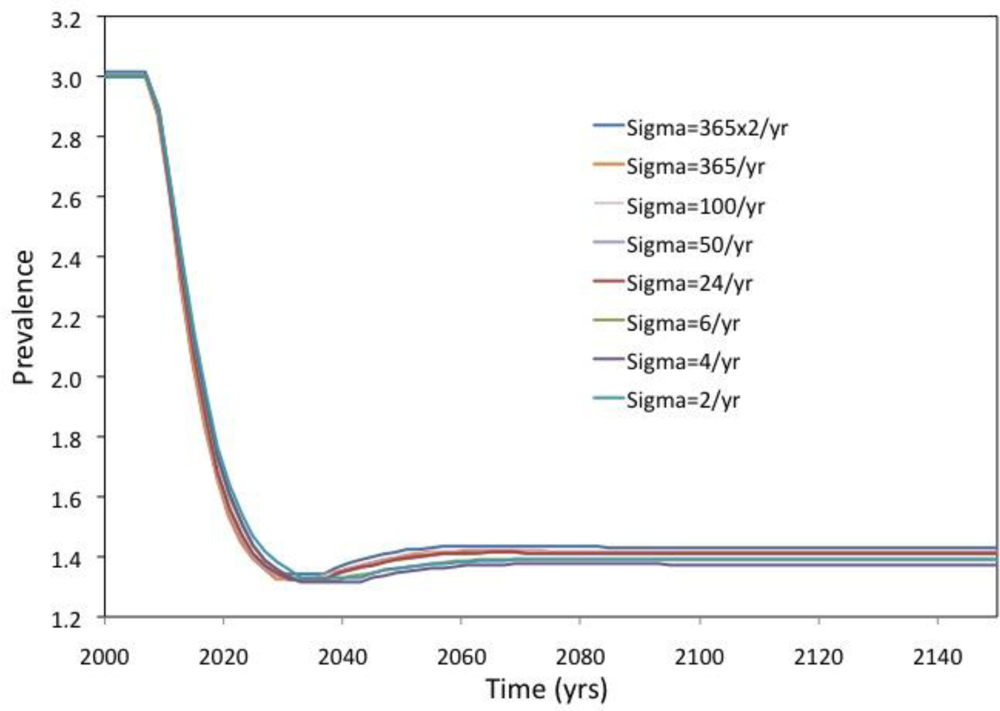
2. Results and Discussion
3. Methods
4. Conclusions
Acknowledgments
References and Notes
- Ault, KA. Human papillomavirus vaccine: an update for gynecologists. Clin. Obstet. Gynecol 2008, 51, 527–532. [Google Scholar]
- Franco, EL; Harper, DM. Vaccination against human papillomavirus infection: a new paradigm in cervical cancer control. Vaccine 2005, 23, 2388–2394. [Google Scholar]
- Ontario Government. Love alone won’t protect your grade 8 daughter from cervical cancer: Ontario’s Grade 8 Vaccination Program.
- Clifford, G; Franceschi, S; Diaz, M; Munoz, N; Villa, LL. Chapter 3: HPV type-distribution in women with and without cervical neoplastic diseases. Vaccine 2006, 24, S26–S34. [Google Scholar]
- Walboomers, J; Jacobs, M; Manos, M; Bosch, F; Kummer, J; Shah, K; Snijder, P; Peto, J; Meijer, C; Munoz, N. Human Papillomavirus is a necessary cause of invasive cervical cancer worldwide. J. Pathol 1999, 189, 1–3. [Google Scholar]
- Bosch, FX; Lorincz, A; Munoz, N; Meijer, CJ; Shah, KV. The casual relation between human papillomavirus and cervical cancer. J. Clin. Pathol 2002, 55, 244–265. [Google Scholar]
- Muñoz, N. Human papillomavirus and cancer: the epidemiological evidence. J. Clin. Virol 2000, 19, 1–5. [Google Scholar]
- Parkin, D; Bray, F; Ferlay, J; Pisano, P. Global cancer statistics, 2002. CA Cancer J. Clin 2002, 55, 74–108. [Google Scholar]
- Sankaranarayanan, R; Ferlay, J. Worldwide burden of gynaecological cancer: the size of the problem. Best Pract. Res. Clin. Obstet. Gynaecol 2006, 20, 207–225. [Google Scholar]
- Bleeker, MCG; Hogenwoning, CJ; Berkhiof, J; Voorhorst, FJ; Hesselink, AT; van Diemen, PM; van den Brule, AJC; Snijders, PJF; Meijer, CJ. Concordance of specific human papillomavirus types in sex partners is more prevalent than would be expected by chance and is associated with increased viral loads. Clin. Infect. Dis 2005, 41, 612–620. [Google Scholar]
- Hughes, JP; Garnett, GP; Koutsky, LA. The theoretical population-level impact of prophylactic human papillomavirus vaccine. Epidemiology 2002, 13, 631–639. [Google Scholar]
- Baseman, JG; Koutsky, LA. Review: The epidemiology of human papillomavirus infections. J. Clin. Virol 2005, 32, S16–S24. [Google Scholar]
- Franco, EL; Villa, LL; Sobrinho, J; Prado, J; Rousseau, M; Desy, M. Epidemiology of acquisition and clearance of cervical human papillomavirus infection in women from a high-risk area for cervical cancer. J. Infect. Dis 1999, 180, 1415–1423. [Google Scholar]
- Giuliano, A; Harris, R; Sedjo, R; Baldwin, S; Roe, D; Papenfuss, MR; Abrahamsen, M; Inserra, P; Olvera, S; Hatch, K. Incidence, prevalence, and clearance of type-specific human papillomavirus infections: the young women's health study. J. Infect. Dis 2002, 186, 462–469. [Google Scholar]
- Ho, GYF; Bierman, R; Beardsley, L; Chang, CJ; Burk, RD. Natural history of cervicovaginal papillomavirus infection in young women. N. Engl. J. Med 1998, 338, 432–428. [Google Scholar]
- Richardson, H; Kelsall, G; Tellier, P; Voyer, H; Abrahamowicz, M; Ferenczy, A; Coutlée, F; Franco, EL. The natural history of type-specific human papillomavirus infections in female university students. Cancer Epidemiol. Biomarker. Prev 2003, 12, 485–490. [Google Scholar]
- Sellors, JW; Mahony, JB; Kaczorowski, J; Lytwyn, A; Bangura, H; Chong, S; Lorincz, A; Dalby, DM; Janjusevic, V; Keller, JL. The Survery of HPV in Ontario Women (SHOW) Group. Prevalence and predictors of human papillomavirus infection in women in Ontario, Canada. Can. Med. Assoc. J 2000, 163, 503–508. [Google Scholar]
- zur Hausen, H. Papillomaviruses causing cancer: evasion from host-cell control in early events in carcinogenesis. J. Nat. Cancer Inst 2000, 92, 690–698. [Google Scholar]
- Bosch, F; de Sanjosé, S. Chapter 1: Human papillomavirus and cervical cancer-burden and assessment of casualty. J. Nat. Cancer Inst. Monogram 2003, 31, 3–13. [Google Scholar]
- Linneham, M; Groce, N. Counseling and educational interventions for women with genital human papillomavirus infection. AIDS Patient Care STDS 2000, 14, 439–445. [Google Scholar]
- Centres for disease control and prevention. Sexually Transmitted Diseases Treatment Guideline 2002. Department of Health and Human Services: Centres for Disease Control and Prevention. 2002.
- Koutsky, LA. Epidemiology of genital human papillomavirus infection. Amer. J. Med 1997, 102, 3–8. [Google Scholar]
- Villa, LL. Prophylactic HPV vaccines reducing the burden of HPV-related diseases. Vaccine 2006, 24, S23–S28. [Google Scholar]
- Foxman, B; Newman, M; Percha, B; Holmes, KK; Aral, SO. Measures of sexual partnerships: lengths, gaps, overlaps, and sexually transmitted infection. Sex. Transm. Dis 2006, 33, 209–214. [Google Scholar]
- Elbasha, EH; Dashbach, EJ; Insinga, RP. Model for assessing human papillomavirus vaccination strategies. Emerg. Infect. Dis 2007, 13, 28–41. [Google Scholar]
- Taira, AV; Neukermans, CP; Sanders, GD. Evaluating human papillomavirus vaccination programs. Emerg. Infect. Dis 2004, 10, 1915–1922. [Google Scholar]
- Barnabas, RV; Laukkanen, P; Koskela, P; Kontule, O; Lehtinen, M; Garnett, GP. Epidemiology of HPV 16 and cervical cancer in Finland and the potential impact of vaccination: mathematical modelling analyses. PLOS Med 2006, 3, 624–632. [Google Scholar]
- Paavonen, J; Naud, P; Salmeron, J; Wheeler, C; Chow, S; Apter, D. Efficacy of human papillomavirus (HPV)-16/18 AS04-adjuvanted vaccine against cervical infection and precancer caused by oncogenic HPV types (PATRICIA): final analysis of a double-blind, randomised study in young women. The Lancet 2009, 374, 301–314. [Google Scholar]
- Singh, A; Wong, T; Howlett, RI. Human papillomavirus vaccines: why the time is right to implement immunization and surveillance programs in Canada. Can. J. Infect. Dis. Med. Microbiol 2008, 19, 294–296. [Google Scholar]
- Brown, DR; Fife, KH; Wheeler, CM; Koutsky, LA; Lupinacci, LM; Railkar, R; Suhr, G; Barr, E; Dicello, A; Li, W; Smith, JF; Tadesse, A; Jansen, KU. Early Assessment of the efficacy of a human papillomavirus types 16 L1 virus-like particle vaccine. Vaccine 2004, 22, 2936–2942. [Google Scholar]
- Burchell, AN; Richardson, H; Mahmud, SM; Trottier, H; Tellier, PT; Hanley, J; Coutlée, F; Franco, EL. Modeling the sexual transmissiblitiy of human papillomavirus infection using stochastic computer simulation and empirical data from a cohort study of young women in Montreal, Canada. Amer. J. Epidemiol 2006, 163, 534–543. [Google Scholar]
- Sanders, GD; Taira, AV. Cost-effectiveness of a potential vaccine for human papillomavirus. Emerg. Infect. Dis 2006, 9, 37–48. [Google Scholar]
- Goldie, SJ; Grima, D; Kohli, M; Wright, TC; Weinstein, M; Franco, EL. A comprehensive natural history model of HPV infection and cervical cancer to estimate the clinical impact of a prophylactic HPV-16/18 vaccine. Int. J. Cancer 2003, 106, 896–904. [Google Scholar]
- Elbasha, EH; Galvani, AP. Vaccination against multiple HPV types. Math. Biosci 2005, 197, 88–117. [Google Scholar]
- Bauch, C. A versatile ODE approximation to a network model for the spread of sexually transmitted diseases. J. Math. Biol 2002, 45, 375–395. [Google Scholar]
- Dietz, K; Hadeler, K. Epidemiological models for sexually transmitted diseases. J. Mathematical Biol 1988, 26, 1–25. [Google Scholar]
- Kretzschmar, M; Morris, M. Concurrent partnership and the spread of HIV. AIDS 1997, 11, 641–648. [Google Scholar]
- Bauch, C; Rand, D. A moment closure model for sexually transmitted disease transmission through a concurrent partnership network. Proc. R. Soc. Lond. B 2000, 267, 2019–2027. [Google Scholar]
- Kretzschmar, M; Dietz, K. The effect of pair formation and variable infectivity on the spread of an infection without recovery. Math. Biosci 1998, 148, 83–113. [Google Scholar]
- Garnett, G; Kim, J; French, K; Goldie, S. Chapter 21: Modelling the impact of HPV vaccines on cervical cancer and screening programmes. Vaccine 2006, 24, S178–S186. [Google Scholar]
- Centres for disease control and prevention. Sexually Transmitted Diseases Treatment Guideline 2002. Department of Health and Human Services, 2008. Available online: http://www.cdc.gov./STD/treatment/6-2002TG.htm\#genitalWarts (accessed on January 22, 2008).
- Woodman, CBJ; Collins, S; Winter, H; Bailey, A; Ellis, J; Prior, P; Yates, M; Rollason, TP; Young, LS. Natural history of cervical human papillomavirus infection in young women: a longitudinal cohort study. The Lancet 2001, 357, 1831–1836. [Google Scholar]

| Symbol | Definition | 3% prevalence scenario | Source |
|---|---|---|---|
| ɛ | Vaccine efficacy | 95% | [11] |
| μ | Rate at which individuals leave the age group of peak sexual activity /yr | 1/15/yr | [2,3] |
| κ | Rate at which individuals are recruited into the age group of peak sexual activity /yr | μN/2 | Derived (see Methods) |
| σ | Pair break-up rate /yr | 2/yr | [27] |
| ρ | Pair formation rate /yr | 33.66/yr | Derived using [27] (see Methods) |
| h | Number of sex acts /yr | 130/yr | [31] |
| β | Transmission rate per sex act | 0.073/act | [41,42], calibrated (see Methods) |
| ω | Rate at which females are vaccinated | 0.05/yr | [42], calibration (see Methods) |
| γ | Infection clearance rate/yr | 1/yr | [14,16,42] |
| δ | Natural immunity waning rate/yr | 1/10/yr | [13,14,16] |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Muller, H.; Bauch, C. When Do Sexual Partnerships Need to Be Accounted for in Transmission Models of Human Papillomavirus? Int. J. Environ. Res. Public Health 2010, 7, 635-650. https://doi.org/10.3390/ijerph7020635
Muller H, Bauch C. When Do Sexual Partnerships Need to Be Accounted for in Transmission Models of Human Papillomavirus? International Journal of Environmental Research and Public Health. 2010; 7(2):635-650. https://doi.org/10.3390/ijerph7020635
Chicago/Turabian StyleMuller, Heidi, and Chris Bauch. 2010. "When Do Sexual Partnerships Need to Be Accounted for in Transmission Models of Human Papillomavirus?" International Journal of Environmental Research and Public Health 7, no. 2: 635-650. https://doi.org/10.3390/ijerph7020635
APA StyleMuller, H., & Bauch, C. (2010). When Do Sexual Partnerships Need to Be Accounted for in Transmission Models of Human Papillomavirus? International Journal of Environmental Research and Public Health, 7(2), 635-650. https://doi.org/10.3390/ijerph7020635




