On Application of the Empirical Bayes Shrinkage in Epidemiological Settings
Abstract
:1. Introduction
2. Methods
2.1. Empirical Bayes Estimator
2.2. Problem with the EBS Estimator
2.3. Simulation Study and Analysis of Variance
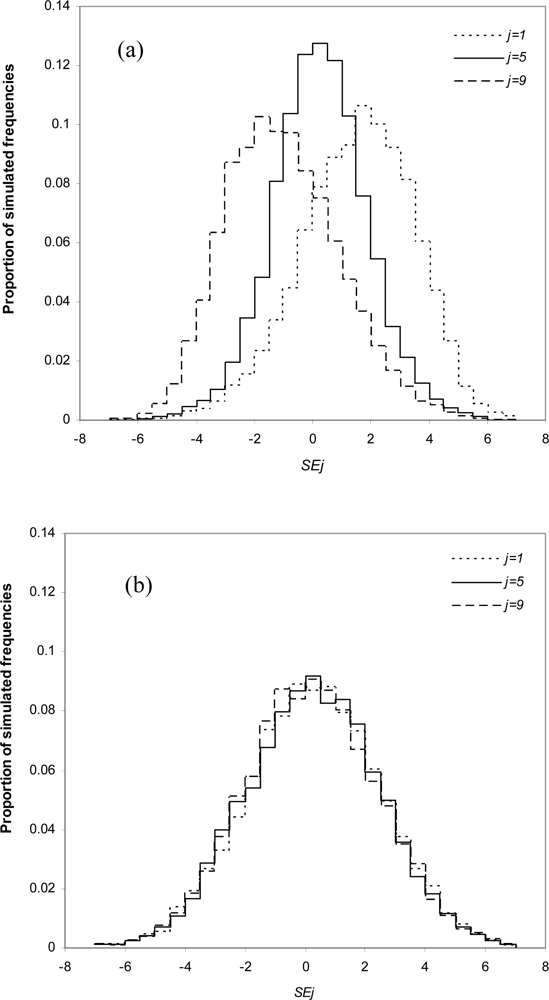
3. Results
3.1. Simulations
3.2. Examples
Example 1: Mumps
Example 2: Birth Weights
4. Discussion
Acknowledgments
References
- Efron, B; Morris, C. Data analysis using Stein’s estimator and its generalisation. J. Am. Stat. Assoc 1975, 70, 311–319. [Google Scholar]
- Steinberg, J. Synthetic Estimates for Small Areas: Statistical Workshop Papers and Discussion; Department of Health, Education and Welfare: Rockville, MD, USA, 1979. [Google Scholar]
- Clayton, D; Kaldor, J. Empirical Bayes estimates of age-standardized relative risks for use in disease mapping. Biometrics 1987, 43, 671–681. [Google Scholar]
- Castner, LA; Schirm, AL. Empirical Bayes Shrinkage Estimates of State Food Stamp Participation Rates for 1998–2000; Mathematica Policy Research: Princeton, NJ, USA, 2003. [Google Scholar]
- Greenland, S. Invited commentary: variable selection versus shrinkage in the control of multiple confounders. Am. J. Epidemiol 2008, 167, 523–529. [Google Scholar]
- Rothman, KJ; Greenland, S; Lash, TL. Modern Epidemiology, 3rd ed; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2008. [Google Scholar]
- Armitage, P; Berry, G; Matthews, JNS. Statistical Methods in Medical Research, 4th ed; Blackwell Publishing: London, UK, 2002. [Google Scholar]
- Efron, B; Morris, C. Stein’s estimation rule and its competitors-an empirical Bayes approach. J. Am. Stat. Assoc 1973, 68, 117–130. [Google Scholar]
- Stein, C. Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1956; Volume 1, pp. 197–208. [Google Scholar]
- Casper, M; Wing, S; Strogatz, D; Davis, CE; Tyroler, HA. Antihypertensive treatment and US trends in stroke mortality, 1962 to 1980. Am. J. Public Health 1992, 82, 1600–1606. [Google Scholar]
- Cislaghi, C; Biggeri, A; Braga, M; Lagazio, C; Marchi, M. Exploratory tools for disease mapping in geographical epidemiology. Stat. Med 1995, 14, 2363–2381. [Google Scholar]
- Chambless, LE; Folsom, AR; Clegg, LX; Sharrett, AR; Nieto, FJ; Shahar, E; Rosamond, W; Evans, G. Carotid wall thickness is predictive of incident clinical stroke. Am. J. Epidemiol 2000, 151, 478–487. [Google Scholar]
- Beckett, LA; Tancredi, DJ. Parametric empirical Bayes estimates of disease prevalence using stratified samples from community populations. Stat. Med 2000, 19, 681–695. [Google Scholar]
- Graham, P. Intelligent smoothing using hierarchical Bayesian models. Epidemiology 2008, 19, 493–495. [Google Scholar]
- Carlin, JB; Louis, TA. Bayes and Empirical Bayes Methods for Data Analysis, 2nd ed; Chapman & Hall: New York, NY, USA, 2000. [Google Scholar]
- Gutmann, S. Stein’s Paradox is impossible in problems with finite sample space. Ann. Stat 1982, 10, 1017–1020. [Google Scholar]
- Greenland, S; Poole, C. Empirical-Bayes and semi-Bayes approaches to occupational and environmental hazard surveillance. Arch. Environ. Health 1994, 49, 9–16. [Google Scholar]
- Fabozzi, FJ; Kolm, PN; Pachamanova, D; Focardi, SM. Robust Portfolio Optimization and Management; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Perlman, MD; Chaudhuri, S. Reversing the Stein Effect; University of Washington: Seattle, WA, USA, 2005.
- Tate, RL. A cautionary note on shrinkage estimates of school and teacher effects. Florida J. Educ. Res 2004, 42, 1–21. [Google Scholar]
- Experimental Estimates of Aboriginal and Torres Strait Islander Australians, 2006; Australian Bureau of Statistics: Canberra, Australia, 2008.
- Efron, B; Morris, C. Limiting the risk of Bayes and empirical Bayes estimators—Part 1: The Bayes case. J. Am. Stat. Assoc 1971, 66, 807–815. [Google Scholar]
- Efron, B; Morris, C. Limiting the risk of Bayes and empirical Bayes estimators—Part 2: The empirical Bayes case. J. Am. Stat. Assoc 1972, 67, 130–139. [Google Scholar]
- Lin, P; Tsai, H. Generalized Bayes minimax estimators of the multivariate normal mean with unknown covariance matrix. Ann. Stat 1973, 1, 142–145. [Google Scholar]
- Stein, CM. Estimation of the mean of a multivariate normal distribution. Ann. Stat 1981, 6, 1135–1151. [Google Scholar]
- Yi-Shi Shao, P; Strawderman, WE. Improving on the James-Stein positive-part estimator. Ann. Stat 1994, 22, 1517–1538. [Google Scholar]
- Hoffmann, K. Stein estimation—a review. Stat. Pap 2000, 41, 127–158. [Google Scholar]
- Sclove, SL. Improved estimators for coefficients in linear regression. J. Am. Stat. Assoc 1968, 63, 596–606. [Google Scholar]
- Sclove, SL; Morris, C; Radhakrishnan, R. Non-optimality of preliminary-test estimators for the mean of a multivariate normal distribution. Ann. Math. Stat 1972, 43, 1481–1490. [Google Scholar]
- Sen, PK; Saleh, AKME. On preliminary test and shrinkage M-estimation in linear models. Ann. Stat 1987, 15, 1580–1592. [Google Scholar]
- Khan, S; Saleh, AKME. On the comparison of the pre-test and shrinkage M-estimation in linear models. Stat. Pap 2001, 42, 451–473. [Google Scholar]
- Saleh, AKME. Theory of Preliminary Test and Stein-type Estimation with Applications; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Morris, C. Parametric empirical Bayes inference: theory and applications. J. Am. Stat. Assoc 1983, 78, 47–55. [Google Scholar]
- Everson, P. A statistician reads the sports pages, Stein’s paradox revisited. Chance 2007, 20, 49–56. [Google Scholar]
- Gruber, MHJ. Improving Efficiency by Shrinkage: The James-Stein and Ridge Regression Estimators; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Hastie, T; Tibshirani, R; Friedman, JH. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2001. [Google Scholar]
- Burton, A; Altman, DG; Royston, P; Holder, RL. The design of simulation studies in medical statistics. Stat. Med 2006, 25, 4279–4292. [Google Scholar]
- Australian National Notifiable Diseases Surveillance System, 2001–2008; Australian Department of Health and Ageing: Canberra, Australia.
- Witte, JS; Greenland, S. Simulation study of hierarchical regression. Stat. Med 1996, 15, 1161–1170. [Google Scholar]
- Greenland, S. When should epidemiologic regressions use random coefficients? Biometrics 2000, 56, 915–921. [Google Scholar]
- West, BT; Welch, KB; Galecki, AT. Linear Mixed Models: A Practical Guide Using Statistical Software; Chapman Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Berger, JO. Statistical Decision Theory and Bayesian Analysis, 2nd ed; Springer: New York, NY, USA, 1985; pp. 364–369. [Google Scholar]
- Ahmed, SE. Shrinkage preliminary test estimation in multivariate normal distributions. J. Stat. Comput. Sim 1992, 43, 177–195. [Google Scholar]
| n | Assessing standard | σ2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0025 | 0.01 | 0.04 | 1 | 25 | 100 | 400 | |||
| θ =j/10 | |||||||||
| f | 600.0 | 150.0 | 37.50 | 1.500 | 0.060 | 0.015 | 0.004 | ||
| 20 | θj | 50.4 | 54.4 | 61.7 | 82.5 | 93.9 | 93.0 | 94.2 | |
| Ȳj | 49.3 | 52.5 | 59.8 | 74.4 | 87.5 | 84.6 | 85.2 | ||
| v͂ | 49.6 | 53.4 | 61.5 | 79.7 | 92.5 | 90.3 | 91.0 | ||
| 40 | θj | 51.1 | 52.9 | 56.1 | 79.7 | 93.7 | 93.2 | 93.7 | |
| Ȳj | 51.7 | 50.7 | 54.3 | 61.5 | 74.1 | 71.9 | 68.9 | ||
| v͂ | 52.1 | 52.0 | 56.1 | 73.1 | 89.6 | 88.3 | 87.8 | ||
| 80 | θj | 52.2 | 50.9 | 54.0 | 74.1 | 92.6 | 92.0 | 93.9 | |
| Ȳj | 52.4 | 48.2 | 50.0 | 50.3 | 49.6 | 47.0 | 48.7 | ||
| v͂ | 53.5 | 49.4 | 53.6 | 66.6 | 83.9 | 83.3 | 82.7 | ||
| θ =j | |||||||||
| f | 60 000 | 15 000 | 3750 | 150.0 | 6.000 | 1.500 | 0.375 | ||
| 20 | θj | 50.4 | 54.4 | 61.7 | 49.7 | 69.7 | 83.9 | 90.7 | |
| Ȳj | 49.3 | 52.5 | 59.8 | 49.8 | 63.5 | 75.3 | 82.3 | ||
| v͂ | 49.6 | 53.4 | 61.5 | 49.9 | 68.1 | 80.8 | 88.7 | ||
| 40 | θj | 51.1 | 52.9 | 56.1 | 50.1 | 66.5 | 77.6 | 86.2 | |
| Ȳj | 51.7 | 50.7 | 54.3 | 50.8 | 56.8 | 60.8 | 65.2 | ||
| v͂ | 52.1 | 52.0 | 56.1 | 50.9 | 62.8 | 73.0 | 80.2 | ||
| 80 | θjj | 52.2 | 50.9 | 54.0 | 48.5 | 62.9 | 71.2 | 85.5 | |
| Ȳj | 52.4 | 48.2 | 50.0 | 51.0 | 46.7 | 48.8 | 49.1 | ||
| v͂ | 53.5 | 49.4 | 53.6 | 51.0 | 54.5 | 65.4 | 74.2 | ||
| θ = 10j | |||||||||
| f | 6 000 000 | 1 500 000 | 375 000 | 15 000 | 600.0 | 150.0 | 37.50 | ||
| 20 | θj | 49.9 | 49.0 | 49.3 | 49.7 | 52.9 | 54.5 | 60.2 | |
| Ȳj | 49.3 | 50.3 | 49.8 | 49.8 | 50.9 | 51.9 | 56.5 | ||
| v͂ | 49.3 | 50.3 | 49.8 | 49.9 | 51.3 | 52.6 | 57.8 | ||
| 40 | θj | 48.4 | 49.0 | 49.5 | 50.1 | 52.1 | 53.0 | 54.5 | |
| Ȳj | 50.7 | 48.9 | 49.1 | 50.8 | 51.0 | 51.8 | 51.2 | ||
| v͂ | 50.7 | 48.9 | 49.2 | 50.9 | 51.8 | 53.2 | 53.6 | ||
| 80 | θj | 50.1 | 49.3 | 49.3 | 48.5 | 52.7 | 52.2 | 54.6 | |
| Ȳ | 50.2 | 50.0 | 50.3 | 51.0 | 49.7 | 50.3 | 47.3 | ||
| v͂ | 50.2 | 50.0 | 50.3 | 51.0 | 50.8 | 52.2 | 51.1 | ||
| n | σ2 | 0.01 | 1 | 100 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| j | 1 | 5 | 9 | 1 | 5 | 9 | 1 | 5 | 9 | ||
| θj | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | ||
| 20 | ȳj | −0.008 | 0.037 | −0.007 | 0.786 | −0.200 | −0.227 | 8.479 | −6.425 | 1.004 | |
| xj | 0.191 | 0.037 | −0.205 | 13.475 | −0.219 | −12.996 | 29.164 | 3.062 | −24.211 | ||
| 40 | ȳj | 0.019 | 0.016 | −0.019 | 0.510 | 0.578 | 0.321 | 3.751 | −7.531 | 0.067 | |
| xj | 0.119 | 0.016 | −0.119 | 8.204 | 0.483 | −7.498 | 28.719 | −1.757 | −28.441 | ||
| 80 | ȳj | −0.012 | 0.017 | −0.011 | 0.271 | 0.161 | −0.017 | −1.264 | −5.765 | −0.045 | |
| xj | 0.037 | 0.017 | −0.061 | 4.683 | 0.170 | −4.397 | 29.172 | −1.436 | −30.025 | ||
| θj | 1 | 5 | 9 | 1 | 5 | 9 | 1 | 5 | 9 | ||
| 20 | ȳj | 0.023 | 0.039 | −0.080 | 0.871 | −0.426 | −0.976 | 1.489 | 4.195 | 0.162 | |
| xj | 0.043 | 0.039 | −0.100 | 2.856 | −0.425 | −2.961 | 129.271 | 2.284 | −126.039 | ||
| 40 | ȳj | −0.013 | 0.046 | −0.041 | 0.515 | −0.934 | −0.286 | 3.159 | 3.994 | −3.299 | |
| xj | −0.003 | 0.046 | −0.051 | 1.513 | −0.932 | −1.283 | 82.075 | 2.813 | −82.005 | ||
| 80 | ȳj | −0.040 | −0.002 | −0.036 | 0.142 | −0.924 | −0.200 | 2.332 | −0.916 | −1.153 | |
| xj | −0.035 | −0.002 | −0.041 | 0.641 | −0.923 | −0.699 | 46.580 | −0.904 | −45.703 | ||
| θj | 10 | 50 | 90 | 10 | 50 | 90 | 10 | 50 | 90 | ||
| 20 | ȳj | −0.089 | −0.008 | −0.025 | −0.956 | 0.198 | −0.331 | 2.691 | 8.139 | −3.101 | |
| xj | −0.087 | −0.008 | −0.027 | −0.756 | 0.198 | −0.531 | 22.794 | 8.100 | −23.191 | ||
| 40 | ȳj | −0.092 | −0.083 | −0.083 | −0.772 | −0.084 | −0.298 | −1.020 | 7.342 | −3.903 | |
| xj | −0.091 | −0.083 | −0.084 | −0.673 | −0.084 | −0.398 | 8.977 | 7.322 | −13.890 | ||
| 80 | ȳj | −0.066 | −0.020 | −0.030 | −0.496 | −0.012 | −0.293 | −1.948 | 4.893 | −6.302 | |
| xj | −0.065 | −0.020 | −0.030 | −0.447 | −0.012 | −0.343 | 3.043 | 4.886 | −11.284 | ||
| n | σ2 | 0.01 | 1 | 100 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| j | 1 | 5 | 9 | 1 | 5 | 9 | 1 | 5 | 9 | ||
| θj | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | ||
| 20 | ȳj | 0.0479 | 0.0497 | 0.0477 | 5.0400 | 5.1221 | 4.8391 | 509.64 | 502.83 | 462.32 | |
| xj | 0.0482 | 0.0493 | 0.0479 | 5.5647 | 2.8272 | 5.2105 | 181.62 | 178.89 | 186.64 | ||
| 40 | ȳj | 0.0248 | 0.0244 | 0.0245 | 2.6060 | 2.4557 | 2.5326 | 248.01 | 256.36 | 247.09 | |
| xj | 0.0249 | 0.0242 | 0.0246 | 2.8567 | 1.7153 | 2.6752 | 95.284 | 86.476 | 94.234 | ||
| 80 | ȳj | 0.0128 | 0.0119 | 0.0128 | 1.2761 | 1.1932 | 1.2172 | 119.23 | 123.92 | 111.17 | |
| xj | 0.0128 | 0.0119 | 0.0128 | 1.3926 | 0.9717 | 1.3115 | 49.919 | 40.804 | 52.251 | ||
| θj | 1 | 5 | 9 | 1 | 5 | 9 | 1 | 5 | 9 | ||
| 20 | ȳj | 0.0517 | 0.0491 | 0.0510 | 5.0175 | 5.2305 | 5.4695 | 485.60 | 495.86 | 530.51 | |
| xj | 0.0517 | 0.0491 | 0.0511 | 5.0747 | 5.1849 | 5.5320 | 537.33 | 267.53 | 548.56 | ||
| 40 | ȳj | 0.0244 | 0.0249 | 0.0271 | 2.5130 | 2.6806 | 2.8059 | 233.65 | 241.30 | 239.03 | |
| xj | 0.0244 | 0.0249 | 0.0271 | 2.5281 | 2.6687 | 2.8173 | 265.57 | 162.31 | 269.45 | ||
| 80 | ȳj | 0.0128 | 0.0125 | 0.0137 | 1.2054 | 1.3085 | 1.3438 | 118.80 | 129.07 | 119.67 | |
| xj | 0.0128 | 0.0125 | 0.0138 | 1.2080 | 1.3055 | 1.3471 | 130.91 | 104.15 | 132.15 | ||
| θj | 10 | 50 | 90 | 10 | 50 | 90 | 10 | 50 | 90 | ||
| 20 | ȳj | 0.0479 | 0.0486 | 0.0469 | 4.7860 | 4.9156 | 5.0841 | 501.95 | 497.18 | 503.44 | |
| xj | 0.0479 | 0.0486 | 0.0469 | 4.7825 | 4.9152 | 5.0854 | 504.31 | 492.75 | 507.06 | ||
| 40 | ȳj | 0.0255 | 0.0261 | 0.0229 | 2.5097 | 2.5017 | 2.6234 | 253.43 | 243.67 | 251.46 | |
| xj | 0.0255 | 0.0261 | 0.0229 | 2.5082 | 2.5016 | 2.6240 | 253.71 | 242.56 | 252.78 | ||
| 80 | ȳj | 0.0120 | 0.0132 | 0.0120 | 1.2461 | 1.2779 | 1.2834 | 126.39 | 116.47 | 118.15 | |
| xj | 0.0120 | 0.0132 | 0.0120 | 1.2456 | 1.2779 | 1.2837 | 126.36 | 116.21 | 118.92 | ||
| State/Territory* | ||||||||
|---|---|---|---|---|---|---|---|---|
| ACT | NSW | NT | Qld | SA | Tas | Vic | WA | |
| 2001 | 0.3 | 0.4 | 0.5 | 0.1 | 0.8 | 0.4 | 0.8 | 1.5 |
| 2002 | 0 | 0.4 | 0.5 | 0.2 | 0.7 | 0 | 0.2 | 0.7 |
| 2003 | 0.6 | 0.5 | 0 | 0.3 | 0.8 | 0 | 0.1 | 0.7 |
| 2004 | 0.9 | 1 | 0 | 0.4 | 0.3 | 0 | 0.1 | 0.5 |
| 2005 | 0.3 | 1.6 | 3.4 | 1.7 | 0.5 | 0 | 0.4 | 1.1 |
| 2006 | 0.3 | 2.3 | 3.3 | 1.4 | 1.3 | 0 | 0.3 | 0.8 |
| 2007 | 1.2 | 4.7 | 28.8 | 1.1 | 1.4 | 0.4 | 0.3 | 5.2 |
| 2008 (year-to-date) | 0 | 1 | 19.1 | 0.6 | 0.9 | 0.4 | 0.3 | 4.5 |
| ȳj | 0.5 | 1.6 | 5.2 | 0.7 | 0.8 | 0.1 | 0.3 | 1.5 |
| Bj | 0.11 | 0.01 | 0.17 | 0.01 | 0.03 | 0.08 | 0.01 | 0.02 |
| xj | 0.6 | 1.6 | 4.6 | 0.7 | 0.8 | 0.2 | 0.3 | 1.5 |
| District* | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ASR | ASU | BD | DR | DU | EA | KD | |||
| NT† | |||||||||
| 2003–2006 | ȳj | 3,182 | 3,381 | 3,137 | 3,058 | 3,326 | 3,121 | 3,186 | 3,198 |
| SD‡ | 33.3 | 27.1 | 72.5 | 26.3 | 8.0 | 27.4 | 46.8 | 113.8 | |
| 2003–2007 | θj | 3,187 | 3,386 | 3,145 | 3,051 | 3,331 | 3,141 | 3,189 | |
| xj | 3,182 | 3,377 | 3,139 | 3,060 | 3,323 | 3,122 | 3,186 | ||
| NT non-Aboriginal | |||||||||
| 2003–2006 | ȳj | 3,494 | 3,421 | 3,322 | 3,324 | 3,347 | 3,504 | 3,320 | 3,390 |
| SD‡ | 119.8 | 25.9 | 162.7 | 33.6 | 8.7 | 73.8 | 53.1 | 108.0 | |
| 2003–2007 | θj | 3,494 | 3,433 | 3,371 | 3,324 | 3,351 | 3,494 | 3,324 | |
| xj | 3,476 | 3,415 | 3,335 | 3,336 | 3,355 | 3,484 | 3,333 | ||
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, Y.; Lee, A.H.; Barnes, T. On Application of the Empirical Bayes Shrinkage in Epidemiological Settings. Int. J. Environ. Res. Public Health 2010, 7, 380-394. https://doi.org/10.3390/ijerph7020380
Zhao Y, Lee AH, Barnes T. On Application of the Empirical Bayes Shrinkage in Epidemiological Settings. International Journal of Environmental Research and Public Health. 2010; 7(2):380-394. https://doi.org/10.3390/ijerph7020380
Chicago/Turabian StyleZhao, Yuejen, Andy H. Lee, and Tony Barnes. 2010. "On Application of the Empirical Bayes Shrinkage in Epidemiological Settings" International Journal of Environmental Research and Public Health 7, no. 2: 380-394. https://doi.org/10.3390/ijerph7020380
APA StyleZhao, Y., Lee, A. H., & Barnes, T. (2010). On Application of the Empirical Bayes Shrinkage in Epidemiological Settings. International Journal of Environmental Research and Public Health, 7(2), 380-394. https://doi.org/10.3390/ijerph7020380




