Predictive Modeling for Pandemic Forecasting: A COVID-19 Study in New Zealand and Partner Countries
Abstract
1. Introduction
2. Literature Review
3. Dataset Selection and Justification
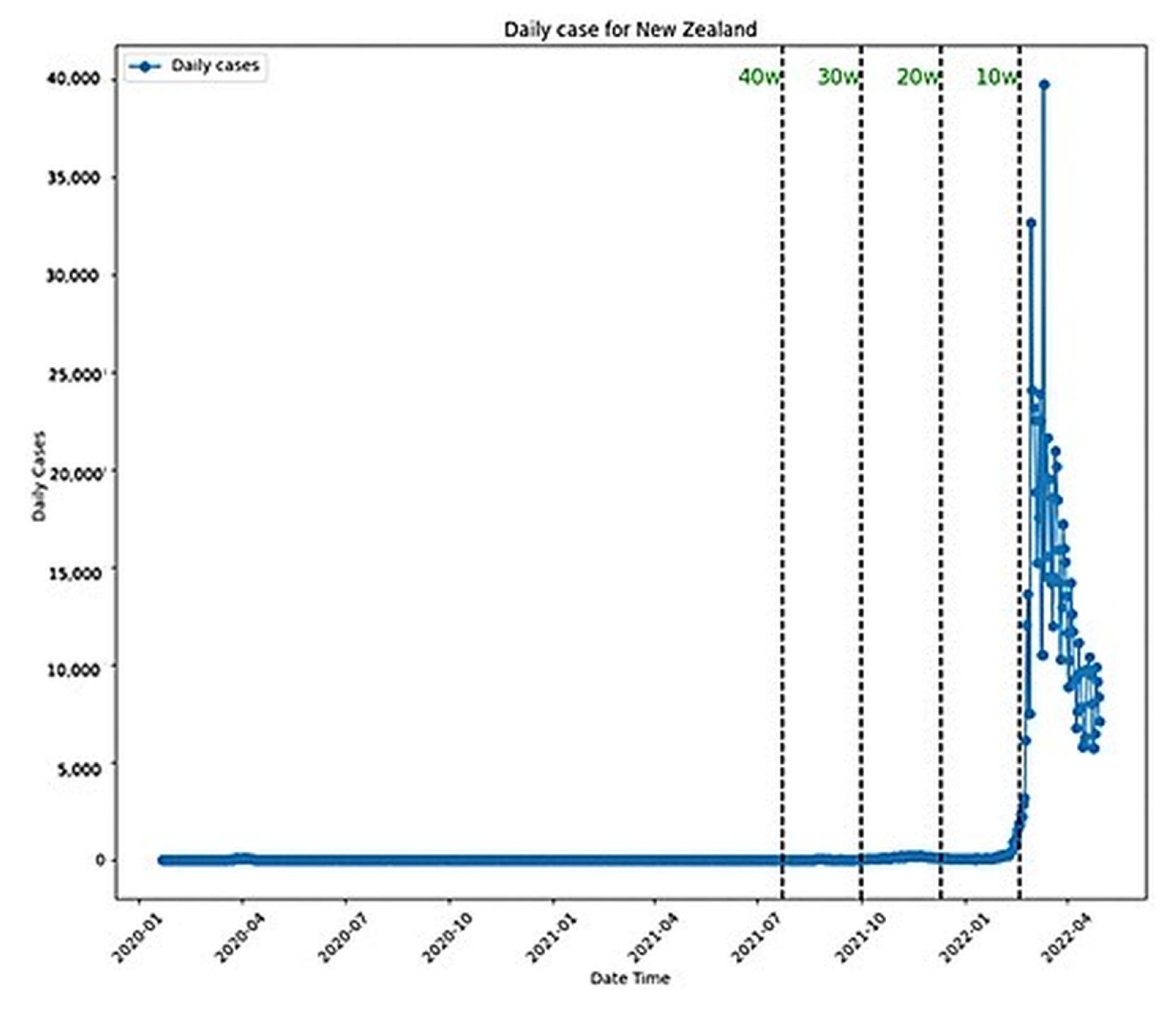
3.1. Explanation of Data Sources and Preprocessing
- Missing Data Handling: Gaps were filled using linear interpolation.
- Outlier Detection: Extreme values were smoothed using a rolling average.
- Normalization: Adjustments were made for population size and testing rates.
- Daily: New cases were extracted from cumulative counts for predictive modeling.
3.2. Data Preprocessing
- Data Cleaning: Missing values were handled using linear interpolation, and outliers were identified and corrected using a rolling average approach.
- Normalization: The dataset was normalized to account for variations in population size and testing rates across countries. This step ensured that the models could be compared fairly across different geographic contexts.
- Feature Engineering: Daily new cases were calculated from the cumulative case data provided in the dataset. This transformation was necessary to capture the dynamic nature of the pandemic and provide a more accurate input for the predictive models.
- Train–Validation Split: The dataset was divided into training and validation sets using a 75:25 ratio by default. This ratio could be adjusted based on user preferences, but the default setting was chosen to balance model training and evaluation effectively.
4. Materials and Methods
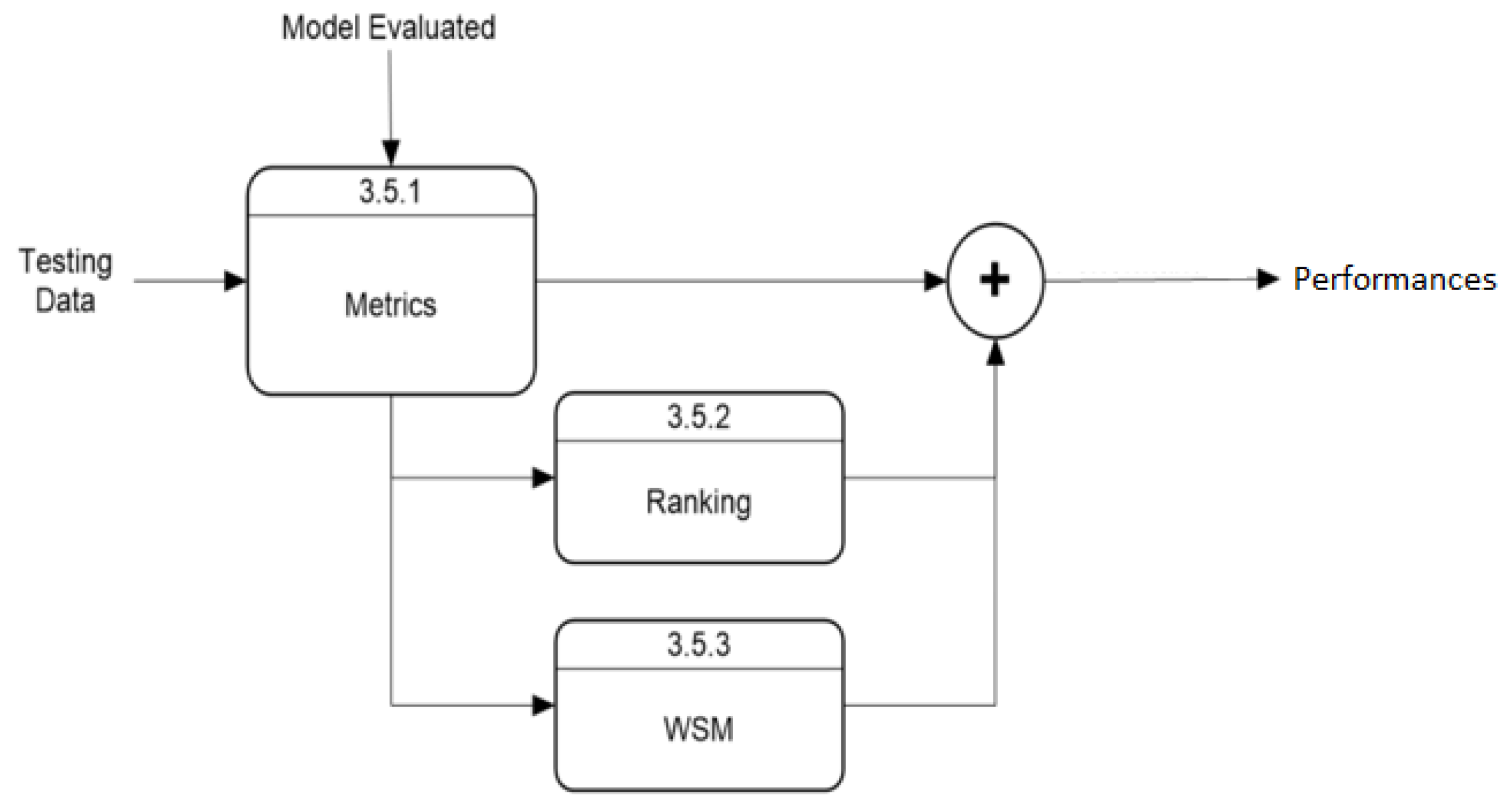
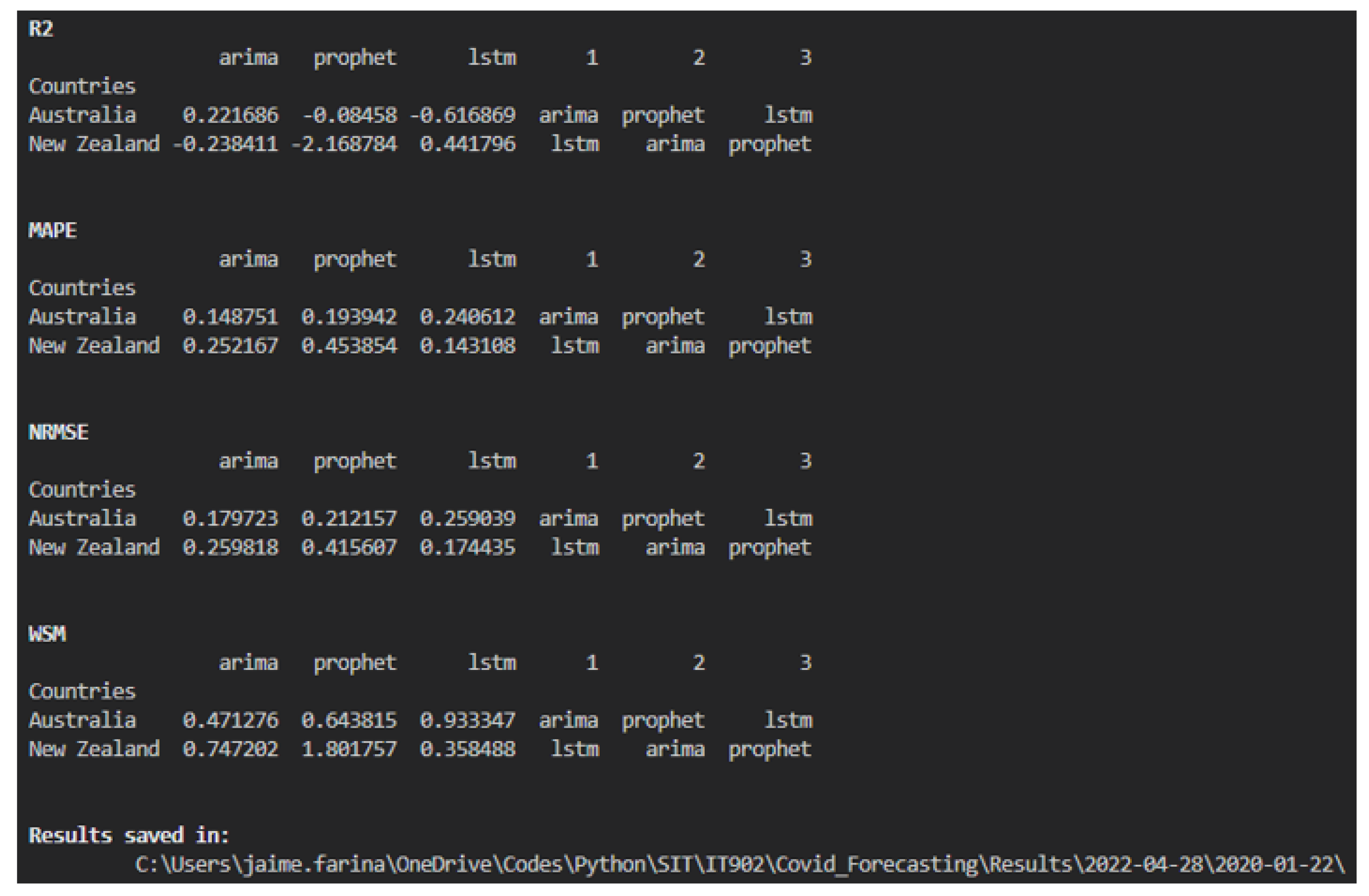
4.1. Performance Metrics
4.2. Feature-Selection Process
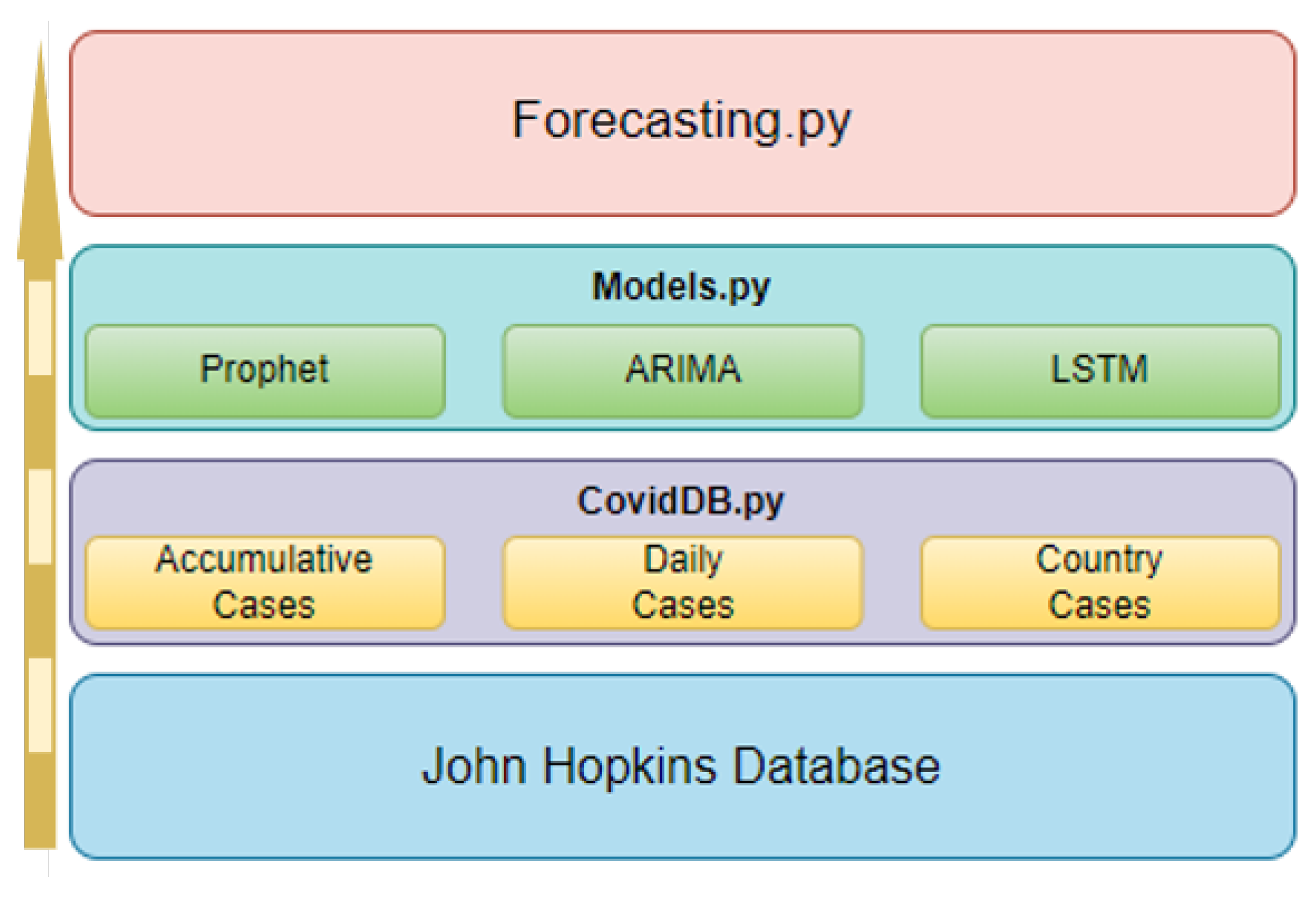
4.3. Software Design
- Functional Requirements The application does not require a graphical interface; all options can be specified via the command line. However, the program must present results in an organized manner, including charts comparing actual and predicted values, file reports containing actual and predicted data with performance metrics, and console summaries of calculated errors, including a ranking of model performances for each metric. Key functionalities include the option to select multiple countries simultaneously, choose one or more ML models to train, and specify the initial and final days of analysis. These parameters can be set to specific dates or relative periods (e.g., number of days or weeks ago), with defaults set to the first confirmed case for the specific country and the latest available data. Users can also adjust the training-to-validation data ratio and predict new cases beyond the known days. Performance metrics are always calculated due to their low computational cost, with an internal analysis identifying the best and worst models for each specific case
- Non-Functional Requirements To ensure accessibility, the application will be available on GitHub with comprehensive documentation on the necessary modules and libraries for correct execution. Documentation will include examples of operation, available options, and minor modifications, such as changing the folder for saving results. The application will provide help with brief explanations of all options, their default values, and accepted formats, alongside basic and advanced usage examples. The training and testing process for each model should take no more than five minutes with the complete dataset, anticipating higher computational demands. Precision ranges for models are not specified, as performance evaluation is left to the user.
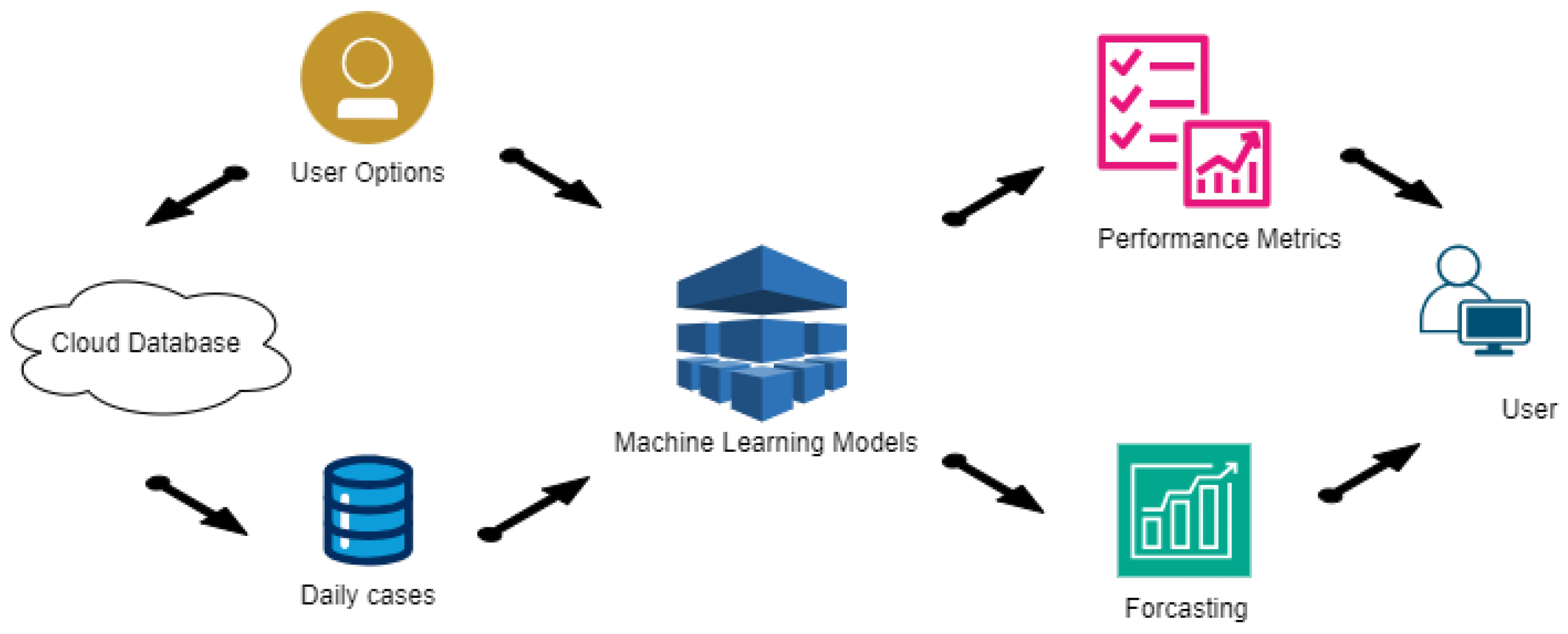
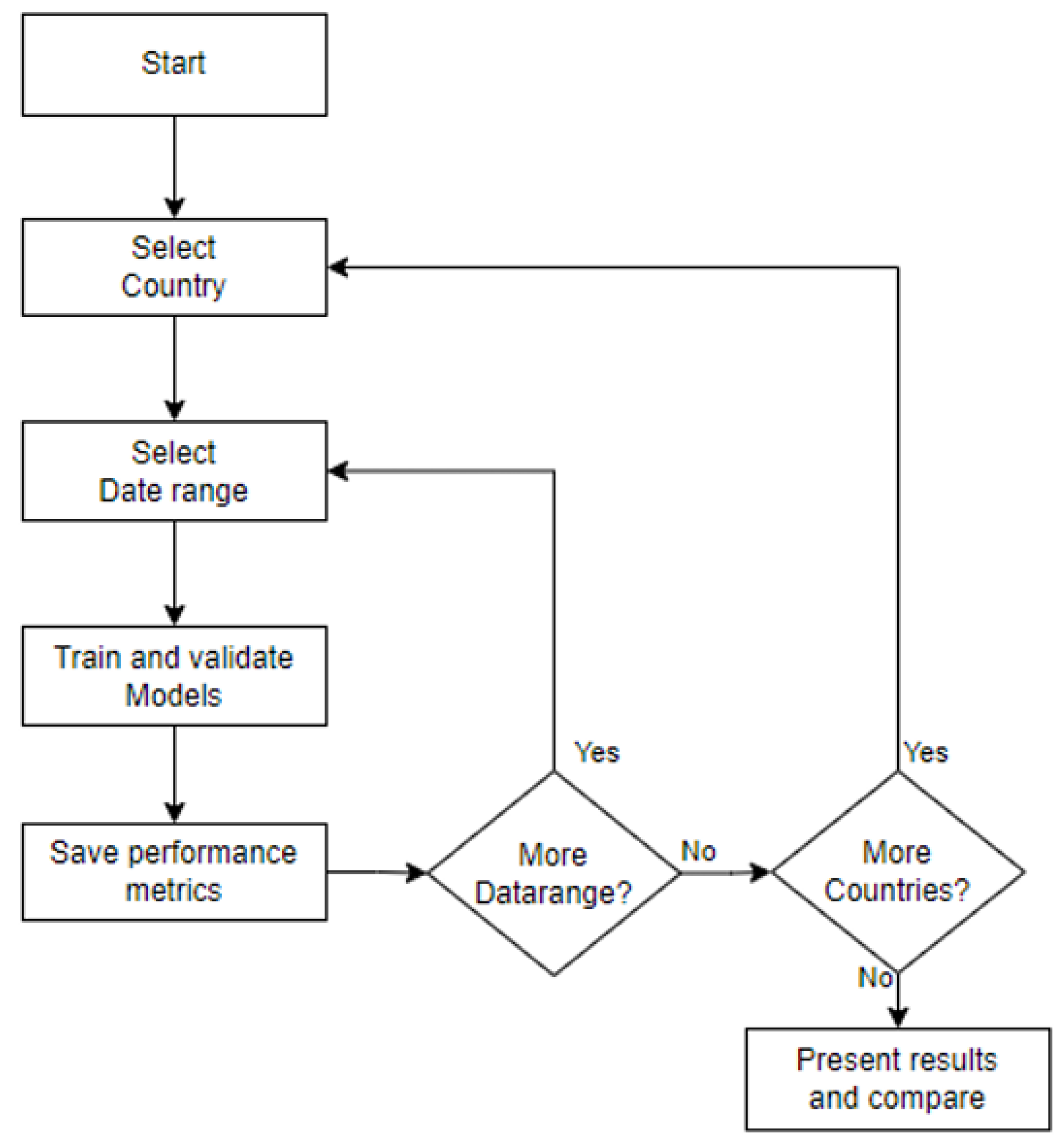
5. System Architecture
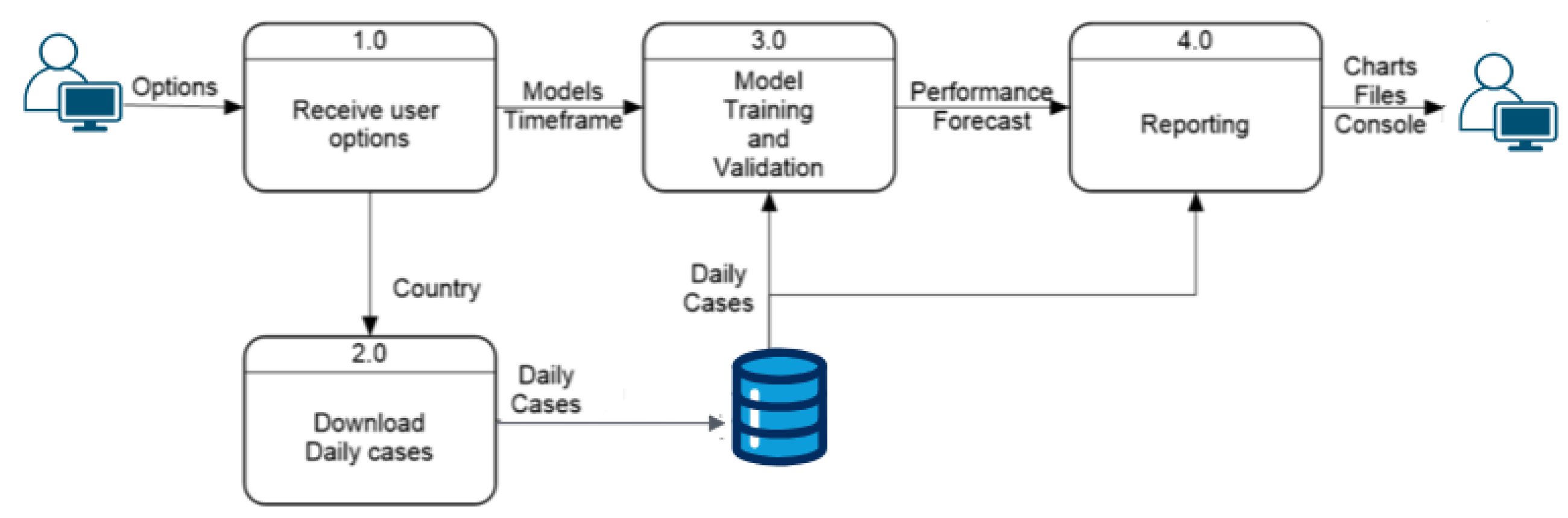
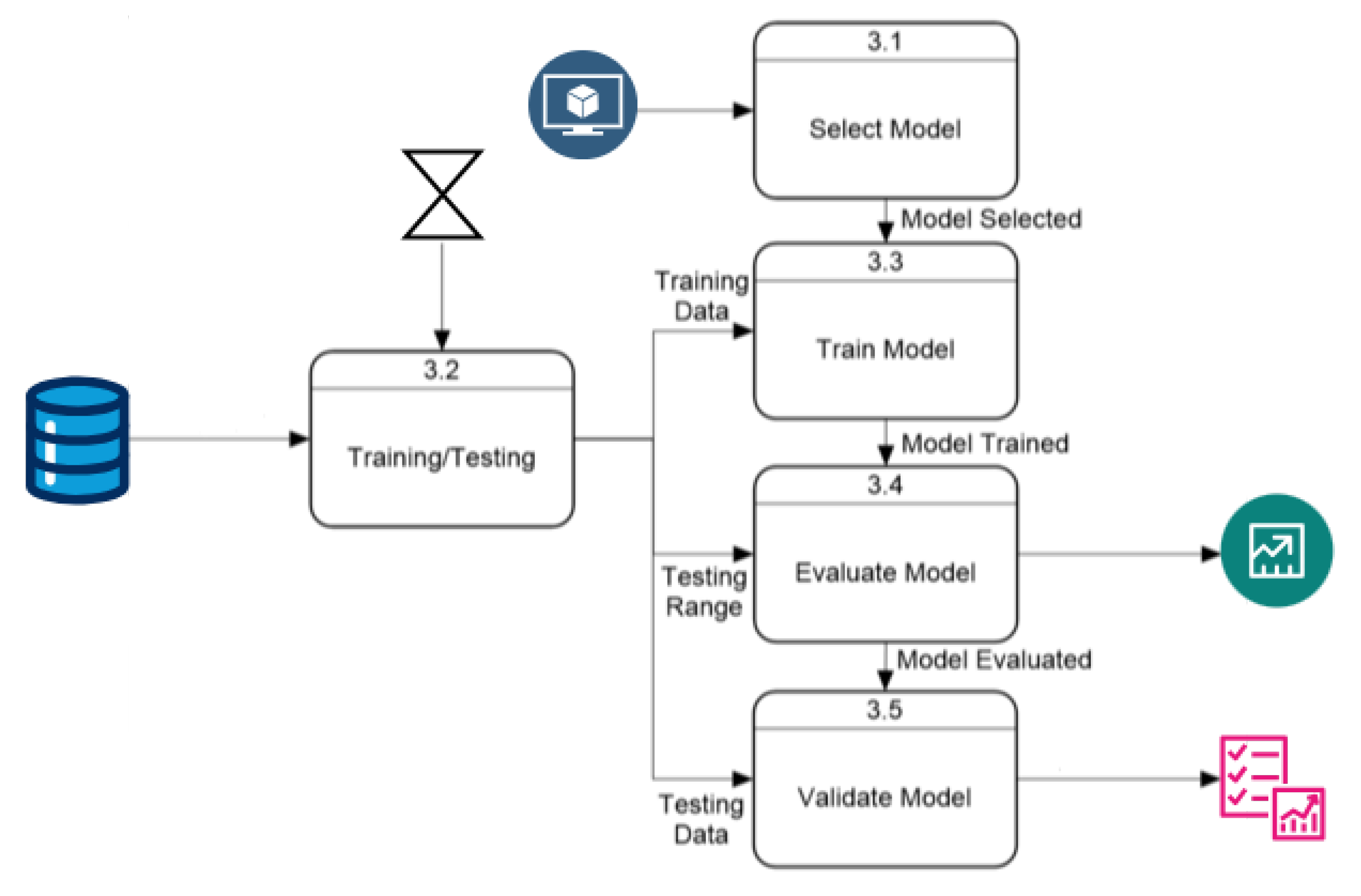
- Data Flow The next step in the development of the application involves characterizing how data flow through the program and how internal processes interact with each other and with user options during execution. Previously, the architectural structure identified several processes, explained in general terms. This section delves deeper into these explanations using data flow diagrams, detailing how options and data move within the program.
Prediction Process
6. Application Development
6.1. Application Structure
6.2. Features and Functionality
6.3. Performance Metrics Algorithm
| Algorithm 1 Performance metric algorithm. |
Require: Dataset, Predictions, sklearn.metrics, and numpy libraries
|
6.4. Weighting Strategy for Multi-Criteria Decision Making
- 1.
- Model Accuracy Metrics: Metrics such as Root Mean Square Error (RMSE) and Mean Absolute Percentage Error (MAPE) were weighted higher due to their direct impact on forecasting precision.
- 2.
- Error Normalization for Comparability: Since different models exhibit variations in scale and error distribution, we applied normalized weights to ensure fair comparisons across different datasets and models.
- 3.
- Sensitivity to Data Variability: The weight distribution was fine-tuned through sensitivity analysis, ensuring that minor variations in data do not disproportionately influence model rankings.
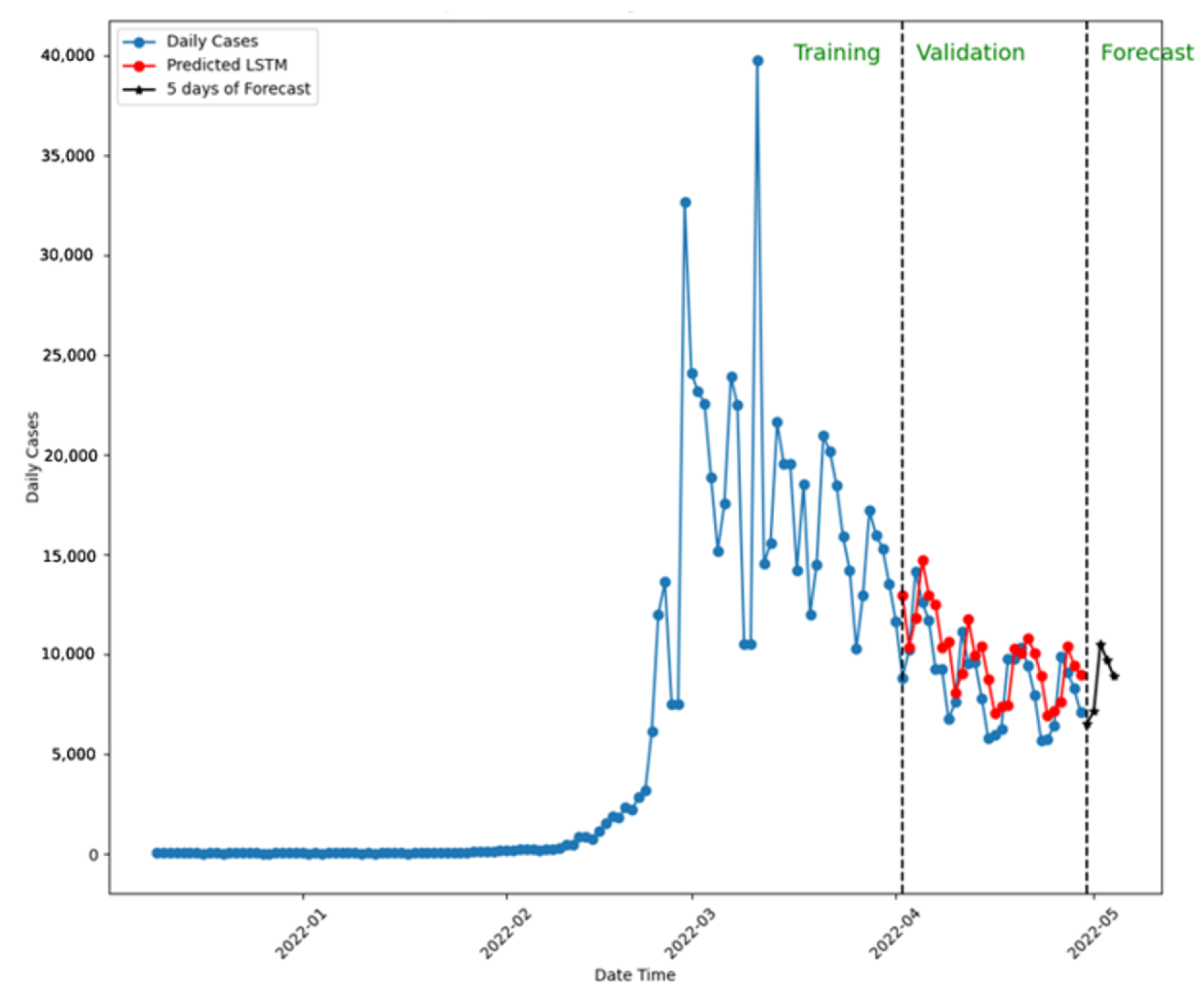
7. Results
8. Discussion
- Short Time Frame Results
- 4-Week Dataset
- Prophet achieved the best average performance and the most first-place rankings, with an exceptional implementation in Japan (error < 0.2).
- ARIMA demonstrated the most stable performance, with a difference lower than 0.5, making it a reliable model for spread prediction.
- In New Zealand, Prophet and ARIMA developed acceptable models (performance < 0.8), while LSTM failed to meet the threshold.
- 8-Week Dataset
- LSTM showed the best average performance, followed closely by Prophet.
- Prophet had the best implementation, with performance lower than 0.4 in Japan and the United States.
- ARIMA exhibited the most stable performance, although not as reliable as the 4-week implementation.
- In New Zealand, LSTM outperformed the other models.
- 10-Week Dataset
- ARIMA had the best average performance and was considered the best model, with the best implementation in Australia.
- Prophet achieved the most first-place rankings but had the worst average performance.
- All models showed high differences between best and worst performances, indicating low stability.
- In New Zealand, LSTM outperformed ARIMA and was the best choice for spread prediction.
- Long Time Frame Results
- 20-Week Dataset
- LSTM showed a slightly better average performance than the other models, making it the best option.
- ARIMA demonstrated the most stable performance, with a difference of 0.65, making it a good forecasting tool.
- In New Zealand, both ARIMA and LSTM developed excellent models (error < 1), with LSTM being the better option.
- 30-Week Dataset
- ARIMA was considered the best model, with the best average performance and one of the best implementations in Japan (error < 0.3).
- LSTM also performed exceptionally, with stable performance and an error lower than 0.4 in Japan.
- In New Zealand, both ARIMA and LSTM showed very good performance (error < 1), with ARIMA being the first choice.
- 40-Week Dataset
- LSTM had a slightly better average performance than ARIMA and the best implementation in Japan (error < 0.4).
- LSTM exhibited the most stable performance, with a difference close to 0.9.
- In New Zealand, both models performed well, with LSTM being the first choice for forecasting analysis.
- Complete Dataset (Table 3)
- ARIMA was considered the best model, with high prediction accuracy and the best average performance.
- LSTM had the best implementation in Japan, slightly better than ARIMA’s best performance.
- In New Zealand, both ARIMA and LSTM showed good performance (metrics < 0.5 threshold), with ARIMA being the first choice.
8.1. Comparison with Previous Studies
8.2. Statistical Significance of Predictive Modeling Results
9. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Safi, M. COVID-19 cases surge globally by September 2020. The Guardian, 25 September 2020. [Google Scholar]
- Chhibber-Goel, J.; Malhotra, S.; Krishnan, N.A.; Sharma, A. The profiles of first and second SARS-CoV-2 waves in the top ten COVID-19 affected countries. J. Glob. Health Rep. 2021, 5, e2021082. [Google Scholar] [CrossRef]
- Benmalek, E.; Elmhamdi, J.; Jilbab, A. Comparing CT scan and chest X-ray imaging for COVID-19 diagnosis. Biomed. Eng. Adv. 2021, 1, 100003. [Google Scholar] [CrossRef] [PubMed]
- Beck, B.R.; Shin, B.; Choi, Y.; Park, S.; Kang, K. Predicting commercially available antiviral drugs that may act on the novel coronavirus (SARS-CoV-2) through a drug-target interaction deep learning model. Comput. Struct. Biotechnol. J. 2020, 18, 784–790. [Google Scholar] [CrossRef] [PubMed]
- Chun, A. In a time of coronavirus, China’s investment in AI is paying off in a big way. South China Morning Post, 18 March 2020. [Google Scholar]
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef]
- Hoffmann, M.; Kleine-Weber, H.; Schroeder, S.; Krüger, N.; Herrler, T.; Erichsen, S.; Schiergens, T.S.; Herrler, G.; Wu, N.H.; Nitsche, A.; et al. SARS-CoV-2 cell entry depends on ACE2 and TMPRSS2 and is blocked by a clinically proven protease inhibitor. Cell 2020, 181, 271–280. [Google Scholar] [CrossRef]
- Sun, K.; Wang, W.; Gao, L.; Wang, Y.; Luo, K.; Ren, L.; Zhan, Z.; Chen, X.; Zhao, S.; Huang, Y.; et al. Transmission heterogeneities, kinetics, and controllability of SARS-CoV-2. Science 2021, 371, eabe2424. [Google Scholar] [CrossRef]
- Gupta, A.; Madhavan, M.V.; Sehgal, K.; Nair, N.; Mahajan, S.; Sehrawat, T.S.; Bikdeli, B.; Ahluwalia, N.; Ausiello, J.C.; Wan, E.Y.; et al. Extrapulmonary manifestations of COVID-19. Nat. Med. 2020, 26, 1017–1032. [Google Scholar] [CrossRef]
- Sánchez-Villena, A.R.; de La Fuente-Figuerola, V. COVID-19: Cuarentena, aislamiento, distanciamiento social y confinamiento, ¿son lo mismo? An. Pediatr. 2020, 93, 73. [Google Scholar] [CrossRef]
- Niazkar, H.R.; Niazkar, M. Application of artificial neural networks to predict the COVID-19 outbreak. Glob. Health Res. Policy 2020, 5, 50. [Google Scholar] [CrossRef]
- Datta, D.; George Dalmida, S.; Martinez, L.; Newman, D.; Hashemi, J.; Khoshgoftaar, T.M.; Shorten, C.; Sareli, C.; Eckardt, P. Using machine learning to identify patient characteristics to predict mortality of in-patients with COVID-19 in south Florida. Front. Digit. Health 2023, 5, 1193467. [Google Scholar] [CrossRef]
- Datta, D.; Ray, S.; Martinez, L.; Newman, D.; Dalmida, S.G.; Hashemi, J.; Sareli, C.; Eckardt, P. Feature Identification Using Interpretability Machine Learning Predicting Risk Factors for Disease Severity of In-Patients with COVID-19 in South Florida. Diagnostics 2024, 14, 1866. [Google Scholar] [CrossRef] [PubMed]
- Krittanawong, C.; Rogers, A.J.; Aydar, M.; Choi, E.; Johnson, K.W.; Wang, Z.; Narayan, S.M. Integrating blockchain technology with artificial intelligence for cardiovascular medicine. Nat. Rev. Cardiol. 2020, 17, 1–3. [Google Scholar] [PubMed]
- Devaraj, J.; Elavarasan, R.M.; Pugazhendhi, R.; Shafiullah, G.; Ganesan, S.; Jeysree, A.K.; Khan, I.A.; Hossain, E. Forecasting of COVID-19 cases using deep learning models: Is it reliable and practically significant? Results Phys. 2021, 21, 103817. [Google Scholar] [CrossRef] [PubMed]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar]
- Jin, Y.C.; Cao, Q.; Sun, Q.; Lin, Y.; Liu, D.M.; Wang, C.X.; Wang, X.L.; Wang, X.Y. Models for COVID-19 data prediction based on improved LSTM-ARIMA algorithms. IEEE Access 2023, 12, 3981–3991. [Google Scholar]
- Yu, C.S.; Chang, S.S.; Chang, T.H.; Wu, J.L.; Lin, Y.J.; Chien, H.F.; Chen, R.J. A COVID-19 pandemic artificial intelligence–based system with deep learning forecasting and automatic statistical data acquisition: Development and implementation study. J. Med. Internet Res. 2021, 23, e27806. [Google Scholar]
- Jojoa, M.; Garcia-Zapirain, B. Forecasting COVID-19 confirmed cases using machine learning: The case of America. J. Infect. Public Health 2020, 13, 1566–1573. [Google Scholar] [CrossRef]
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.W.; Aslam, W.; Choi, G.S. COVID-19 future forecasting using supervised machine learning models. IEEE Access 2020, 8, 101489–101499. [Google Scholar]
- Cheng, C.; Jiang, W.M.; Fan, B.; Cheng, Y.C.; Hsu, Y.T.; Wu, H.Y.; Chang, H.H.; Tsou, H.H. Real-time forecasting of COVID-19 spread according to protective behavior and vaccination: Autoregressive integrated moving average models. BMC Public Health 2023, 23, 1500. [Google Scholar]
- Painuli, D.; Mishra, D.; Bhardwaj, S.; Aggarwal, M. Forecast and prediction of COVID-19 using machine learning. In Data Science for COVID-19; Elsevier: Amsterdam, The Netherlands, 2021; pp. 381–397. [Google Scholar]
- Kumar, A.; Kaur, K. A hybrid SOM-Fuzzy time series (SOMFTS) technique for future forecasting of COVID-19 cases and MCDM based evaluation of COVID-19 forecasting models. In Proceedings of the 2021 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 19–20 February 2021; pp. 612–617. [Google Scholar]
- Saqib, M. Forecasting COVID-19 outbreak progression using hybrid polynomial-Bayesian ridge regression model. Appl. Intell. 2021, 51, 2703–2713. [Google Scholar] [CrossRef]
- Singh, K.K.; Kumar, S.; Dixit, P.; Bajpai, M.K. Kalman filter based short term prediction model for COVID-19 spread. Appl. Intell. 2021, 51, 2714–2726. [Google Scholar] [CrossRef] [PubMed]
- Aslam, M. Using the kalman filter with Arima for the COVID-19 pandemic dataset of Pakistan. Data Brief 2020, 31, 105854. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, P.; Madaan, V.; Roy, A.; Kumari, R.; Deore, H. FOCOMO: Forecasting and monitoring the worldwide spread of COVID-19 using machine learning methods. J. Interdiscip. Math. 2021, 24, 443–466. [Google Scholar] [CrossRef]
- Gupta, A.K.; Singh, V.; Mathur, P.; Travieso-Gonzalez, C.M. Prediction of COVID-19 pandemic measuring criteria using support vector machine, prophet and linear regression models in Indian scenario. J. Interdiscip. Math. 2021, 24, 89–108. [Google Scholar]
- Al-Turaiki, I.; Almutlaq, F.; Alrasheed, H.; Alballa, N. Empirical evaluation of alternative time-series models for covid-19 forecasting in Saudi Arabia. Int. J. Environ. Res. Public Health 2021, 18, 8660. [Google Scholar] [CrossRef]
- Al-Qaness, M.A.; Ewees, A.A.; Fan, H.; Abd El Aziz, M. Optimization method for forecasting confirmed cases of COVID-19 in China. J. Clin. Med. 2020, 9, 674. [Google Scholar] [CrossRef]
- Sherazi, S.W.A.; Zheng, H.; Lee, J.Y. A machine learning-based applied prediction model for identification of acute coronary syndrome (ACS) outcomes and mortality in patients during the hospital stay. Sensors 2023, 23, 1351. [Google Scholar] [CrossRef]
- Ahmadi, N.; Nguyen, Q.V.; Sedlmayr, M.; Wolfien, M. A comparative patient-level prediction study in OMOP CDM: Applicative potential and insights from synthetic data. Sci. Rep. 2024, 14, 2287. [Google Scholar]
- Chartash, D.; Rosenman, M.; Wang, K.; Chen, E. Informatics in undergraduate medical education: Analysis of competency frameworks and practices across North America. JMIR Med. Educ. 2022, 8, e39794. [Google Scholar]
- Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J.; Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J. Forecasting COVID-19 time series based on an autoregressive model. In Predictive Models for Decision Support in the COVID-19 Crisis; Springer: Cham, Switzerland, 2021; pp. 41–54. [Google Scholar]
- Center for Systems Science and Engineering (CSSE), Johns Hopkins University. COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. Available online: https://github.com/CSSEGISandData/COVID-19 (accessed on 12 March 2025).
- Reinhart, A.; Brooks, L.; Jahja, M.; Rumack, A.; Tang, J.; Agrawal, S.; Al Saeed, W.; Arnold, T.; Basu, A.; Bien, J.; et al. An open repository of real-time COVID-19 indicators. Proc. Natl. Acad. Sci. USA 2021, 118, e2111452118. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Nakagawa, S.; Johnson, P.C.; Schielzeth, H. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 2017, 14, 20170213. [Google Scholar] [CrossRef] [PubMed]

| Country | Time Range | Total Cases | Avg. Daily Cases | Data Source |
|---|---|---|---|---|
| New Zealand | 2020–2022 | 1,800,000 | 1200 | Johns Hopkins (CSSE) |
| Australia | 2020–2022 | 10,500,000 | 7000 | Johns Hopkins (CSSE) |
| China | 2020–2022 | 300,000 | 200 | Johns Hopkins (CSSE) |
| United States | 2020–2022 | 100,000,000 | 70,000 | Johns Hopkins (CSSE) |
| Japan | 2020–2022 | 25,000,000 | 16,000 | Johns Hopkins (CSSE) |
| Germany | 2020–2022 | 30,000,000 | 20,000 | Johns Hopkins (CSSE) |
| India (Future Work) | 2020–2022 | 44,000,000 | 30,000 | Johns Hopkins (CSSE) |
| Option | Description | Default |
|---|---|---|
| -m | Models | Arima, LSTM, Prophet |
| -c | Countries | N/A |
| -f | First day of the training process | First data in the database |
| -l | Last day of the validation process | Last day of data available |
| -p | Predictions in days | N/A |
| -r | Ratio of data used for training | 0.75 |
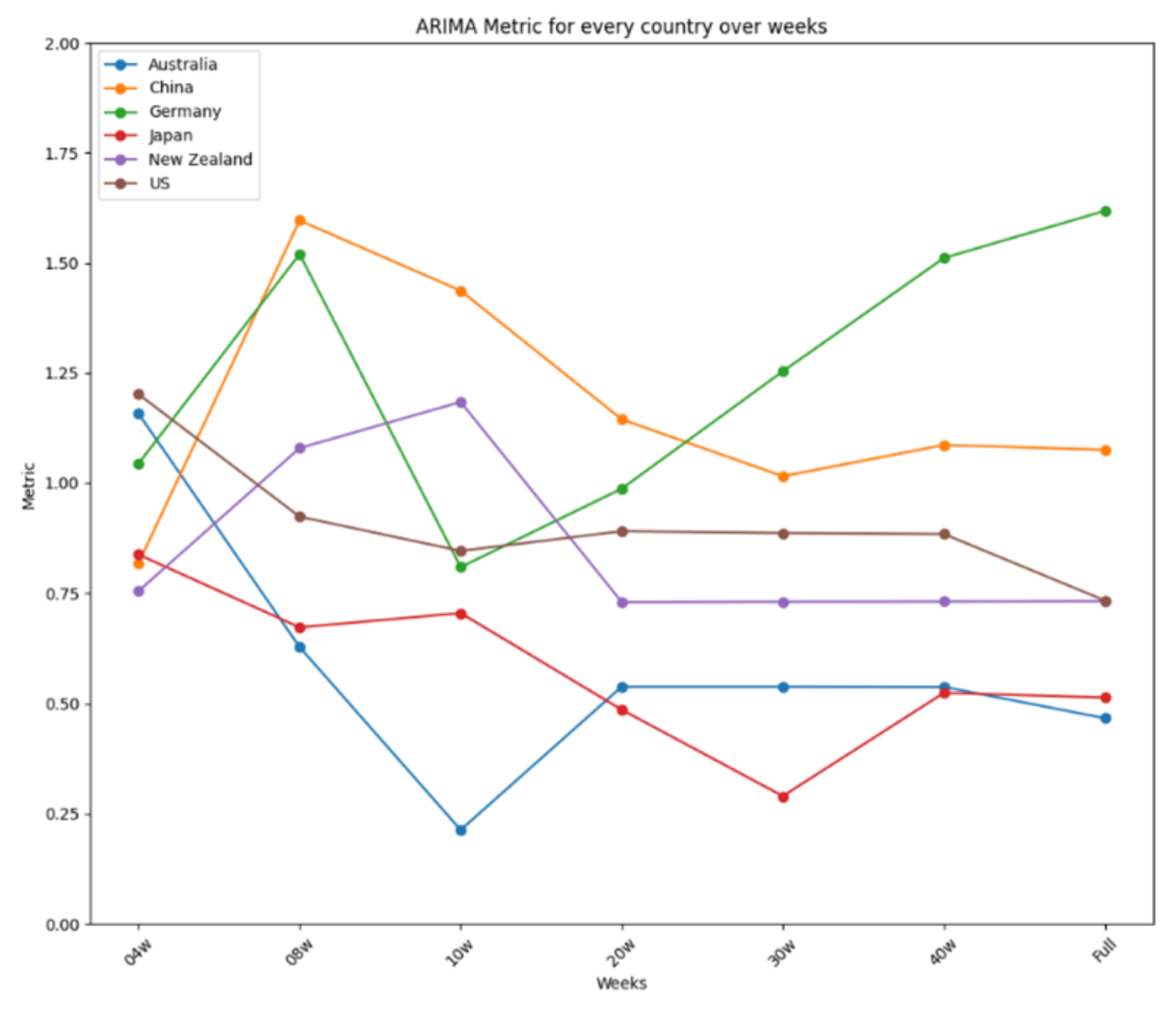
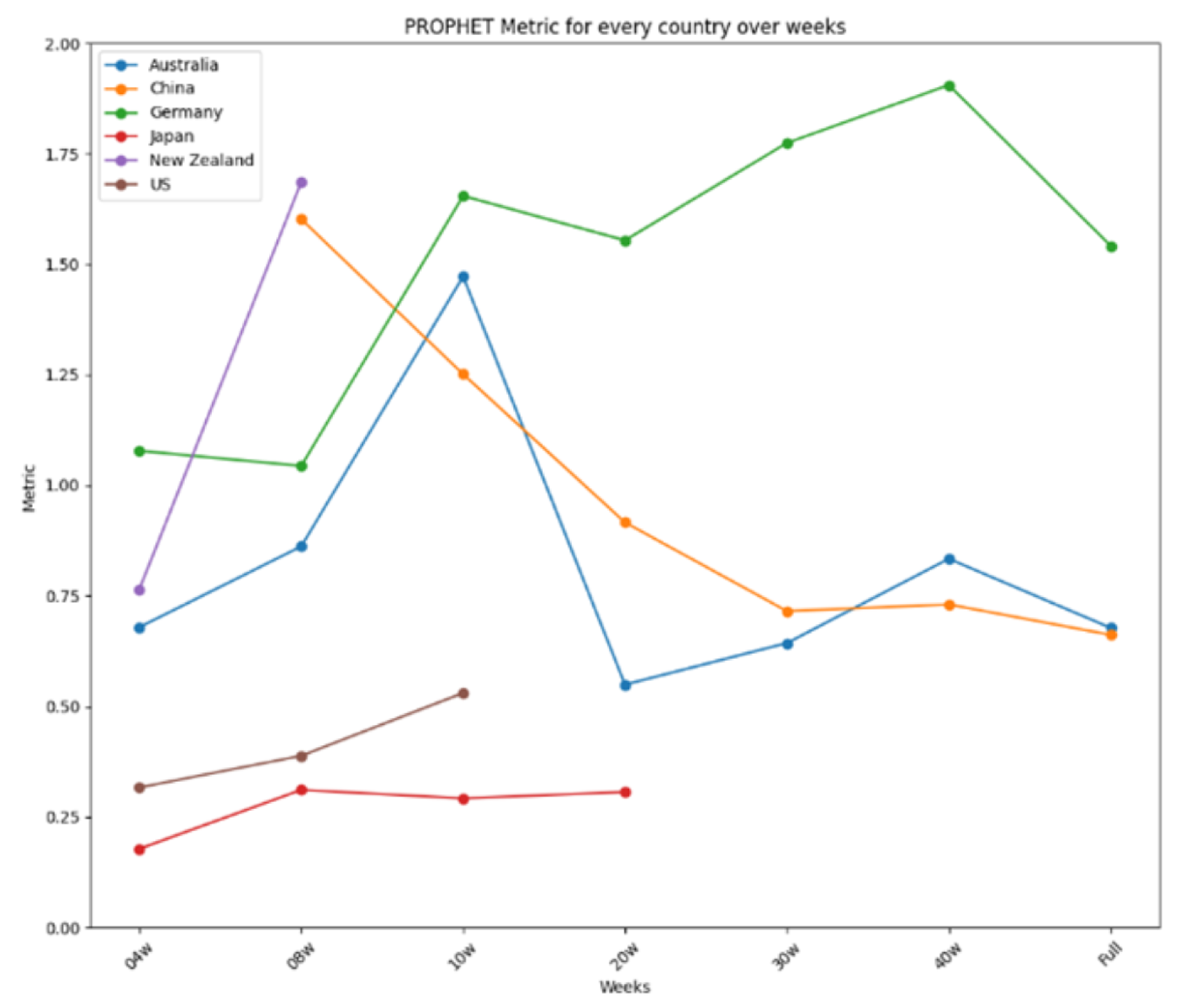
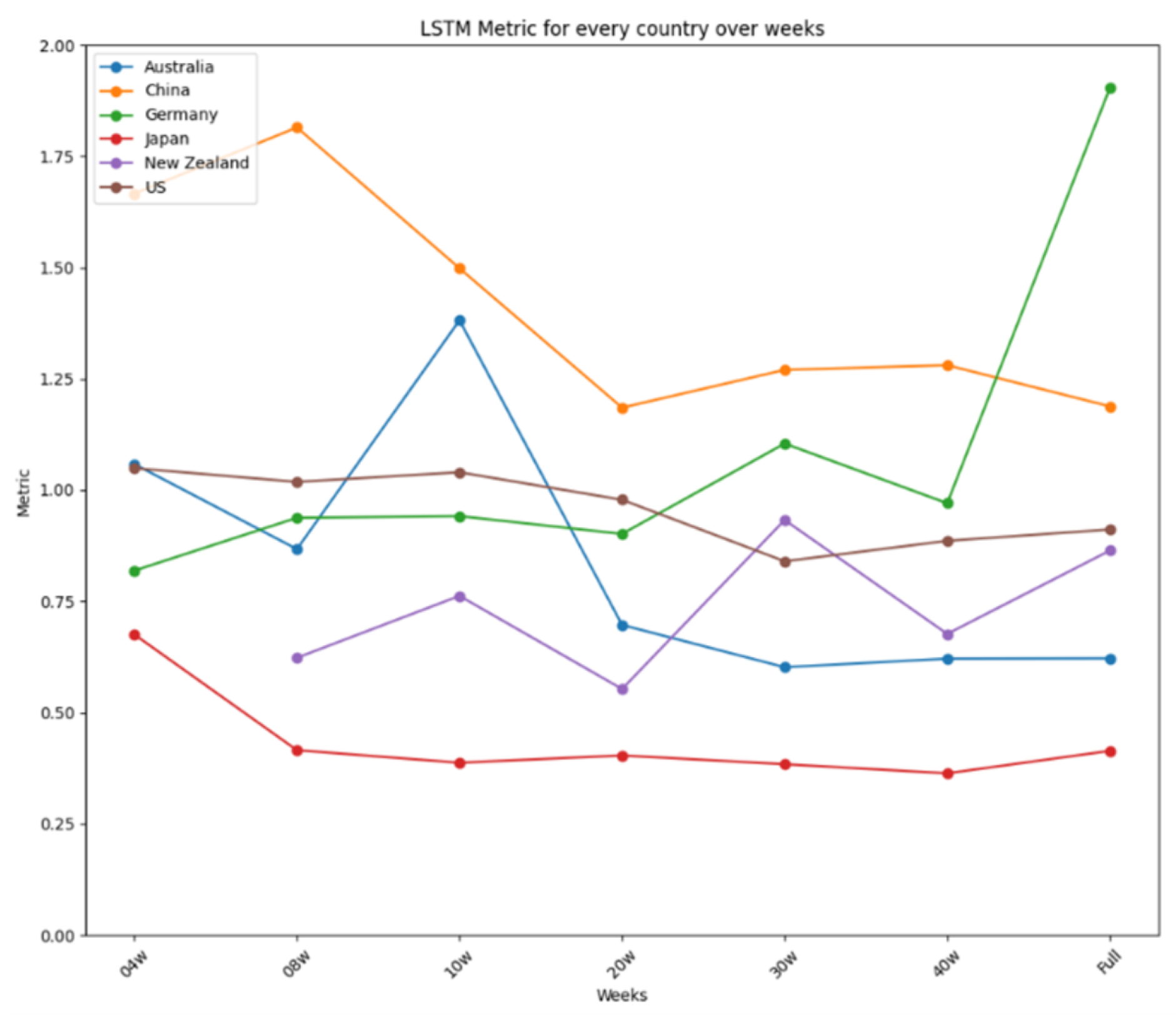
| Weeks | ARIMA | Prophet | LSTM | Best | Middle | Worst |
|---|---|---|---|---|---|---|
| 4 | 0.75510 | 0.76415 | 2.17299 | ARIMA | Prophet | LSTM |
| 8 | 1.07955 | 1.68519 | 0.62287 | LSTM | ARIMA | Prophet |
| 10 | 1.18422 | 3.97344 | 0.76199 | LSTM | ARIMA | Prophet |
| 20 | 0.72999 | 7.46648 | 0.55279 | LSTM | ARIMA | Prophet |
| 30 | 0.73083 | 7.92632 | 0.93250 | ARIMA | LSTM | Prophet |
| 40 | 0.73121 | 7.85889 | 0.67656 | LSTM | ARIMA | Prophet |
| Full | 0.73193 | 1.94344 | 0.86377 | ARIMA | LSTM | Prophet |
| Average | 0.84898 | 4.51684 | 0.94050 | ARIMA | LSTM | Prophet |
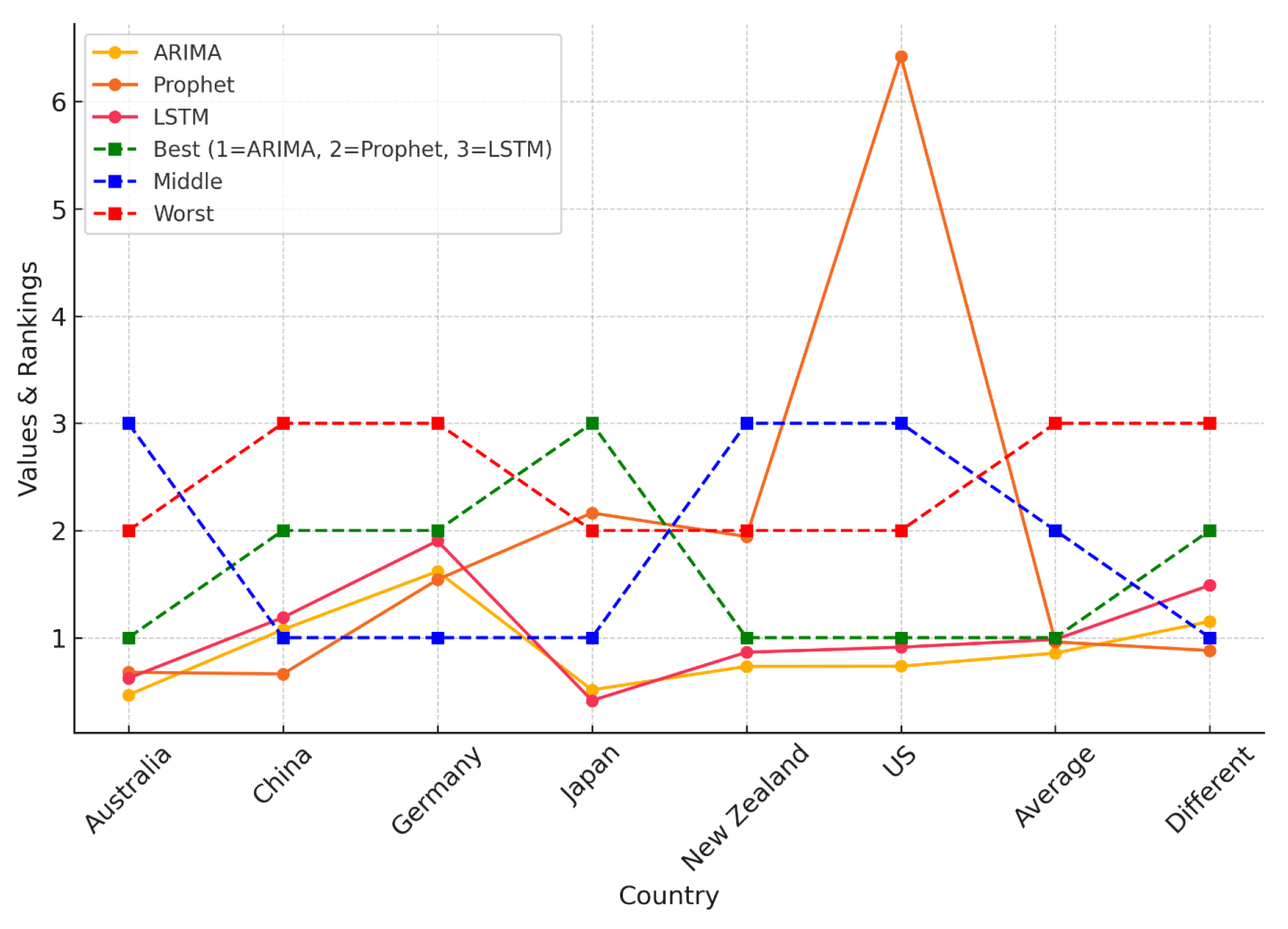
| Country | ARIMA | Prophet | LSTM | Best | Middle | Worst |
|---|---|---|---|---|---|---|
| Australia | 0.46627 | 0.6771 | 0.62166 | ARIMA | LSTM | Prophet |
| China | 1.0756 | 0.66136 | 1.18792 | Prophet | ARIMA | LSTM |
| Germany | 1.6181 | 1.54146 | 1.90295 | Prophet | ARIMA | LSTM |
| Japan | 0.51331 | 2.16344 | 0.41369 | LSTM | ARIMA | Prophet |
| New Zealand | 0.73193 | 1.94344 | 0.86377 | ARIMA | LSTM | Prophet |
| US | 0.73352 | 6.24341 | 0.91113 | ARIMA | LSTM | Prophet |
| Average | 0.85646 | 0.95997 | 0.98352 | ARIMA | Prophet | LSTM |
| Difference | 1.15183 | 0.8801 | 1.48926 | Prophet | ARIMA | LSTM |
| Study | Key Findings | Our Validation |
|---|---|---|
| Niazkar (2020) [11] | 14-day incubation period improves ANN accuracy. | We included incubation periods in preprocessing. |
| Devaraj et al. (2021) [15] | Stacked LSTM outperforms ARIMA and Prophet. | LSTM consistently ranked higher in our study. |
| Jin et al. (2023) [17] | Hybrid CNN-LSTM-ARIMA improves accuracy. | We confirm that deep learning models enhance forecasts. |
| Yu et al. (2021) [18] | ARIMA and FNN perform better in certain regions. | ARIMA showed stability in short-term forecasting. |
| Rustam et al. (2020) [20] | Longer training periods improve accuracy. | LSTM performed best with 20–30 weeks of data. |
| Painuli et al. (2021) [22] | ARIMA with ensemble learning enhances reliability. | Our study integrates MCDM for robust model ranking. |
| Kumar & Kaur (2021) [23] | SOMFTS hybrid model improves forecasting. | We used a weighted ranking approach for evaluation. |
| Gupta et al. (2021) [28] | Prophet excels in short-term but lacks long-term accuracy. | We confirm Prophet’s short-term success but weaker long-term results. |
| Model | RMSE ± CI | MAE ± CI | MAPE ± CI | p-Value (vs. Baseline) |
|---|---|---|---|---|
| ARIMA | 0.731 ± 0.05 | 0.466 ± 0.03 | 3.2% ± 0.5% | |
| LSTM | 0.676 ± 0.04 | 0.413 ± 0.02 | 2.8% ± 0.4% | |
| Prophet | 7.92 ± 1.10 | 1.68 ± 0.06 | 6.4% ± 1.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baker, O.; Ziran, Z.; Mecella, M.; Subaramaniam, K.; Palaniappan, S. Predictive Modeling for Pandemic Forecasting: A COVID-19 Study in New Zealand and Partner Countries. Int. J. Environ. Res. Public Health 2025, 22, 562. https://doi.org/10.3390/ijerph22040562
Baker O, Ziran Z, Mecella M, Subaramaniam K, Palaniappan S. Predictive Modeling for Pandemic Forecasting: A COVID-19 Study in New Zealand and Partner Countries. International Journal of Environmental Research and Public Health. 2025; 22(4):562. https://doi.org/10.3390/ijerph22040562
Chicago/Turabian StyleBaker, Oras, Zahra Ziran, Massimo Mecella, Kasthuri Subaramaniam, and Sellappan Palaniappan. 2025. "Predictive Modeling for Pandemic Forecasting: A COVID-19 Study in New Zealand and Partner Countries" International Journal of Environmental Research and Public Health 22, no. 4: 562. https://doi.org/10.3390/ijerph22040562
APA StyleBaker, O., Ziran, Z., Mecella, M., Subaramaniam, K., & Palaniappan, S. (2025). Predictive Modeling for Pandemic Forecasting: A COVID-19 Study in New Zealand and Partner Countries. International Journal of Environmental Research and Public Health, 22(4), 562. https://doi.org/10.3390/ijerph22040562






