Multi-Objective Optimization Applied to the Design of Sustainable Pedestrian Bridges
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multiobjective Harmony Search
2.2. Problem Formulation and Implementation
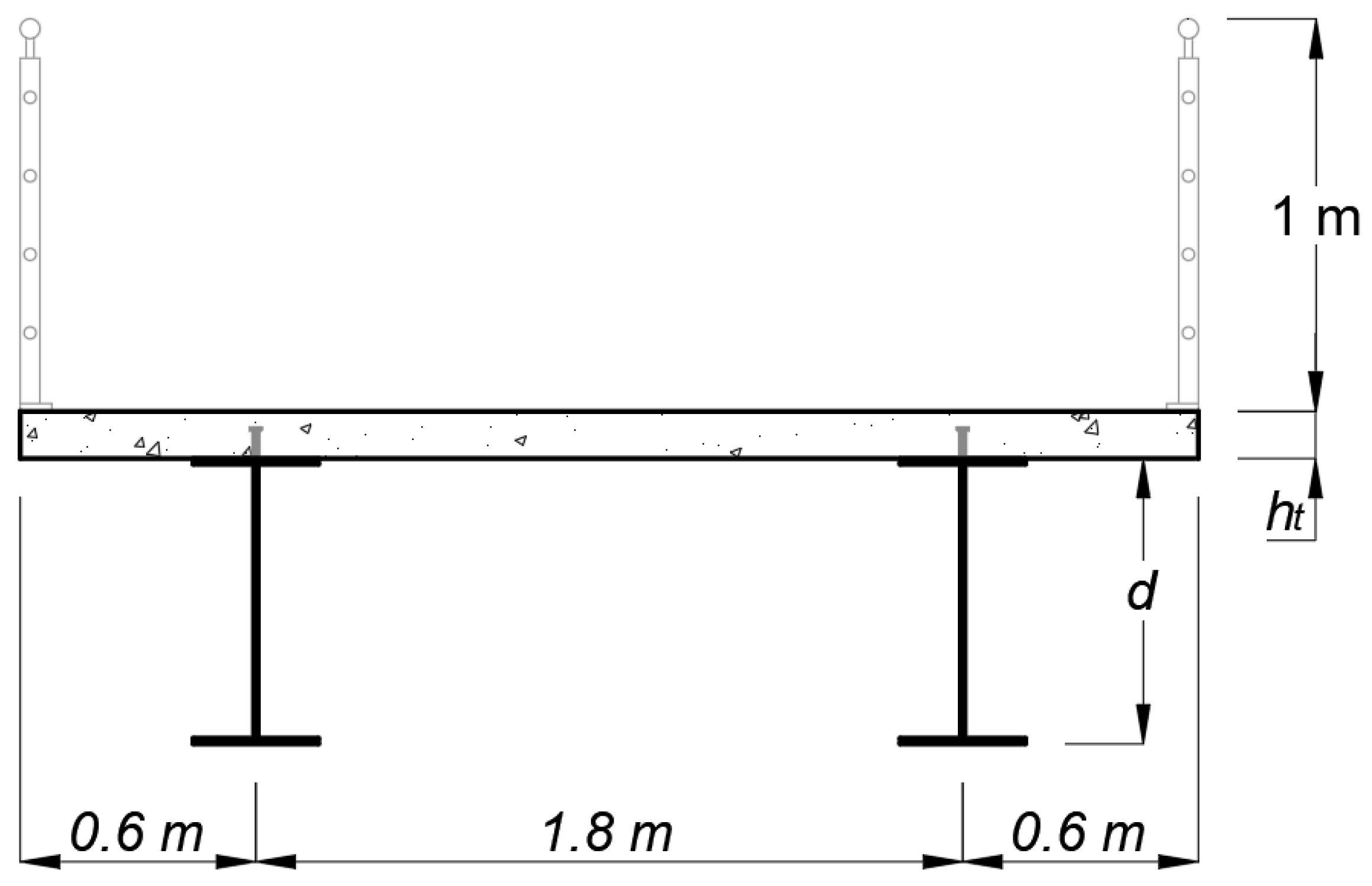
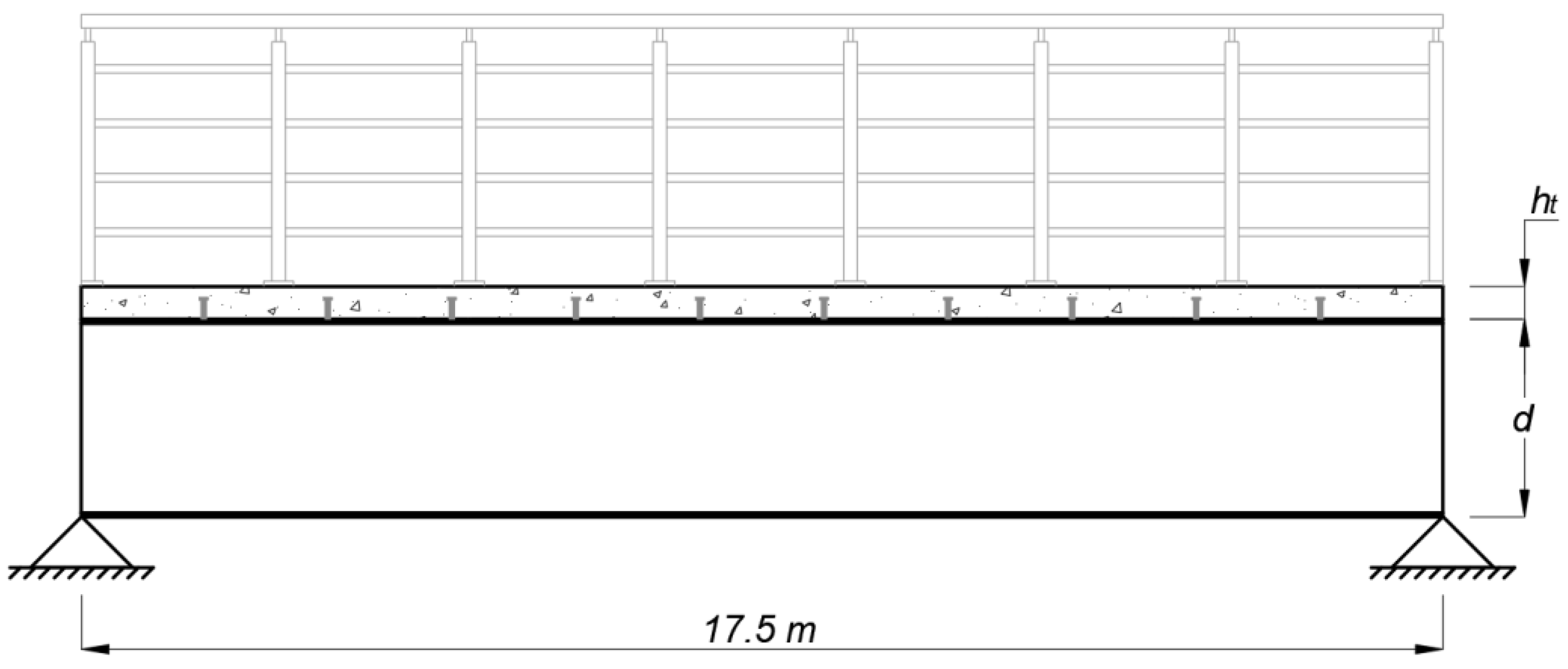
2.2.1. Design Variables
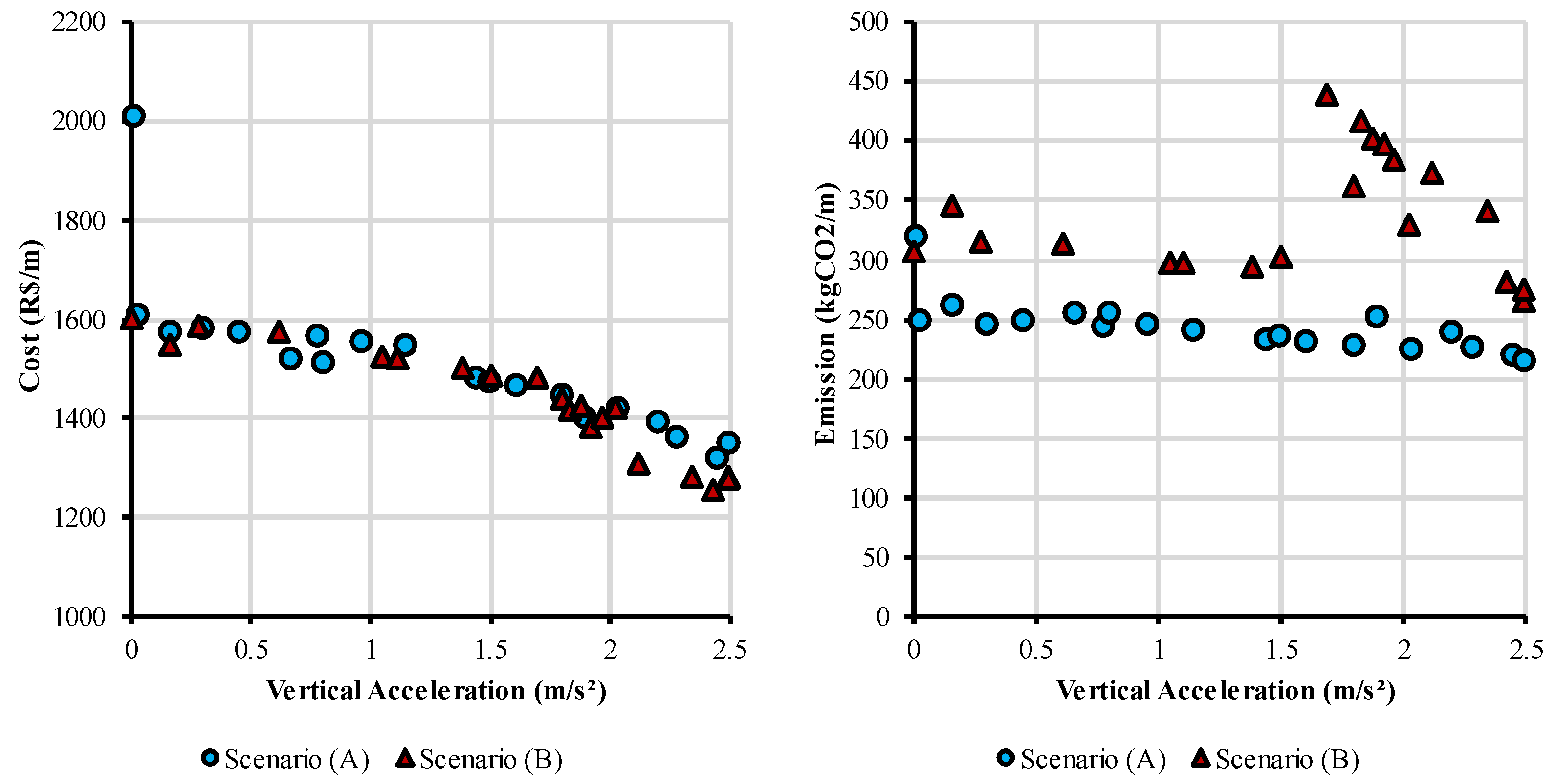
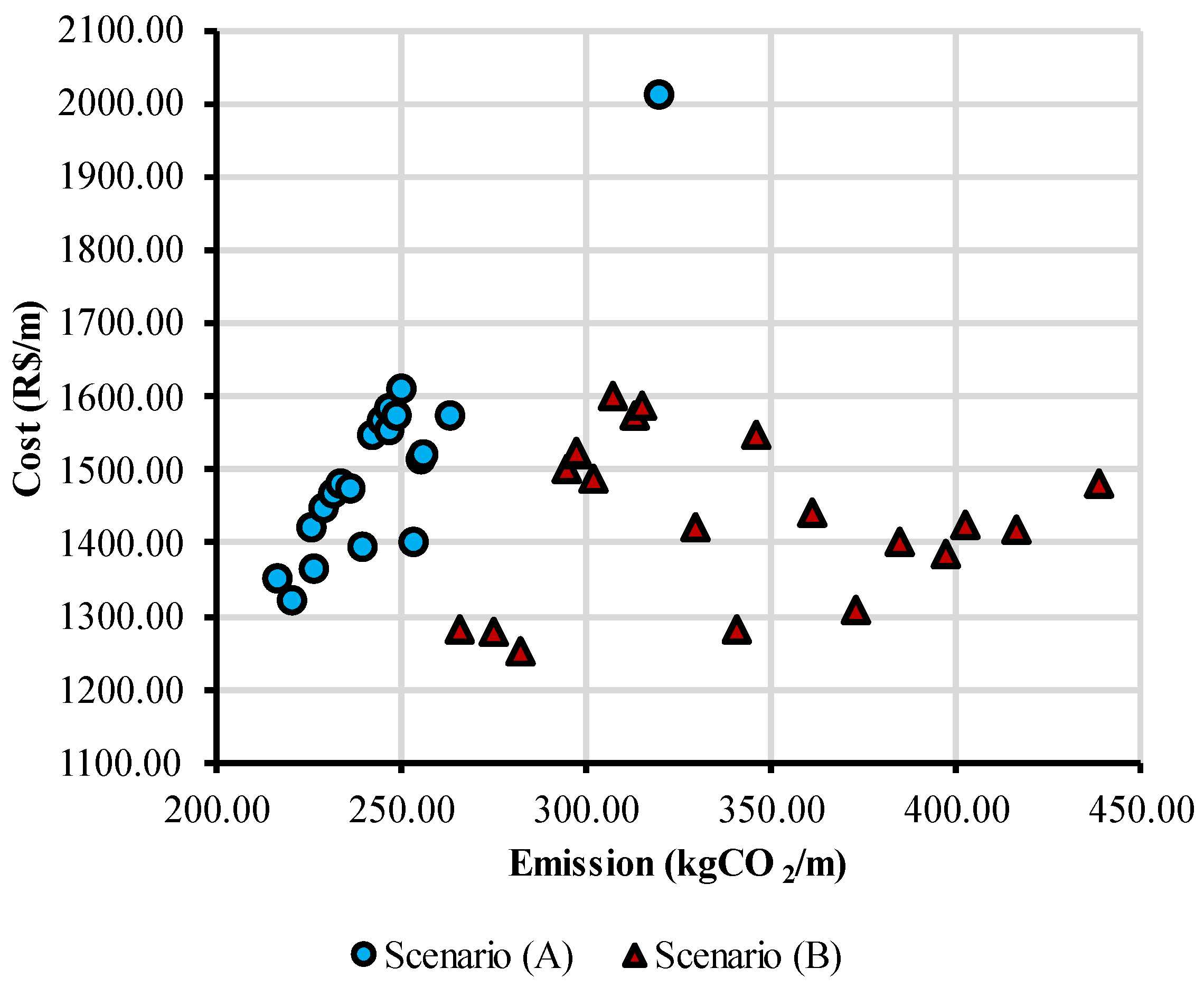
2.2.2. Objective Functions and Emissions Scenarios
- Scenario (A)—unit emissions obtained from the on-site survey for the study region. In Table 2, emission A shows the values considered in this scenario.
- Scenario (B)—unit emissions calculated using the SimaPro software, with Ecoinvent 3.5 database and ReCiPe 2016 method, with adjustments in the processes and quantities to make the values compatible with the same region. These values are displayed as emission B in Table 2.
2.2.3. Verifications and Constraints
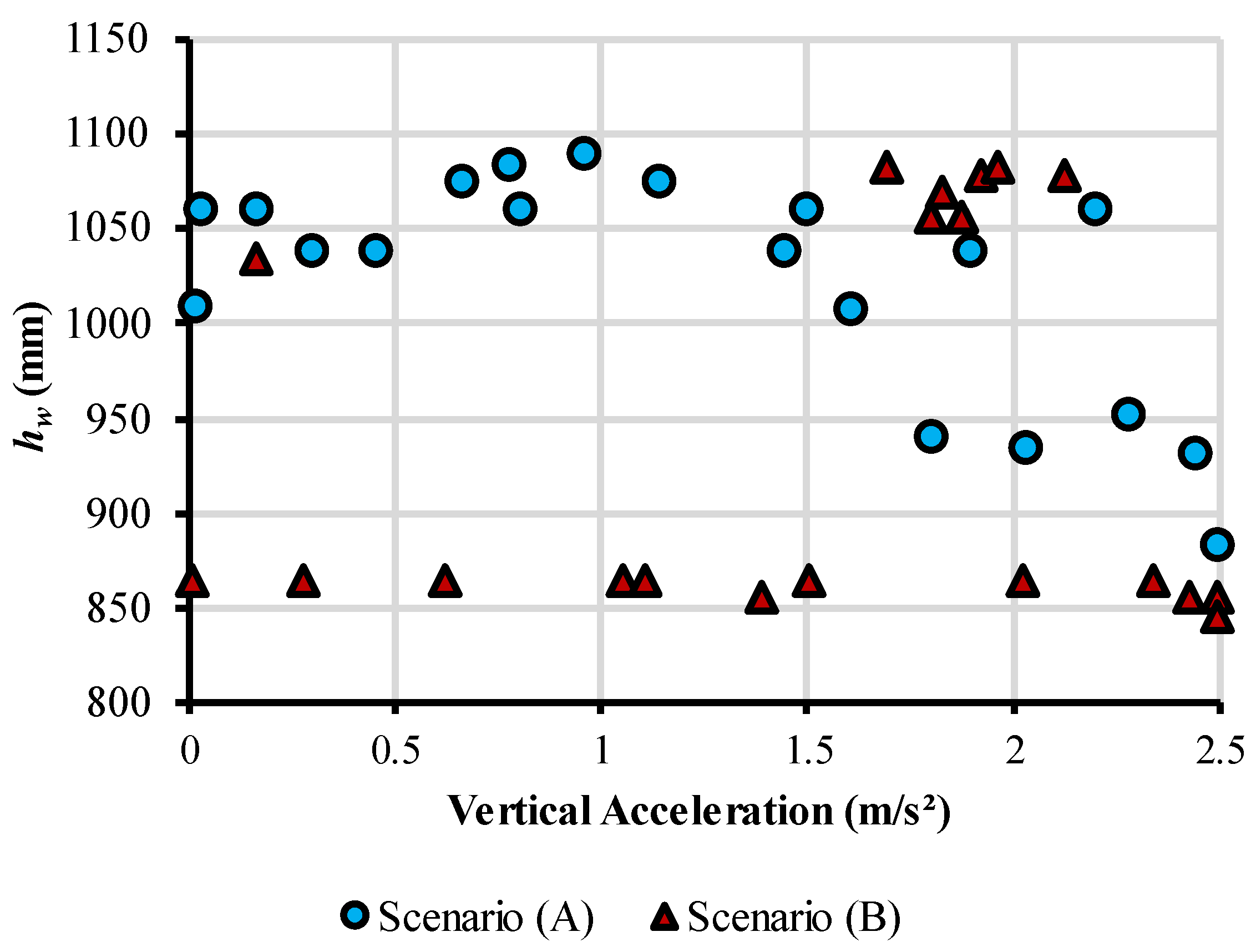
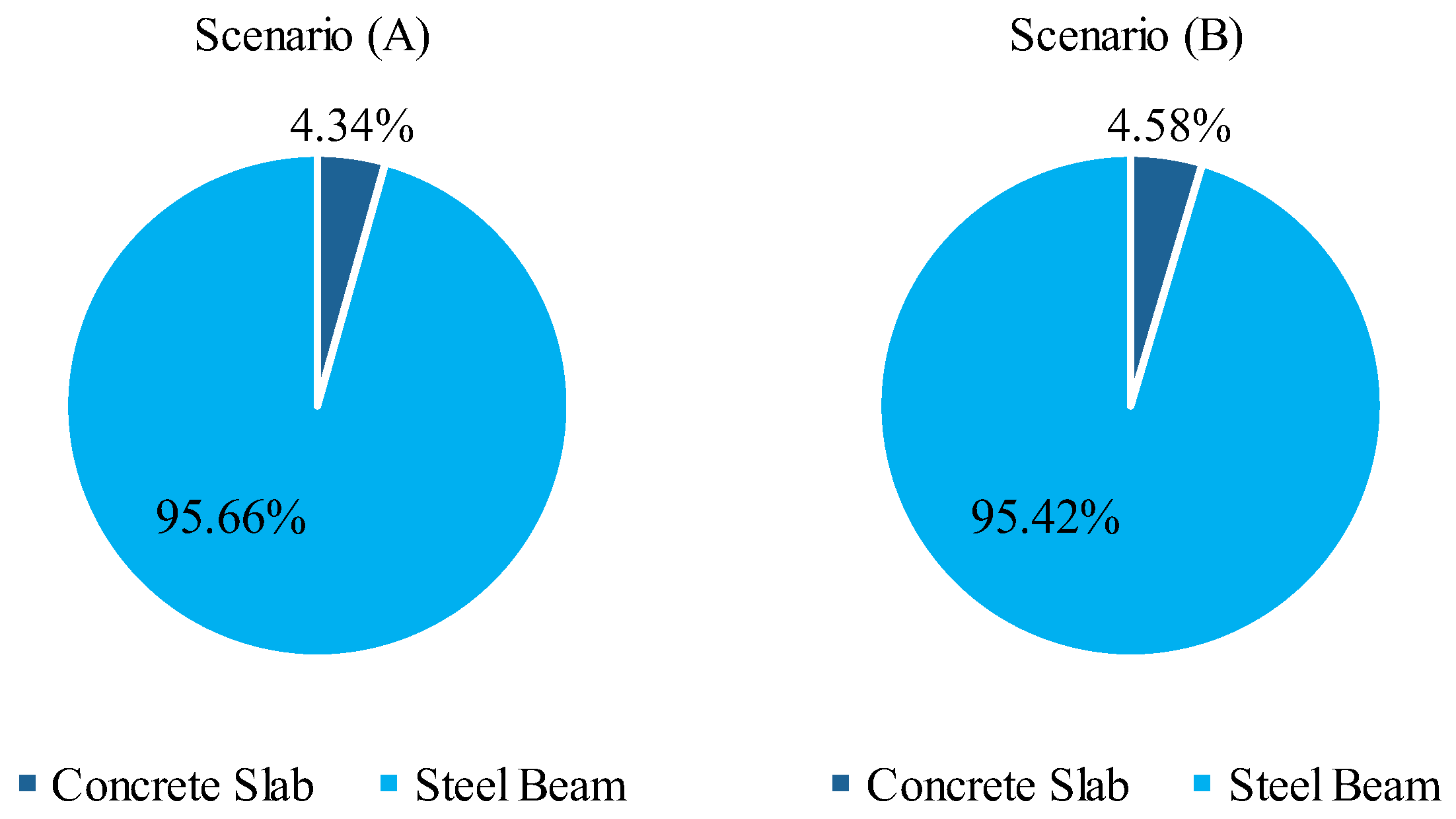
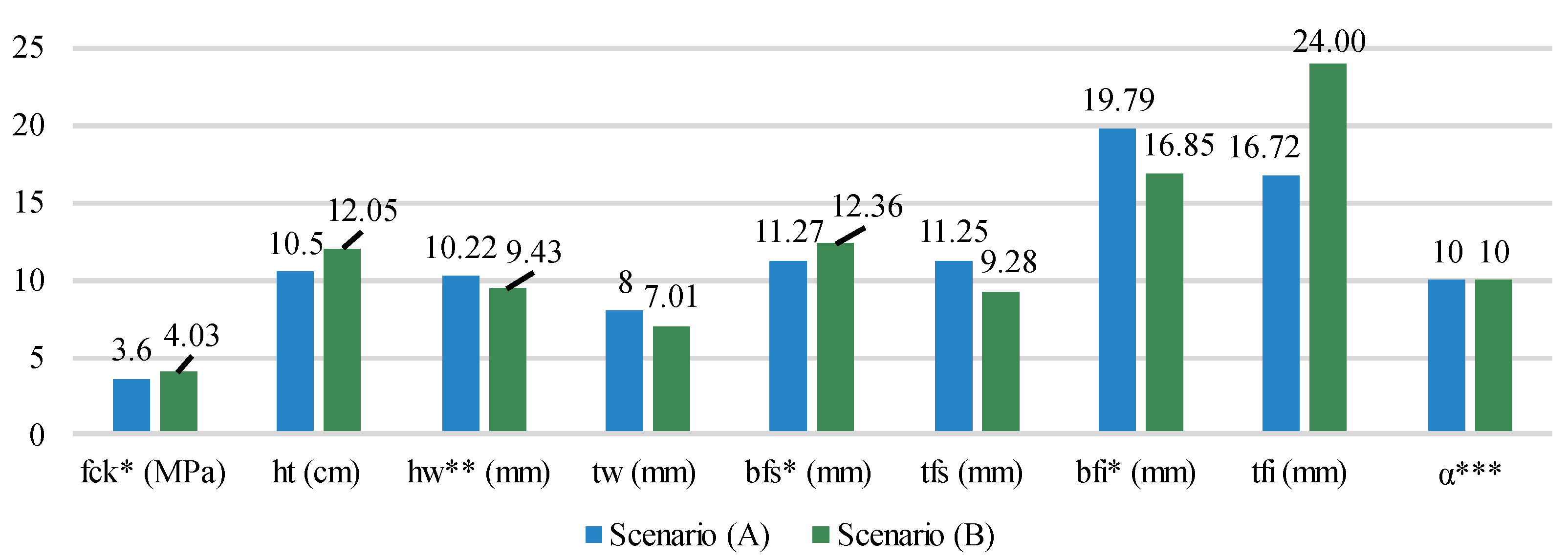
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UNEP. 2022 Global Status Report for Buildings and Construction: Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector; UNEP: Nairobi, Kenya, 2022; ISBN 978-92-807-3984-8. [Google Scholar]
- UN. Transforming our World: The 2030 Agenda for Sustainable Development; UN: New York, NY, USA, 2015; Available online: https://documents-dds-ny.un.org/doc/UNDOC/GEN/N15/291/89/PDF/N1529189.pdf (accessed on 9 August 2022).
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Milani, C.J.; Yepes, V.; Kripka, M. Proposal of Sustainability Indicators for the Design of Small-Span Bridges. Int. J. Environ. Res. Public Health 2020, 17, 4488. [Google Scholar] [CrossRef] [PubMed]
- Kripka, M.; Yepes, V.; Milani, C.J. Selection of Sustainable Short-Span Bridge Design in Brazil. Sustainability 2019, 11, 1307. [Google Scholar] [CrossRef]
- Pedro, R.; Demarche, J.; Miguel, L.; Lopez, R. An efficient approach for the optimization of simply supported steel-concrete composite I-girder bridges. Adv. Eng. Softw. 2017, 112, 31–45. [Google Scholar] [CrossRef]
- Kaveh, A.; Zarandi, M.M.M. Optimal Design of Steel-Concrete Composite I-girder Bridges Using Three Meta-Heuristic Algorithms. Period. Polytech. Civ. Eng. 2019, 63, 317–337. [Google Scholar] [CrossRef]
- Orcesi, A.; Cremona, C.; Ta, B. Optimization of Design and Life-Cycle Management for Steel–Concrete Composite Bridges. Struct. Eng. Int. 2018, 28, 185–195. [Google Scholar] [CrossRef]
- Montoya, M.C.; Hernández, S.; Kareem, A. Aero-structural optimization-based tailoring of bridge deck geometry. Eng. Struct. 2022, 270, 114067. [Google Scholar] [CrossRef]
- Yepes, V.; Dasí-Gil, M.; Martínez-Muñoz, D.; López-Desfilis, V.J.; Martí, J.V. Heuristic Techniques for the Design of Steel-Concrete Composite Pedestrian Bridges. Appl. Sci. 2018, 9, 3253. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Verbeke, P.; Lombaert, G.; De Roeck, G.; Broeck, P.V.D. Numerical and Experimental Evaluation of the Dynamic Performance of a Footbridge with Tuned Mass Dampers. J. Bridg. Eng. 2016, 21, 8. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Sáez, A. Motion-based optimum design of a slender steel footbridge and assessment of its dynamic behavior. Int. J. Steel Struct. 2017, 17, 1459–1470. [Google Scholar] [CrossRef]
- Kilikevičius, A.; Bačinskas, D.; Selech, J.; Matijošius, J.; Kilikevičienė, K.; Vainorius, D.; Ulbrich, D.; Romek, D. The Influence of Different Loads on the Footbridge Dynamic Parameters. Symmetry 2020, 12, 657. [Google Scholar] [CrossRef]
- Kougias, I.P.; Theodossiou, N.P. Multiobjective Pump Scheduling Optimization Using Harmony Search Algorithm (HSA) and Polyphonic HSA. Water Resour. Manag. 2013, 27, 1249–1261. [Google Scholar] [CrossRef]
- Jeddi, B.; Vahidinasab, V. A modified harmony search method for environmental/economic load dispatch of real-world power systems. Energy Convers. Manag. 2017, 78, 661–675. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective Optimization of Water Distribution Networks Using Fuzzy Theory and Harmony Search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Alkhadashi, A.; Mohammad, F.; Zubayr, R.O.; Klalib, H.A.; Balik, P. Multi-objective design optimisation of steel framed structures using three different methods. Int. J. Struct. Integr. 2022, 13, 92–111. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V. Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- Ferenc, T.; Mikulski, T. Parametric optimization of sandwich composite footbridge with U-shaped cross-section. Compos. Struct. 2020, 246, 112406. [Google Scholar] [CrossRef]
- Ferreira, F.; Simões, L. Least Cost Design of Curved Cable-Stayed Footbridges with Control Devices. Structures 2019, 19, 68–83. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Ferreira, F.; Simões, L. Optimum design of a cable-stayed steel footbridge with three dimensional modelling and control devices. Eng. Struct. 2019, 180, 510–523. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Alcalá, J.; Pérez-López, E. Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges. Eng. Struct. 2015, 92, 112–122. [Google Scholar] [CrossRef]
- Tubino, F.; Piccardo, G. Tuned Mass Damper optimization for the mitigation of human-induced vibrations of pedestrian bridges. Meccanica 2015, 50, 809–824. [Google Scholar] [CrossRef]
- Jimenez-Alonso, J.F.; Saez, A. Robust Optimum Design of Tuned Mass Dampers to Mitigate Pedestrian-Induced Vibrations Using Multi-Objective Genetic Algorithms. Struct. Eng. Int. 2017, 27, 492–501. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, L.; Chen, G. Optimal design and application of a MTMD system for a glulam footbridge under human-induced excitation. Eur. J. Wood Wood Prod. 2022, 1–17. [Google Scholar] [CrossRef]
- Santoro, J.F.; Kripka, M. Minimizing environmental impact from optimized sizing of reinforced concrete elements. Comput. Concr. 2020, 25, 111–118. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Medeiros, G.F.; Kripka, M. Modified harmony search and its application to cost minimization of RC columns. Adv. Comput. Des. 2017, 2, 1–13. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Tormen, A.F.; Pravia, Z.M.C.; Ramires, F.B.; Kripka, M. Optimization of steel-concrete composite beams considering cost and environmental impact. Steel Compos. Struct. 2020, 34, 409–421. [Google Scholar] [CrossRef]
- Molina-Pérez, D.; Portilla-Flores, E.A.; Vega-Alvarado, E.; Calva-Yañez, M.B.; Sepúlveda-Cervantes, G. A novel multi-objective harmony search algorithm with pitch adjustment by genotype. Appl. Sci. 2021, 11, 8931. [Google Scholar] [CrossRef]
- Ricart, J.; Hüttemann, G.; Lima, J.; Baran, B. Multiobjective Harmony Search Algorithm Proposals. Electron. Notes Theor. Comput. Sci. 2011, 281, 51–67. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, S. Multi-objective harmony search algorithm for optimal power flow problem. Int. J. Electr. Power Energy Syst. 2011, 33, 745–752. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic algorithms for multiobjective optimization: Formulation, discussion and generalization. In Proceedings of the Genetic Algorithms—Fifth International Conference, San Mateo, CA, USA, 17–22 July 1993; pp. 416–423. [Google Scholar]
- Brazilian Federal Savings Bank (CAIXA). Price and Costs References. National System of Survey of Civil Construction Costs and Indexes (SINAPI). 2022. Available online: https://www.caixa.gov.br/Downloads/sinapi-a-partir-jul-2009-rs/SINAPI_ref_Insumos_Composicoes_RS_112022_Desonerado.zip (accessed on 26 December 2022).
- Worldsteel Association. Sustainability Indicators: 2022 Reports. Available online: https://worldsteel.org/steel-topics/sustainability/sustainability-indicators/ (accessed on 26 December 2022).
- NBR 7187; Design of Concrete Bridges, Viaducts, and Footbridges. ABNT: Rio de Janeiro, Brazil, 2021.
- NBR 7188; Road and Pedestrian Dynamic Loads on Bridges, Viaducts, Footbridges and Other Structures. ABNT: Rio de Janeiro, Brazil, 2013.
- NBR 6123; Forces due to Wind on Buildings. ABNT: Rio de Janeiro, Brazil, 1988.
- NBR 8800; Design of Steel Structures and Composite Structures of Steel and Concrete for Buildings. ABNT: Rio de Janeiro, Brazil, 2008.
- NBR 6118; Design of Concrete Structures—Procedure. ABNT: Rio de Janeiro, Brazil, 2014.
- NBR 5884; Electric Arc Welded Steel Structural I Profile—General Requirements. ABNT: Rio de Janeiro, Brazil, 2013.
- Yepes, V.; Gonzalez-Vidosa, F.; Alcala, J.; Villalba, P. CO2-Optimization Design of Reinforced Concrete Retaining Walls Based on a VNS-Threshold Acceptance Strategy. J. Comput. Civ. Eng. 2012, 26, 378–386. [Google Scholar] [CrossRef]
- de Medeiros, G.F.; Kripka, M. Optimization of reinforced concrete columns according to different environmental impact assessment parameters. Eng. Struct. 2014, 59, 185–194. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| HMS | 20 |
| HMCR | 0.5 |
| PARmin | 0.1 |
| PARmax | 0.9 |
| bwmin | 0.1 |
| bwmax | 0.5 |
| MI | 500,000 |
| Material | Unit | Cost (R$) | Emission A 1 (kgCO2) | Emission B 2 (kgCO2) |
|---|---|---|---|---|
| Concrete 30 MPa | m3 | 533.88 | 157.65 | 348.76 |
| Concrete 45 MPa | m3 | 591.15 | 194.70 | 381.72 |
| Concrete 50 MPa | m3 | 631.60 | 225.78 | 508.63 |
| Reinforcement | kg | 9.68 | 1.05 | 2.10 |
| Steel I-beam | kg | 14.56 | 1.91 | 1.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tres Junior, F.L.; Yepes, V.; Medeiros, G.F.d.; Kripka, M. Multi-Objective Optimization Applied to the Design of Sustainable Pedestrian Bridges. Int. J. Environ. Res. Public Health 2023, 20, 3190. https://doi.org/10.3390/ijerph20043190
Tres Junior FL, Yepes V, Medeiros GFd, Kripka M. Multi-Objective Optimization Applied to the Design of Sustainable Pedestrian Bridges. International Journal of Environmental Research and Public Health. 2023; 20(4):3190. https://doi.org/10.3390/ijerph20043190
Chicago/Turabian StyleTres Junior, Fernando Luiz, Víctor Yepes, Guilherme Fleith de Medeiros, and Moacir Kripka. 2023. "Multi-Objective Optimization Applied to the Design of Sustainable Pedestrian Bridges" International Journal of Environmental Research and Public Health 20, no. 4: 3190. https://doi.org/10.3390/ijerph20043190
APA StyleTres Junior, F. L., Yepes, V., Medeiros, G. F. d., & Kripka, M. (2023). Multi-Objective Optimization Applied to the Design of Sustainable Pedestrian Bridges. International Journal of Environmental Research and Public Health, 20(4), 3190. https://doi.org/10.3390/ijerph20043190









