Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model with Inter-Lane Dependency
Abstract
:1. Introduction
2. Literature Review
- A feasible solution is proposed for SC risk evaluation in serial tunnels of Chinese freeways where there is a lack of traffic flow sensors and an unavailability of crash records.
- The behavioral parameters of CF and LC models are associated with the lighting conditions of different zones in serial tunnels. The link between SC risk in serial tunnels and lighting condition variation is modelled.
- The inter-lane dependency is incorporated into the CF model to describe the impact of traffic turbulence from the PC-occurrence lane on the adjacent lane. The link between SC risk and traffic turbulence from PC is improved for the multilane freeway which conventionally considers the effects of vehicle type heterogeneity and CF-related shockwave on the lane where PC occurs.
3. Model Description
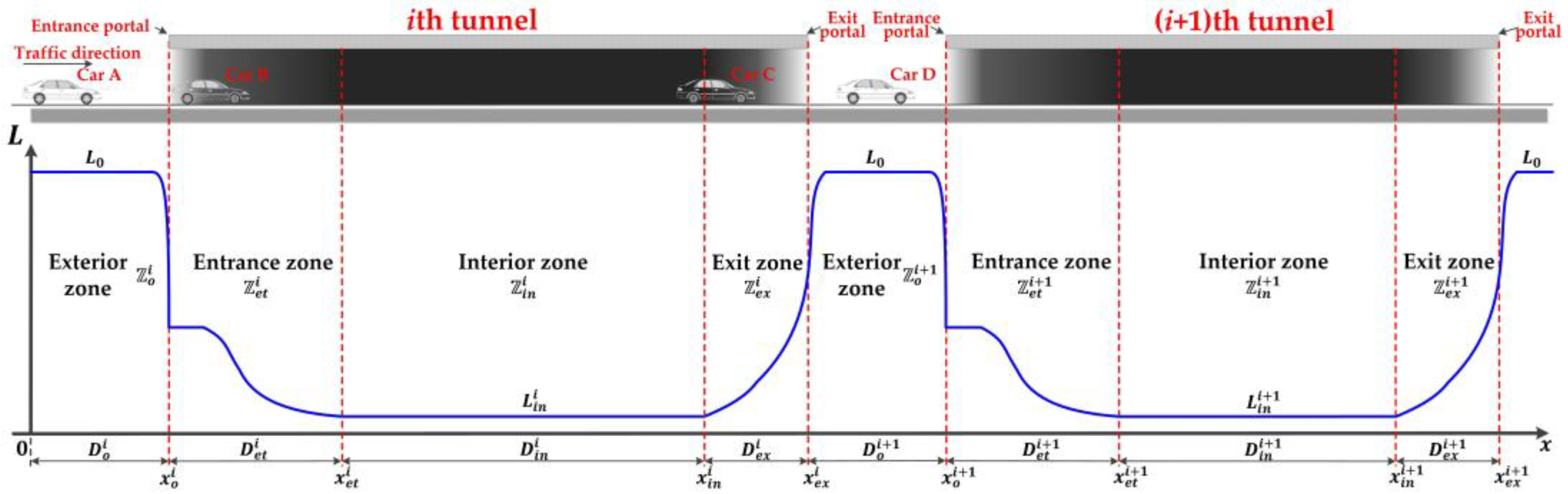
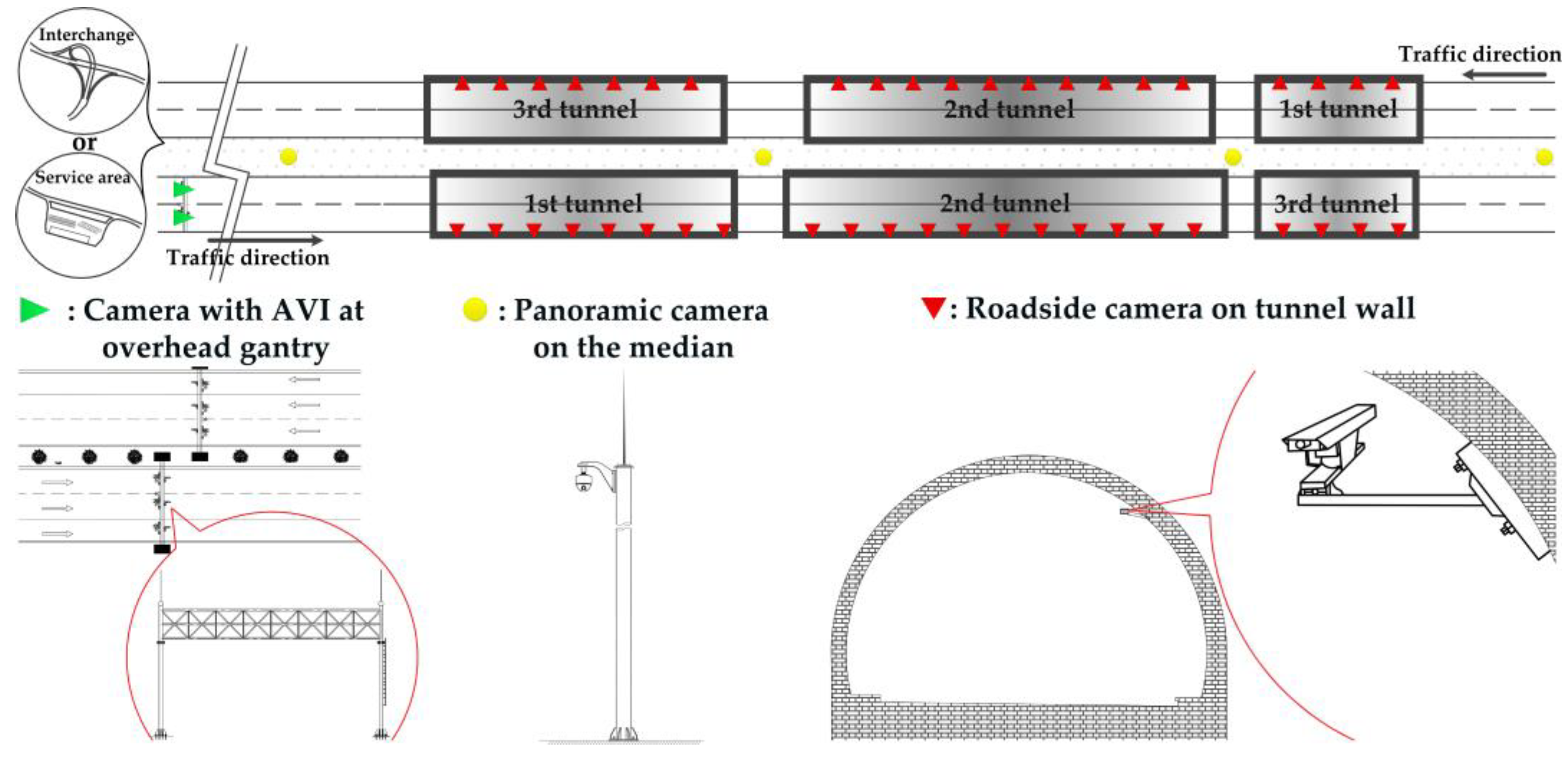
3.1. Definitions, Notations and Assumptions
3.2. Formulation of LMTID
3.2.1. Lighting-Related Behavioral Parameters
3.2.2. CF Part of LMTID
3.2.3. LC Part of LMTID
| Algorithm 1 Recursive evaluation for LCP. |
| Let lateral location of vehicle in LCP , denotes the time step. while , , ; if , , , ; , , , ; , , , ; else , , , ; , , , ; , , , end ; end |
3.3. SSM-Based Crash Risk
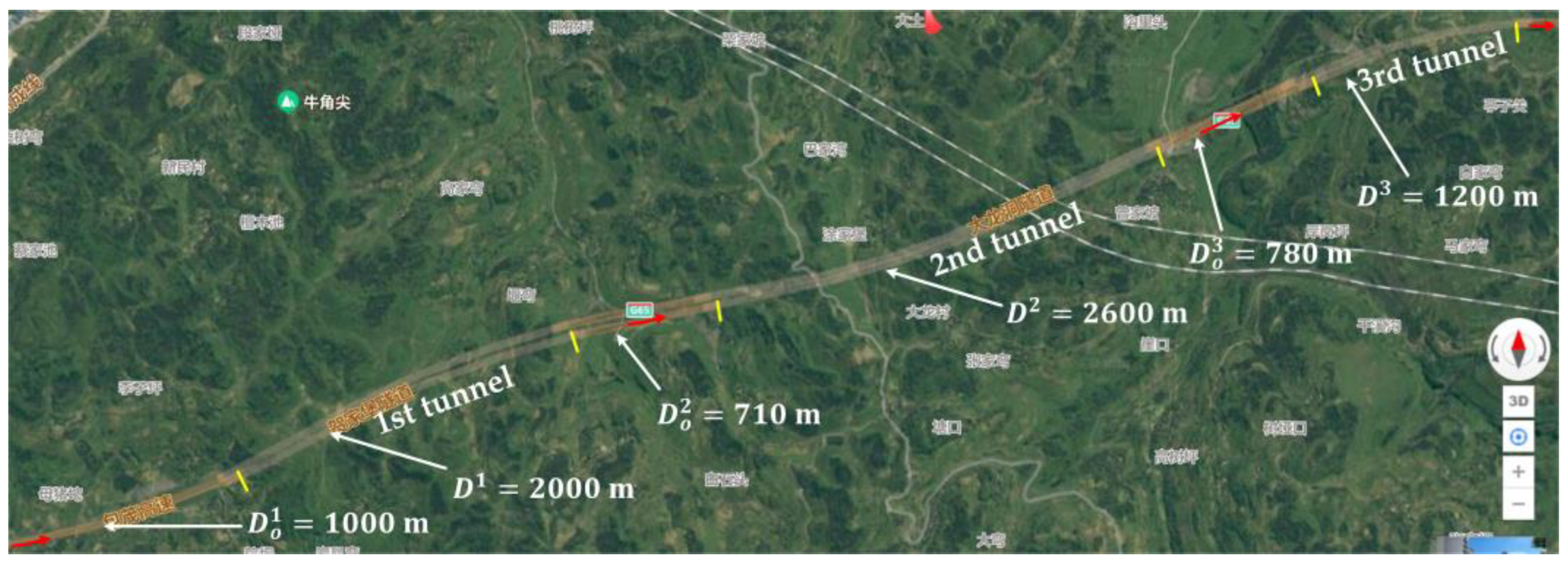
4. Scenarios and Simulations
4.1. Scenarios
4.1.1. Simulation Time Step Comparison
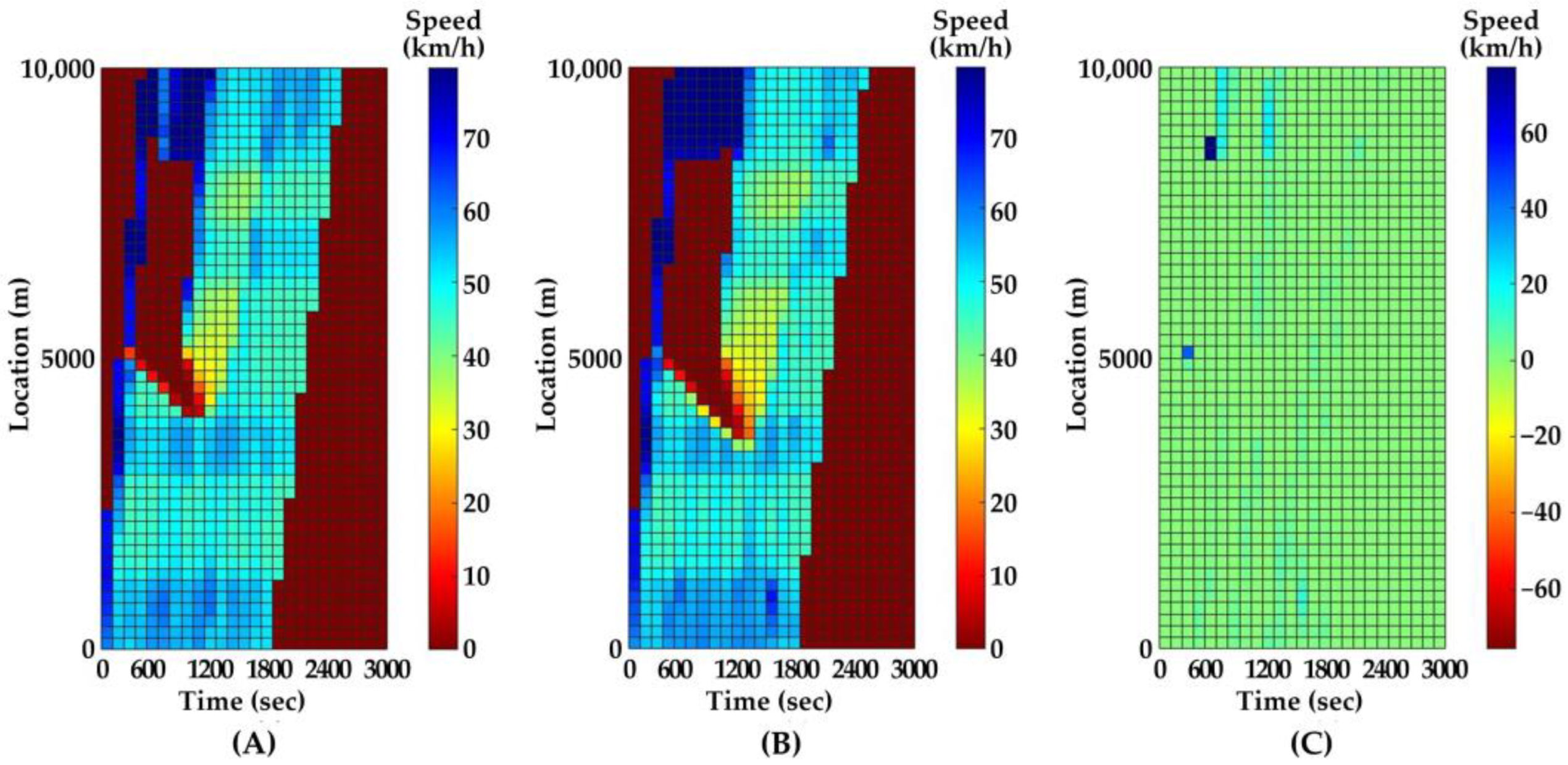
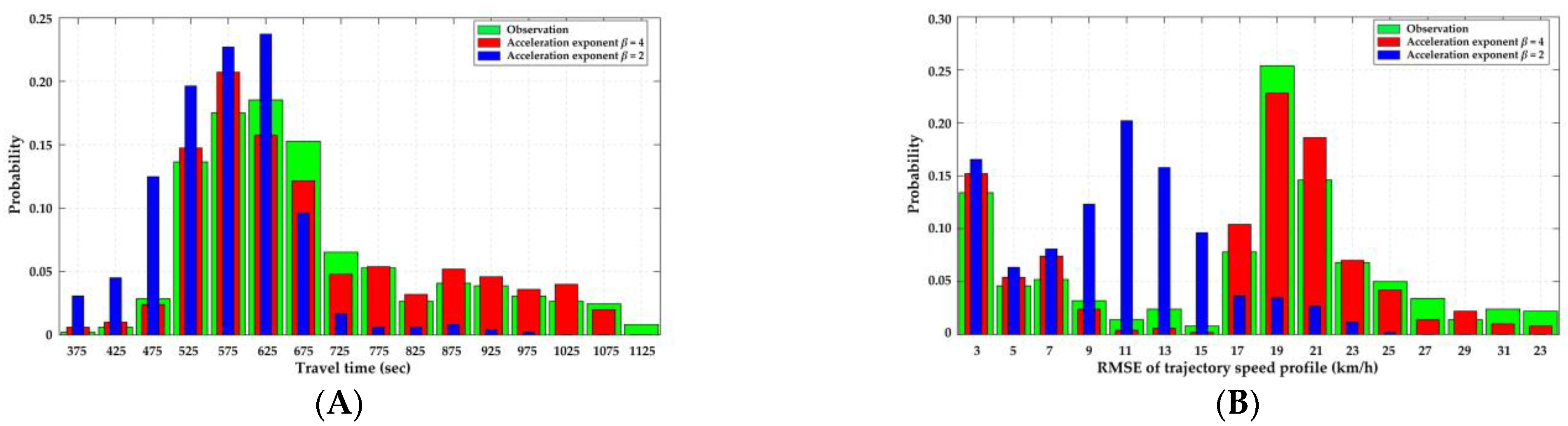
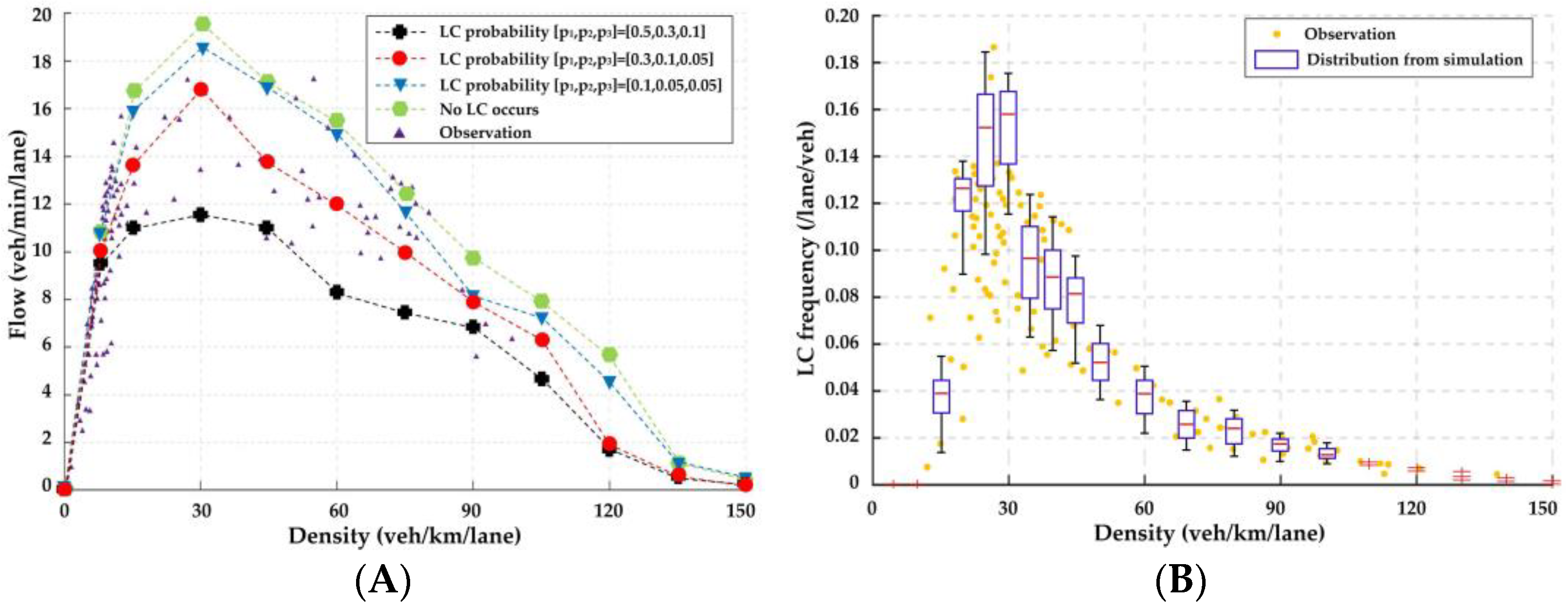
4.1.2. Model Validation
4.1.3. SC Risk under Current Situation and Countermeasures
4.2. Simulations
5. Results and Discussion
5.1. Simulation Time Step Determination
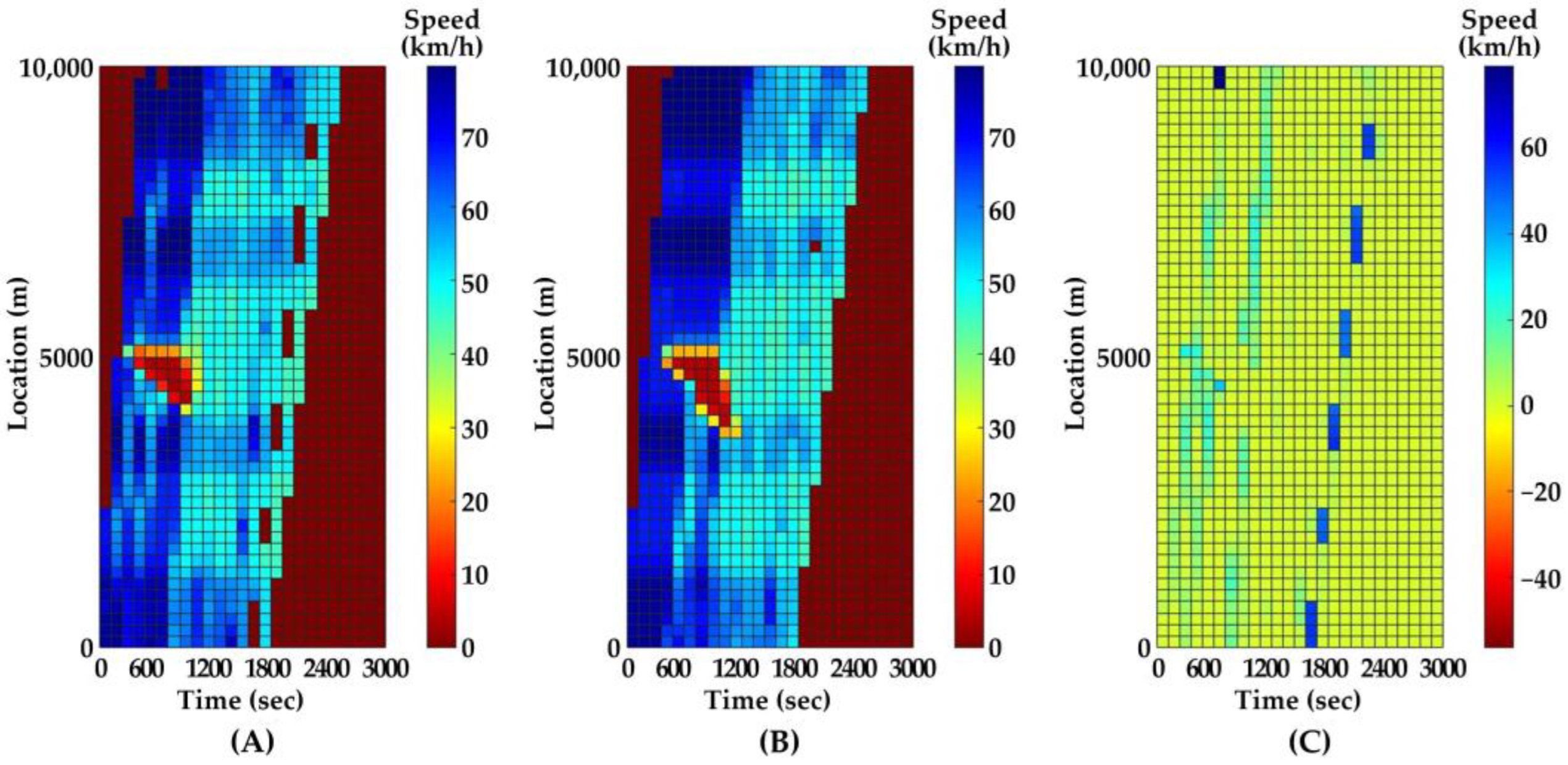
5.2. Model Validation
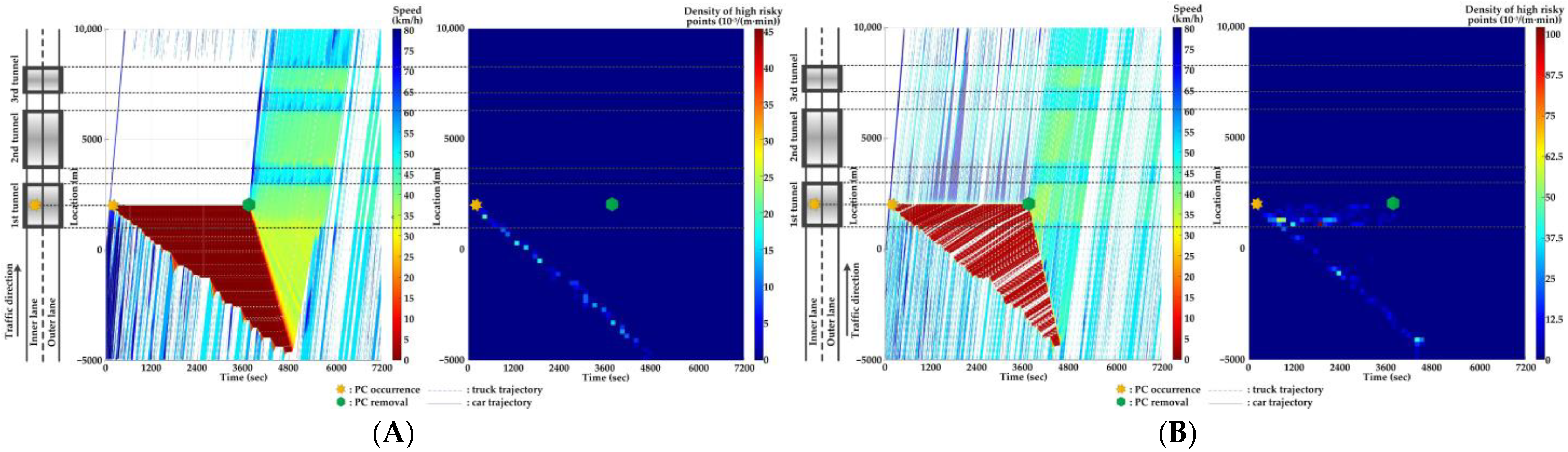
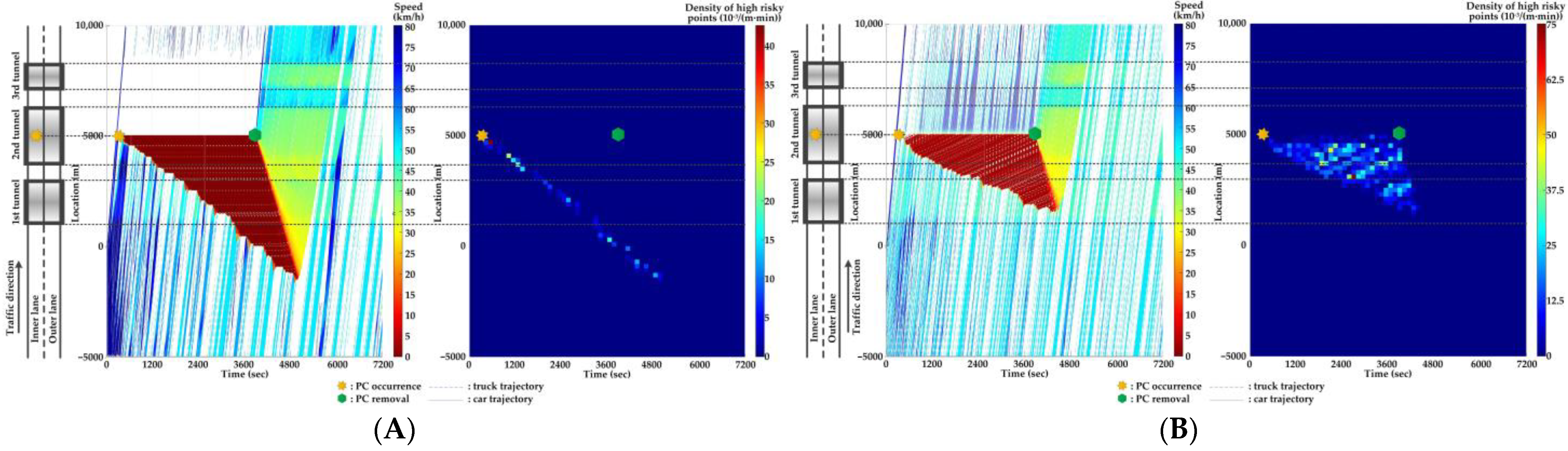
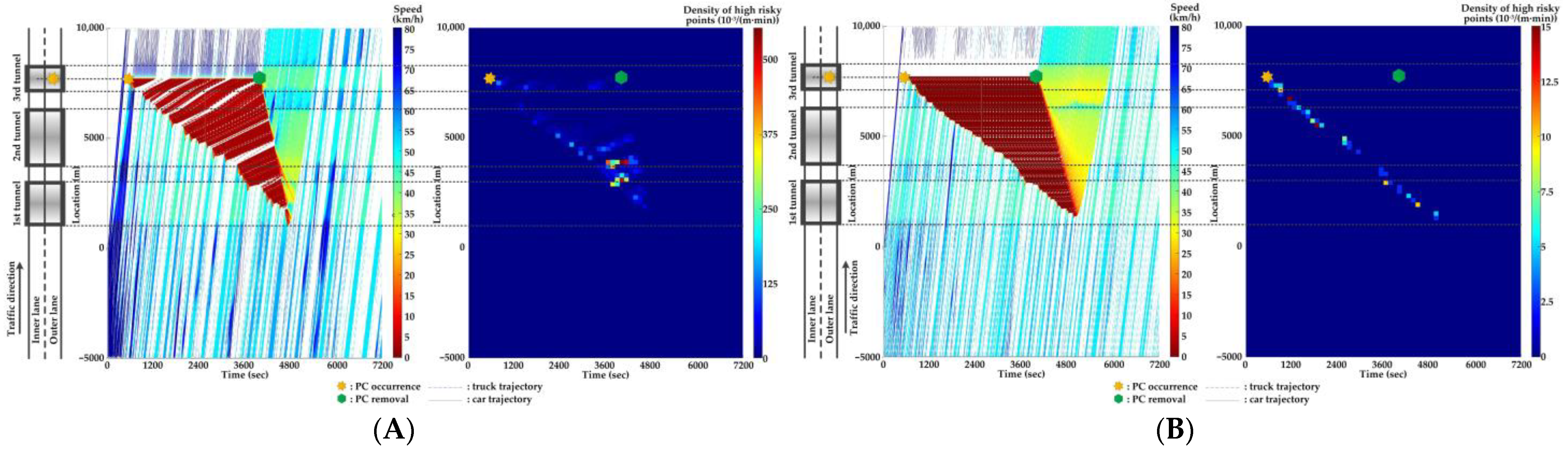
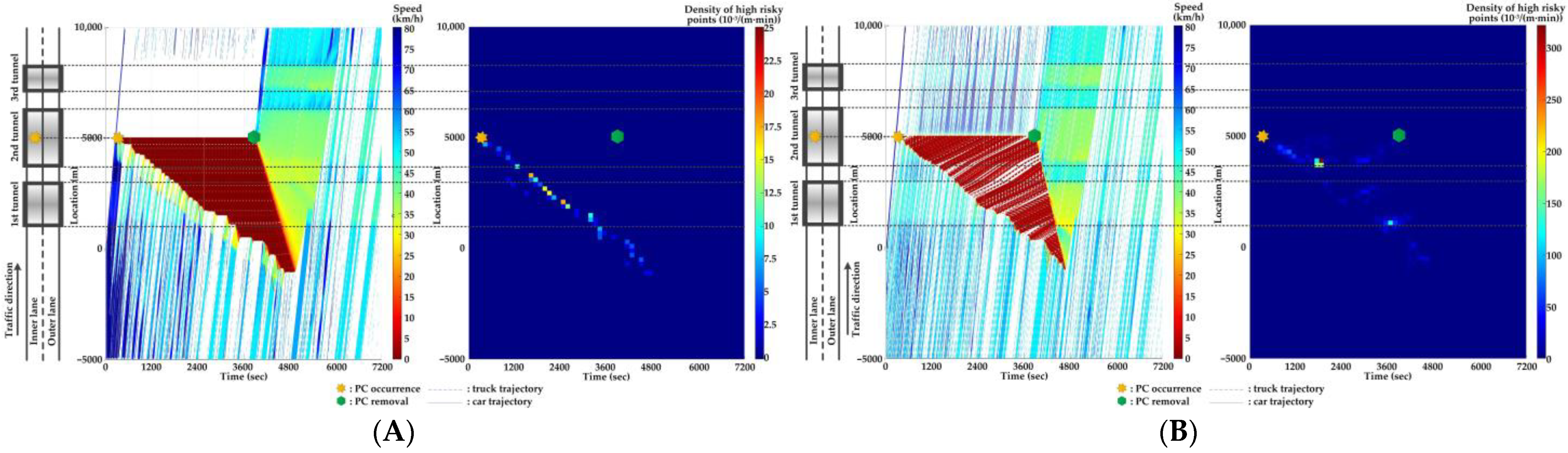
5.3. Features of SC Risks over Time for Different PC Locations in Serial Tunnels
- The stretching tail of the queue incurred by PC occurrence is always the high risky location over time, since the arriving vehicle has to brake to a halt before colliding with the tail of the queue.
- For the lane adjacent to the PC occurrence lane, it has even higher numbers of high-risk points due to the inter-lane dependency and low illumination inside the tunnel. The spatial range of HRPs stretches as the PC-incurred queue on the adjacent lane extends. As a result of the “black hole” and “white hole” effects, the density of HRPs is significantly high near tunnel portals in serial tunnels.
- If PC occurs at the rear location of serial tunnels, the density of SC risk on the PC occurrence lane is relatively low since drivers maintain a slower speed. However, the density of SC risk on the adjacent lane is higher with the stretching PC-incurred queue along serial tunnels, due to the inter-lane dependency and low illumination.
- Periodic oscillations of the traffic flow pattern are presented near tunnel portals where VAs are needed for drivers, demonstrated by the high density traffic flow departing from the PC occurrence location after PC removal.
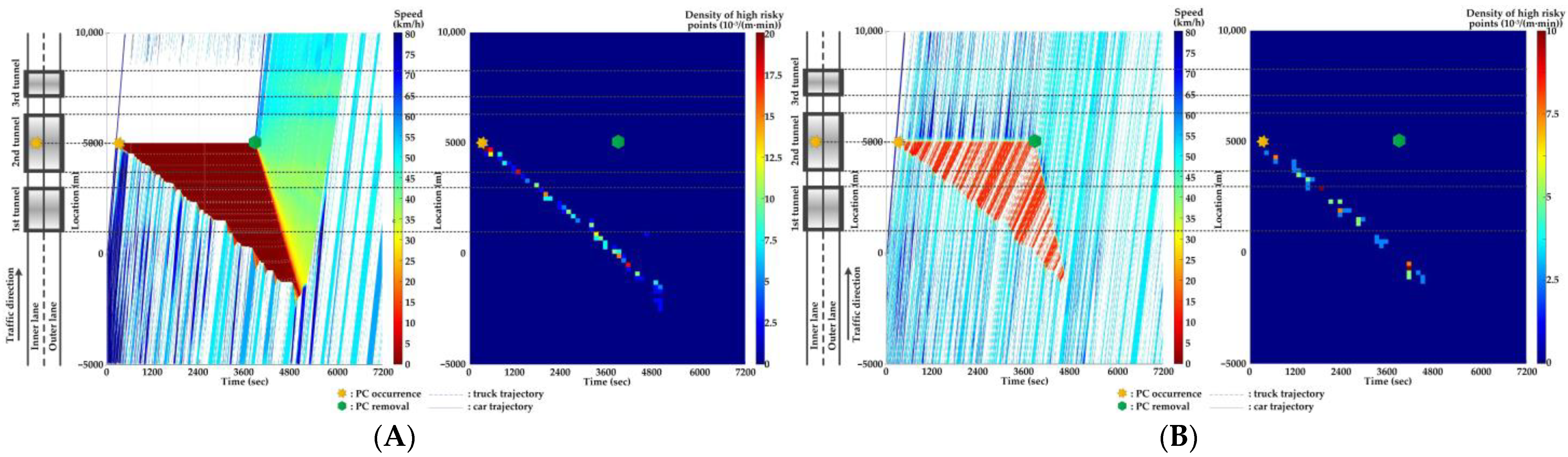
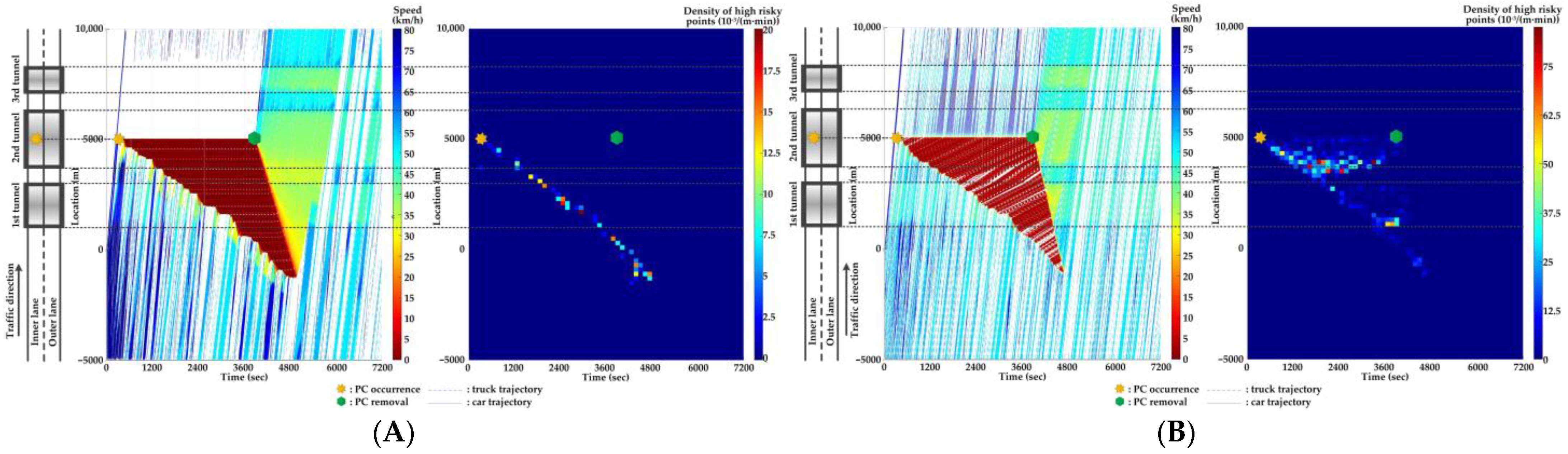
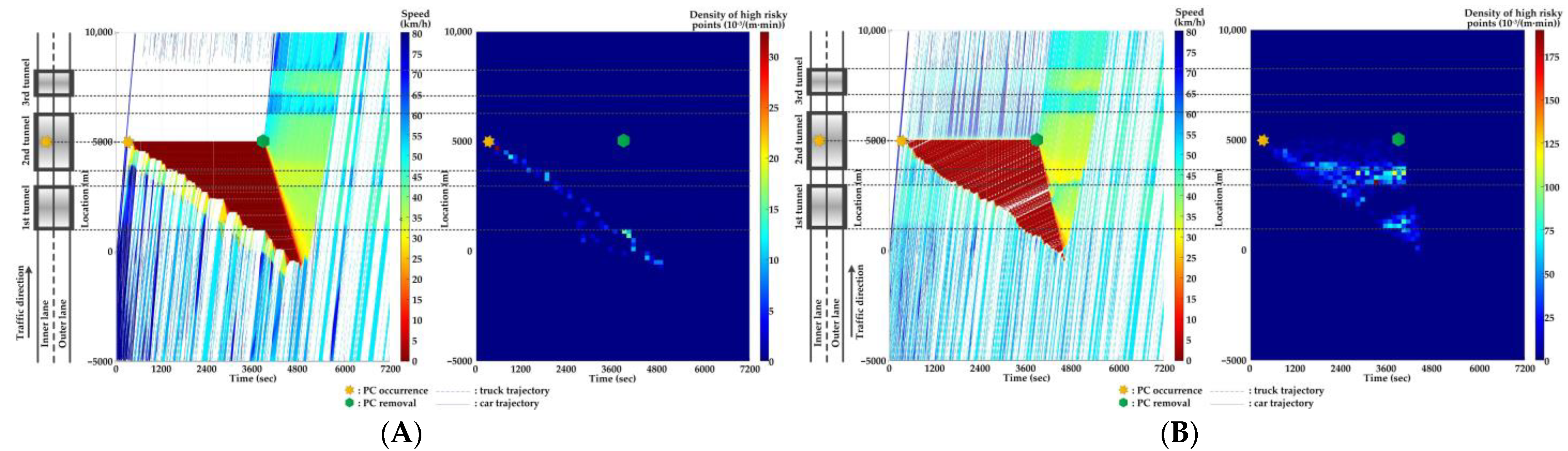
5.4. Comparison of Countermeasures for SC Risk
- In serial tunnels, creating good lighting conditions for drivers is more effective than advanced warnings for a part of drivers in CVs to mitigate the SC risk after PC occurrence.
- Since ATLC can successfully eliminate the “black hole” and “white hole” effects in terms of the daylight theoretically, the SC risk at the tail of the PC-incurred queue is alleviated when tail reaches the portal areas. However, the overall improvement on the PC occurrence lane is not observable. Meanwhile, ATLC can adjust the tunnel lighting inside the tunnel. It can considerably reduce the impact of inter-lane dependency and low illumination on crash risk along the adjacent lane of PC occurrence.
- ASLG for CVs manages to better alleviate the SC risk at the tail of the PC-incurred queue since CVs are able to immediately response to the hazardous traffic flow evolution from PC. However, a few new SC risky locations appear, resulting from the advanced deceleration of CVs whose drivers decide not to change to the adjacent lane. The increase of CV proportions raises the crash risk due to the advanced deceleration of CVs.
- ASLG fails to limit the crash risk along the adjacent lane of PC occurrence since it cannot eliminate the inter-lane dependency after it guides a part of CVs to the adjacent lane. As the proportion of CV rises, the locations and the density of crash risk along the adjacent lane significantly increase.
- A countermeasure combining ATLC with ASLG is promising since it can prevent the “black hole” and “white hole” effects near tunnel portals, inter-lane dependency, and low illumination inside the tunnel, and immediately inform drivers in CVs of the hazardous traffic flow evolution from PC.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calibration of Lighting-Related Behavioral Parameters
Appendix A.1. VA Duration and Desired Speed Reduction in Portal Areas
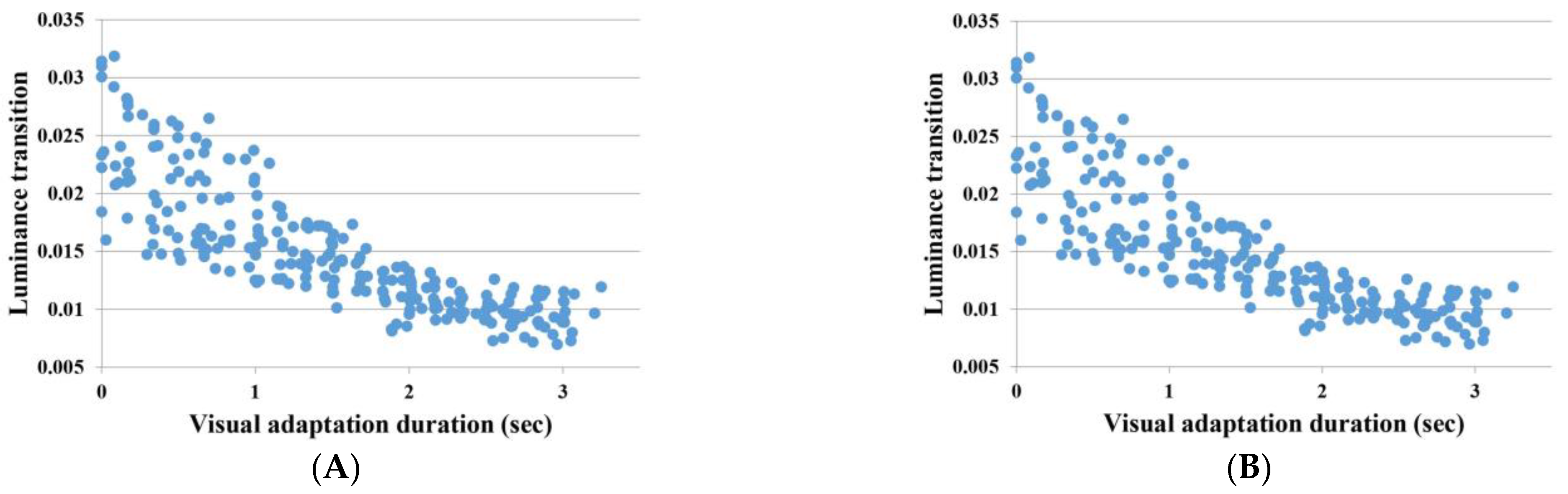
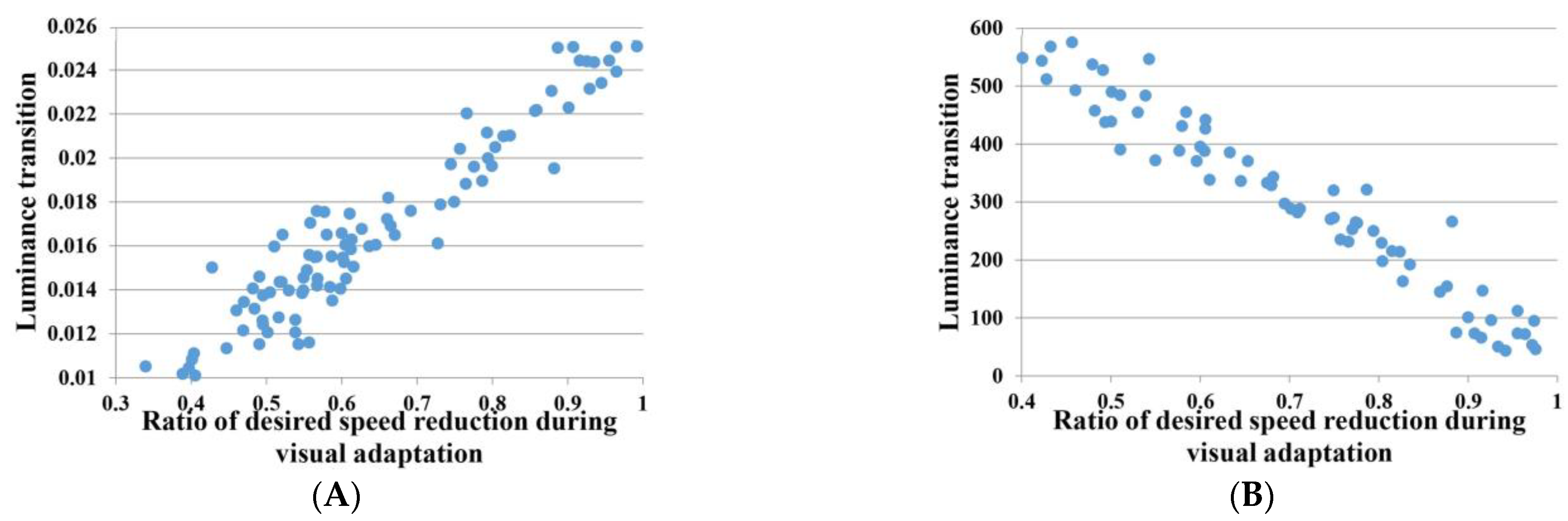
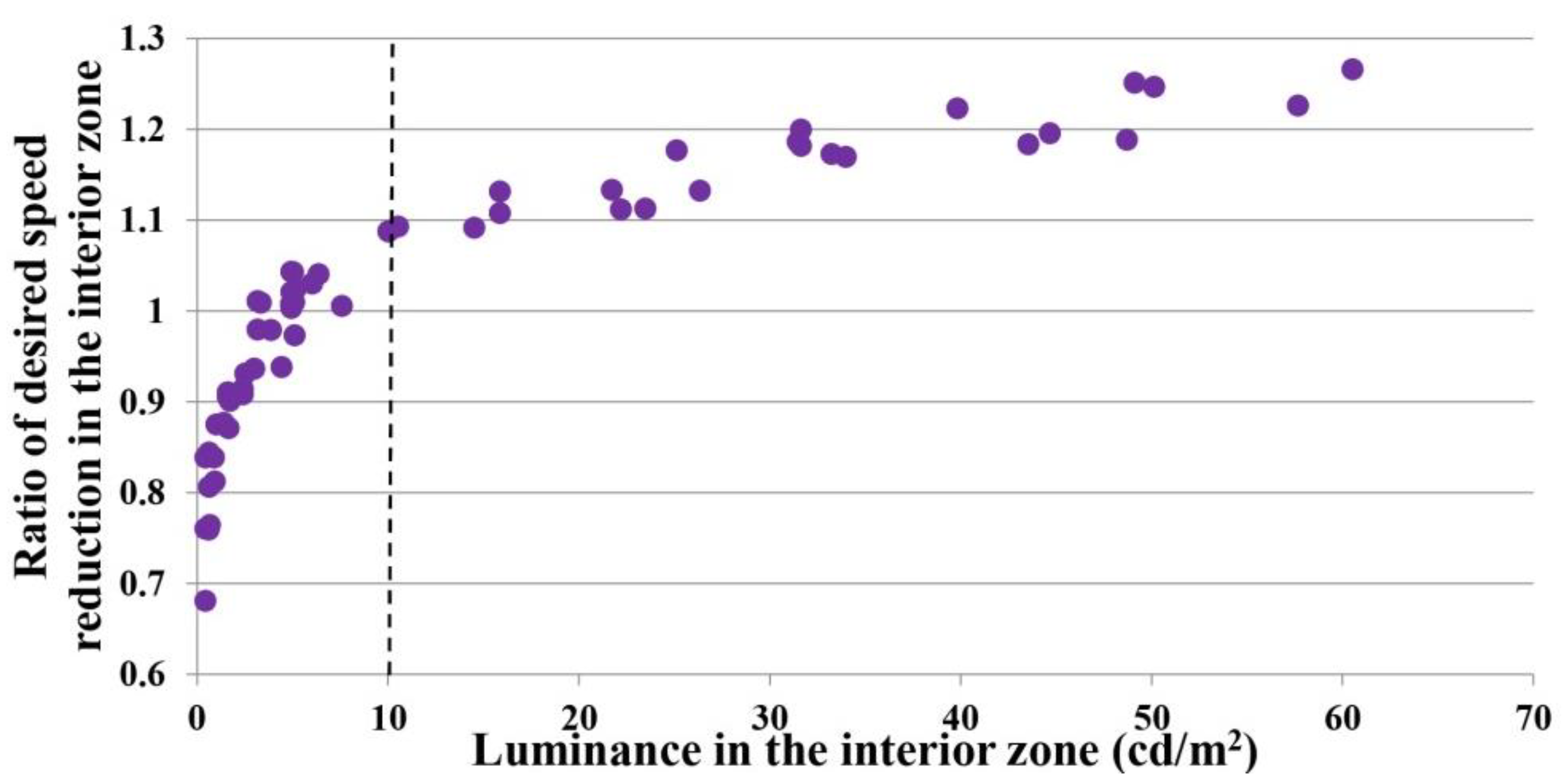
Appendix A.2. Desired Speed Reduction in Interior Zone
References
- Huang, H.; Peng, Y.; Wang, J.; Luo, Q.; Li, X. Interactive risk analysis on crash injury severity at a mountainous freeway with tunnel groups in China. Accid. Anal. Prev. 2018, 111, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Pervez, A.; Wang, Z.; Han, C.; Hu, L.; Huang, H. Crash analysis of Chinese freeway tunnel groups using a five-zone analytic approach. Tunn. Undergr. Space Technol. 2018, 82, 358–365. [Google Scholar] [CrossRef]
- PIARC Technical Committee C3.3, Road Tunnel Operation. Human Factors and Road Tunnel Safety Regarding Users; Report R17; Permanent International Association of Road Congresses (PIARC): Paris, France, 2008. [Google Scholar]
- Zheng, Z.; Du, Z.; Yan, Q.; Xiang, Q.; Chen, G. The impact of rhythm-based visual reference system in long highway tunnels. Saf. Sci. 2017, 95, 75–82. [Google Scholar] [CrossRef]
- He, S.; Liang, B.; Pan, G.; Wang, F.; Cui, L. Influence of dynamic highway tunnel lighting environment on driving safety based on eye movement parameters of the driver. Tunn. Undergr. Space Technol. 2017, 67, 52–60. [Google Scholar] [CrossRef]
- Yu, S.; Shi, L.; Zhang, L.; Liu, Z.; Tu, Y. A solar optical reflection lighting system for threshold zone of short tunnels: Theory and practice. Tunn. Undergr. Space Technol. 2023, 131, 104839. [Google Scholar] [CrossRef]
- Hu, J.; Gao, X.; Wang, R.; Xu, P.; Miao, G. Safety evaluation index on daytime lighting of tunnel entrances. Adv. Mech. Eng. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Lee, J.; Kirytopoulos, K.; Pervez, A.; Huang, H. Understanding drivers’ awareness, habits and intentions inside road tunnels for effective safety policies. Accid. Anal. Prev. 2022, 172, 106690. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Liu, P.; Wang, W.; Xu, C. Development of a variable speed limit strategy to reduce secondary collision risks during inclement weathers. Accid. Anal. Prev. 2014, 72, 134–145. [Google Scholar] [CrossRef]
- Sun, C.; Chilukuri, V. Dynamic incident progression curve for classifying secondary traffic crashes. J. Transp. Eng. 2010, 136, 1153–1158. [Google Scholar] [CrossRef]
- Peng, C.; Xu, C. Combined variable speed limit and lane change guidance for secondary crash prevention using distributed deep reinforcement learning. J. Transp. Saf. Secur. 2022, 14, 2166–2191. [Google Scholar] [CrossRef]
- Xu, C.; Liu, P.; Yang, B.; Wang, W. Real-time estimation of secondary crash likelihood on freeways using high-resolution loop detector data. Transp. Res. Part C Emerg. Technol. 2016, 71, 406–418. [Google Scholar] [CrossRef]
- Xu, C.; Xu, S.; Wang, C.; Li, J. Investigating the factors affecting secondary crash frequency caused by one primary crash using zero-inflated ordered probit regression. Phys. A 2019, 524, 121–129. [Google Scholar] [CrossRef]
- Salek, M.; Jin, W.; Khan, S.; Chowdhury, M.; Gerard, P.; Basnet, S.; Torkjazi, M.; Huynh, N. Assessing the likelihood of secondary crashes on freeways with Adaptive Signal Control System deployed on alternate routes. J. Saf. Res. 2021, 76, 314–326. [Google Scholar] [CrossRef] [PubMed]
- Salum, J.; Kitali, A.; Sando, T.; Alluri, P. Evaluating the impact of Road Rangers in preventing secondary crashes. Accid. Anal. Prev. 2021, 156, 106129. [Google Scholar] [CrossRef] [PubMed]
- Joo, Y.; Kho, S.; Kim, D.; Park, H. A data-driven Bayesian network for probabilistic crash risk assessment of individual driver with traffic violation and crash records. Accid. Anal. Prev. 2022, 176, 106790. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, C.; Jiang, H.; Nie, S.; Chen, L. Transfer learning-based highway crash risk evaluation considering manifold characteristics of traffic flow. Accid. Anal. Prev. 2022, 168, 106598. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B.; Fu, T.; Liu, S.; Stipancic, J. Modeling when and where a secondary accident occurs. Accid. Anal. Prev. 2019, 130, 160–166. [Google Scholar] [CrossRef]
- Park, H.; Haghani, A. Real-time prediction of secondary incident occurrences using vehicle probe data. Transp. Res. Part C Emerg. Technol. 2016, 70, 69–85. [Google Scholar] [CrossRef]
- Li, P.; Abdel-Aty, M. A hybrid machine learning model for predicting real-time secondary crash likelihood. Accid. Anal. Prev. 2022, 165, 106504. [Google Scholar] [CrossRef] [PubMed]
- Peeta, S.; Zhang, P.; Zhou, W. Behavior-based analysis of freeway car-truck interactions and related mitigation strategies. Transp. Res. Part B Methodol. 2005, 39, 417–451. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, S.; Xing, Y.; Lu, J.; Peng, Y.; Zhang, H. The impact of truck proportion on traffic safety using surrogate safety measures in China. J. Adv. Transp. 2020, 2020, 8636417. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, L.; Yang, D. Modeling and simulation of the car-truck heterogeneous traffic flow based on a nonlinear car-following model. Appl. Math. Comput. 2016, 273, 706–717. [Google Scholar] [CrossRef]
- Ponnu, B.; Coifman, B. Speed-spacing dependency on relative speed from the adjacent lane: New insights for car following models. Transp. Res. Part B Methodol. 2015, 82, 74–90. [Google Scholar] [CrossRef]
- Ponnu, B.; Coifman, B. When adjacent lane dependencies dominate the uncongested regime of the fundamental relationship. Transp. Res. Part B Methodol. 2017, 104, 602–615. [Google Scholar] [CrossRef]
- Coifman, B.; Ponnu, B. Adjacent lane dependencies modulating wave velocity on congested freeways-An empirical study. Transp. Res. Part B Methodol. 2020, 142, 84–99. [Google Scholar] [CrossRef]
- Gao, K.; Tu, H.; Sun, L.; Sze, N.; Song, Z.; Shi, H. Impacts of reduced visibility under hazy weather condition on collision risk and car-following behavior: Implications for traffic control and management. Int. J. Sustain. Transp. 2020, 14, 635–642. [Google Scholar] [CrossRef]
- Wang, C.; Xie, Y.; Huang, H.; Liu, P. A review of surrogate safety measures and their applications in connected and automated vehicles safety modeling. Accid. Anal. Prev. 2021, 157, 106157. [Google Scholar] [CrossRef]
- Das, T.; Samandar, M.; Rouphail, N. Longitudinal traffic conflict analysis of autonomous and traditional vehicle platoons in field tests via surrogate safety measures. Accid. Anal. Prev. 2022, 177, 106822. [Google Scholar] [CrossRef]
- Son, S.; Jeong, J.; Park, S.; Park, J. Effects of advanced warning information systems on secondary crash risk under connected vehicle environment. Accid. Anal. Prev. 2020, 148, 105786. [Google Scholar] [CrossRef]
- Qin, L.; Dong, L.; Xu, W.; Zhang, L.; Leon, A. An intelligent luminance control method for tunnel lighting based on traffic volume. Sustainability 2017, 9, 2208. [Google Scholar] [CrossRef]
- Qin, L.; Dong, L.; Xu, W.; Zhang, L.; Yan, Q.; Chen, X. A “vehicle in, light brightens; vehicle out, light darkens” energy-saving control system of highway tunnel lighting. Tunn. Undergr. Space Technol. 2017, 66, 147–156. [Google Scholar] [CrossRef]
- Arun, A.; Haque, M.; Bhaskar, A.; Washington, S.; Sayed, T. A systematic mapping review of surrogate safety assessment using traffic conflict techniques. Accid. Anal. Prev. 2021, 153, 106016. [Google Scholar] [CrossRef] [PubMed]
- Vlahogianni, E.; Karlaftis, M.; Orfanou, F. Modeling the effects of weather and traffic on the risk of secondary incidents. J. Intell. Transp. Syst. 2012, 16, 109–117. [Google Scholar] [CrossRef]
- Imprialou, M.; Orfanou, F.; Vlahogianni, E.; Karlaftis, M. Methods for defining spatiotemporal influence areas and secondary incident detection in freeways. J. Transp. Eng. 2014, 140, 70–80. [Google Scholar] [CrossRef]
- Yang, H.; Ozbay, K.; Xie, K. Assessing the risk of secondary crashes on highways. J. Saf. Res. 2014, 49, 143–149. [Google Scholar] [CrossRef]
- Jalayer, M.; Baratian-Ghorghi, F.; Zhou, H. Identifying and characterizing secondary crashes on the Alabama State highway systems. Adv. Transp. Stud. 2015, 37, 129–140. [Google Scholar]
- Tian, Y.; Chen, H.; Truong, D. A case study to identify secondary crashes on interstate highways in Florida by using geographic information systems (GIS). Adv. Transp. Stud. 2016, 2, 103–112. [Google Scholar]
- Wang, J.; Xie, W.; Liu, B.; Fang, S.; Ragland, D. Identification of freeway secondary accidents with traffic shock wave detected by loop detectors. Saf. Sci. 2016, 87, 195–201. [Google Scholar] [CrossRef]
- Goodall, N. Probability of secondary crash occurrence on freeways with the use of private-sector speed data. Transp. Res. Rec. J. Transp. Res. Board 2017, 2635, 11–18. [Google Scholar] [CrossRef]
- Sarker, A.; Paleti, R.; Mishra, S.; Golias, M.; Freeze, P. Prediction of secondary crash frequency on highway networks. Accid. Anal. Prev. 2017, 98, 108–117. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Xie, K.; Dai, D. Use of ubiquitous probe vehicle data for identifying secondary crashes. Transp. Res. Part C Emerg. Technol. 2017, 82, 138–160. [Google Scholar] [CrossRef]
- Yu, S.; Li, Y.; Xuan, Z.; Li, Y.; Li, G. Real-time risk assessment for road transportation of hazardous materials based on GRU-DNN with multimodal feature embedding. Appl. Sci. 2022, 12, 11130. [Google Scholar] [CrossRef]
- Kitali, A.; Alluri, P.; Sando, T.; Haule, H.; Kidando, E.; Lentz, R. Likelihood estimation of secondary crashes using Bayesian complementary log-log model. Accid. Anal. Prev. 2018, 119, 58–67. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Haghani, A.; Samuel, S.; Knodler, M. Real-time prediction and avoidance of secondary crashes under unexpected traffic congestion. Accid. Anal. Prev. 2018, 112, 39–49. [Google Scholar] [CrossRef]
- Davis, G.; Hourdos, J.; Xiong, H.; Chatterjee, I. Outline for a causal model of traffic conflicts and crashes. Accid. Anal. Prev. 2011, 43, 1907–1919. [Google Scholar] [CrossRef]
- Venthuruthiyil, S.; Chunchu, M. Anticipated Collision Time (ACT): A two-dimensional surrogate safety indicator for trajectory-based proactive safety assessment. Transp. Res. Part C Emerg. Technol. 2022, 139, 103655. [Google Scholar] [CrossRef]
- Ariza, A. Validation of Road Safety Surrogate Measures as a Predictor of Crash Frequency Rates on a Large-Scale Microsimulation Network. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2011. [Google Scholar]
- Shahdah, U.; Saccomanno, F.; Persaud, B. Application of traffic microsimulation for evaluating safety performance of urban signalized intersections. Transp. Res. Part C Emerg. Technol. 2015, 60, 96–104. [Google Scholar] [CrossRef]
- Essa, M.; Sayed, T. Transferability of calibrated microsimulation model parameters for safety assessment using simulated conflicts. Accid. Anal. Prev. 2015, 84, 41–53. [Google Scholar] [CrossRef]
- Fu, C.; Sayed, T. Comparison of threshold determination methods for the deceleration rate to avoid a crash (DRAC)-based crash estimation. Accid. Anal. Prev. 2021, 153, 106051. [Google Scholar] [CrossRef]
- Saifuzzaman, M.; Zheng, Z. Incorporating human-factors in car-following models: A review of recent developments and research needs. Transp. Res. Part C Emerg. Technol. 2014, 48, 379–403. [Google Scholar] [CrossRef]
- Zhigang, D.; Zheng, Z.; Zheng, M.; Ran, B.; Zhao, X. Drivers’ visual comfort at highway tunnel portals: A quantitative analysis based on visual oscillation. Transp. Res. Part D Transp. Environ. 2014, 31, 37–47. [Google Scholar] [CrossRef]
- Mehri, A.; Sajedifar, J.; Abbasi, M.; Naimabadi, A.; Mohammadi, A.A.; Teimori, G.H.; Zakerian, S.A. Safety evaluation of lighting at very long tunnels on the basis of visual adaptation. Saf. Sci. 2019, 116, 196–207. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, S.; Li, D.; Tang, B.; Fang, S. Crash analysis of mountainous freeways with high bridge and tunnel ratios using road scenario-based discretization. PLoS ONE 2020, 15, e0237408. [Google Scholar] [CrossRef]
- Cui, H.; Wang, Y.; Zhu, M.; Li, X. Influence of tunnel group light-dark conversion on dark reaction time. J. Traffic Transp. Eng. 2020, 21, 200–208. (In Chinese) [Google Scholar]
- Yeung, J.; Wong, Y. The effect of road tunnel environment on car following behaviour. Accid. Anal. Prev. 2014, 70, 100–109. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Shen, Y.; Liu, J.; Feng, Z.; Wang, K.; Chen, Q. Drivers’ car-following behaviours in low-illumination conditions. Ergonomics 2021, 64, 199–211. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity. Philos. Trans. Math. Phys. Eng. Sci. 2010, 368, 4585–4605. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Xu, S.; Qian, Y. Stability analysis of an extended intelligent driver model and its simulations under open boundary condition. Phys. A: Stat. Mech. Its Appl. 2015, 419, 526–536. [Google Scholar] [CrossRef]
- Saifuzzaman, M.; Zheng, Z.; Haque, M.; Washington, S. Revisiting the task-capability interface model for incorporating human factors into car-following models. Transp. Res. Part B Methodol. 2015, 82, 1–19. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A. The intelligent driver model with stochasticity—New insights into traffic flow oscillations. Transp. Res. Part B Methodol. 2018, 117, 613–623. [Google Scholar] [CrossRef]
- Xiong, B.; Jiang, R.; Tian, J. Improving two-dimensional intelligent driver models to overcome overly high deceleration in car-following. Phys. A: Stat. Mech. Its Appl. 2019, 534, 122313. [Google Scholar] [CrossRef]
- Sharath, M.; Velaga, N. Enhanced intelligent driver model for two-dimensional motion planning in mixed traffic. Transp. Res. Part C Emerg. Technol. 2020, 120, 102780. [Google Scholar] [CrossRef]
- Yu, G.; Wang, P.; Wu, X.; Wang, Y. Linear and nonlinear stability analysis of a car-following model considering velocity difference of two adjacent lanes. Nonlinear Dyn. 2016, 84, 387–397. [Google Scholar] [CrossRef]
- Jiang, N.; Yu, B.; Cao, F.; Dang, P.; Cui, S. An extended visual angle car-following model considering the vehicle types in the adjacent lane. Phys. A 2021, 566, 125665. [Google Scholar] [CrossRef]
- Rahman, M.; Chowdhury, M.; Xie, Y.; He, Y. Review of microscopic lane-changing models and future research opportunities. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1942–1955. [Google Scholar] [CrossRef]
- Zheng, Z. Recent developments and research needs in modeling lane changing. Transp. Res. Part B Methodol. 2014, 60, 16–32. [Google Scholar] [CrossRef]
- Gipps, P. A model for the structure of lane-changing decisions. Transp. Res. Part B Methodol. 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Zheng, Z.; Ahn, S.; Chen, D.; Laval, J. The effects of lane-changing on the immediate follower: Anticipation, relaxation, and change in driver characteristics. Transp. Res. Part C Emerg. Technol. 2013, 26, 367–379. [Google Scholar] [CrossRef]
- Gazis, D.; Herman, R.; Rothery, R. Nonlinear follow-the-leader models of traffic flow. Oper. Res. 1961, 9, 545–567. [Google Scholar] [CrossRef]
- Lund, I.; Rundmo, T. Cross-cultural comparisons of traffic safety, risk perception, attitudes and behaviour. Saf. Sci. 2009, 47, 547–553. [Google Scholar] [CrossRef]
- Farooq, D.; Moslem, S.; Tufail, R.; Ghorbanzadeh, O.; Duleba, S.; Maqsoom, A.; Blaschke, T. Analyzing the importance of driver behavior criteria related to road safety for different driving cultures. Int. J. Environ. Res. Public Health 2020, 17, 1893. [Google Scholar] [CrossRef] [PubMed]
- Lv, W.; Song, W.; Liu, X.; Ma, J. A microscopic lane changing process model for multilane traffic. Phys. A 2013, 392, 1142–1152. [Google Scholar] [CrossRef]
- Commission internationale de l’éclairage (CIE). Guide for the Lighting of Road Tunnels and Underpasses; CIE 88: 2004; CIE Central Bureau: Vienna, Austria, 2004. [Google Scholar]
- JTG/T D70/2-01-2014; Guidelines for Design of Lighting of Highway Tunnels. Ministry of Transport of the People’s Republic of China: Beijing, China, 2014.
- Abdul Salam, A.; Mezher, K. Energy saving in tunnels lighting using shading structures. In Proceedings of the 2014 International Renewable and Sustainable Energy Conference (IRSEC), Ouarzazate, Morocco, 7–19 October 2014. [Google Scholar]
- Kesting, A.; Treiber, M.; Helbing, D. General lane-changing model MOBIL for car-following models. Transp. Res. Rec. J. Transp. Res. Board 2007, 1999, 86–94. [Google Scholar] [CrossRef]
- Schakel, W.; Knoop, V.; van Arem, B. Integrated lane change model with relaxation and synchronization. Transp. Res. Rec. J. Transp. Res. Board 2012, 2316, 47–57. [Google Scholar] [CrossRef]
- Zhao, P.; Lee, C. Assessing rear-end collision risk of cars and heavy vehicles on freeways using a surrogate safety measure. Accid. Anal. Prev. 2018, 113, 149–158. [Google Scholar] [CrossRef]
- Hayward, J. Near-miss determination through use of a scale of danger. Highw. Res. Rec. 1972, 384, 24–34. [Google Scholar]
- Lu, J.; Grembek, O.; Hansen, M. Learning the representation of surrogate safety measures to identify traffic conflict. Accid. Anal. Prev. 2022, 174, 106755. [Google Scholar] [CrossRef]
- Cooper, D.; Ferguson, N. Traffic studies at T-junctions-a conflict simulation model. Traffic Eng. Control 1976, 17, 306–309. [Google Scholar]
- Cunto, F.; Saccomanno, F. Calibration and validation of simulated vehicle safety performance at signalized intersections. Accid. Anal. Prev. 2008, 40, 1171–1179. [Google Scholar] [CrossRef]
- Weng, J.; Meng, Q.; Yan, X. Analysis of work zone rear-end crash risk for different vehicle-following patterns. Accid. Anal. Prev. 2014, 72, 449–457. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Peng, F.; Ouyang, Y. Measurement and estimation of traffic oscillation properties. Transp. Res. Part B Methodol. 2010, 44, 1–14. [Google Scholar] [CrossRef]
- Manser, M.; Hancock, P. The influence of perceptual speed regulation on speed perception, choice, and control: Tunnel wall characteristics and influences. Accid. Anal. Prev. 2007, 39, 69–78. [Google Scholar] [CrossRef] [PubMed]
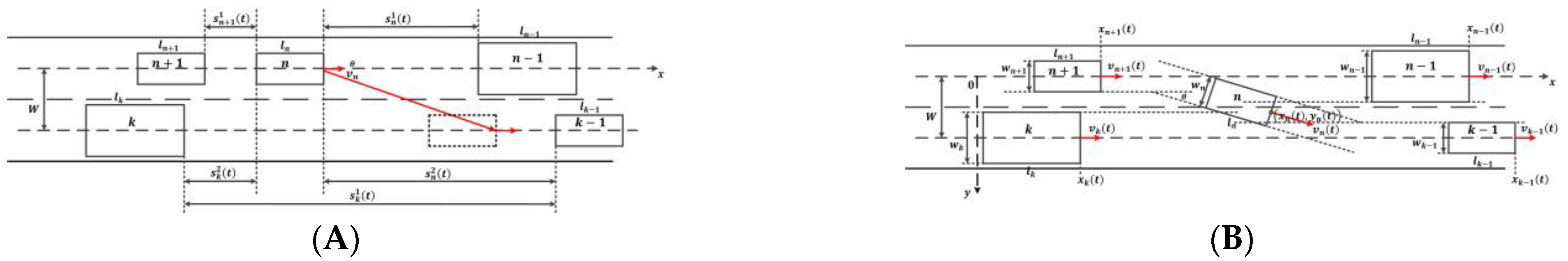





| Distribution Parameters for MADR | Car | Truck |
|---|---|---|
| (m/s2) | 8.45 | 6.82 |
| (m/s2) | 1.40 | 1.40 |
| (m/s2) | 12.68 | 10.05 |
| (m/s2) | 1.23 | 0.60 |
| CC | CT | TC | TT | |
|---|---|---|---|---|
| (s) | 1.2 | 1.4 | 1.8 | 2.0 |
| (m) | 1.04 | 1.62 | 1.23 | 1.89 |
| (km/h) | 80 | 57 | 61 | 52 |
| (m/s2) | 1.01 | 1.03 | 0.78 | 0.74 |
| (m/s2) | 2.26 | 2.12 | 1.70 | 1.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Chen, Y.; Song, L.; Xuan, Z.; Li, Y. Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model with Inter-Lane Dependency. Int. J. Environ. Res. Public Health 2023, 20, 3066. https://doi.org/10.3390/ijerph20043066
Yu S, Chen Y, Song L, Xuan Z, Li Y. Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model with Inter-Lane Dependency. International Journal of Environmental Research and Public Health. 2023; 20(4):3066. https://doi.org/10.3390/ijerph20043066
Chicago/Turabian StyleYu, Shanchuan, Yu Chen, Lang Song, Zhaoze Xuan, and Yi Li. 2023. "Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model with Inter-Lane Dependency" International Journal of Environmental Research and Public Health 20, no. 4: 3066. https://doi.org/10.3390/ijerph20043066
APA StyleYu, S., Chen, Y., Song, L., Xuan, Z., & Li, Y. (2023). Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model with Inter-Lane Dependency. International Journal of Environmental Research and Public Health, 20(4), 3066. https://doi.org/10.3390/ijerph20043066





