Optimization of Ecological Water Replenishment Scheme Based on the Interval Fuzzy Two-Stage Stochastic Programming Method: Boluo Lake National Nature Reserve, Jilin Province, China
Abstract
1. Introduction
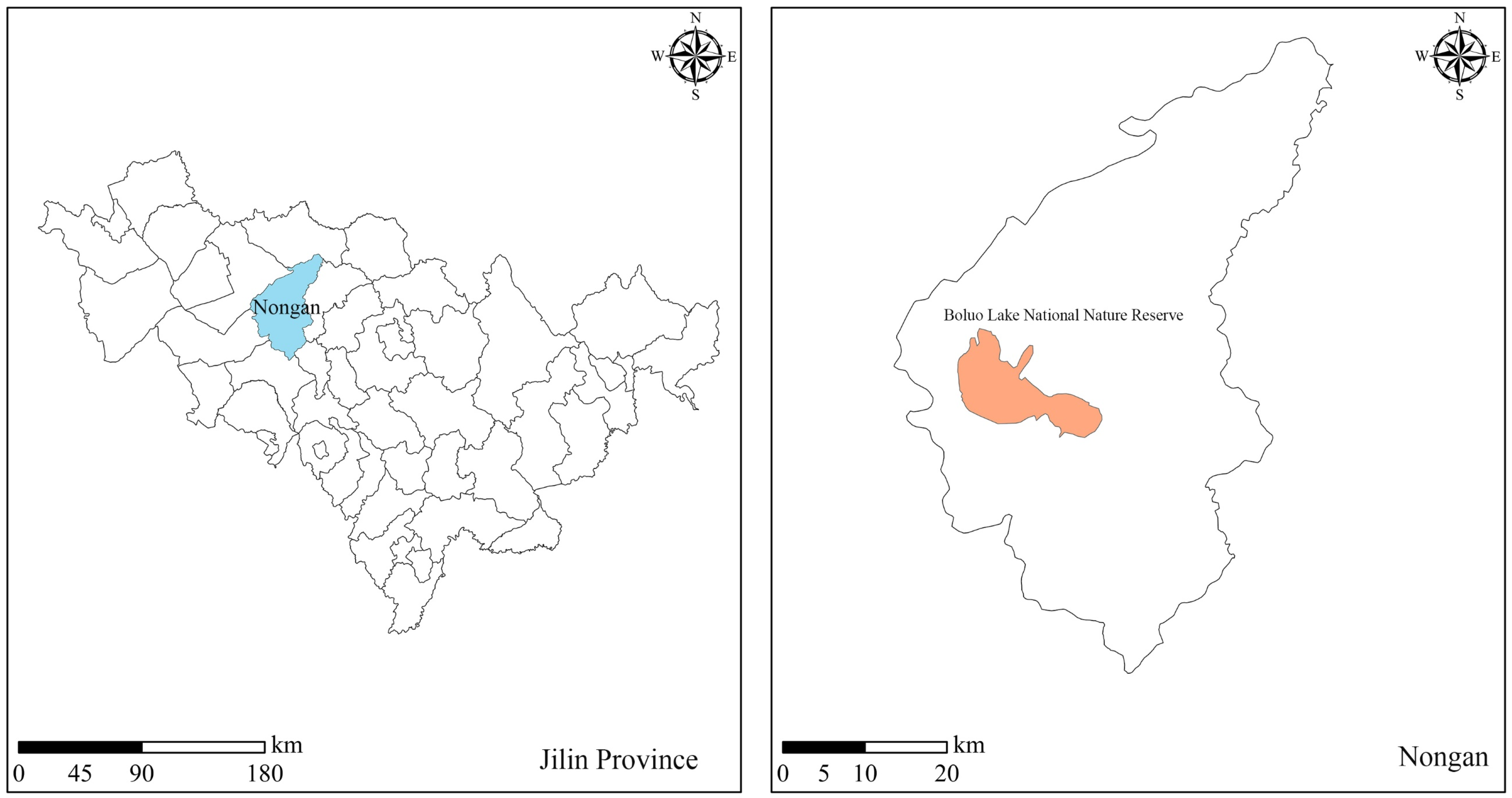
2. Study Area
3. Model Construction
3.1. Overview of Interval Fuzzy Two-Stage Stochastic Programming Methods
3.2. Construction of Optimised Ecological Water Supply Model for Boluo Lake Wetland Based on Interval Fuzzy Two-Stage Stochastic Programming Method
4. Results and Discussion
4.1. Analysis of the Change in Ecological Replenishment Water Quantity Used for Boluo Lake Wetland Water Replenishment Project Based on IFTSP Model
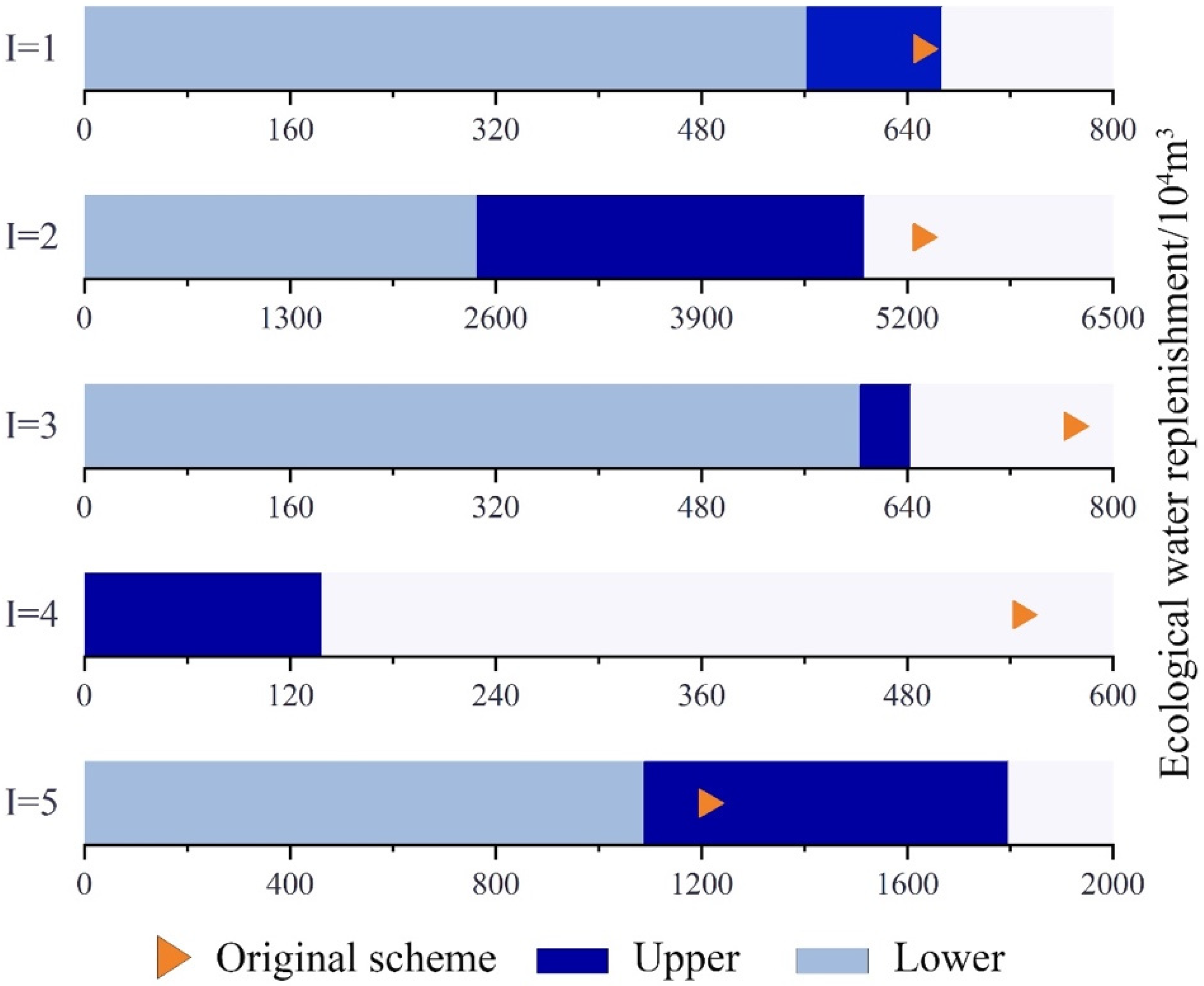
4.1.1. Ecological Replenishment Water Configuration Scheme for Boluo Lake Wetland Water Replenishment Project Based on the IFTSP Method
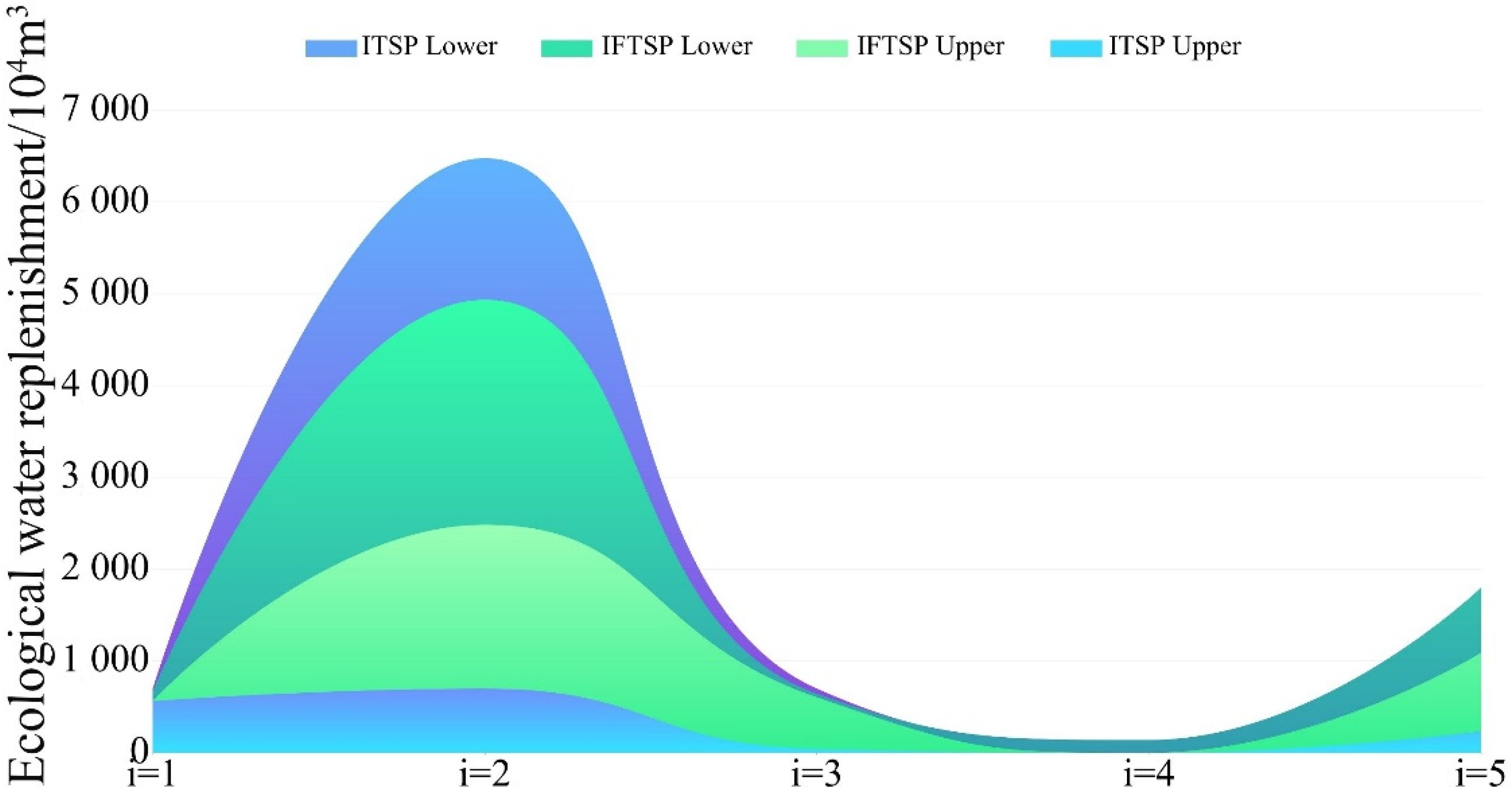
4.1.2. Comparative Analysis of Ecological Recharge Configuration Options for Boluo Lake Wetland Recharge Project by Using IFTSP and ITSP Models
4.2. Analysis of Water Diversion Variation in Boluo Lake Wetland Reserve Recharge Project Based on IFTSP Model
4.2.1. Flood Diversion Water Allocation Scheme for Water Replenishment Project in Boluo Lake Wetland Reserve Based on IFTSP Model
4.2.2. Comparative Analysis of ITSP and IFTSP Models for Diversion of Water from Boluo Lake Wetland Reserve Recharge Project
4.3. Analysis of Ecological Water Replenishment Variation in Boluo Lake Wetland Water Replenishment Project Based on IFTSP Method
4.3.1. Functional Area Allocation Scheme for Water Replenishment Project in Boluo Lake Wetland Reserve Based on IFTSP Model
4.3.2. Comparative Analysis of Changes in Functional Areas in Boluo Lake Wetland Reserve Water Replenishment Project According to ITSP and IFTSP Models
4.4. Comprehensive Comparative Analysis for Boluo Lake Wetland Recharge Project by Using IFTSP and ITSP Models
4.5. Evaluation of Practicability of IFTSP Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, P.; Kumar, S.N. The global governance of water, energy, and food nexus: Allocation and access for competing demands. Int. Environ. Agreem. Politics Law Econ. 2020, 20, 377–391. [Google Scholar] [CrossRef]
- Meng, C.; Wang, X.; Li, Y. An Optimization Model for Water Management Based on Water Resources and Environmental Carrying Capacities: A Case Study of the Yinma River Basin, Northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Ran, L.; Lu, X.X. Redressing China’s strategy of water resource exploitation. Environ. Manag. 2013, 51, 503–510. [Google Scholar] [CrossRef]
- Gong, X.; Zhang, H.; Ren, C.; Sun, D.; Yang, J. Optimization allocation of irrigation water resources based on crop water requirement under considering effective precipitation and uncertainty. Agric. Water Manag. 2020, 239, 106264. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.; Guo, S.; Liu, X.; Guo, P. Inexact nonlinear improved fuzzy chance-constrained programming model for irrigation water management under uncertainty. J. Hydrol. 2018, 556, 397–408. [Google Scholar] [CrossRef]
- Xia, J.; Qiu, B.; Li, Y. Water resources vulnerability and adaptive management in the Huang, Huai and Hai river basins of China. Water Int. 2012, 37, 523–536. [Google Scholar] [CrossRef]
- He, W.; Yang, L.; Li, M.; Meng, C.; Li, Y. Application of an Interval Two-Stage Robust (ITSR) Optimization Model for Optimization of Water Resource Distribution in the Yinma River Basin, Jilin Province, China. Water 2020, 12, 2910. [Google Scholar] [CrossRef]
- Fu, Z.H.; Zhao, H.J.; Wang, H.; Lu, W.T.; Wang, J.; Guo, H.C. Integrated planning for regional development planning and water resources management under uncertainty: A case study of Xining, China. J. Hydrol. 2017, 554, 623–634. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Y.; Zhang, Z.; Wang, P.; Song, X.; Wei, X.; Feng, B. The spatio-temporal variations of surface water quality in China during the “Eleventh Five-Year Plan”. Environ. Monit. Assess. 2015, 187, 64. [Google Scholar] [CrossRef]
- Ren, C.; Zhang, H. A Fuzzy Max–Min Decision Bi-Level Fuzzy Programming Model for Water Resources Optimization Allocation under Uncertainty. Water 2018, 10, 488. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Guo, S.; Zhang, F.; Guo, P. A risk-based fuzzy boundary interval two-stage stochastic water resources management programming approach under uncertainty. J. Hydrol. 2020, 582, 124553. [Google Scholar] [CrossRef]
- Lavoie, R.; Deslandes, J.; Proulx, F. Assessing the ecological value of wetlands using the MACBETH approach in Quebec City. J. Nat. Conserv. 2016, 30, 67–75. [Google Scholar] [CrossRef]
- Berkowitz, J.F.; Green, L.; VanZomeren, C.M.; White, J.R. Evaluating soil properties and potential nitrate removal in wetlands created using an Engineering with Nature based dredged material placement technique. Ecol. Eng. 2016, 97, 381–388. [Google Scholar] [CrossRef]
- Alminagorta, O.; Rosenberg, D.E.; Kettenring, K.M. Systems modeling to improve the hydro-ecological performance of diked wetlands. Water Resour. Res. 2016, 52, 7070–7085. [Google Scholar] [CrossRef]
- Aguilera, H.; Moreno, L.; Wesseling, J.G.; Jiménez-Hernández, M.E.; Castaño, S. Soil moisture prediction to support management in semiarid wetlands during drying episodes. Catena 2016, 147, 709–724. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Bernal, B.; Nahlik, A.M.; Mander, Ü.; Zhang, L.; Anderson, C.J.; Jørgensen, S.E.; Brix, H. Wetlands, carbon, and climate change. Landsc. Ecol. 2012, 28, 583–597. [Google Scholar] [CrossRef]
- Yang, W. A multi-objective optimization approach to allocate environmental flows to the artificially restored wetlands of China’s Yellow River Delta. Ecol. Model. 2011, 222, 261–267. [Google Scholar] [CrossRef]
- Yang, L.; Cong, W.; Meng, C.; Cai, B.; Liu, M. An Interval Fuzzy, Double-Sided, Chance-Constrained Stochastic Programming Model for Planning the Ecological Service Value of Interconnected River Systems. Water 2020, 12, 2649. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H.; Yang, W.; Xing, L.; Tu, G.; Ru, Z.; Xu, Z. The assessment of ecological water replenishment scheme based on the two-dimensional lattice-Boltzmann water age theory. J. Hydro-Environ. Res. 2019, 25, 25–34. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Li, Y.; Bao, A.; Ma, Y. A simulation-based two-stage interval-stochastic pro-gramming model for water resources management in Kaidu-Konqi watershed, China. J. Arid Land 2012, 4, 390–398. [Google Scholar] [CrossRef]
- Li, C.Y.; Zhang, L. An Inexact Two-Stage Allocation Model for Water Resources Management Under Uncertainty. Water Resour. Manag. 2015, 29, 1823–1841. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, L.; Sun, S. Optimization Model of the Ecological Water Replenishment Scheme for Boluo Lake National Nature Reserve Based on Interval Two-Stage Stochastic Programming. Water 2021, 13, 1007. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Scott Yeomans, J. An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; Zeng, G.M.; Maqsood, I.; He, L. An Inexact Two-stage Fuzzy-stochastic Programming Model for Water Resources Management. Water Resour. Manag. 2007, 22, 991–1016. [Google Scholar] [CrossRef]
- Li, M.W.; Li, Y.P.; Huang, G.H. An interval-fuzzy two-stage stochastic programming model for planning carbon dioxide trading under uncertainty. Energy 2011, 36, 5677–5689. [Google Scholar] [CrossRef]
- Cai, B.; Zhang, Y.; Wang, X.; Li, Y. An Optimization Model for a Wetland Restoration Project under Uncertainty. Int. J. Environ. Res. Public Health 2018, 15, 2795. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Yang, Z.F.; Nie, S.L. IFMP: Interval-fuzzy multistage programming for water resources management under uncertainty. Resour. Conserv. Recycl. 2008, 52, 800–812. [Google Scholar] [CrossRef]
- Khalifa, H.A. On two-stage fuzzy random programming for water resources management. Afr. J. Math. Comput. Sci. Res. 2015, 8, 31–36. [Google Scholar] [CrossRef][Green Version]
- Lin, Q.G.; Huang, G.H.; Bass, B.; Qin, X.S. IFTEM: An interval-fuzzy two-stage stochastic optimization model for regional energy systems planning under uncertainty. Energy Policy 2009, 37, 868–878. [Google Scholar] [CrossRef]
- Liao, X.; Meng, C.; Ren, Z.; Zhao, W. Optimization of Ecological Water Supplement Scheme for Improved Suitable Habitat Area for Rare Migratory Birds in Nature Reserves Using Interval-Parameter Fuzzy Two-Stage Stochastic Programming Model. Int. J. Environ. Res. Public Health 2020, 17, 7562. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H. A two-stage mixed-integer fuzzy programming with interval-valued membership functions approach for flood-diversion planning. J. Environ. Manag. 2013, 117, 208–218. [Google Scholar] [CrossRef]
- Khosrojerdi, T.; Moosavirad, S.H.; Ariafar, S.; Ghaeini-Hessaroeyeh, M. Optimal Allocation of Water Resources Using a Two-Stage Stochastic Programming Method with Interval and Fuzzy Parameters. Nat. Resour. Res. 2018, 28, 1107–1124. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H. Interactive two-stage stochastic fuzzy programming for water resources management. J. Environ. Manag. 2011, 92, 1986–1995. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Meng, C.; Cai, B.; Zhao, W. Interval-Parameter Two-Stage Stochastic Programming (IPTSP) Model of Ecological Water Replenishment Scheme in the National Nature Reserve for Improved Suitable Habitat for Rare and Endangered Migrant Birds. Water 2020, 12, 1520. [Google Scholar] [CrossRef]
- Maleki, S.; Soffianian, A.R.; Koupaei, S.S.; Pourmanafi, S.; Saatchi, S. Wetland restoration prioritizing, a tool to reduce negative effects of drought; An application of multicriteria-spatial decision support system (MC-SDSS). Ecol. Eng. 2018, 112, 132–139. [Google Scholar] [CrossRef]
| Lake Bubble | Total Water Replenishment (×104 m3) | ||
|---|---|---|---|
| The Recommended Scheme for Project | IFTSP Model | Range of Variation | |
| Toudaogang Reservoir | 651.46 | [562.40, 667.49] | [−13.67%, 2.46%] |
| Boluo Lake | 5289.64 | [2483.99, 4934.56] | [−53.04%, −6.71%] |
| Mobopao | 768.72 | [603.81, 643.41] | [−21.45%, −16.30%] |
| Yuanbaowapao | 546.50 | [0.00, 138.90] | [−100.00%, −74.58%] |
| Aobaotupao | 1211.64 | [1089.66, 1798.29] | [−10.07%, 48.42%] |
| Name of Lake Bubble | Total Water Replenishment (×104 m3) | ||
|---|---|---|---|
| ITSP Model | IFTSP Model | Reduced Scale of Decision Space | |
| Toudaogang Reservoir | [562.40, 692.94] | [562.40, 667.49] | 19.50% |
| Boluo Lake | [697.50, 6476.21] | [2483.99, 4934.56] | 57.59% |
| Mobopao | [41.60, 698.60] | [603.81, 643.41] | 93.97% |
| Yuanbaowapao | [0.00, 138.90] | [0.00, 138.90] | 0.00% |
| Aobaotupao | [234.40, 1798.29] | [1089.66, 1798.29] | 54.69% |
| Lake Bubble | Flood Diversion Volume (×104 m3) | |||
|---|---|---|---|---|
| The Recommended Scheme for Project | IFTSP Model | |||
| h = 1 | h = 2 | h = 3 | ||
| Toudaogang Reservoir | 0.00 | [270.36, 335.63] | [84.54, 177.12] | [84.54, 177.12] |
| Boluo Lake | 621.00 | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] |
| Mobopao | 295.00 | [269.40, 307.21] | [269.40, 478.80] | [12.60, 12.60] |
| Yuanbaowapao | 2.00 | [206.55, 289.80] | [56.70, 289.80] | [56.70, 56.70] |
| Aobaotupao | 14.00 | [227.37, 556.39] | [227.37, 556.39] | [227.37, 556.39] |
| Total | 932.00 | [973.68, 1489.03] | [638.01, 1502.11] | [381.21, 802.81] |
| Lake Bubble | The Recommended Scheme for Project | ITSP Model | IFTSP Model | ||||
|---|---|---|---|---|---|---|---|
| h = 1 | h = 2 | h = 3 | h = 1 | h = 2 | h = 3 | ||
| Toudaogang Reservoir | 0.00 | [0.00, 335.63] | [0.00, 335.63] | [0.00, 335.63] | [270.36, 335.63] | [84.54, 177.12] | [84.54, 177.12] |
| Boluo Lake | 621.00 | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] |
| Mobopao | 295.00 | [0.00, 431.10] | [0.00, 478.80] | [0.00, 12.60] | [269.40, 307.21] | [269.40, 478.80] | [12.60, 12.60] |
| Yuanbaowapao | 2.00 | [0.00, 289.80] | [0.00, 289.80] | [0.00, 56.70] | [206.55, 289.80] | [56.70, 289.80] | [56.70, 56.70] |
| Aobaotupao | 14.00 | [0.00, 910.70] | [0.00, 910.70] | [0.00, 910.70] | [227.37, 556.39] | [227.37, 556.39] | [227.37, 556.39] |
| Total | 932.00 | [0.00, 1967.23] | [0.00, 2014.93] | [0.00, 1315.63] | [973.68, 1489.03] | [638.01, 1502.11] | [381.21, 802.81] |
| Lake Bubble | Functional Area | Area of Functional Areas (×104 hm2) | ||
|---|---|---|---|---|
| Original Scheme | The Recommended Scheme for Project | IFTSP Model | ||
| Toudaogang Reservoir | Fish pond | [0.03, 0.05] | 0.40 | [0.00, 0.72] |
| Crab pond | [0.00, 0.00] | 0.00 | [0.00, 0.00] | |
| Reed wetland | [0.06, 0.12] | 1.00 | [0.00, 0.96] | |
| Marsh wetland | [0.02, 0.04] | 0.34 | [0.00, 0.33] | |
| Boluo Lake | Fish pond | [0.69, 1.30] | 10.84 | [6.62, 6.96] |
| Crab pond | [0.00, 0.00] | 0.00 | [0.00, 0.44] | |
| Reed wetland | [0.26, 0.48] | 4.00 | [3.65, 3.84] | |
| Marsh wetland | [0.13, 0.24] | 2.00 | [1.92, 2.11] | |
| Mobopao | Fish pond | [0.07, 0.13] | 0.00 | [0.77, 1.04] |
| Crab pond | [0.00, 0.00] | 1.07 | [0.00, 0.00] | |
| Reed wetland | [0.03, 0.06] | 0.50 | [0.00, 0.48] | |
| Marsh wetland | [0.06, 0.12] | 1.00 | [0.00, 0.96] | |
| Yuanbaowapao | Fish pond | [0.00, 0.00] | 0.00 | [0.00, 0.00] |
| Crab pond | [0.00, 0.00] | 0.00 | [0.00, 1.37] | |
| Reed wetland | [0.01, 0.01] | 0.10 | [0.00, 0.10] | |
| Marsh wetland | [0.03, 0.06] | 0.50 | [0.48, 0.66] | |
| Aobaotupao | Fish pond | [0.00, 0.00] | 0.00 | [0.00, 0.00] |
| Crab pond | [0.20, 0.37] | 3.05 | [0.00, 2.14] | |
| Reed wetland | [0.03, 0.06] | 0.50 | [0.00, 0.48] | |
| Marsh wetland | [0.05, 0.09] | 0.76 | [0.00, 0.73] | |
| Lake Bubble | Functional Area | Area of Functional Areas (×104 hm2) | ||
|---|---|---|---|---|
| ITSP Model | IFTSP Model | Range of Variation | ||
| Toudaogang Reservoir | Fish pond | [0.72, 1.04] | [0.00, 0.72] | [−0.72, −0.32] |
| Crab pond | [0.00, 0.68] | [0.00, 0.00] | [0.00, −0.68] | |
| Reed wetland | [0.00, 0.96] | [0.00, 0.96] | [0.00, 0.00] | |
| Marsh wetland | [0.00, 0.33] | [0.00, 0.33] | [0.00, 0.00] | |
| Boluo Lake | Fish pond | [2.94, 8.00] | [6.62, 6.96] | [3.68, −1.04] |
| Crab pond | [0.00, 0.00] | [0.00, 0.44] | [0.00, 0.44] | |
| Reed wetland | [2.07, 3.84] | [3.65, 3.84] | [1.58, 0.00] | |
| Marsh wetland | [1.92, 2.77] | [1.92, 2.11] | [0.00, −0.66] | |
| Mobopao | Fish pond | [0.00, 0.71] | [0.77, 1.04] | [0.77, 0.33] |
| Crab pond | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] | |
| Reed wetland | [0.00, 0.48] | [0.00, 0.48] | [0.00, 0.00] | |
| Marsh wetland | [0.00, 0.96] | [0.00, 0.96] | [0.00, 0.00] | |
| Yuanbaowapao | Fish pond | [0.00, 0.00] | [0.00, 0.00] | [0.00, 0.00] |
| Crab pond | [0.00, 1.14] | [0.00, 1.37] | [0.00, 0.23] | |
| Reed wetland | [0.00, 0.10] | [0.00, 0.10] | [0.00, 0.00] | |
| Marsh wetland | [0.00, 0.48] | [0.48, 0.66] | [0.48, 0.18] | |
| Aobaotupao | Fish pond | [0.00, 2.68] | [0.00, 0.00] | [0.00, −2.68] |
| Crab pond | [0.00, 2.14] | [0.00, 2.14] | [0.00, 0.00] | |
| Reed wetland | [0.48, 1.58] | [0.00, 0.48] | [−0.48, −1.10] | |
| Marsh wetland | [0.00, 0.73] | [0.00, 0.73] | [0.00, 0.00] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; He, W.; Li, Y. Optimization of Ecological Water Replenishment Scheme Based on the Interval Fuzzy Two-Stage Stochastic Programming Method: Boluo Lake National Nature Reserve, Jilin Province, China. Int. J. Environ. Res. Public Health 2022, 19, 5218. https://doi.org/10.3390/ijerph19095218
Yang H, He W, Li Y. Optimization of Ecological Water Replenishment Scheme Based on the Interval Fuzzy Two-Stage Stochastic Programming Method: Boluo Lake National Nature Reserve, Jilin Province, China. International Journal of Environmental Research and Public Health. 2022; 19(9):5218. https://doi.org/10.3390/ijerph19095218
Chicago/Turabian StyleYang, Hao, Wei He, and Yu Li. 2022. "Optimization of Ecological Water Replenishment Scheme Based on the Interval Fuzzy Two-Stage Stochastic Programming Method: Boluo Lake National Nature Reserve, Jilin Province, China" International Journal of Environmental Research and Public Health 19, no. 9: 5218. https://doi.org/10.3390/ijerph19095218
APA StyleYang, H., He, W., & Li, Y. (2022). Optimization of Ecological Water Replenishment Scheme Based on the Interval Fuzzy Two-Stage Stochastic Programming Method: Boluo Lake National Nature Reserve, Jilin Province, China. International Journal of Environmental Research and Public Health, 19(9), 5218. https://doi.org/10.3390/ijerph19095218







