1. Introduction
Pillars are important structural elements in rock and coal underground mining since they can provide temporary or permanent support for tunneling and mining work [
1,
2,
3]. To maximize the extraction rate of mineral resources, dimensions (width and height) of underground pillars must be confined to a certain range, which should still assure stability and safe working conditions throughout the entire life of such projects [
4]. Unstable pillars can result in rock cracking, causing roof collapse, and they could even trigger rock bursts when large amounts of accumulated elastic energy are released [
3,
5]. Increases of mining depth can lead to more frequent pillar instability and failure events; it is therefore expected that new design challenges must be addressed so that new methods to assess rock pillar stability be discussed and developed.
The most common parameter in pillar design and stability estimation is the factor of safety (
FoS), which can be calculated as the ratio of pillar strength to applied pillar stress. Two main methods —the tributary area theory, and numerical simulations—are often employed for pillar stress calculation [
3,
6]; whereas several empirical methods have been developed for pillar strength estimation, as listed in
Table 1. Three basic ‘effects’ related with the ratio of pillar height to width—the linear shape effect, size effect, and power shape effect—were summarized by Lunder [
6]; similarly, Lunder [
6] worked out an empirical equation to assess pillar strength, considering confined and unconfined strength and different ratios of pillar height to width. Similarly, Ahmad and Al-Shayea et al. [
7] proposed new coal pillar strength formulae that consider the interface friction between the roof/floor and pillar, which also have a linear and power shape effect.
Theoretically, a rock or coal pillar is predicted as ‘stable’ when the value of
FoS is greater than 1; otherwise, it is considered ‘unstable’. However, such crisp boundaries are often unreliable, as unstable pillars often occurs when the
FoS value is above 1 (Lunder [
6]), and uncertainties in the ‘capacity’ (strength or resisting force) and ‘demand’ (stress or disturbing force) of a pillar lead to the
FoS being described as a statistical distribution.
Numerical simulation has also been employed to evaluate pillar stability. For instance, York [
15] and Mortazavi and Hassani et al. [
16] employed FLAC
2D to estimate the stability of deep-level pillars considering pillar deformations under natural loading conditions. Li and Li et al. [
17] employed FLAC
3D to obtain the minimum required thickness of crown pillars under sea water pressure; and Martin and Maybee [
18] conducted two-dimensional finite element analyses using Hoek-Brown parameters for pillar strength. Similarly, the finite element method and the discrete fracture network (DFN) approach were integrated by Deng and Yue et al. [
19] and Elmo and Stead [
20] to study the failure of jointed pillars. However, although such numerical methods are powerful tools to model pillar behavior, they have limitations due to the complexity of the models involved and the need for specific calibration.
Many machine learning algorithms have been applied to predict pillar stability. For instance, Tawadrous and Katsabanis [
21] employed Artificial Neural Networks (ANN). Recio-Gordo and Jimenez [
22] presented a probabilistic model based on the theory of linear classifiers that can be used to make probabilistic predictions of pillar behavior in longwall and retreat room and pillar mining. Zhou and Li et al. [
2] employed Fisher Discriminant Analysis (FDA) and Support Vector Machines (SVM), whereas Wattimena and Kramadibrata et al. [
23] and Wattimena [
4] applied logistic regression algorithms. Ghasemi and Ataei et al. [
24] and Ghasemi and Ataei et al. [
25] developed logistic regression and fuzzy logic algorithms in room-and-pillar coal mines. Zhou and Li et al. [
3] employed six machine learning algorithms to evaluate the stability of a rock pillar, and Ghasemi and Kalhori et al. [
26] compared Decision Tree (J48) and SVM algorithms for hard rock pillar stability assessment. Mohanto and Deb [
27] developed a plastic damage index for assessing rib pillar stability in underground metal mines using multi-variate regression and artificial neural network techniques. Ahmad and Al-Shayea et al. [
7] employed random trees and C4.5 decision trees for underground pillar prediction, and Liang and Luo et al. [
28] used new GBDT, XGBoost, and LightGBM algorithms. Dai and Shan et al. [
29] studied an intelligent identification method for coal pillar stability in a fully mechanized caving face of thick coal seams. With a combination of finite difference methods, neural networks, and Monte Carlo simulation techniques, Li and Zhou et al. [
30] studied underground mine hard rock pillar stability.
However, despite their reliable and accurate results, most algorithms are not easily applicable in practice due to their complex training and modeling procedures, and to their ‘black box’ features. The model tree algorithm—which jointly uses decision trees and linear regression methods–was proposed by Quinlan [
31] to overcome such limitations. This algorithm has been successfully applied to numerous geotechnical problems, such as UCS and Young’s Modulus estimation [
32] and hydraulic conductivity [
33]. However, one of the key obstacles to using tree algorithms for pillar stability evaluation is that outcomes should be discrete values such as ‘stable’, ‘unstable’ or ‘failed’. Therefore, those discrete targets must be transformed into continuous values, so that they can be trained using a model tree algorithm for regression analysis.
We propose a Logistic Model Trees (LMT) method [
34] to predict rock and coal pillar stability. This algorithm has the advantage of dealing with the classification problem by jointly using a tree model and a logistic regression algorithm, making it a rational choice in classification and decision-making. One main application of the LMT in geotechnical engineering has been landslide susceptibility prediction [
35,
36,
37], but it has not yet been applied to predict underground pillar stability.
The flowchart of this research is shown in
Figure 1. The rest of this paper is organized as follows.
Section 2 discusses two databases employed in this research, and the selection of input parameters. The LMT method is briefly introduced in
Section 3.
Section 4 discusses the performance and validation of proposed models, and risk and feature importance analyses.
2. Database Description
We compiled two databases that include recorded rock and coal pillar stability events from different types of underground mines. Database A was developed using observations collected by Lunder [
6]. It includes 178 case histories (60 stable, 50 unstable, and 68 failed cases) that came from six hard rock mines in Canada, South Africa, and Sweden. Five main parameters—pillar width,
w; pillar height,
h; ratio of pillar width to height,
r; uniaxial compressive strength of rock, UCS; and average pillar stress,
p—that could affect rock pillar stability were selected and analyzed.
Similarly, Database B was developed based on Van der Merwe [
38] and Van der Merwe [
39], who provided information on 351 case histories of coal pillars (including 274 stable pillars and 77 failed cases) in South African coal mines. It originally contains four parameters related to coal pillar stability analyses —underground depth, H; pillar width,
w; pillar height (mining height),
h; bord width, B—so the ratio of pillar width to height (
r) has been computed to be employed as a parameter in this database.
Although there are other features that could affect the rock and coal pillar stability, such as the geology structure conditions, water and gas contents, other stresses, and fracture information from CT or SEM images [
14,
40,
41,
42], that information is not available for the current pillar stability analysis. Since our models are trained using a limited number of data points are empirical methods, it is expected that their predictions are improved when a more extensive data set and/or more features are employed. Thus, a better calibration of model parameters, and more elaborate models could be established.
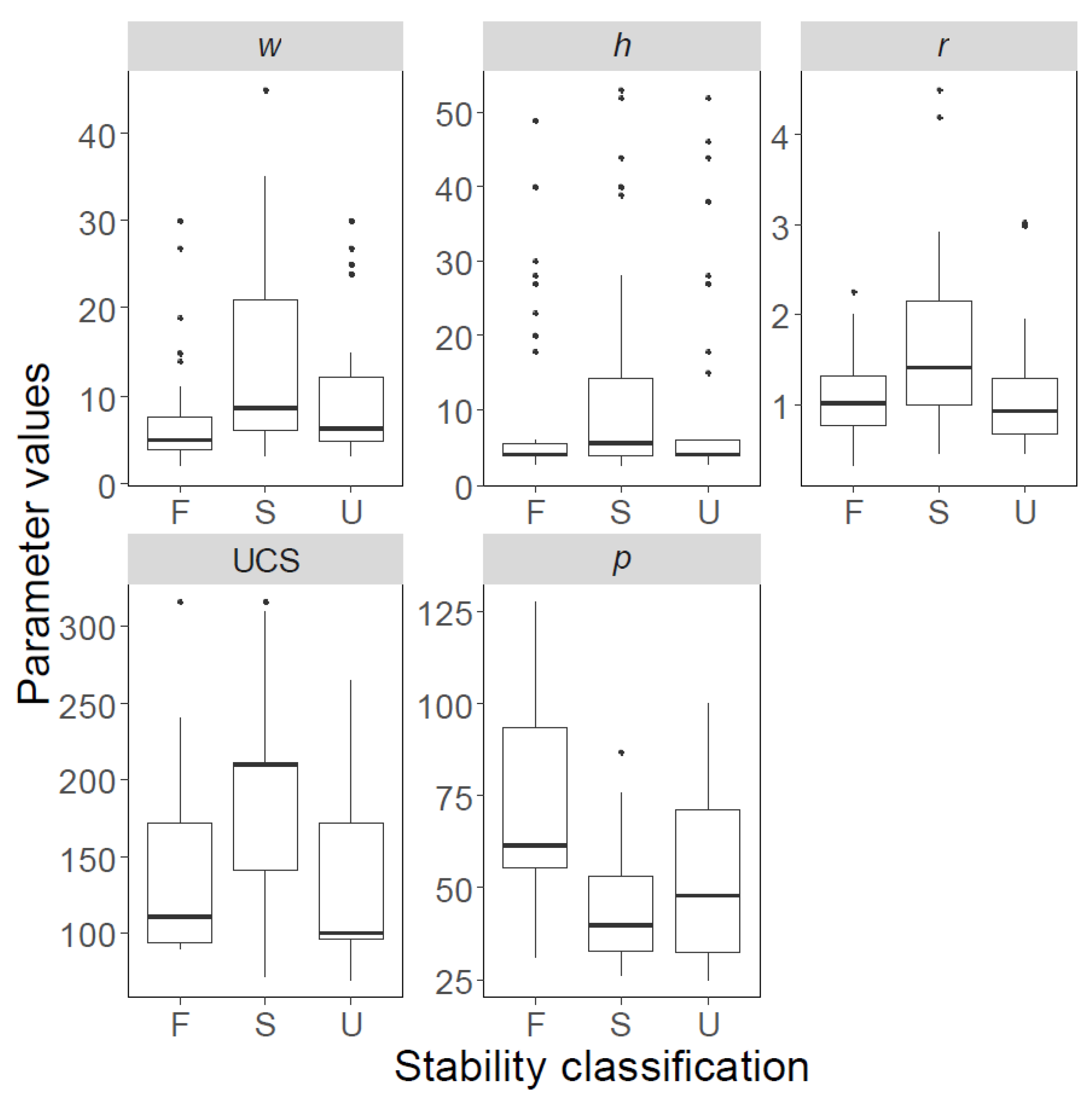
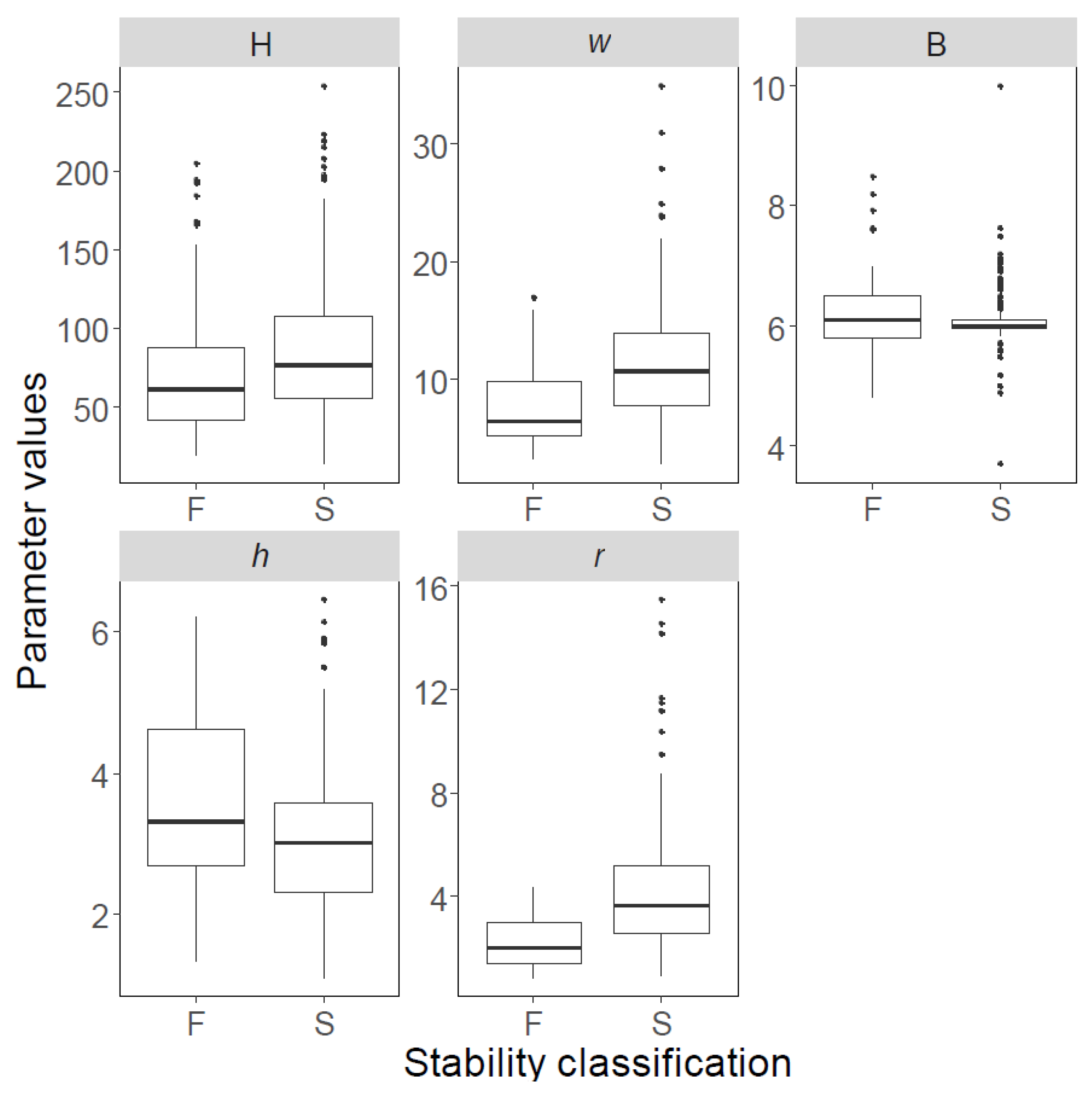
The boxplots of both databases are shown in
Figure 2;
Figure 3, and their statistical features are listed in
Table 2;
Table 3; solid black spots in
Figure 2;
Figure 3 denote “outliers”. The first and third quartiles are indicated using horizontal lines at the bottom and top of the boxes, whereas the bold lines inside the boxes represent median values. Similarly, pillars with ‘failed’, ‘stable’, and ‘unstable’ conditions are shown separately, and labelled using F, S, and U, respectively.
Based on the review and analysis of common techniques to estimate pillar stability using FoS, two categories of parameters were employed in our analyses. One category is the “strength” related parameters: pillar width, w; pillar height or mining height, h; ratio of pillar width to height, r; and uniaxial compressive strength of rock, UCS. The other category includes parameters related to the applied “stress,” including average pillar stress, p; underground depth, H; and bord width, B. With the availability of parameters for the two databases, Models 1 (w, h, r, UCS and p) and 2 (w, h, H, B and r) were established. The detailed analyses of these parameters are discussed in the following subsections.
2.1. Strength-Related Parameters
Pillar width
w and pillar height
h are two key geometrical parameters for stability analysis. The empirical approaches (linear, power, or shape forms) in
Table 1 all included
w,
h, and
r for pillar strength calculation. Zhou and Li et al. [
2] employed
w,
h,
r, and UCS as inputs for FDA and SVM models; Wattimena and Kramadibrata et al. [
23] and Wattimena [
4] used
r as one of the parameters for regression analysis. Moreover, pillar shape, as represented by the
r parameter, could have an influence on increased strength [
3]. Therefore, we consider pillar width
w, pillar height
h, the ratio
r, and UCS as “strength”-related parameters for Model 1. As Database B does not include UCS values, only
w,
h, and
r are employed for Model 2.
2.2. Stress-Related Parameters
The actual stress acting on a pillar may depend on multiple factors such as in situ stresses, mining induced stress changes, geological features, shape and orientation of pillars, spatial relationship between pillars and mine openings, and groundwater conditions [
6]. The tributary area theory introduced by Bunting [
43] calculates the average stress acting on a pillar by simply supposing that the pillar supports its “share” of applied load. Salamon and Munro [
11] proposed a more simplified equation:
where
γ is the unit weight of the rock mass, H is underground depth, B is bord width between pillars, and
w is pillar width.
For Model 1, the average stress has been calculated using the tributary area theory and two-dimensional or three-dimensional finite element modeling in the database, so that it can be directly applied for prediction. For Model 2, H, B, and w are employed to compute the stress condition for coal pillar stability.
Table 4 lists the selected parameters for each model, their corresponding data availability, and types. Theoretically, there may be additional indicators or parameters, such as geological condition, pillar orientation, or mining methods, that could have an influence on pillar stability; however, collecting these data is a major challenge and they have therefore not been employed in this work.
5. Conclusions
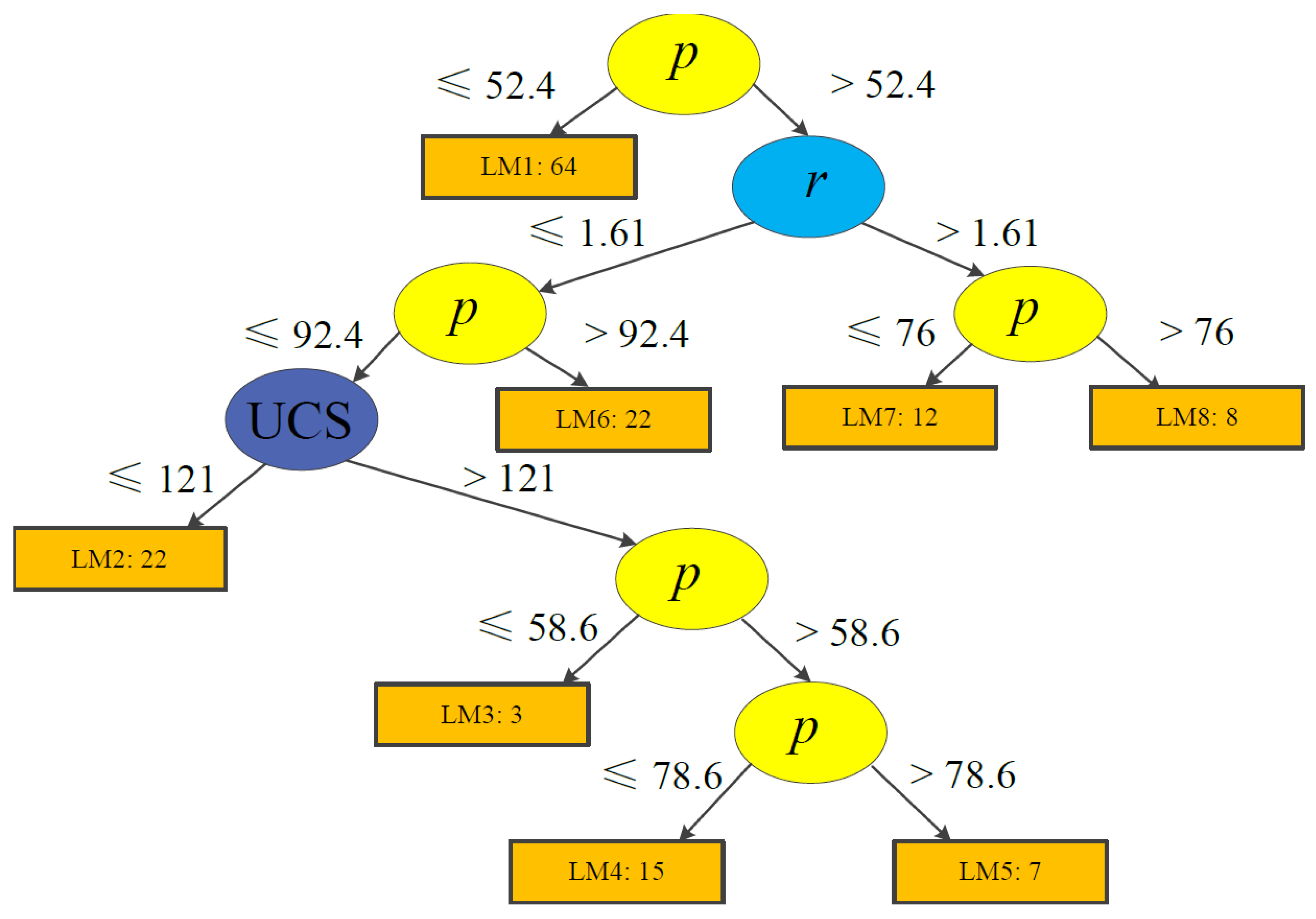
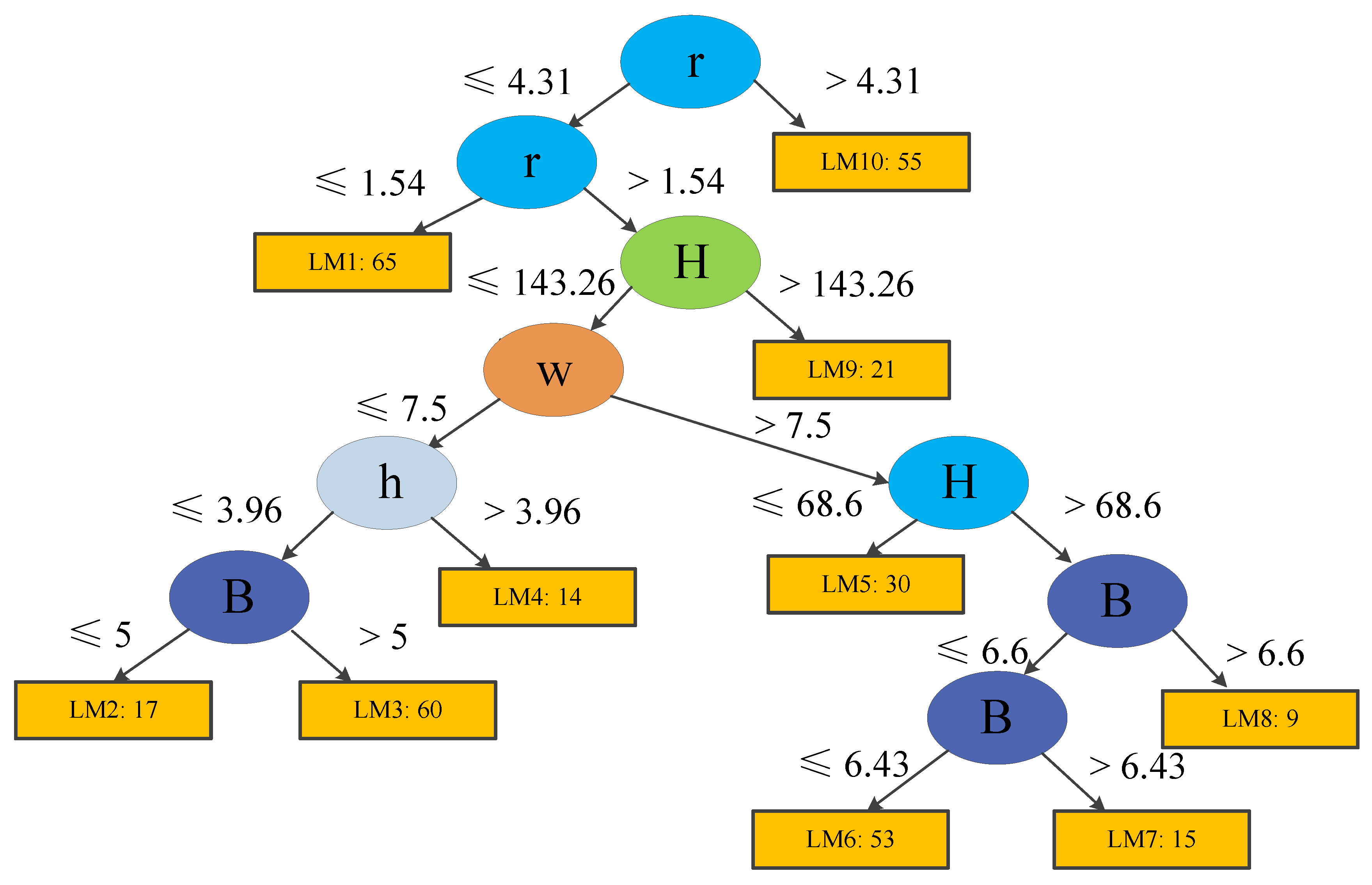
A novel application of Logistic Model Trees (LMT) for instability assessment of underground pillars is presented. Tree structures and the corresponding functions are employed to assess the stability of pillars, given information on several features—including pillar width, pillar height, ratio of pillar width to height, uniaxial compressive strength of rock, average pillar stress, underground depth, and bord width—based on which predictions are conducted. The LMT is learned by LogitBoost, using two sets of case histories from the databases that we compiled from the literature. Results show that both Models 1 and 2 can accurately predict the stability of rock and coal pillars.
The trained tree models were validated using the original databases and 10-fold cross-validation. In addition, nine and twelve new cases—not previously employed for training—were used to further validate the models proposed. Moreover, predictions of several other machine learning methods were also compared with our proposed models. Results showed that the accuracies of the proposed tree models are among the highest and that they are probably adequate for mine site applications. In addition, results suggest that the LMT technique can offer useful information about the probability of pillar failure during underground excavation, so it can be utilized for risk analyses of pillar stability.
Furthermore, feature importance analyses were conducted to appraise the most influential input features for pillar stability. The average pillar stress p was found as the most influential parameter for Model 1, with other factors such as r and UCS also having a critical influence on predictions. For Model 2, r showed the highest effect on the output, followed by H and w. It is expected that these results can lead mine engineers to focus their efforts towards those crucial identified factors.
As the dataset employed for LMT learning and training was limited, it is expected that its predictive capacity could be increased if more case histories are collected. In addition, there are a few minor influencing parameters such as pore-water pressure, gas and water contents of the rocks, etc., which are neglected in this study due to the unavailability of data, and could have been among the selected parameters. More importantly, the application of the proposed models should be within the range of selected parameters.
Finally, the main advantage of LMT compared to other related algorithms commonly employed for pillar stability estimation is that it can be trained easily (even with more input parameters) and that its tree structure, with a LR function in each leaf, explicitly demonstrates the relationship between the inputs and predictive outputs. In addition, it is expected that, with its intuitive features and easy implementation, the LMT can also be employed to solve other geotechnical problems in the future.