Multiple Time Series Fusion Based on LSTM: An Application to CAP A Phase Classification Using EEG
Abstract
:1. Introduction
- -
- Proposal of a novel method for information fusion based on a deep learning model responsible for extracting the features, performing the feature level fusion, and performing the classification. The optimization algorithm tuned the structure of the classifier. Hence, all the fusion and classification procedures were optimized and executed automatically by the deep learning model, which learned the relevant patterns directly from the data.
- -
- Independent evaluation of two optimization algorithms for finding the optimal structure of a deep learning classifier. Optimizing deep learning models is a well-known difficulty in machine learning since the simulations are usually slow. Therefore, there is a need to study suitable algorithms to haste this process.
- -
- Combined examination of subjects free from neurological disorders and subjects with a sleep-related disorder using information (i.e., the signal) from multiple EEG channels to assess the CAP A phases. The state-of-the-art standard is only to examine one channel for the analysis, which is contrary to the specification of the CAP protocol, where the examination should preferably be carried out over multiple channels [1].
- -
- Development of systems tolerant to noise (until a signal-to-noise ratio of 0 dB) and able to handle the loss of 66% of the information, i.e., loss of two channels.
2. Materials and Methods
| Algorithm 1 Pseudocode for the experimental procedure. |
 |
2.1. Studied Population
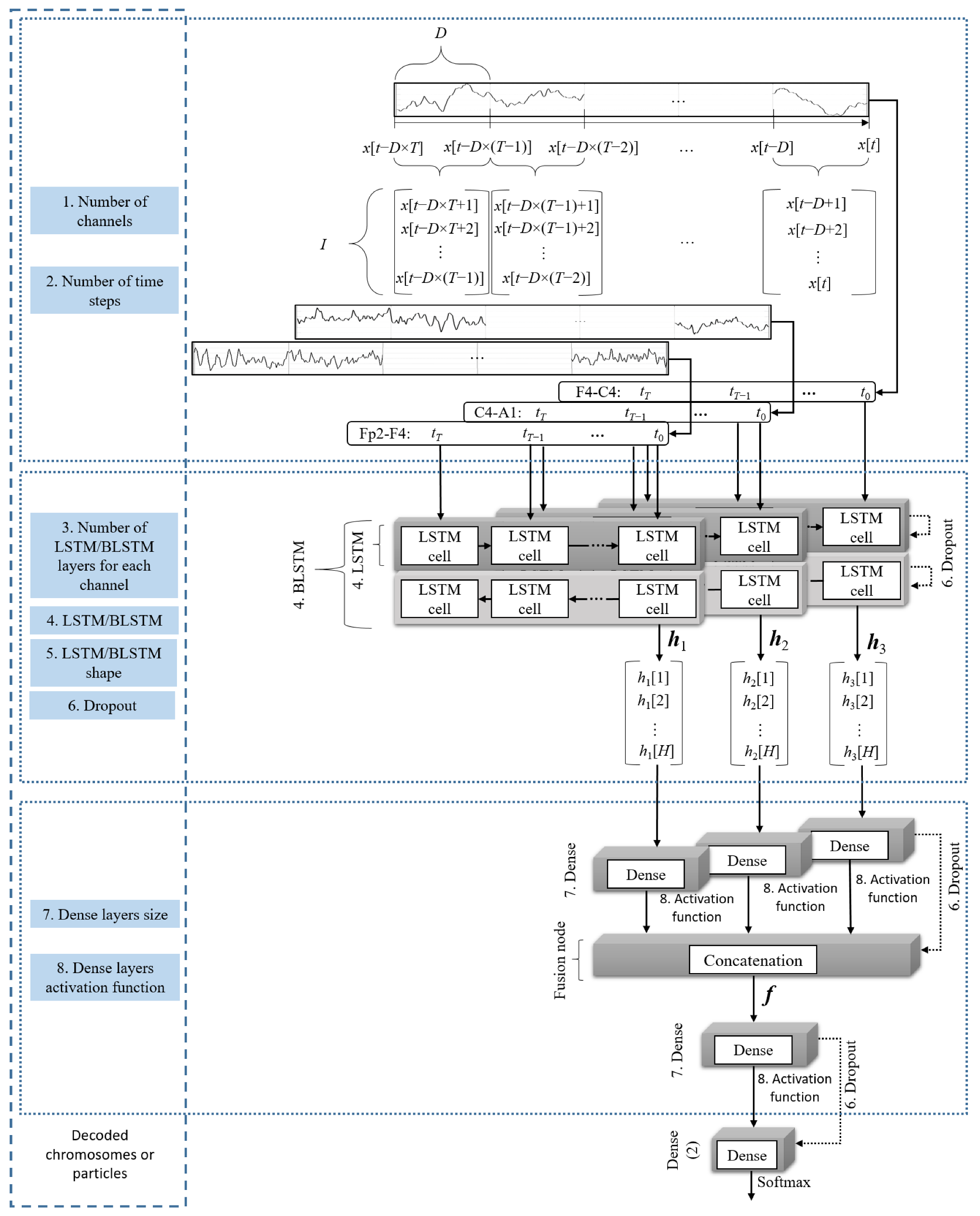
2.2. Classification and Channel Fusion
2.3. Optimization Procedure
2.3.1. Genetic Algorithm
2.3.2. Particle Swarm Optimization
2.4. Performance Metrics and Validation Methodology
2.5. Implementation
3. Experimental Results
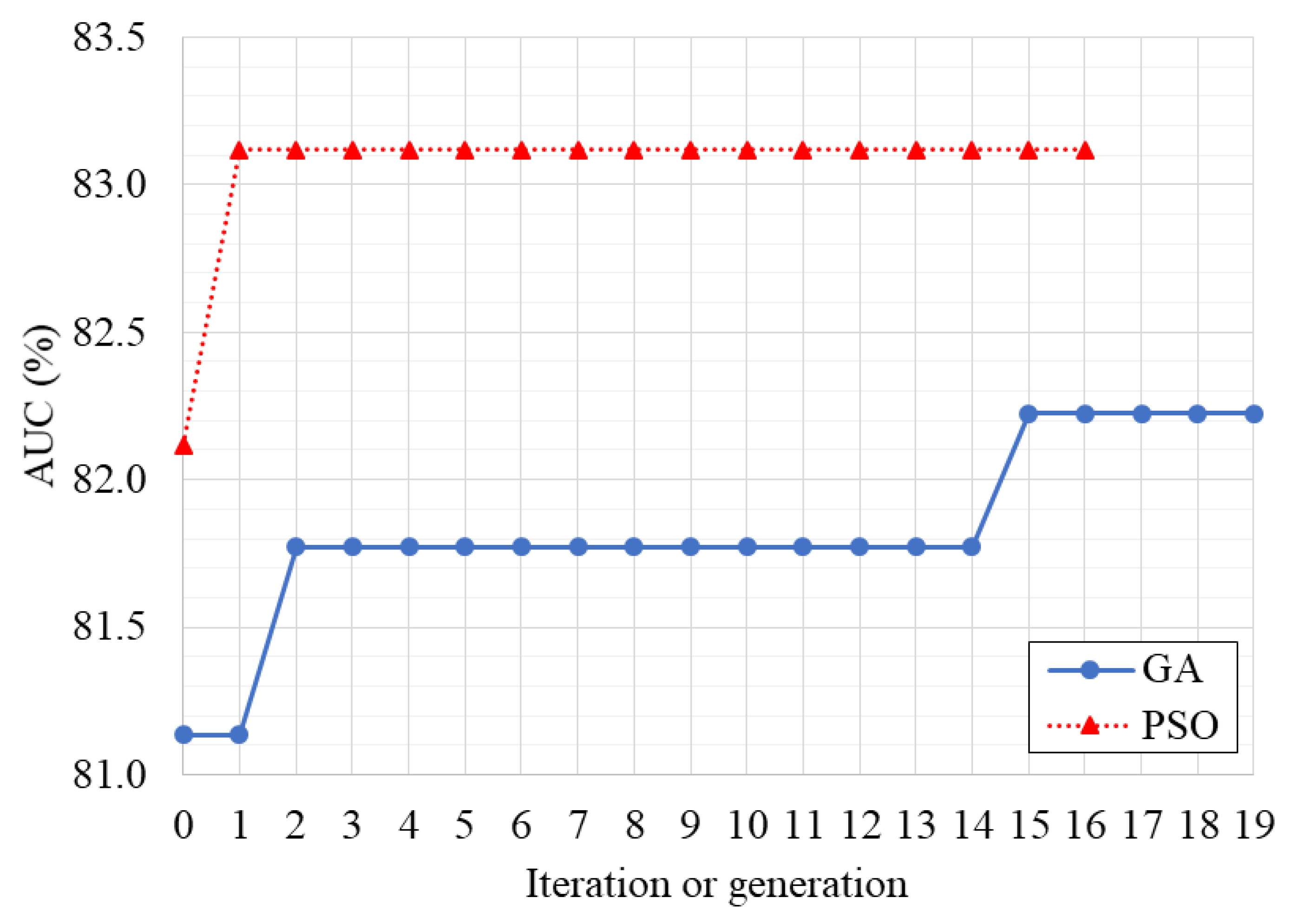
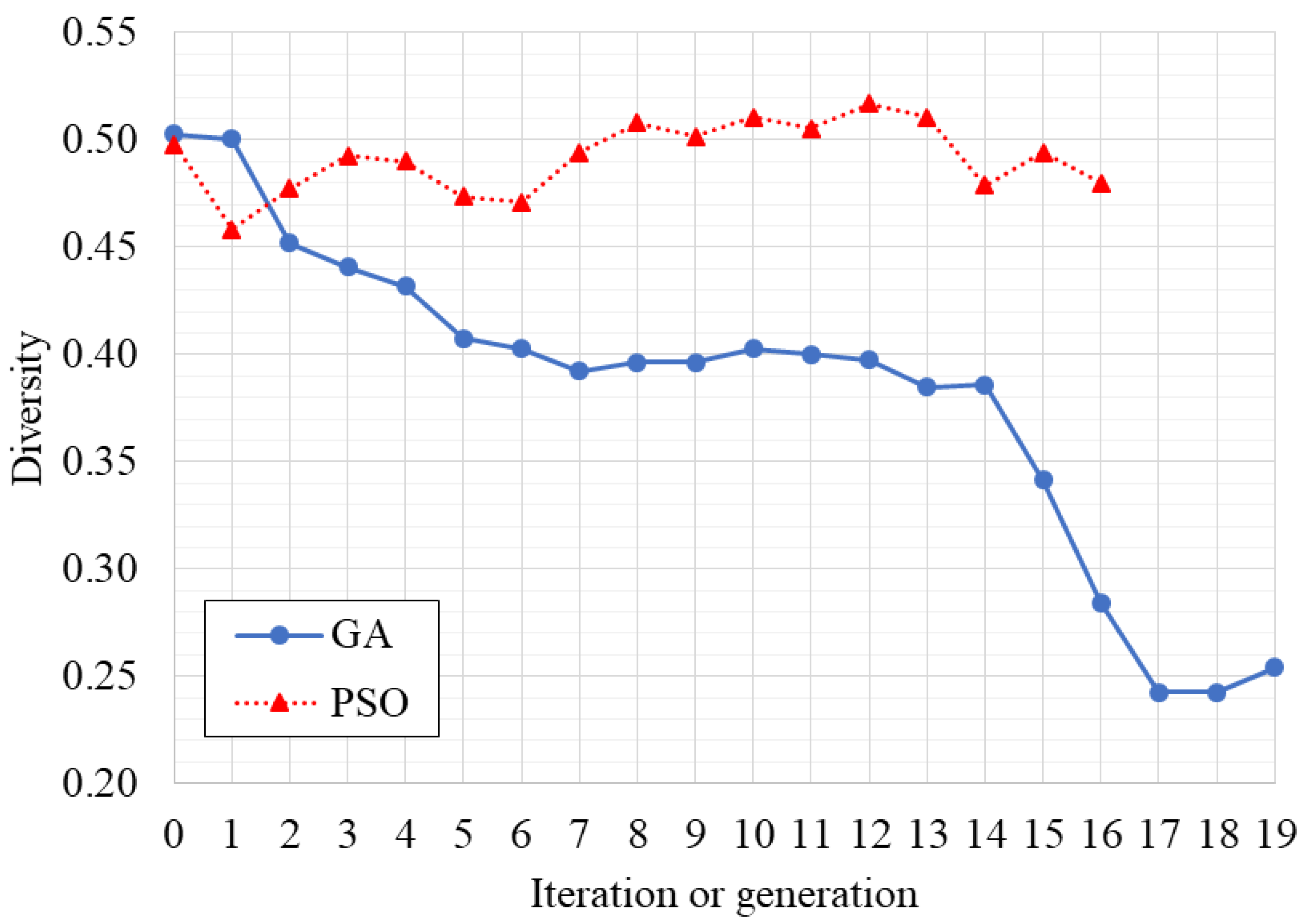
3.1. Optimization of the Classifier
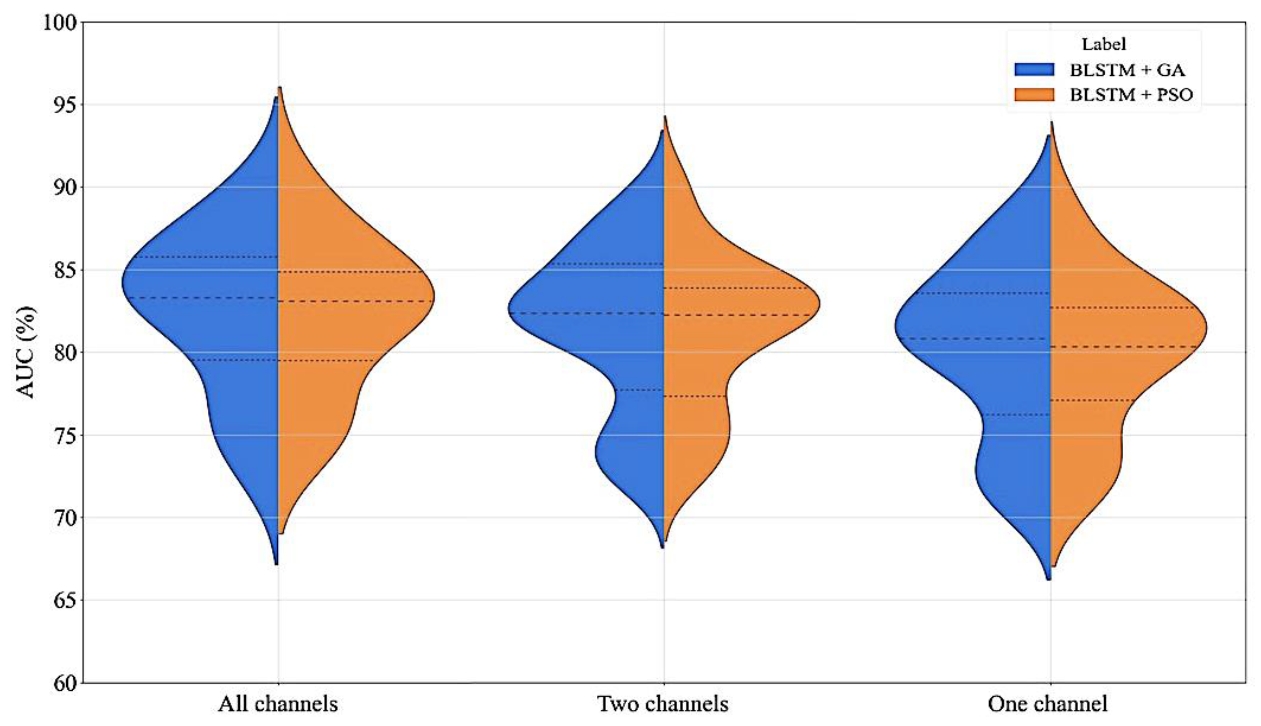
3.2. Performance Assessment
3.3. Robustness Evaluation
4. Discussion
| Work | Population (Subjects) | Examined Channel | Acc (%) | Sen (%) | Spe (%) | Mean (%) |
|---|---|---|---|---|---|---|
| [66] | 15 FND | C4–A1 or C3–A2 | 70 | 51 | 81 | 67 |
| [61] | 8 FND | C4–A1 or C3–A2 | 72 | 52 | 76 | 67 |
| [64] | 6 FND | C4–A1 or C3–A2 | 81 | 76 | 81 | 79 |
| [54] | 12 FND * | - | 81 | 78 | 85 | 81 |
| [67] | 4 FND | C4–A1 or C3–A2 | 82 | 76 | 83 | 80 |
| [68] | 15 FND | C4–A1 or C3–A2 | 83 | 76 | 84 | 81 |
| [65] | 10 FND | F4–C4 | 84 | - | - | - |
| [29] | 4 FND | F4–C4 | 84 | 74 | 86 | 81 |
| [62] | 8 FND | C4–A1 or C3–A2 | 85 | 73 | 87 | 82 |
| [69] | 16 FND | C4–A1 or C3–A2 | 86 | 67 | 90 | 81 |
| [70] | 9 FND + 5 SDP | C4–A1 or C3–A2 | 67 | 55 | 69 | 64 |
| [60] | 27 SDP | C4–A1 and F4–C4 | 73 | - | - | - |
| [63] | 9 FND + 5 SDP | C4–A1 or C3–A2 | 75 | 78 | 74 | 76 |
| [31] | 15 FND + 4 SDP | C4–A1 or C3–A2 | 76 | 75 | 77 | 76 |
| Proposed BLSTM + GA | 8 FND +8 SDP | Fp2–F4, F4–C4, and C4–A1 | 77 | 73 | 77 | 76 |
| Proposed BLSTM + PSO | 8 FND +8 SDP | Fp2–F4, F4–C4, and C4–A1 | 79 | 68 | 81 | 76 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1. Pseudocode for the GA variant used in this work. |
 |
| Algorithm A2. Pseudocode for the PSO algorithm variant used in this work. |
 |
Appendix B
| Number | Locus | Description | Specification |
|---|---|---|---|
| 1 | 0–2 | Number of channels to be fused | 000: Fp2–F4 001: C4–A1 010: F4–C4 011: Fp2–F4 and C4–A1 100: Fp2–F4 and F4–C4 101: F4–C4 and C4–A1 110 or 111: Fp2–F4, F4–C4, and C4–A1 |
| 2 | 3–4 | Number of time steps to be considered by the LSTM | 00: 10 01: 15 10: 20 11: 25 |
| 3 | 5 | Number of LSTM layers for each channel | 0: One 1: Two staked |
| 4 | 6 | Type of LSTM | 0: LSTM 1: BLSTM |
| 5 | 7–8 | Shape of the LSTM layers | 00: 100 01: 200 10: 300 11: 400 |
| 6 | 9–10 | Percentage of dropout for the recurrent and dense layers | 00: 0 01: 5% 10: 10% 11: 15% |
| 7 | 11–12 | Size of the dense layers | 00: 0 01: 200 10: 300 11: 400 |
| 8 | 13–14 | Activation function for the dense layers | 00: tanh 01: Sigmoid 10: ReLU 11: SELU |
References
- Terzano, M.; Parrino, L.; Sherieri, A.; Chervin, R.; Chokroverty, S.; Guilleminault, C.; Hirshkowitz, M.; Mahowald, M.; Moldofsky, H.; Rosa, A.; et al. Atlas, Rules, and Recording Techniques for the Scoring of Cyclic Alternating Pattern (CAP) in Human Sleep. Sleep Med. 2001, 2, 537–553. [Google Scholar] [CrossRef]
- Terzano, M.; Parrino, L. Chapter 8 The Cyclic Alternating Pattern (CAP) in Human Sleep. In Handbook of Clinical Neurophysiology; Elsevier: Amsterdam, The Netherlands, 2005; Volume 6, pp. 79–93. [Google Scholar]
- Terzano, M.; Mancia, D.; Salati, M.; Costani, G.; Decembrino, A.; Parrino, L. The Cyclic Alternating Pattern as a Physiologic Component of Normal NREM Sleep. Sleep 1985, 8, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Halász, P.; Terzano, M.; Parrino, L.; Bódizs, R. The Nature of Arousal in Sleep. J. Sleep Res. 2004, 13, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Parrino, L.; Milioli, G.; Melpignano, A.; Trippi, I. The Cyclic Alternating Pattern and the Brain-Body-Coupling During Sleep. Epileptologie 2016, 33, 150–160. [Google Scholar]
- Parrino, L.; Ferrillo, F.; Smerieri, A.; Spaggiari, M.; Palomba, V.; Rossi, M.; Terzano, M. Is Insomnia a Neurophysiological Disorder? The Role of Sleep EEG Microstructure. Brain Res. Bull. 2004, 63, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Parrino, L.; Paolis, F.; Milioli, G.; Gioi, G.; Grassi, A.; Riccardi, S.; Colizzi, E.; Terzano, M. Distinctive Polysomnographic Traits in Nocturnal Frontal Lobe Epilepsy. Epilepsia 2012, 53, 1178–1184. [Google Scholar] [CrossRef] [PubMed]
- Terzano, M.; Parrino, L.; Boselli, M.; Spaggiari, M.; Di Giovanni, G. Polysomnographic Analysis of Arousal Responses in Obstructive Sleep Apnea Syndrome by Means of the Cyclic Alternating Pattern. J. Clin. Neurophysiol. 1996, 13, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Parrino, L.; Boselli, M.; Buccino, P.; Spaggiari, M.; Giovanni, G.; Terzano, M. The Cyclic Alternating Pattern Plays a Gate-Control on Periodic Limb Movements during Non-Rapid Eye Movement Sleep. J. Clin. Neurophysiol. 1996, 13, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Halász, P.; Terzano, M.; Parrino, L. Décharges de Pointes-Ondes et Microstructure Du Continuum Veille-Sommeil Dans l’épilepsie Généralisée Idiopathique. Neurophysiol. Clin. 2002, 32, 38–53. [Google Scholar] [CrossRef]
- Rundo, J.; Downey III, R. Chapter 25—Polysomnography. In Handbook of Clinical Neurology; Elsevier Science & Technology: Amsterdam, The Netherlands, 2019; Volume 160, pp. 381–392. [Google Scholar]
- Rosa, A.; Alves, G.; Brito, M.; Lopes, M.; Tufik, S. Visual and Automatic Cyclic Alternating Pattern (CAP) Scoring: Inter-Rater Reliability Study. Arq. Neuro-Psiquiatr. 2006, 64, 578–581. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.; Razavi, S. Multisensor Data Fusion: A Review of the State-of-the-Art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Sun, S.; Lin, H.; Ma, J.; Li, X. Multi-Sensor Distributed Fusion Estimation with Applications in Networked Systems: A Review Paper. Inf. Fusion 2017, 38, 122–134. [Google Scholar] [CrossRef]
- Fung, M.; Chen, M.; Chen, Y. Sensor Fusion: A Review of Methods and Applications. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar]
- Gravina, R.; Alinia, P.; Ghasemzadeh, H.; Fortino, G. Multi-Sensor Fusion in Body Sensor Networks: State-of-the-Art and Research Challenges. Inf. Fusion 2017, 35, 68–80. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. Cyclic Alternating Pattern Estimation Based on a Probabilistic Model over an EEG Signal. Biomed. Signal Process. Control 2020, 62, 102063. [Google Scholar] [CrossRef]
- Ravan, M.; Begnaud, J. Investigating the Effect of Short Term Responsive VNS Therapy on Sleep Quality Using Automatic Sleep Staging. IEEE Trans. Biomed. Eng. 2019, 66, 3301–3309. [Google Scholar] [CrossRef]
- Albelwi, S.; Mahmood, A. A Framework for Designing the Architectures of Deep Convolutional Neural Networks. Entropy 2017, 9, 242. [Google Scholar] [CrossRef]
- Mostafa, S.; Mendonça, F.; Ravelo-Garcia, A.; Juliá-Serdá, G.; Morgado-Dias, F. Multi-Objective Hyperparameter Optimization of Convolutional Neural Network for Obstructive Sleep Apnea Detection. IEEE Access 2020, 8, 129586–129599. [Google Scholar] [CrossRef]
- Chiong, R.; Weise, T.; Michalewicz, Z. Variants of Evolutionary Algorithms for Real-World Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Mostafa, S.; Horta, N.; Ravelo-García, A.; Morgado-Dias, F. Analog Active Filter Design Using a Multi Objective Genetic Algorithm. AEU—Int. J. Electron. Commun. 2018, 93, 83–94. [Google Scholar] [CrossRef]
- Tian, G.; Ren, Y.; Zhou, M. Dual-Objective Scheduling of Rescue Vehicles to Distinguish Forest Fires via Differential Evolution and Particle Swarm Optimization Combined Algorithm. IEEE Trans. Int. Transp. Syst. 2016, 17, 3009–3021. [Google Scholar] [CrossRef]
- Fu, Y.; Ding, M.; Zhou, C.; Hu, H. Route Planning for Unmanned Aerial Vehicle (UAV) on the Sea Using Hybrid Differential Evolution and Quantum-Behaved Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. 2013, 43, 1451–1465. [Google Scholar] [CrossRef]
- Senthilnath, J.; Kulkarni, S.; Benediktsson, J.A.; Yang, X. A Novel Approach for Multispectral Satellite Image Classification Based on the Bat Algorithm. IEEE Geosci. Remote Sens. Lett. 2016, 13, 599–603. [Google Scholar] [CrossRef]
- Gregor, M.; Krajčovič, M.; Hnát, J.; Hančinsky, V. Genetic Algorithms in the Design and Planning of Production System. In Proceedings of the 26th Daaam International Symposium on Intelligent Manufacturing and Automation, Zadar, Croatia, 21–24 October 2015. [Google Scholar]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, M.; Ivanov, P.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef] [PubMed]
- Mariani, S.; Grassi, A.; Mendez, M.; Parrino, L.; Terzano, M.; Bianchi, A. Automatic Detection of CAP on Central and Fronto-Central EEG Leads via Support Vector Machines. In Proceedings of the 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011. [Google Scholar]
- Cover, T. The Best Two Independent Measurements Are Not the Two Best. IEEE Trans. Syst. Man Cybern. 1974, 4, 116–117. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. A Portable Wireless Device for Cyclic Alternating Pattern Estimation from an EEG Monopolar Derivation. Entropy 2019, 21, 1203. [Google Scholar] [CrossRef]
- Gers, F.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Panda, S.; Padhy, N. Comparison of Particle Swarm Optimization and Genetic Algorithm for FACTS-Based Controller Design. Appl. Soft Comput. 2008, 8, 1418–1427. [Google Scholar] [CrossRef]
- Jennison, C.; Sheehan, N. Theoretical and Empirical Properties of the Genetic Algorithm as a Numerical Optimizer. J. Comput. Graph. Stat. 1995, 4, 296–318. [Google Scholar]
- Fang, Y.; Li, J. A Review of Tournament Selection in Genetic Programming. In Proceedings of the Advances in Computation and Intelligence—5th International Symposium, ISICA 2010, Wuhan, China, 22–24 October 2010. [Google Scholar]
- Hakimi, D.; Oyewola, D.; Yahaya, Y.; Bolarin, G. Comparative Analysis of Genetic Crossover Operators in Knapsack Problem. J. Appl. Sci. Environ. Manag. 2016, 20, 593–596. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.; Mernik, M. Exploration and Exploitation in Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A Discrete Binary Version of the Particle Swarm Algorithm. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A Modified Particle Swarm Optimizer. In Proceedings of the IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Kennedy, J.; Mendes, R. Population Structure and Particle Swarm Performance. In Proceedings of the IEEE Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; pp. 1671–1676. [Google Scholar]
- Bratton, D.; Kennedy, J. Defining a Standard for Particle Swarm Optimization. In Proceedings of the IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007; pp. 120–127. [Google Scholar]
- Sackett, D.; Haynes, R.; Guyatt, G.; Tugwell, P. Clinical Epidemiology: A Basic Science for Clinical Medicine, 2nd ed.; Lippincott Williams and Wilkins: Philadelphia, PA, USA, 1991. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Shamir, N.; Saad, D.; Marom, E. Preserving the Diversity of a Genetically E Volving Population of Nets U Sing the Functional Behavior of Neurons. Complex Syst. 1993, 7, 327–346. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the International Joint Conference on Articial Intelligence (IJCA), Stanford, QC, Canada, 20–25 August 1995. [Google Scholar]
- Digital Signal Processing Committee, I. Programs for Digital Signal Processing; IEEE Press: New York, NY, USA, 1979. [Google Scholar]
- Muralidharan, K. A Note on Transformation, Standardization and Normalization. IUP J. Oper. Manag. 2010, 9, 116–122. [Google Scholar]
- Hartmann, S.; Baumert, M. Automatic A-Phase Detection of Cyclic Alternating Patterns in Sleep Using Dynamic Temporal Information. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1695–1703. [Google Scholar] [CrossRef]
- Urigüen, J.; Zapirain, B. EEG Artifact Removal—State-of-the-Art and Guidelines. J. Neural Eng. 2015, 12, 031001. [Google Scholar] [CrossRef]
- Largo, R.; Munteanu, C.; Rosa, A. CAP Event Detection by Wavelets and GA Tuning. In Proceedings of the 2005 IEEE International Workshop on Intelligent Signal Processing, Faro, Portugal, 1–3 September 2005. [Google Scholar]
- Harrison, K.R.; Engelbrecht, A.P.; Ombuki-Berman, B.M. Optimal Parameter Regions and the Time-Dependence of Control Parameter Values for the Particle Swarm Optimization Algorithm. Swarm Evol. Comput. 2018, 41, 20–35. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 84–88. [Google Scholar]
- Xin, J.; Chen, G.; Hai, Y. A Particle Swarm Optimizer with Multi-Stage Linearly-Decreasing Inertia Weight. In Proceedings of the 2nd International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009; pp. 505–508. [Google Scholar]
- Kwon, M.; Han, S.; Kim, K.; Jun, S. Super-Resolution for Improving EEG Spatial Resolution Using Deep Convolutional Neural Network—Feasibility Study. Sensors 2019, 19, 5317. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, M.; Temko, A.; Bocchino, A.; O’Mahony, C.; Boylan, G.; Popovici, E. Analysis of a Low-Cost EEG Monitoring System and Dry Electrodes toward Clinical Use in the Neonatal ICU. Sensors 2019, 19, 2637. [Google Scholar] [CrossRef]
- Sharma, M.; Patel, V.; Tiwari, J.; Acharya, U. Automated Characterization of Cyclic Alternating Pattern Using Wavelet-Based Features and Ensemble Learning Techniques with EEG Signals. Diagnostics 2021, 11, 1380. [Google Scholar] [CrossRef]
- Mariani, S.; Manfredini, E.; Rosso, V.; Mendez, M.; Bianchi, A.; Matteucci, M.; Terzano, M.; Cerutti, S.; Parrino, L. Characterization of A Phases during the Cyclic Alternating Pattern of Sleep. Clin. Neurophysiol. 2011, 122, 2016–2024. [Google Scholar] [CrossRef] [PubMed]
- Mariani, S.; Manfredini, E.; Rosso, V.; Grassi, A.; Mendez, M.; Alba, A.; Matteucci, M.; Parrino, L.; Terzano, M.; Cerutti, S.; et al. Efficient Automatic Classifiers for the Detection of A Phases of the Cyclic Alternating Pattern in Sleep. Med. Biol. Eng. Comput. 2012, 50, 359–372. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, F.; Fred, A.; Mostafa, S.; Morgado-Dias, F.; Ravelo-García, A. Automatic Detection of a Phases for CAP Classification. In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM), Funchal, Portugal, 16–18 January 2018. [Google Scholar]
- Niknazar, H.; Seifpour, S.; Mikaili, M.; Nasrabadi, A.; Banaraki, A. A Novel Method to Detect the A Phases of Cyclic Alternating Pattern (CAP) Using Similarity Index. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015. [Google Scholar]
- Barcaro, U.; Bonanni, E.; Maestri, M.; Murri, L.; Parrino, L.; Terzano, M. A General Automatic Method for the Analysis of NREM Sleep Microstructure. Sleep Med. 2004, 5, 567–576. [Google Scholar] [CrossRef]
- Mendonça, F.; Mostafa, S.; Morgado-Dias, F.; Ravelo-Garcia, A. Cyclic Alternating Pattern Estimation from One EEG Monopolar Derivation Using a Long Short-Term Memory. In Proceedings of the 2019 International Conference in Engineering Applications (ICEA), Sao Miguel, Portugal, 8–11 July 2019. [Google Scholar]
- Mariani, S.; Bianchi, A.; Manfredini, E.; Rosso, V.; Mendez, M.; Parrino, L.; Matteucci, M.; Grassi, A.; Cerutti, S.; Terzano, M. Automatic Detection of A Phases of the Cyclic Alternating Pattern during Sleep. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010. [Google Scholar]
- Hartmann, S.; Baumert, M. Improved A-Phase Detection of Cyclic Alternating Pattern Using Deep Learning. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019. [Google Scholar]
- Mariani, S.; Grassi, A.; Mendez, M.; Milioli, G.; Parrino, L.; Terzano, M.; Bianchi, A. EEG Segmentation for Improving Automatic CAP Detection. Clin. Neurophysiol. 2013, 124, 1815–1823. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, S.; Mendonça, F.; Ravelo-García, A.; Morgado-Dias, F. Combination of Deep and Shallow Networks for Cyclic Alternating Patterns Detection. In Proceedings of the 2018 13th APCA International Conference on Automatic Control and Soft Computing (CONTROLO), Ponta Delgada, Portugal, 4–6 June 2018. [Google Scholar]


| Measure | Population (Subjects) | Mean | Standard Deviation | Range (Minimum–Maximum) | ||
|---|---|---|---|---|---|---|
| Age (years) | 8 FND | 32.25 | 5.85 | 23.00 | - | 41.00 |
| 8 SDP | 33.50 | 15.04 | 16.00 | - | 67.00 | |
| 8 FND + 8 SDP | 32.88 | 11.43 | 16.00 | - | 67.00 | |
| A-phase time (seconds) | 8 FND | 3235.63 | 748.10 | 2235.00 | - | 4281.00 |
| 8 SDP | 4764.75 | 1069.05 | 3861.00 | - | 6901.00 | |
| 8 FND + 8 SDP | 4000.19 | 1198.25 | 2235.00 | - | 6901.00 | |
| REM time (seconds) | 8 FND | 6997.50 | 1888.91 | 4530.00 | - | 11,430.00 |
| 8 SDP | 5703.75 | 1816.08 | 2640.00 | - | 8430.00 | |
| 8 FND + 8 SDP | 6350.63 | 1962.53 | 2640.00 | - | 11,430.00 | |
| NREM time (seconds) | 8 FND | 20,715.00 | 2822.07 | 17,280.00 | - | 26,040.00 |
| 8 SDP | 22,106.25 | 2459.24 | 18,210.00 | - | 26,910.00 | |
| 8 FND + 8 SDP | 21,410.63 | 2736.76 | 17,280.00 | - | 26,910.00 | |
| Number | Parameters | Using GA | Using PSO |
|---|---|---|---|
| 1 | Number of channels to be fused | 3 (Fp2–F4, F4–C4, and C4–A1) | 3 (Fp2–F4, F4–C4, and C4–A1) |
| 2 | Number of time steps to be considered by the LSTM | 10 | 25 |
| 3 | Number of LSTM layers for each channel | 1 | 1 |
| 4 | Type of LSTM | BLSTM | BLSTM |
| 5 | Shape of the LSTM layers | 100 | 100 |
| 6 | Percentage of dropout for the recurrent and dense layers | 15% | 5% |
| 7 | Size of the dense layers | 300 | 200 |
| 8 | Activation function for the dense layers | Sigmoid | ReLu |
| Performance Metric | Population (Subjects) | Configuration Found by GA | Configuration Found by PSO |
|---|---|---|---|
| Acc (%) | 8 FND + 8 SDP | 76.52 ± 4.75 (68.08–85.30) | 79.43 ± 4.91 (69.25–87.29) |
| 8 FND | 76.53 ± 4.88 (70.67–87.01) | 77.24 ± 6.34 (69.16–86.16) | |
| 8 SDP | 77.66 ± 4.55 (71.72–85.91) | 79.33 ± 4.74 (71.50–85.35) | |
| Sen (%) | 8 FND + 8 SDP | 72.93 ± 9.77 (52.64–84.99) | 68.14 ± 11.26 (49.36–82.46) |
| 8 FND | 70.04 ± 9.67 (54.86–80.02) | 62.79 ± 12.79 (37.60–80.76) | |
| 8 SDP | 70.67 ± 12.21 (51.73–85.12) | 65.14 ± 14.27 (43.46–85.51) | |
| Spe (%) | 8 FND + 8 SDP | 77.07 ± 5.96 (66.69–88.12) | 81.21 ± 6.71 (68.79–93.35) |
| 8 FND | 77.28 ± 6.05 (69.65–89.22) | 79.02 ± 8.40 (67.90–91.95) | |
| 8 SDP | 78.69 ± 6.60 (70.83–90.74) | 81.90 ± 7.10 (69.83–93.73) | |
| AUC (%) | 8 FND + 8 SDP | 82.37 ± 4.75 (72.79–89.81) | 82.25 ± 4.53 (74.37–90.69) |
| 8 FND | 80.31 ± 4.67 (72.94–87.84) | 78.13 ± 3.89 (71.86–83.82) | |
| 8 SDP | 82.26 ± 4.75 (74.16–89.52) | 81.69 ± 4.96 (74.54–91.10) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendonça, F.; Mostafa, S.S.; Freitas, D.; Morgado-Dias, F.; Ravelo-García, A.G. Multiple Time Series Fusion Based on LSTM: An Application to CAP A Phase Classification Using EEG. Int. J. Environ. Res. Public Health 2022, 19, 10892. https://doi.org/10.3390/ijerph191710892
Mendonça F, Mostafa SS, Freitas D, Morgado-Dias F, Ravelo-García AG. Multiple Time Series Fusion Based on LSTM: An Application to CAP A Phase Classification Using EEG. International Journal of Environmental Research and Public Health. 2022; 19(17):10892. https://doi.org/10.3390/ijerph191710892
Chicago/Turabian StyleMendonça, Fábio, Sheikh Shanawaz Mostafa, Diogo Freitas, Fernando Morgado-Dias, and Antonio G. Ravelo-García. 2022. "Multiple Time Series Fusion Based on LSTM: An Application to CAP A Phase Classification Using EEG" International Journal of Environmental Research and Public Health 19, no. 17: 10892. https://doi.org/10.3390/ijerph191710892
APA StyleMendonça, F., Mostafa, S. S., Freitas, D., Morgado-Dias, F., & Ravelo-García, A. G. (2022). Multiple Time Series Fusion Based on LSTM: An Application to CAP A Phase Classification Using EEG. International Journal of Environmental Research and Public Health, 19(17), 10892. https://doi.org/10.3390/ijerph191710892










