Did You Just Cough? Visualization of Vapor Diffusion in an Office Using Computational Fluid Dynamics Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometry Model
2.2. Computational Model and Boundary Conditions
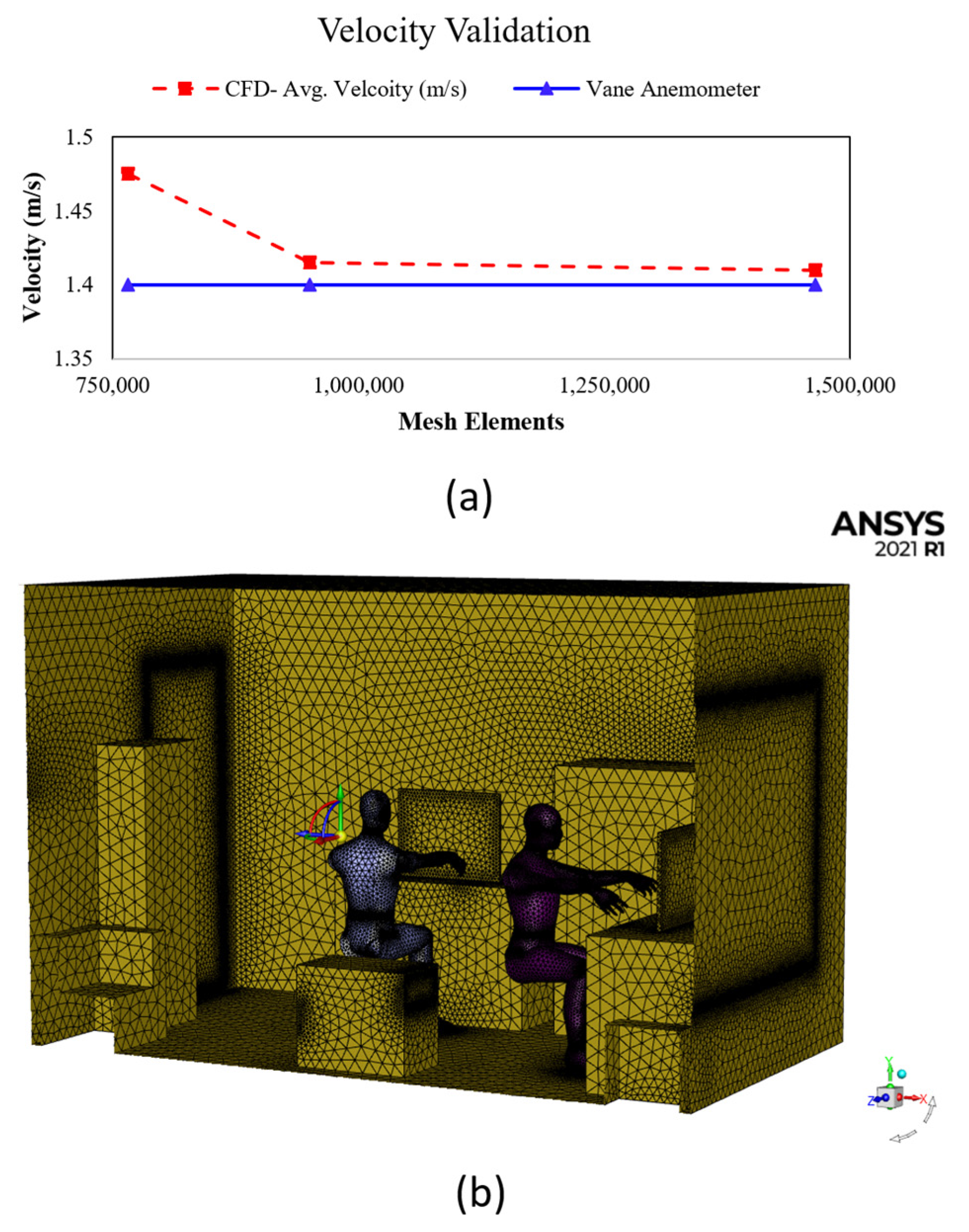
2.3. Grid Indpendence and Validation
3. Results and Discussion
3.1. Velocity Contours
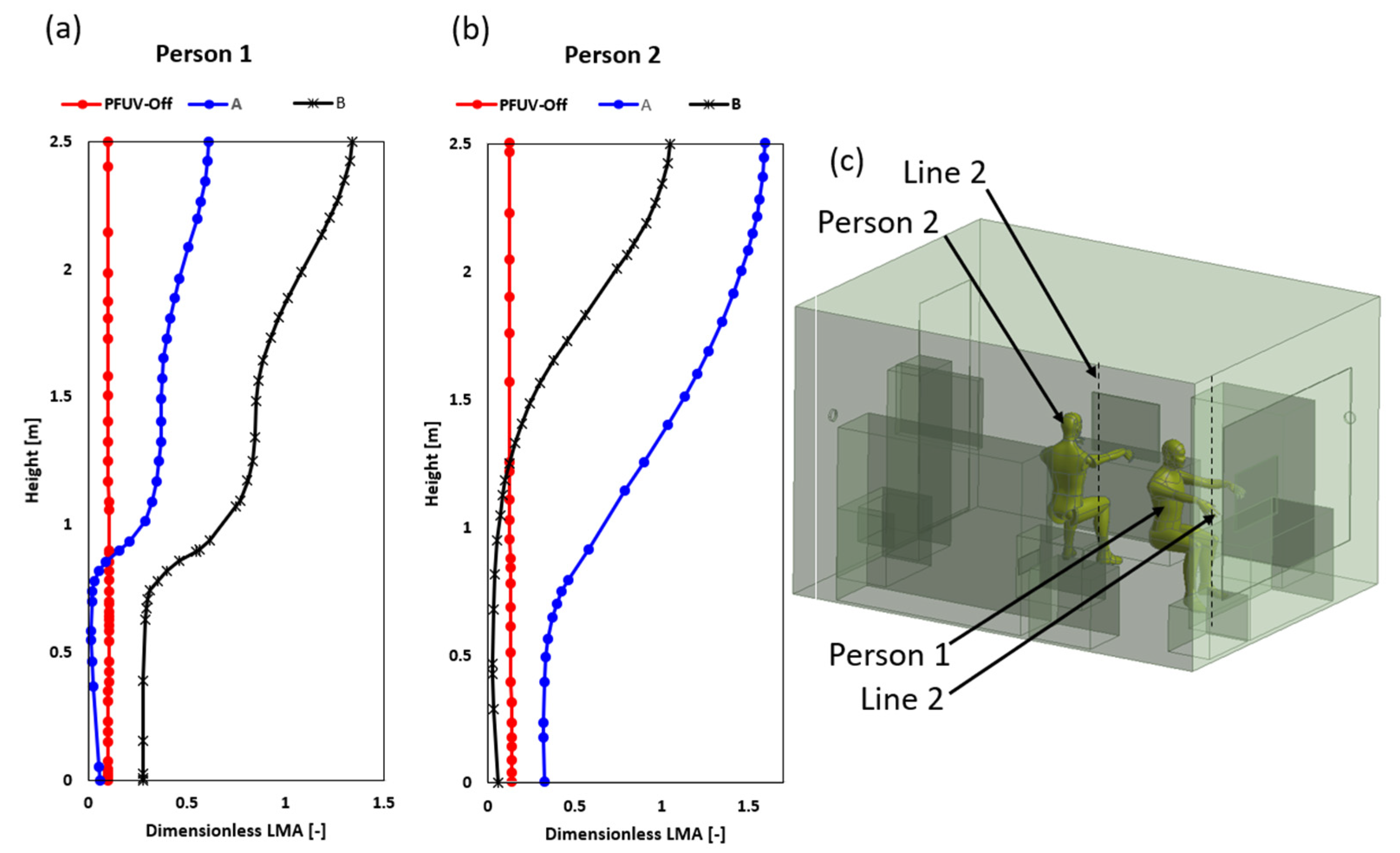
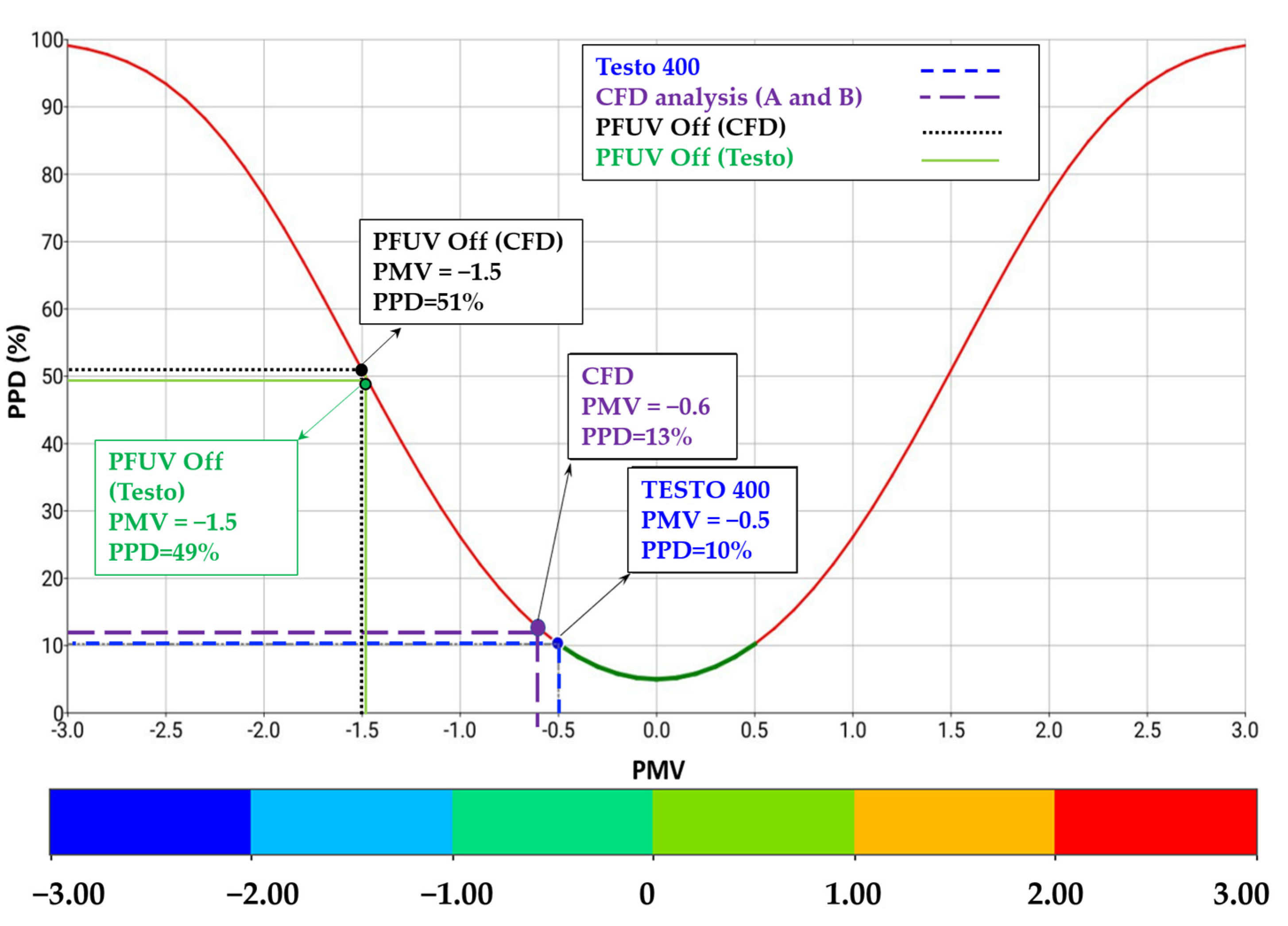
3.2. Measures of Air Mixing and Thermal Comfort
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Di Gilio, A.; Palmisani, J.; Pulimeno, M.; Cerino, F.; Cacace, M.; Miani, A.; de Gennaro, G. CO2 concentration monitoring inside educational buildings as a strategic tool to reduce the risk of SARS-CoV-2 airborne transmission. Environ. Res. 2021, 202, 111560. [Google Scholar] [CrossRef]
- Al-Rawi, M.; Lazonby, A.; Smith, C. Prototyping a low-cost residential air quality device using ultraviolet germicidal irradiation (UVGI) light. HardwareX 2022, 11, 00251. [Google Scholar] [CrossRef]
- Luo, H.; Zhong, L. Ultraviolet germicidal irradiation (UVGI) for in-duct airborne bioaerosol disinfection: Review and analysis of design factors. Build. Environ. 2021, 197, 107852. [Google Scholar] [CrossRef]
- World Health Organisation. Update of WHO Global Air Quality Guidelines. 2021. Available online: https://www.euro.who.int/en/health-topics/environment-and-health/air-quality/activities/update-of-who-global-air-quality-guidelines (accessed on 15 May 2022).
- Shan, X.; Luo, N.; Sun, K.; Hong, T.; Lee, Y.; Lu, W. Coupling CFD and building energy modelling to optimize the operation of a large open office space for occupant comfort. Sustain. Cities Soc. 2020, 60, 102257. [Google Scholar] [CrossRef]
- Gao, N.; Niu, J. Transient CFD simulation of the respiration process and inter-person exposure assessment. Build. Environ. 2006, 41, 1214–1222. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, S.; Kim, M.K.; Srebric, J. A Review of CFD Analysis Methods for Personalized Ventilation (PV) in Indoor Built Environments. Sustainability 2019, 11, 4166. [Google Scholar] [CrossRef]
- Cheng, X.; Su, R.; Shen, X.; Deng, T.; Zhang, D.; Chang, D.; Zhang, B.; Qiu, S. Modeling of indoor airflow around thermal manikins by multiple-relaxation-time lattice Boltzmann method with LES approaches. Numer. Heat Transf. Part A Appl. 2019, 77, 215–231. [Google Scholar] [CrossRef]
- Ai, Z.; Melikov, A. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: A review. Indoor Air. 2008, 28, 500–524. [Google Scholar] [CrossRef]
- Liu, S.; Novoselac, A. Lagrangian particle modeling in the indoor environment: A comparison of RANS and LES turbulence methods (RP-1512). HVACR Res. 2014, 20, 480–495. [Google Scholar] [CrossRef]
- Ivanov, M.; Mijorski, S. Assessment of Transient CFD Techniques for Virtual Thermal Manikins’ Breathing Simulations. Environ. Processes 2019, 6, 241–251. [Google Scholar] [CrossRef]
- Ivanov, M.; Mijorski, S. Geometrical form assessment of a CFD based breathing thermal manikins, designed by simplified polygonal shapes. E3S Web Conf. 2019, 85, 02002. [Google Scholar] [CrossRef]
- Olmedo, I.; Nielsen, P.; Ruiz de Adana, M.; Jensen, R. The risk of airborne cross-infection in a room with vertical low-velocity ventilation. Indoor Air. 2012, 23, 62–73. [Google Scholar] [CrossRef]
- Anthony, T.; Anderson, K. Computational Fluid Dynamics Investigation of Human Aspiration in Low-Velocity Air: Orientation Effects on Mouth-Breathing Simulations. Ann. Occup. Hyg. 2013, 57, 740–757. [Google Scholar] [CrossRef]
- Park, D.; Chang, S. Effects of combined central air conditioning diffusers and window-integrated ventilation system on indoor air quality and thermal comfort in an office. Sustain. Cities Soc. 2020, 61, 102292. [Google Scholar] [CrossRef]
- Li, Y.; Tong, Z. Development of real-time adaptive model-free extremum seeking control for CFD-simulated thermal environment. Sustain. Cities Soc. 2021, 74, 103166. [Google Scholar] [CrossRef]
- Shan, X.; Xu, W.; Lee, Y.; Lu, W. Evaluation of thermal environment by coupling CFD analysis and wireless-sensor measurements of a full-scale room with cooling system. Sustain. Cities Soc. 2019, 45, 395–405. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, H.; Niu, J. Investigating Indoor Air Quality and Thermal Comfort Using a Numerical Thermal Manikin. Indoor Built Environ. 2007, 16, 7–17. [Google Scholar] [CrossRef]
- Licina, D.; Melikov, A.; Sekhar, C.; Tham, K. Air temperature investigation in microenvironment around a human body. Build. Environ. 2015, 92, 39–47. [Google Scholar] [CrossRef]
- Mirzaie, M.; Lakzian, E.; Khan, A.; Warkiani, M.; Mahian, O.; Ahmadi, G. COVID-19 spread in a classroom equipped with partition –A CFD approach. J. Hazard. Mater. 2021, 420, 126587. [Google Scholar] [CrossRef]
- Dao, H.; Kim, K. Behavior of cough droplets emitted from COVID-19 patient in hospital isolation room with different ventilation configurations. Built Environ. 2022, 209, 108649. [Google Scholar] [CrossRef]
- Hassan, A.; Megahed, N. COVID-19 and urban spaces: A new integrated CFD approach for public health opportunities. Built Environ. 2021, 204, 108131. [Google Scholar] [CrossRef]
- Cao, Y.; Aldawi, F.; Sinaga, N.; Moria, H.; Dizaji, H.; Wae-hayee, M. Single solar chimney technology as a natural free ventilator; energy-environmental case study for Hong Kong. Case Stud. Therm. Eng. 2021, 26, 101173. [Google Scholar] [CrossRef]
- Slurink, I.A.L.; Smaardijk, V.R.; Kop, W.J.; Kupper, N.; Mols, F.; Schoormans, D.; Soedamah-Muthu, S.S. Changes in Perceived Stress and Lifestyle Behaviors in Response to the COVID-19 Pandemic in The Netherlands: An Online Longitudinal Survey Study. Int. J. Environ. Res. Public Health 2022, 19, 4375. [Google Scholar] [CrossRef]
- Lindert, L.; Kühn, L.; Kuper, P.; Choi, K.-E. Organizational Health Literacy in the Context of Employee Health: An Expert-Panel-Guided Scoping Review Protocol. Int. J. Environ. Res. Public Health 2022, 19, 4381. [Google Scholar] [CrossRef]
- Simons, S.W.; Waters, J.R. Local ventilation effectiveness parameters in air distribution system design. Build. Serv. Eng. Res. Technol. 1998, 19, 135–140. [Google Scholar] [CrossRef]
- Al-Rawi, M. The thermal comfort sweet-spot: A case study in a residential house in Waikato, New Zealand. Case Stud. Therm. Eng. 2021, 28, 101530. [Google Scholar] [CrossRef]




| Boundary Element | Type | Dimensions L × H × W (mm) | Heat Transfer | Substance Concentration |
|---|---|---|---|---|
| Office | wall | 3900 × 2500 × 2900 | Adiabatic, No slip wall | n/a |
| Laptop 1 + 2 | wall | 650 × 500 × 20 | 260 Watt (130 Watt each) | n/a |
| TV | wall | 800 × 600 × 80 | 130 Watt | n/a |
| Desk 1 | wall | 1300 × 800 × 600 | Adiabatic | n/a |
| Desk 2 | wall | 1200 × 800 × 470 | Adiabatic | n/a |
| Door Outlet | Outlet | 800 × 20 | Opening Pressure 18 , 50% | Air: 50% Vapor: 50% |
| Sofa, furniture | wall | - | Adiabatic | n/a |
| Light | wall | Diameter = 200 mm | 40 Watt (LED) | n/a |
| Boundary Element | Type | Dimensions L × H × W (mm) | Heat Transfer | Substance Concentration |
|---|---|---|---|---|
| PFUV Dehumidifier | wall | 640 × 540 × 370 | Adiabatic | n/a |
| PFUV Outlet | Outlet | 320 × 160 | Velocity = 1.4 m/s , 50% | Air: 100% |
| PFUV Inlet | Inlet | 320 × 140 | Velocity = 0.5 m/s | Air: 50% Vapor: 50% |
| Person 1 (Nose) | Inlet | Diameter = 30 mm | Volume flow rate 0.0015 m3/s | Air: 50% Vapor: 50% |
| Person 2 (Mouth) | Outlet | Diameter = 40 mm | Function (0–22.352 m/s) for 10 s coughing , 100% | Vapor: 100% |
| Person 1 | wall | Area = 0.375 m2 | Heat Flux = 44 W/m2 (For uninfected) | n/a |
| Person 2 | wall | Area = 0.375 m2 | Heat Flux = 44 W/m2 (For infected) | n/a |
| Element Size (m) | Mesh Elements | Vane Anemometer (m/s) | Outlet Velocity (m/s) PFUV Dehumidifier | % Error |  |
| 0.03 | 765,532 | 1.4 | 1.475 | 5.084 | |
| 0.02 | 950,253 | 1.4 | 1.415 | 1.06 | |
| 0.01 | 1,465,125 | 1.4 | 1.41 | 0.709 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Rawi, M.; Al-Jumaily, A.M.; Lazonby, A. Did You Just Cough? Visualization of Vapor Diffusion in an Office Using Computational Fluid Dynamics Analysis. Int. J. Environ. Res. Public Health 2022, 19, 9928. https://doi.org/10.3390/ijerph19169928
Al-Rawi M, Al-Jumaily AM, Lazonby A. Did You Just Cough? Visualization of Vapor Diffusion in an Office Using Computational Fluid Dynamics Analysis. International Journal of Environmental Research and Public Health. 2022; 19(16):9928. https://doi.org/10.3390/ijerph19169928
Chicago/Turabian StyleAl-Rawi, Mohammad, Ahmed M. Al-Jumaily, and Annette Lazonby. 2022. "Did You Just Cough? Visualization of Vapor Diffusion in an Office Using Computational Fluid Dynamics Analysis" International Journal of Environmental Research and Public Health 19, no. 16: 9928. https://doi.org/10.3390/ijerph19169928
APA StyleAl-Rawi, M., Al-Jumaily, A. M., & Lazonby, A. (2022). Did You Just Cough? Visualization of Vapor Diffusion in an Office Using Computational Fluid Dynamics Analysis. International Journal of Environmental Research and Public Health, 19(16), 9928. https://doi.org/10.3390/ijerph19169928







