What Cause Large Spatiotemporal Differences in Carbon Intensity of Energy-Intensive Industries in China? Evidence from Provincial Data during 2000–2019
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Measurement of EIICI
3.2. Spatial Differences and Spatial Autocorrelation
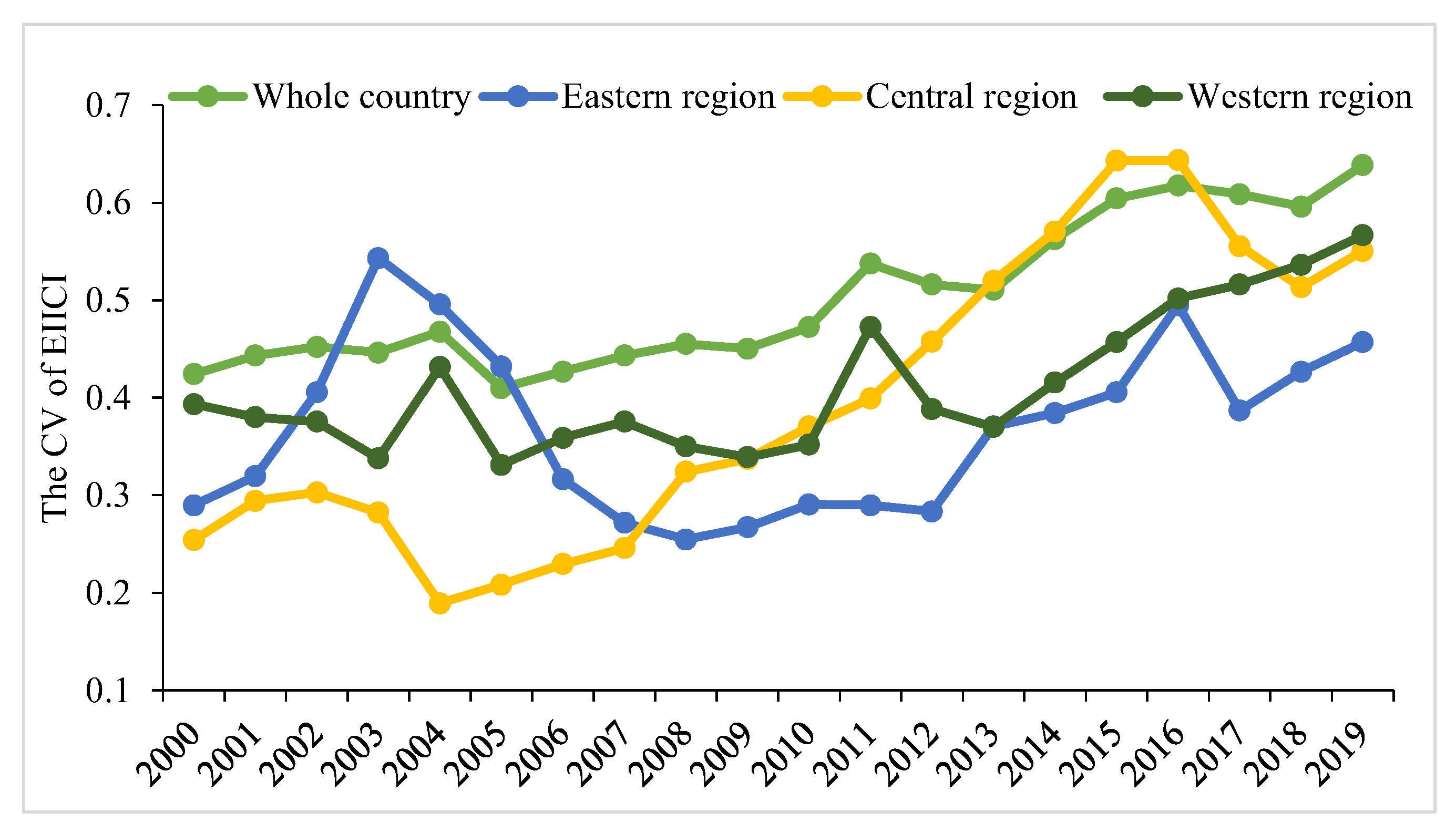
3.2.1. Coefficient of Variation
3.2.2. Spatial Autocorrelation
3.3. Spatial Econometric Model
3.4. Model Specification
3.5. Data Source and Description
4. Spatiotemporal Differences of EIICI
- (1)
- From 2000 to 2019, the EIICI showed a significant phased downward trend
- (2)
- At the provincial scale, the EIICI shows a significant downward trend, but there are gradually expanding spatial differences
- (3)
- At the regional scale, the EIICI shows a pattern of regional differences in the coexistence of “high in the west and low in the east” and “high in the north and low in the south”
- (4)
- EIICI has significant positive spatial autocorrelation
5. Estimation Results and Discussion of Drivers
5.1. Model Test
5.2. Analysis of Estimation Results
5.2.1. Results of SDM Model
5.2.2. Direct and Indirect Effects
6. Conclusions
7. Implications and Future Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kerr, R.A. Global warming is changing the world. Science 2007, 316, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Iyer, G.C.; Clarke, L.E.; Edmonds, J.A.; Flannery, B.P.; Hultman, N.E.; McJeon, H.C.; Victor, D.G. Improved representation of investment decisions in assessments of CO2 mitigation. Nat. Clim. Chang. 2015, 5, 436–440. [Google Scholar] [CrossRef]
- Adegoke, C.W.; Sojobi, A.O. Climate change impact on infrastructure in Osogbo metropolis, south-west Nigeria. J. Emerg. Trends Eng. Appl. Sci. 2015, 6, 156–165. [Google Scholar]
- Zhao, Y.; Chen, R.; Zang, P.; Huang, L.; Ma, S.; Wang, S. Spatiotemporal patterns of global carbon intensities and their driving forces. Sci. Total Environ. 2021, 818, 151690. [Google Scholar] [CrossRef]
- Han, Y.; Jin, B.; Qi, X.; Zhou, H. Influential Factors and Spatiotemporal Characteristics of Carbon Intensity on Industrial Sectors in China. Int. J. Environ. Res. Public Health 2021, 18, 2914. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Li, X.; Zhou, J.; Wang, S.; Liu, B. Some developments and new insights of environmental problems and deep mining strategy for cleaner production in mines. J. Clean. Prod. 2019, 210, 1562–1578. [Google Scholar] [CrossRef]
- State Council Information Office of the People’s Republic of China, China’s Energy Development in the New Era; People’s Publishing House: Beijing, China, 2020.
- Mi, Z.; Wei, Y.M.; Wang, B.; Meng, J.; Liu, Z.; Shan, Y.; Liu, J.; Guan, D. Socioeconomic impact assessment of China’s CO2 emissions peak prior to 2030. J. Clean. Prod. 2017, 142, 2227–2236. [Google Scholar] [CrossRef]
- Liu, H.C.; Fan, J.; Zhou, K.; Wang, Q. Exploring regional differences in the impact of high energy-intensive industries on CO2 emissions: Evidence from a panel analysis in China. Environ. Sci. Pollut. Res. 2019, 26, 26229–26241. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, M.; Wang, Z.; Jin, F. The impact of energy-intensive industries on air quality in China’s industrial agglomerations. J. Geogr. Sci. 2021, 31, 584–602. [Google Scholar] [CrossRef]
- Jiang, Z.; Lin, B. China’s energy demand and its characteristics in the industrialization and urbanization process: A reply. Energy Policy 2013, 60, 583–585. [Google Scholar] [CrossRef]
- Du, G.; Sun, C.; Ouyang, X.; Zhang, C. A decomposition analysis of energy-related CO2 emissions in Chinese six high-energy intensive industries. J. Clean. Prod. 2018, 184, 1102–1112. [Google Scholar] [CrossRef]
- Hussain, J.; Khan, A.; Zhou, K. The impact of natural resource depletion on energy use and CO2 emission in Belt & Road Initiative countries: A cross-country analysis. Energy J. 2020, 199, 117409. [Google Scholar]
- Schönsleben, P.; Vodicka, M.; Bunse, K.; Ernst, F.O. The changing concept of sustainability and economic opportunities for energy-intensive industries. CIRP Ann. 2010, 59, 477–480. [Google Scholar] [CrossRef]
- Team, P.; Carbon, P.; Neutrality, C. Analysis of a Peaked Carbon Emission Pathway in China Toward Carbon Neutrality. Engineering 2021, 7, 1673–1677. [Google Scholar]
- Jiang, X.; Duan, Y.; Green, C. Regional disparity in energy intensity of China and the role of industrial and export structure. Resour. Conserv. Recycl. 2017, 120, 209–218. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Zhou, Y.; Chen, Y.; Yang, C.; Chen, Z.; Wu, J. Spatiotemporal variations of CO2 emissions and their impact factors in China: A comparative analysis between the provincial and prefectural levels. Appl. Energy 2019, 233, 170–181. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F. The effects of trade openness on decoupling carbon emissions from economic growth–Evidence from 182 countries. J. Clean. Prod. 2021, 279, 123838. [Google Scholar] [CrossRef]
- Li, R.; Wang, Q.; Liu, Y.; Jiang, R. Per-capita carbon emissions in 147 countries: The effect of economic, energy, social, and trade structural changes. Sustain. Prod. Consum. 2021, 27, 1149–1164. [Google Scholar] [CrossRef]
- Zaidi, S.A.H.; Hussain, M.; Zaman, Q.U. Dynamic linkages between financial inclusion and carbon emissions: Evidence from selected OECD countries. Resour. Environ. Sustain. 2021, 4, 100022. [Google Scholar] [CrossRef]
- Adedoyin, F.F.; Gumede, M.I.; Bekun, F.V.; Etokakpan, M.U.; Balsalobre-Lorente, D. Modelling coal rent, economic growth and CO2 emissions: Does regulatory quality matter in BRICS economies? Sci. Total Environ. 2020, 710, 136284. [Google Scholar] [CrossRef]
- Xue, B.; Geng, Y.; Müller, K.; Lu, C.; Ren, W. Understanding the causality between carbon dioxide emission, fossil energy consumption and economic growth in developed countries: An empirical study. Sustainability 2014, 6, 1037–1045. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, Y.; Zhu, Z. Spatio-Temporal Heterogeneity of Carbon Emissions and Its Key Influencing Factors in the Yellow River Economic Belt of China from 2006 to 2019. Int. J. Environ. Res. Public Health 2022, 19, 4185. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, B.; Liu, T. Empirical analysis on the factors influencing national and regional carbon intensity in China. Renew. Sustain. Energy Rev. 2016, 55, 34–42. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, L.C.; Wu, G.; Tsai, H.T.; Wei, Y.M. Changes in carbon intensity in China: Empirical findings from 1980–2003. Ecol. Econ. 2007, 62, 683–691. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Ye, X.; Wei, Y.D. Spatiotemporal dynamics of carbon intensity from energy consumption in China. J. Geogr. Sci. 2014, 24, 631–650. [Google Scholar] [CrossRef]
- Ouyang, X.; Lin, B. An analysis of the driving forces of energy-related carbon dioxide emissions in China’s industrial sector. Renew. Sustain. Energy Rev. 2015, 45, 838–849. [Google Scholar] [CrossRef]
- Ma, M.; Cai, W. What drives the carbon mitigation in Chinese commercial building sector? Evidence from decomposing an extended Kaya identity. Sci. Total Environ. 2018, 634, 884–899. [Google Scholar] [CrossRef] [PubMed]
- Chi, Y.; Zhou, W.; Tang, S.; Hu, Y. Driving Factors of CO2 Emissions in China’s Power Industry: Relative Importance Analysis Based on Spatial Durbin Model. Energies 2022, 15, 2631. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Han, R.; Chang, Y.; Sun, X. Spatial Heterogeneity of Factors Influencing CO2 Emissions in China’s Energy-intensive industries. Sustainability 2021, 13, 8304. [Google Scholar] [CrossRef]
- Zhu, R.; Zhao, R.; Sun, J.; Xiao, L.; Jiao, S.; Chuai, X.; Zhang, L.; Yang, Q. Temporospatial pattern of carbon emission efficiency of China’s energy-intensive industries and its policy implications. J. Clean. Prod. 2021, 286, 125507. [Google Scholar] [CrossRef]
- Feng, K.; Davis, S.J.; Sun, L.; Hubacek, K. Drivers of the US CO2 emissions 1997–2013. Nat. Commun. 2015, 6, 7714. [Google Scholar] [CrossRef] [PubMed]
- Ge, F.; Li, J.; Zhang, Y.; Ye, S.; Han, P. Impacts of Energy Structure on Carbon Emissions in China, 1997–2019. Int. J. Environ. Res. Public Health 2022, 19, 5850. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.X.; Hao, P.; Yao, P.Y. Non-linear relationship between economic growth and CO2 emissions in China: An empirical study based on panel smooth transition regression models. Int. J. Environ. Res. Public Health 2017, 14, 1568. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, C. The impact of urbanization on CO2 emissions in China: An empirical study using 1980–2014 provincial data. Environ. Sci. Pollut. Res. 2018, 25, 2457–2465. [Google Scholar] [CrossRef]
- Xu, G.Y.; Song, D.Y. An empirical study on the environmental Kuznets curve for China’s carbon emissions: Based on provincial panel data. Chin. J. Popul. Resour. Environ. 2011, 9, 66–76. [Google Scholar]
- Wang, S.; Zeng, J.; Liu, X. Examining the multiple impacts of technological progress on CO2 emissions in China: A panel quantile regression approach. Renew. Sustain. Energy Rev. 2019, 103, 140–150. [Google Scholar] [CrossRef]
- Li, P.; Ouyang, Y. Quantifying the role of technical progress towards China’s 2030 carbon intensity target. J. Environ. Plan. Manag. 2021, 64, 379–398. [Google Scholar] [CrossRef]
- Zhang, L.W.; Sojobi, A.O.; Kodur, V.K.R.; Liew, K.M. Effective utilization and recycling of mixed recycled aggregates for a greener environment. J. Clean. Prod. 2019, 236, 117600. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.; Poon, J.; He, Z. China’s carbon dioxide emission and drivers: A spatial analysis. J. Clean. Prod. 2019, 211, 640–651. [Google Scholar] [CrossRef]
- Yang, Y.M.; Wang, Z.; Wang, L.Y.; Liu, C. Analysis of the determinants of carbon intensity on regional differences. Acta Sci. Circumstantiate 2016, 36, 3436–3444. [Google Scholar]
- Lin, H.; Wang, X.; Bao, G.; Xiao, H. Heterogeneous Spatial Effects of FDI on CO2 Emissions in China. Earths Future 2022, 10, e2021EF002331. [Google Scholar] [CrossRef]
- Guan, D.; Hubacek, K.; Weber, C.L.; Peters, G.P.; Reiner, D.M. The drivers of Chinese CO2 emissions from 1980 to 2030. Glob. Environ. Chang. 2008, 18, 626–634. [Google Scholar] [CrossRef]
- Xu, S.C.; He, Z.X.; Long, R.Y. Factors that influence carbon emissions due to energy consumption in China: Decomposition analysis using LMDI. Appl. Energy 2014, 127, 182–193. [Google Scholar] [CrossRef]
- Xie, S.H.; Wang, L.X.; Shao, Z.L. Analysis on Industrial Difference and Motivation Factor of Carbon intensity. Res. Environ. Sci. 2013, 26, 1252–1258. [Google Scholar]
- Lin, B.; Long, H. Emissions reduction in China’s chemical industry e based on LMDI. Renew. Sustain. Energy Rev. 2016, 53, 1348–1355. [Google Scholar] [CrossRef]
- Lin, B.; Ouyang, X. Analysis of energy-related CO2 (carbon dioxide) emissions and reduction potential in the Chinese non-metallic mineral products industry. Energy J. 2014, 68, 688–697. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, Y.; Shi, X.; Zhang, Z.; Zhang, W. Structural and technological determinants of carbon intensity reduction of China’s electricity generation. Environ. Sci. Pollut. Res. 2021, 28, 13469–13486. [Google Scholar] [CrossRef]
- Wang, H.; Ang, B.W.; Su, B. A multi-region structural decomposition analysis of global CO2 emission intensity. Ecol. Econ. 2017, 142, 163–176. [Google Scholar] [CrossRef]
- Wachsmann, U.; Wood, R.; Lenzen, M.; Schaeffer, R. Structural decomposition of energy use in Brazil from 1970 to 1996. Appl. Energy 2009, 86, 578–587. [Google Scholar] [CrossRef]
- Wang, S.; Fang, C.; Wang, Y. Spatiotemporal variations of energy-related CO2 emissions in China and its influencing factors: An empirical analysis based on provincial panel data. Renew. Sustain. Energy Rev. 2016, 55, 505–515. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Chen, Z. Will China make a difference in its carbon intensity reduction targets by 2020 and 2030? Appl. Energy 2017, 203, 874–882. [Google Scholar] [CrossRef]
- Tobler, W. On the first law of geography: A reply. Ann. Assoc. Am. Geogr. 2004, 94, 304–310. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s Recent Emission Pattern Shifts. Earth’s Future 2021, 9, e2021EF002241. [Google Scholar] [CrossRef]
- Liao, S.; Wang, D.; Xia, C.; Tang, J. China’s provincial process CO2 emissions from cement production during 1993–2019. Sci. Data 2022, 9, 165. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.C.; Fan, J.; Zeng, Y.X.; Wang, W.Z. The evolution of tea spatial agglomeration in China: An analysis based on different geographical scales. J. Mt. Sci. 2018, 15, 2590–2602. [Google Scholar] [CrossRef]
- Zhou, K.; Wu, J.; Liu, H. Spatiotemporal variations and determinants of water pollutant discharge in the Yangtze River Economic Belt, China: A spatial econometric analysis. Environ. Pollut. 2021, 271, 116320. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Elhorst, J.P. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014; Volume 479, p. 480. [Google Scholar]
- Holdren, J.P.; Ehrlich, P.R. Human Population and the Global Environment: Population growth, rising per capita material consumption, and disruptive technologies have made civilization a global ecological force. Am. Sci. 1974, 62, 282–292. [Google Scholar]
- Li, J.; Cheng, J.; Wen, Y.; Cheng, J.; Ma, Z.; Hu, P.; Jiang, S. The Cause of China’s Haze Pollution: City Level Evidence Based on the Extended STIRPAT Model. Int. J. Environ. Res. Public Health 2022, 19, 4597. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J.; Zhong, C.; Ji, D.; Huang, W. Satellite-derived spatiotemporal PM2.5 concentrations and variations from 2006 to 2017 in China. Sci. Total Environ. 2020, 712, 134577. [Google Scholar] [CrossRef]
- Fantom, N.J.; Serajuddin, U. The World Bank’s Classification of Countries by Income; World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2016. [Google Scholar]
- Li, L.; Liu, X.; Ge, J.; Chu, X.; Wang, J. Regional differences in spatial spillover and hysteresis effects: A theoretical and empirical study of environmental regulations on haze pollution in China. J. Clean. Prod. 2019, 230, 1096–1110. [Google Scholar] [CrossRef]
- Lin, J.; Mou, D. Analysis of the optimal spatial distribution of natural gas under ‘transition from coal to gas’ in China. Resour. Energy Econ. 2021, 66, 101259. [Google Scholar] [CrossRef]
- Meng, B.; Liu, Y.; Andrew, R.; Zhou, M.; Hubacek, K.; Xue, J.; Peters, G.; Gao, Y. More than half of China’s CO2 emissions are from micro, small and medium-sized enterprises. Appl. Energy 2018, 230, 712–725. [Google Scholar] [CrossRef]
- Chen, D.; Chen, S.; Jin, H. Industrial agglomeration and CO2 emissions: Evidence from 187 Chinese prefecture-level cities over 2005–2013. J. Clean. Prod. 2018, 172, 993–1003. [Google Scholar] [CrossRef]

| Variable | Symbol | Unit | Min | Mean | Max | SD |
|---|---|---|---|---|---|---|
| Carbon intensity of energy-intensive industries | EIICI | Tons/104 yuan | 0.410 | 5.100 | 23.83 | 4.010 |
| Economic level | ECON | Yuan | 2759 | 34,702 | 160,000 | 27,385 |
| Urbanization | URB | % | 20.35 | 51.06 | 89.60 | 15.02 |
| Technological innovation | INN | Yuan/person | 10.53 | 686.5 | 11,256 | 1187 |
| Energy structure | ES | % | 1.210 | 47.19 | 92.64 | 17.84 |
| Environmental regulation | ER | 104 yuan/tons | 0.020 | 1.700 | 52.09 | 5.310 |
| Industrial agglomeration | AGG | % | 18.06 | 39.09 | 75.77 | 13.10 |
| Firm size | FZ | 104 yuan | 797.5 | 8071 | 31,533 | 6466 |
| Regions | Provinces |
|---|---|
| Eastern region | Beijing, Tianjin, Hebei, Liaoning, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, Hainan |
| Central region | Shanxi, Jilin, Heilongjiang, Anhui, Jiangxi, Henan, Hubei, Hunan |
| Western region | Inner Mongolia, Guangxi, Chongqing, Sichuan, Guizhou, Yunnan, Shannxi, Gansu, Qinghai, Ningxia, Xinjiang |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
|---|---|---|---|---|---|---|---|---|---|---|
| Moran’I | 0.282 | 0.304 | 0.389 | 0.213 | 0.270 | 0.345 | 0.294 | 0.303 | 0.355 | 0.312 |
| Z statistics | 2.772 | 2.964 | 3.746 | 2.185 | 2.728 | 3.355 | 2.955 | 3.022 | 3.482 | 3.066 |
| p value | 0.006 | 0.003 | 0.000 | 0.029 | 0.006 | 0.001 | 0.003 | 0.003 | 0.000 | 0.002 |
| Year | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| Moran’I | 0.363 | 0.275 | 0.323 | 0.312 | 0.345 | 0.332 | 0.366 | 0.338 | 0.366 | 0.377 |
| Z statistics | 3.505 | 2.842 | 3.169 | 3.059 | 3.369 | 3.265 | 3.581 | 3.306 | 3.562 | 3.649 |
| p value | 0.000 | 0.004 | 0.002 | 0.002 | 0.001 | 0.001 | 0.000 | 0.001 | 0.000 | 0.000 |
| Statistics | Mixed Effects | Spatial Fixed Effects | Time-Period Fixed Effects | Two-Way Fixed Effects |
|---|---|---|---|---|
| R2 | 0.747 | 0.825 | 0.767 | 0.863 |
| Log-L | −201.402 | −191.128 | −44.622 | −20.799 |
| LM-lag | 107.829 (0.000) *** | 201.835 (0.000) *** | 51.732 (0.000) *** | 51.866 (0.000) *** |
| Robust LM-lag | 1.358(0.561) | 3.513 (0.086) * | 2.741 (0.107) | 4.948 (0.015) ** |
| LM-error | 608.595 (0.000) *** | 644.876 (0.000) *** | 326.733 (0.000) *** | 353.689 (0.000) *** |
| Robust LM-error | 501.123 (0.000) *** | 445.782 (0.000) *** | 275.515 (0.000) *** | 304.771 (0.000) *** |
| W1 | W2 | W3 | |
|---|---|---|---|
| LnECON | −0.390 *** (−5.41) | −0.397 *** (−5.98) | −0.443 *** (−5.63) |
| LnURB | −0.120 (−1.07) | −0.0383 (−0.37) | −0.355 ** (−2.75) |
| LnINN | −0.0839 ** (−2.97) | −0.0947 *** (−3.51) | −0.132 *** (−4.41) |
| LnES | 0.375 *** (11.53) | 0.363 *** (11.44) | 0.310 *** (7.90) |
| LnER | 0.0164 (0.96) | 0.0195 (1.25) | 0.0278 (1.54) |
| LnAGG | −0.117 (−1.96) | −0.172 *** (−3.31) | 0.0129 (0.20) |
| LnFZ | −0.191 *** (−5.48) | −0.125 *** (−3.98) | −0.122 ** (−3.15) |
| ρ | 0.249 *** (4.35) | 0.484 *** (10.80) | 0.285 *** (5.32) |
| W*LnECON | 0.373 ** (2.82) | 0.0972 (0.64) | 0.419 (1.57) |
| W*LnURB | −0.389 (−1.85) | 0.140 (0.56) | 0.787 * (2.13) |
| W*LnINN | −0.318 *** (−5.12) | −0.546 *** (−8.28) | 0.0407(0.46) |
| W*LnES | −0.0922 (−1.32) | −0.105 (−1.13) | −0.0627 (−0.69) |
| W*LnER | 0.0411 * (2.54) | 0.0479 *** (3.29) | 0.0278 (1.61) |
| W*LnAGG | 0.506 ** (3.05) | 0.479 * (2.12) | 1.307 *** (7.06) |
| W*LnFZ | −0.198 (−1.92) | −0.0595 (−0.61) | −0.291 ** (−3.22) |
| σ2 | 0.0204 *** (17.17) | 0.0169 *** (17.56) | 0.0229 *** (17.31) |
| Adj. R2 | 0.894 | 0.917 | 0.858 |
| Log Likelihood | 312.595 | 361.723 | 281.396 |
| N | 600 | 600 | 600 |
| LR_Direct | LR_Indirect | LR_Total | |
|---|---|---|---|
| LnECON | −0.397 *** (−5.83) | 0.0952 (0.61) | −0.301 (−1.71) |
| LnURB | −0.0443 (−0.43) | 0.159 (0.66) | 0.115 (0.45) |
| LnINN | −0.0915 *** (−3.56) | −0.508 *** (−7.91) | −0.599 *** (−9.11) |
| LnES | 0.320 *** (10.87) | 0.0897 ** (2.72) | 0.410 *** (3.69) |
| LnER | 0.0187 (1.20) | 0.0334 ** (2.53) | 0.0521 (1.73) |
| LnAGG | −0.176 *** (−3.34) | 0.0804 * (2.35) | −0.0951 (−0.66) |
| LnFZ | −0.126 *** (−3.90) | −0.053 (−0.54) | −0.179 (−1.75) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Shen, Y.; Liu, H. What Cause Large Spatiotemporal Differences in Carbon Intensity of Energy-Intensive Industries in China? Evidence from Provincial Data during 2000–2019. Int. J. Environ. Res. Public Health 2022, 19, 10235. https://doi.org/10.3390/ijerph191610235
Xu X, Shen Y, Liu H. What Cause Large Spatiotemporal Differences in Carbon Intensity of Energy-Intensive Industries in China? Evidence from Provincial Data during 2000–2019. International Journal of Environmental Research and Public Health. 2022; 19(16):10235. https://doi.org/10.3390/ijerph191610235
Chicago/Turabian StyleXu, Xin, Yuming Shen, and Hanchu Liu. 2022. "What Cause Large Spatiotemporal Differences in Carbon Intensity of Energy-Intensive Industries in China? Evidence from Provincial Data during 2000–2019" International Journal of Environmental Research and Public Health 19, no. 16: 10235. https://doi.org/10.3390/ijerph191610235
APA StyleXu, X., Shen, Y., & Liu, H. (2022). What Cause Large Spatiotemporal Differences in Carbon Intensity of Energy-Intensive Industries in China? Evidence from Provincial Data during 2000–2019. International Journal of Environmental Research and Public Health, 19(16), 10235. https://doi.org/10.3390/ijerph191610235






