Cohen’s Kappa Coefficient as a Measure to Assess Classification Improvement following the Addition of a New Marker to a Regression Model
Abstract
:1. Introduction
2. Materials and Methods
- κ > 0 indicates better reclassification after adding a new variable,
- κ < 0 indicates worse reclassification after adding a new variable,
- κ = 0 indicates that there are no changes in the reclassification.
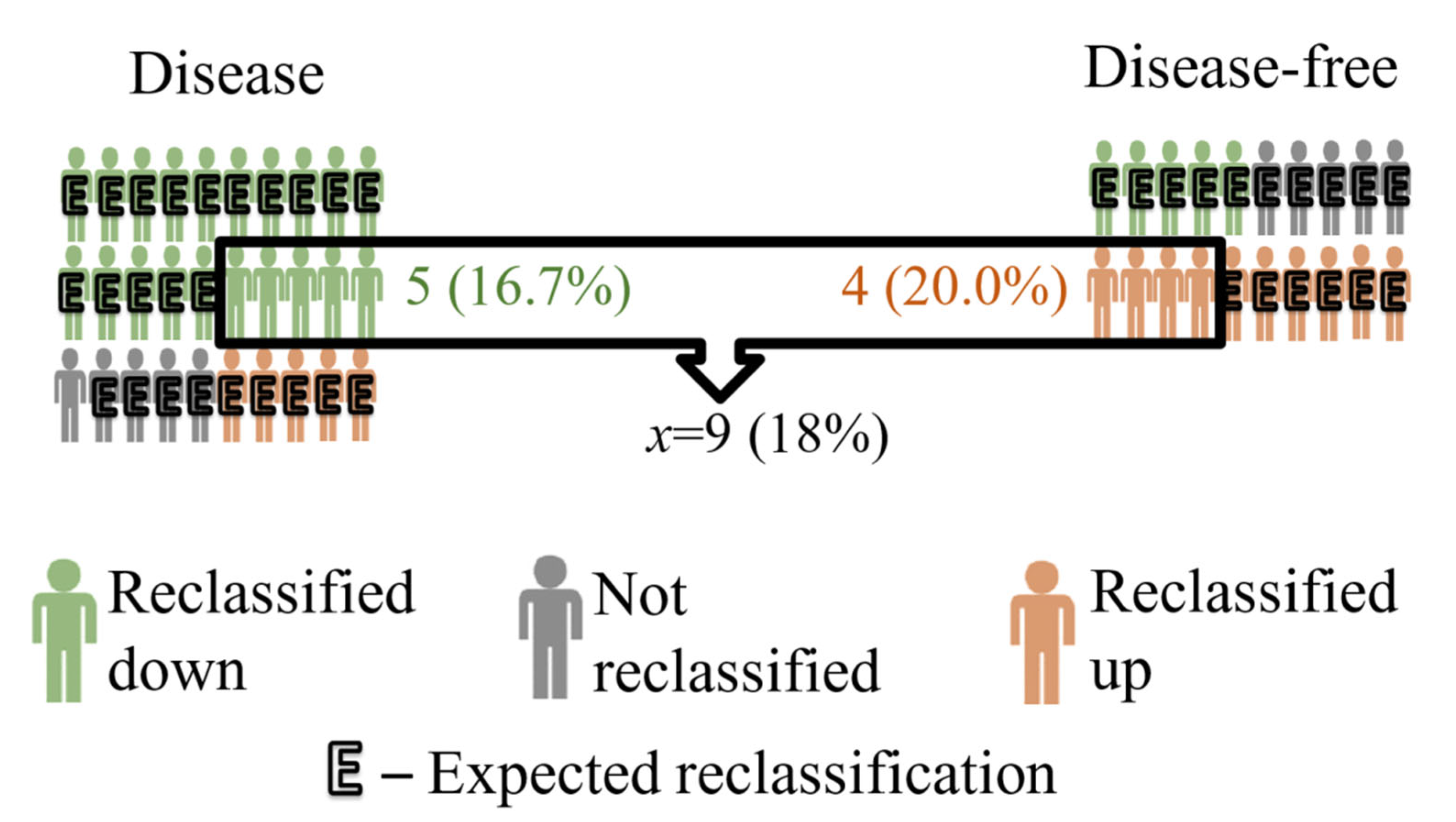
2.1. Example
2.2. Plan of Simulation Study
2.3. Selection of Candidates for Extended Models
2.4. Construction of the Basic Model
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Steyerberg, E.W.; Harrell, F.E. Prediction Models Need Appropriate Internal, Internal-External, and External Validation. J. Clin. Epidemiol. 2016, 69, 245–247. [Google Scholar] [CrossRef] [PubMed]
- Altman, N.; Krzywinski, M. Interpreting P Values. Nat. Methods 2017, 14, 213–214. [Google Scholar] [CrossRef]
- Sullivan, G.M.; Feinn, R. Using Effect Size—Or Why the P Value Is Not Enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef] [PubMed]
- American Psychological Association (Ed.) Publication Manual of the American Psychological Association, 6th ed.; American Psychological Association: Washington, DC, USA, 2010; ISBN 978-1-4338-0559-2. [Google Scholar]
- Bakker, A.; Cai, J.; English, L.; Kaiser, G.; Mesa, V.; Van Dooren, W. Beyond Small, Medium, or Large: Points of Consideration When Interpreting Effect Sizes. Educ. Stud. Math. 2019, 102, 1–8. [Google Scholar] [CrossRef]
- Durlak, J.A. How to Select, Calculate, and Interpret Effect Sizes. J. Pediatric Psychol. 2009, 34, 917–928. [Google Scholar] [CrossRef]
- Sun, S.; Pan, W.; Wang, L.L. A Comprehensive Review of Effect Size Reporting and Interpreting Practices in Academic Journals in Education and Psychology. J. Educ. Psychol. 2010, 102, 989–1004. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; L. Erlbaum Associates: Hillsdale, NJ, USA, 1988; ISBN 978-0-8058-0283-2. [Google Scholar]
- Trafimow, D.; Marks, M. Editorial. Basic Appl. Soc. Psychol. 2015, 37, 1–2. [Google Scholar] [CrossRef]
- Scott, W.A. Reliability of Content Analysis: The Case of Nominal Scale Coding. Public Opin. Q. 1955, 19, 321–325. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Barlow, W.; Lai, M.Y.; Azen, S.P. A Comparison of Methods for Calculating a Stratified Kappa. Stat. Med. 1991, 10, 1465–1472. [Google Scholar] [CrossRef]
- Cohen, J. Weighted Kappa: Nominal Scale Agreement Provision for Scaled Disagreement or Partial Credit. Psychol. Bull. 1968, 70, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Donner, A.; Klar, N. The Statistical Analysis of Kappa Statistics in Multiple Samples. J. Clin. Epidemiol. 1996, 49, 1053–1058. [Google Scholar] [CrossRef]
- Graham, P. Modelling Covariate Effects in Observer Agreement Studies: The Case of Nominal Scale Agreement. Stat. Med. 1995, 14, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Lipsitz, S.R.; Laird, N.M.; Brennan, T.A. Simple Moment Estimates of the κ-Coefficient and Its Variance. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1994, 43, 309–323. [Google Scholar] [CrossRef]
- Klar, N.; Lipsitz, S.R.; Ibrahim, J.G. An Estimating Equations Approach for Modelling Kappa. Biom. J. J. Math. Methods Biosci. 2000, 42, 45–58. [Google Scholar] [CrossRef]
- Williamson, J.M.; Lipsitz, S.R.; Manatunga, A.K. Modeling Kappa for Measuring Dependent Categorical Agreement Data. Biostatistics 2000, 1, 191–202. [Google Scholar] [CrossRef]
- Chmura Kraemer, H.; Periyakoil, V.S.; Noda, A. Kappa Coefficients in Medical Research. Statist. Med. 2002, 21, 2109–2129. [Google Scholar] [CrossRef]
- Cook, N.R. Use and Misuse of the Receiver Operating Characteristic Curve in Risk Prediction. Circulation 2007, 115, 928–935. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’Agostino, R.B.; Pencina, K.M.; Janssens, A.C.J.W.; Greenland, P. Interpreting Incremental Value of Markers Added to Risk Prediction Models. Am. J. Epidemiol. 2012, 176, 473–481. [Google Scholar] [CrossRef]
- Austin, P.C.; Steyerberg, E.W. Predictive Accuracy of Risk Factors and Markers: A Simulation Study of the Effect of Novel Markers on Different Performance Measures for Logistic Regression Models. Stat. Med. 2013, 32, 661–672. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’ Agostino, R.B.; D’ Agostino, R.B.; Vasan, R.S. Evaluating the Added Predictive Ability of a New Marker: From Area under the ROC Curve to Reclassification and Beyond. Stat. Med. 2008, 27, 157–172. [Google Scholar] [CrossRef] [PubMed]
- Pencina, M.J.; D’Agostino, R.B.; Steyerberg, E.W. Extensions of Net Reclassification Improvement Calculations to Measure Usefulness of New Biomarkers. Stat. Med. 2011, 30, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Pencina, M.J.; Steyerberg, E.W.; D’Agostino, R.B. Net Reclassification Index at Event Rate: Properties and Relationships. Stat. Med. 2017, 36, 4455–4467. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.S.; Fan, J.; Feng, Z.; Gerds, T.; Hilden, J. The Net Reclassification Index (NRI): A Misleading Measure of Prediction Improvement Even with Independent Test Data Sets. Stat. Biosci. 2015, 7, 282–295. [Google Scholar] [CrossRef]
- Hilden, J.; Gerds, T.A. A Note on the Evaluation of Novel Biomarkers: Do Not Rely on Integrated Discrimination Improvement and Net Reclassification Index. Stat. Med. 2014, 33, 3405–3414. [Google Scholar] [CrossRef]
- Kerr, K.F.; Wang, Z.; Janes, H.; McClelland, R.L.; Psaty, B.M.; Pepe, M.S. Net Reclassification Indices for Evaluating Risk-Prediction Instruments: A Critical Review. Epidemiology 2014, 25, 114–121. [Google Scholar] [CrossRef]
- Leening, M.J.G.; Vedder, M.M.; Witteman, J.C.M.; Pencina, M.J.; Steyerberg, E.W. Net Reclassification Improvement: Computation, Interpretation, and Controversies: A Literature Review and Clinician’s Guide. Ann. Intern. Med. 2014, 160, 122–131. [Google Scholar] [CrossRef]
- Cook, N.R. Clinically Relevant Measures of Fit? A Note of Caution. Am. J. Epidemiol. 2012, 176, 488–491. [Google Scholar] [CrossRef]
- Pepe, M.S.; Janes, H.; Li, C.I. Net Risk Reclassification P Values: Valid or Misleading? J. Natl. Cancer Inst. 2014, 106, dju041. [Google Scholar] [CrossRef]
- Burch, P.M.; Glaab, W.E.; Holder, D.J.; Phillips, J.A.; Sauer, J.-M.; Walker, E.G. Net Reclassification Index and Integrated Discrimination Index Are Not Appropriate for Testing Whether a Biomarker Improves Predictive Performance. Toxicol. Sci. 2017, 156, 11–13. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’Agostino, R.B.; Vasan, R.S. Statistical Methods for Assessment of Added Usefulness of New Biomarkers. Clin. Chem. Lab. Med. 2010, 48, 1703–1711. [Google Scholar] [CrossRef] [PubMed]
- Thomas, L.E.; O’Brien, E.C.; Piccini, J.P.; D’Agostino, R.B.; Pencina, M.J. Application of Net Reclassification Index to Non-Nested and Point-Based Risk Prediction Models: A Review. Eur. Heart J. 2019, 40, 1880–1887. [Google Scholar] [CrossRef]
- Cao, H.; Sen, P.K.; Peery, A.F.; Dellon, E.S. Assessing Agreement with Multiple Raters on Correlated Kappa Statistics. Biom. J. 2016, 58, 935–943. [Google Scholar] [CrossRef]
- Mahmood, S.S.; Levy, D.; Vasan, R.S.; Wang, T.J. The Framingham Heart Study and the Epidemiology of Cardiovascular Disease: A Historical Perspective. Lancet 2014, 383, 999–1008. [Google Scholar] [CrossRef]
- Piepoli, M.F.; Hoes, A.W.; Agewall, S.; Albus, C.; Brotons, C.; Catapano, A.L.; Cooney, M.-T.; Corrà, U.; Cosyns, B.; Deaton, C.; et al. 2016 European Guidelines on Cardiovascular Disease Prevention in Clinical Practice: The Sixth Joint Task Force of the European Society of Cardiology and Other Societies on Cardiovascular Disease Prevention in Clinical Practice (Constituted by Representatives of 10 Societies and by Invited Experts)Developed with the Special Contribution of the European Association for Cardiovascular Prevention & Rehabilitation (EACPR). Eur. Heart J. 2016, 37, 2315–2381. [Google Scholar] [CrossRef] [PubMed]
- Conroy, R.M.; Pyörälä, K.; Fitzgerald, A.P.; Sans, S.; Menotti, A.; De Backer, G.; De Bacquer, D.; Ducimetière, P.; Jousilahti, P.; Keil, U.; et al. Estimation of Ten-Year Risk of Fatal Cardiovascular Disease in Europe: The SCORE Project. Eur. Heart J. 2003, 24, 987–1003. [Google Scholar] [CrossRef]
- Zdrojewski, T.; Jankowski, P.; Bandosz, P.; Bartuś, S.; Chwojnicki, K.; Drygas, W.; Gaciong, Z.; Hoffman, P.; Kalarus, Z.; Kaźmierczak, J.; et al. [A new version of cardiovascular risk assessment system and risk charts calibrated for Polish population]. Kardiol. Pol. 2015, 73, 958–961. [Google Scholar] [CrossRef]
- Demler, O.V.; Pencina, M.J.; D’Agostino, R.B. Misuse of DeLong Test to Compare AUCs for Nested Models. Stat. Med. 2012, 31, 2577–2587. [Google Scholar] [CrossRef]
- Den Ruijter, H.M.; Peters, S.A.E.; Anderson, T.J.; Britton, A.R.; Dekker, J.M.; Eijkemans, M.J.; Engström, G.; Evans, G.W.; de Graaf, J.; Grobbee, D.E.; et al. Common Carotid Intima-Media Thickness Measurements in Cardiovascular Risk Prediction: A Meta-Analysis. JAMA 2012, 308, 796–803. [Google Scholar] [CrossRef]
- Kavousi, M.; Elias-Smale, S.; Rutten, J.H.W.; Leening, M.J.G.; Vliegenthart, R.; Verwoert, G.C.; Krestin, G.P.; Oudkerk, M.; de Maat, M.P.M.; Leebeek, F.W.G.; et al. Evaluation of Newer Risk Markers for Coronary Heart Disease Risk Classification: A Cohort Study. Ann. Intern. Med. 2012, 156, 438–444. [Google Scholar] [CrossRef]
- Yeboah, J.; McClelland, R.L.; Polonsky, T.S.; Burke, G.L.; Sibley, C.T.; O’Leary, D.; Carr, J.J.; Goff, D.C.; Greenland, P.; Herrington, D.M. Comparison of Novel Risk Markers for Improvement in Cardiovascular Risk Assessment in Intermediate-Risk Individuals. JAMA 2012, 308, 788–795. [Google Scholar] [CrossRef] [PubMed]
- Cook, N.R. Comments on ‘Evaluating the Added Predictive Ability of a New Marker: From Area under the ROC Curve to Reclassification and beyond’ by M. J. Pencina et al., Statistics in Medicine (DOI: 10.1002/Sim.2929). Stat. Med. 2008, 27, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Cook, N.R.; Paynter, N.P. Performance of Reclassification Statistics in Comparing Risk Prediction Models. Biom. J. 2011, 53, 237–258. [Google Scholar] [CrossRef] [PubMed]
- Paynter, N.P.; Cook, N.R. A Bias-Corrected Net Reclassification Improvement for Clinical Subgroups. Med. Decis. Mak. 2013, 33, 154–162. [Google Scholar] [CrossRef] [PubMed]
- Merry, A.H.H.; Boer, J.M.A.; Schouten, L.J.; Ambergen, T.; Steyerberg, E.W.; Feskens, E.J.M.; Verschuren, W.M.M.; Gorgels, A.P.M.; van den Brandt, P.A. Risk Prediction of Incident Coronary Heart Disease in The Netherlands: Re-Estimation and Improvement of the SCORE Risk Function. Eur. J. Prev. Cardiol. 2012, 19, 840–848. [Google Scholar] [CrossRef] [PubMed]
- Siontis, G.C.M.; Tzoulaki, I.; Siontis, K.C.; Ioannidis, J.P.A. Comparisons of Established Risk Prediction Models for Cardiovascular Disease: Systematic Review. BMJ 2012, 344, e3318. [Google Scholar] [CrossRef]
| Observed Frequency | ||||
| disease-free | diseased | total | ||
| reclassification | down | aO | bO | # down |
| no changes | cO | dO | # no changes | |
| up | eO | fO | # up | |
| total | # disease-free | # diseased | n | |
| Expected frequency * | ||||
| reclassification | down | aE | bE | |
| no changes | cE | dE | ||
| up | eE | fE | ||
| Observed Frequency | |||||
| disease-free | hidden category | diseased | total | ||
| reclassification | down | aO | 0 | bO | # down |
| no changes | cO | 0 | dO | # no changes | |
| up | eO | 0 | fO | # up | |
| total | # disease-free | 0 | # diseased | n | |
| Expected frequency * | |||||
| reclassification | down | aE | 0 | bE | |
| no changes | cE | 0 | dE | ||
| up | eE | 0 | fE | ||
| Observed Frequency | |||||
| disease-free | hidden category | diseased | total | ||
| reclassification | down | aO = 20 | 0 | bO = 5 | aO + bO = 25 |
| no changes | cO = 5 | 0 | dO = 5 | cO + dO = 10 | |
| up | eO = 5 | 0 | fO = 10 | eO + fO = 15 | |
| total | aO + cO + eO = 30 | 0 | bO + dO + fO = 20 | n = 50 | |
| Expected frequency * | |||||
| reclassification | down | aE = 15 | 0 | bE = 10 | |
| no changes | cE = 6 | 0 | dE = 4 | ||
| up | eE = 9 | 0 | fE = 6 | ||
| Independent Variables | Frequency (%) | p-Value | OR [95%CI] | R2 # | BASIC MODEL * |
|---|---|---|---|---|---|
| CANDIDATES FOR THE BASIC MODEL | |||||
| 1. BMI | 0.02 | BMI | |||
| underweight | 21 (0.5) | 0.2287 | 1.7 [0.72, 4.05] | ||
| standard | 931 (23.5) | reference | |||
| overweight | 1780 (44.8) | <0.0001 | 1.52 [1.29, 1.79] | ||
| obesity | 1239 (31.2) | <0.0001 | 1.97 [1.65, 2.35] | ||
| 2. place of residence | 0.0003 | ||||
| rural area | 1496 (37.7) | 0.3207 | 0.94 [0.82, 1.07] | ||
| urban area | 2475 (62.3) | reference | |||
| 3. marital status | 0.0004 | ||||
| single | 1143 (28.8) | 0.1202 | 0.9 [0.78, 1.03] | ||
| in a relationship | 2828 (71.2) | reference | |||
| 4. income | 0.007 | income | |||
| low | 1034 (26.0) | 0.0007 | 0.77 [0.67, 0.9] | ||
| average | 2226 (56.1) | reference | |||
| high | 711 (17.9) | 0.0001 | 0.7 [0.59, 0.83] | ||
| 5. daily activity | 0.003 | daily activity | |||
| passive | 1335 (33.6) | 0.0035 | 1.29 [1.09, 1.53] | ||
| mixed | 1793 (43.8) | 0.6809 | 0.97 [0.82, 1.14] | ||
| active | 897 (22.6) | reference | |||
| CANDIDATES FOR THE NEW MODELS | |||||
| ADDITIONAL | |||||
| 6. education | 0.04 | ||||
| basic | 830 (20.9) | reference | |||
| professional | 1065 (26.8) | <0.0001 | 0.63 [0.52, 0.76] | ||
| medium | 1408 (35.5) | <0.0001 | 0.45 [0.38, 0.53] | ||
| higher | 668 (16.8) | <0.0001 | 0.40 [0.33, 0.49] | ||
| 7. SCORE | 0.39 | ||||
| high | 2573 (64.8) | <0.0001 | 22.66 [18.27, 28.12] | ||
| low | 1398 (35.2) | reference | |||
| RANDOM | assumed parameters | ||||
| 8. uniform | interval: [0, 100] | 0.3049 | 1.00 [1.00, 1.00] | 0.0003 | |
| 9. normal | mean (sd) = 0 (1) | 0.4043 | 1.03 [0.96, 1.09] | 0.0003 | |
| 10. Poisson | λ = 4 | 0.0443 | 1.03 [1.00, 1.07] | 0.001 | |
| 11. exponential | λ = 1 | 0.5114 | 1.02 [0.96, 1.09] | 0.0001 | |
| 12. binomial | p = 0.1 | 0.7362 | 0.96 [0.78, 1.19] | 0.00003 | |
| 13. binomial | p = 0.5 | 0.6574 | 0.97 [0.86, 1.10] | 0.00009 | |
| Model | Wald Test p-Value | Likelihood Ratio Test p-Value | AUC [95%CI] | AUC Change after Adding Marker p-Value |
|---|---|---|---|---|
| basic | 0.59 [0.57, 0.60] | |||
| basic + education | (p < 0.0001 for each category) | <0.0001 | 0.63 [0.61, 0.65] | <0.0001 |
| basic + SCORE | <0.0001 | <0.0001 | 0.79 [0.78, 0.81] | <0.0001 |
| basic + uniform | 0.2532 | 0.2532 | 0.59 [0.57, 0.61] | 0.3989 |
| basic + normal | 0.5251 | 0.5251 | 0.59 [0.57, 0.60] | 0.7074 |
| basic + Poisson | 0.0550 | 0.0549 | 0.59 [0.57, 0.61] | 0.3206 |
| basic + exponential | 0.4761 | 0.4764 | 0.59 [0.57, 0.61] | 0.4795 |
| basic + binomial (p = 0.1) | 0.7848 | 0.7847 | 0.59 [0.57, 0.60] | 0.4742 |
| basic + binomial (p = 0.5) | 0.8866 | 0.8866 | 0.59 [0.57, 0.60] | 0.6523 |
| Model | x Number (% from n) | p-Value * | κ [95%CI] | p-Value # | NRI [95%CI] |
|---|---|---|---|---|---|
| basic + education | 311 (7.82) | <0.0001 | 0.16 [0.13, 0.19] | <0.0001 | 0.32 [0.26, 0.38] |
| basic + SCORE | 1035 (26.06) | <0.0001 | 0.50 [0.48, 0.53] | <0.0001 | 1.06 [1.01, 1.10] |
| basic + uniform | 30 (0.74) | 0.3470 | 0.01 [−0.02, 0.05] | 0.3470 | 0.03 [−0.03, 0.09] |
| basic + normal | 17 (0.41) | 0.6068 | 0.01 [−0.02, 0.04] | 0.6068 | 0.02 [−0.05, 0.08] |
| basic + Poisson | 54 (1.35) | 0.0876 | 0.03 [0.00, 0.06] | 0.0874 | 0.05 [−0.01, 0.12] |
| basic + exponential | −22 (−0.55) | 0.4733 | −0.01 [−0.04, 0.02] | 0.4736 | 0.02 [−0.04, 0.08] |
| basic + binomial (p = 0.1) | 0 (0.00) | 0.6690 | 0.00 [−0.02, 0.02] | 0.6684 | 0.01 [−0.03, 0.05] |
| basic + binomial (p = 0.5) | 14 (0.35) | 0.6574 | 0.01 [−0.02, 0.04] | 0.6574 | 0.01 [−0.05, 0.08] |
| Model | x Number (% from n) | p-Value * | Unit-κ [95%CI] | p-Value # | Unit-NRI [95%CI] |
|---|---|---|---|---|---|
| basic + education | 310 (7.8) | <0.0001 | 0.15 [0.12, 0.18] | <0.0001 | 0.31 [0.26, 0.38] |
| basic + SCORE | 1035 (26.1) | <0.0001 | 0.50 [0.48, 0.53] | <0.0001 | 1.05 [1.01, 1.10] |
| basic + uniform | 24 (0.6) | 0.1965 | 0.007 [−0.004, 0.018] | 0.1984 | 0.02 [−0.01, 0.06] |
| basic + normal | −6 (−0.2) | 0.3595 | −0.002 [−0.005, 0.002] | 0.3599 | −0.006 [−0.019, 0.007] |
| basic + Poisson | 30 (0.7) | 0.1588 | 0.010 [−0.004, 0.023] | 0.1590 | 0.030 [−0.011, 0.072] |
| basic + exponential | 8 (0.2) | 0.2918 | 0.002 [−0.002, 0.006] | 0.2950 | 0.008 [−0.07, 0.023] |
| basic + binomial (p = 0.1) | 0 (0) | 1.0000 | 0.000 [0.000, 0.000] | NA | 0.000 [0.000, 0.000] |
| basic + binomial (p = 0.5) | 0 (0) | 1.0000 | 0.000 [0.000, 0.000] | NA | 0.000 [0.000, 0.000] |
| Model | x Number (% from n) | p-Value * | κ (p) [95%CI] | p-Value # | NRI (p) [95%CI] |
|---|---|---|---|---|---|
| basic + education | 52 (1.3) | 0.0012 | 0.01 [0.01, 0.02] | <0.0001 | 0.06 [0.03, 0.09] |
| basic + SCORE | 397 (10.0) | <0.0001 | 0.13 [0.11. 0.14] | <0.0001 | 0.40 [0.37. 0.44] |
| basic + uniform | −6 (−0.2) | 0.3936 | −0.002 [−0.001, 0,002] | 0.3934 | −0.007 [−0.022, 0.009] |
| basic + normal | 2 (0.1) | 0.3332 | 0.001 [−0.001, 0.002] | 0.2749 | 0.004 [−0.003, 0.011] |
| basic + Poisson | 9 (0.2) | 0.2882 | 0.002 [−0.002, 0.007] | 0.2879 | 0.009 [−0.008, 0.026] |
| basic + exponential | 4 (0.1) | 0.1987 | 0.001 [−0.001, 0.002] | 0.1999 | 0.004 [−0.002, 0.010] |
| basic + binomial (p = 0.1) | 0 (0.0) | 0.9092 | 0.000 [−0.002, 0.002] | 0.9998 | 0.000 [−0.004, 0.004] |
| basic + binomial (p = 0.5) | 0 (0.0) | 1.0000 | 0.000 [0.000, 0.000] | NA | 0.000 [0.000, 0.000] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Więckowska, B.; Kubiak, K.B.; Jóźwiak, P.; Moryson, W.; Stawińska-Witoszyńska, B. Cohen’s Kappa Coefficient as a Measure to Assess Classification Improvement following the Addition of a New Marker to a Regression Model. Int. J. Environ. Res. Public Health 2022, 19, 10213. https://doi.org/10.3390/ijerph191610213
Więckowska B, Kubiak KB, Jóźwiak P, Moryson W, Stawińska-Witoszyńska B. Cohen’s Kappa Coefficient as a Measure to Assess Classification Improvement following the Addition of a New Marker to a Regression Model. International Journal of Environmental Research and Public Health. 2022; 19(16):10213. https://doi.org/10.3390/ijerph191610213
Chicago/Turabian StyleWięckowska, Barbara, Katarzyna B. Kubiak, Paulina Jóźwiak, Wacław Moryson, and Barbara Stawińska-Witoszyńska. 2022. "Cohen’s Kappa Coefficient as a Measure to Assess Classification Improvement following the Addition of a New Marker to a Regression Model" International Journal of Environmental Research and Public Health 19, no. 16: 10213. https://doi.org/10.3390/ijerph191610213
APA StyleWięckowska, B., Kubiak, K. B., Jóźwiak, P., Moryson, W., & Stawińska-Witoszyńska, B. (2022). Cohen’s Kappa Coefficient as a Measure to Assess Classification Improvement following the Addition of a New Marker to a Regression Model. International Journal of Environmental Research and Public Health, 19(16), 10213. https://doi.org/10.3390/ijerph191610213






