Abstract
To scientifically and quantitatively evaluate the degree of urban storm resilience and improve the level of urban stormwater resilience, based on the resilience theory, starting from the three attributes of resilience (resistance, recovery and adaptability), this paper establishes the framework of urban resilience evaluation indicator system under the background of stormwater disaster. Firstly, the weight of the indicator system is analyzed by the Delphi method and cloud model, and then the urban stormwater recilience evaluation model is constructed by using the cloud model and approximate ideal solution ranking method. Through the fuzzy description, the corresponding quantitative value is given to the qualitative indicator, so that the stormwater resilience of the city can be measured by accurate values. Finally, the feasibility of the model is verified by case analysis. The results show that the urban stormwater resilience evaluation theory and method based on cloud model and approximate ideal solution ranking method have important guiding significance to improve the level of urban stormwater resilience.
1. Introduction
In recent years, the impact of climate change on cities has become more and more serious. In particular, natural disasters such as heavy rain and flood brought by extreme weather have posed a huge threat to the public safety of cities around the world [1]. In such a context, the research related to resilience science opens up a new perspective for the study of urban security. Among them, the evaluation of urban stormwater resilience is a major research hotspot. Based on the basic theory of resilience, this research evaluates the ability of cities to deal with the flood damage from various aspects and dimensions, finds out the weaknesses in each structure and link of the city, and finally puts forward the corresponding improvement suggestions and measures [2].
With the deepening of the research on the discipline of resilience, scholars from all over the world began to refine the evaluation of urban stormwater resilience into specific indicators, and scientifically evaluate the degree of urban stormwater resilience with quantitative indicators, making the design of an urban stormwater resilience evaluation system more comprehensive and scientific. For example, in 2013, Orencio and other scholars constructed a resilience index system for coastal communities to cope with flood disasters and elaborated the corresponding seven aspects that affect the resilience of coastal communities [3]. Then, the AHP method (analytic hierarchy process) was used to calculate the resilience index of cities. In 2016, Kotzee and Reyers proposed a comprehensive index covering economic, social, ecological, and infrastructure indicators related to stormwater resilience, and mapped the spatial distribution of resilience from the perspective of system adaptability and vulnerability [4]. In the same year, Qasim and other scholars established a four-layer community flood disaster resilience index of social, economic, institutional and physical [5], and evaluated and analyzed the community resilience index in three districts of Khyber Pakhtunkhwa Province by using expert evaluation method. In 2017, Miguez and Verol designed a stormwater toughness index model tool with the help of the multi-criterion method and hydrodynamic model, which can quantitatively express the toughness index of different stormwater management schemes [6]. Yu Kongjian proposed three key strategies for stormwater resilience urban construction: absorption, deceleration, and adaptation, and verified their effectiveness through field experimental projects [7]. According to the characteristics of Weimar Ilmpark, Tian Lu analyzed the necessity and potential of stormwater management in this area and proposed corresponding improvement strategies for the construction of stormwater resilience cities in China based on urban resilience theory [8]. Zhou Yinan et al. constructed a set of storm flood resilience urban design systems, which includes the optimization of land use, urban organizational structure, establishment of multi-functional space and integration of an urban system, extending the boundary of traditional urban design and providing a new choice for performance eco-city design [9]. Ma Kun et al. constructed a stormwater management model based on the toughness theory, and then proposed a corresponding stormwater management construction model by calculating the flood-bearing capacity of the study area [10]. The research on urban storm flood resilience started late in China, and the assessment of urban storm flood resilience mainly focuses on qualitative research.
In this paper, the urban stormwater resilience assessment system is taken as the research object, and the influence degree of natural disasters and safety production technology level on the urban stormwater resilience is mainly studied. Therefore, the purpose of this paper is to improve the city’s ability to resist natural disasters by effectively evaluating the resilience of urban rainwater, so as to provide a theoretical basis for strategic thinking and countermeasures for the construction of resilient cities.
2. Related Theories and Methods
2.1. Resilience and Stormwater Resilience
Resilience means “rebound or retreat.” In the 1970s, Canadian ecologist Hollin first applied the concept of resilience in the field of systems ecology to express “the ability of an ecosystem to recover to its original structural stability after being impacted by the outside world” [11]. With the deepening of relevant research and interdisciplinary exchanges, the concept of resilience has gradually expanded to the fields of human beings, social ecology, urban economy, urban and rural planning. At the same time, scholars’ interpretation of the connotation of resilience is becoming more and more thorough and perfect. The academia generally believes that resilience has three basic elements, namely, the system’s defense ability to resist external shocks, the resilience ability to recover to its original structure after bearing external disturbances, and the better adaptability to withstand the risk impact of the next disaster.
The concept of stormwater resilience originates from system ecology and is a kind of resistance, resilience, adaptability and self-learning ability to cope with extreme natural disasters such as flood and waterlogging, with a certain degree of redundancy [12]. The concept and connotations of stormwater resilience are not uniform and fixed, and mostly change with the change in practice and application objects [13]. For example, Bell believes that the stormwater resilience of buildings refers to the ability of buildings to withstand the damage of rain and flood [14]. Tourbier believes that storm flood resilience in planning spatial dimension can be summarized from four aspects: society, structure, space and risk management, mainly including flood control engineering, green space management, institutional management, flood area planning, storm runoff control and financial insurance assistance [15]. Batica et al. believed that regional or community storm flood resilience is a restorative and adaptive learning organization in physical, natural, social, institutional and economic aspects within a certain range [16]. Liao Guixian et al. believe that storm flood resilience can be interpreted as the ability of a city to withstand floods, including the resistance ability of traditional flood prevention projects, flood adaptation organization ability to prevent casualties and property losses, and management ability to maintain urban infrastructure and social and economic stability [17].
2.2. Cloud Model
Cloud model is a cognitive model based on normal distribution function and membership function [18]. It is based on probability statistics and fuzzy set theory to realize the two-way conversion between qualitative concepts and quantitative data. It can effectively represent the concepts of fuzziness, randomness and uncertainty, and has been widely used in the fields of weight calculation, time series mining and decision evaluation [19]. Let U be a quantitative domain expressed by precise numerical values and C be a qualitative concept on the domain U. If the quantitative value is x ∈ U, and x is a random realization of the qualitative concept C, then the membership degree of x to C [0,1] is a random number with a stable tendency. Where there is X, the distribution of X in the domain U is called the subordinate cloud, which is called cloud for short. The result of a random numerical conversion of the qualitative concept through a specific algorithm using the digital characteristics of the cloud is called a cloud drop. A cloud drop contains an element X in the field U and its membership degree to concept C in this conversion, denoted as (x, ‘).
Normality is the most important property of the cloud model. Expectation Ex, entropy En and hyperentropy He are used to describe the three digital features of cloud model. A cloud model can usually be written as C = (Ex, En, He). Among them, the point that can best represent the qualitative concept of Expected Ex in the domain space is the most typical sample point for the quantization of the concept. Entropy En represents the measurable granularity of a qualitative concept. In general, the larger the entropy is, the more macroscopic the concept is. Entropy also reflects the uncertainty of the qualitative concept. Hyperentropy He represents the entropy of entropy and is a measure of entropy’s uncertainty. It reflects the randomness of samples representing qualitative concept values and reveals the association between fuzziness and randomness. In particular, when He = 0, the cloud model degenerates into the form of normal membership function.
Reverse cloud generator is a transformation model from quantitative value to qualitative concept. Its principle is that a certain number of precise values can be reasonably converted into appropriate qualitative language values (Ex, En, He) from statistical “cloud drops”. It is a mapping from quantitative to qualitative. This is a reverse and indirect process, which provides a favorable means for fuzzy comprehensive evaluation. Figure 1 is its schematic diagram.
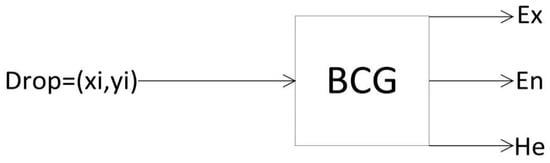
Figure 1.
Schematic diagram of reverse cloud generator.
2.3. TOPSIS
The approximate ideal solution ranking method is a commonly used and effective method in multi-objective decision analysis [20]. Its basic principle is to rank the evaluated objects based on the distance between positive and negative ideal solutions in multi-objective decision problems. If all the indicators of the positive ideal solution are optimal, it can be understood as a virtual optimal solution while the negative ideal solution is completely opposite. The TOPSIS method evaluates the relative merits and demerits of the evaluation object according to the distance memory ranking between the evaluation object and the idealized target. If the evaluation object is closest to the positive ideal solution, it is the optimal value; otherwise, it is the worst value [21]. The steps to calculate the degree of closeness by using the approximate ideal solution ordering method (TOPSIS) are as follows:
(1) Build the initial evaluation matrix
In this matrix, each row represents an index grade, and each column represents an evaluation index. Assume that there are n evaluation indexes and m index grades, then the initial evaluation matrix can be constructed as follows:
The element xij in the initial evaluation matrix A can be expressed as the score value of the ith index relative to the j criteria.
Normalized numerical processing is carried out on the initial judgment matrix A, and then we can find the normalized initial judgment matrix of Aij:
(2) Construction of weighted standardized decision matrix
Using the cloud model and Delphi method, the relative weight W of each index factor is obtained.
Each column of the matrix Aij is multiplied by the weight Wj to find the weighted normalization decision matrix Bij.
(3) Closeness degree analysis
The positive and negative ideal solutions S+ and S− are calculated. They are respectively expressed as:
Here, represents the positive ideal solution, represents the weighted standardized decision matrix, J = (J = 1, 2, 3 … m)/j represents benefit attribute, J′ = (j = 1, 2, 3 … m)/j represents the cost attribute.
Here, represents the negative ideal solution, represents the weighted standardized decision matrix, J = (J = 1, 2, 3 … m)/j represents benefit attribute, J′ = (j = 1, 2, 3 … m)/j represents the cost attribute.
Calculate the distance between each evaluation index and the positive ideal solution Si+ and the negative ideal solution Si−. The calculation formula is as follows:
Here, represents the distance between each evaluation index and the positive ideal solution, represents the weighted standardized decision matrix, and represents the maximum value.
Here, represents the distance between each evaluation index and the positive ideal solution, represents the weighted standardized decision matrix, and represents the maximum value.
The closeness degree between each evaluation index grade and the positive ideal solution is calculated by the following formula:
3. Construction of Urban Stormwater Resilience Evaluation Index System
Based on relevant domestic and foreign literature [22,23,24,25,26,27] and the actual situation of major cities in China in dealing with rain flood damage, the evaluation index system of urban storm flood resilience was established from three dimensions of resistance, recovery and adaptability.
Resistance refers to the ability of a city to withstand the impact of rain and flood damage. Considering urban flood control facilities, for example, traditional urban flood control facilities only include some basic engineering facilities such as levees and dams, which do not meet the standards of building resilient cities. The construction of resilient cities not only requires more high-standard and strict urban flood control engineering facilities [23], but also requires urban residents to have self-consciousness, good flood resistance awareness, and certain personal flood control capacity [24]. Only by meeting the above conditions can we ensure that residents can react quickly and take corresponding flood control measures actively when the rain and flood damage comes, so as to reduce unnecessary economic losses and casualties.
Recovery refers to the ability of a city to change from an unbalanced state to a balanced state in time. It is intuitively shown as the ability of a city to eliminate the adverse effects caused by rain and flood (such as sewage, stagnant water, garbage and disease.) and restore the normal order of the city in a timely manner. Among them, urban infrastructure [23], residents’ education level [24], social capital [25], resource access [25], urban governance [26] and other factors will affect the speed and degree of urban recovery, which is an important factor to measure the resilience of a city.
Adaptability refers to a city’s ability to adjust itself to different levels of storm flooding. The city is formed by the interaction between man and nature, mutual feedback, through the establishment of good natural ecological system, and a developed city drainage system, and a new type of non-spot resource recycling system can improve the adaptability of a city for rain flood hazard, and among them, the good natural ecological system can effectively promote the regional climate and automatically adjust ability and the ability of ecological water culvert [27]. A developed urban drainage system has a certain degree of water storage capacity and can discharge urban rainwater to rivers, lakes and seas outside the city in a timely fashion. The new stormwater resource recycling system can make full use of stormwater resources through water storage and water purification, thus promoting the harmonious development of man and nature in the city.
Based on the above analysis, a set of evaluation index systems of urban resilience under the background of rain flood damage is constructed. The first-level index (target layer) is urban storm flood resilience, and the second-level index (decision-making layer) is resistance, resilience and adaptability. The third-level indicators are selected with reference to China Statistical Yearbook [28], with a total of 18 items, as shown in Table 1.

Table 1.
Urban stormwater resilience evaluation index system.
The selection basis of three-level indicators under resistance is that the level of education will affect the people’s awareness of flood fighting and flood control, broad and high-quality urban roads are conducive to rescue and evacuation in and after accidents, the action ability of the elderly and children is low, which will affect the emergency evacuation and rescue ability of the city, and flood control engineering facilities are important infrastructures to resist flood disasters
The selection basis of three-level indicators under recovery is that the employment rate will directly affect the city’s per capita GDP, and the city needs strong human and economic support to recover from the impact of rain and flood disasters. The level and ability of urban medical treatment will affect the rescue rate of the injured after rain and flood disasters.
The selection basis of three-level indicators under adaptability is that the good education level of urban residents will greatly promote the improvement of urban learning and adaptability. The urban green area and the water area of lakes and rivers will affect the ecological water cycle function and climate quality of the city, and the total urban water storage and comprehensive production capacity are conducive to the purification and treatment of rainwater.
4. Establishment of Urban Stormwater Resilience Evaluation Model
4.1. Cloud Model Combines with Delphi Method to Calculate the Weight of Indicators
The traditional index weight determination method is highly subjective. To reduce the subjectivity of weight determination, the cloud weight (Ex, En, He) method is selected in this paper to soften the traditional weight. Ex is expected to be the traditional weight, and entropy En and hyperentropy He are the parameters used to soften the weight.
(1) Delphi method
Relevant professionals and mostly experts and scholars were invited to weigh the indicators in the evaluation index system of urban rainwater toughness, and the importance of the lower index (such as the index layer) to the upper index (such as the criterion layer) was given a score based on 0–1.
(2) Cloud weight solution and correction
A reverse cloud generator algorithm is used to process the expert rating results to obtain the cloud weight corresponding to each index and generate the corresponding cloud map. The thicker the cloud in the cloud map, the higher the superentropy value and the greater the dispersion of cloud droplets, which indicates that the experts’ scoring results differ greatly, and the persuasion is low. Suggestions should be put forward on the experts’ scoring results and a new round of grading revision should be carried out to modify the index cloud weight. According to the procedure of “expert rating—result collection—cloud image judgment—opinion feedback—expert rating”, the cloud image is constantly improved to reduce the dispersion of cloud droplets, reduce the subjectivity of index cloud weight, and improve the accuracy and scientificity of evaluation results.
(3) Weight normalization processing
After calculating the index cloud weights of each layer of the urban stormwater toughness evaluation index system, it is necessary to normalize the index cloud weights of the same layer according to Equation (9).
is the cloud weight of indicators at each layer, is the sum of the cloud weight of indicators at the same layer, and is the indicator weight after normalization.
The steps to determine the weight of each index by combining the cloud model and the Delphi method are as follows:
According to the steps to determine the weights of urban rainwater resilience assessment indicators in the previous section, 10 experts in the industry were invited to score the importance of the lower level indicators relative to the upper level, that is, the importance of Bi(i = 1, 2, 3) relative to A, and Ci relative to BI. Ten points of the expert weight scoring table were issued and, ten copies were recycled. Finally, the cloud model is used to reverse the cloud generator to obtain the cloud weight of the lower layer relative to the upper index.
The evaluation index system of urban rainwater resilience involves a total of 18 indexes, which will not be described in this paper due to space limitation. Here, the determination process of the cloud weight between the resistance index of the criterion layer and the target layer is taken as an example to illustrate. The expert grading table is shown in Table 2.

Table 2.
Weight grading table of Bi relative to A.
Python programming language is used to implement reverse cloud generator algorithm, and the weight scoring results of B1 are processed to obtain the first score result’s cloud weight (0.9180, 0.0421, 0.0170). At the same time, the forward generator is used to generate the cloud map of the weight of B1 cloud, as shown in Figure 2. According to the weighted cloud map of B1 cloud, it can be seen that the cloud is thicker and the cloud drops are more dispersed, which means that there are big differences among experts when evaluating the importance of resistance relative to the toughness of urban rainwater in the scoring process. To improve the consistency of experts’ recognition of the cloud weight scoring results and reduce the subjective randomness of the scoring results, experts were invited to score again. After repeated feedback and correction, the cloud drop layer thickness in Figure 2 is obviously getting smaller and smaller, and the expert opinions are gradually unified. The cloud weight of resistance relative to urban stormwater resilience is (0.9230, 0.0163, 0.0065).
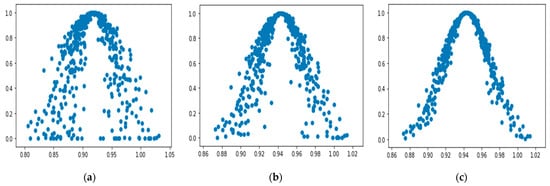
Figure 2.
Process diagram of cloud weight correction. (a) Experts score for the first time; (b) experts score for the second time; (c) experts score for the third time.
The above process is repeated to determine the index cloud weights of each layer of the urban storm flood resilience assessment index system and continuously revise them. Finally, the normalization process is conducted to obtain the index cloud weights of each layer of the urban storm flood resilience assessment index system, as shown in Table 3.

Table 3.
Urban stormwater resilience assessment index system cloud weight.
The index weights of each layer in the urban stormwater resilience assessment index system are summarized as shown in Table 4.

Table 4.
Weight table of urban stormwater resilience evaluation indicators.
4.2. The Indicator Closeness Degree Was Calculated by TOPSIS Method
4.2.1. Fuzzy Description of Resilience Indicator Grade
Because the units and orders of magnitude of each indicator are inconsistent, we set four ranges for each three-level indicator by referring to the standard ranges of each indicator in various provinces in China and assign corresponding scores to each range. Among them, 1 indicates that the index is lower than the national average, 2 and 3 indicate that the index is around the national average, and 4 indicates that the index is higher than the national average. We divided the fuzzy grade description of each resilience indicator into four levels, among which the first level indicates that the city has the lowest level of storm flood resilience, and the city under this level will face great flood risk and the subsequent recovery process will be very slow. Level 2 indicates that the level of storm flood resilience of a city is relatively poor. Cities under this level are still facing great flood risk, and uncontrollable accident consequences may occur when the rainstorm comes. Level 3 indicates that the city’s flood resilience level is in a good stage. Any city under this level has a certain resistance capacity and can be controlled in a relatively quick time once it is attacked by the flood. Level 4 indicates that the city has the highest degree of flood resilience, and a city under this level can make corresponding prediction measures in advance by virtue of its strong resistance and adaptability to avoid large losses.
Due to the limited space, only the fuzzy description of each third-level indicator under the second-level indicator is displayed. For the fuzzy description of the remaining third-level indicators. See the Supplementary Material.
(1) Fuzzy description of resistance indicator grade
The proportion of population over 60 years old and under 18 years old C1 value standard: the proportion of population over 60 years old and under 18 years old in the total population of the city. The fuzzy description of C1 is shown in Table 5.

Table 5.
Fuzzy description of the percentage of the population aged over 60 and under 18.
(2) Fuzzy description of recovery indicator grade
Per capita GDP C7 value standard: measure the GDP ranking obtained by the National Bureau of Statistics to judge the level of the city’s per capita GDP. The fuzzy description of C7 is shown in Table 6.

Table 6.
Fuzzy description of GDP per capita.
(3) Fuzzy description of adaptability indicator grade
Per capita public green area C12 value standard: the average area of public green space occupied by each resident in the city. The fuzzy description of C12 is shown in Table 7.

Table 7.
Fuzzy description of per capita public green area.
(4) Secondary indicator evaluation grade value
The evaluation index grades of resistance are shown in Table 8.

Table 8.
Values of resistance evaluation indicator grades.
The evaluation index grades of recovery are shown in Table 9.

Table 9.
Values of recovery evaluation indicator grades.
The evaluation index grades of adaptability are shown in Table 10.

Table 10.
Values of adaptability evaluation indicator grades.
4.2.2. Standard for Resilience Grade of Urban Stormwater
According to the grade fuzzy description of resilience index, the initial evaluation matrix AK was constructed.
Set the resistance evaluation matrix as A1,
The distance S1+, S1−, and closeness degree Ei+ between the resistance indicator class value and the positive and negative ideal solution were calculated, as Table 11 shown.

Table 11.
Resistance grade standard.
Set the recovery evaluation matrix as A2,
The distance S1+, S1−, and closeness degree Ei+ between the recovery indicator class value and the positive and negative ideal solution were calculated, as Table 12 shown.

Table 12.
Recovery grade standard.
Set the adaptability evaluation matrix as A3,
The distance S1+, S1−, and closeness degree Ei+ between the adaptability indicator class value and the positive and negative ideal solution were calculated, as Table 13 shown.

Table 13.
Adaptability grade standard.
To sum up, the urban stormwater resilience grade standard is shown in Table 14.

Table 14.
Urban stormwater resilience grade standard.
According to Table 14, the grading standards of urban stormwater resilience can be obtained as follows:
Level 1: 0 ≤ Ei+ < 0.3896
Level 2: 0.3896 ≤ Ei+ < 0.7194
Level 3: 0.7194 ≤ Ei+ < 1
Level 4: Ei+ = 1
In the first level, the resilience of urban stormwater is at the least ideal state. Once in the first level, the system will be faced with huge flood risk or the disaster resistance and recovery ability of the system is very poor, which will cause extremely serious consequences. Level 2 refers to the situation in which the resilience of urban stormwater is relatively poor. The system in level 2 is still facing great flood risk and will cause uncontrollable accident consequences once the rainstorm occurs. Level 3 refers to the situation in which the resilience of urban stormwater is relatively good. The system in level 3 is capable of resisting floods to a certain extent, and it can be controlled within a certain period of time once the rainstorm occurs. Level 4 is the ideal condition of urban stormwater resilience. The system in level 4 can predict and avoid or respond to the flood in time, so that it will not cause great losses. The system has a strong learning ability and can draw experience from the flood disaster suffered by the system, which makes the resilience level of the system higher and higher.
5. Example Analysis and Discussion
Taking the heavy rainstorm in Beijing on 7.21 as an example, this paper comprehensively evaluated the rainwater toughness of Beijing at that time by applying the cloud model TOPSIS resilience evaluation model, found out the weak links in the response to the rainwater and flood damage of Beijing at that time and put forward corresponding suggestions.
5.1. Rainstorm Flood Resilience Indicator Grade of Beijing
Through referring to relevant literature, we have mastered the relevant data of Beijing before the heavy rainstorm on July 21, and now we have classified the three-level indicators of rainstorm resilience in Beijing, as Table 15 shown.

Table 15.
Grade classification of stormwater resilience indicators in Beijing.
5.2. Stormwater Resilience Assessment in Beijing
According to Formula (1), the initial evaluation matrix A of stormwater resilience in Beijing is obtained.
Then, the initial evaluation matrix A is dimensionless to obtain the standard decision matrix B.
According to Formula (4) to Formula (8), the distance S1+, S1−, and the closeness degree E1+ between the value of stormwater resilience capacity indicator grade in Beijing and the positive and negative ideal solutions are obtained, as shown in Table 16.

Table 16.
Urban stormwater resilience grade standard.
Through calculation, the final result of the stormwater resilience assessment of Beijing is 0.5196, which means that the stormwater resilience level of Beijing is at the second level. In other words, the stormwater resilience level of Beijing is relatively poor. Once a flood with large precipitation occurs, uncontrollable accident consequences will be caused.
It can be seen from the fuzzy description of the stormwater resilience indicator of Beijing above that the indicator score of the pumping and discharging capacity of pumps, the surface area of lakes and rivers, the capacity of reservoirs and the comprehensive production capacity of water plants in the central urban area of Beijing is only 1. This indicates that the water storage of Beijing is low, and the capacity of self-production of water and the drainage capacity of the urban system are at the downstream level. In recent years, although projects such as “South-to-North Water Diversion” have been carried out to supply water from water-rich areas to water-poor cities, when extreme weather disasters such as 7.21 come, cities with low stormwater resilience still find it difficult to resist the impact and pressure brought about by disasters, and bear relatively serious consequences. This reflects that the key for a city to cope with the hazards of natural disasters is to improve the resilience of the city itself.
According to the above numerical results and analysis, it is suggested that the relevant urban management departments should improve the pumping and discharging capacity of urban water pumps and the comprehensive production capacity of water plants, so as to strengthen the drainage capacity of urban systems and increase the total water storage of the city and at the same time, strengthen the protection of urban rivers and waters, publicize the importance of water resources protection and encourage urban people to actively participate in the protection of urban water resources, so as to avoid the drying up and degradation of urban rivers and waters to the greatest extent. It is believed that with the effective implementation of these measures, the resilience level of urban stormwater will be significantly improved.
6. Conclusions
(1) According to the safety assessment methods developed by our predecessors and relevant literature and data, according to the actual situation of urban flood resistance and relevant national regulations, the indicators affecting urban rain and flood resilience are analyzed, and a three-level indicator system is constructed. The first-level indicators are urban rain and flood resilience, the second-level indicators are resistance, recovery and adaptability, and there are 18 third-level indicators in total. The indicator system of the model is relatively perfect, and the weight of each evaluation indicator is effectively unified.
(2) The cloud model and Delphi method are used to obtain the relative weight of evaluation indicators at all levels. The relative weight value indicates the influence degree of each subordinate indicator on the final goal. By comparing the relative weight value, we can find the vulnerable points in the overall system, and then provide targeted management measures and suggestions for relevant departments.
(3) Through the fuzzy description of the resilience indicator level and using the approximate ideal solution ranking method (TOPSIS method), the distance and closeness between each level indicator and the positive and negative ideal solution can be obtained. The calculated closeness can be used to represent the high or low degree of urban stormwater resilience.
(4) The constructed cloud TOPSIS evaluation model is applied to Beijing under the Severe Rainstorm on July 21. Through an all-round data search, sorting and calculation, it is finally determined that the stormwater resilience of Beijing was at the second level at that time.
Due to a relatively small number of quantitative indicators, which fail to cover all aspects that affect urban resilience, and individual indicators are limited by regions, the applicability of the model established in this paper is limited. The next step is to construct an indicator system from multi-dimensional considerations to improve the applicability of the model. In addition, the characteristics of this paper that are absolute values are used to indicate that it can contrast the evaluation indicator and the national average gap, but considering that the relative characteristics are used to indicate if some indicators can be according to different population scales, area size, and organizational structure, the results of the city are also needed to be considered in future research work.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ijerph19010038/s1, Fuzzy description of other three-level indicators.
Author Contributions
H.Q. wrote the manuscript, contributed to the theory of the study and contributed significantly to analysis and manuscript preparation. J.P. performed the data analyses, helped perform the analysis with constructive discussions and contributed to software and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China (No.52004258), and the APC was funded by The National Natural Science Foundation of China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Robin, L. Climate change and urban resilience. Curr. Opin. Environ. Sustain. 2011, 3, 164–168. [Google Scholar]
- Solecki, W.; Leichenko, R.; O’Brien, K. Climate change adaptation strategies and disaster risk reduction in cities: Connections, contentions, and synergies. Curr. Opin. Environ. Sustain. 2011, 3, 135–141. [Google Scholar] [CrossRef]
- Orencio, P.M.; Fujii, M. A localized disaster-resilience index to assess coastal communities based on an analytic hierarchy process (AHP). Int. J. Disaster Risk Reduct. 2013, 3, 62–75. [Google Scholar] [CrossRef]
- Kotzee, I.; Reyers, B. Piloting a social-ecological index for measuring flood resilience: A composite index approach. Ecol. Indic. 2016, 60, 45–53. [Google Scholar] [CrossRef]
- Qasim, S.; Qasim, M.; Shrestha, R.P.; Khan, A.N.; Tun, K. Community resilience to flood hazards in Khyber Pukhthunkhwa province of Pakistan. Int. J. Disaster Risk Reduct. 2016, 18, 100–106. [Google Scholar] [CrossRef]
- Miguez, M.G.; Veról, A.P. A catchment scale Integrated Flood Resilience Index to support decision making in urban flood control design. Environ. Plan. 2017, 44, 925–946. [Google Scholar] [CrossRef]
- Kongjian, Y.U. Three Key Strategies to Achieve A Sponge City: Retention, Slow Down and Adaptation. South Archit. 2015, 1, 4–7. [Google Scholar]
- Tian, L.; Wang, Y.C. Research on Stormwater Management of Cultural Heritage Ilmpark in Weimar Germany Based on Urban Resilience. Nat. Resour. 2015, 6, 398–404. [Google Scholar]
- Zhou, Y.; Li, B. Form Follows Water: A Study on Stormwater Resilient Urban Design. China City Plan. Rev. 2017, 26, 32–39. [Google Scholar]
- Kun, M.A.; Tang, X.; Ren, Y.; Ge, Y.; Deng, M. Study on construction strategy of storm water management in hilly land based on resilience theory. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2018, 42, 139–145. [Google Scholar]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef] [Green Version]
- De Bruijn, K.M. Resilience and Flood Risk Management, A Systems Approach Applied to Lowland Rivers; Delft University Press: Delft, The Netherlands, 2005. [Google Scholar]
- Bruijn, K.D.; Buurman, J.; Mens, M.; Dahm, R.; Klijn, F. Resilience in practice: Five principles to enable societies to cope with extreme weather events. Environ. Sci. Policy 2017, 70, 21–30. [Google Scholar] [CrossRef]
- Bowker, P.; Wallingford, H. Improving the Flood Resilience of Buildings through Improved Materials, Methods and Details. 2005. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.189.3455&rep=rep1&type=pdf (accessed on 12 November 2021).
- Tourbier, J. A Methodology to Define Flood Resilience. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012. [Google Scholar]
- Batica, J.; Gourbesville, P. Methodology for Flood Resilience Index Development. In Proceedings of the International Conference on Flood Resilience Experiences in Asia & Europe-icfr, Brisbane, Australia, 26 June–1 July 2011. [Google Scholar]
- Liao, K.H.; Lin, H.; Yang, W. A Theory on Urban Resilience to Floods-A Basis for Alternative Planning Practices. Urban Plan. Int. 2015, 17, 388–395. [Google Scholar] [CrossRef]
- Wang, S.G.; Sun, Q.B.; Zhang, G.W.; Yang, F. Uncertain QoS-Aware Skyline Service Selection Based on Cloud Model. J. Softw. 2012, 23, 1397–1412. [Google Scholar] [CrossRef]
- Xu, C.L.; Wang, G.Y.; Zhang, Q.H. A New Multi-Step Backward Cloud Transformation Algorithm Based on Normal Cloud Model. Fundam. Inform. 2014, 133, 55–85. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.; Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making. Lect. Notes Econ. Math. Syst. 1981, 404, 287–288. [Google Scholar]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Systems 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Zhe, L.Z. Research on Natural Disaster Risk Assessment Index System and Method. China Saf. Sci. J. 2010, 11, 61–65. [Google Scholar]
- Joerin, J.; Shaw, R.; Takeuchi, Y.; Krishnamurthy, R. Assessing community resilience to climate-related disasters in Chennai, India. Int. J. Disaster Risk Reduct. 2012, 1, 44–54. [Google Scholar] [CrossRef]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. Community and regional resilience: Perspective from hazards, disaters and emergency. Community Reg. Resil. Initiat. Tenn. 2008, 1, 383–398. [Google Scholar]
- Jabareen, Y. Planning the resilient city: Concepts and strategies for coping with climate change and environmental risk. Cities 2013, 31, 220–229. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, B. Resilient Urban Design For Flood Control. Planners 2017, 33, 90–97. [Google Scholar]
- Gao, M.A.; Mu, Y. China Statistical Yearbook: Retrospect and Prospect of Construction on the Window of Government Statistics. Stat. Res. 2012, 29, 38–43. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).