Controlling COVID-19 Outbreaks with Financial Incentives
Abstract
1. Introduction
2. Mathematical Model and Numerical Solution Algorithm
3. Computational Experiments
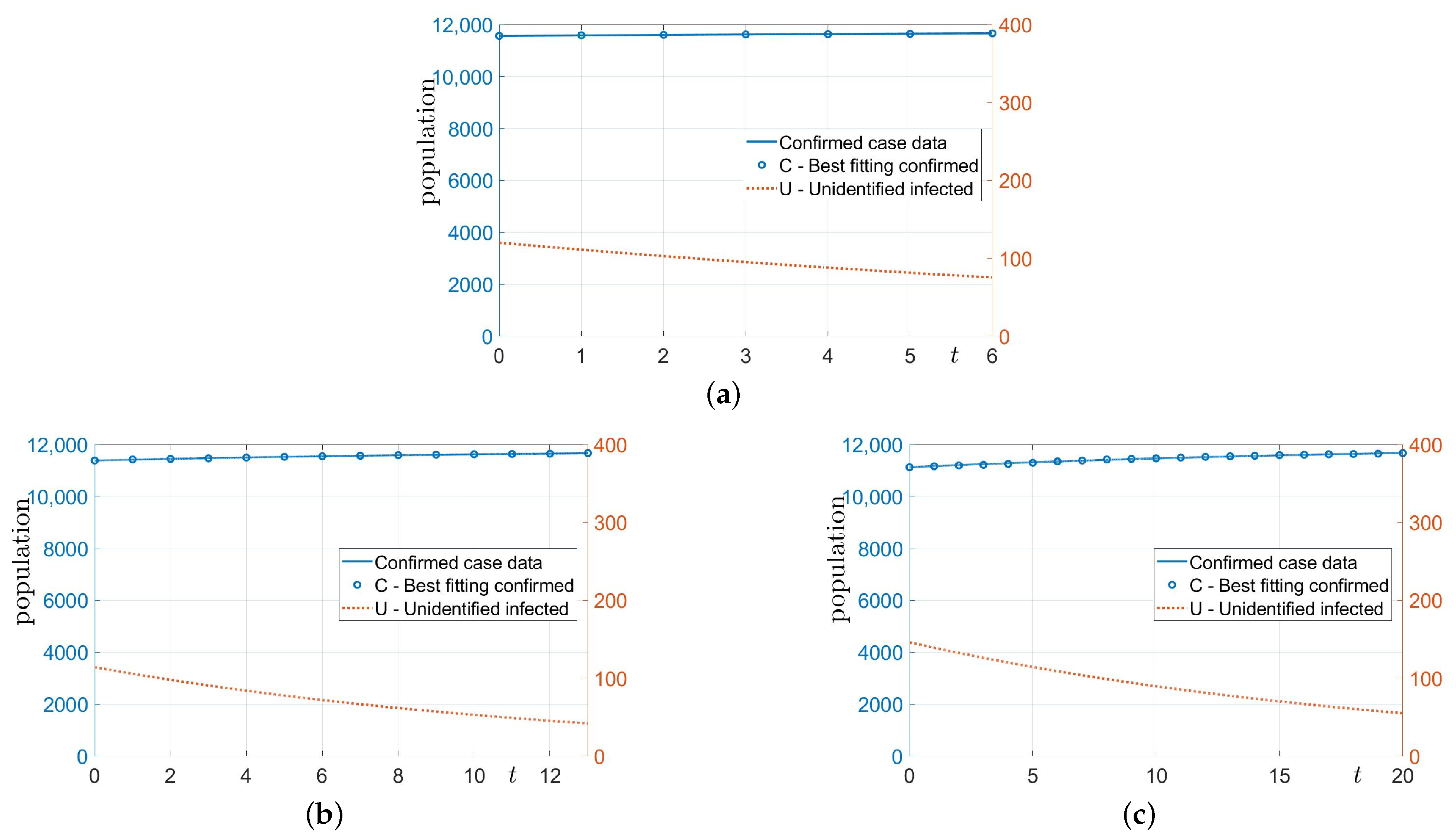
3.1. Estimation without Financial Incentives
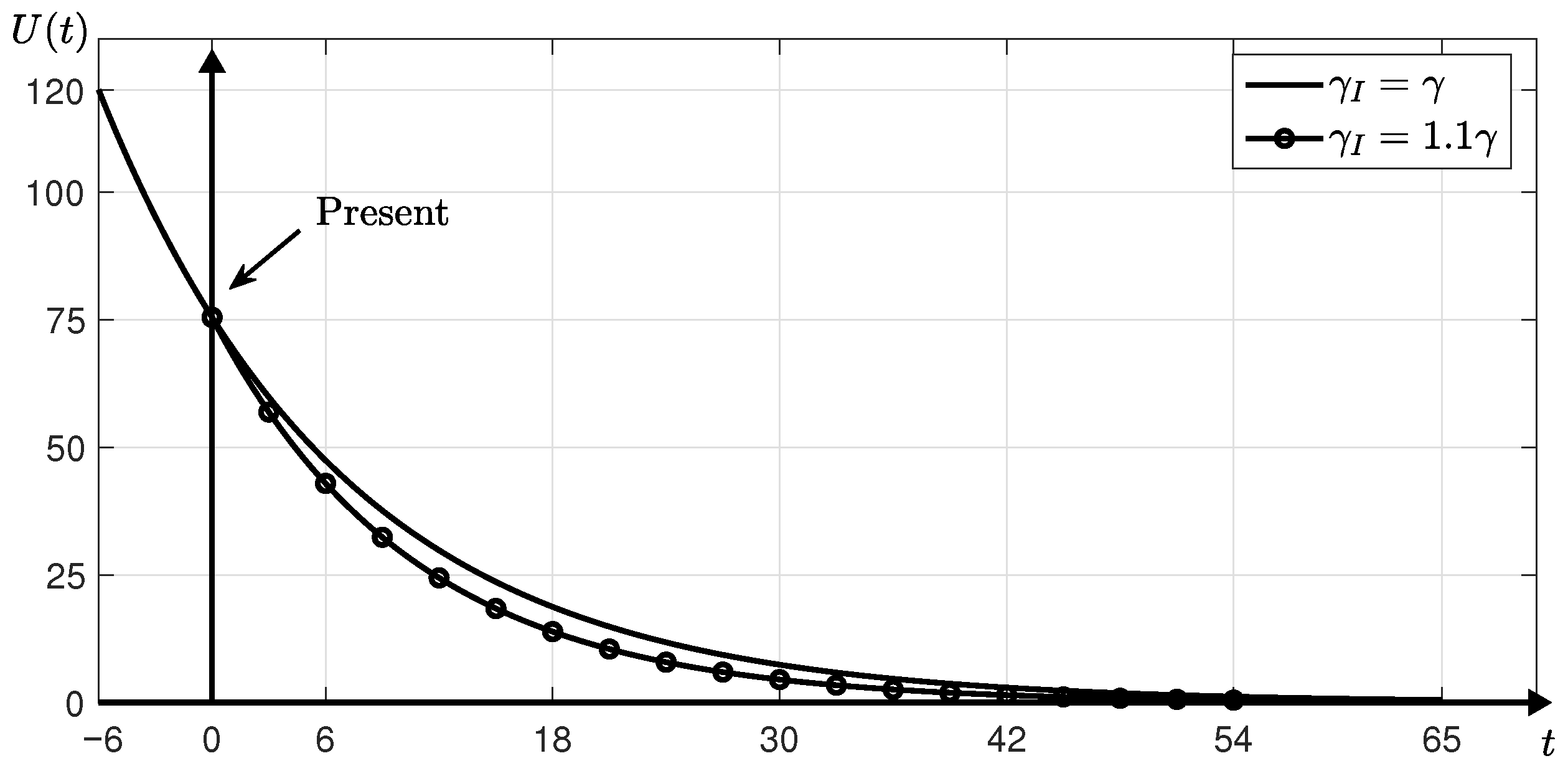
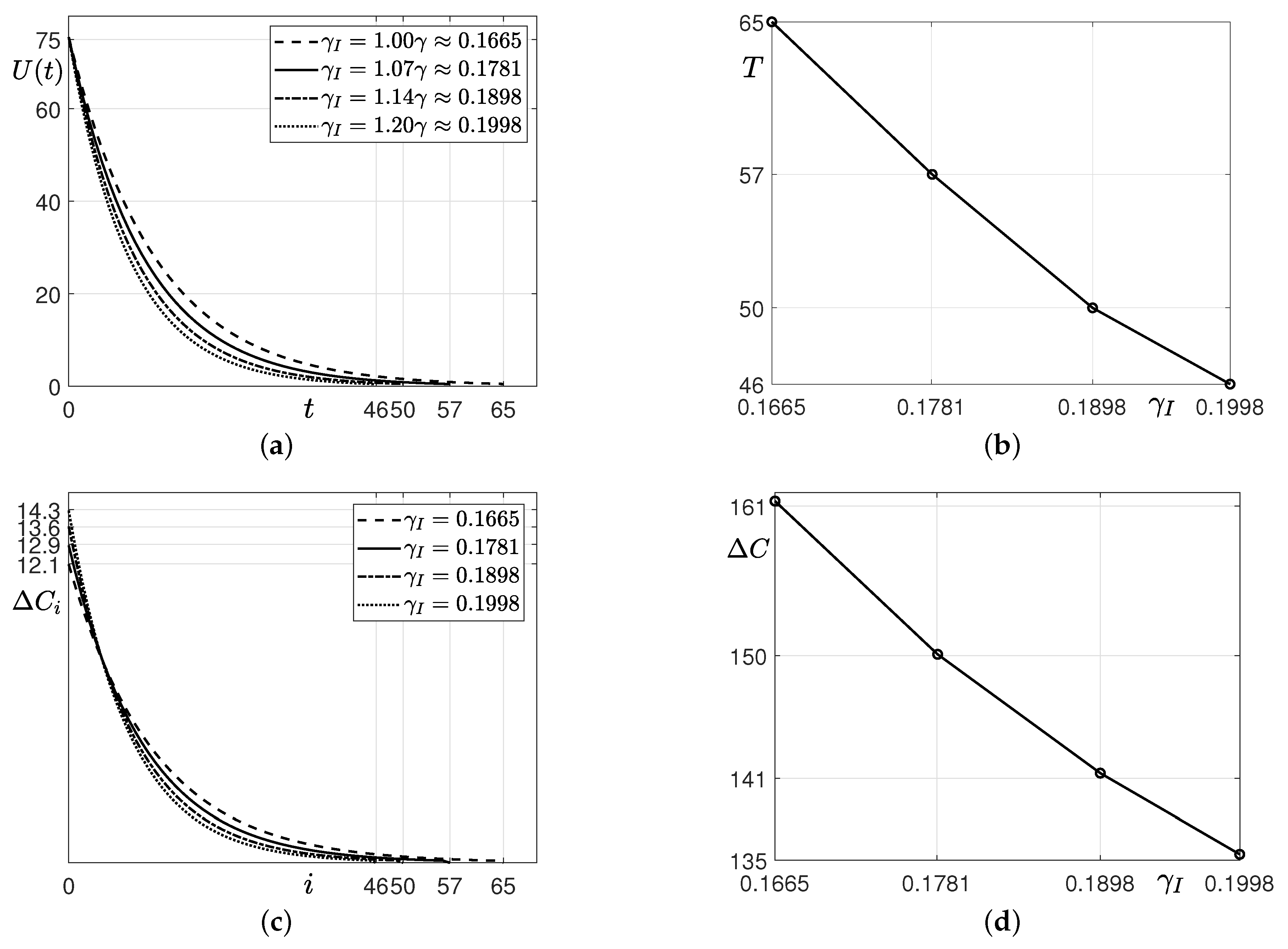
3.2. Estimation with Financial Incentives
- Step 1.
- Before the implementation of the incentive policy, we first estimate and using the SUC model with the number of confirmed cases up to now. Here, is fixed.
- Step 2.
- Assuming that financial incentives are provided, we compute , and T using the SUC model and the iterative method until . Here, we use the same parameters as those used and obtained in Step 1 except for . Instead of , we use that is greater than 0.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data
| No | Date | Cases | No | Date | Cases | No | Date | Cases | No | Date | Cases |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25-March | 8910 | 30 | 23-April | 9677 | 59 | 22-May | 9941 | 88 | 20-June | 10,945 |
| 2 | 26-March | 8957 | 31 | 24-April | 9681 | 60 | 23-May | 9960 | 89 | 21-June | 10,985 |
| 3 | 27-March | 9023 | 32 | 25-April | 9687 | 61 | 24-May | 9977 | 90 | 22-June | 10,996 |
| 4 | 28-March | 9115 | 33 | 26-April | 9688 | 62 | 25-May | 9990 | 91 | 23-June | 11,012 |
| 5 | 29-March | 9171 | 34 | 27-April | 9691 | 63 | 26-May | 10,006 | 92 | 24-June | 11,043 |
| 6 | 30-March | 9185 | 35 | 28-April | 9693 | 64 | 27-May | 10,043 | 93 | 25-June | 11,066 |
| 7 | 31-March | 9268 | 36 | 29-April | 9697 | 65 | 28-May | 10,111 | 94 | 26-June | 11,093 |
| 8 | 01-April | 9327 | 37 | 30-April | 9697 | 66 | 29-May | 10,166 | 95 | 27-June | 11,124 |
| 9 | 02-April | 9375 | 38 | 01-May | 9698 | 67 | 30-May | 10,193 | 96 | 28-June | 11,164 |
| 10 | 03-April | 9415 | 39 | 02-May | 9698 | 68 | 31-May | 10,208 | 97 | 29-June | 11,194 |
| 11 | 04-April | 9392 | 40 | 03-May | 9701 | 69 | 01-June | 10,238 | 98 | 30-June | 11,217 |
| 12 | 05-April | 9433 | 41 | 04-May | 9701 | 70 | 02-June | 10,274 | 99 | 01-July | 11,252 |
| 13 | 06-April | 9464 | 42 | 05-May | 9701 | 71 | 03-June | 10,320 | 100 | 02-July | 11,296 |
| 14 | 07-April | 9494 | 43 | 06-May | 9701 | 72 | 04-June | 10,353 | 101 | 03-July | 11,348 |
| 15 | 08-April | 9523 | 44 | 07-May | 9702 | 73 | 05-June | 10,387 | 102 | 04-July | 11,384 |
| 16 | 09-April | 9539 | 45 | 08-May | 9703 | 74 | 06-June | 10,430 | 103 | 05-July | 11,427 |
| 17 | 10-April | 9561 | 46 | 09-May | 9720 | 75 | 07-June | 10,483 | 104 | 06-July | 11,449 |
| 18 | 11-April | 9579 | 47 | 10-May | 9746 | 76 | 08-June | 10,516 | 105 | 07-July | 11,469 |
| 19 | 12-April | 9587 | 48 | 11-May | 9775 | 77 | 09-June | 10,551 | 106 | 08-July | 11,499 |
| 20 | 13-April | 9596 | 49 | 12-May | 9797 | 78 | 10-June | 10,594 | 107 | 09-July | 11,526 |
| 21 | 14-April | 9611 | 50 | 13-May | 9819 | 79 | 11-June | 10,634 | 108 | 10-July | 11,548 |
| 22 | 15-April | 9627 | 51 | 14-May | 9845 | 80 | 12-June | 10,677 | 109 | 11-July | 11,568 |
| 23 | 16-April | 9638 | 52 | 15-May | 9867 | 81 | 13-June | 10,720 | 110 | 12-July | 11,589 |
| 24 | 17-April | 9646 | 53 | 16-May | 9876 | 82 | 14-June | 10,751 | 111 | 13-July | 11,608 |
| 25 | 18-April | 9655 | 54 | 17-May | 9882 | 83 | 15-June | 10,774 | 112 | 14-July | 11,622 |
| 26 | 19-April | 9658 | 55 | 18-May | 9887 | 84 | 16-June | 10,795 | 113 | 15-July | 11,633 |
| 27 | 20-April | 9664 | 56 | 19-May | 9896 | 85 | 17-June | 10,826 | 114 | 16-July | 11,647 |
| 28 | 21-April | 9668 | 57 | 20-May | 9920 | 86 | 18-June | 10,877 | 115 | 17-July | 11,668 |
| 29 | 22-April | 9673 | 58 | 21-May | 9930 | 87 | 19-June | 10,909 |
Appendix B. MATLAB Code
References
- Lai, C.C.; Shih, T.P.; Ko, W.C.; Tang, H.J.; Hsueh, P.R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and corona virus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef] [PubMed]
- Younes, A.B.; Hasan, Z. COVID-19: Modeling, prediction, and control. Appl. Sci. 2020, 10, 3666. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Coronavirus Disease 2019 (COVID-19) Situation Report 179, accesed 17 July 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200717-covid-19-sitrep-179.pdf?sfvrsn=2f1599fa_28 (accessed on 6 January 2021).
- Novel Coronavirus (COVID-19) Situation Reports Published by the Korea Disease Control and Prevention Agency (KDCA). Available online: http://www.kdca.go.kr/board/board.es?mid=a20501000000&bid=0015 (accessed on 6 January 2021).
- Khalifa, S.A.; Mohamed, B.S.; Elashal, M.H.; Du, M.; Guo, Z.; Zhao, C.; Musharraf, S.G.; Boskabady, M.H.; El-Seedi, H.H.R.; Efferth, T.; et al. Comprehensive overview on multiple strategies fighting COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 5813. [Google Scholar] [CrossRef] [PubMed]
- Ha, B.T.T.; La Quang, N.; Mirzoev, T.; Tai, N.T.; Thai, P.Q.; Dinh, P.C. Combating the COVID-19 Epidemic: Experiences from Vietnam. Int. J. Environ. Res. Public Health 2020, 17, 3125. [Google Scholar] [CrossRef] [PubMed]
- Pung, R.; Chiew, C.J.; Young, B.E.; Chin, S.; Chen, M.I.; Clapham, H.E.; Cook, A.R.; Maurer-Stroh, S.; Toh, M.P.H.S.; Poh, C.; et al. Investigation of three clusters of COVID-19 in Singapore: Implications for surveillance and response measures. Lancet 2020, 395, 1039–1046. [Google Scholar] [CrossRef]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Guzzetta, G.; Poletti, P.; Ajelli, M.; Trentini, F.; Marziano, V.; Cereda, D.; Tirani, M.; Diurno, G.; Bodina, A.; Barone, A.; et al. Potential short-term outcome of an uncontrolled COVID-19 epidemic in Lombardy, Italy, February to March 2020. Eurosurveillance 2020, 25, 2000293. [Google Scholar] [CrossRef]
- Xie, K.; Liang, B.; Dulebenets, M.A.; Mei, Y. The impact of risk perception on social distancing during the COVID-19 pandemic in China. Int. J. Environ. Res. Public Health 2020, 17, 6256. [Google Scholar]
- Ghinai, I.; McPherson, T.D.; Hunter, J.C.; Kirking, H.L.; Christiansen, D.; Joshi, K.; Rubin, R.; Morales-Estrada, S.; Black, S.R.; Pacilli, M.; et al. First known person-to-person transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in the USA. Lancet 2020, 395, 1137–1144. [Google Scholar] [CrossRef]
- Peeri, N.C.; Shrestha, N.; Rahman, M.S.; Zaki, R.; Tan, Z.; Bibi, S.; Baghbanzadeh, M.; Aghamohammadi, N.; Zhang, W.; Haque, U. The SARS, MERS and novel coronavirus (COVID-19) epidemics, the newest and biggest global health threats: What lessons have we learned? Int. J. Epidemiol. 2020, 49, 717–726. [Google Scholar] [CrossRef]
- Day, M. Covid-19: Identifying and isolating asymptomatic people helped eliminate virus in Italian village. BMJ 2020, 368. [Google Scholar] [CrossRef] [PubMed]
- Sjödin, H.; Wilder-Smith, A.; Osman, S.; Farooq, Z.; Rocklöv, J. Only strict quarantine measures can curb the coronavirus disease (COVID-19) outbreak in Italy, 2020. Eurosurveillance 2020, 25, 2000280. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Shao, Q.; Li, D.; Sun, M. How the individuals’ risk aversion affect the epidemic spreading. Appl. Math. Comput. 2020, 369, 124894. [Google Scholar] [CrossRef]
- Reuters News. Available online: https://www.reuters.com/article/us-china-health-rewards/china-city-offers-1400-reward-for-virus-patients-who-report-to-authorities-idUSKCN20L0GE (accessed on 6 January 2021).
- Chamie, G.; Ndyabakira, A.; Marson, K.G.; Emperador, D.M.; Kamya, M.R.; Havlir, D.V.; Kwarisiima, D.; Thirumurthy, H. A pilot randomized trial of incentive strategies to promote HIV retesting in rural Uganda. PLoS ONE 2020, 15, e0233600. [Google Scholar] [CrossRef] [PubMed]
- Adamson, B.; El-Sadr, W.; Dimitrov, D.; Gamble, T.; Beauchamp, G.; Carlson, J.J.; Garrison, L.; Donnell, D. The cost-effectiveness of financial incentives for viral suppression: HPTN 065 study. Value Health 2019, 22, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Rat-Aspert, O.; Fourichon, C. Modelling collective effectiveness of voluntary vaccination with and without incentives. Prev. Vet. Med. 2010, 93, 265–275. [Google Scholar] [CrossRef]
- Lee, C.; Li, Y.; Kim, J. The susceptible-unidentified infected-confirmed (SUC) epidemic model for estimating unidentified infected population for COVID-19. Chaos Soliton. Fract. 2020, 139, 110090. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack–McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, J.B.; Li, H. Global dynamics of an SIQR model with vaccination and elimination hybrid strategies. Mathematics 2018, 6, 328. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, Y.; Islam, S. Complex dynamics of an SEIR epidemic model with saturated incidence rate and treatment. Physica A 2018, 493, 210–227. [Google Scholar] [CrossRef]
- Wu, M.; Dai, W.; Lu, Z.; Zhao, Y.; Wang, M. The method for risk evaluation in assembly process based on the discrete-time SIRS epidemic model and information entropy. Entropy 2019, 21, 1029. [Google Scholar] [CrossRef]
- Nistal, R.; De la Sen, M.; Alonso-Quesada, S.; Ibeas, A. On a new discrete SEIADR model with mixed controls: Study of its properties. Mathematics 2019, 7, 18. [Google Scholar] [CrossRef]

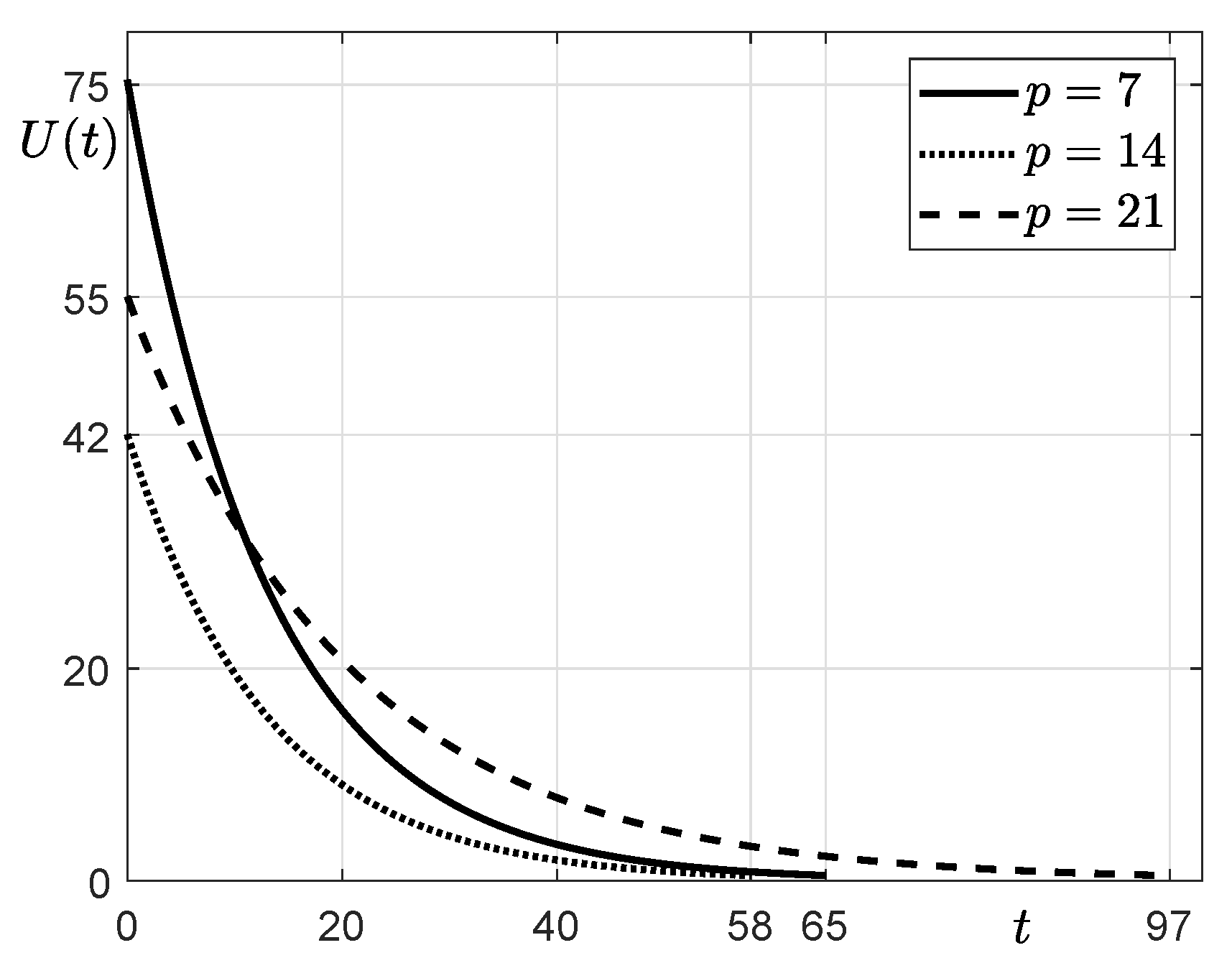
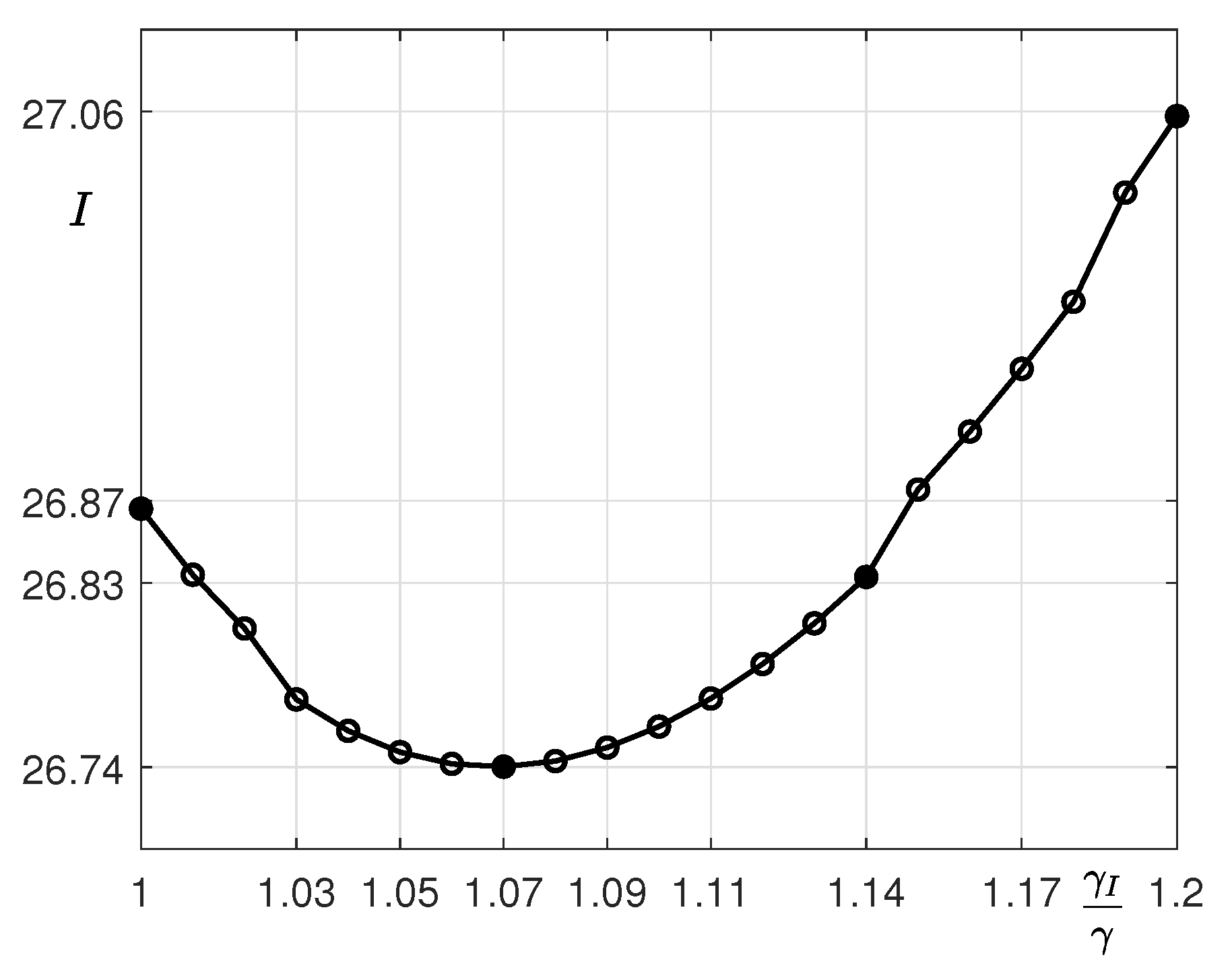
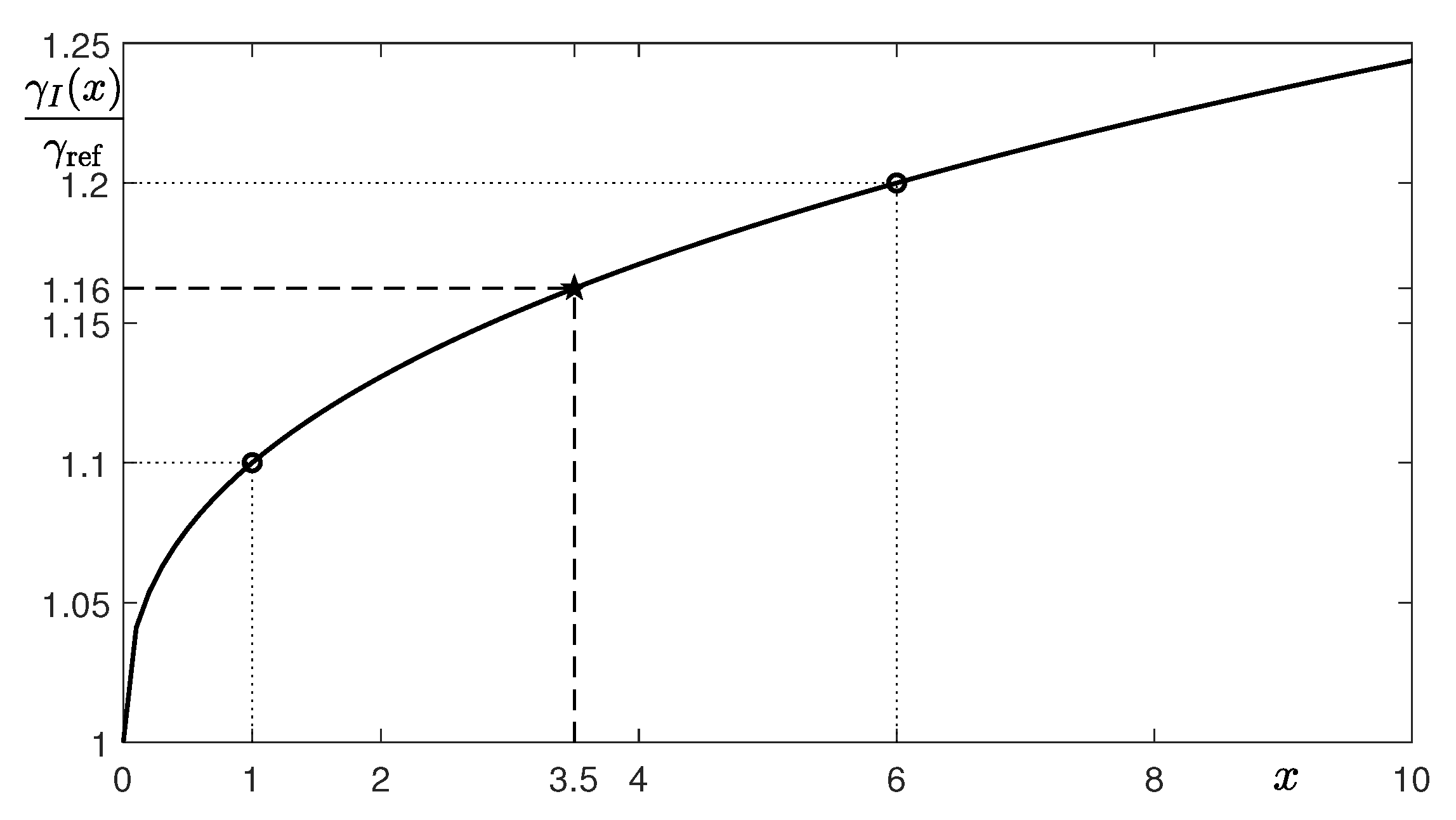
| p | 7 | 14 | 21 |
|---|---|---|---|
| C | 11,664 | 11,664 | 11,675 |
| U | 75 | 42 | 55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Kwak, S.; Kim, J. Controlling COVID-19 Outbreaks with Financial Incentives. Int. J. Environ. Res. Public Health 2021, 18, 724. https://doi.org/10.3390/ijerph18020724
Lee C, Kwak S, Kim J. Controlling COVID-19 Outbreaks with Financial Incentives. International Journal of Environmental Research and Public Health. 2021; 18(2):724. https://doi.org/10.3390/ijerph18020724
Chicago/Turabian StyleLee, Chaeyoung, Soobin Kwak, and Junseok Kim. 2021. "Controlling COVID-19 Outbreaks with Financial Incentives" International Journal of Environmental Research and Public Health 18, no. 2: 724. https://doi.org/10.3390/ijerph18020724
APA StyleLee, C., Kwak, S., & Kim, J. (2021). Controlling COVID-19 Outbreaks with Financial Incentives. International Journal of Environmental Research and Public Health, 18(2), 724. https://doi.org/10.3390/ijerph18020724






