A Framework for Weather-Driven Dengue Virus Transmission Dynamics in Different Brazilian Regions
Abstract
1. Introduction
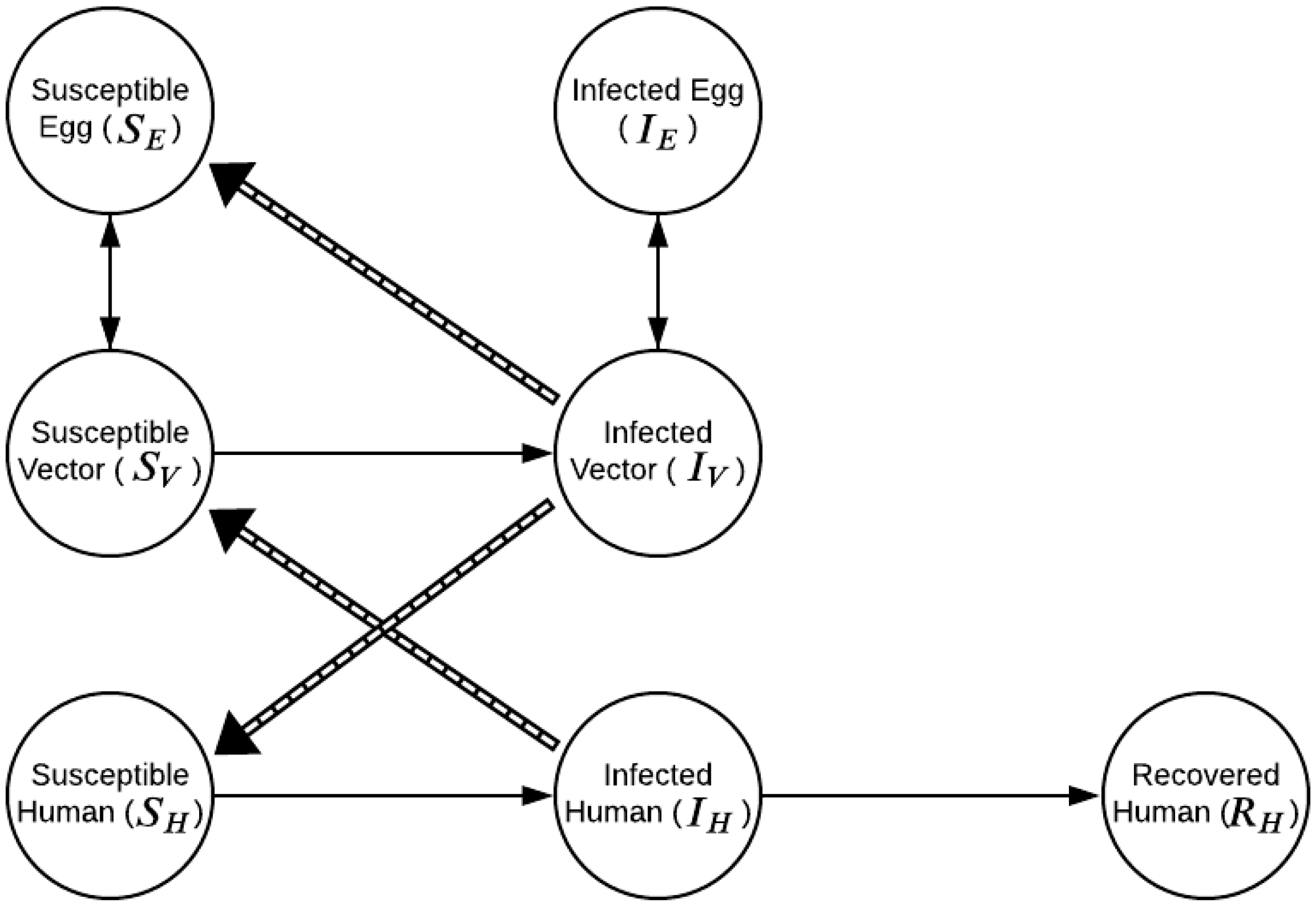
2. Materials and Methods
2.1. Initial Conditions
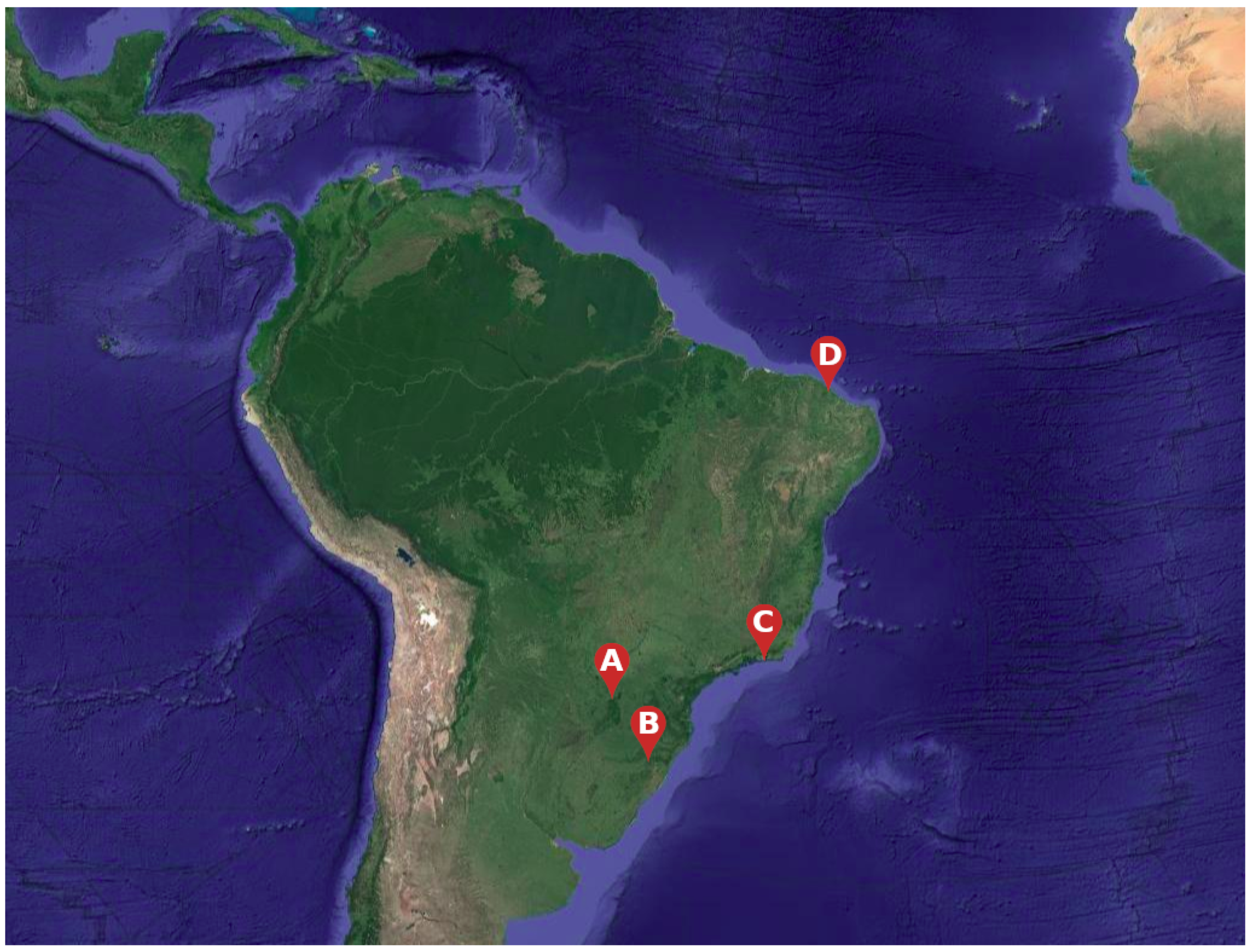
2.2. Case Studies
2.3. Data
2.3.1. Epidemiological Data
2.3.2. Temperature Data
2.3.3. Rainfall Data
2.4. Model Calibration
3. Results
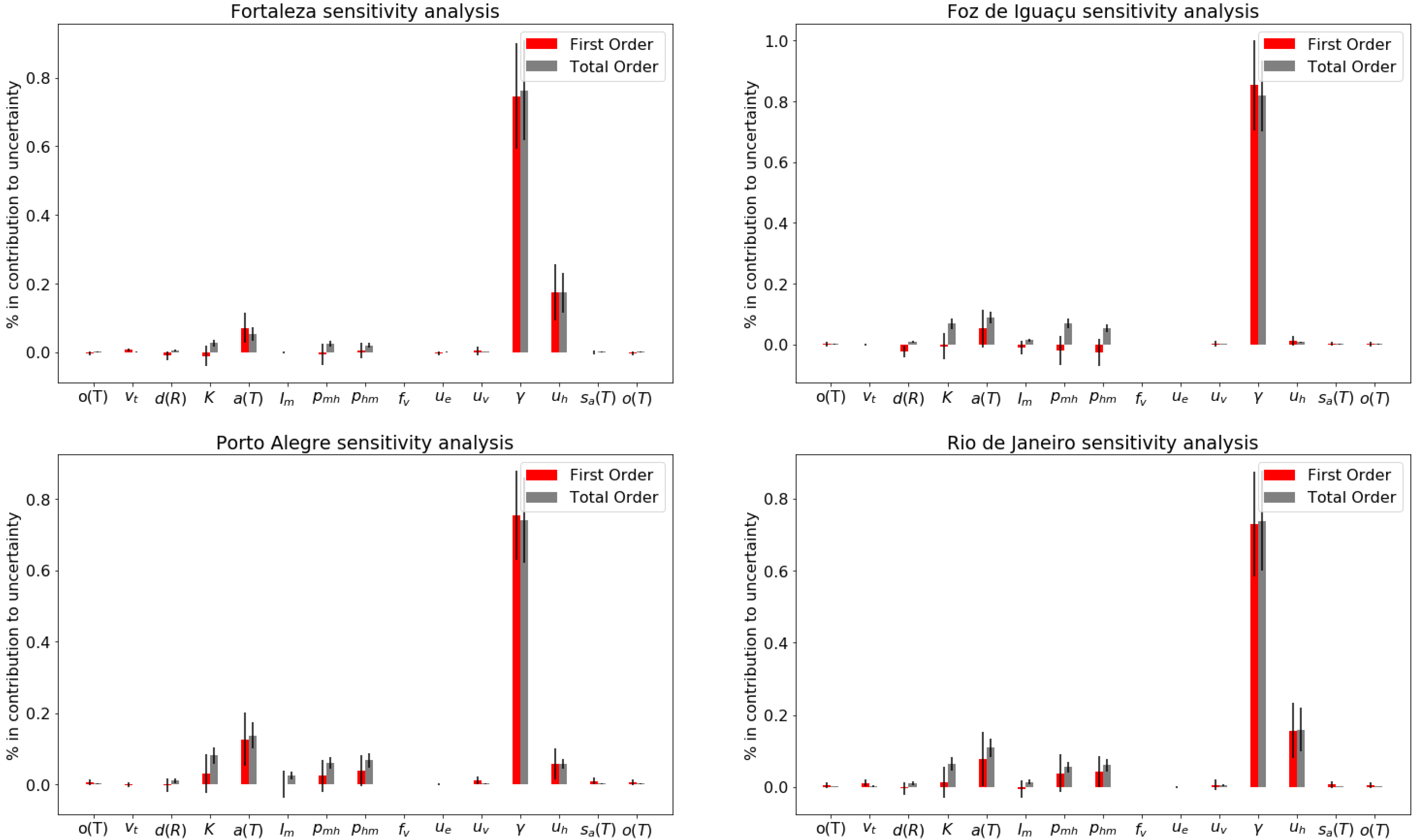
3.1. Sensitivity Analysis
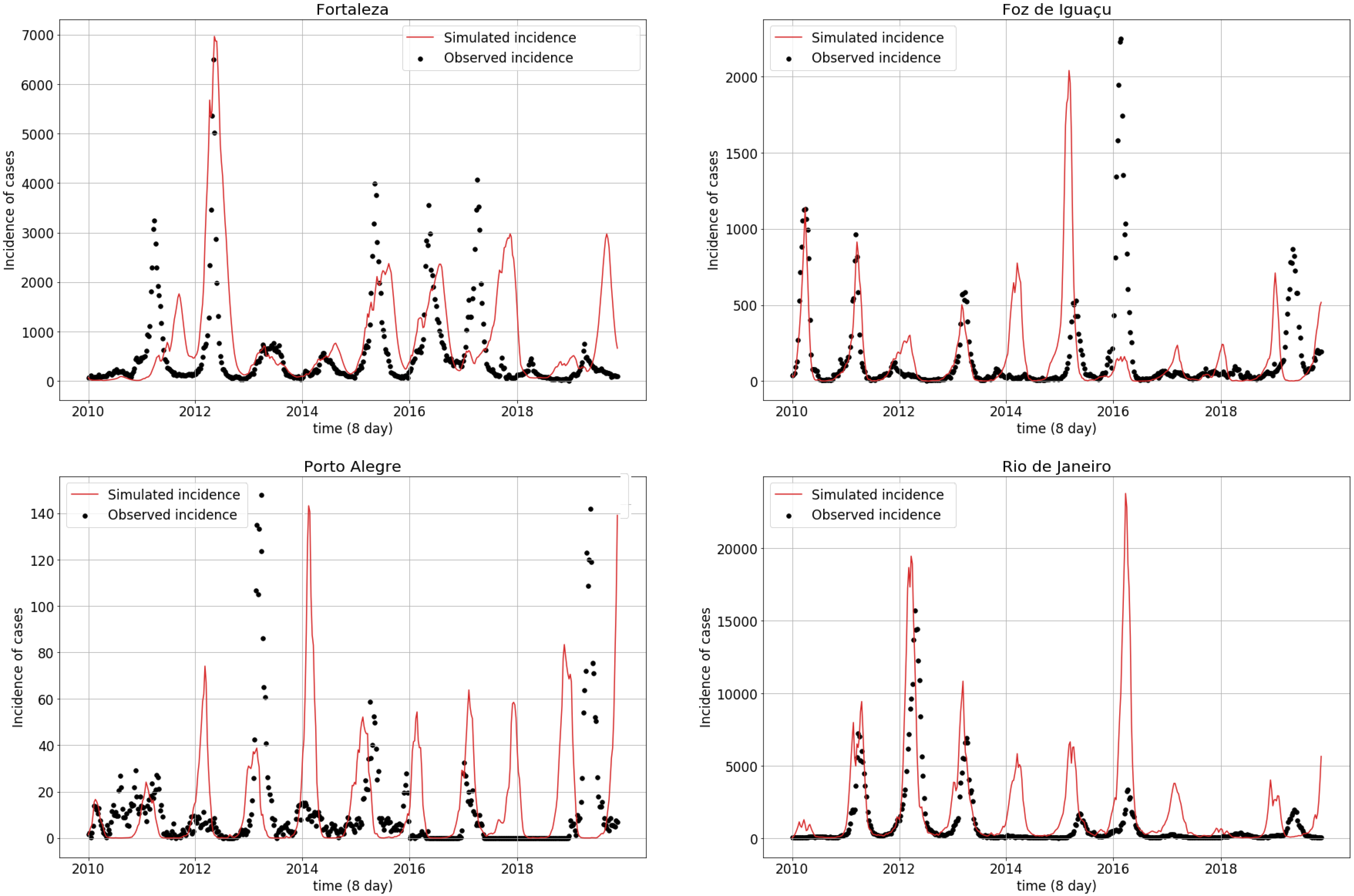
3.2. Calibration Process
3.3. Vertical Transmission
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gubler, D.J. Dengue, urbanization and globalization: The unholy trinity of the 21st century. Trop. Med. Health 2011, 39, S3–S11. [Google Scholar] [CrossRef]
- DA, S. Aedes albopictus and arboviruses: A concise review of the literature. J. Am. Mosq. Control Assoc. 1986, 2, 424–428. [Google Scholar]
- Focks, D.; Haile, D.; Daniels, E.; Mount, G. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): Simulation results and validation. J. Med. Entomol. 1993, 30, 1018–1028. [Google Scholar] [CrossRef]
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes aegypti: Formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68, 1945–1974. [Google Scholar] [CrossRef]
- Lima, T.; Carneiro, T.; Silva, L.; Lana, R.; Codeço, C.; Reis, I.; Maretto, R.; Santos, L.; Monteiro, A.M.; Medeiros, L.; et al. A framework for modeling and simulating Aedes aegypti and dengue fever dynamics. In Proceedings of the Winter Simulation Conference 2014, Savannah, GA, USA, 7–10 December 2014; pp. 1481–1492. [Google Scholar]
- Side, S.; Noorani, M.S.M. A SIR model for spread of dengue fever disease (simulation for South Sulawesi, Indonesia and Selangor, Malaysia). World J. Model. Simul. 2013, 9, 96–105. [Google Scholar]
- Huber, J.H.; Childs, M.L.; Caldwell, J.M.; Mordecai, E.A. Seasonal temperature variation influences climate suitability for dengue, chikungunya, and Zika transmission. PLoS Negl. Trop. Dis. 2018, 12, e0006451. [Google Scholar] [CrossRef]
- Chanprasopchai, P.; Tang, I.M.; Pongsumpun, P. SIR model for dengue disease with effect of dengue vaccination. Comput. Math. Methods Med. 2018, 2018, 9861572. [Google Scholar] [CrossRef] [PubMed]
- Natal, D. Bioecologia do Aedes aegypti. Biológico 2002, 64, 205–207. [Google Scholar]
- Nelson, M.J. Aedes Aegypti: Biology and Ecology. 1986. Available online: https://iris.paho.org/handle/10665.2/28514 (accessed on 25 June 2021).
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7, e49085. [Google Scholar] [CrossRef] [PubMed]
- Laura, L.; Supriatna, A.K.; Khumaeroh, M.S.; Anggriani, N. Biological and mechanical transmission models of dengue fever. Commun. Biomath. Sci. 2019, 2, 12–22. [Google Scholar] [CrossRef]
- Rueda, L.; Patel, K.; Axtell, R.; Stinner, R. Temperature-dependent development and survival rates of Culex quinquefasciatus and Aedes aegypti (Diptera: Culicidae). J. Med. Entomol. 1990, 27, 892–898. [Google Scholar] [CrossRef] [PubMed]
- Tun-Lin, W.; Burkot, T.; Kay, B. Effects of temperature and larval diet on development rates and survival of the dengue vector Aedes aegypti in north Queensland, Australia. Med. Vet. Entomol. 2000, 14, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.M.; Burke, D.S.; Harrison, B.A.; Whitmire, R.E.; Nisalak, A. Effect of temperature on the vector efficiency of Aedes aegypti for dengue 2 virus. Am. J. Trop. Med. Hyg. 1987, 36, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Chirombo, J.; Tompkins, A.M. Relative importance of climatic, geographic and socio-economic determinants of malaria in Malawi. Malar. J. 2013, 12, 416. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.; Reiner, R.C.; Brady, O.J.; Messina, J.P.; Gilbert, M.; Pigott, D.M.; Yi, D.; Johnson, K.; Earl, L.; Marczak, L.B.; et al. Past and future spread of the arbovirus vectors Aedes aegypti and Aedes albopictus. Nat. Microbiol. 2019, 4, 854–863. [Google Scholar] [CrossRef]
- Trpiš, M. Dry season survival of Aedes aegypti eggs in various breeding sites in the Dar es Salaam area, Tanzania. Bull. World Health Organ. 1972, 47, 433. [Google Scholar]
- Hii, Y.L.; Zhu, H.; Ng, N.; Ng, L.C.; Rocklöv, J. Forecast of dengue incidence using temperature and rainfall. PLoS Negl. Trop. Dis. 2012, 6, e1908. [Google Scholar] [CrossRef]
- Buckner, E.A.; Alto, B.W.; Lounibos, L.P. Vertical transmission of Key West dengue-1 virus by Aedes aegypti and Aedes albopictus (Diptera: Culicidae) mosquitoes from Florida. J. Med. Entomol. 2013, 50, 1291–1297. [Google Scholar] [CrossRef]
- Adams, B.; Boots, M. How important is vertical transmission in mosquitoes for the persistence of dengue? Insights from a mathematical model. Epidemics 2010, 2, 1–10. [Google Scholar] [CrossRef]
- Pan American Health Organization. Epidemiological Update: Dengue and other Arboviruses—10 June 2020. World Health Organ. Reg. Off. Am. 2020, 1, 15. [Google Scholar]
- Pan American Health Organization. Epidemiological Update Dengue, 11 November 2019. World Health Organ. Reg. Off. Am. 2019, 1, 15. [Google Scholar]
- Esteva, L.; Yang, H.M. Assessing the effects of temperature and dengue virus load on dengue transmission. J. Biol. Syst. 2015, 23, 1550027. [Google Scholar] [CrossRef]
- Zaslavsky, R.; de Goulart, B.N.G. Pendulum migration and healthcare in border area. Ciência Saúde Coletiva 2017, 22, 3981–3986. [Google Scholar] [CrossRef]
- Magori, K.; Legros, M.; Puente, M.E.; Focks, D.A.; Scott, T.W.; Lloyd, A.L.; Gould, F. Skeeter Buster: A stochastic, spatially explicit modeling tool for studying Aedes aegypti population replacement and population suppression strategies. PLoS Negl. Trop. Dis. 2009, 3, e508. [Google Scholar] [CrossRef]
- Do Estado do Rio de Janeiro, G. Informações de Saúde. 2020. Available online: http://sistemas.saude.rj.gov.br/tabnetbd/dhx.exe?taxas/sim_taxas_mortalidade_valores.def (accessed on 25 June 2021).
- Bosio, C.F.; Thomas, R.E.; Grimstad, P.R.; Rai, K.S. Variation in the efficiency of vertical transmission of dengue-1 virus by strains of Aedes albopictus (Diptera: Culicidae). J. Med. Entomol. 1992, 29, 985–989. [Google Scholar] [CrossRef] [PubMed]
- Joshi, V.; Mourya, D.; Sharma, R. Persistence of dengue-3 virus through transovarial transmission passage in successive generations of Aedes aegypti mosquitoes. Am. J. Trop. Med. Hyg. 2002, 67, 158–161. [Google Scholar] [CrossRef] [PubMed]
- Lequime, S.; Paul, R.E.; Lambrechts, L. Determinants of arbovirus vertical transmission in mosquitoes. PLoS Pathog. 2016, 12, e1005548. [Google Scholar] [CrossRef] [PubMed]
- Neira, M.; Lacroix, R.; Cáceres, L.; Kaiser, P.E.; Young, J.; Pineda, L.; Black, I.; Sosa, N.; Nimmo, D.; Alphey, L.; et al. Estimation of Aedes aegypti (Diptera: Culicidae) population size and adult male survival in an urban area in Panama. Memórias Inst. Oswaldo Cruz 2014, 109, 879–886. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.A.; Brenner, R.J.; Hayes, J.; Daniels, E. Transmission thresholds for dengue in terms of Aedes aegypti pupae per person with discussion of their utility in source reduction efforts. Am. J. Trop. Med. Hyg. 2000, 62, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Pan American Health Organization. Dengue Guidelines for Diagnosis, Treatment, Prevention and Control: New Edition; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Mordecai, E.A.; Cohen, J.M.; Evans, M.V.; Gudapati, P.; Johnson, L.R.; Lippi, C.A.; Miazgowicz, K.; Murdock, C.C.; Rohr, J.R.; Ryan, S.J.; et al. Detecting the impact of temperature on transmission of Zika, dengue, and chikungunya using mechanistic models. PLoS Negl. Trop. Dis. 2017, 11, e0005568. [Google Scholar] [CrossRef]
- Briere, J.F.; Pracros, P.; Le Roux, A.Y.; Pierre, J.S. A novel rate model of temperature-dependent development for arthropods. Environ. Entomol. 1999, 28, 22–29. [Google Scholar] [CrossRef]
- Alto, B.W.; Juliano, S.A. Precipitation and temperature effects on populations of Aedes albopictus (Diptera: Culicidae): Implications for range expansion. J. Med. Entomol. 2001, 38, 646–656. [Google Scholar] [CrossRef]
- Brasil. Base de Dados. 2020. Available online: http://basededados.turismo.gov.br/ (accessed on 25 June 2021).
- Codeco, C.; Coelho, F.; Cruz, O.; Oliveira, S.; Castro, T.; Bastos, L. Infodengue: A nowcasting system for the surveillance of arboviruses in Brazil. Revue d’Épidémiologie Santé Publique 2018, 66, S386. [Google Scholar] [CrossRef]
- Brasil. Censo Demográfico. 2010. Available online: https://www.ibge.gov.br/ (accessed on 25 June 2021).
- Caprara, A.; De Oliveira Lima, J.W.; Rocha Peixoto, A.C.; Vasconcelos Motta, C.M.; Soares Nobre, J.M.; Sommerfeld, J.; Kroeger, A. Entomological impact and social participation in dengue control: A cluster randomized trial in Fortaleza, Brazil. Trans. R. Soc. Trop. Med. Hyg. 2015, 109, 99–105. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra Land Surface Temperature/Emissivity 8-Day L3 Global 1km SIN Grid V006. NASA EOSDIS Land Processes DAAC 2015. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Câmara, F.P.; Gomes, A.F.; Santos, G.T.D.; Câmara, D.C.P. Clima e epidemias de dengue no Estado do Rio de Janeiro. Rev. Soc. Bras. Med. Trop. 2009, 42, 137–140. [Google Scholar] [CrossRef]
- Conte, C.H. Comércio e deslocamento pendular: Posicionamentos sobre a rede urbana de Foz do Iguaçu. Rev. Geoaraguaia 2013, 3, 126–147. [Google Scholar]
- Peris, A.F.; Lugnani, A.C. Um estudo sobre o eixo Cascavel–Foz do Iguaçu na região oeste do Paraná. Rev. Parana. Desenvolv. 2011, 104, 79–102. [Google Scholar]
- Hasenack, H.; Flores, F.E.V. Relações entre temperatura do ar e variáveis do ambiente urbano de Porto Alegre, RS. Pesqui. Geociências 1994, 21, 3–11. [Google Scholar] [CrossRef][Green Version]
- Google Maps. South America Map. 2021. Available online: https://www.google.com/maps/place/Goi%C3%A1s/@-19.6461803,-67.8237896,4.5z (accessed on 25 June 2021).
- Martinez-Romero, N.; Osorio-Peralta, O.; Santamaria-Vite, I. Natural gas network optimization and sensibility analysis. In Proceedings of the SPE International Petroleum Conference and Exhibition in Mexico, Villahermosa, Mexico, 10 February 2002; Society of Petroleum Engineers: Richardson, TX, USA, 2002. [Google Scholar]
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Chávez, J.P.; Götz, T.; Siegmund, S.; Wijaya, K.P. An SIR-Dengue transmission model with seasonal effects and impulsive control. Math. Biosci. 2017, 289, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Götz, T.; Altmeier, N.; Bock, W.; Rockenfeller, R.; Wijaya, K.P. Modeling dengue data from Semarang, Indonesia. Ecol. Complex. 2017, 30, 57–62. [Google Scholar] [CrossRef]
- Rashkov, P.; Venturino, E.; Aguiar, M.; Stollenwerk, N.; Kooi, B.W. On the role of vector modeling in a minimalistic epidemic model. Math. Biosci. Eng. 2019, 16, 4314–4338. [Google Scholar] [CrossRef] [PubMed]
- Osorio, S.R.; Bermúdez, E.A.; Loaiza, A.M.; Armenia, Q.C. A simulation model for the chikungunya with vectorial capacity. Appl. Math. Sci. 2015, 9, 6953–6960. [Google Scholar] [CrossRef]
- Defterli, Ö. Modeling the impact of temperature on fractional order dengue model with vertical transmission. Int. J. Optim. Control Theor. Appl. 2020, 10, 85–93. [Google Scholar] [CrossRef]
- Phaijoo, G.R.; Gurung, D.B. Modeling impact of temperature and human movement on the persistence of dengue disease. Comput. Math. Methods Med. 2017, 2017, 1747134. [Google Scholar] [CrossRef]
- Beltrán-Silva, S.; Chacón-Hernández, S.; Moreno-Palacios, E.; Pereyra-Molina, J. Clinical and differential diagnosis: Dengue, chikungunya and Zika. Rev. Méd. Hosp. Gen. México 2018, 81, 146–153. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Mattar, C.; Barichivich, J.; Santamaría-Artigas, A.; Takahashi, K.; Malhi, Y.; Sobrino, J.A.; Van Der Schrier, G. Record-breaking warming and extreme drought in the Amazon rainforest during the course of El Niño 2015–2016. Sci. Rep. 2016, 6, 33130. [Google Scholar] [CrossRef]
- Gagnon, A.S.; Bush, A.B.; Smoyer-Tomic, K.E. Dengue epidemics and the El Niño southern oscillation. Clim. Res. 2001, 19, 35–43. [Google Scholar] [CrossRef]
- Tipayamongkholgul, M.; Fang, C.T.; Klinchan, S.; Liu, C.M.; King, C.C. Effects of the El Niño-Southern Oscillation on dengue epidemics in Thailand, 1996–2005. BMC Public Health 2009, 9, 422. [Google Scholar] [CrossRef] [PubMed]
- Petrova, D.; Rodó, X.; Sippy, R.; Ballester, J.; Mejía, R.; Beltrán-Ayala, E.; Borbor-Cordova, M.J.; Vallejo, G.M.; Olmedo, A.J.; Stewart-Ibarra, A.M.; et al. The 2018–2019 weak El Niño: Predicting the risk of a dengue outbreak in Machala, Ecuador. Int. J. Climatol. 2020, 41, 3813–3823. [Google Scholar] [CrossRef]
- Dieng, H.; Rahman, G.S.; Hassan, A.A.; Salmah, M.C.; Satho, T.; Miake, F.; Boots, M.; Sazaly, A. The effects of simulated rainfall on immature population dynamics of Aedes albopictus and female oviposition. Int. J. Biometeorol. 2012, 56, 113–120. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Definition | Value | Source |
|---|---|---|---|
| Mosquito sex ratio | [26] | ||
| Egg mortality rate (8 day) | [3] | ||
| Vertical transmission rate | [21] | ||
| Dengue recovery rate (8 day) | 1 | [33] | |
| Infected immigrants | |||
| Human birth and mortality rate (8 day) | [27] | ||
| K | Carrying Capacity | [31] |
| Variable | Definition | Function | a | b | c | Source |
|---|---|---|---|---|---|---|
| Biting rate (8 day) | Brière | [34] | ||||
| Oviposition rate per 8 days | Brière | [34] | ||||
| Aquatic survival rate | Quadratic | [34] | ||||
| human to mosquito infection prob. per bite | Brière | [34] | ||||
| mosquito to human infection prob. per bite | Brière | [34] | ||||
| Adult mosquito mortality rate (8 day) | Quadratic | [34] | ||||
| Development rate | Quadratic | [36] |
| Municipality | Tourists (8 day) | |||
|---|---|---|---|---|
| Rio de Janeiro | 327,259 | 40 | 21,535 | |
| Fortaleza | 70 | 2099 | ||
| Porto Alegre | 171,628 | 2 | 14,325 | |
| Foz do Iguaçu | 256,088 | 37,332 | 35 | 15,892 |
| Municipality | K | ||||
|---|---|---|---|---|---|
| Rio de Janeiro | |||||
| Fortaleza | 3 | ||||
| Porto Alegre | |||||
| Foz do Iguaçu | 3 |
| Municipality | Observed Attack Rate (%) | Simulated Attack Rate (%) |
|---|---|---|
| Rio de Janeiro | ||
| Fortaleza | ||
| Porto Alegre | ||
| Foz do Iguaçu |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, L.D.; Lana, R.M.; Coelho, F.C. A Framework for Weather-Driven Dengue Virus Transmission Dynamics in Different Brazilian Regions. Int. J. Environ. Res. Public Health 2021, 18, 9493. https://doi.org/10.3390/ijerph18189493
Alves LD, Lana RM, Coelho FC. A Framework for Weather-Driven Dengue Virus Transmission Dynamics in Different Brazilian Regions. International Journal of Environmental Research and Public Health. 2021; 18(18):9493. https://doi.org/10.3390/ijerph18189493
Chicago/Turabian StyleAlves, Leon Diniz, Raquel Martins Lana, and Flávio Codeço Coelho. 2021. "A Framework for Weather-Driven Dengue Virus Transmission Dynamics in Different Brazilian Regions" International Journal of Environmental Research and Public Health 18, no. 18: 9493. https://doi.org/10.3390/ijerph18189493
APA StyleAlves, L. D., Lana, R. M., & Coelho, F. C. (2021). A Framework for Weather-Driven Dengue Virus Transmission Dynamics in Different Brazilian Regions. International Journal of Environmental Research and Public Health, 18(18), 9493. https://doi.org/10.3390/ijerph18189493






