Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks
Abstract
1. Introduction
1.1. Framework
1.2. Radon Related Concepts
1.2.1. Mechanisms and Factors That Boost Radon Leakage into Enclosed Spaces
1.2.2. Criteria for the Application of Corrective Measures
1.2.3. Radon Gas Detection Systems
1.3. Use of Expert Systems in Decision-Support Tools
1.3.1. Expert Systems Applied to the Interpretation of External Factors and Environmental Conditions
1.4. Decision Trees
- Step 1: Start from the root node that contains all the independent variables.
- Step 2: For each independent variable find all the potential splitting points by defining a series of regions or nodes that do not overlap each other, and that are associated to the observable values linked to the predictor variable in each one of those regions.
- Step 3: For each one of the previously identified nodes, the subset S that allows one to minimize the impurity of the node into two descending branches giving place to two child nodes, must be found. As it has already been mentioned, the impurity parameter represents the sum of the squared deviations between the dependent variables’ values and the mean value for the region or node [85]. A group might be considered as pure when all its elements belong to the same region, and as impure when all of its elements belong to different regions [85]. When a node is pure, it might be said that a terminal node—or leaf—has been reached. However, when a node is impure it is necessary to determine if it is wished to stop and accept the obtained group, or else continue performing splits considering other independent variables [85]. As it has been already mentioned, there are several indices to measure impurity—such as Gini for classification problems [85]—but in this case, because a regression case will be applied, the RSS metric becomes important, aiming to its minimization as a metric for more homogeneous nodes.
- Step 4: The former process is repeated recursively through the recursive binary splitting method, selecting the predictor variable and the splitting point that guarantees a lower total RSS value by using the subsequent nodes until the tree reaches the maximum size that was assigned to it.
- Step 5: If a stop criterion is reached then the iteration is halted; else the command will return again to Step 2. In relation to the stop criteria, it is necessary to be careful because an early stop might result in a tree that is very small as to represent the structure of the starting data. On the contrary, a late stop might produce a tree that is too large, or even unstable, and with no useful meaning whatsoever [85].
- Step 6: Finally, after obtaining the value associated to a prediction line, it is proceeded to calculate the root-mean-square error (RMSE) in order to determine the accuracy and precision of the proposed regression model, by calculating the square root of the mean value of the sum of the squared differences between the predicted and the actual values. That is, starting from the initial data, a measure is established of how far away the predicted and the actual values are [95].
2. Materials and Methods
2.1. Definition of the Methodology
2.1.1. Previous Considerations
2.1.2. Conceptual Design and Description of the Proposed Methodology
Data Collection
- Environmental and atmospheric sensors.
- Radon sensor.
Data Reading, Processing and Interpretation
Monitoring and Alert Generation
- Preventive actions
- ○
- Activate forced evacuation and mechanical ventilation.
- ○
- De-activate forced evacuation.
- ○
- Natural ventilation.
- Checking actions
- ○
- Check sensors.
- ○
- Check inference.
- ○
- Check exposure time.
2.2. Implementation of the Methodology
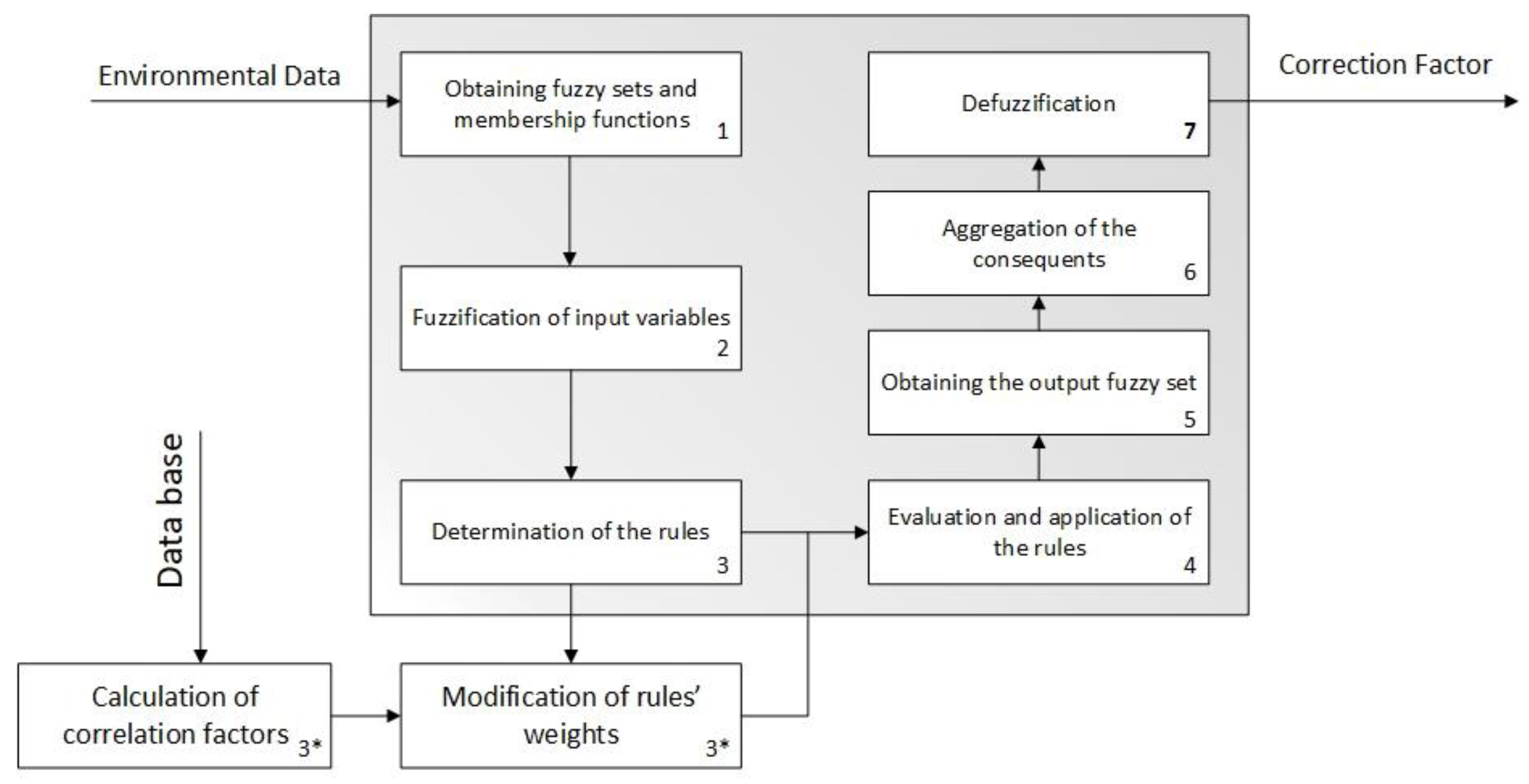
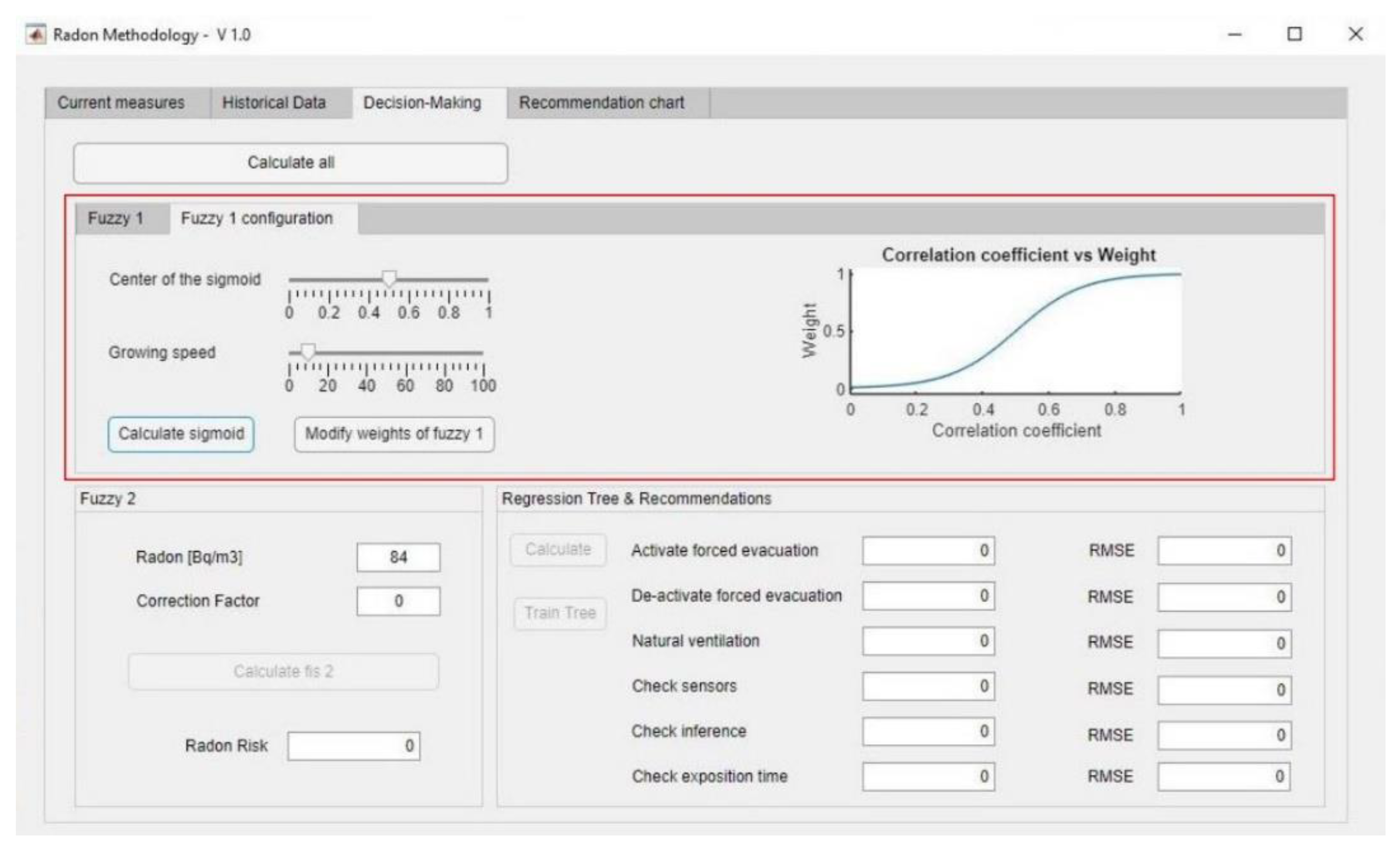
2.2.1. First Inference System—Correction Factor
Calculation
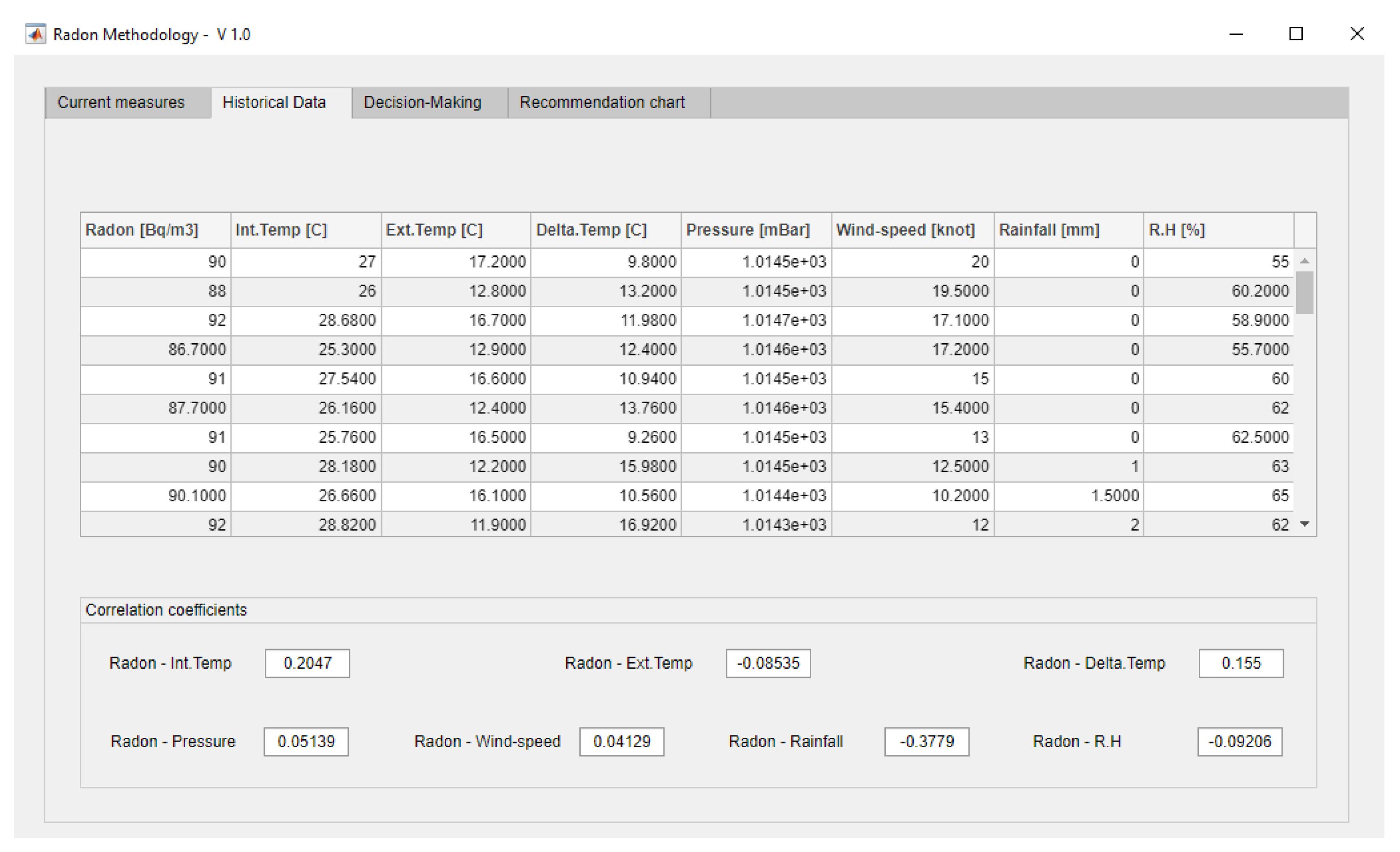
Determination of the Correlation Coefficient
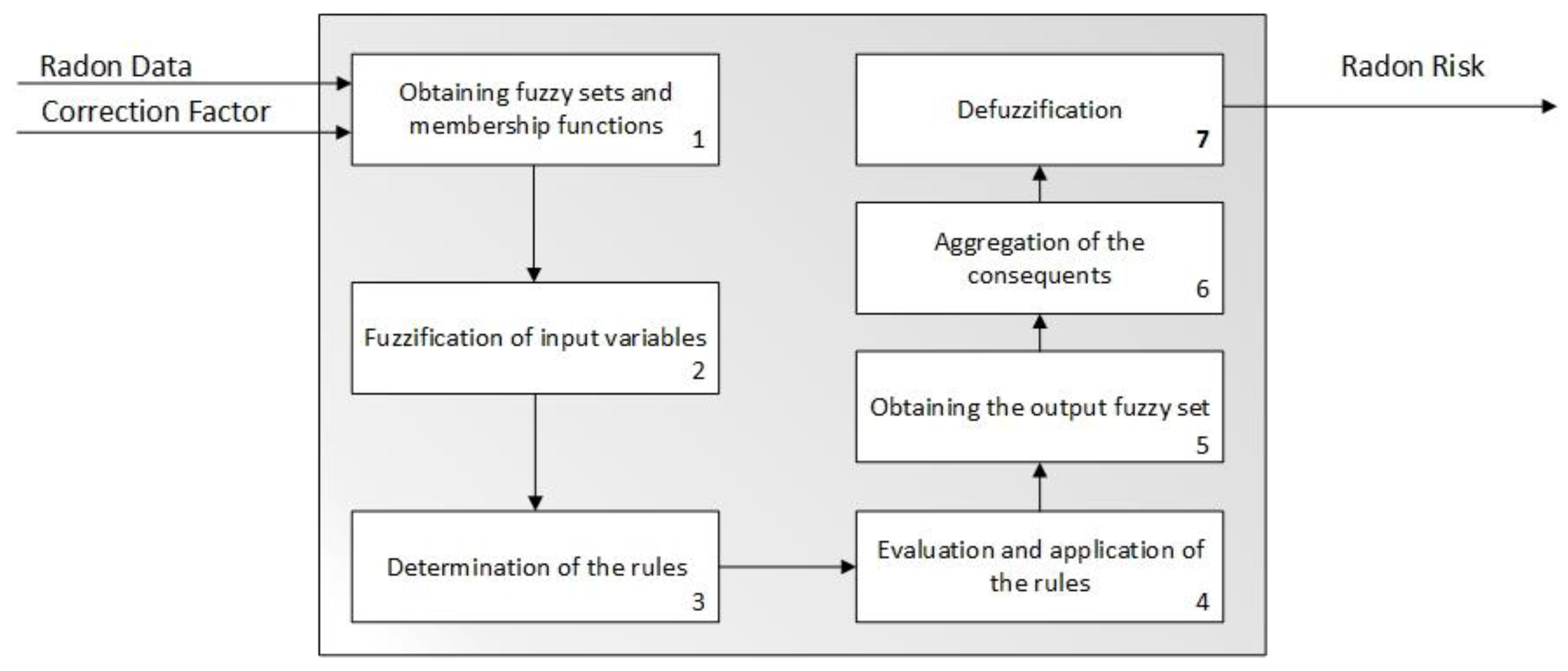
2.2.2. Second Inference System—Radon Risk
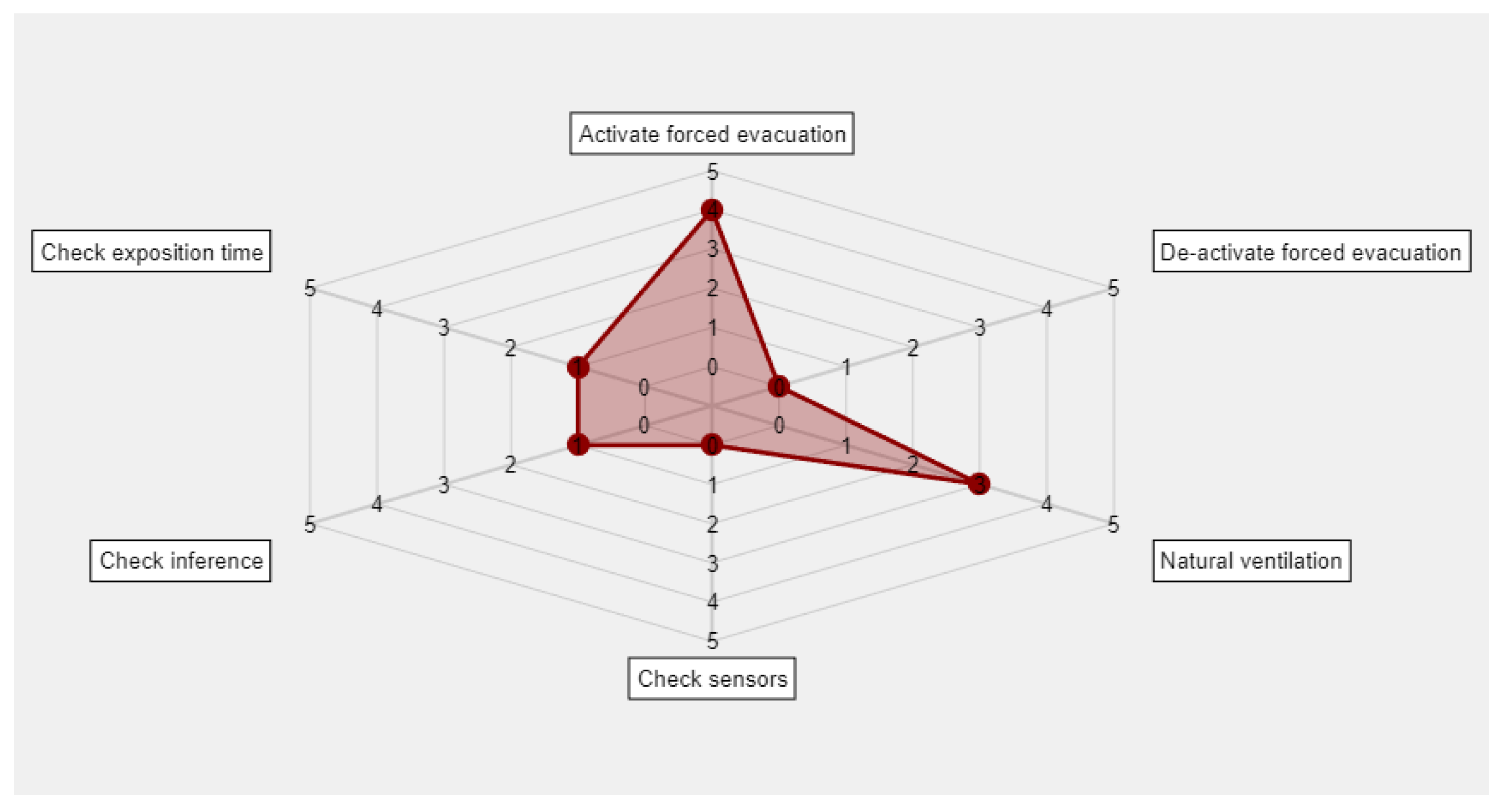
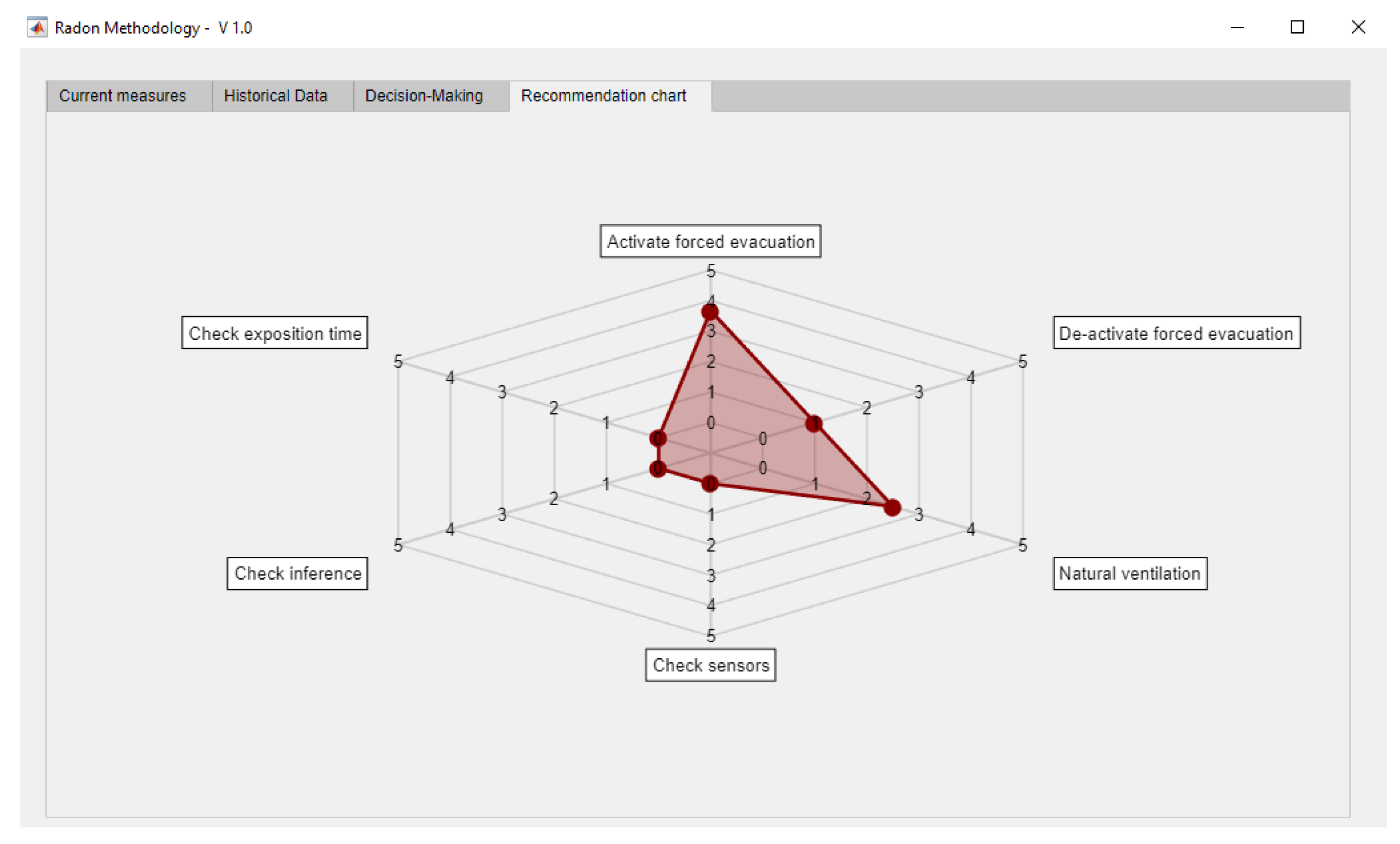
2.2.3. Regression Trees and Generation of the Spider-Web Diagram—Establishment of Recommendations
3. Case Study and Results
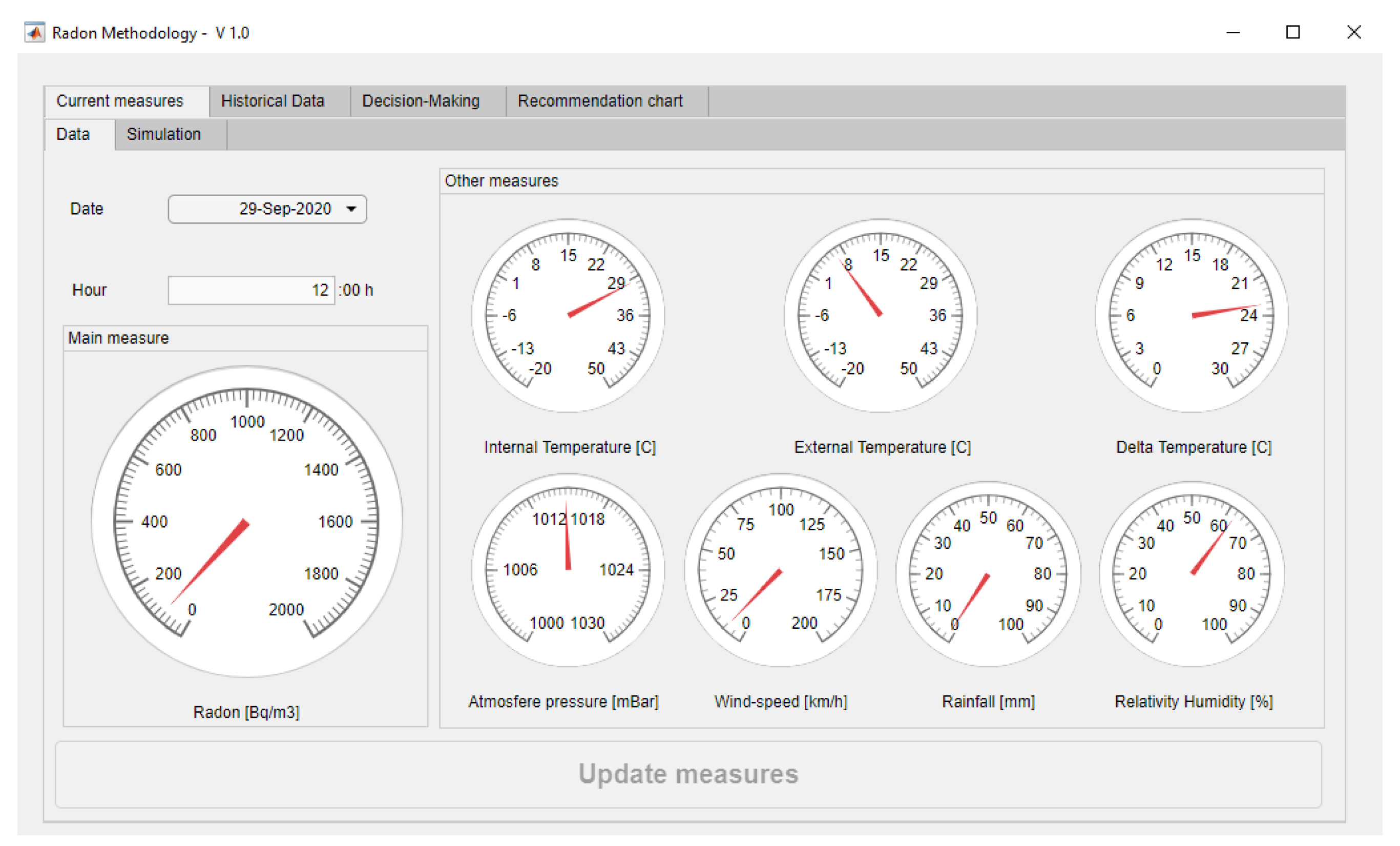
3.1. Data Collection
3.2. Data Reading, Processing and Interpretation
- Radon concentration value: 84 Bq/m3.
- Indoor temperature: 29.6 °C.
- Outdoor temperature: 6.5 °C.
- Atmospheric pressure: 1014.8 mbar.
- Wind speed: 9.5 km/h.
- Collected rainfall: 1.2 mm.
- Relative humidity: 62.3%.
- Correlation coefficient of radon concentration vs. indoor temperature: 0.2047.
- Correlation coefficient of radon concentration vs. outdoor temperature: −0.08535.
- Correlation coefficient of radon concentration vs. temperature difference: 0.155.
- Correlation coefficient of radon concentration vs. atmospheric pressure: 0.05139.
- Correlation coefficient of radon concentration vs. wind speed: 0.04129.
- Correlation coefficient of radon concentration vs. rainfall: −0.3779.
- Correlation coefficient of radon concentration vs. relative humidity: −0.09206.
3.3. Monitoring and Alert Generation
- Activate forced evacuation: 3.667/5.
- De-activate forced evacuation: 1/5.
- Natural ventilation: 2.5/5.
- Check sensors: 0/5.
- Check inference: 0/5.
- Check exposure time: 0/5.
4. Discussion
- Unlike early warning systems, the use of expert systems combined with decision trees is not aimed only at minimizing the impact of radon gas concentrations, but it also intends to mitigate the existing effects and to enrich the knowledge base of the system, in a way that allows to keep inserting and identifying factors influencing those gas concentrations.
- When defined as expert systems, the decisions will always be subject to a final review because, even if they may be understood as multi-criteria decision methods, in no case they encompass all the criteria, viewpoints and scenarios that could show up. So, its preventive effects would be a consequence of its evolution as knowledge-based systems, while their derived decisions will always be interpreted by the users, who at any moment may modify them, either inside or outside the methodology.
- The incorporation of modification mechanisms that are not related to the re-programming of the software artifact is one of the key points of the methodology. It clearly increases its versatility of use as well as its adaptation to different scenarios and circumstances. Said scenarios, in principle related to buildings with a residential use and their associated environmental metrics, may be extended with a mere re-definition of the membership functions and the dependent variables, defining through these all the specific circumstances for each scenario where the methodology is wished to be applied. For example, if its use were focused on underground mines then it would be necessary to re-define the intervals and qualifiers of the input variables to the first inference system, as well as removing and considering recommended actions according to their origins. In any case, those changes would be easily implemented.
- The necessary interpretation of the results derived from the algorithm establishes the nature of expert systems, enriches their knowledge base, and incorporates a qualitative control on the uncertainty that is associated to the definition and application of the methodology. With all that, the uncertainty that is inherent both to data collection and to their qualitative interpretation is reduced. Not only the uncertainty from the randomness of measurements is reduced, but also the epistemic is—this one related to the lack of information—and the one related with the own interaction of the systems, algorithms and data collection processes as well. The fact of supervising the risk determination by means of a correction factor, and the constant monitoring that is provided by the definition of the membership functions, allows an expert user to continuously improve the prediction capability of the methodology.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. WHO Handbook on Indoor Radon: A Public Health Perspective; WHO Press: Geneva, Switzerland, 2009; ISBN 978-92-4-154767-3. [Google Scholar]
- Thompson, R.E. Radon. In Encyclopedia of Toxicology, 3rd ed.; Elsevier Academic Press: Burlington, MA, USA, 2014; ISBN 9780123864543. [Google Scholar]
- Blanco-Novoa, O.; Fernández-Caramés, T.M.; Fraga-Lamas, P.; Castedo, L. A cost-effective IoT system for monitoring indoor radon gas concentration. Sensors 2018, 18, 2198. [Google Scholar] [CrossRef] [PubMed]
- Al-Zoughool, M.; Krewski, D. Health effects of radon: A review of the literature. Int. J. Radiat. Biol. 2009, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Lubin, J.H.; Boice, J.D.; Edling, C.; Hornung, R.W.; Howe, G.R.; Kunz, E.; Kusiak, R.A.; Morrison, H.I.; Radford, E.P.; Samet, J.M.; et al. Lung cancer in radon-exposed miners and estimation of risk from indoor exposure. J. Natl. Cancer Inst. 1995, 87, 817–827. [Google Scholar] [CrossRef] [PubMed]
- Pavia, M.; Bianco, A.; Pileggi, C.; Angelillo, I.F. Meta-Analysis of residential exposure to radon gas and lung cancer. Bull. World Health Organ. 2003, 81, 732–738. [Google Scholar] [CrossRef]
- Darby, S.; Hill, D.; Auvinen, A.; Barros-Dios, J.M.; Baysson, H.; Bochicchio, F.; Deo, H.; Falk, R.; Forastiere, F.; Hakama, M.; et al. Radon in homes and risk of lung cancer: Collaborative analysis of individual data from 13 European case-control studies. Br. Med. J. 2005, 330, 223–226. [Google Scholar] [CrossRef]
- Krewski, D.; Lubin, J.H.; Zielinski, J.M.; Alavanja, M.; Catalan, V.S.; Field, R.W.; Klotz, J.B.; Létourneau, E.G.; Lynch, C.F.; Lyon, J.L.; et al. A combined analysis of north American case-control studies of residential radon and lung cancer. J. Toxicol. Environ. Health 2006, 69, 533–597. [Google Scholar] [CrossRef]
- Lantz, P.M.; Mendez, D.; Philbert, M.A. Radon, smoking, and lung cancer: The need to refocus radon control policy. Am. J. Public Health 2013, 103, 443–447. [Google Scholar] [CrossRef]
- García-Tobar, J. Influencia de las condiciones meteorológicas sobre el nivel de radón a corto plazo en un laboratorio subterráneo. Nova Sci. 2014, 6, 78. [Google Scholar] [CrossRef]
- Castro Bernárdez, M. Exposición a Radón Residencial y Cáncer de Pulmón: Un Estudio de Casos y Controles en el Área Sanitaria de Ourense. Ph.D. Thesis, Universidade de Santiago de Compostela, Santiago de Compostela, Spain, 2015. [Google Scholar]
- López-Abente, G.; Núñez, O.; Fernández-Navarro, P.; Barros-Dios, J.M.; Martín-Méndez, I.; Bel-Lan, A.; Locutura, J.; Quindós, L.; Sainz, C.; Ruano-Ravina, A. Residential radon and cancer mortality in Galicia, Spain. Sci. Total Environ. 2018, 610–611, 1125–1132. [Google Scholar] [CrossRef]
- Barbosa-Lorenzo, R.; Ruano-Ravina, A.; Cerdeira Caramés, S.; Barros-Dios, J.M. Residential radon and lung cancer. An ecologic study in Galicia, Spain. Med. Clínica 2015, 144, 304–308. [Google Scholar] [CrossRef]
- Torres-Durán, M. Radón Residencial y Riesgo de Cáncer de Pulmón en Nunca Fumadores. Un Estudio Multicéntrico de Casos y Controles en el Noroeste de España. Ph.D. Thesis, Universidade de Santiago de Compostela, Santiago de Compostela, Spain, 2015. [Google Scholar]
- Quindos, L.S.; Fernandez, P.L.; Soto, J. National survey on indoor radon in Spain. Environ. Int. 1991, 17, 449–453. [Google Scholar] [CrossRef]
- Barros-Dios, J.M.; Barreiro, M.A.; Ruano-Ravina, A.; Figueiras, A. Exposure to residential radon and lung cancer in Spain: A population-based: Case-Control study. Am. J. Epidemiol. 2002, 156, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Barros-Dios, J.M.; Ruano-Ravina, A.; Gastelu-Iturri, J.; Figueiras, A. Factors underlying residential radon concentration: Results from Galicia, Spain. Environ. Res. 2007, 103, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Quindós, L.S.; Fernández, P.L.; Sainz, C.; Fuente, I.; Nicolás, J.; Quindós, L.; Arteche, J. Indoor radon in a Spanish region with different gamma exposure levels. J. Environ. Radioact. 2008, 99, 1544–1547. [Google Scholar] [CrossRef]
- Cortina, D.; Durán, I.; Llerena, J.J. Measurements of indoor radon concentrations in the Santiago de Compostela area. J. Environ. Radioact. 2008, 99, 1583–1588. [Google Scholar] [CrossRef] [PubMed]
- Martins, L.M.O.; Gomes, M.E.P.; Neves, L.J.P.F.; Pereira, A.J.S.C. The influence of geological factors on radon risk in groundwater and dwellings in the region of Amarante (Northern Portugal). Environ. Earth Sci. 2013, 68, 733–740. [Google Scholar] [CrossRef]
- Martins, L.M.O.; Gomes, M.E.P.; Teixeira, R.J.S.; Pereira, A.J.S.C.; Neves, L.J.P.F. Indoor radon risk associated to post-tectonic biotite granites from Vila Pouca de Aguiar pluton, northern Portugal. Ecotoxicol. Environ. Saf. 2016, 133, 164–175. [Google Scholar] [CrossRef]
- US EPA A Citizen’s Guide to Radon; US EPA: Washington, DC, USA, 2012.
- Pereira, F.; Lopes, S.I.; Carvalho, N.B.; Curado, A. RnProbe: A LoRa-Enabled IoT Edge Device for Integrated Radon Risk Management. IEEE Access 2020, 8, 203488–203502. [Google Scholar] [CrossRef]
- Lucas, P.J.F.; van der Gaag, L.C. Principles of Expert Systems; Addison-Wesley: Wokingham, UK, 1991; ISBN 0-201-41640-9. [Google Scholar]
- Pfeifer, R.; Lüthi, H.-J. Decision Support Systems and Expert Systems: A Complementary Relationship? In Expert Systems and Artificial Intelligence in Decision Support Systems; Springer: Dordrecht, The Netherlands, 1987; pp. 41–51. [Google Scholar]
- Font, L.L.; Baixeras, C.; Domingo, C.; Fernandez, F. Experimental and theoretical study of radon levels and entry mechanisms in a Mediterranean climate house. Radiat. Meas. 1999, 31, 277–282. [Google Scholar] [CrossRef]
- Font, L.L.; Baixeras, C.; Jönsson, G.; Enge, W.; Ghose, R. Application of a radon model to explain indoor radon levels in a Swedish house. Radiat. Meas. 1999, 31, 359–362. [Google Scholar] [CrossRef]
- Font, L.; Baixeras, C. The RAGENA dynamic model of radon generation, entry and accumulation indoors. Sci. Total Environ. 2003, 307, 55–69. [Google Scholar] [CrossRef]
- Ávila, T.V. Radiaciones Ionizantes y su Impacto. Primer Simposio Internacional sobre Medioambiente (ISE 2017); Repositorio Institucional de la Universidad Politécnica Salesiana: Cuenca, Ecuador, 2018. [Google Scholar]
- Barreira, F. Concentration of atmospheric radon and wind direction. Nature 1961, 190, 1092–1093. [Google Scholar] [CrossRef]
- Virk, H.S.; Walia, V.; Sharma, A.K.; Kumar, N.; Kumar, R. Correlation of radon anomalies with microseismic events in Kangra and Chamba valleys of N-W Himalaya. Geofis. Int. 2000, 39, 221–227. [Google Scholar] [CrossRef]
- Sakashita, T.; Doi, M.; Nakamura, Y.; Iida, T. A case study of radon-222 transport from continental North-East Asia to the Japanese islands in winter by numerical analysis. J. Environ. Radioact. 2004, 72, 245–257. [Google Scholar] [CrossRef]
- Groves-Kirkby, C.J.; Crockett, R.G.M.; Denman, A.R.; Phillips, P.S. Climatic and Seasonal Influences on Radon Time Series in an Environment of Low Anthropogenic Activity; The University of Northampton: Northampton, UK, 2006; pp. 1–10. [Google Scholar]
- Eaton, R.S.; Scott, A.G. Understanding radon transport into houses. Radiat. Prot. Dosimetry 1984, 7, 251–253. [Google Scholar] [CrossRef]
- Nazaroff, W.W.; Feustel, H.; Nero, A.V.; Revzan, K.L.; Grimsrud, D.T.; Essling, M.A.; Toohey, R.E. Radon transport into a detached one-story house with a basement. Atmos. Environ. 1985, 19, 31–46. [Google Scholar] [CrossRef]
- Linares-Alemparte, P.; García-Ortega, S. Influence of Ventilation on Radon Concentration in a Study Case in Spain. In Proceedings of the 40th AIVC—8th TightVent—6th Venticool Conference, Ghent, Belgium, 15–16 October 2019. [Google Scholar]
- Zhang, Z.; Smith, B.; Steck, D.J.; Guo, Q.; Field, R.W. Variation in yearly residential radon concentrations in the upper Midwest. Health Phys. 2007, 93, 288–297. [Google Scholar] [CrossRef]
- Borgoni, R.; Cremonesi, A.; Quatto, P.; Somà, G.; Bartolo, D.; Alberici, A. Radon Indoor in Lombardy: A Geostatistical Approach for Identifying Prone Areas; Geomatics Workbooks: Roma, Italy, 2018. [Google Scholar]
- Pantelić, G.; Čeliković, I.; Živanović, M.; Vukanac, I.; Nikolić, J.; Cinelli, G.; Gruber, V. Literature Review of Indoor Radon Surveys in Europe; JRC114370; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar]
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. Report No. A/RES/70/1; United Nations: New York, NY, USA, 2015. [Google Scholar]
- EUR-Lex. Council Directive 2013/59/Euratom of 5 December 2013 Laying Down Basic Safety Standards for Protection Against the Dangers Arising from Exposure to Ionising Radiation, and Repealing Directives 89/618/Euratom, 90/641/Eu, 96/29/Euratom, 97/43/Euratom and 2003/122/Euratom. Available online: https://eur-lex.europa.eu/eli/dir/2013/59/oj (accessed on 11 February 2020).
- Documento BOE-A-2019-18528; Real Decreto 732/2019, de 20 de Diciembre, por el Que se Modifica el Código Técnico de la Edificación, Aprobado por el Real Decreto 314/2006, de 17 de Marzo. Available online: https://www.boe.es/diario_boe/txt.php?id=BOE-A-2019-18528 (accessed on 24 March 2020).
- Tommasino, L. Passive Sampling and Monitoring of Radon and Other Gases. Radiat. Prot. Dosimetry 1998, 78, 55–58. [Google Scholar] [CrossRef]
- Cothern, C.R.; Smith, J.E., Jr. (Eds.) Environmental Radon; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 35, ISBN 978-1-4899-0475-1. [Google Scholar]
- Miles, J. Methods of radon measurement and devices. In Proceedings of the 4th European Conference on Protection against Radon at Home and at Work, Prague, Czech Republic, 28 June–2 July 2004. [Google Scholar]
- Alvarellos, A.; Gestal, M.; Dorado, J.; Rabuñal, J.R. Developing a secure low-cost radon monitoring system. Sensors 2020, 20, 752. [Google Scholar] [CrossRef]
- US Nuclear Regulatory Commission. Multi-Agency Radiation Survey and Site Investigation Manual (MARSSIM); 30026032; US Nuclear Regulatory Commission: Washington, DC, USA, 2000. [CrossRef]
- Mazed, D.; Ciolini, R.; Curzio, G.; Del Gratta, A. A new active method for continuous radon measurements based on a multiple cell proportional counter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 582, 535–545. [Google Scholar] [CrossRef]
- Burstein, F.; Holsapple, C.W. Handbook on Decision Support Systems 1; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Burstein, F.; Holsapple, C.W. Handbook on Decision Support Systems 2; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Bonczek, R.H.; Holsapple, C.W.; Whinston, A.B.; Carter, H. Foundations of Decision Support Systems; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Hevner, A.R.; Chatterjee, S. Design Research in Information Systems: Theory and Practice; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-6107-5. [Google Scholar]
- Krishnamoorthy, C.S.; Rajeev, S. Artificial Intelligence and Expert Systems for Engineers; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Liao, S.H. Expert system methodologies and applications-a decade review from 1995 to 2004. Expert Syst. Appl. 2005, 28, 93–103. [Google Scholar] [CrossRef]
- Kumar, Y.; Jain, Y. Research Aspects of Expert System. Int. J. Comput. Bus. Res. 2012, 1, 1–11. [Google Scholar]
- Merritt, D. Building Expert Systems in Prolog; Springer: New York, NY, USA, 1989; ISBN 978-1-4613-8913-2. [Google Scholar]
- Marston, M.; Allen, J.; Mistree, F. The decision support problem technique: Integrating descriptive and normative approaches in decision based design. Eng. Valuat. Cost Anal. 2000, 3, 107–129. [Google Scholar]
- Allen, J.K.; Seepersad, C.C.; Choi, H.-J.; Panchal, J.H.; McDowell, D.L.; Mistree, F. Decision Making in Engineering Design. In Integrated Design of Multiscale, Multifunctional Materials and Products; Elsevier: Burlington, MA, USA, 2010. [Google Scholar]
- Mistree, F.; Smith, W.F.; Bras, B.; Allen, J.K.; Muster, D. Decision-Based Design: A Contemporary Paradigm for Ship Design. Trans. Soc. Nav. Archit. Mar. Eng. 1990, 98, 565–597. [Google Scholar]
- Chien, C.F.; Kim, K.H.; Liu, B.; Gen, M. Advanced decision and intelligence technologies for manufacturing and logistics. J. Intell. Manuf. 2012, 23, 2133–2135. [Google Scholar] [CrossRef]
- Hazelrigg, G.A. A Framework for Decision-Based Engineering Design. J. Mech. Des. 1998, 120, 653–658. [Google Scholar] [CrossRef]
- Lewis, K.; Chen, W.; Schmidt, L. Decision Making in Engineering Design; ASME Press: New York, NY, USA, 2006; ISBN 978-0791802465. [Google Scholar]
- Myers, W. Introduction to Expert Systems. IEEE Expert 1986, 1, 100–109. [Google Scholar] [CrossRef]
- Buchanan, B.G. Expert systems: Working systems and the research literature. Expert Syst. 1986, 3, 32–50. [Google Scholar] [CrossRef]
- Todd, B.S. An Introduction to Expert Systems; Oxford University Computing Laboratory: Oxford, UK, 1992. [Google Scholar]
- Hevner, A.R.; March, S.T.; Park, J.; Ram, S. Design science in information systems research. MIS Q. Manag. Inf. Syst. 2004, 28, 75–105. [Google Scholar] [CrossRef]
- Brambley, M.R.; Hanlon, R.L.; Parker, G.B. Expert Systems: A New Approach to Radon Mitigation Training and Quality Assurance; 22031214; Pacific Northwest Lab.: Richland, WA, USA, 1990. [Google Scholar]
- Reffat, R.M.; Harkness, E.L. Expert system for environmental quality evaluation. J. Perform. Constr. Facil. 2001, 15, 109–114. [Google Scholar] [CrossRef]
- Shoom, G.B.; Bowen, D.G. IAQES: An expert system for indoor air quality problem resolution. In Proceedings of the Fifth Annual AI Systems in Government Conference, Washington, DC, USA, 6–11 May 1990; pp. 127–133. [Google Scholar]
- Ikram, A.; Qamar, U. Developing an expert system based on association rules and predicate logic for earthquake prediction. Knowl. Based Syst. 2015, 75, 87–103. [Google Scholar] [CrossRef]
- Sato, S.-Y.; Kobayashi, H.; Utsumi, Y. Diagnosis of indoor air quality and ventilation design utilizing expert system. Build. Simul. 1999, 6, 831–838. [Google Scholar]
- Fang, H.-Y.; Mikroudis, G.K.; Pamukcu, S. Multi-Domain Expert Systems for Hazardous Waste Site Investigations. In Expert Systems in Environmental Planning; Springer: Berlin/Heidelberg, Germany, 1993; pp. 217–232. [Google Scholar]
- Fang, H.-Y. Expert systems for assessment of radon gas. In Proceedings of the ASCE Environmental Engineering National Conference, Austin, TX, USA, 10–12 July 1989; Molina, J., Ed.; pp. 97–104. [Google Scholar]
- Fang, H.Y.; Mikroudis, G.K. “Modular Expert System: An Expert System between Expert Systems”; Envirotronics Corporation International: Grand Rapids, MI, USA, 1989. [Google Scholar]
- Fang, H.Y.; Mikroudis, G.K.; Pamukcu, S. A unified approach to the assessment of waste disposal sites. Comput. Geotech. 1987, 3, 129–156. [Google Scholar] [CrossRef]
- Fang, H.Y.; Mikroudis, G.K. Multi-Domains and multi-experts in knowledge based expert systems. In Proceedings of the 1st International Symposium on Environmental Geotechnology, Allentown, PA, USA; 1987; pp. 355–361. [Google Scholar]
- Byrne, P.H. Development of an Advisory System for Indoor Radon Mitigation. Master’s Thesis, Portland State University, Portland, OR, USA, 1991. [Google Scholar] [CrossRef]
- Murphy, K.; Packer, C.; Stevens, A.; Simpson, S. Effective early warning systems for new and emerging health technologies: Developing an evaluation framework and an assessment of current systems. Int. J. Technol. Assess. Health Care 2007, 23, 324–330. [Google Scholar] [CrossRef]
- Zschau, J.; Küppers, A. (Eds.) Early Warning Systems for Natural Disaster Reduction; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-642-63234-1. [Google Scholar]
- Lin, C.S.; Khan, H.A.; Chang, R.Y.; Wang, Y.C. A new approach to modeling early warning systems for currency crises: Can a machine-learning fuzzy expert system predict the currency crises effectively? J. Int. Money Financ. 2008, 27, 1098–1121. [Google Scholar] [CrossRef][Green Version]
- Waidyanatha, N. Towards a typology of integrated functional Early Warning Systems. Int. J. Crit. Infrastruct. 2010, 6, 31–51. [Google Scholar] [CrossRef]
- Velikov, I. Development of an Early Warning Expert System. In Proceedings of the 5th International Conference on Application of Information and Communication Technology and Statistics in Economy and Education (ICAICTSEE-2015), Sofia, Bulgaria, 13–14 November 2015. [Google Scholar]
- Shanon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–623. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984; ISBN 9781351460491. [Google Scholar]
- Ma, X. Using Classification and Regression Trees: A Practical Primer; Information Age Publishing, INC: Charlotte, NC, USA, 2018. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees: Theory and Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2008; ISBN 9789812771711. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Lewis, R.J. An Introduction to Classification and Regression Tree (CART) Analysis Introduction to CART. In Proceedings of the 2000 Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, 22–25 May 2000. [Google Scholar]
- Lemon, S.C.; Roy, J.; Clark, M.A.; Friedmann, P.D.; Rakowski, W. Classification and Regression Tree Analysis in Public Health: Methodological Review and Comparison with Logistic Regression. Ann. Behav. Med. 2003, 26, 172–181. [Google Scholar] [CrossRef]
- Xingong, W.; Vipin, K. (Eds.) The Top Ten Algorithms in Data Mining; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Loh, W.-Y. Classification and Regression Tree Methods. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Chichester, UK, 2014. [Google Scholar]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Questier, F.; Put, R.; Coomans, D.; Walczak, B.; Heyden, Y.V. The use of CART and multivariate regression trees for supervised and unsupervised feature selection. Chemom. Intell. Lab. Syst. 2005, 76, 45–54. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Casal-Guisande, M.; Comesaña-Campos, A.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. Design and Development of a Methodology Based on Expert Systems, Applied to the Treatment of Pressure Ulcers. Diagnostics 2020, 10, 614. [Google Scholar] [CrossRef]
- Comesaña-Campos, A.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J. The Value Index as a decision support tool applied to a new system for evaluating and selecting design alternatives. Expert Syst. Appl. 2018, 113. [Google Scholar] [CrossRef]
- Comesaña-Campos, A.; Casal-Guisande, M.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases. Int. J. Environ. Res. Public Health 2020, 17, 8644. [Google Scholar] [CrossRef] [PubMed]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man. Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Mamdani, E.H. Advances in the linguistic synthesis of fuzzy controllers. Int. J. Man. Mach. Stud. 1976, 8, 669–678. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis. IEEE Trans. Comput. 1977, C–26, 1182–1191. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2010; ISBN 9781119994374. [Google Scholar]
- Thunnissen, D.P. Propagating and Mitigating Uncertainty in the Design of Complex Multidisciplinary Systems. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2005. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Dagnino, S.J. Correlación. Revista Chilena de Anestesia 2014, 43. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- MATLAB & Simulink. R2020b—Actualizaciones de las Familias de Productos MATLAB y Simulink. Available online: https://es.mathworks.com/products/new_products/latest_features.html (accessed on 22 October 2020).
- MATLAB. Fuzzy Logic Toolbox. Available online: https://www.mathworks.com/products/fuzzy-logic.html (accessed on 29 May 2020).
- GitHub. NewGuy012/spider_plot: Create a Spider or Radar Plot with Individual Axes. Available online: https://github.com/NewGuy012/spider_plot (accessed on 22 October 2020).
- Hintenlang, D.E. Influence of ventilation strategies on indoor radon concentrations based on a semiempirical model for florida-style houses. Health Phys. 1994, 66, 427–432. [Google Scholar] [CrossRef] [PubMed]



| Technology | Air Sampling | Measurement Technique | Duration of Studies | Description of the Technology |
|---|---|---|---|---|
| Activated carbon detector | Passive | Integrating [44] | Short-term studies (periods generally shorter than one week) | These are based on the capability of active carbon to retain radon gas [46]. After their use, the amount of gamma radiation emitted may be determined in a laboratory. |
| Electret ion chamber detector | Active and passive variants | Integrating | Depending on the ion chamber design, it may allow to carry out short-term or long-term studies [47] | This type of devices measure the ionization produced when radon atoms disintegrate inside the chamber [47]. |
| Track-etch detector | Passive | Integrating [44] | Long-term studies | After exposed, the detector is chemically and/or electrochemically etched and analysed in a laboratory to obtain the average radon concentration from the density of tracks produced by radon and its progeny [46]. |
| Scintillation cells | Active | Grab or Continuous [44] | Commonly used for carrying out continuous measurements [3] for both short and long cycles | It consists of a cylindrical device coated with a luminescent material [47], with one of the walls being transparent, and activated by alpha emissions [46]. The emitted photons are captured and amplified by a photomultiplier tube [46,47], thus allowing to determine the radon gas concentration level in air [46]. |
| Gas-filled detector | Active and passive variants | Grab or continuous [48] | May be used both for short and for long measurement periods | It is a device in which an interaction is produced between the radioactive particles derived from the radon gas present in a chamber, generating ion couples that are attracted to charged electrodes [47]. It may use different gas mixes such as air, argon with a small amount of methane, and argon or helium with small amounts of any halogen element [47]. |
| Solid-state detector | Active and passive variants | Grab or continuous | Can be used both for short and long measurement cycles. | It is based on the interaction of the emitted radiation with a semi-conductor material that produces electron-hole couples that are then collected by charged electrodes [47]. Depending on the type of design it may focus on one or another radiation type, with germanium and silicon being the most commonly used materials [47]. |
| Guideline 1: Design an Artifact (the Proposed Methodology) |
| The artifact, meaning the methodology as detailed in Section 2.2, consists in a helping tool aimed to the process for the prevention of high indoor concentrations of radon gas. In the first place, the calculation is made for the correction factor, from the information collected by a set of sensors, by means of a fuzzy logic-based inference system. Later, said correction factor is combined with the current radon gas concentration within a second inference system, also based on fuzzy logic, from which the radon risk level is obtained. Finally, from the calculated values and the data history it is possible to train regression models based on a decision tree, that will be used to perform recommendations on the levels at which the corrective measures should be applied to reduce the concentration of radon gas. With the objective of automating the calculations and facilitating the understanding of the proposed methodology, the implementation of the system has been carried out into a software artifact defined using the MATLAB® environment developed by The MathWorks, Inc, Natick, MA, US. |
| Guideline 2: Relevance of the problem |
| The problem derived from the inhalation of radon gas results nowadays to be unquestionable, because it is recognized as the second-leading cause of lung cancer after smoking [1,5,6,7,8,9,11]. That is why it becomes very important the development of a methodology that allows to detect and anticipate potential situations in which the current radon gas concentration might get increased inside a building. |
| Guideline 3: Assessment of the design |
| The application of the new methodology is shown in the case study described in Section 3. |
| Guideline 4: Contributions to the field of research |
| The contributions to the field of expert systems are presented in Section 4 and Section 5 of this article. |
| Guideline 5: Rigour in the research |
| The conceptual development of the presented methodology, together with its classification within the field of investigation, has been defined in Section 1. In the same way, the mathematical foundations of this work are supported on the use of fuzzy inference systems, given their proved effectiveness and their capability for handling uncertainty in decision-making processes. |
| Guideline 6: Design as a search |
| In Section 1, the methodology has been framed within the state of the art that is inherent to the field of study. |
| Guideline 7: Communication of the research |
| In Section 5, the main contributions of the new method are presented, as will be the future lines of work. |
| Prevention of Exposure to Harmful Radon Gas Concentrations | ||
|---|---|---|
| Design Needs for the Artifact | Technical Requirements | Restrictions Associated to the Environment |
| The methodological process, from data collection to its interpretation, will need as little user interaction as possible | Programming the sensor data reading, and the automatic filtering and labelling of information Programming the autonomous-operation inference models | Errors or corrections that need the intervention of an expert |
| It must have an interface where the recommendations are shown in a graphical way | Graphical interface | The user must have available a device to run the software |
| It must collect environmental information and store it in a convenient way | Definition of a knowledge base supported by common database systems | The applicable restrictions from the devices and the environments where the software is implemented |
| It must process recursively the information | Continuous reading/writing on the database systems | None |
| It must calculate a risk value associated to the exposure to radon gas | Conjoint implementation of the inference systems together with the regression tree | Limitations associated to the algorithms themselves |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerqueiro-Pequeño, J.; Comesaña-Campos, A.; Casal-Guisande, M.; Bouza-Rodríguez, J.-B. Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks. Int. J. Environ. Res. Public Health 2021, 18, 269. https://doi.org/10.3390/ijerph18010269
Cerqueiro-Pequeño J, Comesaña-Campos A, Casal-Guisande M, Bouza-Rodríguez J-B. Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks. International Journal of Environmental Research and Public Health. 2021; 18(1):269. https://doi.org/10.3390/ijerph18010269
Chicago/Turabian StyleCerqueiro-Pequeño, Jorge, Alberto Comesaña-Campos, Manuel Casal-Guisande, and José-Benito Bouza-Rodríguez. 2021. "Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks" International Journal of Environmental Research and Public Health 18, no. 1: 269. https://doi.org/10.3390/ijerph18010269
APA StyleCerqueiro-Pequeño, J., Comesaña-Campos, A., Casal-Guisande, M., & Bouza-Rodríguez, J.-B. (2021). Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks. International Journal of Environmental Research and Public Health, 18(1), 269. https://doi.org/10.3390/ijerph18010269






