Enhancing Sustainability and Resilience through Multi-Level Infrastructure Planning
Abstract
1. Introduction
1.1. Implementation Planning as a Part of Resilient Planning
1.2. Implementation Planning and Decentralization
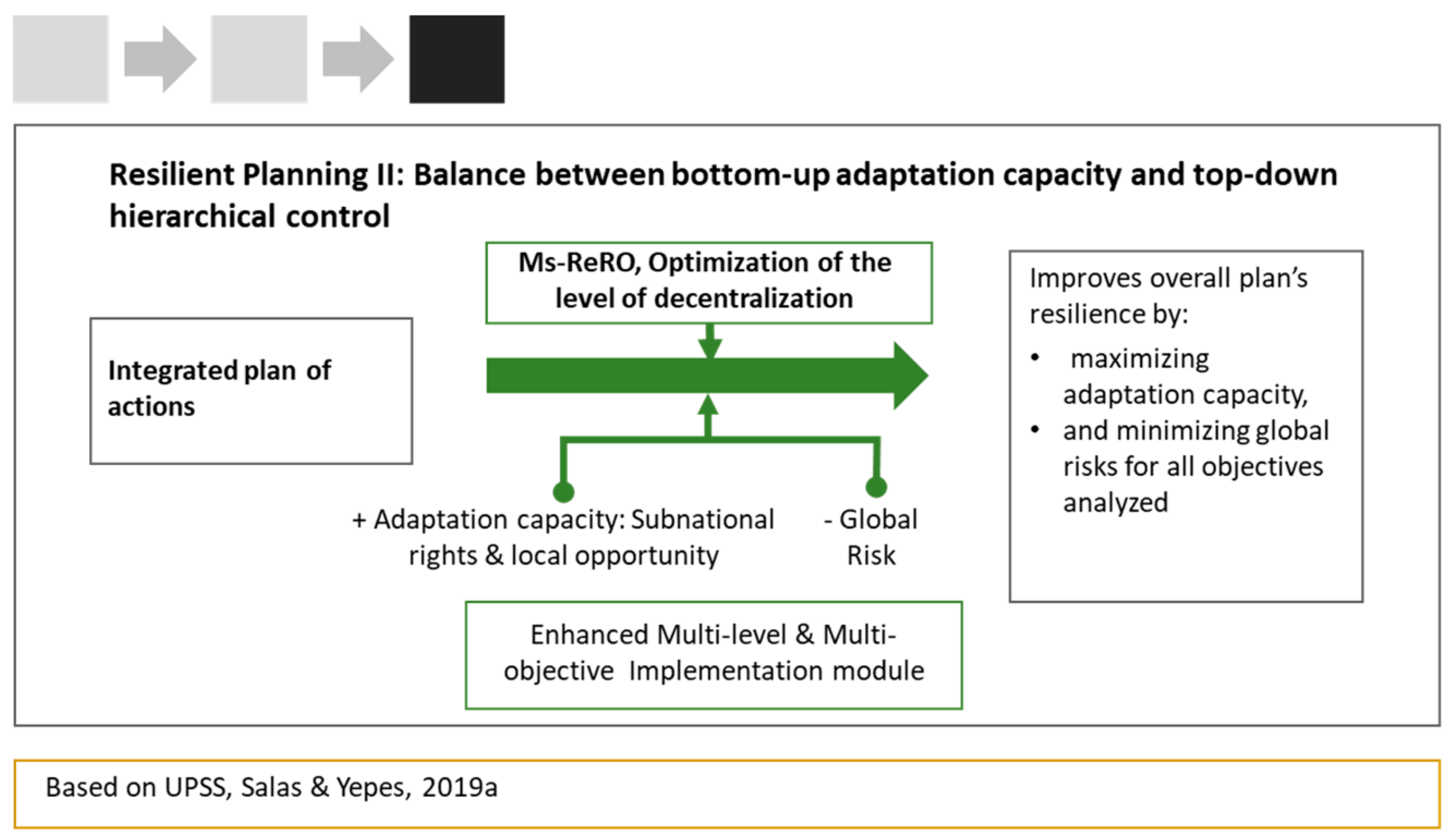
1.3. Decentralized Systems: Balancing Adaptive Capacity and Hierarchical Control
2. Methods
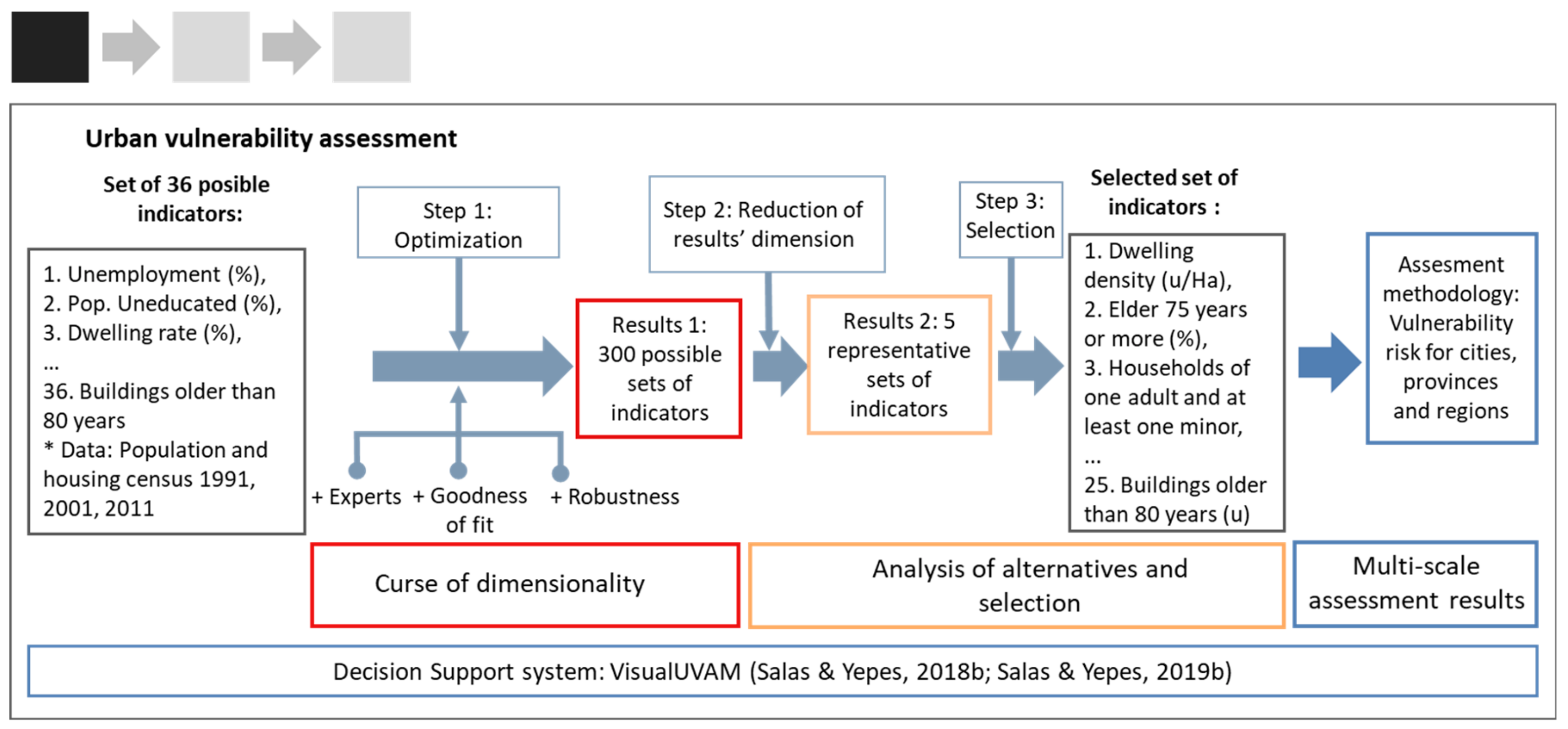
2.1. Step 1: Urban Vulnerability Assessment
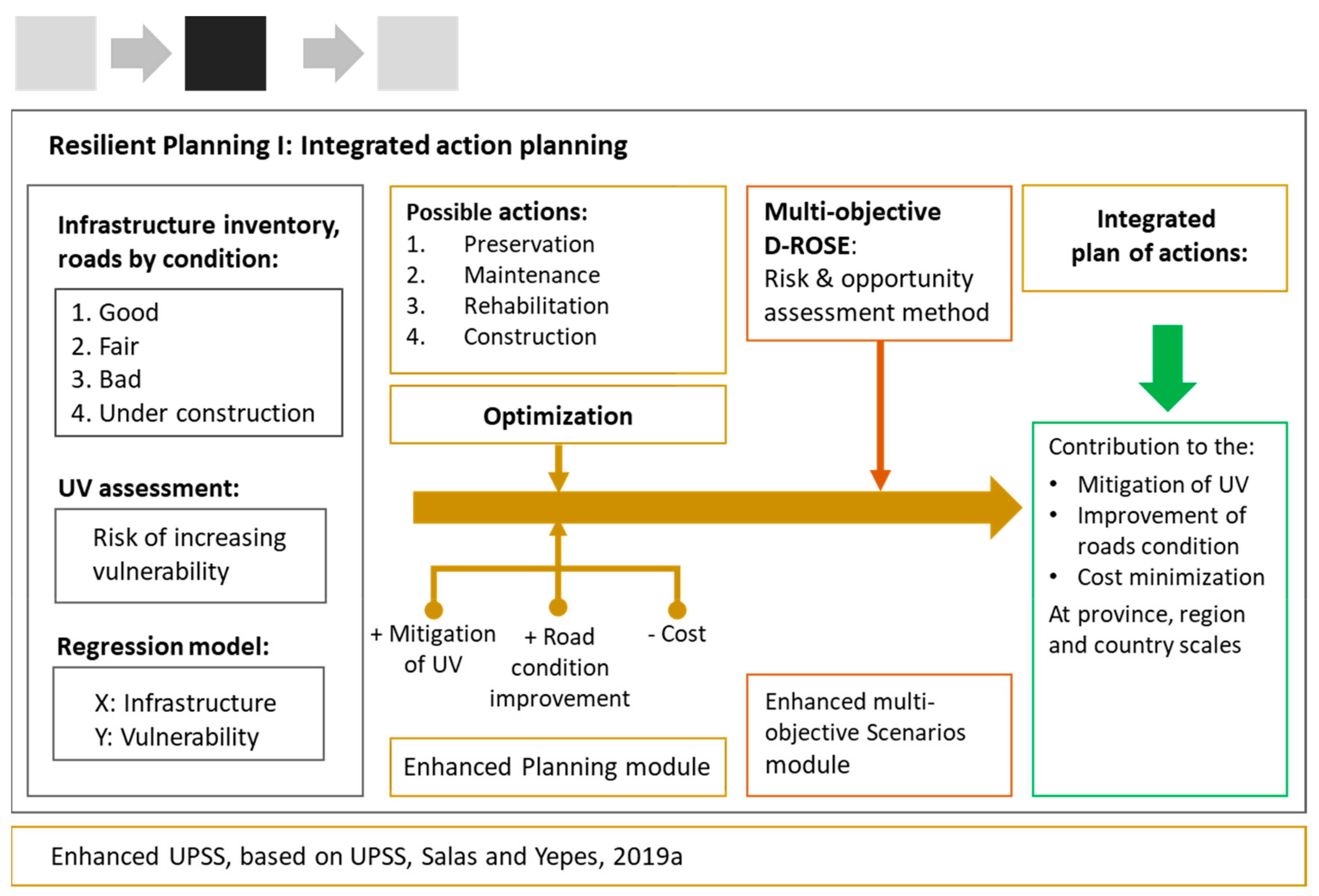
2.2. Step 2: Resilient Planning I—Action Planning
2.2.1. Planning Module: Generation of Planning Alternatives
2.2.2. Scenario Module: Evaluation of Risk and Opportunities
2.3. Step 3: Resilient Planning II—Implementation Planning
3. Case Study: Resilient Road Network Planning in Provinces of Spain
3.1. Information Collection Process
3.1.1. Information Required for Urban Vulnerability Assessment
3.1.2. Information Required for Urban Infrastructure Planning
3.2. Running of the Process
3.2.1. Step 1: Urban Vulnerability Assessment
3.2.2. Step 2: Action Planning
3.2.3. Step 3: Implementation Planning
4. Results
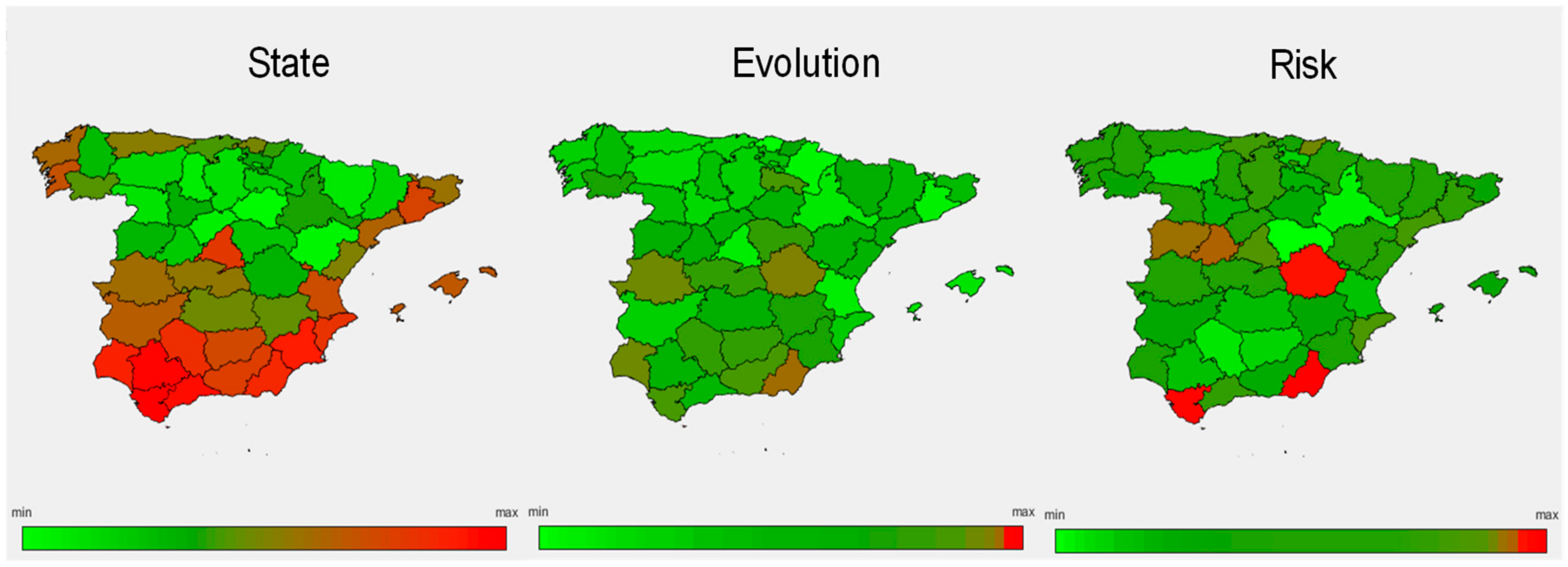
4.1. Step 1: Urban Vulnerability Assessment
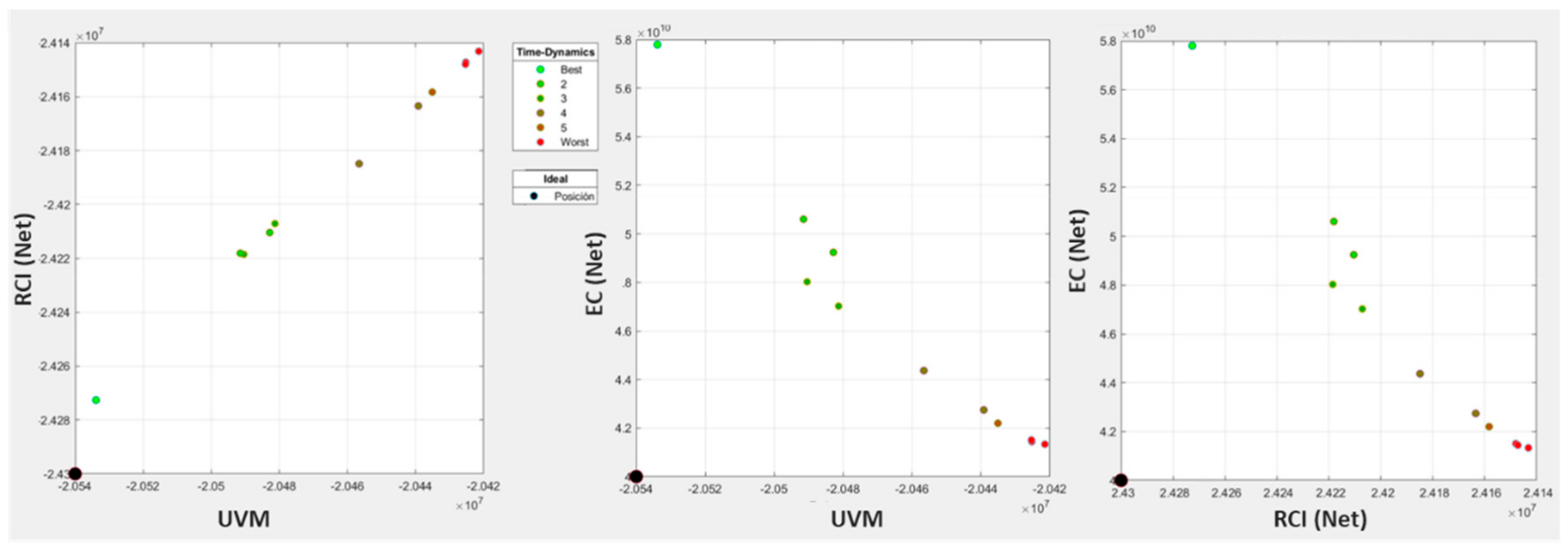
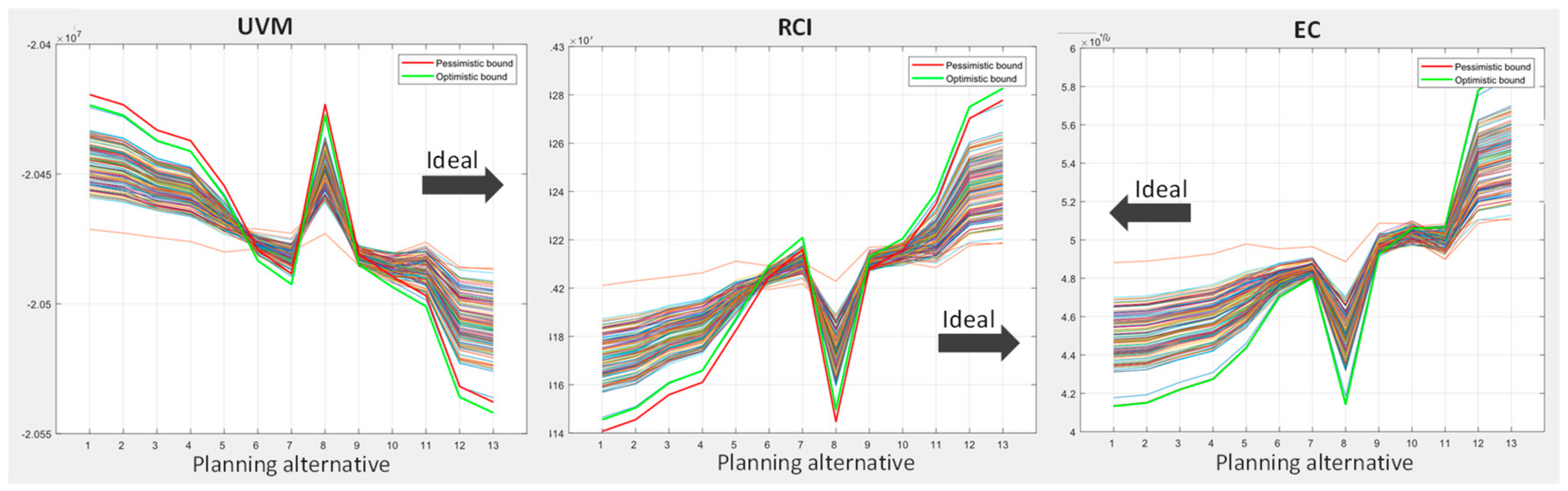
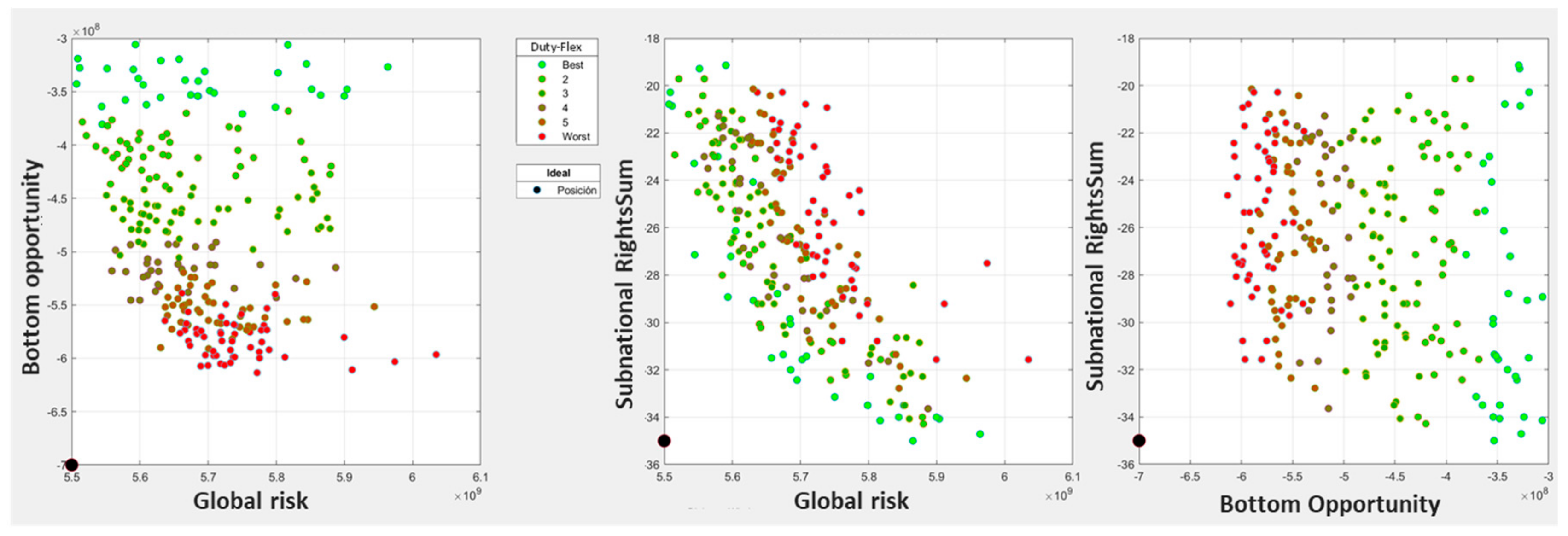
4.2. Step 2: Planning of Actions
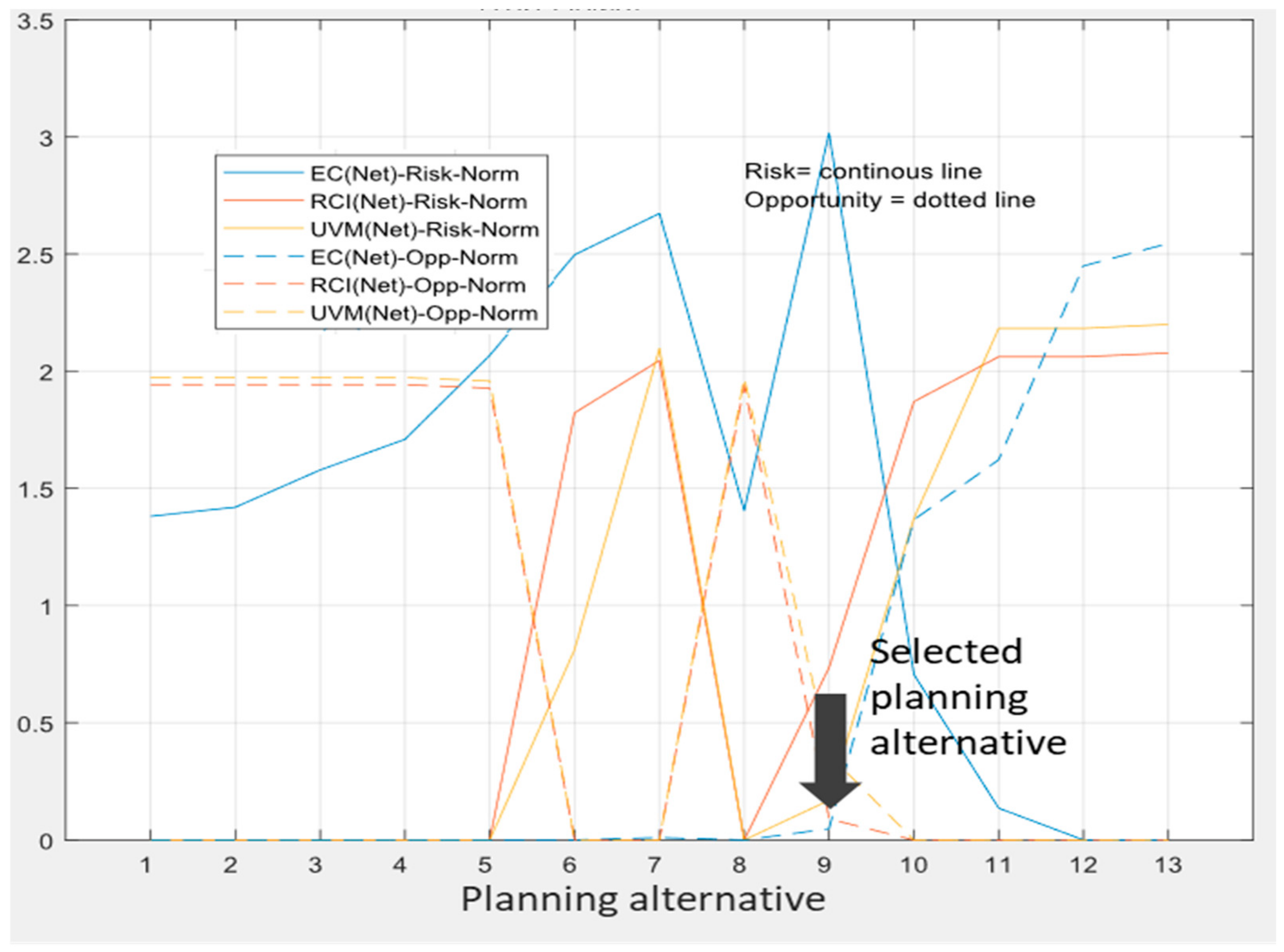
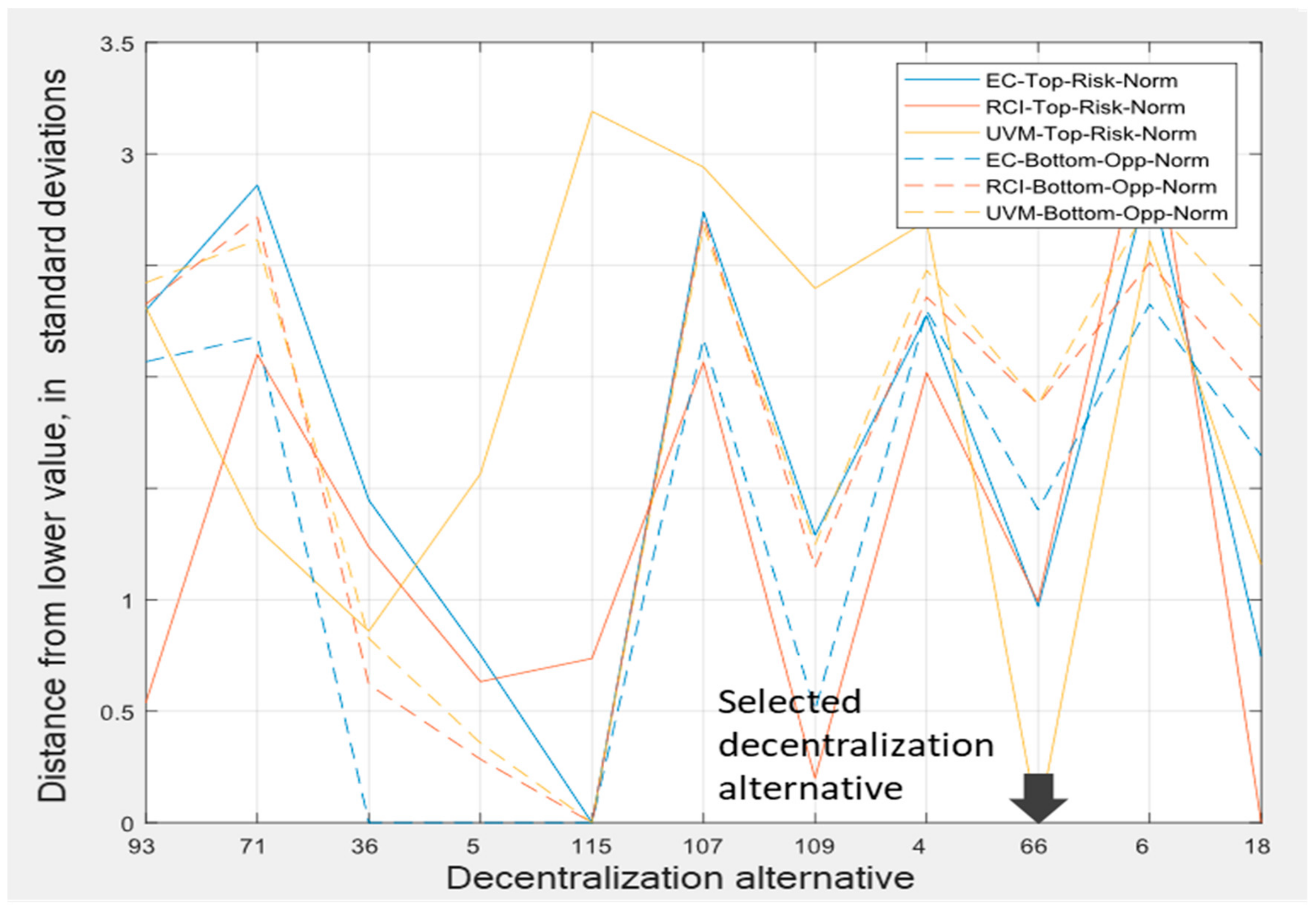
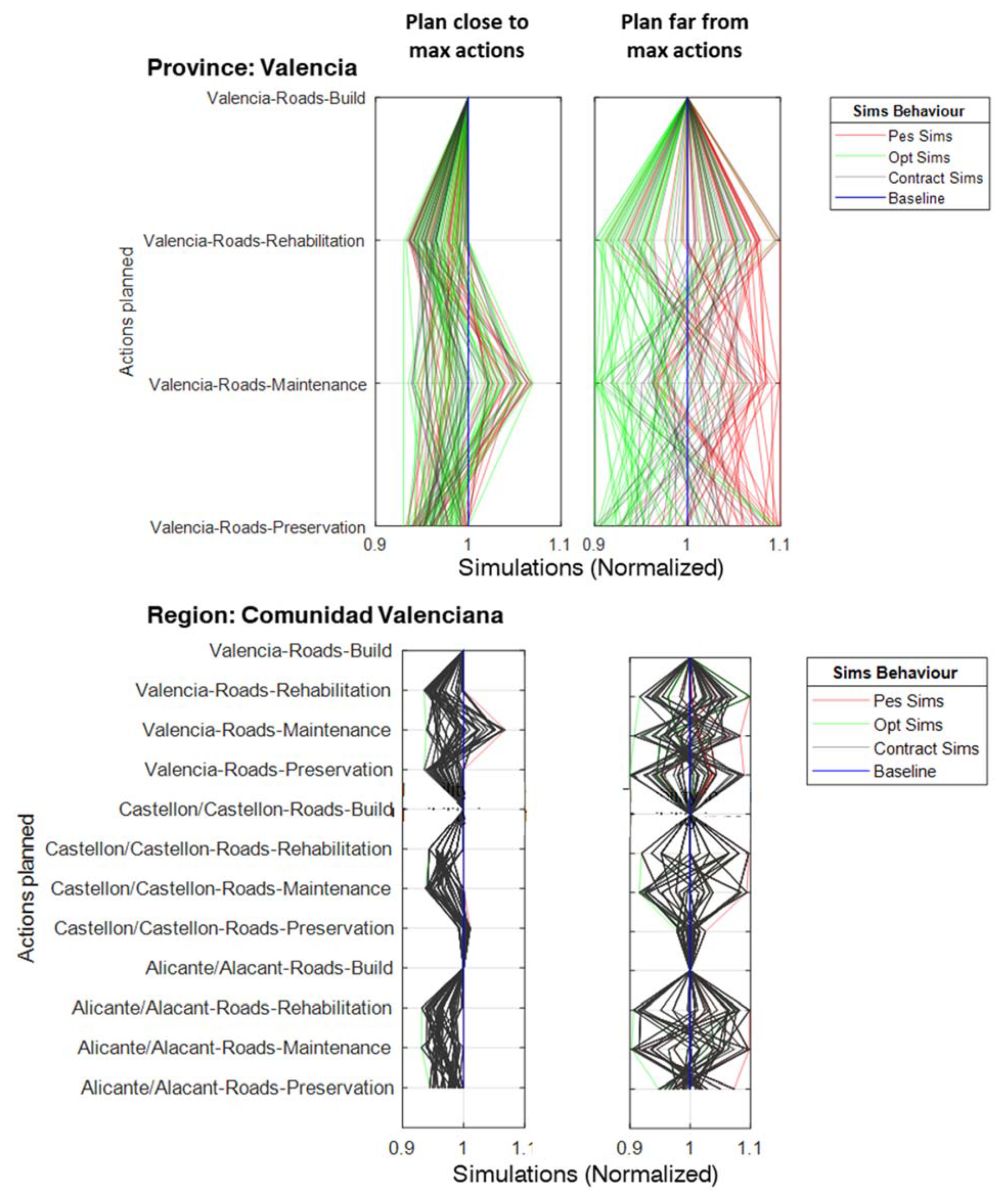
4.3. Step 3 Implementation Planning
5. Discussion
5.1. Action Planning
5.2. Implementation Planning
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holling, C.S. From complex regions to complex worlds. Ecol. Soc. 2004, 9, 11. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. Resilient urban planning: Major principles and criteria. Energy Procedia 2014, 61, 1491–1495. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, B. Resilient Planning Frame for Building Resilient Cities. In Building Resilient Cities in China: The Nexus between Planning and Science; Chen, X., Pan, Q., Eds.; Springer: Dordrecht, The Netherlands, 2015; Volume 113, pp. 33–41. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. MS-ReRO and D-ROSE methods: Assessing relational uncertainty and evaluating scenarios’ risks and opportunities on multi-scale infrastructure systems. J. Clean. Prod. 2019, 216, 607–623. [Google Scholar] [CrossRef]
- Schulz, A.; Zia, A.; Koliba, C. Adapting bridge infrastructure to climate change: institutionalizing resilience in intergovernmental transportation planning processes in the Northeastern USA. Mitig. Adapt. Strateg. Glob. Chang. 2017, 22, 175–198. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. Resilience-Oriented Urban Planning. Lect. Notes Energy 2018, 65, 3–27. [Google Scholar] [CrossRef]
- Gonzales, P.; Ajami, N.K. An integrative regional resilience framework for the changing urban water paradigm. Sustain. Cities Soc. 2017, 30, 128–138. [Google Scholar] [CrossRef]
- Leigh, N.G.; Lee, H. Sustainable and Resilient Urban Water Systems: The Role of Decentralization and Planning. Sustainability 2019, 11, 918. [Google Scholar] [CrossRef]
- Rogers, C.D.F. Engineering future liveable, resilient, sustainable cities using foresight. Proc. Inst. Civ. Eng. Civ. Eng. 2018, 171, 3–9. [Google Scholar] [CrossRef]
- Wagenaar, H.; Wilkinson, C. Enacting Resilience: A Performative Account of Governing for Urban Resilience. Urban Stud. 2015, 52, 1265–1284. [Google Scholar] [CrossRef]
- Wei, Y.D.; Li, H.; Yue, W. Urban land expansion and regional inequality in transitional China. Landsc. Urban Plan. 2017, 163, 17–31. [Google Scholar] [CrossRef]
- France-Mensah, J.; O’Brien, W.J. Developing a Sustainable Pavement Management Plan: Tradeoffs in Road Condition, User Costs, and Greenhouse Gas Emissions. J. Manag. Eng. 2019, 35. [Google Scholar] [CrossRef]
- Mao, X.; Wang, J.; Yuan, C.; Yu, W.; Gan, J. A Dynamic Traffic Assignment Model for the Sustainability of Pavement Performance. Sustainability 2019, 11, 170. [Google Scholar] [CrossRef]
- Torres-Machi, C.; Pellicer, E.; Yepes, V.; Chamorro, A. Towards a sustainable optimization of pavement maintenance programs under budgetary restrictions. J. Clean. Prod. 2017, 148, 90–102. [Google Scholar] [CrossRef]
- Torres-Machi, C.; Osorio, A.; Godoy, P.; Chamorro, A.; Mourgues, C.; Videla, C. Sustainable Management Framework for Transportation Assets: Application to Urban Pavement Networks. Ksce J. Civ. Eng. 2018, 22, 4095–4106. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Opudo, J.; Nyambenya, S. Comparison of Fuzzy AHP and Fuzzy TOPSIS for Road Pavement Maintenance Prioritization: Methodological Exposition and Case Study. Adv. Civ. Eng. 2015. [Google Scholar] [CrossRef]
- Gomes, S.V.; Cardoso, J.L.; Azevedo, C.L. Portuguese mainland road network safety performance indicator. Case Stud. Transp. Policy 2018, 6, 416–422. [Google Scholar] [CrossRef]
- Heinitz, F.M. Consistency of state road network master plan development steps. Case Stud. Transp. Policy 2018, 6, 400–415. [Google Scholar] [CrossRef]
- Rezaei, A.; Tahsili, S. Urban Vulnerability Assessment Using AHP. Adv. Civ. Eng. 2018. [Google Scholar] [CrossRef]
- Masi, A.; Santarsiero, G.; Chiauzzi, L. Development of a seismic risk mitigation methodology for public buildings applied to the hospitals of Basilicata region (Southern Italy). Soil Dyn. Earthq. Eng. 2014, 65, 30–42. [Google Scholar] [CrossRef]
- Beilin, R.; Wilkinson, C. Introduction: Governing for urban resilience. Urban Stud. 2015, 52, 1205–1217. [Google Scholar] [CrossRef]
- Cedergren, A.; Johansson, J.; Svegrup, L.; Hassel, H. Local success, global failure: Challenges facing the recovery operations of critical infrastructure breakdowns. In Proceedings of the 25th European Safety and Reliability Conference, Zurich, Switzerland, 7–10 September 2015; pp. 4343–4348. Available online: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84959017927&partnerID=40&md5=e6ef4cacb9260cde65a111ae0d36a90a. (accessed on 27 July 2019).
- Cedergren, A.; Johansson, J.; Hassel, H. Challenges to critical infrastructure resilience in an institutionally fragmented setting. Saf. Sci. 2018, 110, 51–58. [Google Scholar] [CrossRef]
- Regmi, B.R.; Star, C.; Leal Filho, W. Effectiveness of the Local Adaptation Plan of Action to support climate change adaptation in Nepal. Mitig. Adapt. Strateg. Glob. Chang. 2016, 21, 461–478. [Google Scholar] [CrossRef]
- Frank, J.; Martínez-Vázquez, J. Decentralization and Infrastructure: From Gaps to Solutions. In Decentralization and Infrastructure in the Global Economy: From Gaps to Solutions; Routledge: London, UK, 2015. [Google Scholar] [CrossRef]
- Charbit, C.; Gamper, C. Coordination of infrastructure investment across levels of government. In Decentralization and Infrastructure in the Global Economy: From Gaps to Solutions; Routledge: London, UK, 2015. [Google Scholar] [CrossRef]
- Lehmann, P.; Brenck, M.; Gebhardt, O.; Schaller, S.; Süßbauer, E. Barriers and opportunities for urban adaptation planning: analytical framework and evidence from cities in Latin America and Germany. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 75–97. [Google Scholar] [CrossRef]
- Jain, M.; Korzhenevych, A. Spatial Disparities, Transport Infrastructure, and Decentralization Policy in the Delhi Region. J. Urban Plan. Dev. 2017, 143. [Google Scholar] [CrossRef]
- Wilkinson, C.; Porter, L.; Colding, J. Metropolitan planning and resilience thinking: A practitioner’s perspective. Crit. Plan. 2010, 17, 25–44. [Google Scholar]
- Hurtado, S.D.G. Is EU urban policy transforming urban regeneration in Spain? Answers from an analysis of the Iniciativa Urbana (2007–2013). Cities 2017, 60, 402–414. [Google Scholar] [CrossRef]
- Newman, J.P.; Dandy, G.C.; Maier, H.R. Multiobjective optimization of cluster-scale urban water systems investigating alternative water sources and level of decentralization. Water Resour. Res. 2014, 50, 7915–7938. [Google Scholar] [CrossRef]
- Ganzle, S.; Stead, D.; Sielker, F.; Chilla, T. Macro-regional Strategies, Cohesion Policy and Regional Cooperation in the European Union: Towards a Research Agenda. Political Stud. Rev. 2019, 17, 161–174. [Google Scholar] [CrossRef]
- Roozbahani, A.; Zahraie, B.; Tabesh, M. Integrated risk assessment of urban water supply systems from source to tap. Stoch. Environ. Res. Risk Assess. 2013, 27, 923–944. [Google Scholar] [CrossRef]
- Gupta, J.; Bergsma, E.; Termeer, C.J.A.M.; Biesbroek, G.R.; van den Brink, M.; Jong, P.; Klostermann, J.E.M.; Meijerink, S.; Nooteboom, S. The adaptive capacity of institutions in the spatial planning, water, agriculture and nature sectors in the Netherlands. Mitig. Adapt. Strateg. Glob. Chang. 2016, 21, 883–903. [Google Scholar] [CrossRef]
- Rigillo, M.; Cervelli, E. Mapping Urban Vulnerability: the Case Study of Gran Santo Domingo, Dominican Republic. Adv. Eng. Forum 2014, 11, 142–148. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. Urban vulnerability assessment: Advances from the strategic planning outlook. J. Clean. Prod. 2018, 179, 544–558. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. A discursive, many-objective approach for selecting more-evolved urban vulnerability assessment models. J. Clean. Prod. 2018, 176, 1231–1244. [Google Scholar] [CrossRef]
- Zhao, P.; Chapman, R.; Randal, E.; Howden-Chapman, P. Understanding resilient urban futures: A systemic modelling approach. Sustainability 2013, 5, 3202–3223. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. VisualUVAM: A Decision Support System Addressing the Curse of Dimensionality for the Multi-Scale Assessment of Urban Vulnerability in Spain. Sustainability 2019, 11, 2191. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. Ranking-dominance and many-objective optimization. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3983–3990. [Google Scholar] [CrossRef]
- Navarro, I.J.; Martí, J.V.; Yepes, V. Reliability-based maintenance optimization of corrosion preventive designs under a life cycle perspective. Environ. Impact Assess. Rev. 2019, 74, 23–34. [Google Scholar] [CrossRef]
- Adger, W.N. Vulnerability. Glob. Environ. Chang. 2006, 16, 268–281. [Google Scholar] [CrossRef]
- Santos, J.; Ferreira, A.; Flintsch, G. A multi-objective optimization-based pavement management decision-support system for enhancing pavement sustainability. J. Clean. Prod. 2017, 164, 1380–1393. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, W.; Cai, K.; Gao, X.; Zhang, X.; Liu, J.; Wang, Z.; Li, D. Analysis of the Spatial Distribution Characteristics of Urban Resilience and Its Influencing Factors: A Case Study of 56 Cities in China. Int. J. Environ. Res. Public Health 2019, 16, 4442. [Google Scholar] [CrossRef]
- Baudrit, C.; Taillandier, F.; Tran, T.T.P.; Breysse, D. Uncertainty Processing and Risk Monitoring in Construction Projects Using Hierarchical Probabilistic Relational Models. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 97–115. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision-the analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Singh, R.P.; Nachtnebel, H.P. Analytical hierarchy process (AHP) application for reinforcement of hydropower strategy in Nepal. Renew. Sustain. Energy Rev. 2016, 55, 43–58. [Google Scholar] [CrossRef]
- Convertino, M.; Muñoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Model. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Groen, E.A.; Bokkers, E.A.M.; Heijungs, R.; de Boer, I.J.M. Methods for global sensitivity analysis in life cycle assessment. Int. J. Life Cycle Assess. 2017, 22, 1125–1137. [Google Scholar] [CrossRef]
- Evelyne Groen, Global Sensitivity Analysis. Available online: https://evelynegroen.github.io/Code/globalsensitivity.html (accessed on 1 February 2020).
- Convertino, M.; Valverde, L.J., Jr. Portfolio Decision Analysis Framework for Value-Focused Ecosystem Management. PLoS ONE 2013, 8, e65056. [Google Scholar] [CrossRef]
- García-Segura, T.; Penadés-Plà, V.; Yepes, V. Sustainable bridge design by metamodel-assisted multi-objective optimization and decision-making under uncertainty. J. Clean. Prod. 2018, 202, 904–915. [Google Scholar] [CrossRef]
- McGlashan, A.; Verrinder, G.; Verhagen, E. Working towards More Effective Implementation, Dissemination and Scale-Up of Lower-Limb Injury-Prevention Programs: Insights from Community Australian Football Coaches. Int. J. Environ. Res. Public Health 2018, 15, 351. [Google Scholar] [CrossRef]
- Yepes, V.; Torres-Machi, C.; Chamorro, A.; Pellicer, E. Optimal pavement maintenance programs based on a hybrid Greedy Randomized Adaptive Search Procedure Algorithm. J. Civ. Eng. Manag. 2016, 22, 540–550. [Google Scholar] [CrossRef]
- Sierra, L.A.; Yepes, V.; Pellicer, E. A review of multi-criteria assessment of the social sustainability of infrastructures. J. Clean. Prod. 2018, 187, 496–513. [Google Scholar] [CrossRef]
- Sierra, l.A.; Pellicer, E.; Yepes, V. Social sustainability in the life cycle of Chilean public infrastructure. J. Constr. Eng. Manag. 2016, 142, 05015020. [Google Scholar] [CrossRef]
- Sierra, L.A.; Yepes, V.; García-Segura, T.; Pellicer, E. Bayesian network method for decision-making about the social sustainability of infrastructure projects. J. Clean. Prod. 2018, 176, 521–534. [Google Scholar] [CrossRef]

| Infrastructure/Explanatory Variables: | Possible Action Variables: | |||||||
|---|---|---|---|---|---|---|---|---|
| Description | Id | Unit | Type | Treatment Cost (€/m2) | SLI (*) | PCI-CS (**) | Treatment/Period (***) | Period Cost |
| Net Infrastructures: | ||||||||
| Road condition variables | ||||||||
| Road condition: Good | 1 | m2 | Preservation | 1.02 | 3 | 85 | 4 | 4 |
| Road condition: Fair | 2 | m2 | Maintenance | 23.24 | 10 | 60 | 1 | 23 |
| Road condition: Poor | 3 | m2 | Rehabilitation | 66.74 | 25 | 25 | 1 | 67 |
| Road condition: Total | 4 | m2 | Construction | 496 | 25 | 95 | 1 | 496 |
| Initial Road Network Inventory | Actions Planned | Final Road Network Inventory (*) | ||||
|---|---|---|---|---|---|---|
| Condition | Quantity (*) | Type | Quantity (*) | Variation | Total | |
| Region: Comunidad Valenciana | Good | 101.43 | Preservation | 90.34 | 14.34 | 115.78 |
| Fair | 14.70 | Maintenance | 12.77 | −3.61 | 11.09 | |
| Poor | 2.58 | Rehabilitation | 2.46 | 10.56 | 13.14 | |
| Construction | 10.21 | |||||
| Province 1: Alicante | Good | 40.26 | Preservation | 36.93 | 3.49 | 43.75 |
| Fair | 2.83 | Maintenance | 2.68 | 0.50 | 3.33 | |
| Poor | 0.32 | Rehabilitation | 0.30 | 3.18 | 3.50 | |
| Construction | 3.83 | 0.00 | ||||
| Province 2: Castellón | Good | 20.97 | Preservation | 16.05 | −2.85 | 18.12 |
| Fair | 0.29 | Maintenance | 0.25 | 4.63 | 4.92 | |
| Poor | 0.09 | Rehabilitation | 0.07 | 4.89 | 4.98 | |
| Construction | 1.75 | 0.00 | ||||
| Province 3: Valencia | Good | 40.20 | Preservation | 37.35 | 13.71 | 53.90 |
| Fair | 11.58 | Maintenance | 9.84 | −8.73 | 2.84 | |
| Poor | 2.17 | Rehabilitation | 2.09 | 2.49 | 4.67 | |
| Construction | 4.62 | 0.00 | ||||
| Parameter | PDF (*) | Sensitivity Index | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Economic Cost | Road Condition Improv. | Mitigation of UV | ||||||||
| 1 (**) | 2 (**) | 3 (**) | 1 (**) | 2 (**) | 3 (**) | 1 (**) | 2 (**) | 3 (**) | ||
| Rights: | ||||||||||
| Regions (***) | 5, 5, 21 | 8.50% | 0.58% | 13.67% | 5.71% | 0.12% | 13.67% | 10.88% | 2.03% | 13.67% |
| Provinces | 4, 4, 14 | 1.34% | 87.61% | 86.33% | 74.64% | 99.34% | 86.33% | 1.73% | 96.82% | 86.33% |
| Duties: | ||||||||||
| National | 1, 1, 3 | 0.51% | 0.01% | 0.00% | 0.11% | 0.00% | 0.00% | 0.12% | 0.00% | 0.00% |
| Region | 1, 1, 3 | 1.80% | 0.01% | 0.00% | 0.47% | 0.01% | 0.00% | 0.01% | 0.00% | 0.00% |
| Provinces | 1, 2, 6 | 87.85% | 11.79% | 0.00% | 19.07% | 0.53% | 0.00% | 87.26% | 1.15% | 0.00% |
| Rights: | Region | Provinces | Duties: | Region | Provinces | |
|---|---|---|---|---|---|---|
| Range | 14% | 5% | Range | 3% | 5% | |
| Actions | Lb (*) | Ub (*) | Objectives (**) | Lb | Ub | |
| Country and Region: Comunidad Valenciana | Preservation | 77.69 | 101.43 | UVM(Net) (−) | −8.77 x 103 | −9.31 x 103 |
| Maintenance | 10.98 | 14.49 | RCI(Net) (+) | 9.73 x 103 | 1.03 x 104 | |
| Rehabilitation | 2.12 | 2.56 | EC(Net) (−) | 5.59 x 109 | 5.94 x 109 | |
| Construction | 8.78 | 8.25 | ||||
| Region and Province 1: Alicante | Preservation | 35.09 | 40.26 | UVM(Net) (−) | −2.49 x 103 | −2.75 x 103 |
| Maintenance | 2.55 | 2.63 | RCI(Net) (+) | 3.10 x 103 | 3.42 x 103 | |
| Rehabilitation | 0.29 | 0.32 | EC(Net) (−) | 1.98 x 109 | 2.19 x 109 | |
| Construction | 3.64 | 1.41 | ||||
| Region and Province 2: Castellón | Preservation | 15.25 | 20.97 | UVM(Net) (−) | 3.13 | 3.46 |
| Maintenance | 0.24 | 0.29 | RCI(Net) (+) | 3.38 x 102 | 3.74 x 102 | |
| Rehabilitation | 0.06 | 0.07 | EC(Net) (−) | 8.79 x 108 | 9.71 x 108 | |
| Construction | 1.67 | 2.07 | ||||
| Region and Province 3: Valencia | Preservation | 35.48 | 40.20 | UVM(Net) (−) | −6.10 x 103 | −6.74 x 103 |
| Maintenance | 9.35 | 11.58 | RCI(Net) (+) | 6.09 x 103 | 6.73 x 103 | |
| Rehabilitation | 1.98 | 2.17 | EC(Net) (−) | 2.62 x 109 | 2.89 x 109 | |
| Construction | 4.39 | 4.77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas, J.; Yepes, V. Enhancing Sustainability and Resilience through Multi-Level Infrastructure Planning. Int. J. Environ. Res. Public Health 2020, 17, 962. https://doi.org/10.3390/ijerph17030962
Salas J, Yepes V. Enhancing Sustainability and Resilience through Multi-Level Infrastructure Planning. International Journal of Environmental Research and Public Health. 2020; 17(3):962. https://doi.org/10.3390/ijerph17030962
Chicago/Turabian StyleSalas, Jorge, and Víctor Yepes. 2020. "Enhancing Sustainability and Resilience through Multi-Level Infrastructure Planning" International Journal of Environmental Research and Public Health 17, no. 3: 962. https://doi.org/10.3390/ijerph17030962
APA StyleSalas, J., & Yepes, V. (2020). Enhancing Sustainability and Resilience through Multi-Level Infrastructure Planning. International Journal of Environmental Research and Public Health, 17(3), 962. https://doi.org/10.3390/ijerph17030962






