1. Introduction
Over the past decades, global supply chain (GSC) activity has grown tremendously as a result of decreased trade barriers and free trade agreements among countries. A GSC refers to the combination of supply chains on a global scale; it requires a global vision focused on extending the supply chain system to the whole world and selecting the most competitive partners around the world. Recent developments in the trade barrier debate and growing uncertainty about trade policies across countries are forcing companies to rethink their global operations. In addition, worldwide environmental and resource crises have become increasingly prominent in recent years, and global closed-loop supply chain management with the main characteristics of “recycling and remanufacturing” has attracted extensive attention from governments, companies and academia [
1]. Many scholars have conducted extensive research on the issue from a global perspective, particularly the integrated optimization problem of the global closed-loop supply chain [
2]. Alternately, with complicated commercial competition and the rapid development of the Internet, constantly trying to innovate business models is one of the ways for companies to succeed in fierce global competition, more and more companies establish online channels to sell products accompanied with their traditional retail channels. A recent survey reported that approximately 42% of the top-ranking companies sell their products to consumers through online sales channels in various industries [
3,
4]. Further, the dual-channel collection model has also become a measure for major companies. Compared with any traditional single-channel collection model, the dual-channel collection model can achieve better market penetration [
5]. The combination of dual-channel sales and collection models (physical retail and collection channels + online sales and collection channels) is the main development trend of global closed-loop supply chains in recent years. The retailer’s collection strategies, as well as the manufacturer’s collection and remanufacturing strategies, have significant and complex influences on the operation and performance of the whole chain [
6]. Therefore, it is of great theoretical and practical significance to study the integrated optimization problem of a dual-channel global closed-loop supply chain.
A GSC is a supply chain that transcends the borders of a single country. It mainly implements a series of interconnected business activities scattered around the world, including the purchase of raw materials and parts, the acquisition and processing of final products, activities to enhance product value-added, distribution, and information exchange between various commercial entities to reduce costs and expand revenue [
7]. A GSC can achieve diversified customer docking and then help suppliers obtain relevant information and create knowledge through their close relationships with the customer base, thereby promoting product development [
8]. Therefore, to achieve more effective competition, an increasing number of companies rely on relationships with GSC partners. A strong supply chain relationship can reveal unknown customer needs over time through in-depth interaction with customers and thus jointly create the relationship capital required to deepen knowledge [
9]. However, GSCs are difficult to manage and control. In the context of globalization, larger geographic distances increase costs and complicate inventory decisions [
10]. Of course, differences in culture, language, and conventions will also reduce the effectiveness of coordination with customers and suppliers to a certain extent [
11]. Similarly, developing countries’ inadequate infrastructure in transportation and telecommunications, as well as backward equipment and technology, pose many challenges for developed countries to achieve global supply chains [
12]. In addition, the GSC also has unique risks affecting performance, including the changes in the regulatory environment and the instability of factors such as costs, delivery, quality, and flexibility [
13]. These risks are factored into consideration when designing global supply chains. Summarizing the previous research work of GSC, it usually takes multi-factory companies as the research object, focusing on enterprise decision-making models, and paying special attention to the connection between headquarters and branches. As an applied research, the GSC research work is guided by the current needs of multinational companies. It mainly answers the question: For multinational companies to conduct business activities in different regions, how do they make decisions to achieve optimality? That is, the multinational company decision problem. To help managers address these issues, the research community has developed many GSC design models. First of all, the decision of supplier selection has become the primary solution to global supply chain design problems [
14]. In addition, the integration of decisions throughout the chain also affects the design of global supply chains [
15]. Integrating business processes is an effective measure, mainly by integrating replenishment plans between companies by managing inventory and collaboration plans with suppliers, as well as sharing promotion information with replenishing companies. It also includes redesigning supply strategies, coordinating with suppliers, redistributing distribution strategies, and coordinating with customers. However, the benefits of GSCs may be hindered by the aforementioned improvement plans [
16]. Therefore, this study aims to effectively design a GSC based on the relationships among the partners, and the optimal decision is to produce the maximum return.
In recent years, research on the closed-loop supply chain has developed from the original closed-loop supply chain with single-channel sales and collection model to the current dual-channel closed-loop supply chain with dual-channel sales and collection model. To ensure the stable operation of the supply chain, many scholars and practitioners have conducted in-depth research on how to achieve closed-loop supply chain coordination. Among them, government subsidization [
17,
18], and relevant contracts and mechanisms [
5,
19] are considered as two direct and important measures to coordinate the supply chain. Government can encourage manufacturers to adopt the required channel structure by setting appropriate subsidy levels, the optimal price and the percentage of subsidy allocation will affect the final demand price of the remanufactured product. The customs contract and profit sharing contract can increase the profit of both online and offline channels of supply chain members by reasonably setting the proportion of revenue sharing and cost sharing, and finally achieve a win-win situation between dealers and collectors. In addition, other factors, such as service value [
20], also affect the coordination and stability of the supply chain to a certain extent. Generally speaking, the causes of closed-loop supply chain coordination problems include information asymmetry, decentralized decision-making, high ambiguity, limited rationality, and socialist behavior. To solve these problems, we should seek solutions from the perspective of system, technology and culture, seeking information sharing, collaborative logistics and trust. Among them, the correct choice of sales and collection channel model is considered as one of the key measures to effectively coordinate the closed-loop supply chain [
19]. In the forward network, a single sales channel where a retailer sells products directly to customers is a traditional sales model. Due to the rapid development of the Internet, e-commerce has gradually become popular, and manufacturers have also started retail businesses. Chen et al. [
21] call the phenomenon of manufacturers selling products directly to customers through online channels as manufacturer encroachment, and they also found that manufacturer encroachment behavior can bring more profit to manufacturers than information asymmetry. Therefore, as e-commerce technology continues to mature, the dual-channel sales model, which combines offline retailer sales with online manufacturer sales, has gradually become a measure taken by major companies. In the reverse network, there are three common types of collection models implemented by companies for returned products, including retailer, manufacturer and third-party collection. Wan and Hong [
22] build a game model to analyze the optimal pricing and collection policies for retailers and third-party collection. There is no doubt that dual-channel collection will cause the existence of a competitive relationship between the collecting entities, which will affect the profit of the collecting entities to a certain extent. Zheng et al. [
23] point out that collection competition will reduce the amount of total collection and the expected profit for all supply chain members. The expected profits can only be improved if the two collection agencies can still carry out intensive collection work without considering the reward and punishment mechanism. Liu et al. [
16] also believe that there is collection competition between dual collection channels, to choose the most appropriate dual-channel collection model, they study the closed-loop supply chain reverse channel selection decision problems in a pairwise combination of the three collection modes. It is found that the manufacturer and retailer dual collection model is the best choice regardless of the intensity of competition. Later, Modak et al. [
24] confirm this conclusion by analyzing and comparing the above three collection models for second-hand products. It turns out that third party participation in second-hand product collection is always detrimental. In addition, some rare collection models, such as collector collection [
25] and backup supplier collection [
26], have not been popularized due to fewer businesses using them.
Supply chain network design is one of the most critical planning problems in supply chain management. Network design helps the supply chain to determine the location of production-, storage-, and transportation-related facilities, as well as the capacity and functionality of the equipment, which are critical for the long-term operation of the supply chain. For a general supply chain network, according to its characteristics, the supply chain can be categorized as a green, sustainable, risky, resilient, or uncertain supply chain. The implementation plan and goals of its network design vary according to its characteristics. Rezaee et al. [
27] propose a planning model to design green supply chains in a carbon environment. Varsei and Polyakovskiy [
28] build a supply chain analysis model to solve wine supply chain network design issues considering three aspects of sustainability. Babazadeh et al. [
29] propose a model to design a biodiesel supply chain network at risk. Rezapour et al. [
30] design a nonlinear model to solve the design problem of resilient automobile supply chain networks, they use three strategies to reduce the risk of outages. Zokaee et al. [
10] build a model for the supply chain design based on the uncertainty, to determine the strategic "location" and tactical "allocation" decisions of the supply chain. Compared with the general supply chain, the closed-loop supply chain reduces the pollution emissions and surplus waste by closing the flow of materials, while providing services to customers at a lower cost, its network design is also gradually being valued. For the single objective optimization model, minimizing costs is generally considered the primary goal of designing closed-loop supply chains [
31,
32,
33]. Li et al. [
31] establish a nonlinear model to study the inventory decision problems of closed-loop systems with third-party logistics services, it aims to determine the location of the mixed distribution collection center while minimizing the total cost of the system. Rad et al. [
32] construct a mathematical model, in which multi-period, multi-product and single-objective characteristics are taken into account; it is mainly used to determine the production plan, inventory level, flow between facilities, transportation type, procurement quantity, etc., by minimizing the cost of the system. For the multi-objective optimization model, environmental impact is generally considered as the second objective function, and the environmental impact is usually measured by the carbon dioxide emissions and the green performance of the system [
34,
35,
36]. Chen et al. [
34] develop a deterministic model to solve the problem of the multi-objective design for the solar industry; the single-period, single-product and multi-objective model is provided to find the balance between total costs and total carbon dioxide emissions, as well as determine the factory location selection, capacity expansion, technology selection, and purchase and order fulfillment decision problems. Tosarkani and Amin [
35] extend the original multi-period, multi-product and single-objective optimization model and consider the green performance related to the collection center. The objective is to maximize the green factors of the system on the basis of maximizing the profit of the supply chain. Other objective functions, such as sales loss [
37] and social performance [
38], can also be optimized according to the actual research problems. The acceleration of economic globalization has led to the emergence of GSCs. Due to the complexity of GSCs, only some scholars have conducted research related to network design. Hasani and Khosrojerdi [
11] develop a mixed integer nonlinear model for designing GSC networks under uncertainty. They propose six flexible strategies to mitigate the risks of related outages to extract management insights. Urata et al. [
13] propose an Asian GSC network design method, which can minimize material-based carbon dioxide emissions costs and determine suppliers, plant locations, and databases that meet low-carbon material supply needs. Amin and Baki [
12] consider global factors such as exchange rates and tariffs, and propose a GSC network design model based on uncertain demand. Due to the difficulty of managing and controlling GSCs, research on the network design of these supply chains is not very mature, especially in terms of the design and optimization of dual-channel global closed-loop supply chains.
In order to better solve the closed-loop supply chain network design model, the
-constraint method is used in this paper. The
-constraint method can generate all effective solutions to the problem, and the decision maker selects the most suitable one from them. Many studies have verified the effectiveness of this method. Talaei et al. [
39] apply the
-constraint method to solve the bi-objective optimization model. They list three advantages of the method. First, with the change of
, the model can get different optimal solutions. Second, the scale of objective function does not affect the optimal solution. Third, this method is very suitable for solving non-convex models. Jindal and Sangwan [
36] use the interactive
-constraint method to solve the proposed multi-objective optimization model. They think that since the decision-makers only participate in the second stage of the solution, this method can have a good decision-making effect when the decision-maker interaction is difficult. Yang et al. [
40] put forward an improved
-constraint method to solve the model. The improved method can adjust the value of
according to the size of infeasible individuals, which can effectively prevent the unreasonable setting of
value. At the same time, it can switch freely to participate in a global and local search, which can balance the convergence. Shafiekhani et al. [
41] propose the augmented
-constraint method to solve the bi-objective optimization problem. The augmented
-constraint method can avoid the emergence of various weak solutions due to changing the value of
, and reduce the repetition of the solution process to accelerate the whole process. Tabar et al. [
42] also use the augmented
-constraint method to solve the proposed optimization model. They think that the augmented
-constraint method does not change the original feasible region in the process of solving, and can produce non inferior solutions. At the same time, the scaling of the objective function does not affect the process and result of the solution. Osorio et al. [
43] propose an augmented
-constraint method combined the with sample average approximation method to solve linear programming model. Each
can be used to solve a sample average approximation problem. The resulting Pareto front can be composed of the assignment of one target and the expected value of another. This method can avoid the emergence of weak solutions and accelerate the whole process of solving. Dorotić et al. [
44] combine the
-constraint method with the weighted sum method for the multi-objective optimization problem, and then they use the inflection point method to select the solution closest to the Pareto optimal solution from the effective solutions. This method can realize the visualization of the Pareto front and obtain the compromise solution based on all possible results. Fan et al. [
45] propose an improved
-constraint processing method, which is combined with a multi-objective evolutionary algorithm to solve optimization problems. The integration method can dynamically adjust the value of
according to the ratio of feasible to total solutions, so as to ensure the balance between feasible and infeasible regions.
The integrated optimization is one of the fundamental activities and infrastructure construction for supply chain management, which affects the operational efficiency. In addition, product collection helps reduce production costs, reduce energy consumption, and protect the environment, the optimization of a global closed-loop supply chain with dual-channels can effectively control the operation of the forward and reverse supply networks, as well as promote a close relationship between product sales and product collection. Therefore, this paper establishes a single-product, multi-period, multi-objective mixed-integer linear programming model, and a dual-channel sales and dual-channel collection model are designed. The model integrates three conflicting objective functions: the economic factors are measured by net present value (NPV), the environmental impact is calculated by the total amount of emissions, and social welfare is measured by the social sustainability indicator. In addition, the optimization of the objective functions can solve the strategic decision problem, including the determination of the network structure, entity capacity, the flow of products and components between entities, returned product collection levels, and production, remanufacturing and inventory levels. Finally, a proposed solution method, i.e., the -constraint method, is provided, in which three different size test problems are assessed. The result verifies the applicability and robustness of the solution method and provides management advice for other supply chain managers.
3. Results
To verify the effectiveness and practicability of the method so that companies of all sizes can be considered, three differently scaled dual-channel models are explored using the proposed
-constraint method. Assume that the model can be expanded to include up to three CPUs (C1, C2, C3), four factories (F1, F2, F3, F4), two warehouses (W1, W2), four retailers (R1, R2, R3, R4), four consumers (O1, O2), three collection centers (L1, L2, L3), two disassembly centers (D1, D2), and four refurbishing centers (E1, E2, E3, E4). The sizes of the test problems assumed are shown in
Table 5.
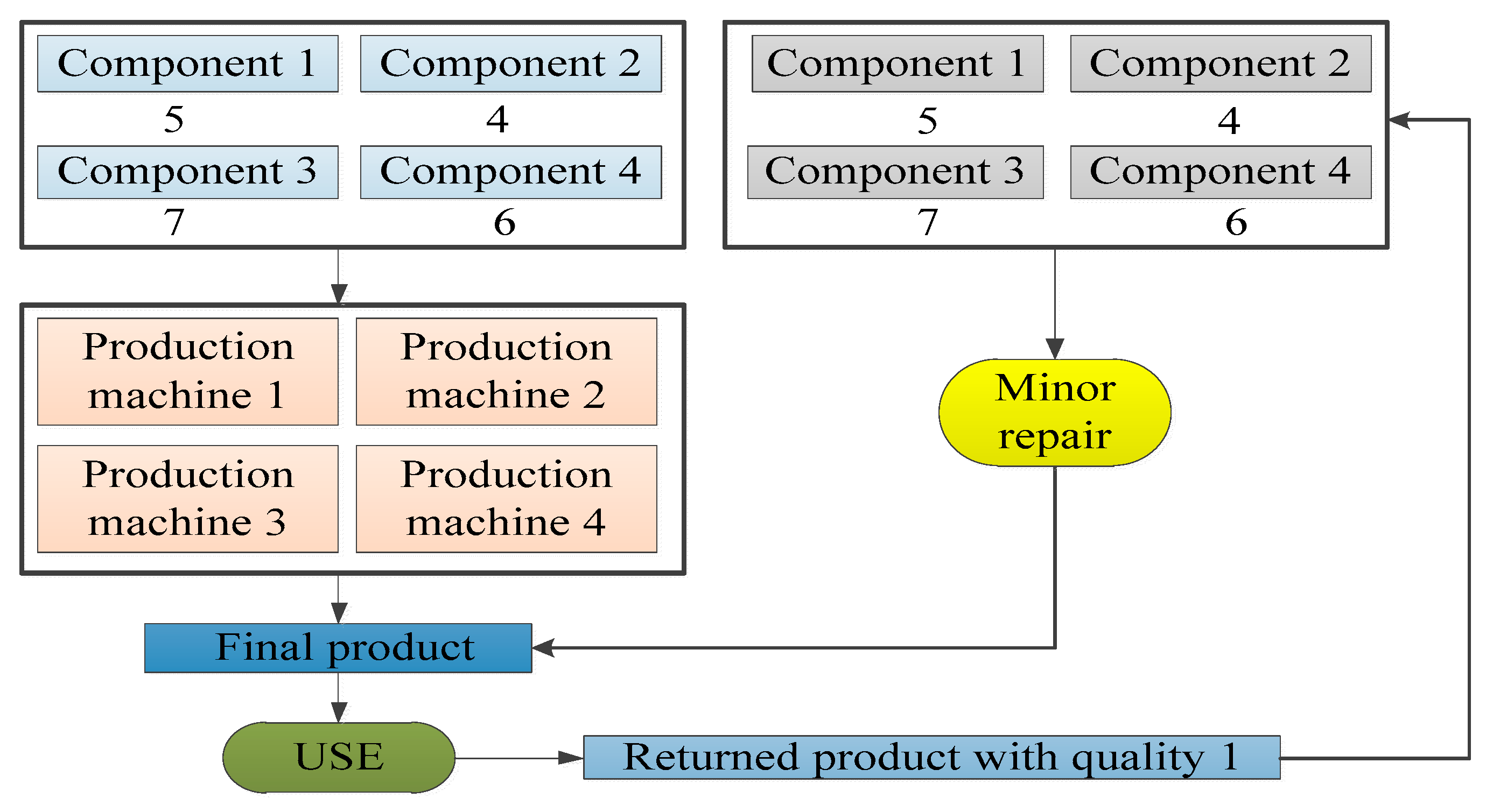
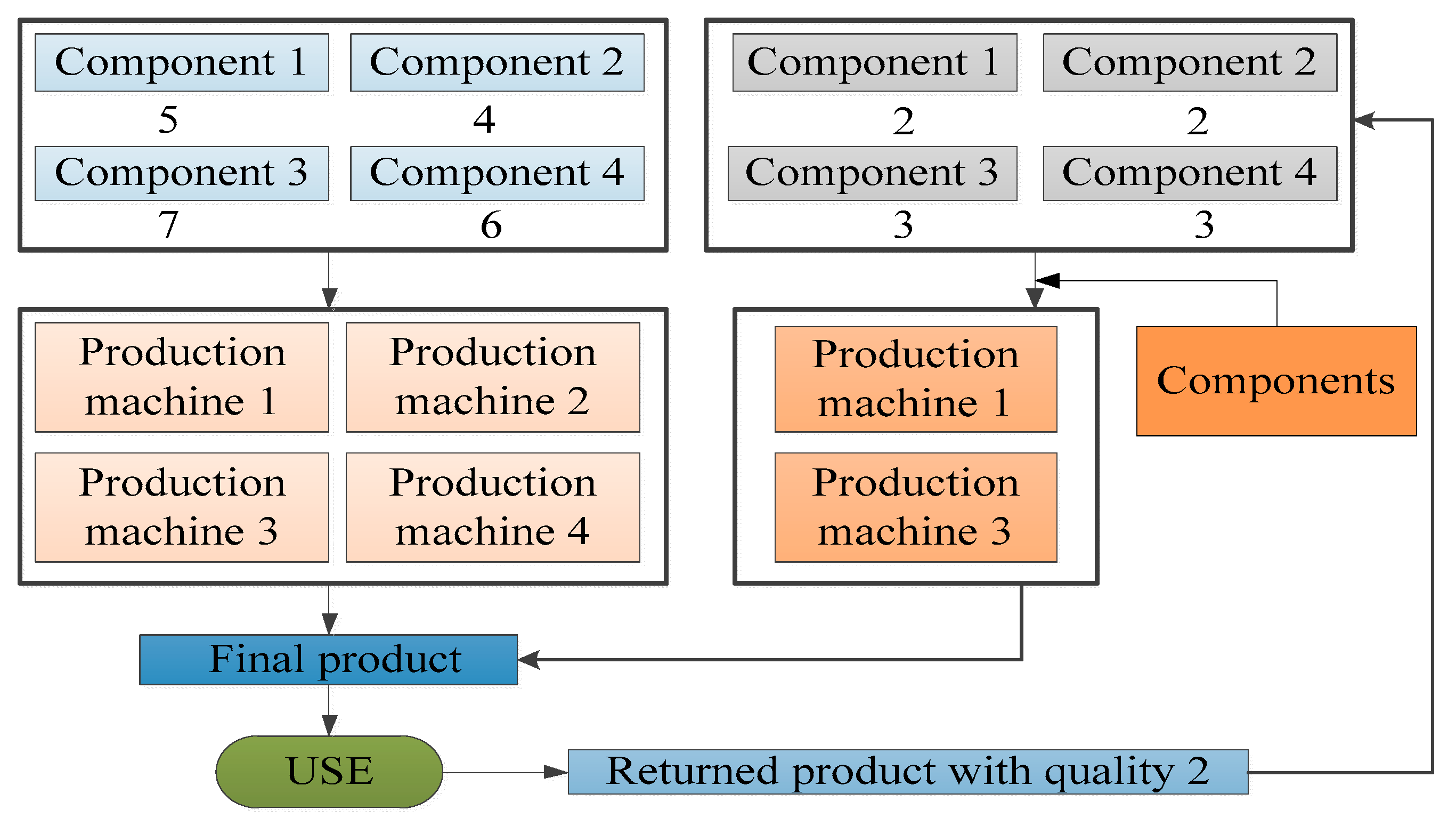
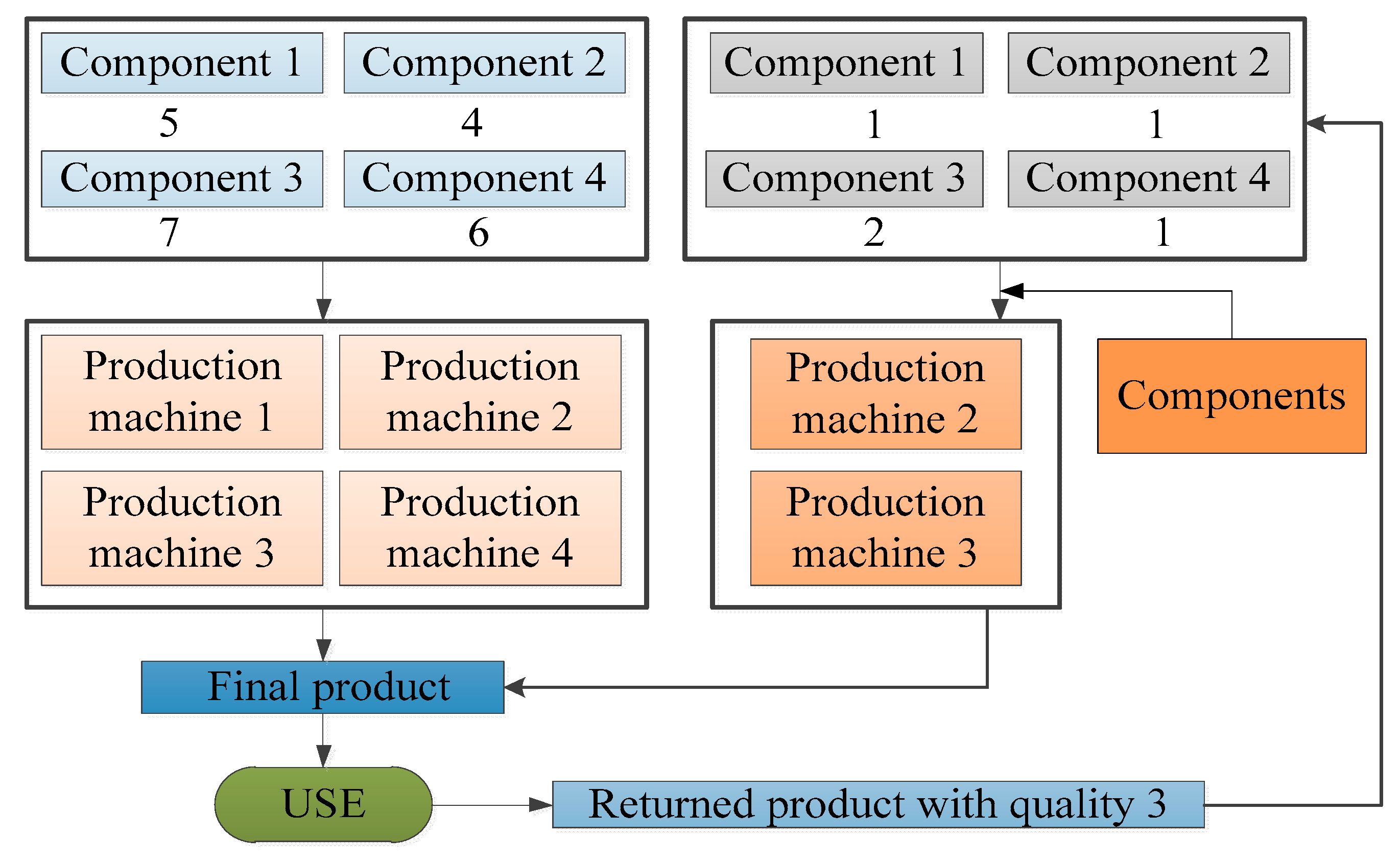
Suppose that a company produces and sells one type of product (FP), which is produced from four types of components (M1, M2, M3, M4), including five units of M1, four units of M2, seven units of M3 and six units of M4 and that the production process needs to be completed on four production machines (P1, P2, P3, P4). Then, the products will be collected after use, and the returned products can be divided into three different levels of quality (RP1, RP2, RP3), where a returned product with quality 1 requires only minor repairs without the need to use production machines and the remaining returned products will be disassembled into various components. One unit of returned product with quality 2 can be disassembled to obtain two units of M1, two units of M2, three units of M3 and three units of M4, and one unit of returned product with quality 3 can be disassembled to obtain one unit of M1, one unit of M2, two units of M3 and one unit of M4. Finally, by replenishing the missing components, one unit of the remanufactured product can be obtained, the minor repair process for returned products with quality 1 can be completed without replenishing components, the production process for returned products with quality 2 can be completed by P1 and P3, and the remanufacturing process for the returned products with quality 3 can be completed by P2 and P3. These processes are shown in
Figure 2,
Figure 3 and
Figure 4.
Table 6 describes the composition of products, and the demand for the machines used for producing and remanufacturing products.
Table 7 describes the capacity characteristics of entities within the analysis boundary, including the maximum and minimum supply capacity of the CPUs, as well as the maximum receiving capacity for the components, products and returned products of other entities.
Table 8 depicts the cost, revenue and proportion characteristics associated with the components, the production, the refurbishing, recycling, disposal and transportation costs, and the related proportions of the components.
Table 9 depicts the cost characteristics associated with the final products and returned products, including the cost of disassembly and collection for the returned products, as well as the production machine operating cost and transportation cost for the products and returned products.
Table 10 lists the construction and worker characteristics associated with the entities within the analysis boundary, including the entity construction costs, amount of
emissions generated during entity construction, number of workers required, and wages of workers. Then, the distance between entities is shown in
Table 11. Next,
Table 12 provides the amount of
emissions associated with supply chain activities, including production, minor repairs, remanufacturing, disassembly, refurbishing, and disposal.
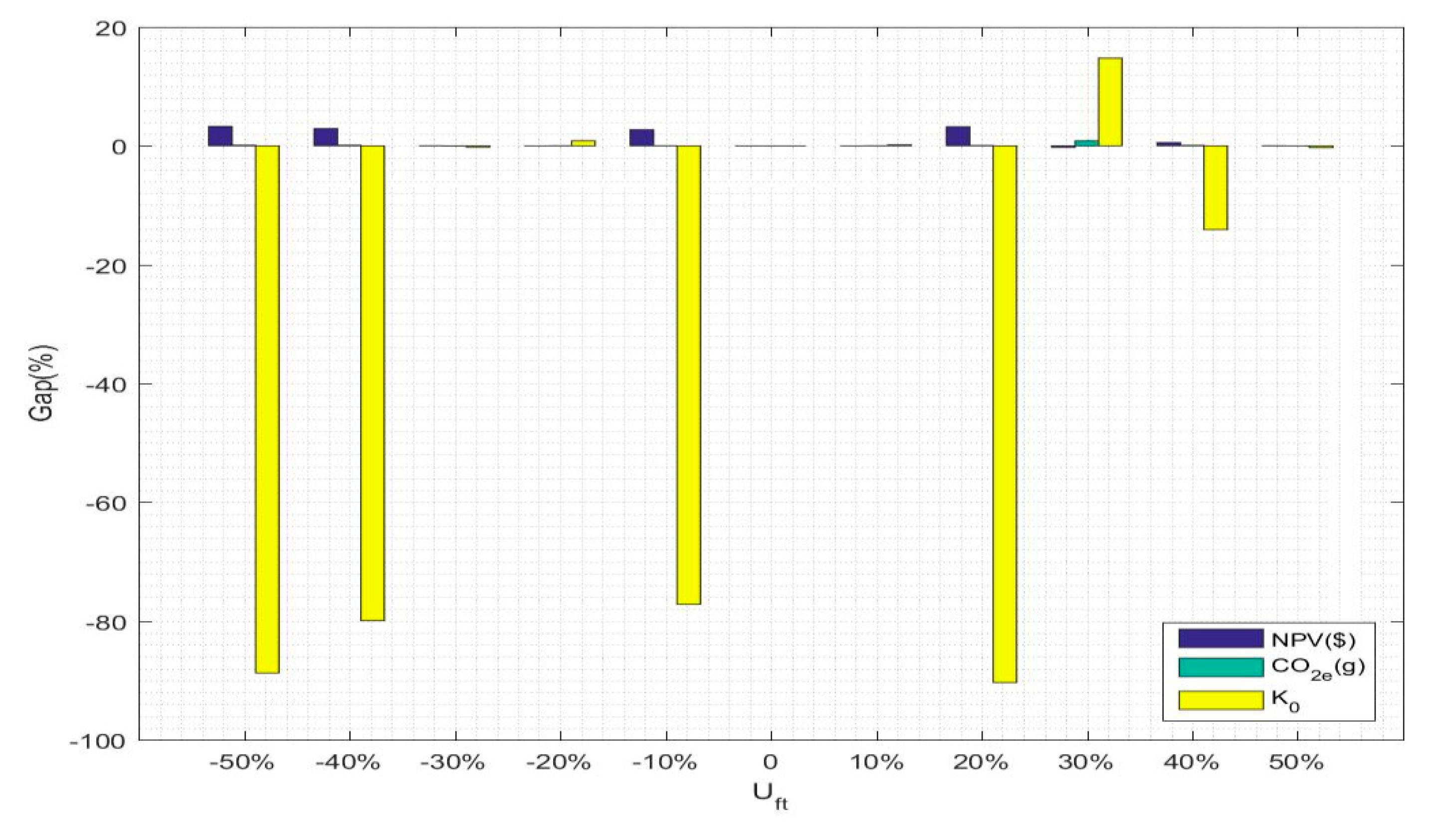
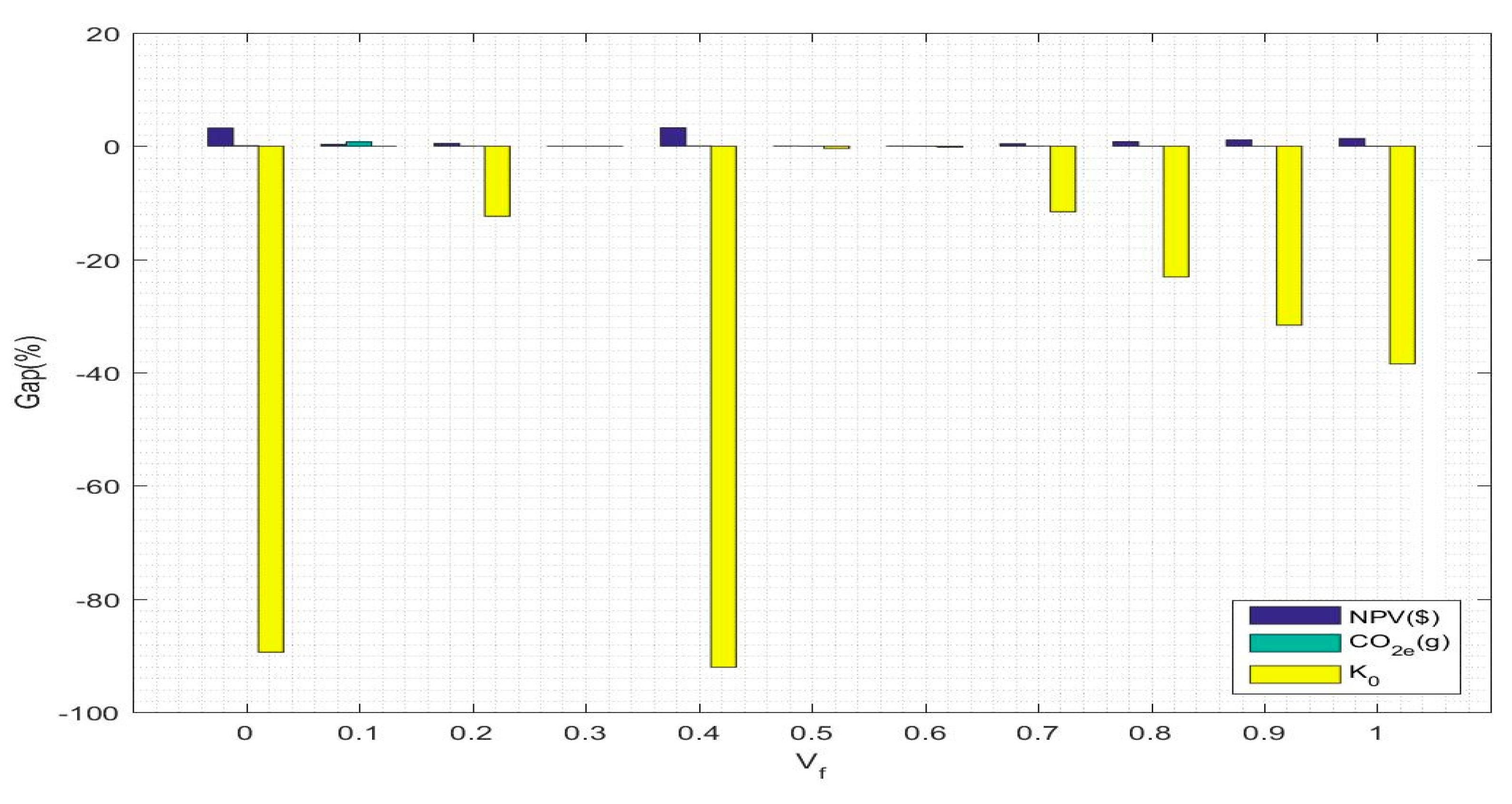
Although the size of the test problem is constantly increasing, the parameter values of the three test problems are fixed, which allows for an evaluation of the influence of the proposed method on differently scaled models. In addition, a test problem with a time period of one year, i.e., 52 weeks, is studied, and the total time range is three years.
Next, some time-related parameters are introduced. For this type of product, the inventory holding cost in the warehouse changes with time. In the three years studied, the inventory holding cost per unit product is $5, $6 and $7, respectively. Due to the upgrading of products and maturing production technology, the unit selling price of the product decreases with time and is $500, $480 and $450, respectively, which is consistent with the selling price of the retailers and warehouses. In addition, the cost of leasing increases year by year, at $10,000, $12,000 and $13,000, respectively, per year for a store. The demand for the product also increases year by year in the three years, reaching 1000, 1200 and 1400, respectively. More importantly, due to the increased awareness of the public regarding energy conservation in recent years, a large number of returned products are collected to complete the remanufacturing process of new products, and the return rate of the product reaches 30%.
In each factory, four production machines are used to complete the production and remanufacturing activities, and mass production of the products is carried out. The cost of acquisition for four production machines varies according to the tasks they perform and their effects: $7000, $6000, $9000 and $12,000. For these four production machines, six, nine, five and seven workers are required to complete the manufacturing activities during the operation. At the same time, to facilitate transportation and ensure the timeliness of the arrival of the components and products, the company has set up its own transport fleet to complete all transport activities, replacing the original third-party logistics provider’s transportation model, and the transport personnel are transport workers at the transport entity. At present, to make the number of trucks sufficient to meet the existing traffic volume and not waste resources, the number of trucks, depending on the size of the problem being studied, is 8, 14 and 16, and the cost of each truck is $80,000. There is no doubt that trucking will produce harmful substances that pollute the environment. Here, only emissions are considered. For a transport distance of 1 km, the emissions per truck are 400 g. For production machines and trucks, the residual value will decrease with an increase in the service life. At the end of the three years studied, the residual ratio of the four machines is 35%, 38%, 30% and 41%, and the residual ratio of these trucks is 35%. For entities within the analysis boundary, the residual ratio varies with the type of entity, and the ratios are 44%, 42%, 48%, 38%, 36% and 35%.
The regional index values of extended producer responsibilities and employment practices are considered to be location-dependent on the hybrid collection facility and subject to the size of the test problem. Therefore, the index values of extended producer responsibilities for the three differently sized test problems are 0.8, 0.85 and 0.92, and the index values of the employment practices for the three differently sized test problems are 0.6, 0.73, 0.9. In addition, the weights of the four social sustainability criteria, which are used to calculate the social benefits, can be calculated through AHP, where the pairwise comparison matrix of the social sustainability goal and criteria is obtained by surveying and consulting different manufacturers in the study area. Therefore, the relative weights of the four criteria are calculated as 0.16, 0.18, 0.53 and 0.13. Finally, the interest rate and tax rate are considered to be in line with the development goal of the supply chain and are consistent with the requirements of social development at 10% and 25%, respectively.