Predicting the Epidemiological Outbreak of the Coronavirus Disease 2019 (COVID-19) in Saudi Arabia
Abstract
1. Introduction
2. Related Work
3. Methodology
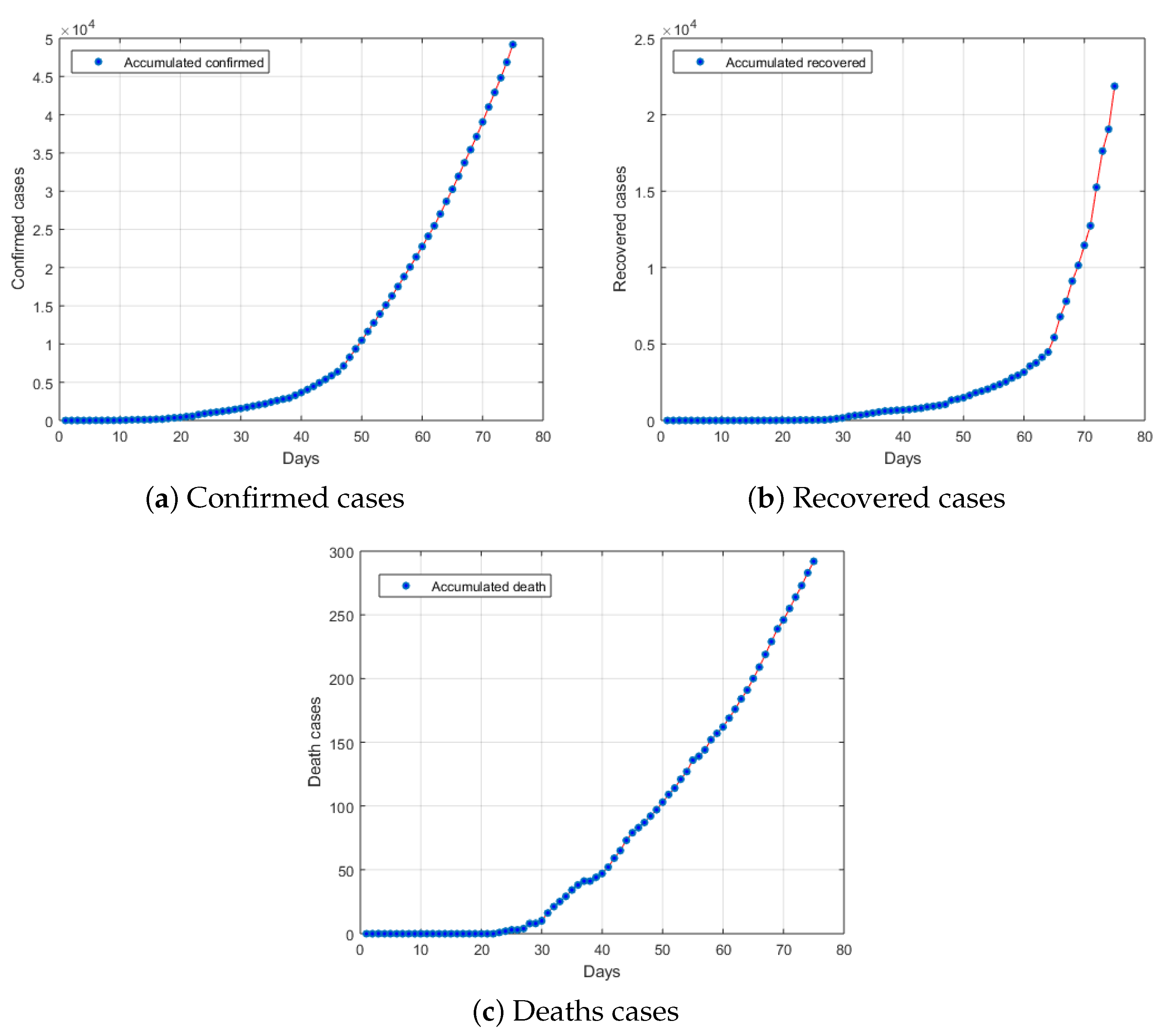
3.1. Data
3.2. Models
3.2.1. Logistic Growth Model
3.2.2. Susceptible-Infected-Recovered Model
- Susceptible (S): group of individuals that not currently infected but may catch the disease.
- Infected (I): group of individuals that are currently infectious.
- Recovered or Removed (R): group of individuals that are no longer infectious. They are either recovered, become immune, or have died.
- Duration of infectiousness;
- Probability of infection being transmitted during contact between an infected person and a susceptible person;
- The average rate of contact between infected and susceptible individuals.
4. Results
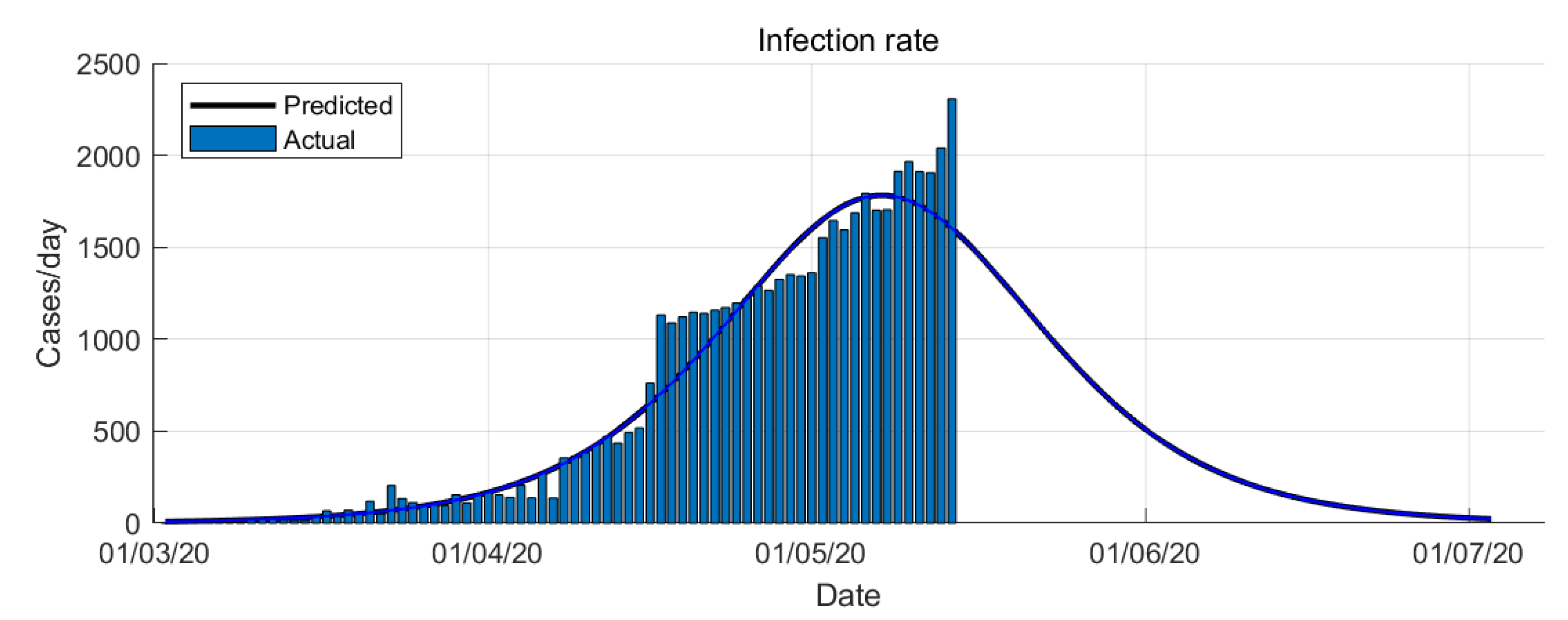
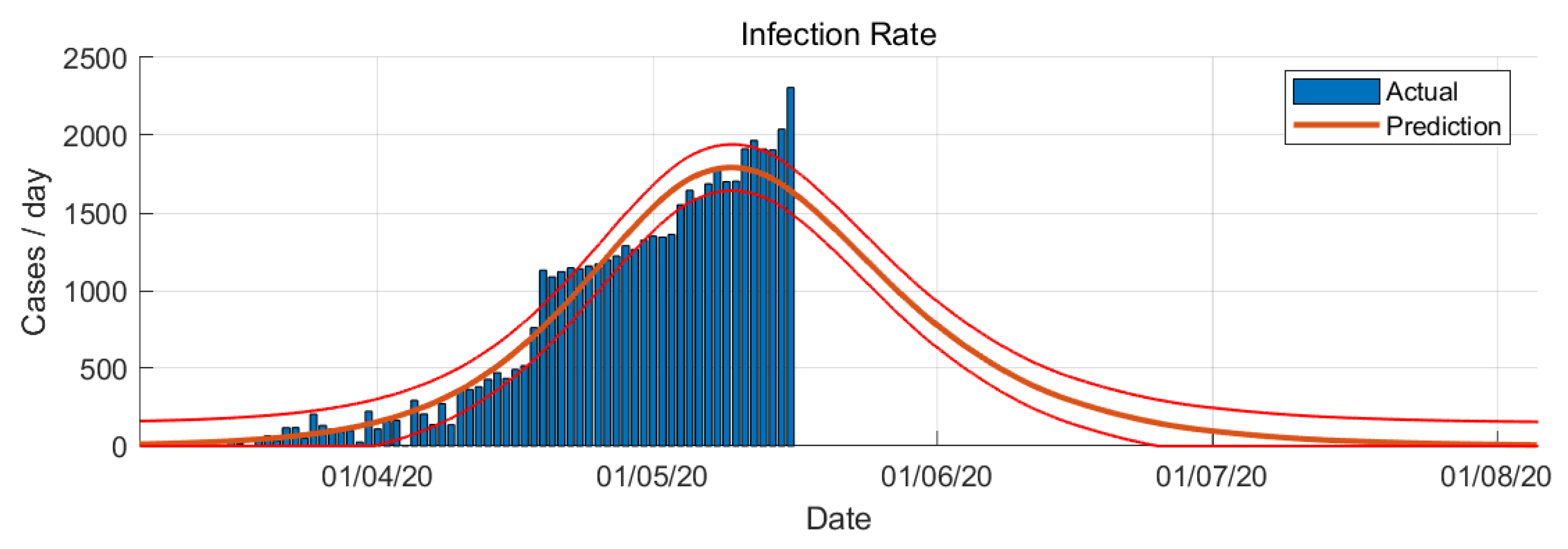
4.1. Results of Logistic Growth Model
- Red: fast growth phase;
- Yellow: transition to steady-state phase;
- Green: ending phase (plateau stage).
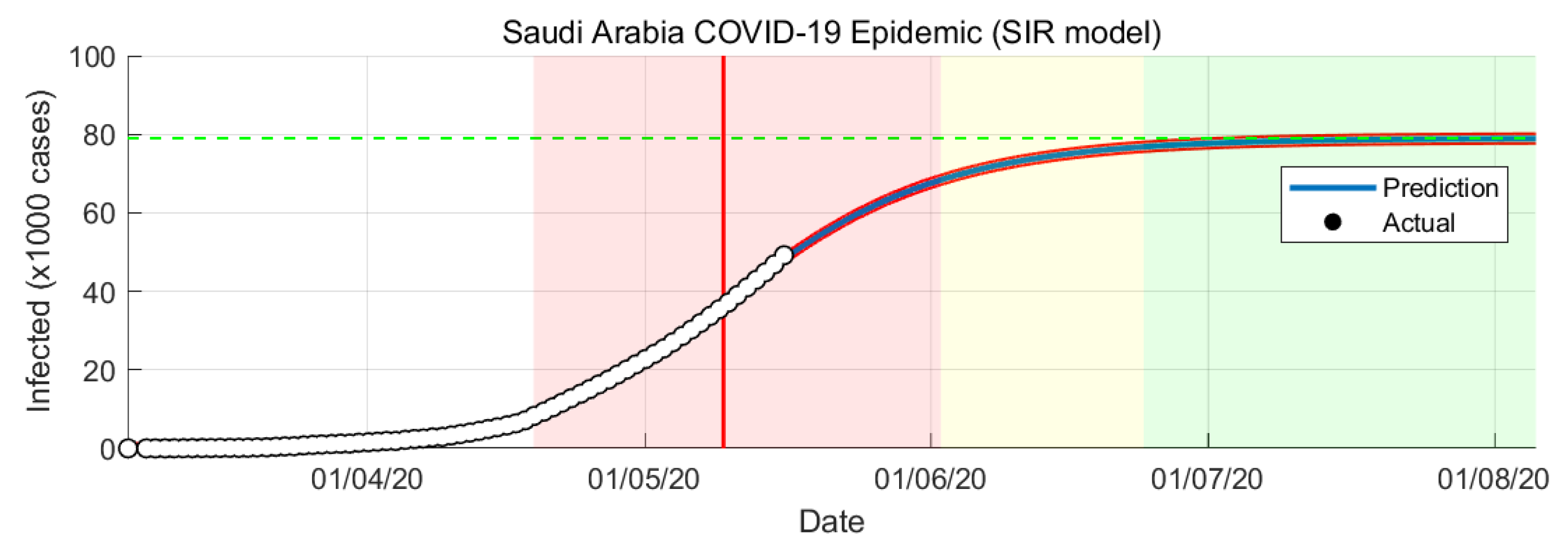
4.2. Results of Susceptible-Infected-Recovered Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Liu, Q.; Guo, D. Emerging coronaviruses: Genome structure, replication, and pathogenesis. J. Med. Virol. 2020, 92, 418–423. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.Y.; Li, J.L.; Yang, X.L.; Chmura, A.A.; Zhu, G.; Epstein, J.H.; Mazet, J.K.; Hu, B.; Zhang, W.; Peng, C.; et al. Isolation and characterization of a bat SARS-like coronavirus that uses the ACE2 receptor. Nature 2013, 503, 535–538. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.F.; Shi, Z.; Zhang, S.; Field, H.; Daszak, P.; Eaton, B.T. Review of bats and SARS. Emerg. Infect. Dis. 2006, 12, 1834. [Google Scholar] [CrossRef] [PubMed]
- Novel Coronavirus (2019-nCoV); World Health Organization: Geneva, Switzerland, 2020.
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Du, Z.; Wang, L.; Cauchemez, S.; Xu, X.; Wang, X.; Cowling, B.J.; Meyers, L.A. Risk for Transportation of 2019 Novel Coronavirus (COVID-19) from Wuhan to Cities in China. medRxiv 2020. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- COVID-19 Coronavirus Pandemic. Available online: https://www.worldometers.info/coronavirus/ (accessed on 17 April 2020).
- Shanafelt, D.W.; Jones, G.; Lima, M.; Perrings, C.; Chowell, G. Forecasting the 2001 foot-and-mouth disease epidemic in the UK. EcoHealth 2018, 15, 338–347. [Google Scholar] [CrossRef]
- Wang, W.; Ruan, S. Simulating the SARS outbreak in Beijing with limited data. J. Theor. Biol. 2004, 227, 369–379. [Google Scholar] [CrossRef]
- Chowell, G.; Simonsen, L.; Viboud, C.; Kuang, Y. Is West Africa approaching a catastrophic phase or is the 2014 Ebola epidemic slowing down? Different models yield different answers for Liberia. PLoS Curr. 2014, 6. [Google Scholar] [CrossRef]
- Pell, B.; Kuang, Y.; Viboud, C.; Chowell, G. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics 2018, 22, 62–70. [Google Scholar] [CrossRef]
- Al-qaness, M.A.; Ewees, A.A.; Fan, H.; Abd El Aziz, M. Optimization Method for Forecasting Confirmed Cases of COVID-19 in China. J. Clin. Med. 2020, 9, 674. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Feng, W. Trend and forecasting of the COVID-19 outbreak in China. arXiv 2020, arXiv:2002.05866. [Google Scholar]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 2020, 5, 256–263. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Cao, P.; Du, P.; Wu, Z.; Zhuang, Z.; Yang, L.; Yu, X.; Zhou, Q.; Feng, X.; Wang, X.; et al. Early estimation of the case fatality rate of COVID-19 in mainland China: A data-driven analysis. Ann. Transl. Med. 2020, 8, 128. [Google Scholar] [CrossRef]
- Batista, M. Estimation of the final size of the COVID-19 epidemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. arXiv 2020, arXiv:2002.12298. [Google Scholar] [CrossRef]
- Zhao, S.; Musa, S.S.; Lin, Q.; Ran, J.; Yang, G.; Wang, W.; Lou, Y.; Yang, L.; Gao, D.; He, D.; et al. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of January 2020: A data-driven Modelling analysis of the early outbreak. J. Clin. Med. 2020, 9, 388. [Google Scholar] [CrossRef]
- Nishiura, H.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Miyama, T.; Kinoshita, R.; Linton, N.M.; Jung, S.m.; Yuan, B.; Suzuki, A.; et al. The rate of underascertainment of novel coronavirus (2019-nCoV) infection: Estimation using Japanese passengers data on evacuation flights. J. Clin. Med. 2020, 9, 419. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef]
- Thompson, R.N. Novel coronavirus outbreak in Wuhan, China, 2020: Intense surveillance Is vital for preventing sustained transmission in new locations. J. Clin. Med. 2020, 9, 498. [Google Scholar] [CrossRef]
- Jung, S.m.; Akhmetzhanov, A.R.; Hayashi, K.; Linton, N.M.; Yang, Y.; Yuan, B.; Kobayashi, T.; Kinoshita, R.; Nishiura, H. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: Inference using exported cases. J. Clin. Med. 2020, 9, 523. [Google Scholar] [CrossRef] [PubMed]
- Haberman, R. Mathematical Models: Mechanical Vibrations, Population Dynamics, and Traffic Flow; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998; Volume 21. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1927, 115, 700–721. [Google Scholar]
- Hamer, W.H. Epidemic Disease in England: The Evidence of Variability and of Persistency of Type; Bedford Press: Bedford, UK, 1906. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Batista, M. Estimation of the final size of the second phase of the coronavirus epidemic by the logistic model. medRxiv 2020. [Google Scholar] [CrossRef]
- Le Page, M. Will heat kill the coronavirus? New Sci. 2020, 245, 6–7. [Google Scholar] [CrossRef]


| Date | New | Accumulated Confirmed | Accumulated Recovered | Accumulated Deaths | |
|---|---|---|---|---|---|
| 2/3/2020 | 1 | 1 | 1 | 0 | |
| 4/3/2020 | 1 | 2 | 0 | 0 | |
| 5/3/2020 | 3 | 5 | 0 | 0 | |
| 6/3/2020 | 2 | 7 | 0 | 0 | |
| 7/3/2020 | 4 | 11 | 0 | 0 | |
| 8/3/2020 | 4 | 15 | 0 | 0 | |
| 9/3/2020 | 5 | 20 | 0 | 0 | |
| 10/3/2020 | 1 | 21 | 1 | 0 | |
| 11/3/2020 | 24 | 45 | 0 | 0 | |
| 12/3/2020 | 17 | 62 | 0 | 0 | |
| 13/3/2020 | 24 | 86 | 1 | 0 | |
| 14/3/2020 | 17 | 103 | 1 | 0 | |
| 15/3/2020 | 15 | 118 | 2 | 0 | |
| 16/3/2020 | 15 | 133 | 2 | 0 | |
| 17/3/2020 | 38 | 171 | 0 | 0 | |
| 18/3/2020 | 67 | 238 | 6 | 0 | |
| 19/3/2020 | 36 | 274 | 8 | 0 | |
| 20/3/2020 | 70 | 344 | 8 | 0 | |
| 21/3/2020 | 48 | 392 | 16 | 0 | |
| 22/3/2020 | 119 | 511 | 17 | 0 | |
| 23/3/2020 | 51 | 562 | 19 | 0 | |
| 24/3/2020 | 205 | 767 | 28 | 1 | |
| 25/3/2020 | 133 | 900 | 29 | 2 | |
| 26/3/2020 | 112 | 1012 | 33 | 3 | |
| 27/3/2020 | 92 | 1104 | 35 | 3 | |
| 28/3/2020 | 99 | 1203 | 37 | 4 | |
| 29/3/2020 | 96 | 1299 | 66 | 8 | |
| 30/3/2020 | 154 | 1453 | 115 | 8 | |
| 31/3/2020 | 110 | 1563 | 165 | 10 | |
| 1/4/2020 | 157 | 1720 | 264 | 16 | |
| 2/4/2020 | 165 | 1885 | 328 | 21 | |
| 3/4/2020 | 154 | 2039 | 351 | 25 | |
| 4/4/2020 | 140 | 2179 | 420 | 29 | |
| 5/4/2020 | 206 | 2385 | 488 | 34 | |
| 6/4/2020 | 138 | 2523 | 551 | 38 | |
| 7/4/2020 | 272 | 2795 | 615 | 41 | |
| 8/4/2020 | 137 | 2932 | 631 | 41 | |
| 9/4/2020 | 355 | 3287 | 666 | 44 | |
| 10/4/2020 | 364 | 3651 | 685 | 47 | |
| 11/4/2020 | 382 | 4033 | 720 | 52 | |
| 12/4/2020 | 429 | 4462 | 761 | 59 | |
| 13/4/2020 | 472 | 4934 | 805 | 65 | |
| 14/4/2020 | 435 | 5369 | 889 | 73 | |
| 15/4/2020 | 493 | 5862 | 931 | 79 |
| Date | New | Accumulated Confirmed | Accumulated Recovered | Accumulated Deaths |
|---|---|---|---|---|
| 16/4/2020 | 518 | 6380 | 990 | 83 |
| 17/4/2020 | 762 | 7142 | 1049 | 87 |
| 18/4/2020 | 1132 | 8274 | 1329 | 92 |
| 19/4/2020 | 1088 | 9362 | 1398 | 97 |
| 20/4/2020 | 1122 | 10,484 | 1490 | 103 |
| 21/4/2020 | 1147 | 11,631 | 1640 | 109 |
| 22/4/2020 | 1141 | 12,772 | 1812 | 114 |
| 23/4/2020 | 1158 | 13,930 | 1925 | 121 |
| 24/4/2020 | 1172 | 15,102 | 2049 | 127 |
| 25/4/2020 | 1197 | 16,299 | 2215 | 136 |
| 26/4/2020 | 1223 | 17,522 | 2357 | 139 |
| 27/4/2020 | 1289 | 18,811 | 2531 | 144 |
| 28/4/2020 | 1266 | 20,077 | 2784 | 152 |
| 29/4/2020 | 1325 | 21,402 | 2953 | 157 |
| 30/4/2020 | 1351 | 22,753 | 3163 | 162 |
| 1/5/2020 | 1344 | 24,097 | 3555 | 169 |
| 2/5/2020 | 1362 | 25,459 | 3765 | 176 |
| 3/5/2020 | 1552 | 27,011 | 4134 | 184 |
| 4/5/2020 | 1645 | 28,656 | 4476 | 191 |
| 5/5/2020 | 1595 | 30,251 | 5431 | 200 |
| 6/5/2020 | 1687 | 31,938 | 6783 | 209 |
| 7/5/2020 | 1793 | 33,731 | 7798 | 219 |
| 8/5/2020 | 1701 | 35,432 | 9120 | 229 |
| 9/5/2020 | 1704 | 37,136 | 10,144 | 239 |
| 10/5/2020 | 1912 | 39,048 | 11,457 | 246 |
| 11/5/2020 | 1966 | 41,014 | 12,737 | 255 |
| 12/5/2020 | 1911 | 42,925 | 15,257 | 264 |
| 13/5/2020 | 1905 | 44,830 | 17,622 | 273 |
| 14/5/2020 | 2039 | 46,869 | 19,051 | 283 |
| 15/5/2020 | 2307 | 49,176 | 21,869 | 292 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alboaneen, D.; Pranggono, B.; Alshammari, D.; Alqahtani, N.; Alyaffer, R. Predicting the Epidemiological Outbreak of the Coronavirus Disease 2019 (COVID-19) in Saudi Arabia. Int. J. Environ. Res. Public Health 2020, 17, 4568. https://doi.org/10.3390/ijerph17124568
Alboaneen D, Pranggono B, Alshammari D, Alqahtani N, Alyaffer R. Predicting the Epidemiological Outbreak of the Coronavirus Disease 2019 (COVID-19) in Saudi Arabia. International Journal of Environmental Research and Public Health. 2020; 17(12):4568. https://doi.org/10.3390/ijerph17124568
Chicago/Turabian StyleAlboaneen, Dabiah, Bernardi Pranggono, Dhahi Alshammari, Nourah Alqahtani, and Raja Alyaffer. 2020. "Predicting the Epidemiological Outbreak of the Coronavirus Disease 2019 (COVID-19) in Saudi Arabia" International Journal of Environmental Research and Public Health 17, no. 12: 4568. https://doi.org/10.3390/ijerph17124568
APA StyleAlboaneen, D., Pranggono, B., Alshammari, D., Alqahtani, N., & Alyaffer, R. (2020). Predicting the Epidemiological Outbreak of the Coronavirus Disease 2019 (COVID-19) in Saudi Arabia. International Journal of Environmental Research and Public Health, 17(12), 4568. https://doi.org/10.3390/ijerph17124568





