Rainfall-Induced Landslide Prediction Using Machine Learning Models: The Case of Ngororero District, Rwanda
Abstract
1. Introduction
2. Materials and Methods
2.1. Area of Study
2.2. Data Acquisition and Landslide Inventory
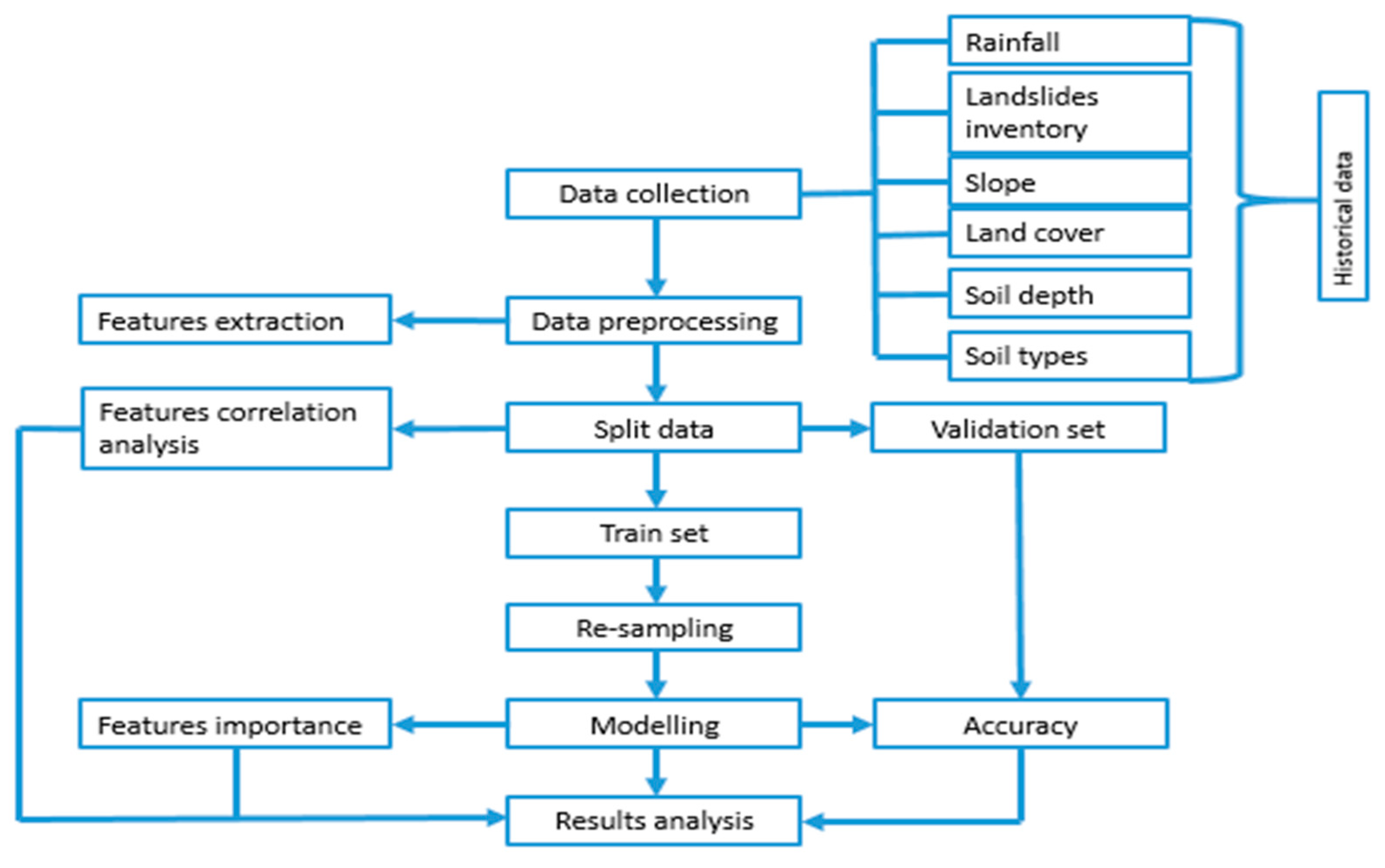
2.2.1. Data Collection
2.2.2. Dataset
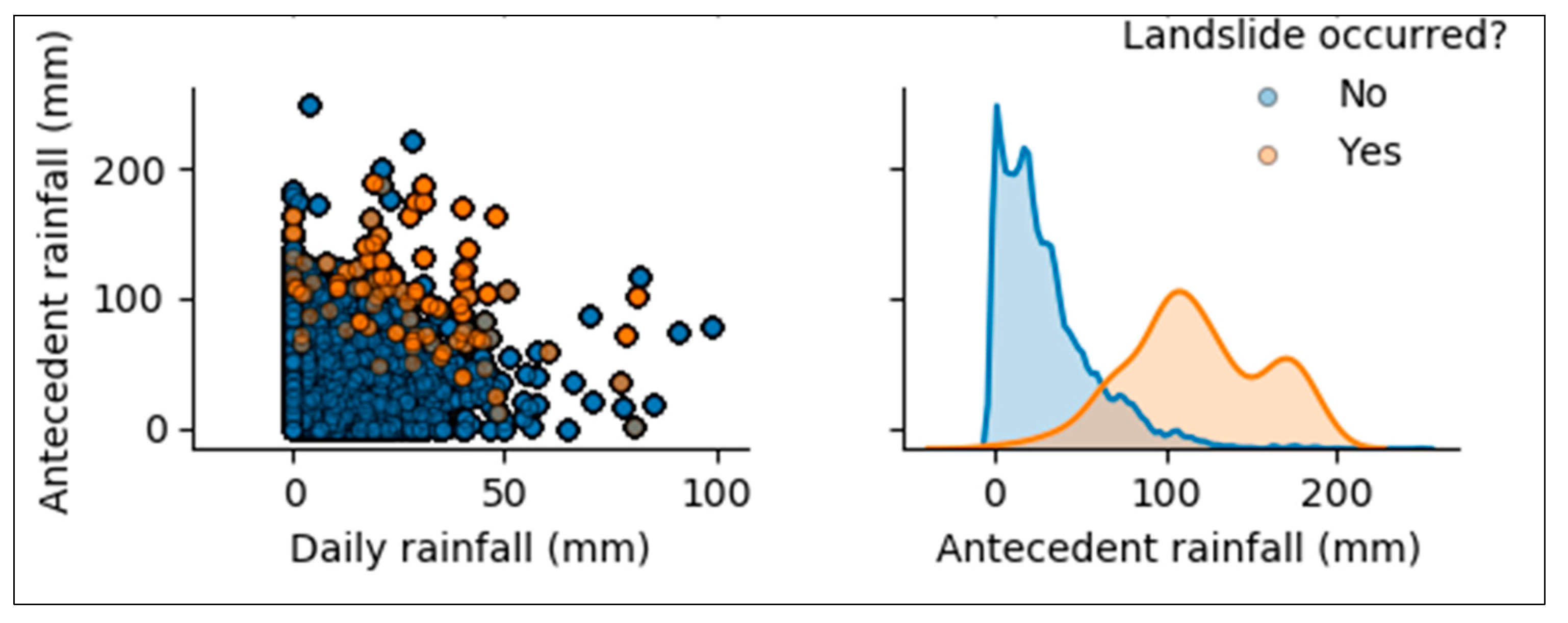
2.2.3. Rainfall
2.2.4. Antecedent Rainfall
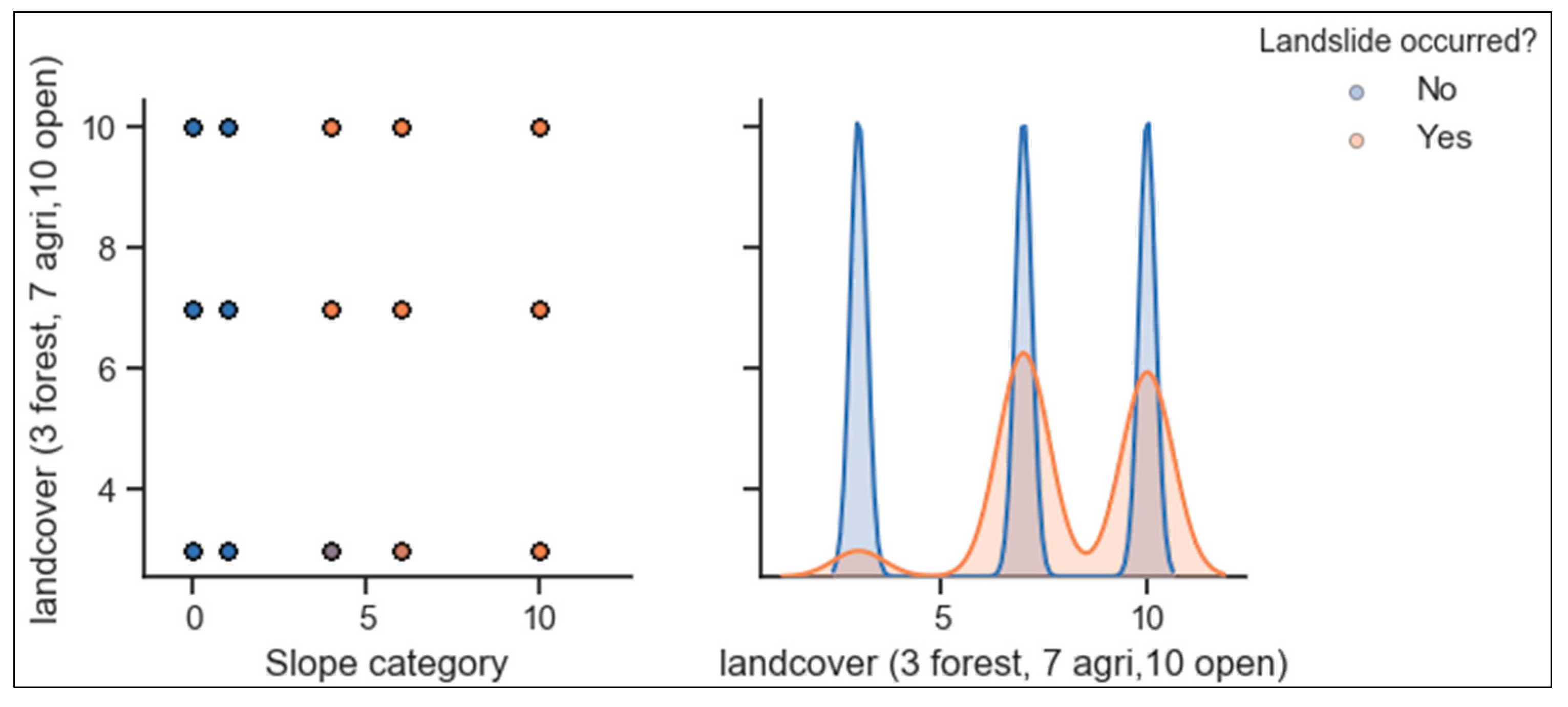
2.2.5. Slope
2.2.6. Soil Type
2.2.7. Soil Depth
2.2.8. Land Cover
2.2.9. Landslide Incidences
2.2.10. Splitting Dataset into a Training and a Test Dataset
2.2.11. Training and Testing the Models
2.2.12. Results Analysis
2.3. Machine Learning Models
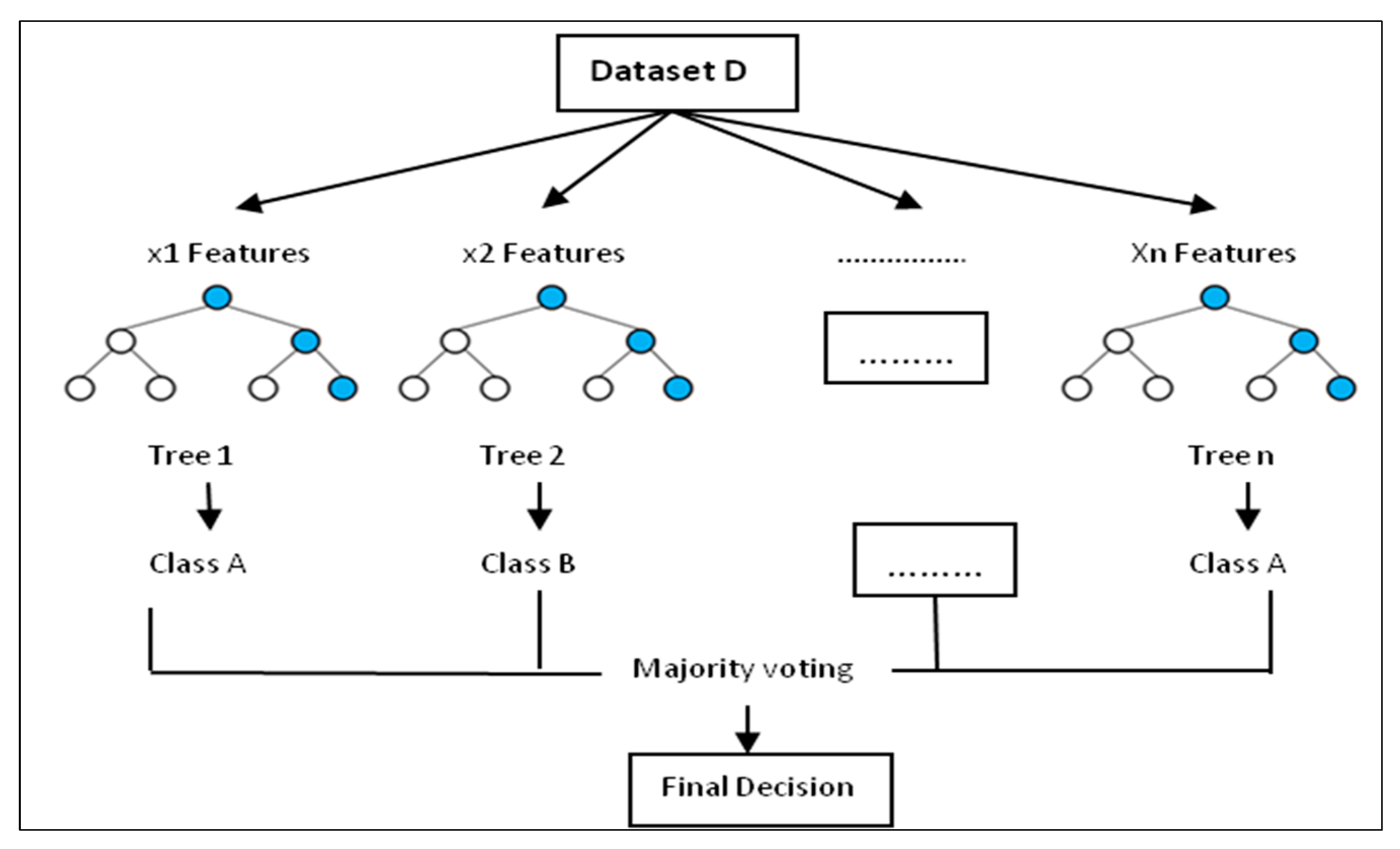
2.3.1. Random Forest
2.3.2. Logistic Regression
2.4. Re-Sampling
2.5. Preliminary Analysis Using Exploratory Data Analysis (EDA)
2.6. Models Evaluation
3. Results
3.1. Preliminary Analysis: Correlation Among Features Used in the Models
3.2. Models Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Douglas, I.; Alam, K.; Maghenda, M.; Mcdonnell, Y.; McLean, L.; Campbell, J. Unjust waters: Climate change, flooding and the urban poor in Africa. Environ. Urban. 2008, 20, 187–205. [Google Scholar] [CrossRef]
- Nahayo, L.; Li, L.; Mupenzi, C. Spatial Distribution of Landslides Vulnerability for the Risk Management in Ngororero District of Rwanda. EAJST Special 2018, 8, 1–14. [Google Scholar]
- MIDIMAR. Republic of Rwanda Refugee Affairs National Contingency Plan for Floods; MIDIMAR: Kigali, Rwanda, 2014. [Google Scholar]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Luo, G.; Nahayo, L.; Huang, X.; Cai, P. Landslide susceptibility assessment using spatial multi-criteria evaluation model in Rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Xue, X.; Hong, Y.; Gourley, J.J.; Lu, N.; Wan, Z.; Hong, Z.; Wooten, R. iCRESTRIGRS: A coupled modeling system for cascading flood-landslide disaster forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 1–23. [Google Scholar] [CrossRef]
- Ministry in charge of emergency management. The National Risk Atlas of Rwanda. Available online: http://minema.gov.rw/uploads/tx_download/National_Risk_Atlas_of_Rwanda_electronic_version.pdf (accessed on 15 March 2018).
- Jeong, S.; Lee, K.; Kim, J.; Kim, Y. Analysis of rainfall-induced landslide on unsaturated soil slopes. Sustainability 2017, 9, 1280. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Hong, M.; Kim, J.; Jeong, S. Rainfall intensity-duration thresholds for landslide prediction in South Korea by considering the effects of antecedent rainfall. Landslides 2018, 15, 523–534. [Google Scholar] [CrossRef]
- Diakakis, M. Rainfall thresholds for flood triggering. The case of Marathonas in Greece. Nat. Hazards 2012, 60, 789–800. [Google Scholar] [CrossRef]
- Nahayo, L.; Mupenzi, C.; Kayiranga, A.; Karamage, F.; Ndayisaba, F.; Nyesheja, E.M.; Li, L. Early alert and community involvement: Approach for disaster risk reduction in Rwanda. Nat. Hazards 2017, 86, 505–517. [Google Scholar] [CrossRef]
- Lee, S.; Ryu, J.H.; Won, J.S.; Park, H.J. Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Staley, D.M.; Kean, J.W.; Cannon, S.H.; Schmidt, K.M.; Laber, J.L. Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California. Landslides 2013, 10, 547–562. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Lee, M.-J. Rainfall and Landslide Correlation Analysis and Prediction of Future Rainfall Base on Climate Change. In Geohazards Caused by Human Activity; InTech: London, UK, 2016. [Google Scholar]
- Republic of Rwanda Western Province Ngororero District. Available online: www.ngororero.gov.rw (accessed on 17 September 2019).
- Modeling, H. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in hydrological modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale. A Review. 2013, 17, 392–406. [Google Scholar]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar] [CrossRef]
- Data Ngororero - African Center of Excellence in Internet of Things. Available online: https://aceiot.ur.ac.rw/spip.php?article103 (accessed on 26 March 2020).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Chen, Z.; Ren, F.; Feng, L.; Du, Q. Optimizing the predictive ability of machine learning methods for landslide susceptibility mapping using smote for Lishui city in Zhejiang province, China. Int. J. Environ. Res. Public Health 2019, 16, 368. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.C.; Lee, S.; Jung, H.S.; Lee, S. Landslide susceptibility mapping using random forest and boosted tree models in Pyeong-Chang, Korea. Geocarto Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Random Forest Classifier - Machine Learning Global Software Support. Available online: https://www.globalsoftwaresupport.com/random-forest-classifier/ (accessed on 26 March 2020).
- Lin, W.; Wu, Z.; Lin, L.; Wen, A.; Li, J. An ensemble random forest algorithm for insurance big data analysis. IEEE Access 2017, 5, 16568–16575. [Google Scholar] [CrossRef]
- Louppe, G. Understanding random forests: From theory to practice. Ph.D. Thesis, University of Liege, Liege, Belgium, July 2014. [Google Scholar]
- Gorsevski, P.V.; Gessler, P.E.; Foltz, R.B.; Elliot, W.J. Spatial prediction of landslide hazard using logistic regression and ROC analysis. Trans. GIS 2006, 10, 395–415. [Google Scholar] [CrossRef]
- Mathew, J.; Jha, V.K.; Rawat, G.S. Landslide susceptibility zonation mapping and its validation in part of Garhwal Lesser Himalaya, India, using binary logistic regression analysis and receiver operating characteristic curve method. Landslides 2009, 6, 17–26. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth-Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V. Conditioning factor determination for mapping and prediction of landslide susceptibility using machine learning algorithms. Proc. SPIE 2019, 11156, 19. [Google Scholar] [CrossRef]
- Pham, B.T.; Son, L.H.; Hoang, T.A.; Nguyen, D.M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Lombardo, L.; Mai, P.M. Presenting logistic regression-based landslide susceptibility results. Eng. Geol. 2018, 244, 14–24. [Google Scholar] [CrossRef]
- Capparelli, G.; Versace, P. FLaIR and SUSHI: Two mathematical models for early warning of landslides induced by rainfall. Landslides 2011, 8, 67–79. [Google Scholar] [CrossRef]
- Thai Pham, B.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Ahmad, B.B.; Quoc, N.K.; Lee, S. Landslide susceptibility assessment by novel hybrid machine learning algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gayen, A.; Park, S.; Lee, C.W.; Lee, S. Assessment of landslide-prone areas and their zonation using logistic regression, LogitBoost, and naïvebayes machine-learning algorithms. Sustainability 2018, 10, 3697. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Landslide susceptibility mapping based on random forest and boosted regression tree models, and a comparison of their performance. Appl. Sci. 2019, 9, 942. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Bao, Y.; Han, X.; Zhan, J.; Peng, W. Landslide susceptibility mapping using logistic regression analysis along the Jinsha river and its tributaries close to Derong and Deqin County, southwestern China. ISPRS Int. J. Geo-Information 2018, 7, 438. [Google Scholar] [CrossRef]
- Utomo, D.; Chen, S.F.; Hsiung, P.A. Landslide prediction with model switching. Appl. Sci. 2019, 9, 1839. [Google Scholar] [CrossRef]
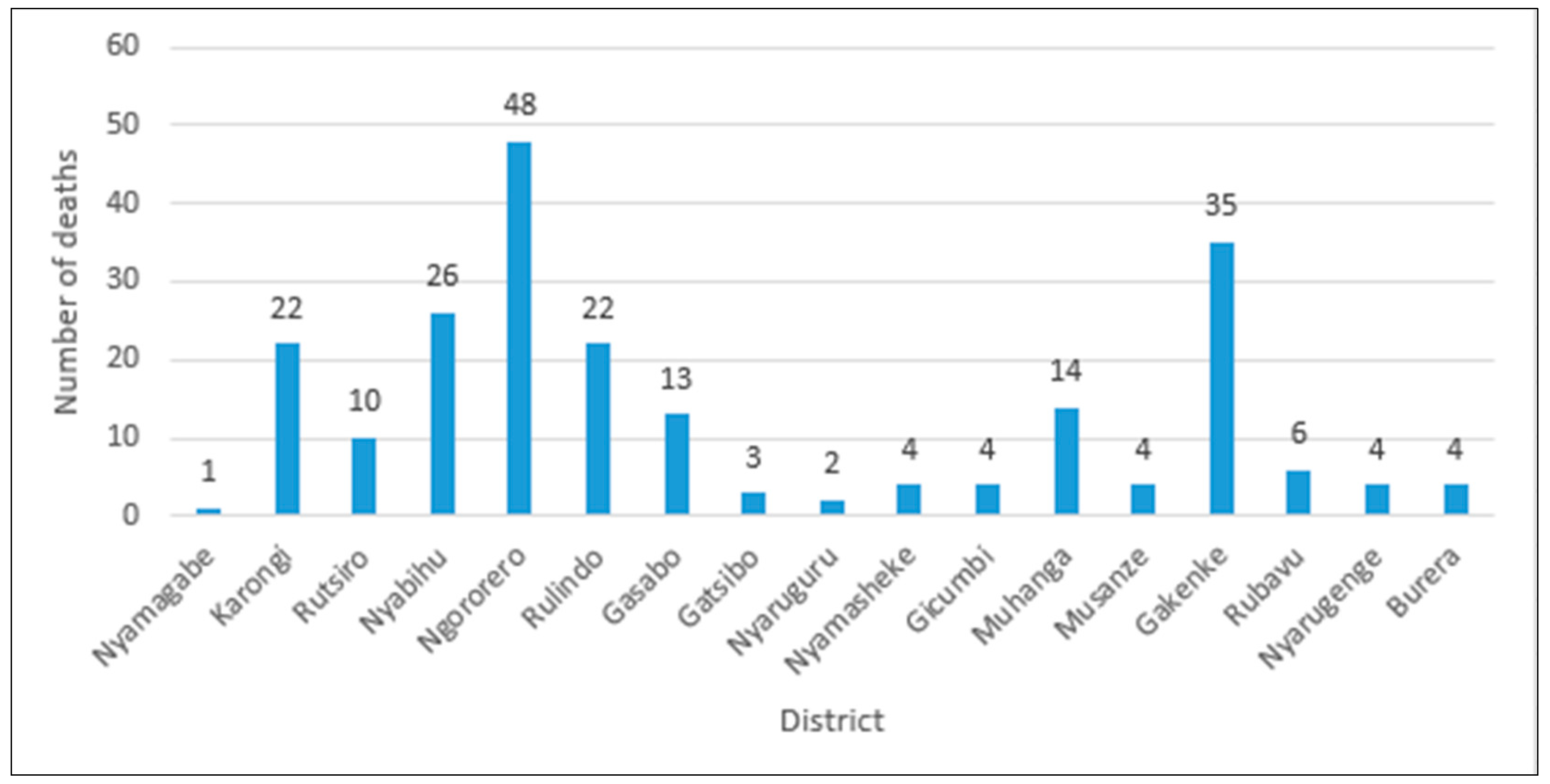

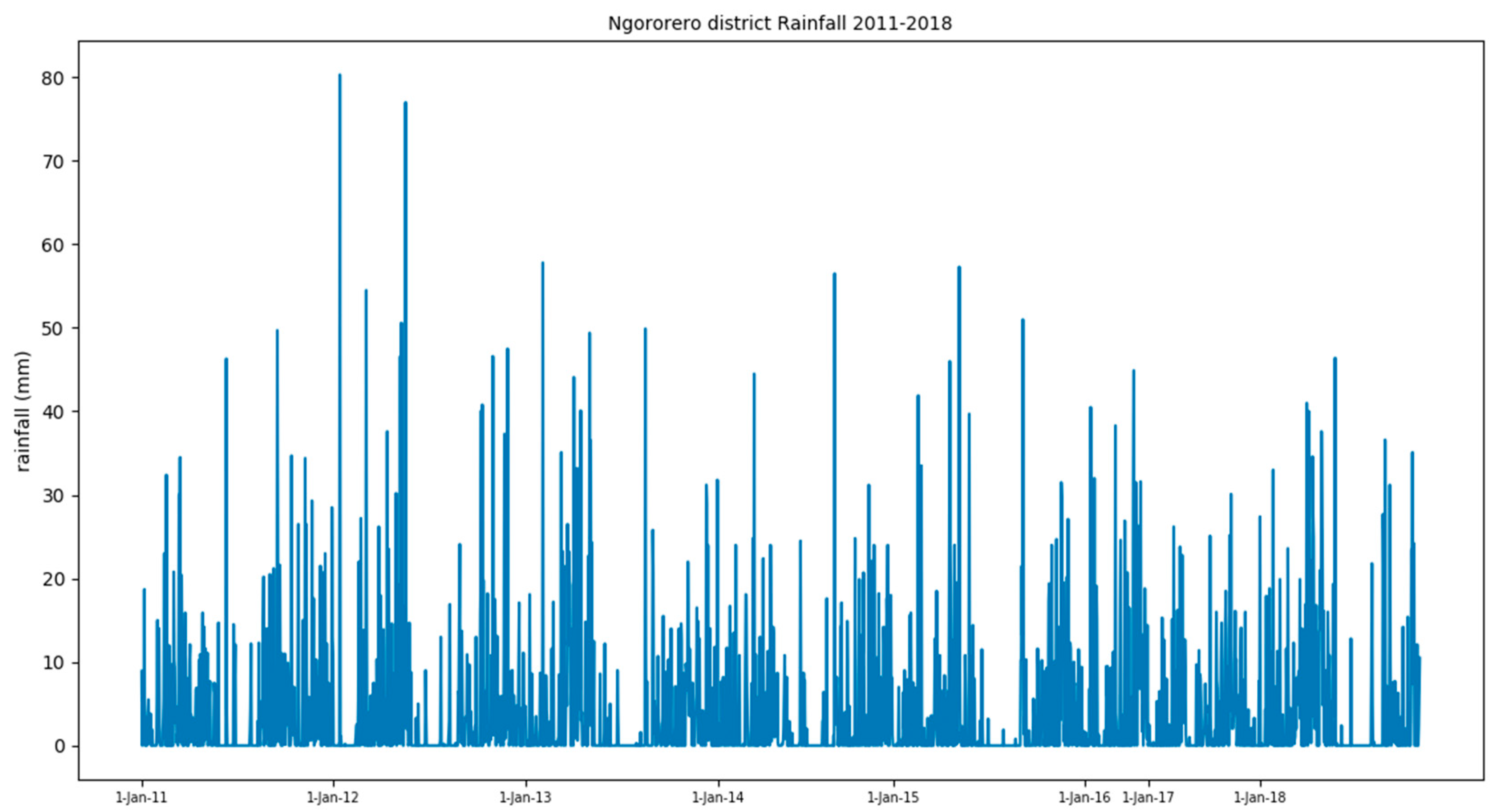
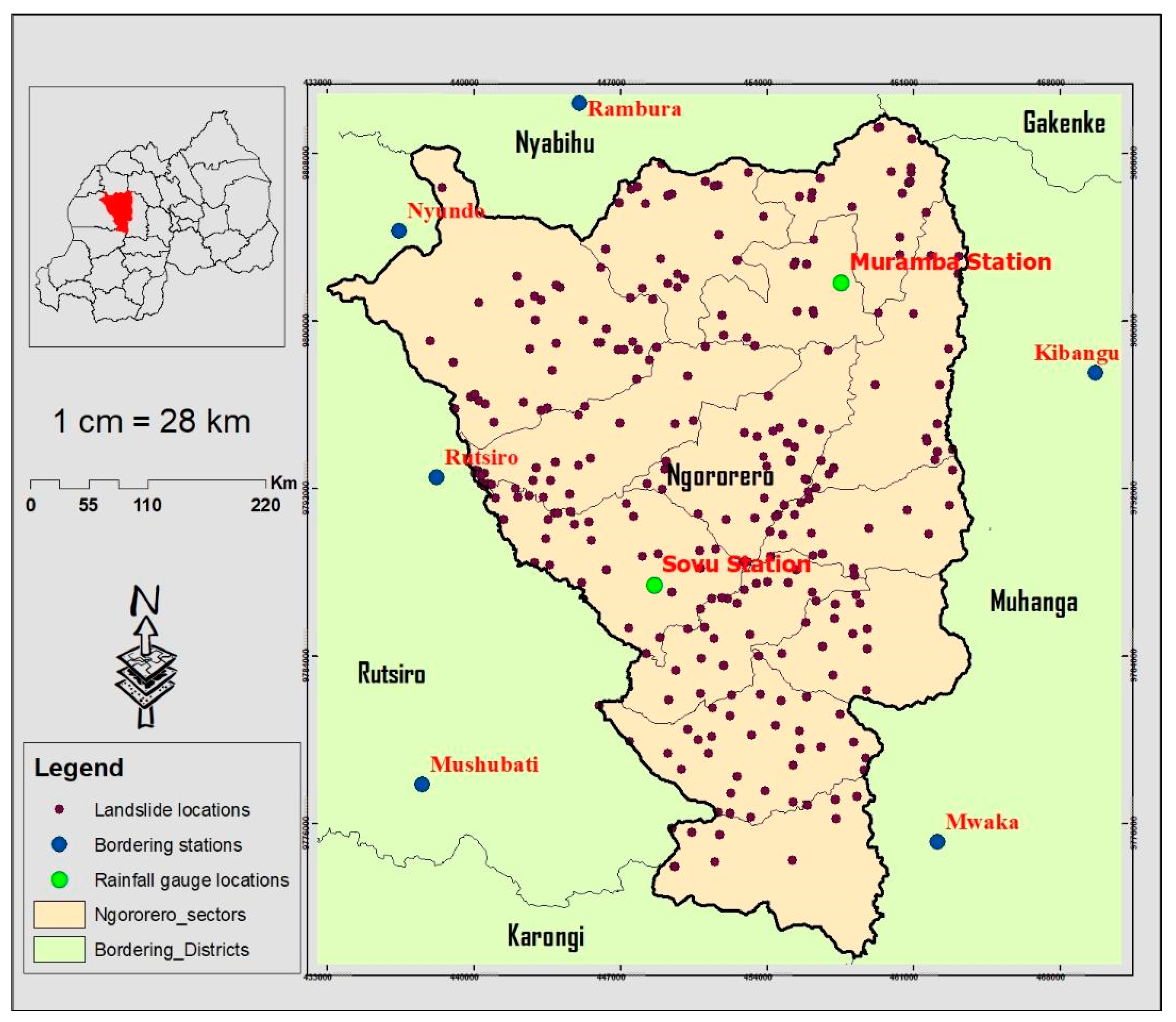
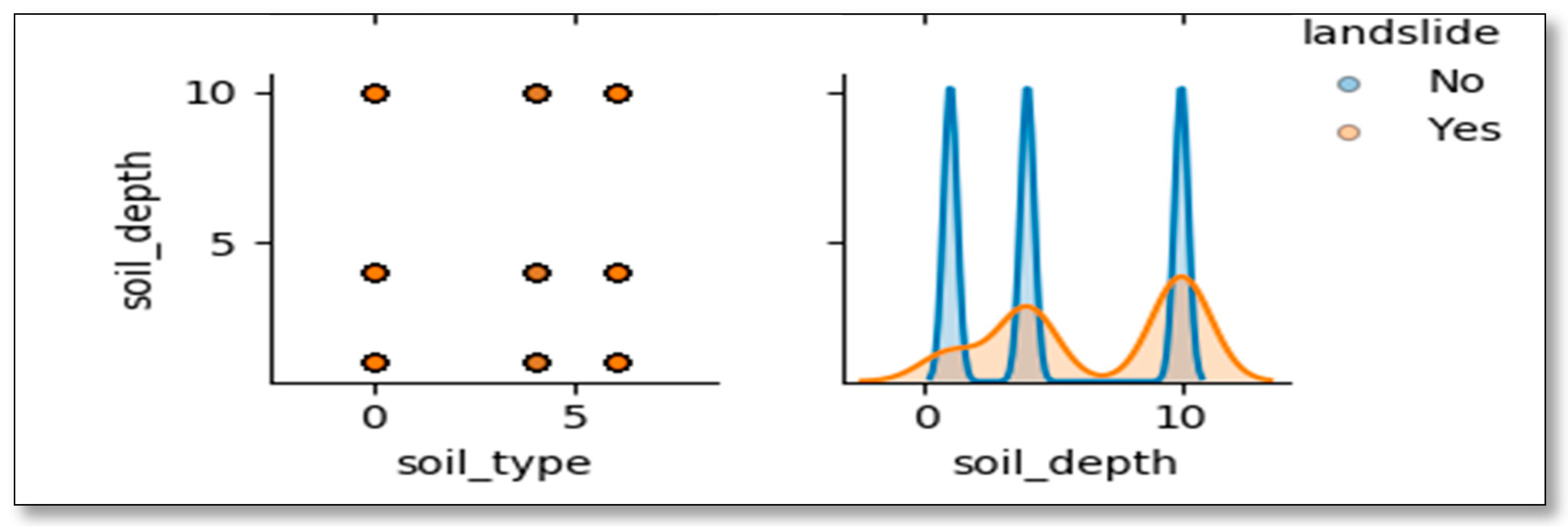
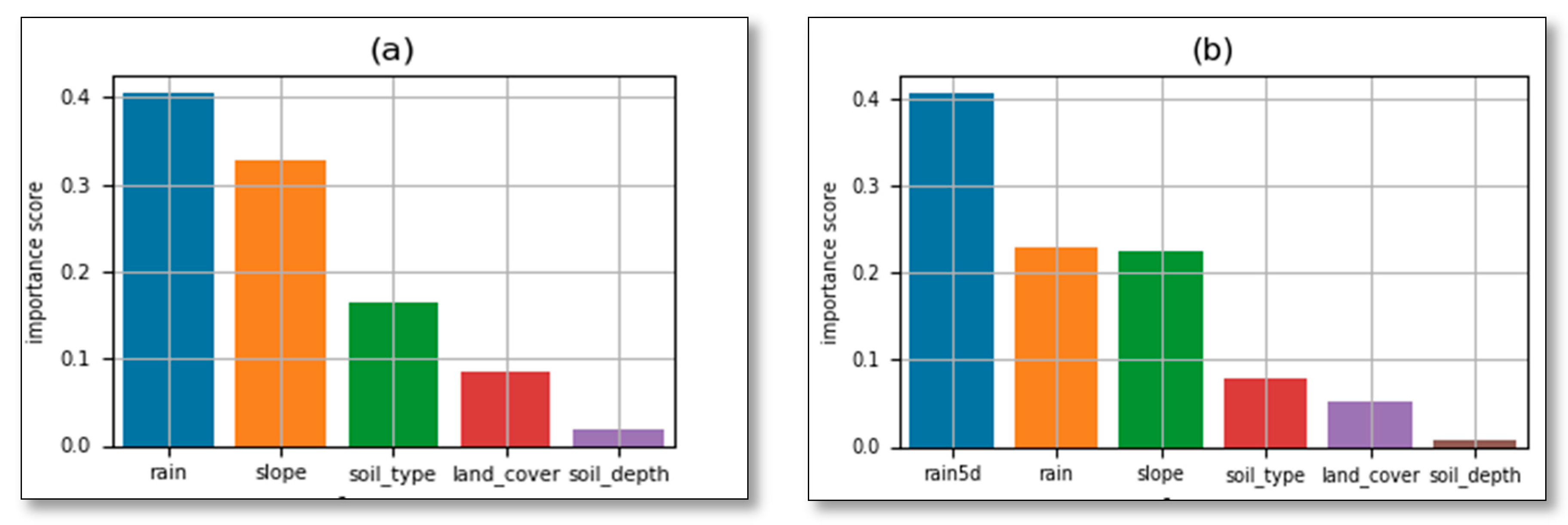
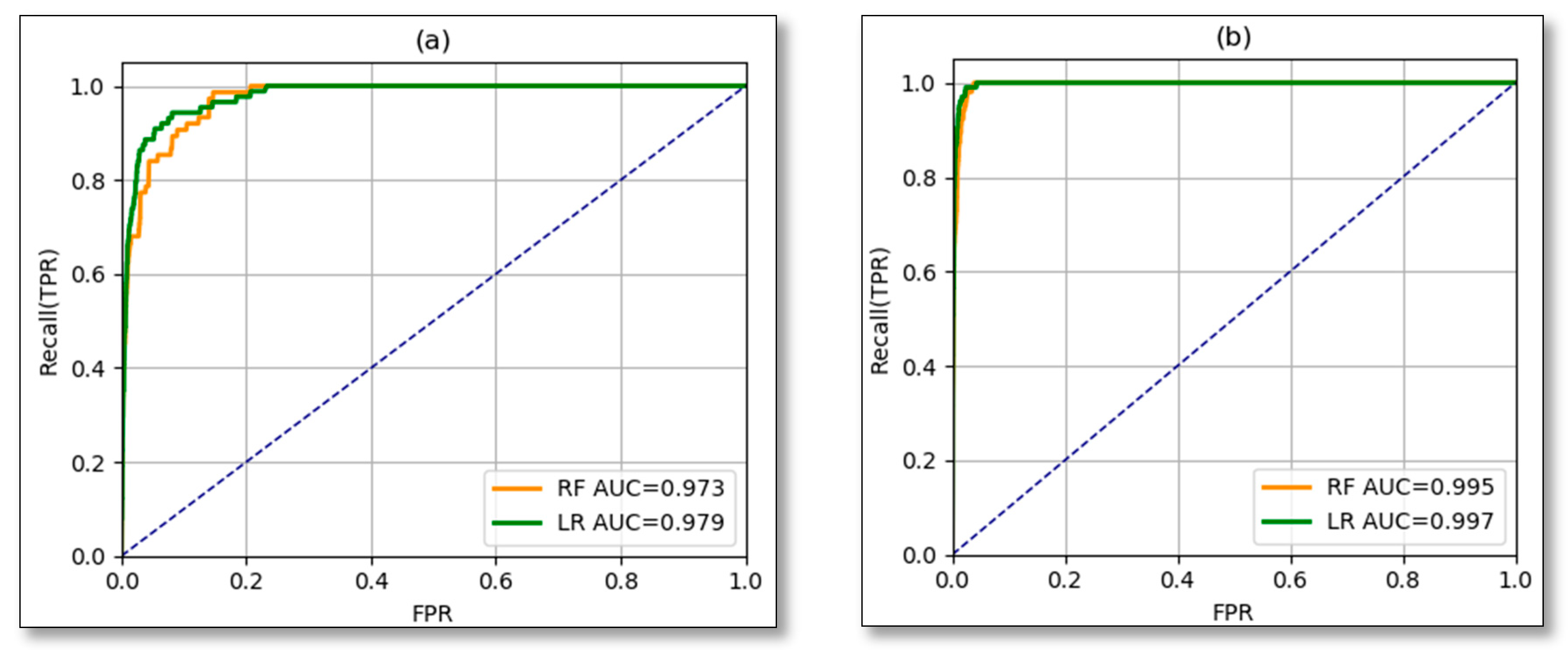
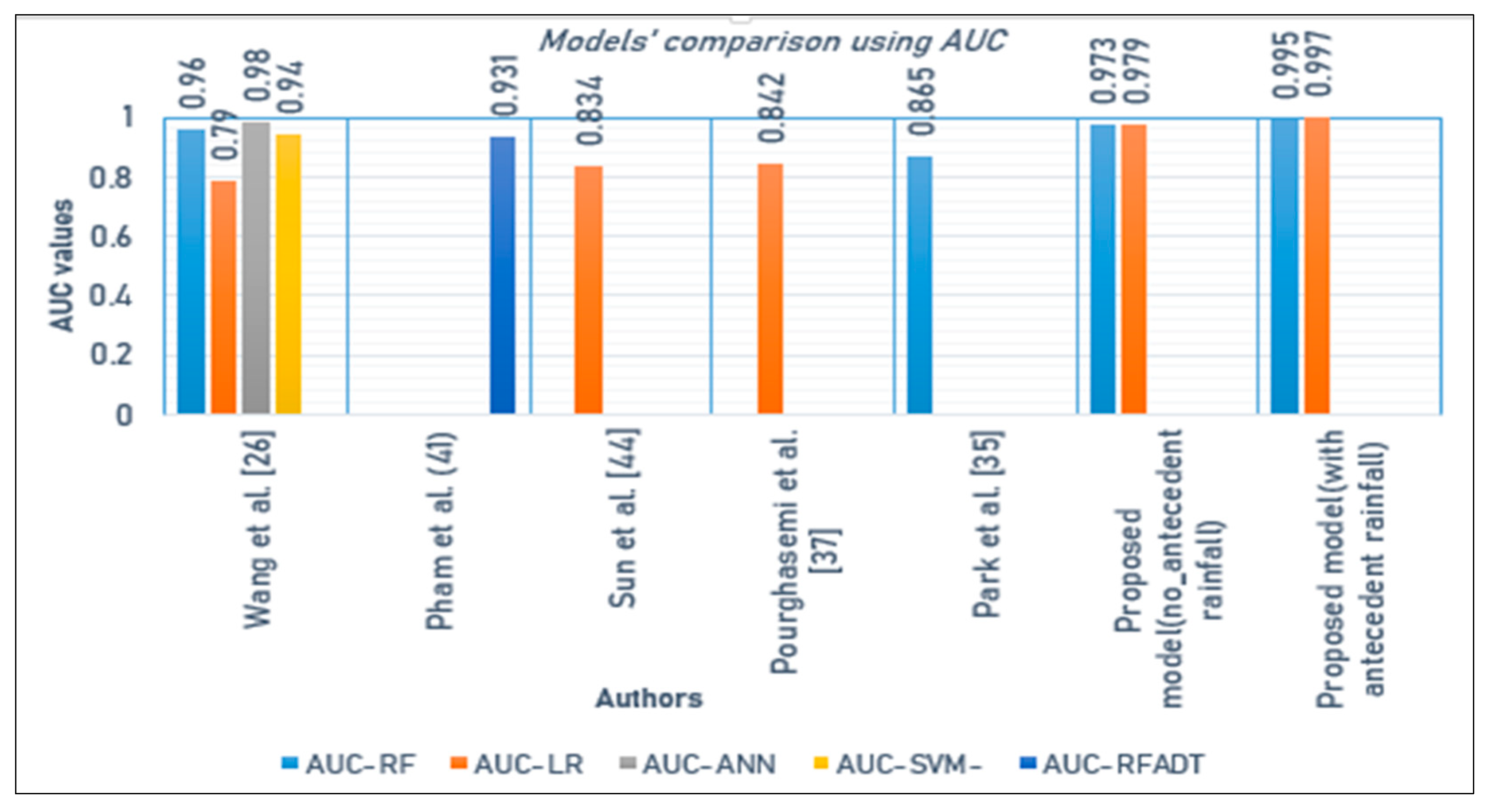
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Total |
|---|---|---|---|---|---|---|---|---|---|
| Number of death | 19 | 14 | 31 | 0 | 10 | 64 | 7 | 77 | 222 |
| Slope | Soil | Land | |||||
|---|---|---|---|---|---|---|---|
| Slope Angle (Degree) | Score | Soil Type | Score | Soil Depth (cm) | Score | Land Cover | Score |
| 0–10 | 0 | Clay | 0 | <50 | 1 | Forest plantation | 3 |
| >10–15 | 1 | Sand | 4 | >50–100 | 4 | Agriculture | 7 |
| >15–20 | 4 | Silt | 6 | >100 | 10 | Open land | 10 |
| >20–25 | 6 | ||||||
| >25–45 | 10 | ||||||
| 1-Day Rainfall (Without Antecedent Rainfall) | 5-Days Antecedent Rainfall Included | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fold | Accuracy (using cross-validation) | Accuracy (using train/test ratios) | Accuracy (using cross-validation) | Accuracy (using train/test ratios) | ||||||
| RF | LR | Ratio | RF | LR | RF | LR | Ratio | RF | LR | |
| 1 | 0.9530 | 0.9466 | 0.80 & 0.20 | 0.9414 | 0.9322 | 0.9875 | 0.9877 | 0.80 & 0.20 | 0.9742 | 0.9836 |
| 2 | 0.9536 | 0.9466 | 0.75 & 0.25 | 0.9398 | 0.9330 | 0.9871 | 0.9882 | 0.75 & 0.25 | 0.9759 | 0.9835 |
| 3 | 0.9531 | 0.9459 | 0.70 & 0.30 | 0.9399 | 0.9352 | 0.9876 | 0.9878 | 0.70 & 0.30 | 0.9744 | 0.9838 |
| 4 | 0.952 | 0.9457 | 0.65 & 0.35 | 0.9394 | 0.9392 | 0.9870 | 0.9879 | 0.65 & 0.35 | 0.9767 | 0.9838 |
| 5 | 0.9530 | 0.9467 | 0.60 & 0.40 | 0.9469 | 0.9413 | 0.9876 | 0.9879 | 0.60 & 0.40 | 0.9740 | 0.9840 |
| Av. | 0.9530 | 0.9463 | 0.55 & 0.45 | 0.9409 | 0.9415 | 0.9874 | 0.9879 | 0.55 & 0.45 | 0.9744 | 0.9837 |
| Std | 0.0003 | 0.0004 | 0.0028 | 0.0041 | 0.0002 | 0.0001 | 0.001 | 0.0001 | ||
| Performance Metric | 1-Day Rainfall, Antecedent Rainfall Excluded (%) | 5-Days Antecedent Rainfall Included (%) | ||
|---|---|---|---|---|
| RF | LR | RF | LR | |
| Recall (TPR) | 84.61 | 90.38 | 95.19 | 96.15 |
| Specificity (TNR) | 93.91 | 93.92 | 97.64 | 98.38 |
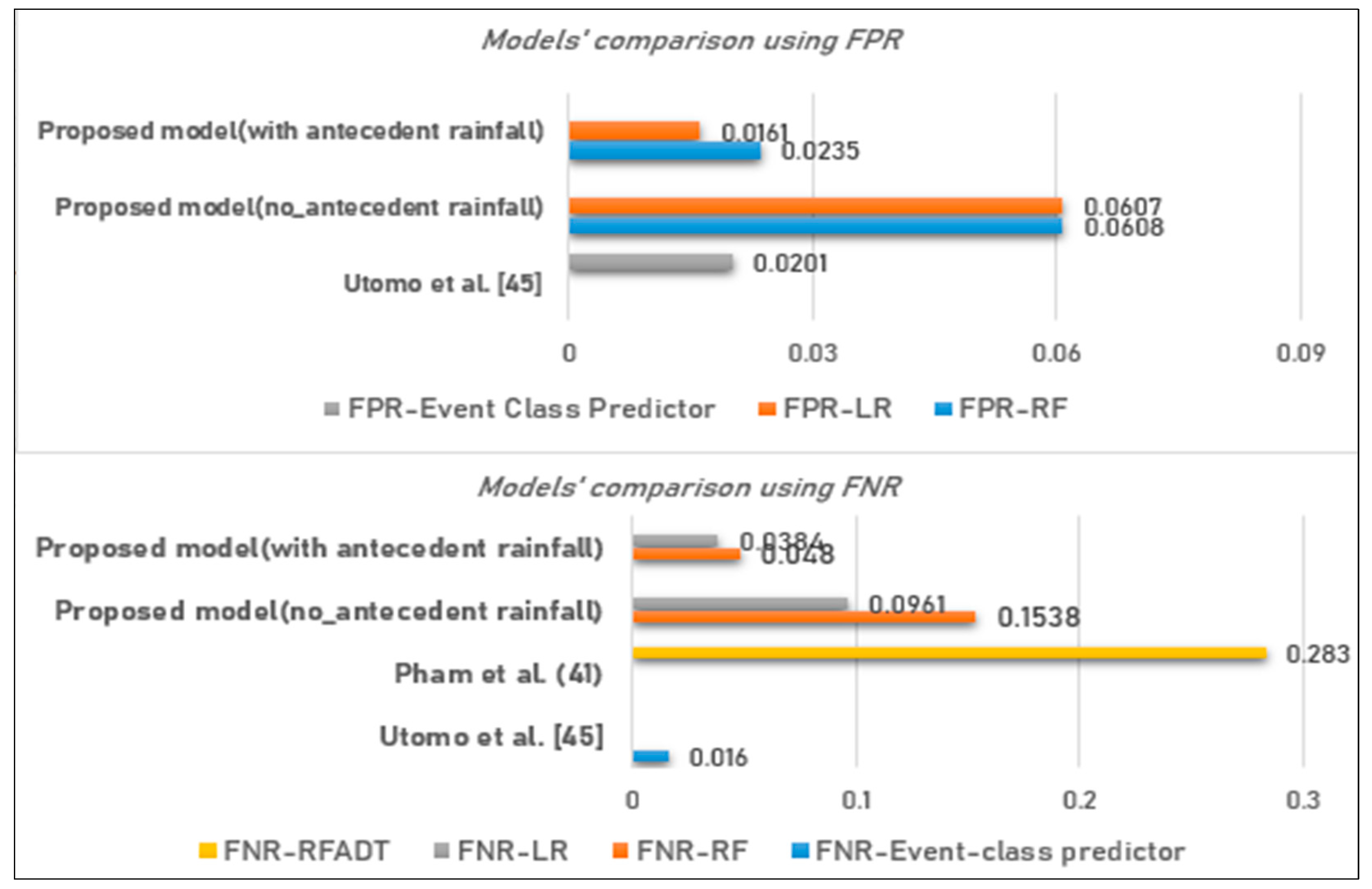
| False Positive Rate (FPR) | 6.08 | 6.07 | 2.35 | 1.61 |
| False Negative Rate (FNR) | 15.38 | 9.61 | 4.80 | 3.84 |
| Intercept | Daily Rainfall | Antecedent Rainfall (5-Days) | Slope | Soil Type | Soil Depth | Land Cover |
|---|---|---|---|---|---|---|
| −7.06 | 1.32 | 2.47 | −9.34 | −2.90 | −4.10 | −4.37 |
| −9.29 | −5.39 | −1.85 | −1.12 | |||
| 1.20 | 1.23 | −1.10 | −1.56 | |||
| 3.87 | ||||||
| 6.49 |
| Random Forest | Logistic Regression | |||||
|---|---|---|---|---|---|---|
| Correct Predictions (%) | ||||||
| Performance Metric | Without Antecedent Rainfall | With Antecedent Rainfall | Improvement (%) | Without Antecedent Rainfall | With Antecedent Rainfall | Improvement (%) |
| Recall (TPR) | 84.61 | 95.19 | 10.58 | 90.38 | 96.15 | 5.77 |
| Specificity (TNR) | 93.91 | 97.64 | 3.73 | 93.92 | 98.38 | 4.46 |
| Incorrect Predictions (%) | ||||||
| False Positives | 6.08 | 2.35 | 3.73 | 6.07 | 1.61 | 4.46 |
| False Negatives | 15.38 | 4.80 | 10.58 | 9.61 | 3.84 | 5.77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuradusenge, M.; Kumaran, S.; Zennaro, M. Rainfall-Induced Landslide Prediction Using Machine Learning Models: The Case of Ngororero District, Rwanda. Int. J. Environ. Res. Public Health 2020, 17, 4147. https://doi.org/10.3390/ijerph17114147
Kuradusenge M, Kumaran S, Zennaro M. Rainfall-Induced Landslide Prediction Using Machine Learning Models: The Case of Ngororero District, Rwanda. International Journal of Environmental Research and Public Health. 2020; 17(11):4147. https://doi.org/10.3390/ijerph17114147
Chicago/Turabian StyleKuradusenge, Martin, Santhi Kumaran, and Marco Zennaro. 2020. "Rainfall-Induced Landslide Prediction Using Machine Learning Models: The Case of Ngororero District, Rwanda" International Journal of Environmental Research and Public Health 17, no. 11: 4147. https://doi.org/10.3390/ijerph17114147
APA StyleKuradusenge, M., Kumaran, S., & Zennaro, M. (2020). Rainfall-Induced Landslide Prediction Using Machine Learning Models: The Case of Ngororero District, Rwanda. International Journal of Environmental Research and Public Health, 17(11), 4147. https://doi.org/10.3390/ijerph17114147







