Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020
Abstract
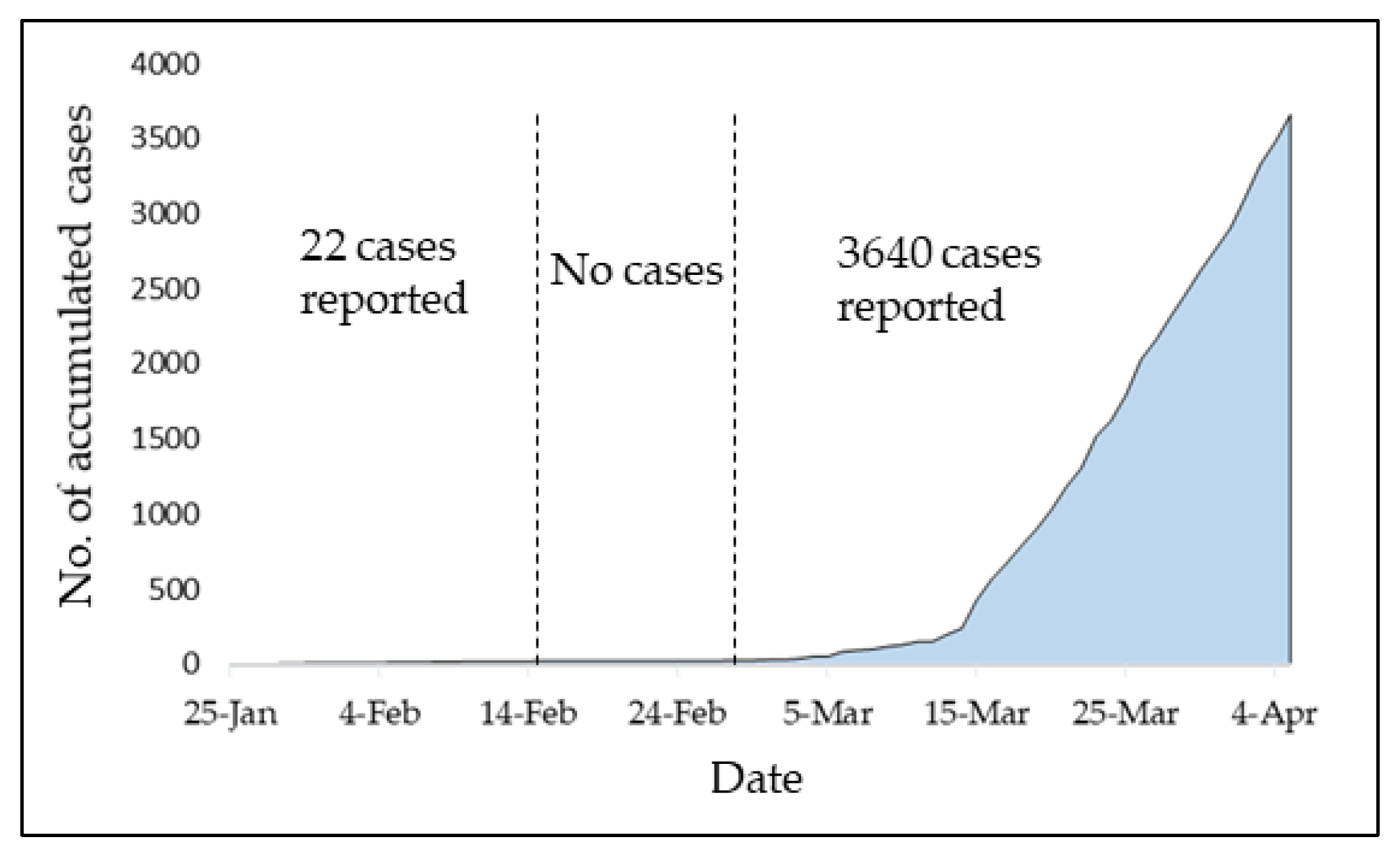
1. Introduction
2. Methods
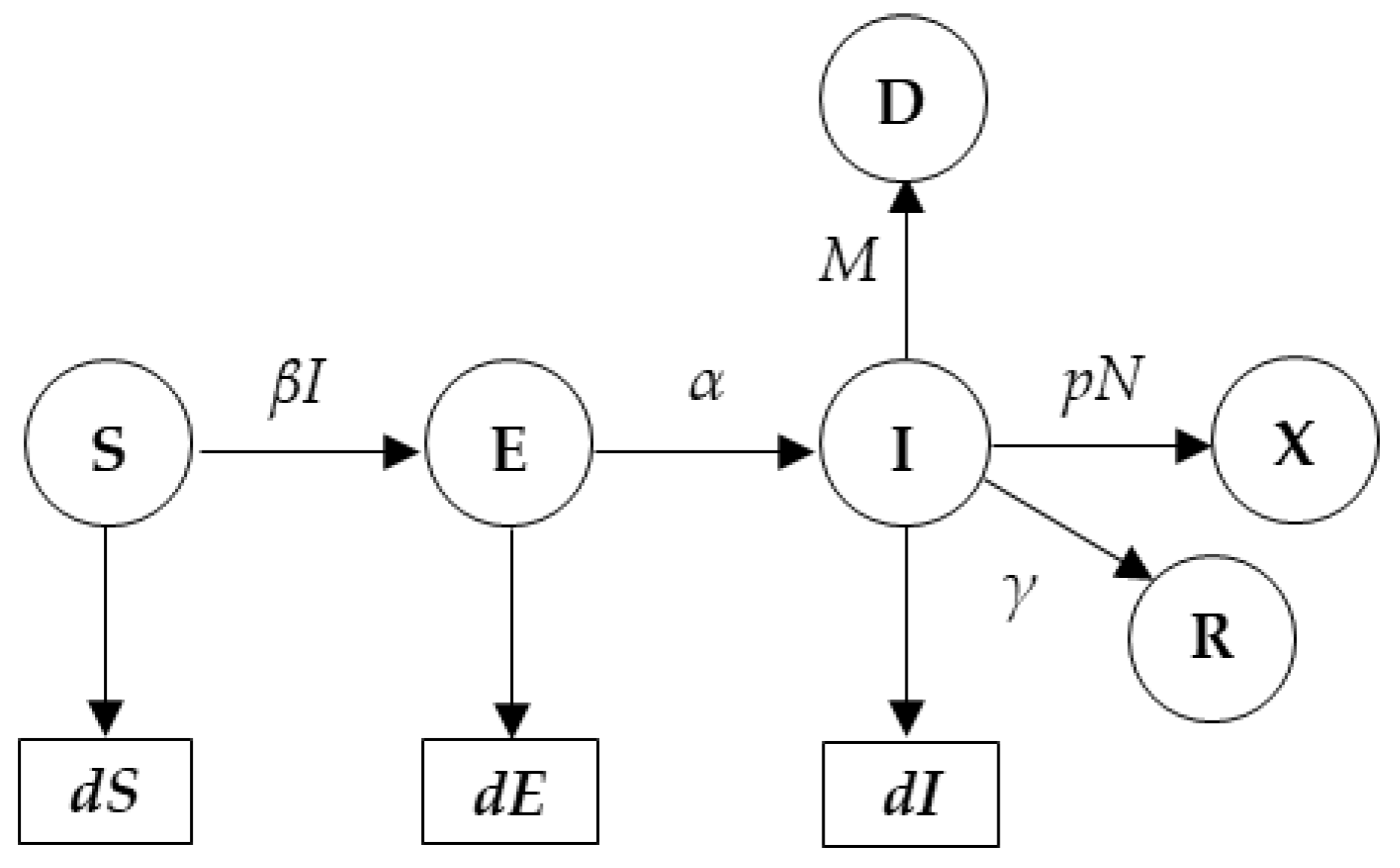
2.1. SEIR Model for Peak Prediction
dE(t)/d(t) = βS(t)I(t) − αE(t),
dI(t)/d(t) = αE(t) − γI(t) − MI(t),
dR(t)/d(t) = γI(t),
dD(t)/d(t) = MI(t)
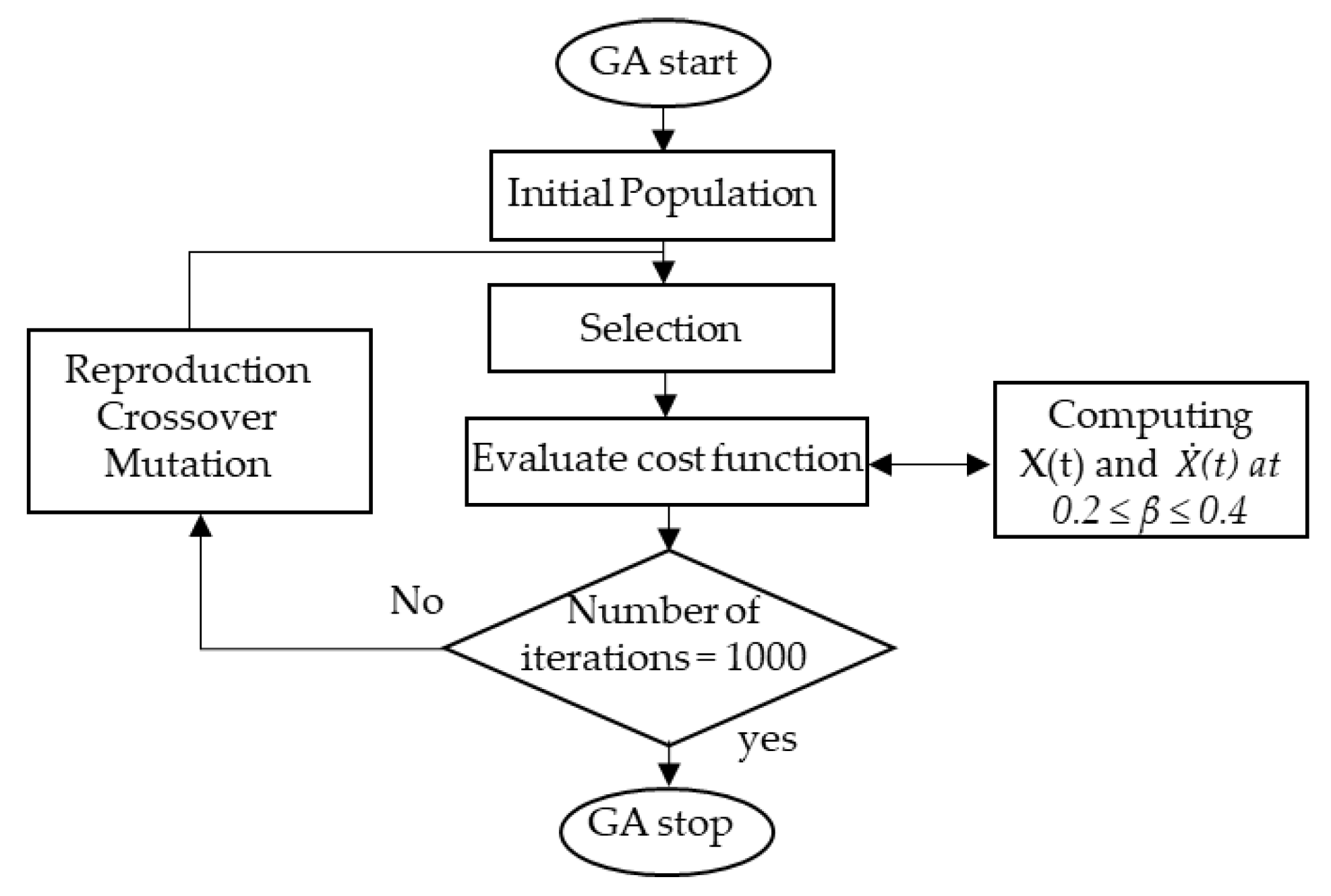
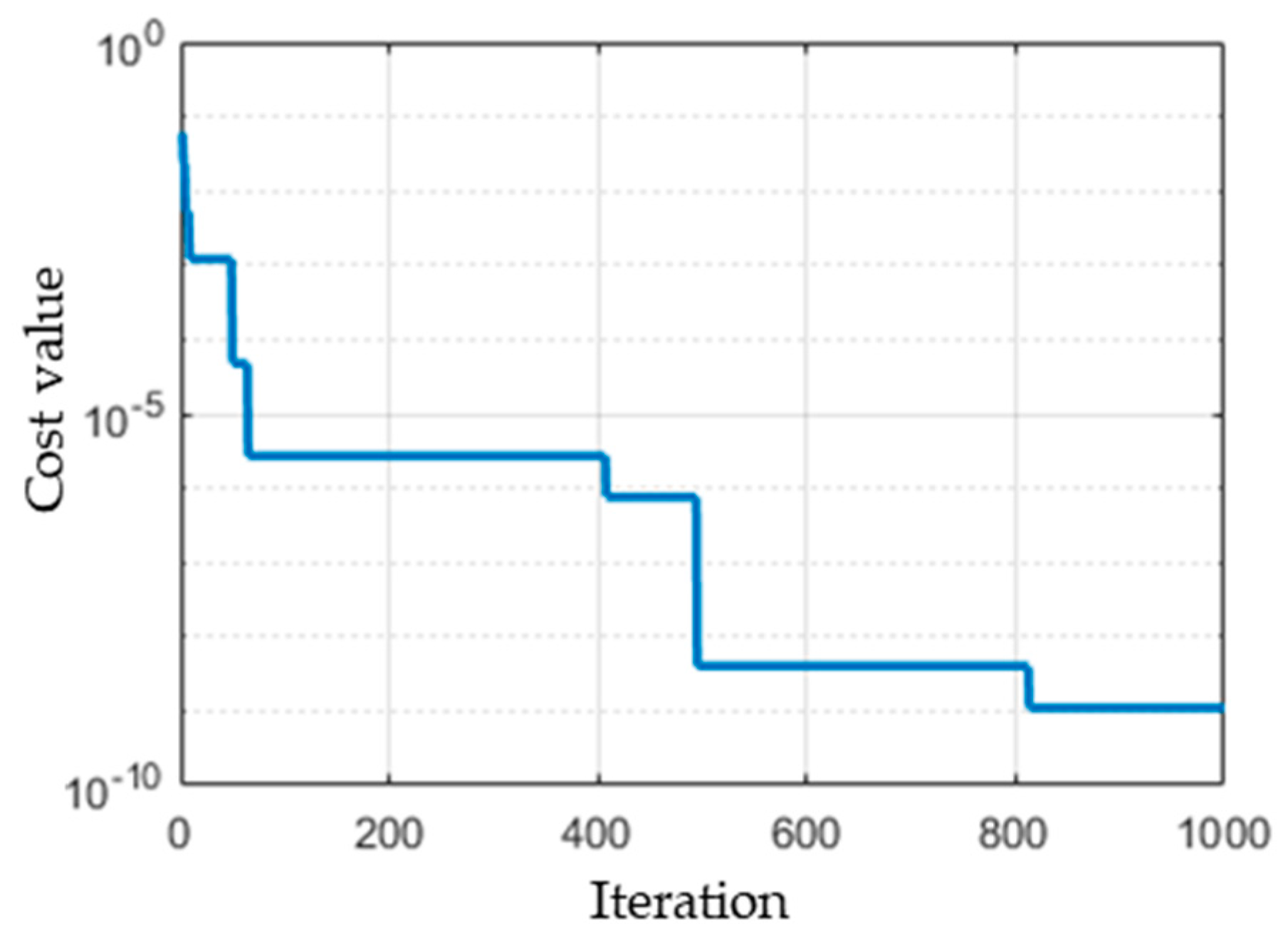
2.2. β. Estimation Using GA
- Population initialization: In order to find a solution to the problem of the cost function, the GA initially creates a number of populations that randomly encodes the chromosomes (individuals). Then, the cost values of the generated population are evaluated.
- Selection: In this process, each individual identified by its associated cost is ranked and the corresponding individual fitness is selected. According to fitness, the best chromosomes from the population are then selected such that better fitness has a bigger chance to be selected. Subsequently, the solutions selected from one population are implemented to form a new population. This process is motivated by the new population potentially being better than the previous one. The selection process is performed using a certain function that fixes the generation gap. The selected individuals are then recombined.
- Crossover: To make new offspring (children) for the following iteration, the selected individuals (parents) have to undergo a crossover with a crossover probability. However, if there is no crossover performed, the offspring is an exact copy of the parents.
- Mutation: In this process, the information in the chromosomes is randomly modified. The genes occasionally mutate to be converted to novel genes. Based on mutation, it is possible to control the multifariousness of the population as well as to enhance the search capacity of the search scheme.
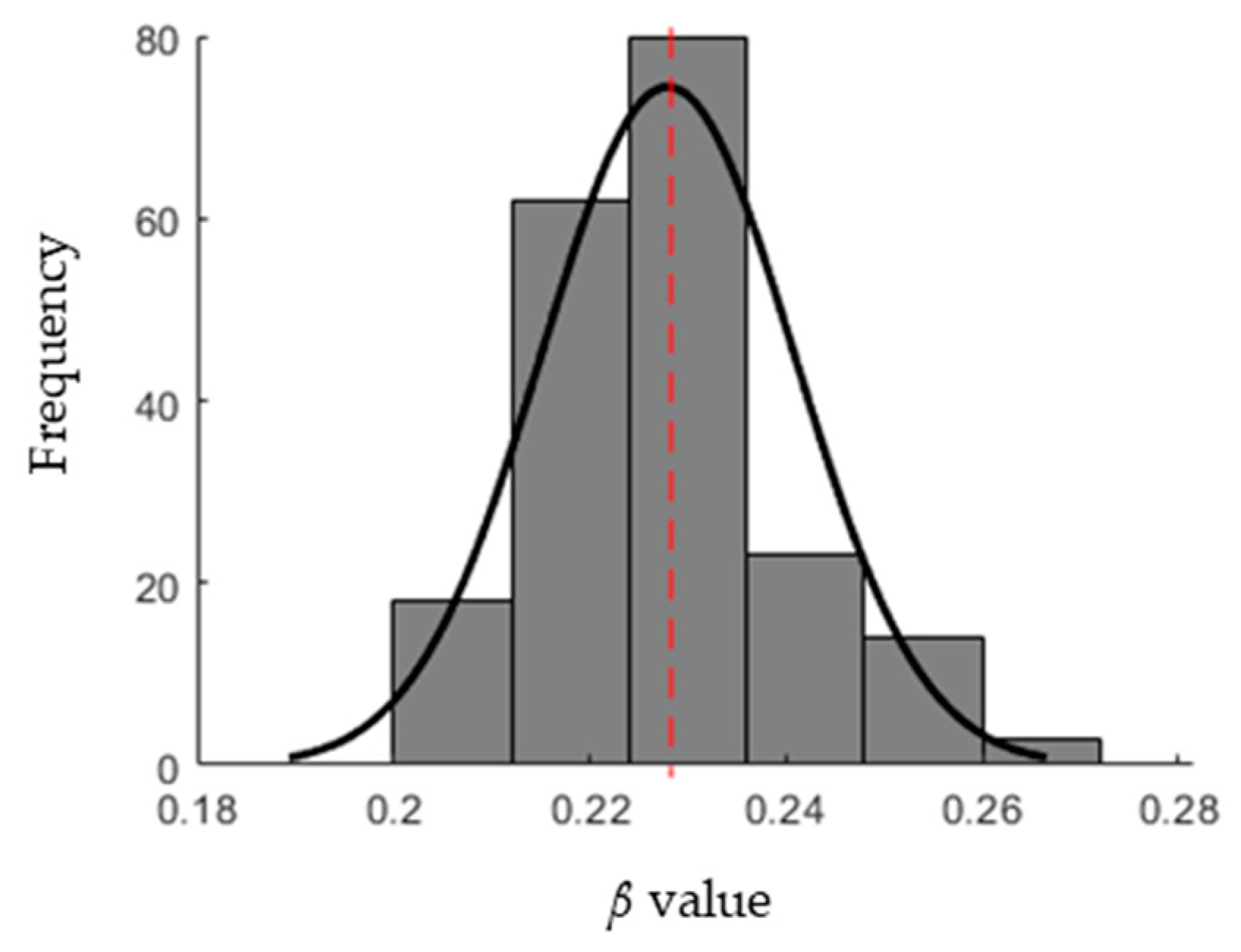
- Evaluation: For each individual, the cost function of the optimization problem is calculated. The stopping criterion of the GA is the number of iterations after which the process is stopped. For each iteration, the β value that has the minimum cost function is recorded. The distribution of the β values is then approximated by a normal distribution with a mean and standard deviation.
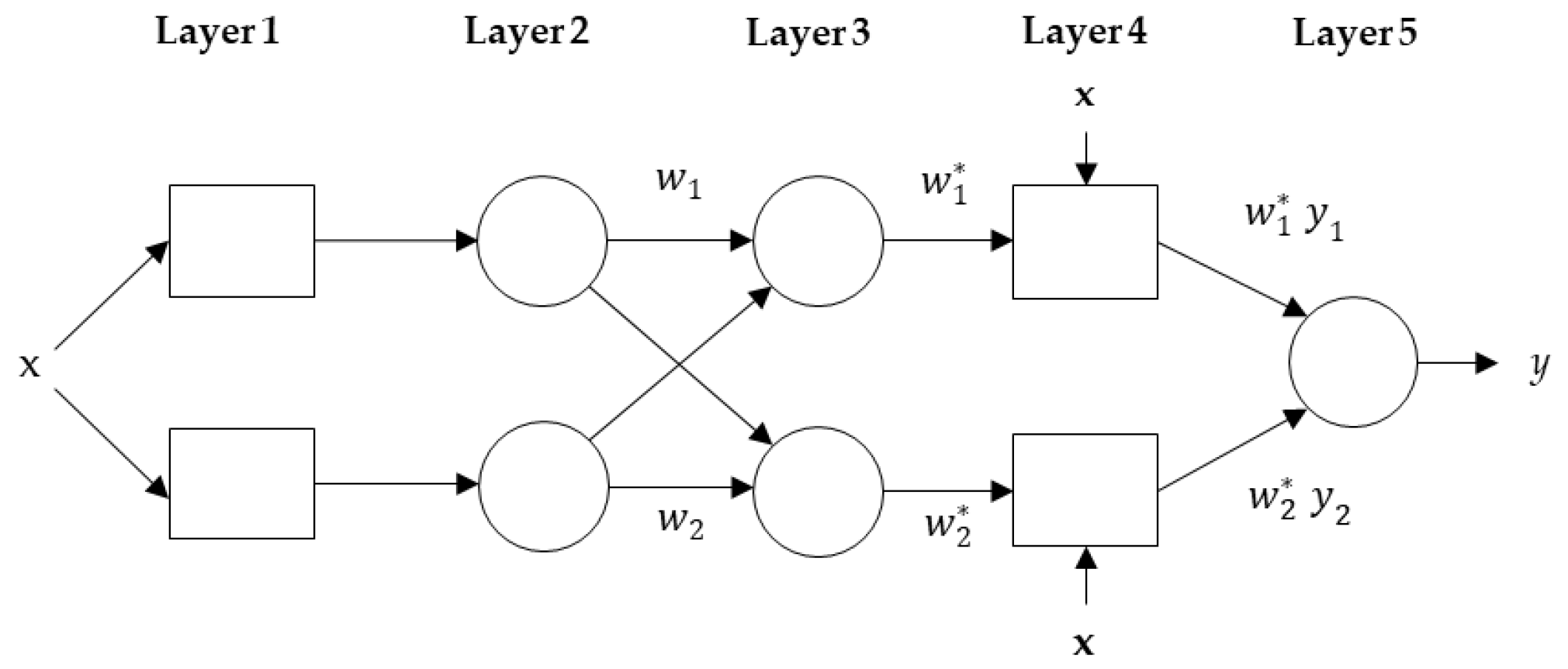
2.3. ANFIS for Short-Term Forecasting
3. Results
3.1. Infection Rate (β) Estimation
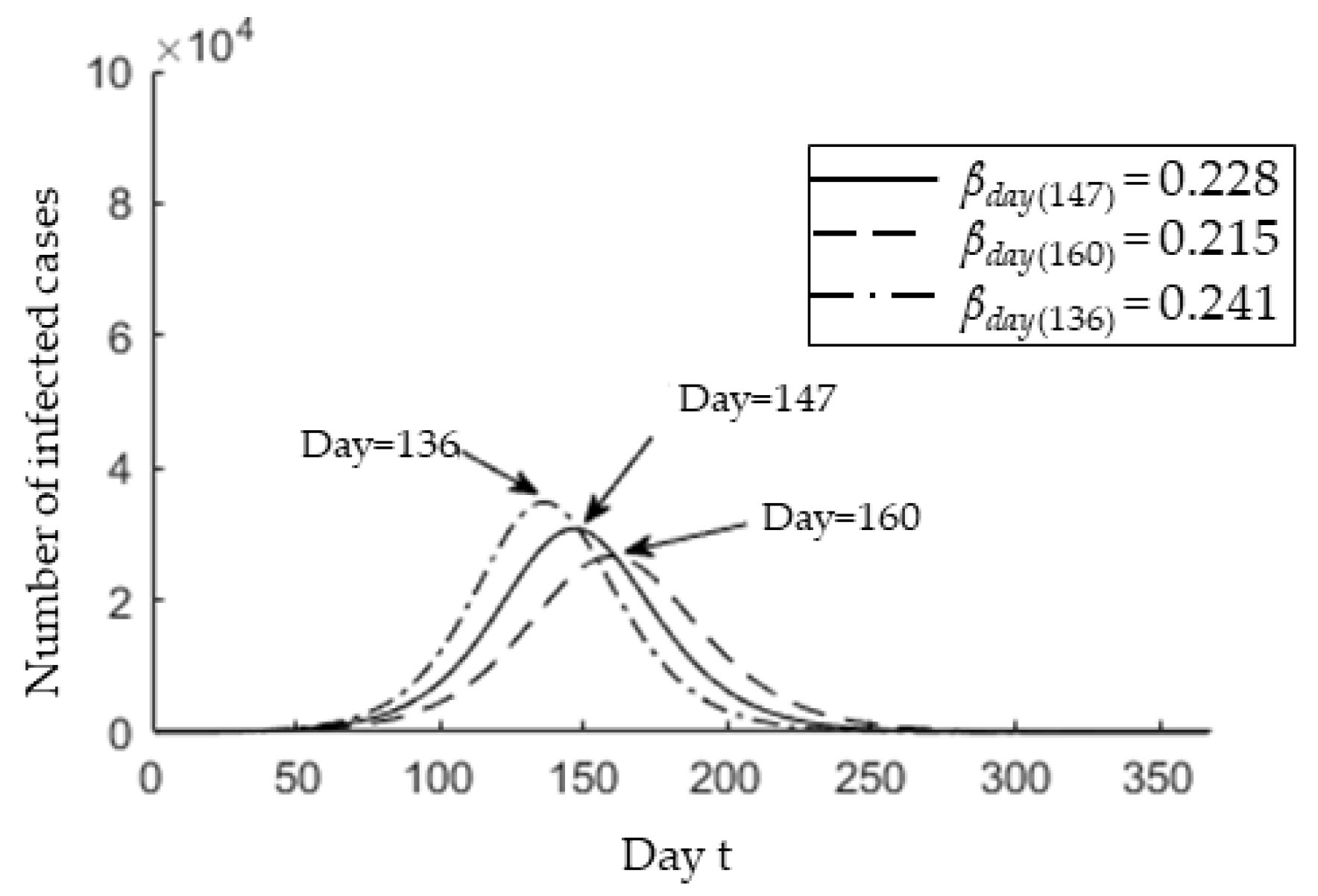
3.2. Epedimic Peak Prediction
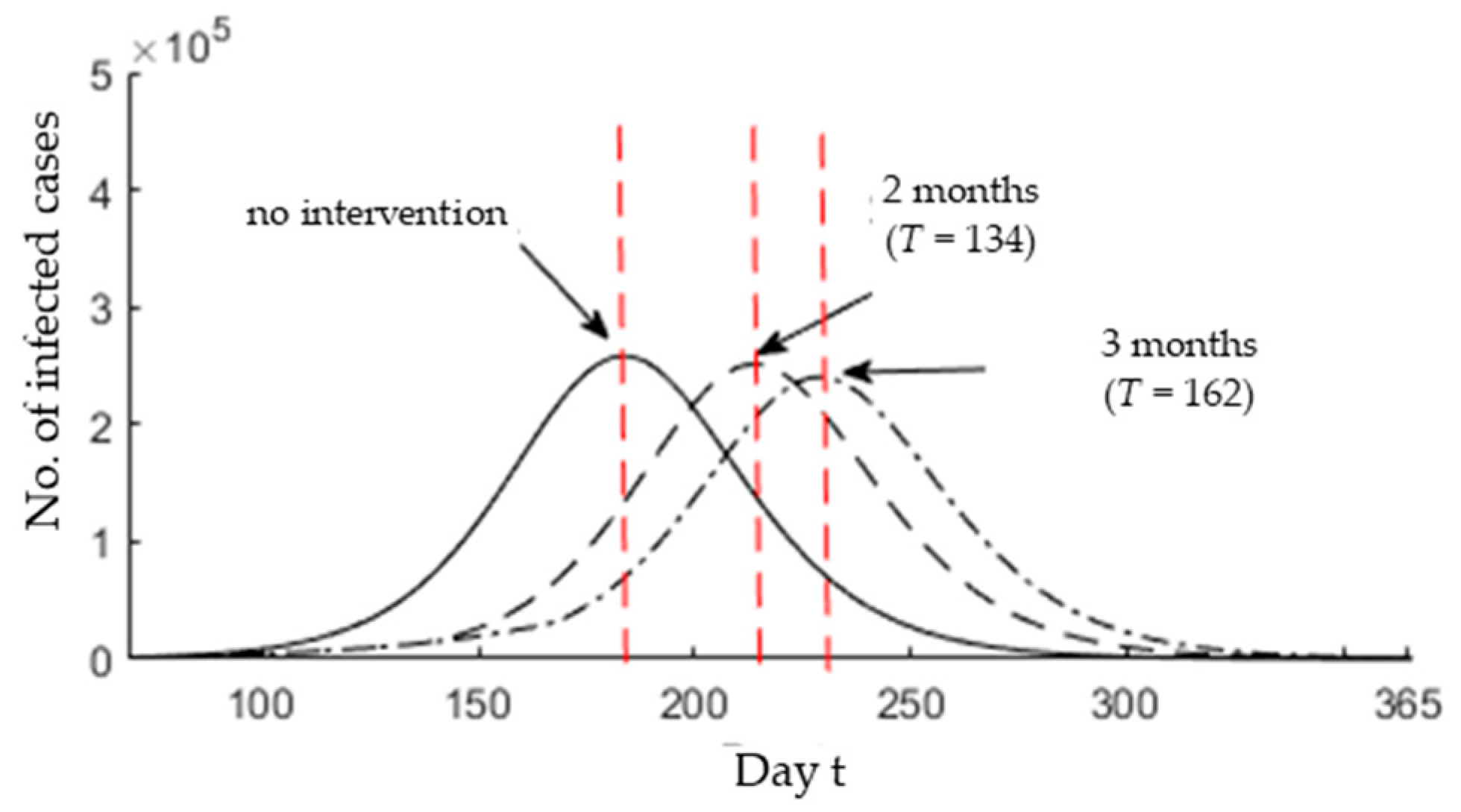
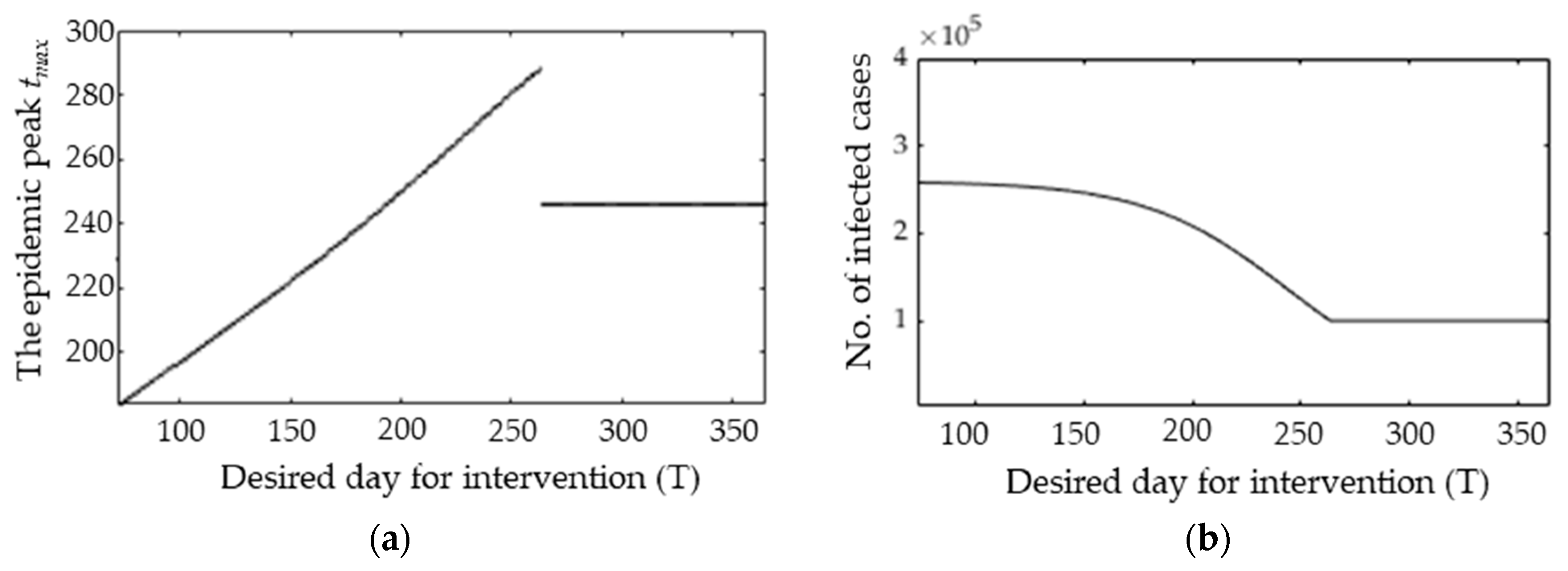
3.3. Epidemic Peak after Possible Interventions
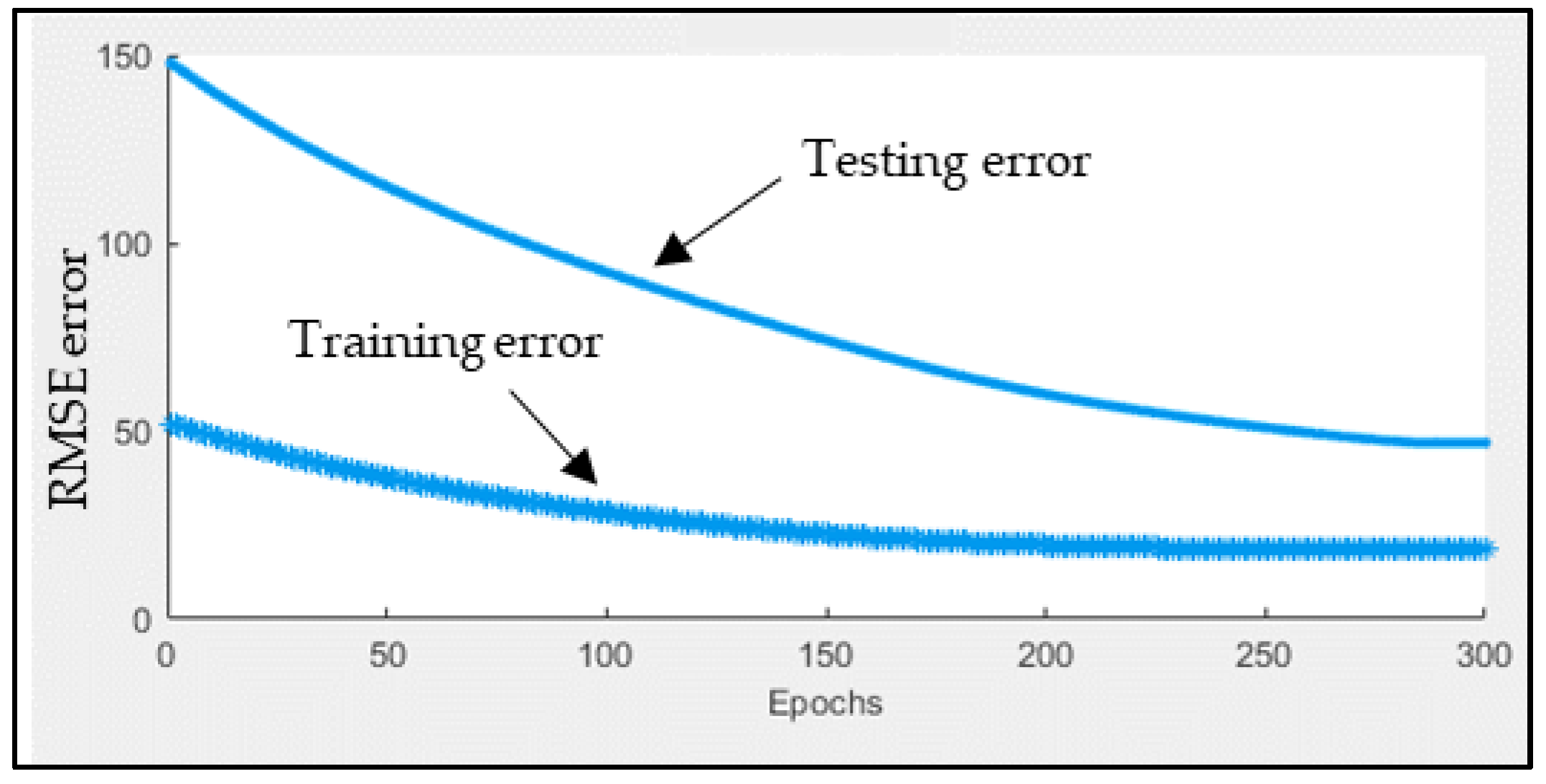
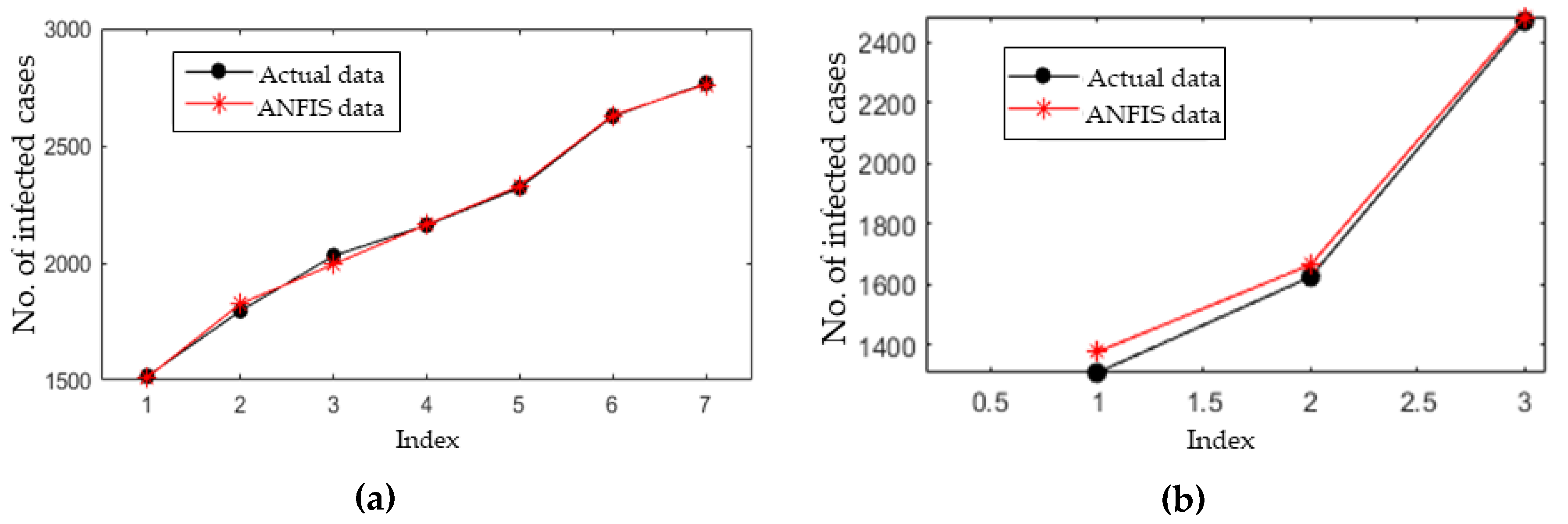
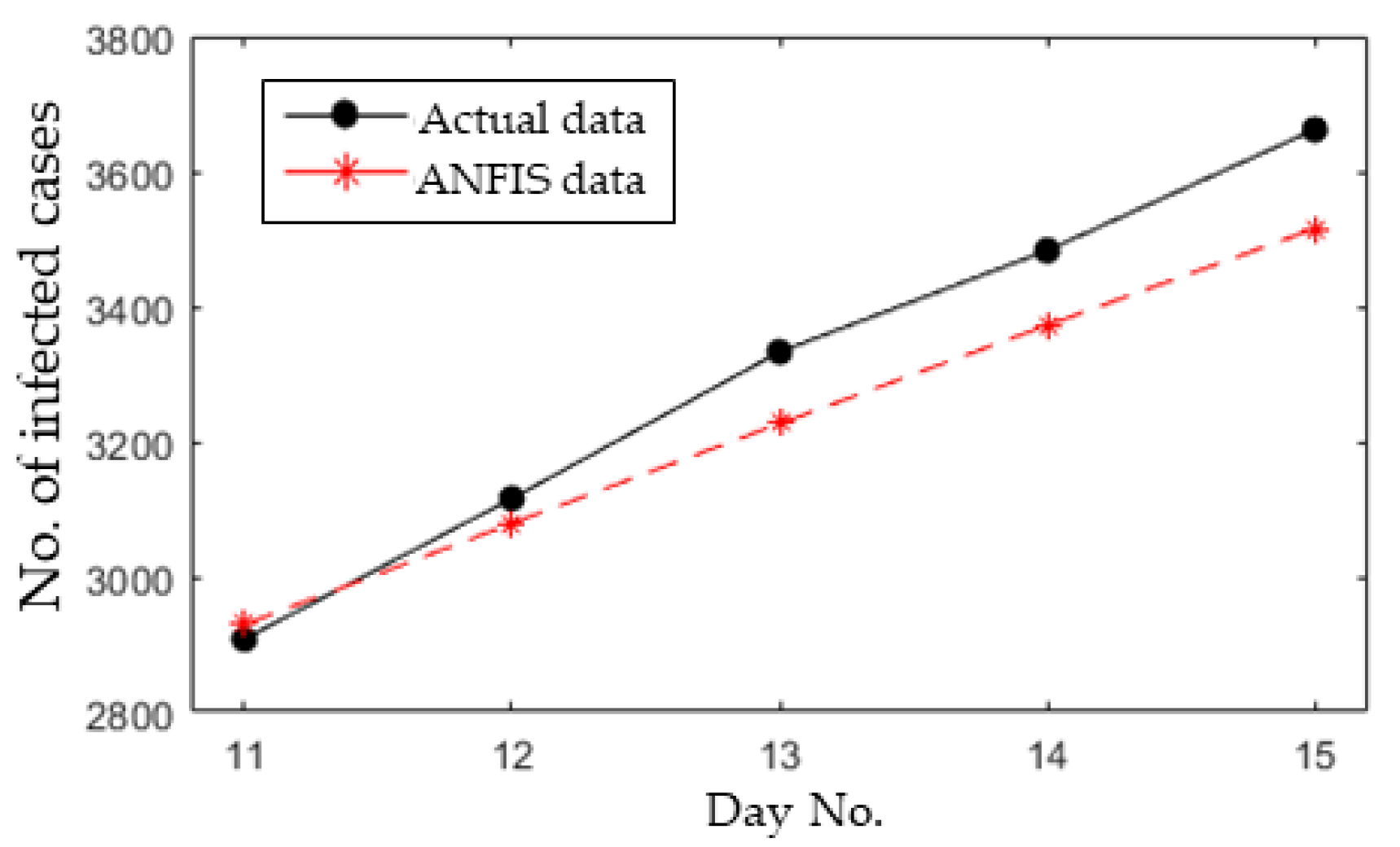
3.4. Short-Term Forecasting
4. Discussion
- The number of people who had contact with COVID-19 patients is enormous, as reported in [48]. This could make the process of tracking and isolating more complex. Based on the information reported by Chinese medical doctors involved in Wuhan, the critical cases form 10% of the total number of infected people. The early diagnosis and treatment would reduce the flow of COVID-19 patients into the ICU unit [49].
- Poor experience in treating and managing cases with different levels of infection. For instance, severe cases should be kept under monitoring with intensive care, while mild cases without clear symptoms should be kept with less intensive care in the hospitals. However, patients under investigation should be placed in special isolation outside the hospitals. This kind of management would ease the treating process with the currently available equipment [50].
- The current MCO implemented in Malaysia is limited to aiding the awareness of the people to the danger of COVID-19. For the first 10 days of the MCO, 60% of the public has obeyed the MCO issued by the government [51]. Thus, more restrictions are needed to enforce the MCO. By increasing the public awareness, the infection rate will be reduced, which would result in decreasing the reproductive number and delaying the epidemic peak.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data availability
Appendix A
References
- Gallego, V.; Nishiura, H.; Sah, R.; Rodriguez-Morales, A.J. The COVID-19 outbreak and implications for the Tokyo 2020 Summer Olympic Games. Travel Med. Infect. Dis. 2020, 34, 101604. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Deng, L.; Zhang, L.; Cai, Y.; Cheung, C.W.; Xia, Z. Review of the clinical characteristics of coronavirus disease 2019 (COVID-19). J. Gen. Intern. Med. 2020, 35, 1545–1549. [Google Scholar] [CrossRef] [PubMed]
- Updates on the Coronavirus Disease 2019 (COVID-19) Situation in Malaysia. Available online: http://www.moh.gov.my/index.php/database_stores/attach_download/337/1378 (accessed on 22 March 2020).
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020, 382, 970–971. [Google Scholar] [CrossRef]
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.M.; Yan, P.; Chowell, G. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: February 13–23, 2020. J. Clin. Med. 2020, 9, 596. [Google Scholar] [CrossRef] [PubMed]
- Guzzetta, G.; Poletti, P.; Ajelli, M.; Trentini, F.; Marziano, V.; Cereda, D.; Tirani, M.; Diurno, G.; Bodina, A.; Barone, A. Potential short-term outcome of an uncontrolled COVID-19 epidemic in Lombardy, Italy, February to March 2020. Eurosurveillance 2020, 25, 2000293. [Google Scholar] [CrossRef]
- Huang, N.E.; Qiao, F. A data driven time-dependent transmission rate for tracking an epidemic: A case study of 2019-nCoV. Sci. Bull. 2020, 65, 425. [Google Scholar] [CrossRef]
- Peng, L.; Yang, W.; Zhang, D.; Zhuge, C.; Hong, L. Epidemic analysis of COVID-19 in China by dynamical modeling. arXiv 2020, arXiv:2002.06563v1. [Google Scholar]
- Tian, S.; Hu, N.; Lou, J.; Chen, K.; Kang, X.; Xiang, Z.; Chen, H.; Wang, D.; Liu, N.; Liu, D. Characteristics of COVID-19 infection in Beijing. J. Infect. 2020, 4, 401–406. [Google Scholar] [CrossRef]
- Qin, L.; Sun, Q.; Wang, Y.; Wu, K.-F.; Chen, M.; Shia, B.-C.; Wu, S.-Y. Prediction of Number of Cases of 2019 Novel Coronavirus (COVID-19) Using Social Media Search Index. Int. J. Environ. Res. Public Health 2020, 17, 2365. [Google Scholar] [CrossRef]
- Kuniya, T. Prediction of the Epidemic Peak of Coronavirus Disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [PubMed]
- Rovetta, A.; Bhagavathula, A.S. Modelling the epidemiological trend and behavior of COVID-19 in Italy. medRxiv 2020. [Google Scholar] [CrossRef]
- Olfatifar, M.; Houri, H.; Shojaee, S.; Pourhoseingholi, M.A.; Al-Ali, W.; Luca, B.; Ashtari, S.; Shahrokh, S.; Vahedian, A.; Asadzadeh Aghdaei, H. The Required Confronting Approaches Efficacy and Time to Control Iranian COVID-19 Outbreak. Arch. Clin. Inf. Dis. 2020, 15, e102633. [Google Scholar] [CrossRef]
- Li, X.; Zhao, X.; Sun, Y. The lockdown of Hubei Province causing different transmission dynamics of the novel coronavirus (2019-nCoV) in Wuhan and Beijing. medRxiv 2020. [Google Scholar] [CrossRef]
- Hu, Z.; Ge, Q.; Jin, L.; Xiong, M. Artificial intelligence forecasting of covid-19 in China. Available online: https://arxiv.org/abs/2002.07112 (accessed on 13 May 2020).
- Li, X.; Xu, B.; Shaman, J. The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus. Int. J. Environ. Res. Public Health 2019, 16, 1890. [Google Scholar] [CrossRef]
- Davidian, M.; Giltinan, D.M. Nonlinear Models for Repeated Measurement Data; CRC Press: Boca Raton, FL, USA, 1995; Volume 62. [Google Scholar]
- Capaldi, A.; Behrend, S.; Berman, B.; Smith, J.; Wright, J.; Lloyd, A.L. Parameter estimation and uncertainty quantication for an epidemic model. Math. Biosci. Eng. 2012, 9, 553–576. [Google Scholar]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Smirnova, A.; deCamp, L.; Chowell, G. Forecasting epidemics through nonparametric estimation of time-dependent transmission rates using the SEIR model. Bull. Math. Biol. 2019, 81, 4343–4365. [Google Scholar] [CrossRef]
- Sun, H.; Qiu, Y.; Yan, H.; Huang, Y.; Zhu, Y.; Chen, S.X. Tracking and Predicting COVID-19 Epidemic in China Mainland. medRxiv 2020, 17, 20. [Google Scholar]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.-M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: A statistical analysis of publicly available case data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef] [PubMed]
- Current Population Estimates, Malaysia, 2018–2019. Available online: https://www.dosm.gov.my/v1/index.php?r=column/cthemeByCat&cat=155&bul_id=aWJZRkJ4UEdKcUZpT2tVT090Snpydz09&menu_id=L0pheU43NWJwRWVSZklWdzQ4TlhUUT09 (accessed on 20 March 2020).
- Covid-19: Malaysia to Receive New Test Kit from South Korea. Available online: https://www.thestar.com.my/news/nation/2020/04/05/covid-19-malaysia-to-receive-new-test-kit-from-south-korea (accessed on 12 April 2020).
- Latest COVID-19 Statistic in Malaysia by MOH. Available online: http://www.moh.gov.my/index.php/pages/view/2019-ncov-wuhan (accessed on 25 March 2020).
- Jung, S.-M.; Akhmetzhanov, A.R.; Hayashi, K.; Linton, N.M.; Yang, Y.; Yuan, B.; Kobayashi, T.; Kinoshita, R.; Nishiura, H. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: Inference using exported cases. J. Clin. Med. 2020, 9, 523. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.H. Notes on R0; Department of Anthropological Sciences: Stanford, CA, USA, 2007. [Google Scholar]
- Tuncer, N.; Gulbudak, H.; Cannataro, V.L.; Martcheva, M. Structural and practical identifiability issues of immuno-epidemiological vector–host models with application to rift valley fever. Bull. Math. Biol. 2016, 78, 1796–1827. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, F.; Isa, N.A.M.; Osman, M.K.; Hussain, Z. Performance comparison of gradient descent and Genetic Algorithm based Artificial Neural Networks training. In Proceedings of the 2010 10th International Conference on Intelligent Systems Design and Applications, Cairo, Egypt, 29 November–1 December 2010; pp. 604–609. [Google Scholar]
- Sorsa, A.; Peltokangas, R.; Leiviska, K. Real-coded genetic algorithms and nonlinear parameter identification. In Proceedings of the 2008 4th International IEEE Conference Intelligent Systems, Varna, Bulgaria, 6–8 September 2008; pp. 10–42. [Google Scholar]
- Kilinc, M.; Caicedo, J.M. Finding Plausible Optimal Solutions in Engineering Problems Using an Adaptive Genetic Algorithm. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.; Mansor, Z. Identifying the most significant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Dashti, A.; Asghari, M.; Shirazian, S. H2-selective mixed matrix membranes modeling using ANFIS, PSO-ANFIS, GA-ANFIS. Int. J. Hydrog. Energy 2017, 42, 15211–15225. [Google Scholar] [CrossRef]
- Yi, H.-S.; Park, S.; An, K.-G.; Kwak, K.-C. Algal bloom prediction using extreme learning machine models at artificial weirs in the Nakdong River, Korea. Int. J. Environ. Res. Public Health 2018, 15, 2078. [Google Scholar] [CrossRef] [PubMed]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
- Piepho, H.P. A coefficient of determination (R2) for generalized linear mixed models. Biom. J. 2019, 61, 860–872. [Google Scholar] [CrossRef]
- Coronavirus Disease 2019 (COVID-19) Situation Report–46. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200306-sitrep-46-covid-19.pdf?sfvrsn=96b04adf_2 (accessed on 20 March 2020).
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef]
- Majumder, M.; Mandl, K.D. Early transmissibility assessment of a novel coronavirus in Wuhan, China. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Zhang, S.; Diao, M.; Yu, W.; Pei, L.; Lin, Z.; Chen, D. Estimation of the reproductive number of Novel Coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int. J. Infect. Dis. 2020, 93, 201–204. [Google Scholar] [CrossRef]
- Liu, Y.; Gayle, A.A.; Wilder-Smith, A.; Rocklöv, J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020, 27, 1–4. [Google Scholar]
- Liu, T.; Hu, J.; Kang, M.; Lin, L.; Zhong, H.; Xiao, J.; He, G.; Song, T.; Huang, Q.; Rong, Z. Transmission dynamics of 2019 novel coronavirus (2019-nCoV). bioRexiv 2020, 1, 919787. [Google Scholar] [CrossRef]
- Read, J.M.; Bridgen, J.R.; Cummings, D.A.; Ho, A.; Jewell, C.P. Novel coronavirus 2019-nCoV: Early estimation of epidemiological parameters and epidemic predictions. MedRxiv 2020. (preprint). [Google Scholar] [CrossRef]
- It’s a ‘False Hope’ Coronavirus Will Disappear in the Summer Like the Flu. Available online: https://www.msn.com/en-us/health/health-news/its-a-false-hope-coronavirus-will-disappear-in-the-summer-like-the-flu-who-says/ar-BB10QrLc (accessed on 12 March 2020).
- Efforts to Contain Covid-19 No Longer Possible. Available online: https://www.nst.com.my/news/nation/2020/03/575003/efforts-contain-covid-19-no-longer-possible-dr-lee (accessed on 16 March 2020).
- Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19). Available online: https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf (accessed on 12 March 2020).
- World Health Organization. Clinical Management of Severe Acute Respiratory Infection (SARI) When COVID-19 Disease Is Suspected: Interim Guidance, 13 March 2020; World Health Organization: Geneva, Switzerland, 2020.
- Only 60pc Complied with MCO; Police May Take Sterner Action. Available online: https://www.malaymail.com/news/malaysia/2020/03/19/ismail-sabri-four-in-10-malaysians-violating-movement-control-order/1848077/ (accessed on 19 March 2020).
- Gilliland, M. The Business Forecasting Deal: Exposing Myths, Eliminating Bad Practices, Providing Practical Solutions; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 27. [Google Scholar]

| Coefficient | Description | Value |
|---|---|---|
| α | Onset rate | 0.2 |
| γ | Removal rate | 0.1 |
| M | Mortality rate | 0.016 |
| N | Malaysia population | 32.6 × 106 |
| p | Identification rate | 0.084 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Population size | 200 | Mutation rate | 0.02 |
| Number of iterations | 1000 | Mutation percentage | 0.9 |
| Crossover percentage | 0.95 |
| Parameter | Method/Value | Parameter | Method/Value |
|---|---|---|---|
| Fuzzy structure | Sugeno-type | No. of epochs | 300 |
| Rules clustering | Grid partition | Input | Day number |
| MF type | Gaussian | Output | Infected cases |
| Optimization method | Hybrid | Output MF | constant |
| Parameter | Training Data | Testing Dataset |
|---|---|---|
| RMSE | 18.53 | 46.87 |
| NRMSE | 0.012 | 0.032 |
| MAPE | 1.31% | 2.79% |
| R2 | 0.9973 | 0.9998 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsayed, A.; Sadir, H.; Kamil, R.; Sari, H. Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020. Int. J. Environ. Res. Public Health 2020, 17, 4076. https://doi.org/10.3390/ijerph17114076
Alsayed A, Sadir H, Kamil R, Sari H. Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020. International Journal of Environmental Research and Public Health. 2020; 17(11):4076. https://doi.org/10.3390/ijerph17114076
Chicago/Turabian StyleAlsayed, Abdallah, Hayder Sadir, Raja Kamil, and Hasan Sari. 2020. "Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020" International Journal of Environmental Research and Public Health 17, no. 11: 4076. https://doi.org/10.3390/ijerph17114076
APA StyleAlsayed, A., Sadir, H., Kamil, R., & Sari, H. (2020). Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020. International Journal of Environmental Research and Public Health, 17(11), 4076. https://doi.org/10.3390/ijerph17114076





