Analyzing the Effect of Government Subsidy on the Development of the Remanufacturing Industry
Abstract
1. Introduction
2. Literature Review
3. Model Setting
3.1. Government
3.2. OEM
3.3. Consumers
4. Model Analysis
4.1. Setting 1: Only Remanufactured Products Exist in the Market
4.1.1. The Government Does Not Have a Budget Constraint
4.1.2. The Government Has a Budget Constraint
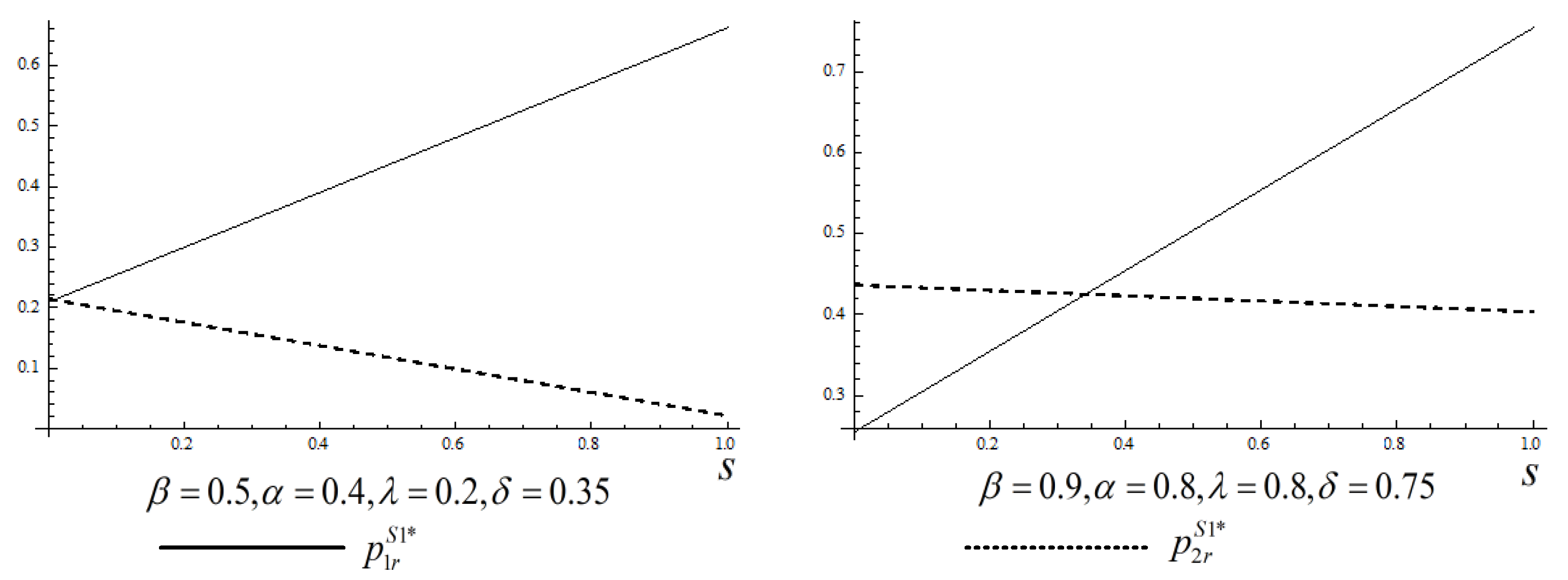
4.2. Setting 2: New and Remanufactured Products Coexist in the Market
4.2.1. The Government Does Not Have a Budget Constraint
4.2.2. The Government Has a Budget Constraint
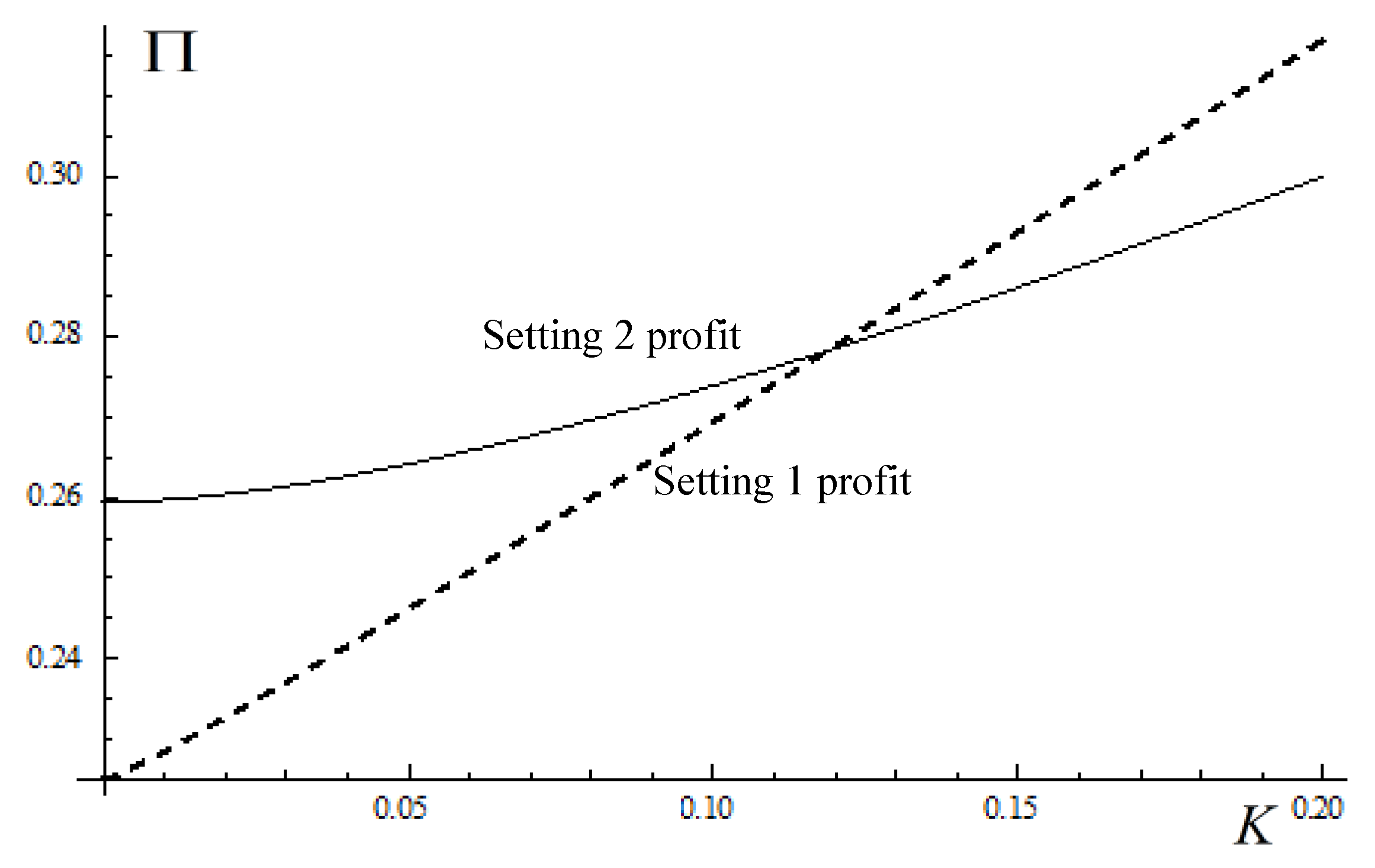
5. Discussion on Government Subsidy with a Budget Constraint
6. Managerial Implications
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Agrawal, V.V.; Atasu, A.; Van Wassenhove, L.N. OM Forum—New opportunities for operations management research in sustainability. Manuf. Serv. Oper. Manag. 2019, 21, 1–12. [Google Scholar] [CrossRef]
- Yang, M.; Smart, P.; Kumar, M.; Jolly, M.; Evans, S. Product-service systems business models for circular supply chains. Prod. Plan. Control 2018, 29, 498–508. [Google Scholar] [CrossRef]
- Guide, V.D.R.; Harrison, T.P.; Van Wassenhove, L.N. The challenge of closed-loop supply chains. Interfaces 2003, 33, 3–6. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Geyer, R.; Van Wassenhove, L.N.; Atasu, A. The economics of remanufacturing under limited component durability and finite product life cycles. Manag. Sci. 2007, 53, 88–100. [Google Scholar] [CrossRef]
- Giutini, R.; Gaudette, K. Remanufacturing: The next great opportunity for boosting US productivity. Bus. Horiz. 2003, 46, 41–48. [Google Scholar] [CrossRef]
- Atasu, A.; Sarvary, M.; Van Wassenhove, L.N. Remanufacturing as a marketing strategy. Manag. Sci. 2008, 54, 1731–1746. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Deng, H.; Keong Leong, G.; Huang, T. A dual channel, quality-based price competition model for the WEEE recycling market with government subsidy. Omega 2016, 59, 290–302. [Google Scholar] [CrossRef]
- Debo, L.G.; Toktay, L.B.; Van Wassenhove, L.N. Market segmentation and product technology selection for remanufacturable products. Manag. Sci. 2005, 51, 1193–1205. [Google Scholar] [CrossRef]
- Guide, V.D.R.; Muyldermans, L.; Van Wassenhove, L.N. Hewlett-packard company unlocks the value potential from time-sensitive returns. Interfaces 2005, 35, 281–293. [Google Scholar] [CrossRef][Green Version]
- Abbey, J.D.; Meloy, M.G.; Guide, V.D.R.; Atalay, S. Remanufactured products in closed-loop supply chains for consumer goods. Prod. Oper. Manag. 2015, 24, 488–503. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, Y. Does the entry of third-party remanufacturers always hurt original equipment manufacturers? Decis. Sci. 2016, 47, 762–780. [Google Scholar] [CrossRef]
- NDRC. Notice on Initiating the Pilot Program of ‘‘Trade Old for Remanufactured” for Remanufactured Products. 2013. Available online: https://www.ndrc.gov.cn/fggz/tzgg/ggkx/201309/t20130901_1070296.html (accessed on 19 May 2020).
- NDRC. Announcement on the Qualified Pilot Enterprises, Product Models and Promotional Price for Promoting Remanufacturing Products (Remanufactured Automobile Engine and Gearbox). 2015. Available online: https://www.ndrc.gov.cn/xwdt/dt/sjdt/201507/t20150701_1130482.html (accessed on 19 May 2020).
- Huang, Y.; Gokpinar, B.; Tang, C.S.; Yoo, O.S. Selling innovative products in the presence of externalities. Prod. Oper. Manag. 2018, 27, 1236–1250. [Google Scholar] [CrossRef]
- Jacobsen, N.B. Industrial symbiosis in Kalundborg, Denmark: A quantitative assessment of economic and environmental aspects. J. Ind. Ecol. 2008, 10, 239–255. [Google Scholar] [CrossRef]
- Agrawal, V.V.; Ülkü, S. The role of modular upgradability as a green design strategy. Manuf. Serv. Oper. Manag. 2013, 15, 640–648. [Google Scholar] [CrossRef]
- Agrawal, V.V.; Bellos, I. The potential of servicizing as a green business model. Manag. Sci. 2017, 63, 1545–1562. [Google Scholar] [CrossRef]
- Guo, R.; Lee, H.L.; Swinney, R. Responsible sourcing in supply chains. Manag. Sci. 2016, 62, 2722–2744. [Google Scholar] [CrossRef]
- Alizadeh-Basban, N.; Taleizadeh, A.A. A hybrid circular economy—Game theoretical approach in a dual-channel green supply chain considering sale’s effort, delivery time, and hybrid remanufacturing. J. Clean. Prod. 2020, 250, 119521. [Google Scholar] [CrossRef]
- Miao, Z.; Mao, H.; Fu, K.; Wang, Y. Remanufacturing with trade-ins under carbon regulations. Comput. Oper. Res. 2016, 89, 253–268. [Google Scholar] [CrossRef]
- Alev, I.; Agrawal, V.V.; Atasu, A. Extended producer responsibility for durable products. Manuf. Serv. Oper. Manag. 2020, 22, 364–382. [Google Scholar] [CrossRef]
- Lobel, R.; Perakis, G. Consumer choice model for forecasting demand and designing incentives for solar technology. Work. Pap. 2011. Available online: http://ssrn.com/abstract=1748424 (accessed on 19 May 2020).
- Krass, D.; Nedorezov, T.; Ovchinnikov, A. Environmental taxes and the choice of green technology. Prod. Oper. Manag. 2013, 22, 1035–1055. [Google Scholar] [CrossRef]
- Taylor, T.A.; Xiao, W. Subsidizing the distribution channel: Donor funding to improve the availability of malaria drugs. Manag. Sci. 2014, 60, 2461–2477. [Google Scholar] [CrossRef]
- Cohen, M.C.; Lobel, R.; Perakis, G. The impact of demand uncertainty on consumer subsidies for green technology adoption. Manag. Sci. 2016, 62, 1235–1258. [Google Scholar] [CrossRef]
- Levi, R.; Perakis, G.; Romero, G. On the effectiveness of uniform subsidies in increasing market consumption. Manag. Sci. 2017, 63, 40–57. [Google Scholar] [CrossRef]
- Yu, J.J.; Tang, C.S.; Shen, Z.-J.M. Improving consumer welfare and manufacturer profit via government subsidy programs: Subsidizing consumers or manufacturers? Manuf. Serv. Oper. Manag. 2018, 20, 752–766. [Google Scholar] [CrossRef]
- Yu, J.J.; Tang, C.S.; Sodhi, M.S.; Knuckles, J. Optimal subsidies for development supply chains. Manuf. Serv. Oper. Manag. 2019. [Google Scholar] [CrossRef]
- Zhu, X.; Ren, M.; Chu, W.; Chiong, R. Remanufacturing subsidy or carbon regulation? An alternative toward sustainable production. J. Clean. Prod. 2019, 239, 117988. [Google Scholar] [CrossRef]
- Cao, J.; Chen, X.; Zhang, X.; Gao, Y.; Zhang, X.; Kumar, S. Overview of remanufacturing industry in China: Government policies, enterprise, and public awareness. J. Clean. Prod. 2020, 242, 118450. [Google Scholar] [CrossRef]
- Hu, X.; Yang, Z.; Sun, J.; Zhang, Y. Carbon tax or cap-and-trade: Which is more viable for Chinese remanufacturing industry? J. Clean. Prod. 2020, 243, 118606. [Google Scholar] [CrossRef]
- Katz, M.L.; Shapiro, C. Network externalities, competition, and compatibility. Am. Econ. Rev. 1985, 75, 424–440. [Google Scholar]
- Candogan, O.; Bimpikis, K.; Ozdaglar, A. Optimal pricing in networks with externalities. Oper. Res. 2012, 60, 883–905. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Z. Consumer choice models with endogenous network effects. Manag. Sci. 2017, 63, 3944–3960. [Google Scholar] [CrossRef]
- Gao, S.Y.; Lim, W.S.; Tang, C.S. Entry of copycats of luxury brands. Mark. Sci. 2017, 36, 272–289. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Guide, V.D.R., Jr.; Li, J. The potential for cannibalization of new products sales by remanufactured products. Decis. Sci. 2010, 41, 547–572. [Google Scholar] [CrossRef]
- Subramanian, R.; Subramanyam, R. Key factors in the market for remanufactured products. Manuf. Serv. Oper. Manag. 2012, 14, 315–326. [Google Scholar] [CrossRef]
- Yan, X.; Chao, X.; Lu, Y.; Zhou, S.X. Optimal policies for selling new and remanufactured products. Prod. Oper. Manag. 2017, 26, 1746–1759. [Google Scholar] [CrossRef]
- Ma, Z.-J.; Zhou, Q.; Dai, Y.; Sheu, J.-B. Optimal pricing decisions under the coexistence of “trade old for new” and “trade old for remanufactured” programs. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 337–352. [Google Scholar] [CrossRef]
- Ma, Z.-J.; Zhou, Q.; Dai, Y.; Guan, G.-F. To license or not to license remanufacturing business? Sustainability 2018, 10, 347. [Google Scholar] [CrossRef]
- Aaker, J.; Fournier, S.; Brasel, S.A. When good brands do bad. J. Consum. Res. 2004, 31, 1–16. [Google Scholar] [CrossRef]
- Ovchinnikov, A. Revenue and cost management for remanufactured products. Prod. Oper. Manag. 2011, 20, 824–840. [Google Scholar] [CrossRef]
- Gromet, D.M.; Kunreuther, H.; Larrick, R.P. Political ideology affects energy-efficiency attitudes and choices. Proc. Natl. Acad. Sci. USA 2013, 110, 9314–9319. [Google Scholar] [CrossRef]
- Souza, G.C. Closed-loop supply chains: A critical review, and future research. Decis. Sci. 2013, 44, 7–38. [Google Scholar] [CrossRef]
- Majumder, P.; Groenevelt, H. Competition in remanufacturing. Prod. Oper. Manag. 2001, 10, 125–141. [Google Scholar] [CrossRef]
- Vorasayan, J.; Ryan, S.M. Optimal price and quantity of refurbished products. Prod. Oper. Manag. 2009, 15, 369–383. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing new and remanufactured products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y. Optimal policies for new and green remanufactured short-life-cycle products considering consumer behavior. J. Clean. Prod. 2019, 214, 483–505. [Google Scholar] [CrossRef]
- Wu, L.; Liu, L.; Wang, Z. Competitive remanufacturing and pricing strategy with contrast effect and assimilation effect. J. Clean. Prod. 2020, 257, 120333. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Yuen, K.F. Analyzing the Effect of Government Subsidy on the Development of the Remanufacturing Industry. Int. J. Environ. Res. Public Health 2020, 17, 3550. https://doi.org/10.3390/ijerph17103550
Zhou Q, Yuen KF. Analyzing the Effect of Government Subsidy on the Development of the Remanufacturing Industry. International Journal of Environmental Research and Public Health. 2020; 17(10):3550. https://doi.org/10.3390/ijerph17103550
Chicago/Turabian StyleZhou, Qin, and Kum Fai Yuen. 2020. "Analyzing the Effect of Government Subsidy on the Development of the Remanufacturing Industry" International Journal of Environmental Research and Public Health 17, no. 10: 3550. https://doi.org/10.3390/ijerph17103550
APA StyleZhou, Q., & Yuen, K. F. (2020). Analyzing the Effect of Government Subsidy on the Development of the Remanufacturing Industry. International Journal of Environmental Research and Public Health, 17(10), 3550. https://doi.org/10.3390/ijerph17103550





