Artificial Intelligence-Empowered Mobilization of Assessments in COVID-19-like Pandemics: A Case Study for Early Flattening of the Curve
Abstract
1. Introduction
2. Background and Motivation
3. AI-Empowered Preparedness for Pandemic Outbreaks
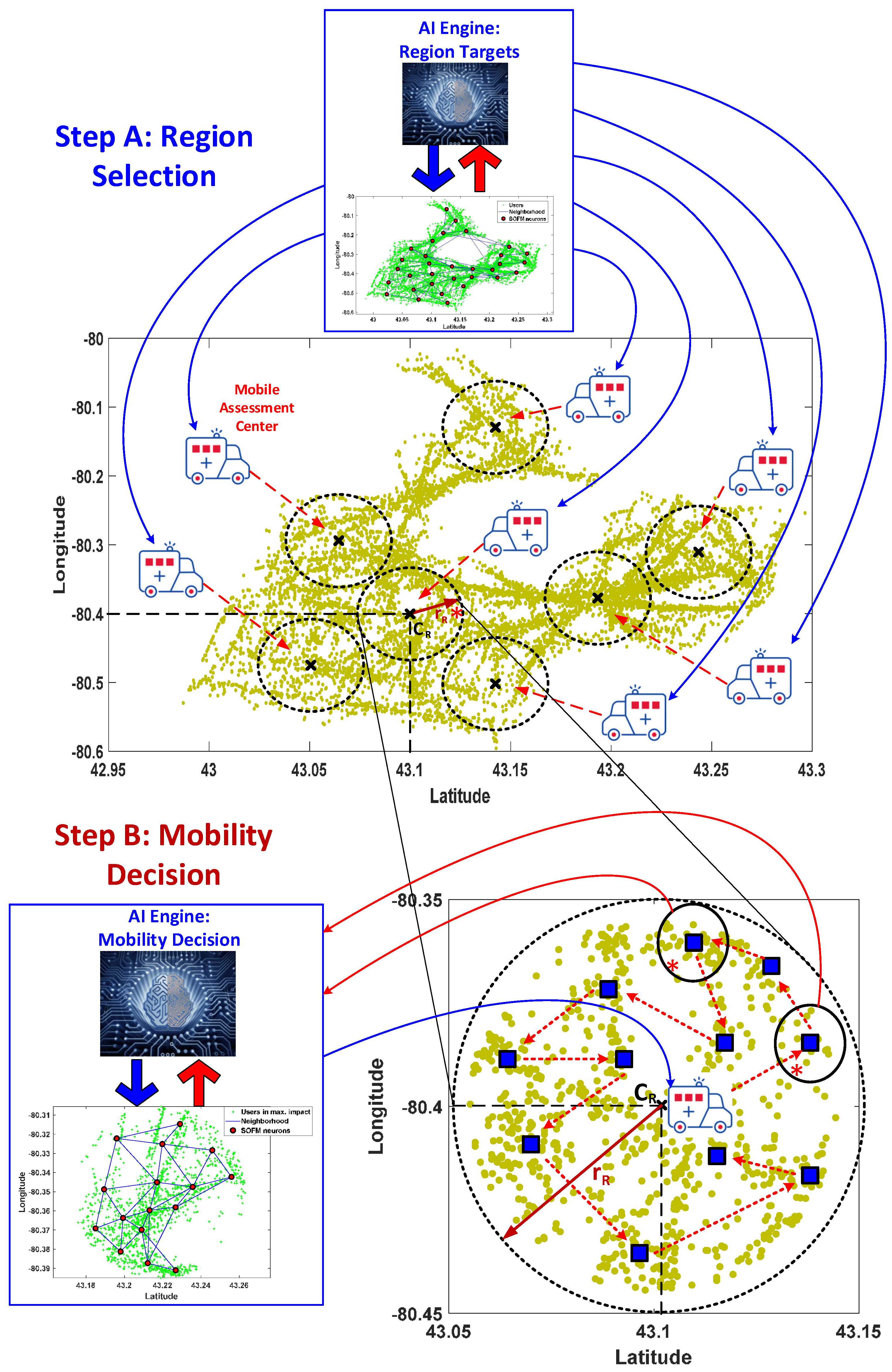
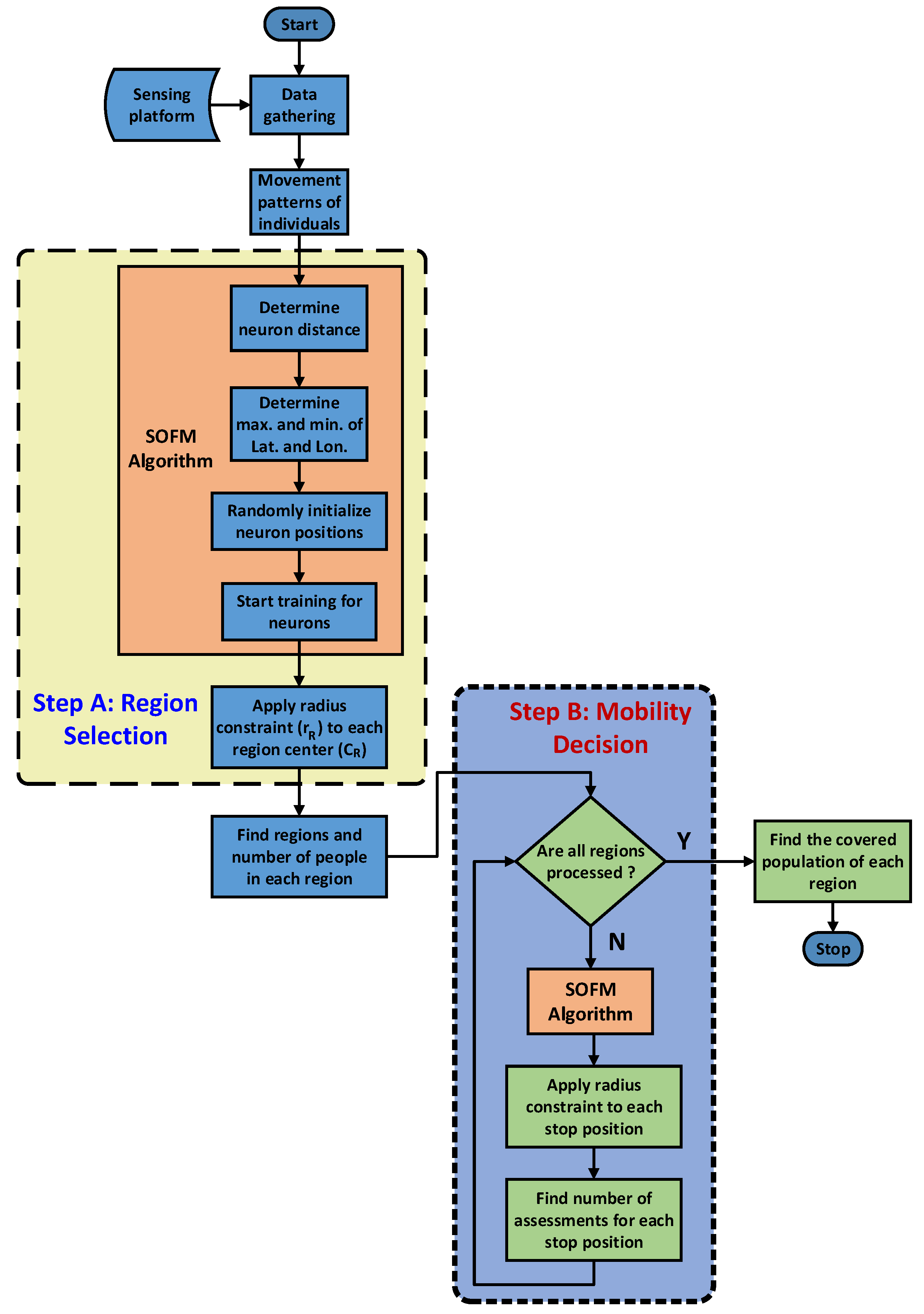
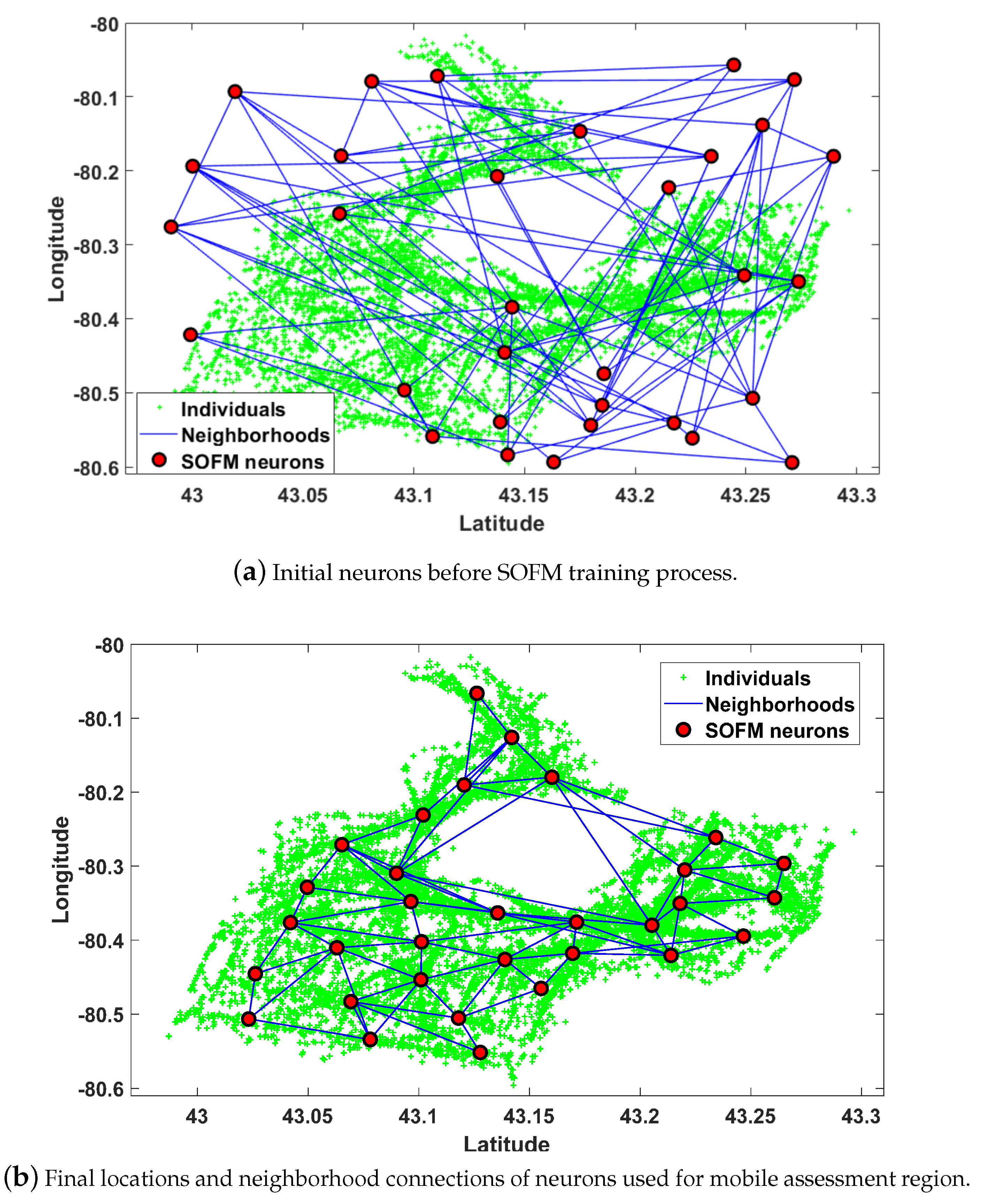
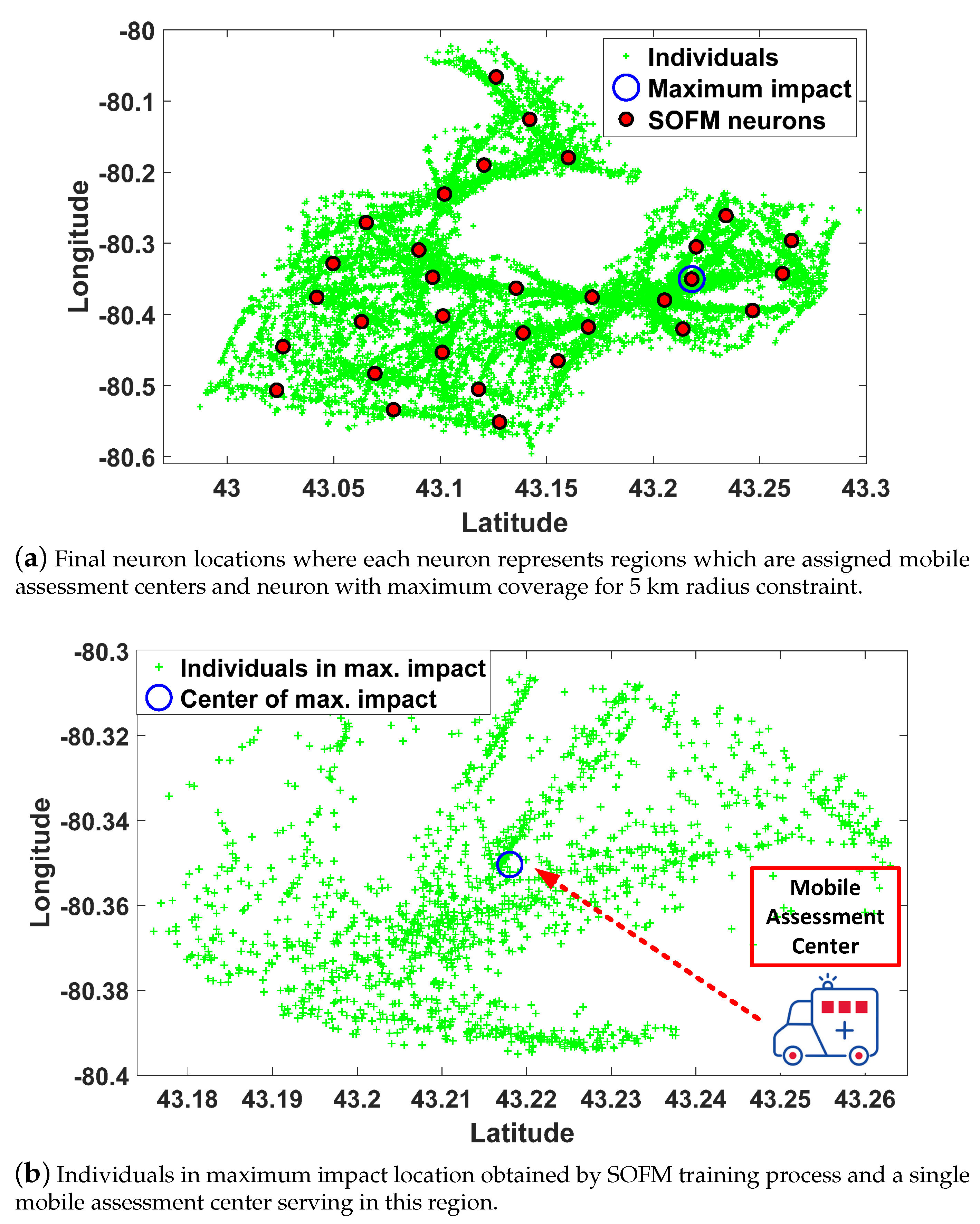
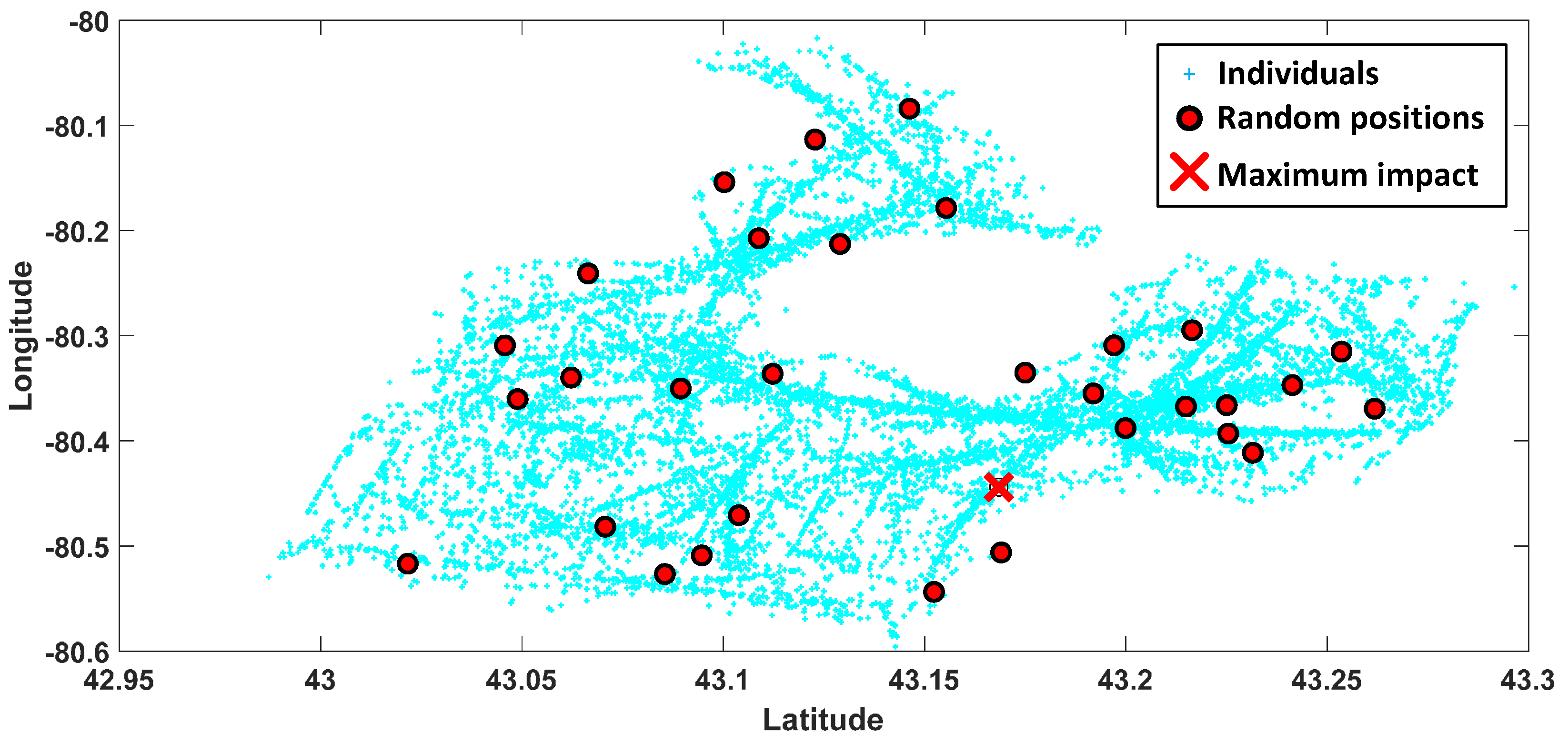
3.1. Step A: Region Selection
3.2. Step B: Mobility Decision
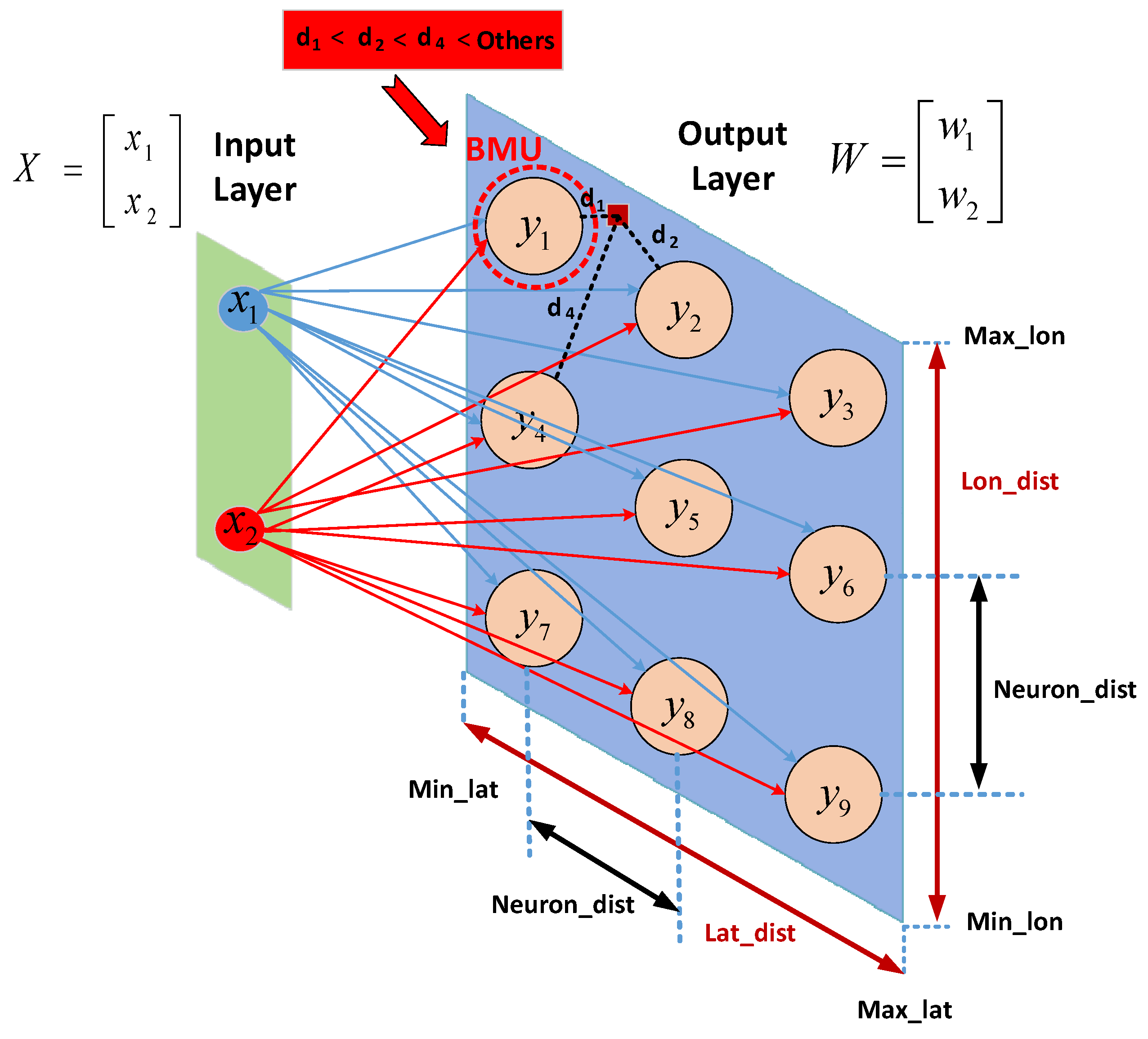
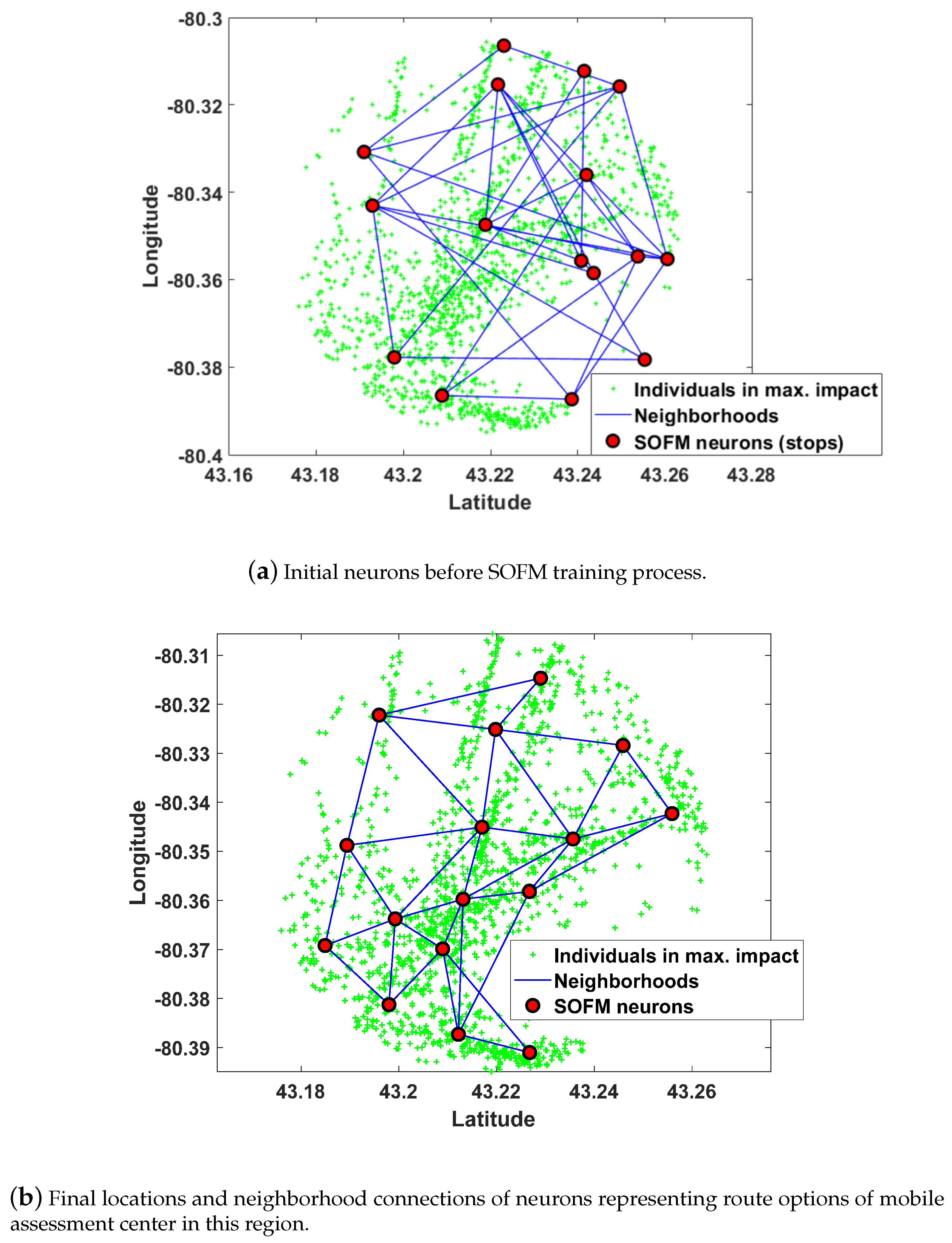
3.3. Self Organizing Feature Map for Route Planning
4. Simulation Settings for COVID-19
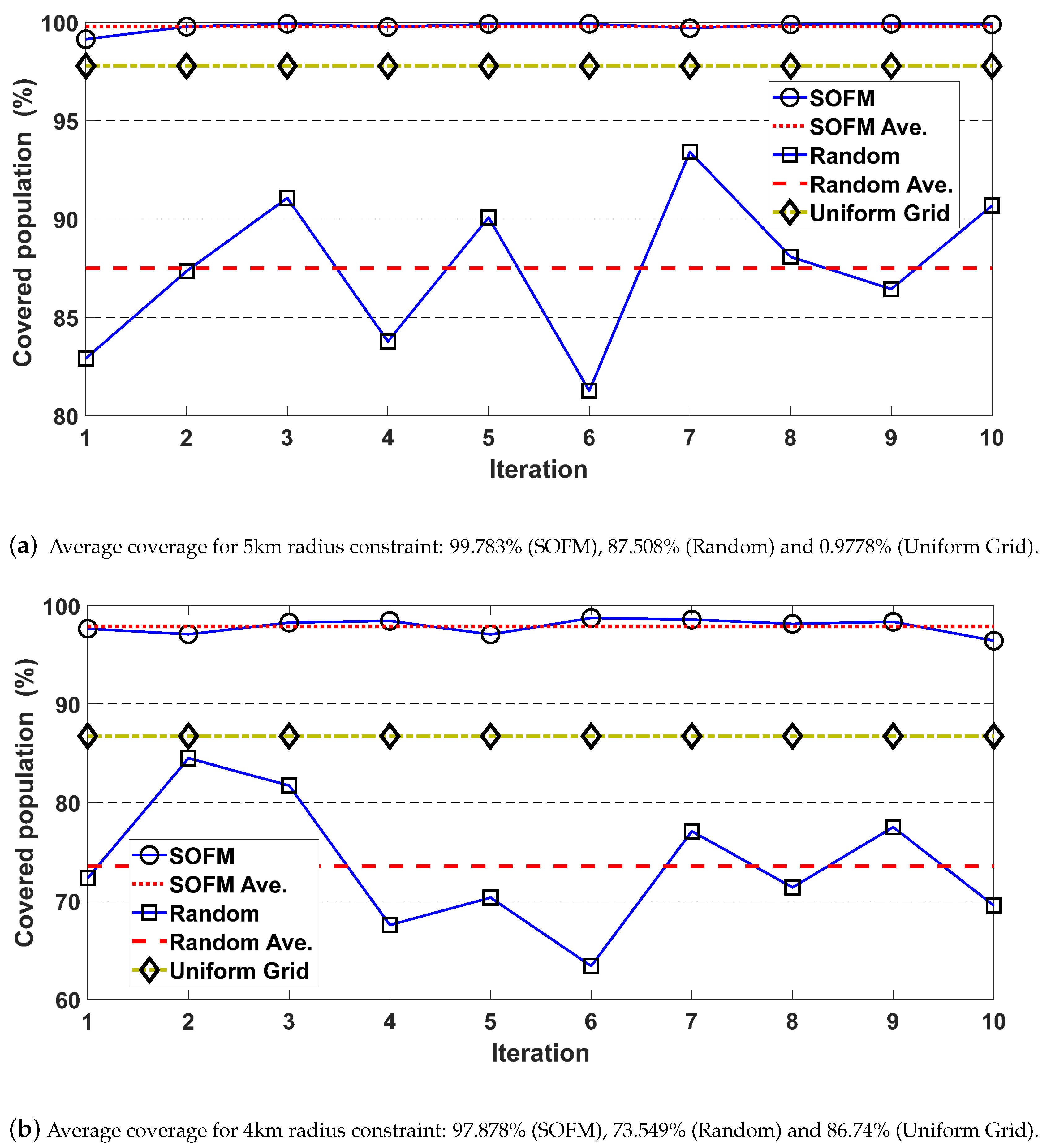
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, H.; Liu, S.M.; Yu, X.H.; Tang, S.L.; Tang, C.K. Coronavirus disease 2019 (COVID-19): Current status and future perspective. Int. J. Antimicrob. Agents 2020, 105951. [Google Scholar] [CrossRef] [PubMed]
- Shim, E.; Tariq, A.; Choi, W.; Lee, Y.; Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Wood, D.A.; Sathananthan, J.; Gin, K.; Mansour, S.; Ly, H.Q.; ur Rehman Quraishi, A.; Lavoie, A.; Lutchmedial, S.; Nosair, M.; Bagai, A.; et al. Precautions and Procedures for Coronary and Structural Cardiac Interventions during the COVID-19 Pandemic: Guidance from Canadian Association of Interventional Cardiology. Can. J. Cardiol. 2020, 36, 780–783. [Google Scholar] [CrossRef] [PubMed]
- Woodul, R.L.; Delamater, P.L.; Emch, M. Hospital surge capacity for an influenza pandemic in the triangle region of North Carolina. Spat. Spatio-Temporal Epidemiol. 2019, 30, 100285. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101922. [Google Scholar] [CrossRef] [PubMed]
- Panovska-Griffiths, J.; Grieco, L.; van Leeuwen, E.; Baguelin, M.; Pebody, R.; Utley, M. Are we prepared for the next influenza pandemic? Lessons from modelling different preparedness policies against four pandemic scenarios. J. Theor. Biol. 2019, 481, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Hsih, W.H.; Cheng, M.Y.; Ho, M.W.; Chou, C.H.; Lin, P.C.; Chi, C.Y.; Liao, W.C.; Chen, C.Y.; Leong, L.Y.; Tien, N.; et al. Featuring COVID-19 cases via screening symptomatic patients with epidemiologic link during flu season in a medical center of central Taiwan. J. Microbiol. Immunol. Infect. 2020. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, B.S.; Steiner, M.T.A.; Fenerich, A.T.; Lima, R.H.P. Data mining and machine learning techniques applied to public health problems: A bibliometric analysis from 2009 to 2018. Comput. Ind. Eng. 2019, 138, 106120. [Google Scholar] [CrossRef]
- Nishiura, H.; Kobayashi, T.; Suzuki, A.; Jung, S.M.; Hayashi, K.; Kinoshita, R.; Yang, Y.; Yuan, B.; Akhmetzhanov, A.R.; Linton, N.M.; et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef] [PubMed]
- Bellavista, P.; De Benedetto, J.; De Rolt, C.R.; Foschini, L.; Montanari, R. LTE proximity discovery for supporting participatory mobile health communities. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhang, Y.; Simsek, M.; Kantarci, B. Self Organizing Feature Map for Fake Task Attack Modelling in Mobile Crowdsensing. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Panovska-Griffiths, J.; Grieco, L.; van Leeuwen, E.; Grove, P.; Utley, M. A method for evaluating the cost-benefit of different preparedness planning policies against pandemic influenza. MethodsX 2020, 100870. [Google Scholar] [CrossRef] [PubMed]
- Chavez, S.; Long, B.; Koyfman, A.; Liang, S.Y. Coronavirus Disease (COVID-19): A primer for emergency physicians. Am. J. Emerg. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Neill, D.B. New Directions in Artificial Intelligence for Public Health Surveillance. IEEE Intell. Syst. 2012, 27, 56–59. [Google Scholar] [CrossRef]
- Agrebi, S.; Larbi, A. Chapter 18—Use of artificial intelligence in infectious diseases. In Artificial Intelligence in Precision Health; Barh, D., Ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 415–438. [Google Scholar]
- Bruzzone, A.G.; Massei, M.; Madeo, F.; Tarone, F.; Petuhova, J. Intelligent Agents for Pandemic Modeling. In Proceedings of the 2011 Emerging M&S Applications in Industry and Academia Symposium; Society for Computer Simulation International: San Diego, CA, USA, 2011; pp. 23–30. [Google Scholar]
- Wong, Z.S.; Zhou, J.; Zhang, Q. Artificial Intelligence for infectious disease Big Data Analytics. Infect. Dis. Health 2019, 24, 44–48. [Google Scholar] [CrossRef]
- Somanchi, S.; Neill, D.B. Graph Structure Learning from Unlabeled Data for Early Outbreak Detection. IEEE Intell. Syst. 2017, 32, 80–84. [Google Scholar] [CrossRef]
- Jiang, D.; Hao, M.; Ding, F.; Fu, J.; Li, M. Mapping the transmission risk of Zika virus using machine learning models. Acta Trop. 2018, 185, 391–399. [Google Scholar] [CrossRef]
- Jia, W.; Li, X.; Tan, K.; Xie, G. Predicting the outbreak of the hand-foot-mouth diseases in China using recurrent neural network. In Proceedings of the 2019 IEEE International Conference on Healthcare Informatics (ICHI), Xi’an, China, 10–13 June 2019; pp. 1–4. [Google Scholar]
- Xia, H.; Nagaraj, K.; Chen, J.; Marathe, M.V. Synthesis of a high resolution social contact network for Delhi with application to pandemic planning. Artif. Intell. Med. 2015, 65, 113–130. [Google Scholar] [CrossRef]
- Nieto-Chaupis, H. Face To Face with Next Flu Pandemic with a Wiener-Series-Based Machine Learning: Fast Decisions to Tackle Rapid Spread. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 7–9 January 2019; pp. 0654–0658. [Google Scholar]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Kohonen, T. Exploration of very large databases by self-organizing maps. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; Volume 1, pp. PL1–PL6. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Moler, C. COVID-19 Simulator. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/59085-cleve_lab (accessed on 30 March 2020).
- Fiandrino, C.; Capponi, A.; Cacciatore, G.; Kliazovich, D.; Sorger, U.; Bouvry, P.; Kantarci, B.; Granelli, F.; Giordano, S. CrowdSenSim: A simulation platform for mobile crowdsensing in realistic urban environments. IEEE Access 2017, 5, 3490–3503. [Google Scholar] [CrossRef]


| Types of Individuals | Explanation |
| Mobile | Susceptible, on the move |
| Static | Susceptible, stay at home |
| Infected | Infects other susceptible individuals within distance "radius" |
| Immune | Was infected for "duration" steps. No longer infectious |
| Controllable Parameters | Explanation |
| n = 1566 | population size |
| infected = 0.001 | initial infected fraction of population |
| static = 0.20 | static individuals ratio |
| radius = 0.03 | infectious distance |
| duration = 200 days | time of infection |
| speed = 0.03 | spread speed |
| barrier = 0.0 | barrier height |
| Day | Mobile | Static | Infected | Immune |
|---|---|---|---|---|
| 0 | 1252 | 313 | 1 | 0 |
| 1 | 1251 | 313 | 2 | 0 |
| 2 | 1250 | 313 | 3 | 0 |
| 3 | 1249 | 313 | 4 | 0 |
| 4 | 1248 | 313 | 5 | 0 |
| 5 | 1246 | 312 | 8 | 0 |
| 6 | 1243 | 311 | 12 | 0 |
| 7 | 1237 | 309 | 20 | 0 |
| 8 | 1228 | 306 | 32 | 0 |
| 9 | 1222 | 303 | 41 | 0 |
| 10 | 1216 | 302 | 48 | 0 |
| 11 | 1209 | 301 | 56 | 0 |
| 12 | 1201 | 299 | 66 | 0 |
| 13 | 1196 | 297 | 73 | 0 |
| 14 | 1181 | 296 | 89 | 0 |
| 15 | 1168 | 293 | 105 | 0 |
| 16 | 1158 | 293 | 115 | 0 |
| 17 | 1145 | 288 | 133 | 0 |
| 18 | 1132 | 288 | 146 | 0 |
| 19 | 1120 | 282 | 164 | 0 |
| 20 | 1098 | 277 | 191 | 0 |
| 21 | 1077 | 274 | 215 | 0 |
| 22 | 1056 | 273 | 237 | 0 |
| 23 | 1043 | 271 | 252 | 0 |
| 24 | 1026 | 263 | 277 | 0 |
| 25 | 1005 | 263 | 298 | 0 |
| 26 | 981 | 261 | 324 | 0 |
| 27 | 966 | 258 | 342 | 0 |
| 28 | 943 | 256 | 367 | 0 |
| 29 | 928 | 252 | 386 | 0 |
| 30 | 914 | 248 | 404 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simsek, M.; Kantarci, B. Artificial Intelligence-Empowered Mobilization of Assessments in COVID-19-like Pandemics: A Case Study for Early Flattening of the Curve. Int. J. Environ. Res. Public Health 2020, 17, 3437. https://doi.org/10.3390/ijerph17103437
Simsek M, Kantarci B. Artificial Intelligence-Empowered Mobilization of Assessments in COVID-19-like Pandemics: A Case Study for Early Flattening of the Curve. International Journal of Environmental Research and Public Health. 2020; 17(10):3437. https://doi.org/10.3390/ijerph17103437
Chicago/Turabian StyleSimsek, Murat, and Burak Kantarci. 2020. "Artificial Intelligence-Empowered Mobilization of Assessments in COVID-19-like Pandemics: A Case Study for Early Flattening of the Curve" International Journal of Environmental Research and Public Health 17, no. 10: 3437. https://doi.org/10.3390/ijerph17103437
APA StyleSimsek, M., & Kantarci, B. (2020). Artificial Intelligence-Empowered Mobilization of Assessments in COVID-19-like Pandemics: A Case Study for Early Flattening of the Curve. International Journal of Environmental Research and Public Health, 17(10), 3437. https://doi.org/10.3390/ijerph17103437






