Using Low-Cost Air Quality Sensor Networks to Improve the Spatial and Temporal Resolution of Concentration Maps
Abstract
1. Introduction
2. Methodology
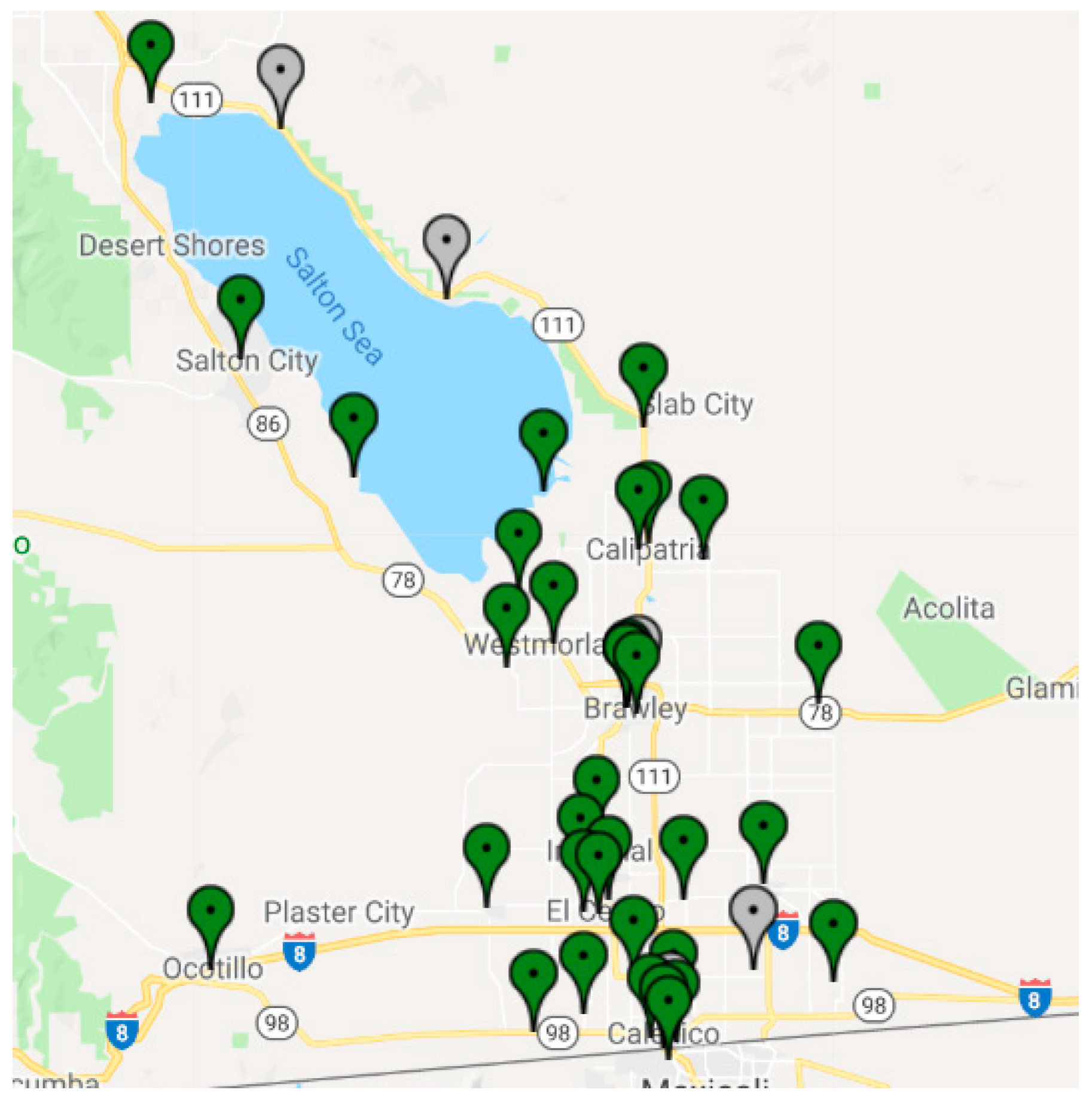
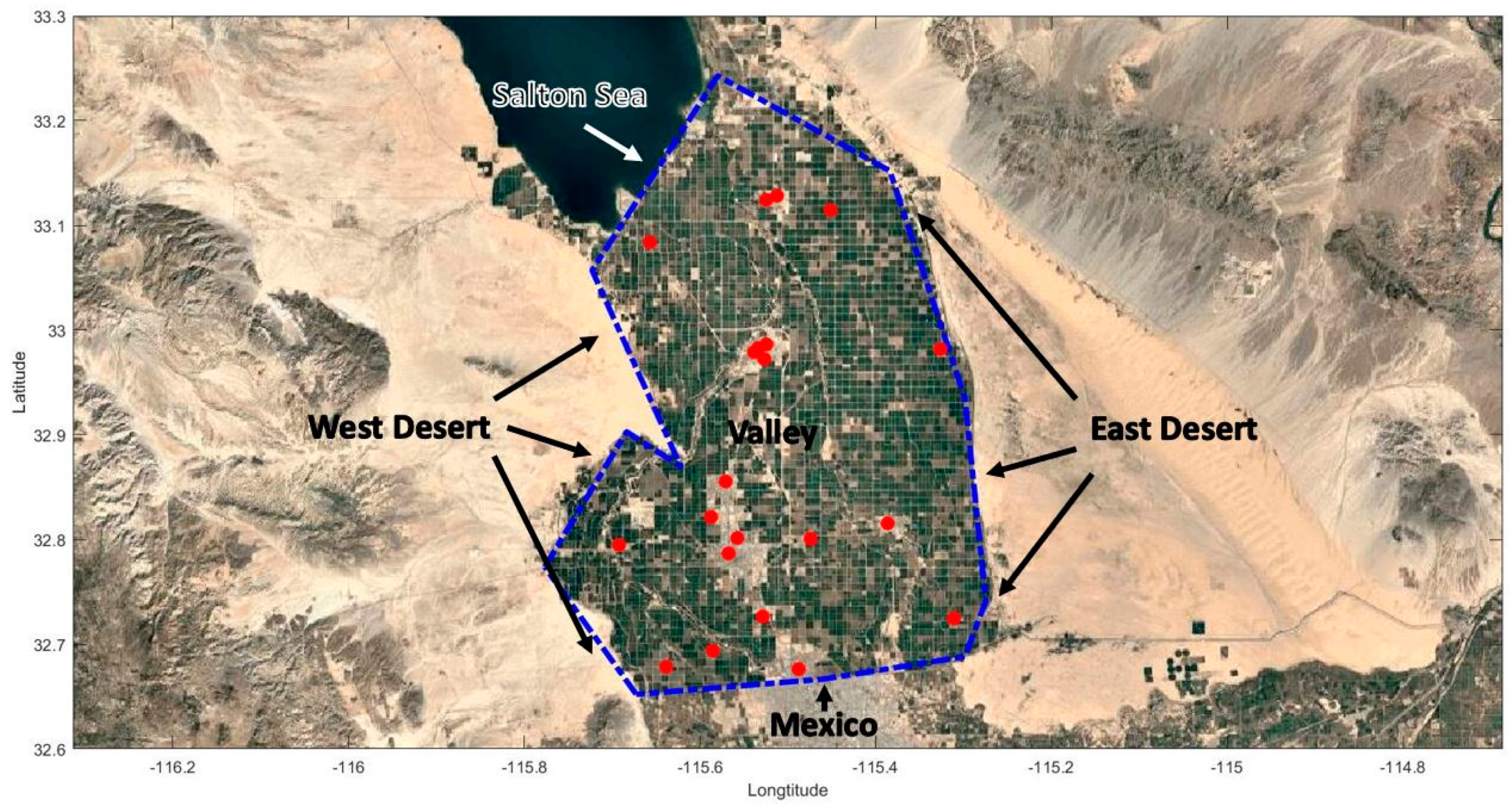
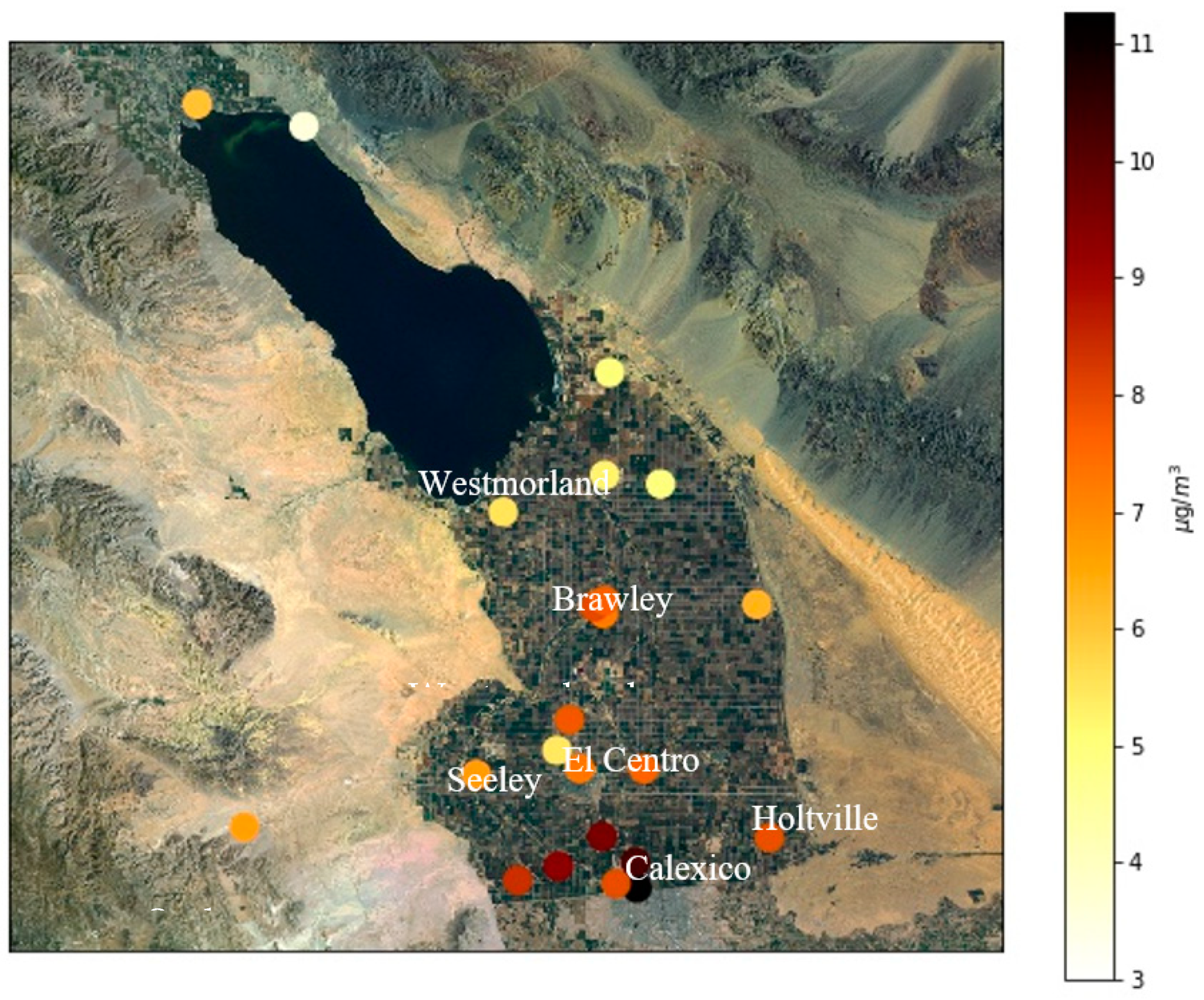
2.1. Sensor and Source Locations
2.2. Modeling Approach
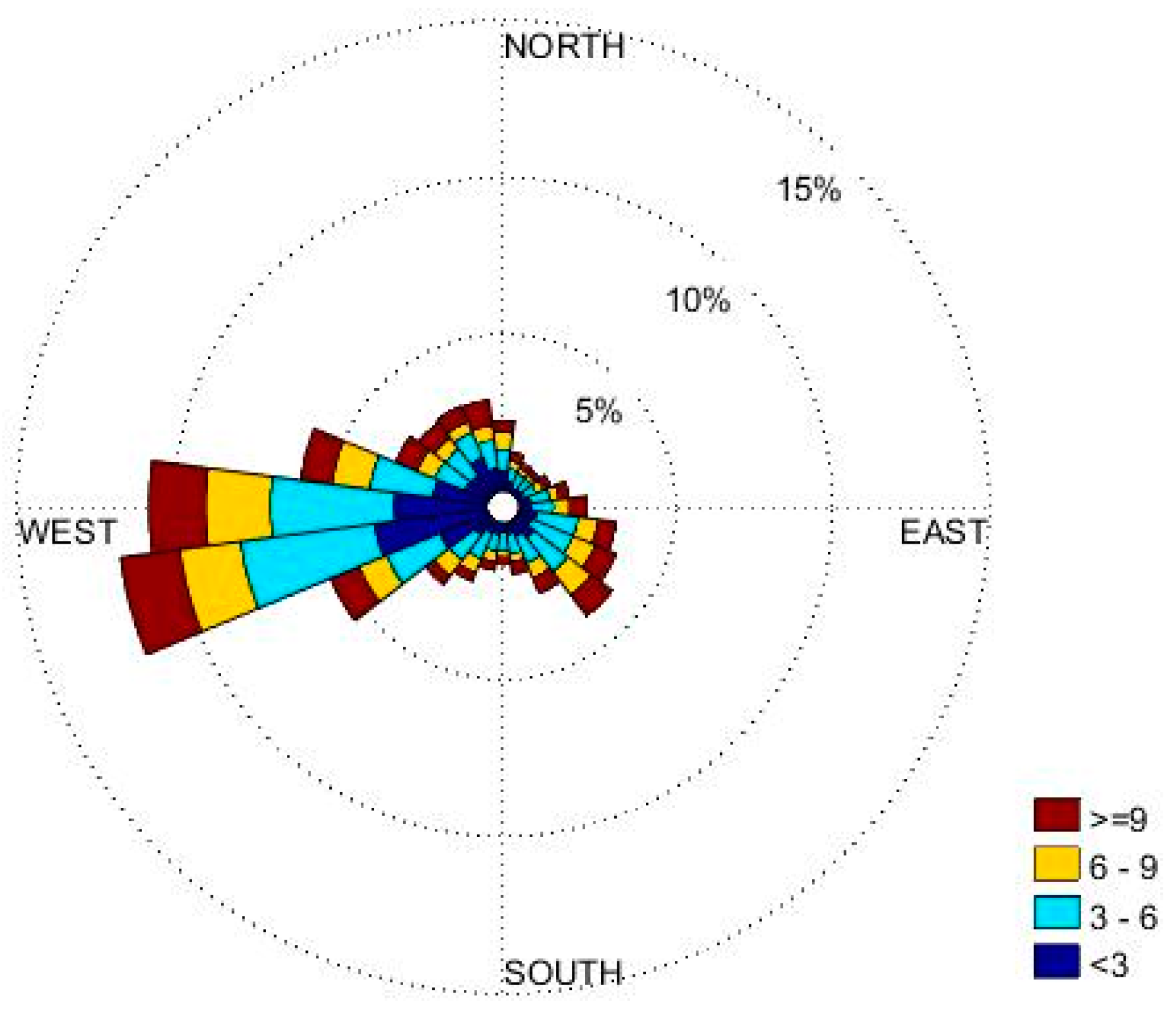
2.3. Meteorological Inputs
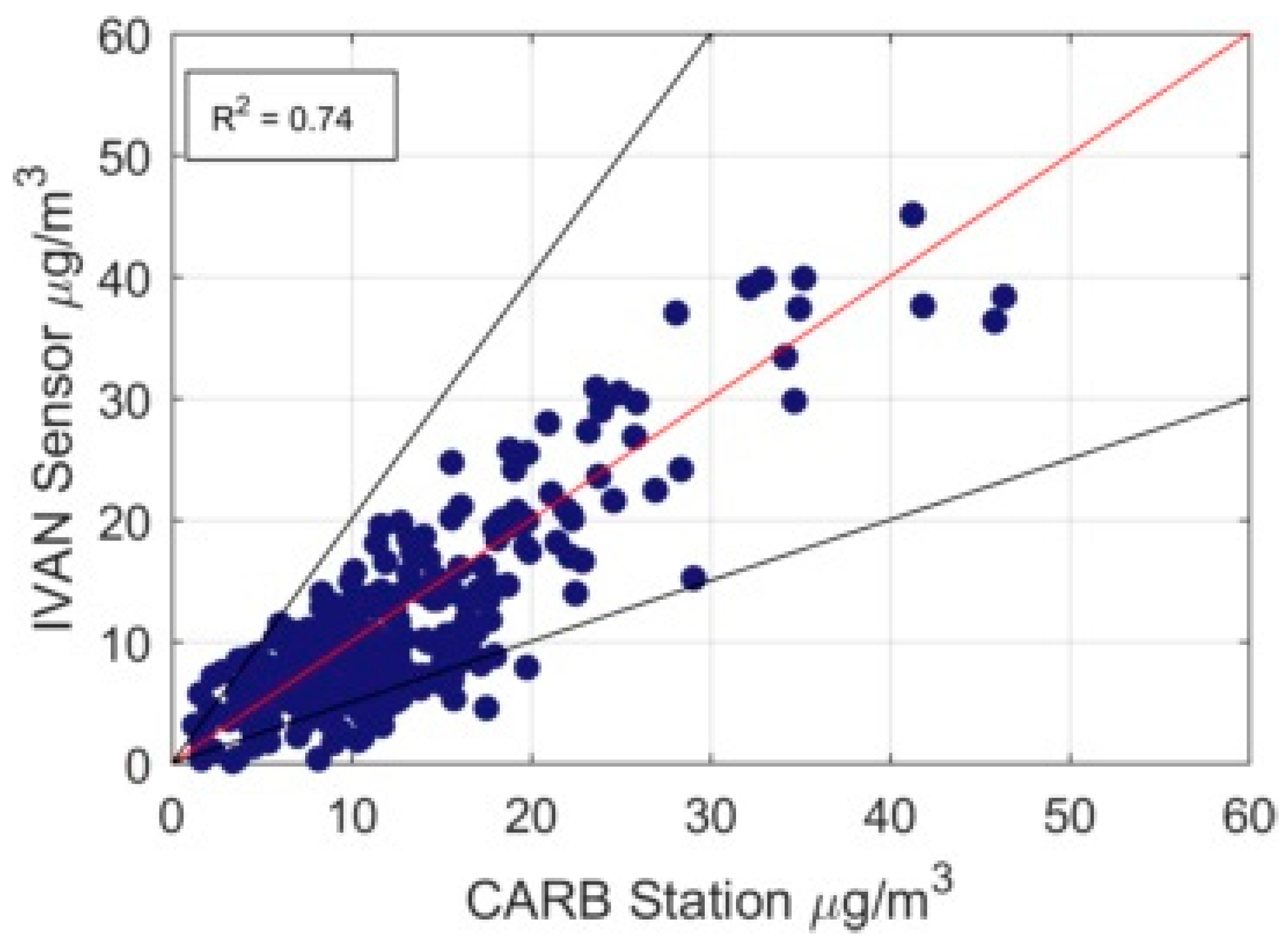
2.4. Concentration Measurement
3. Results and Discussion
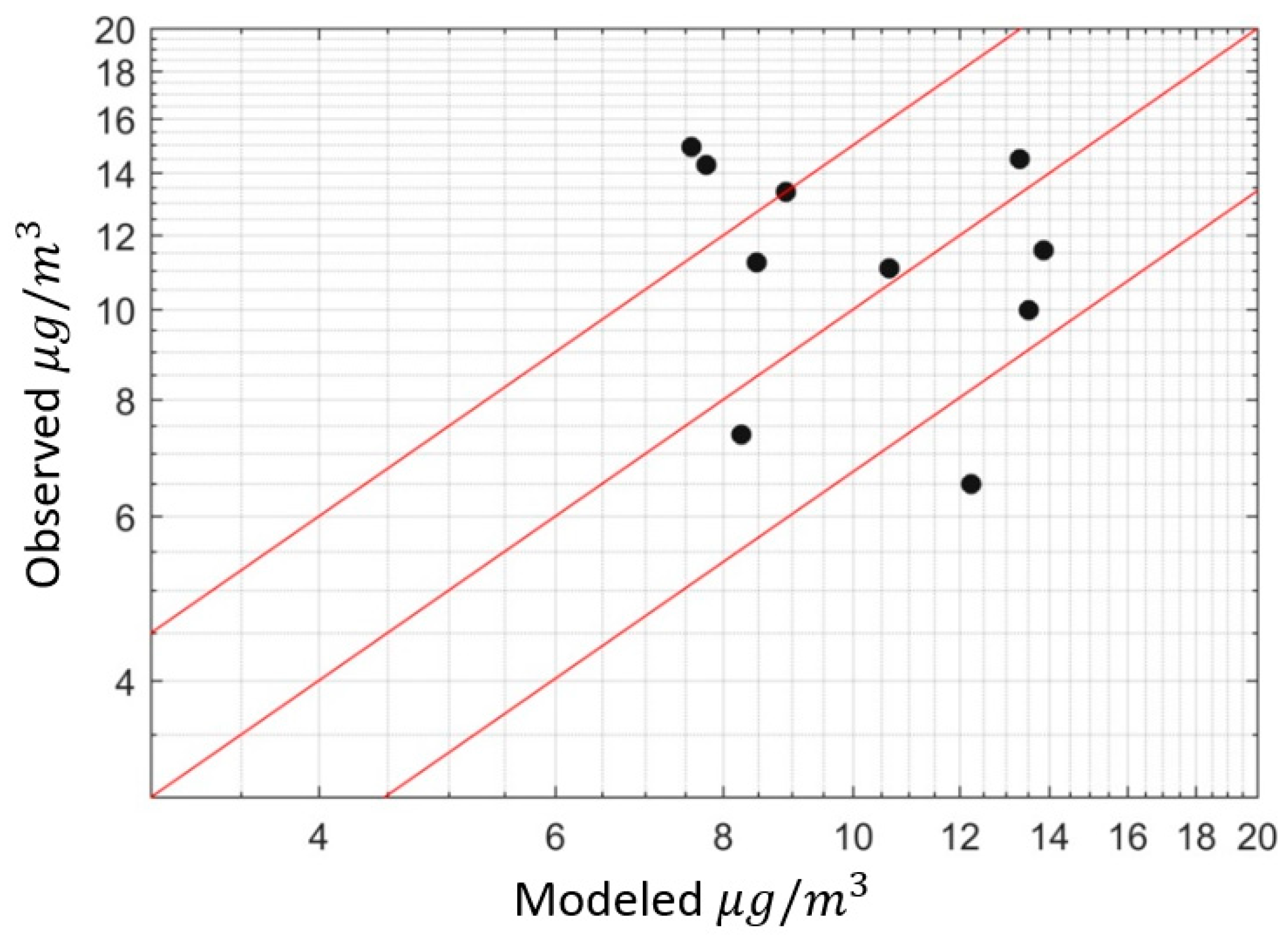
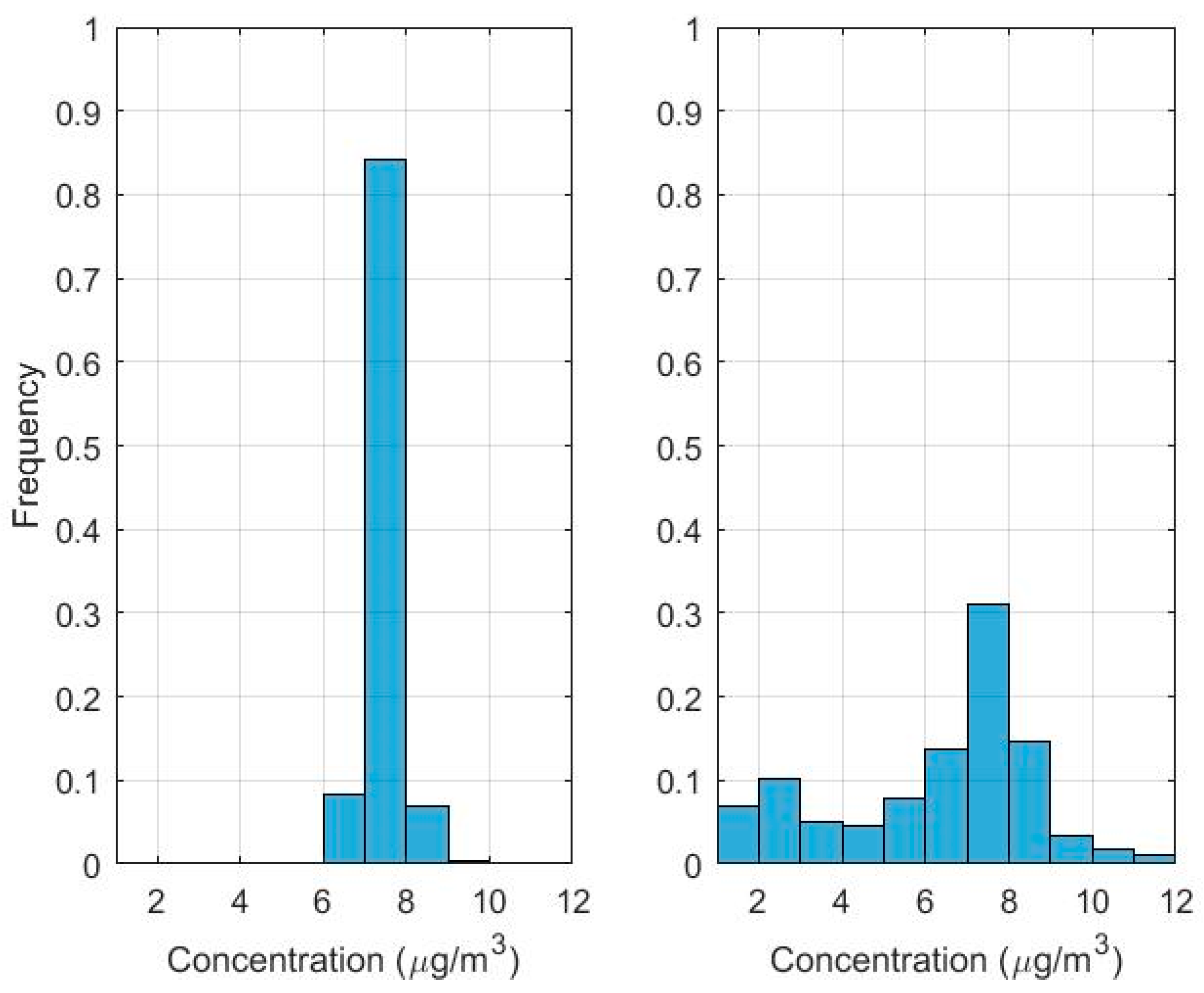
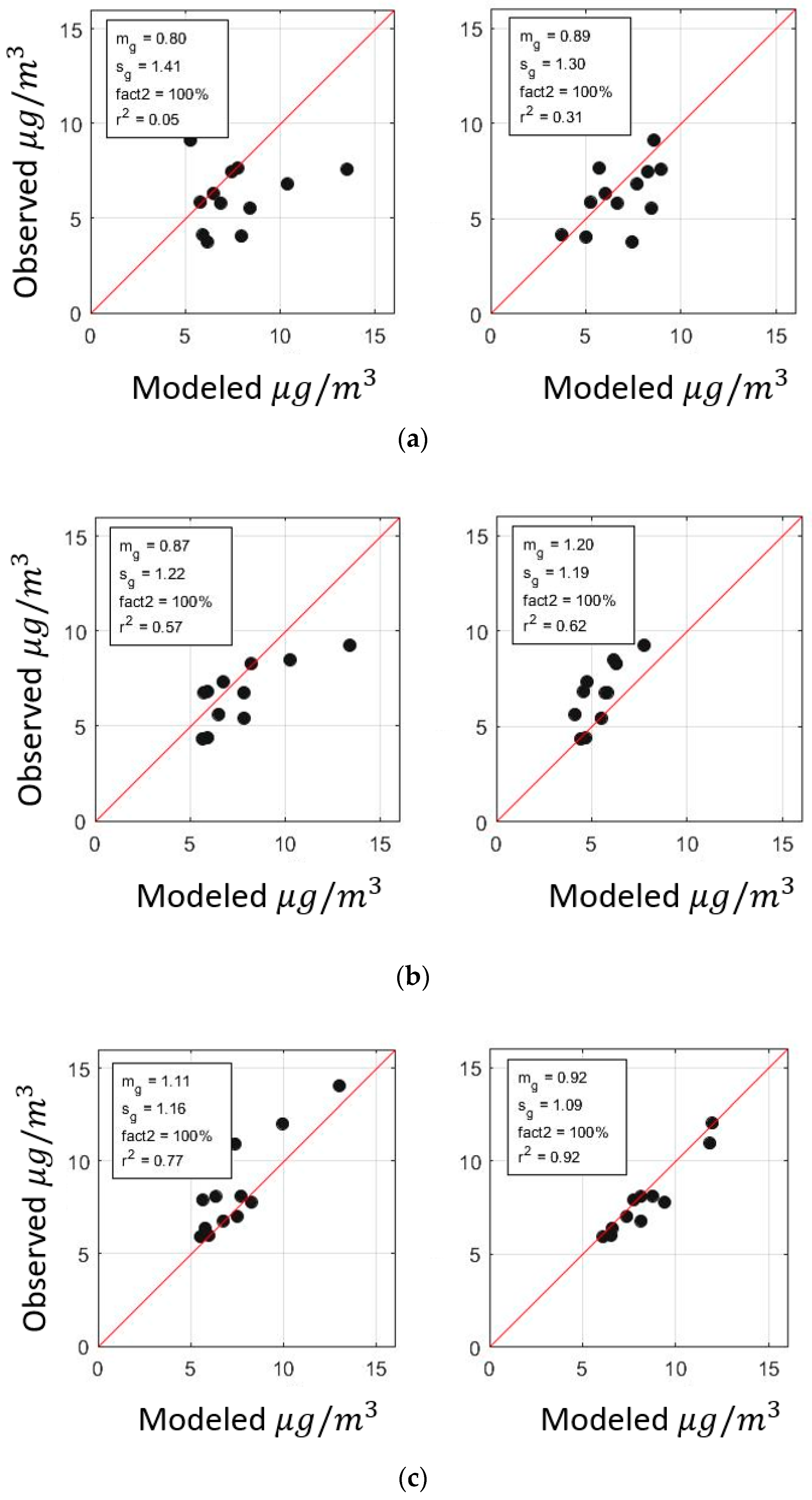
3.1. Modeling Results
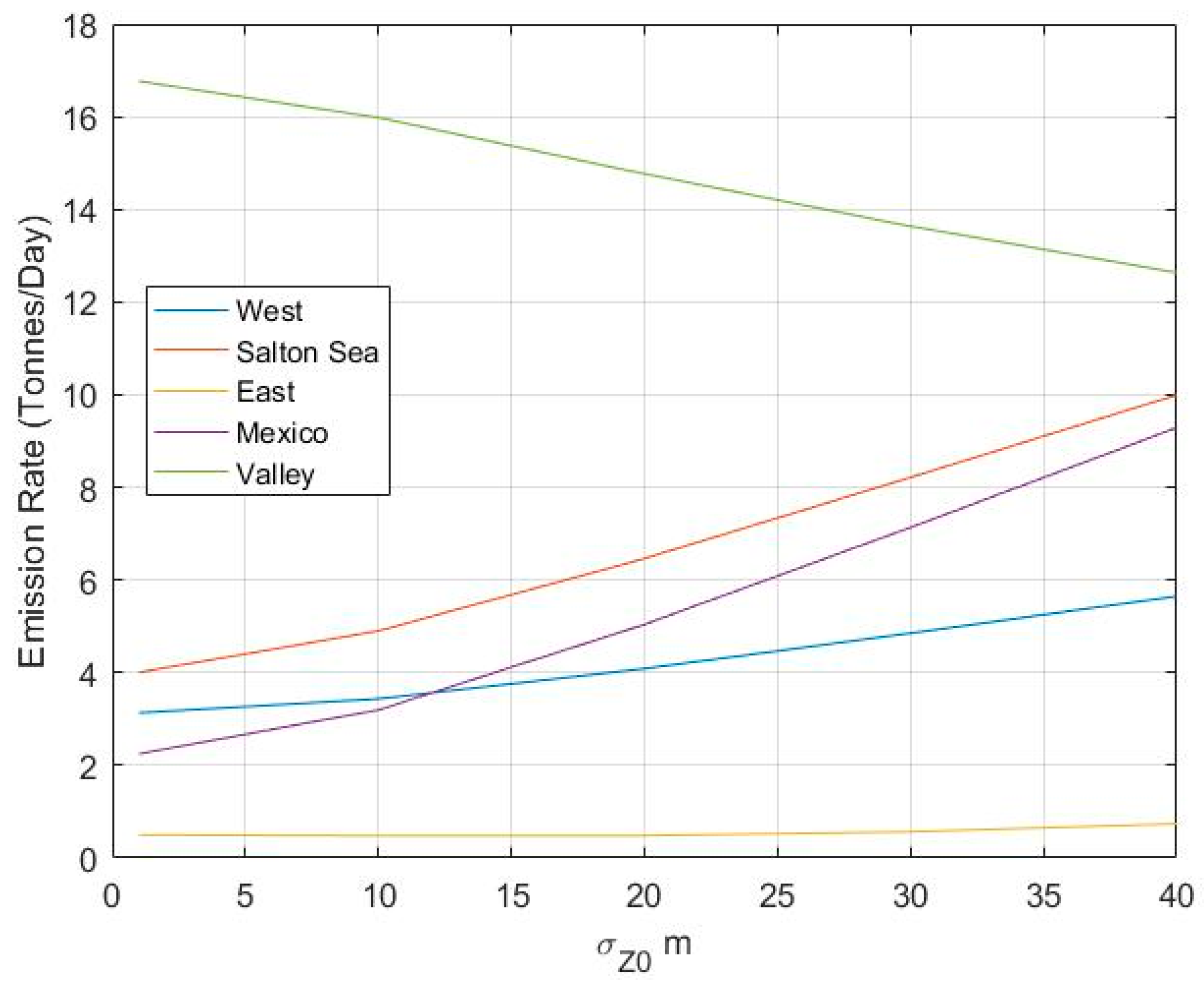
3.2. Sensitivity of the Model to
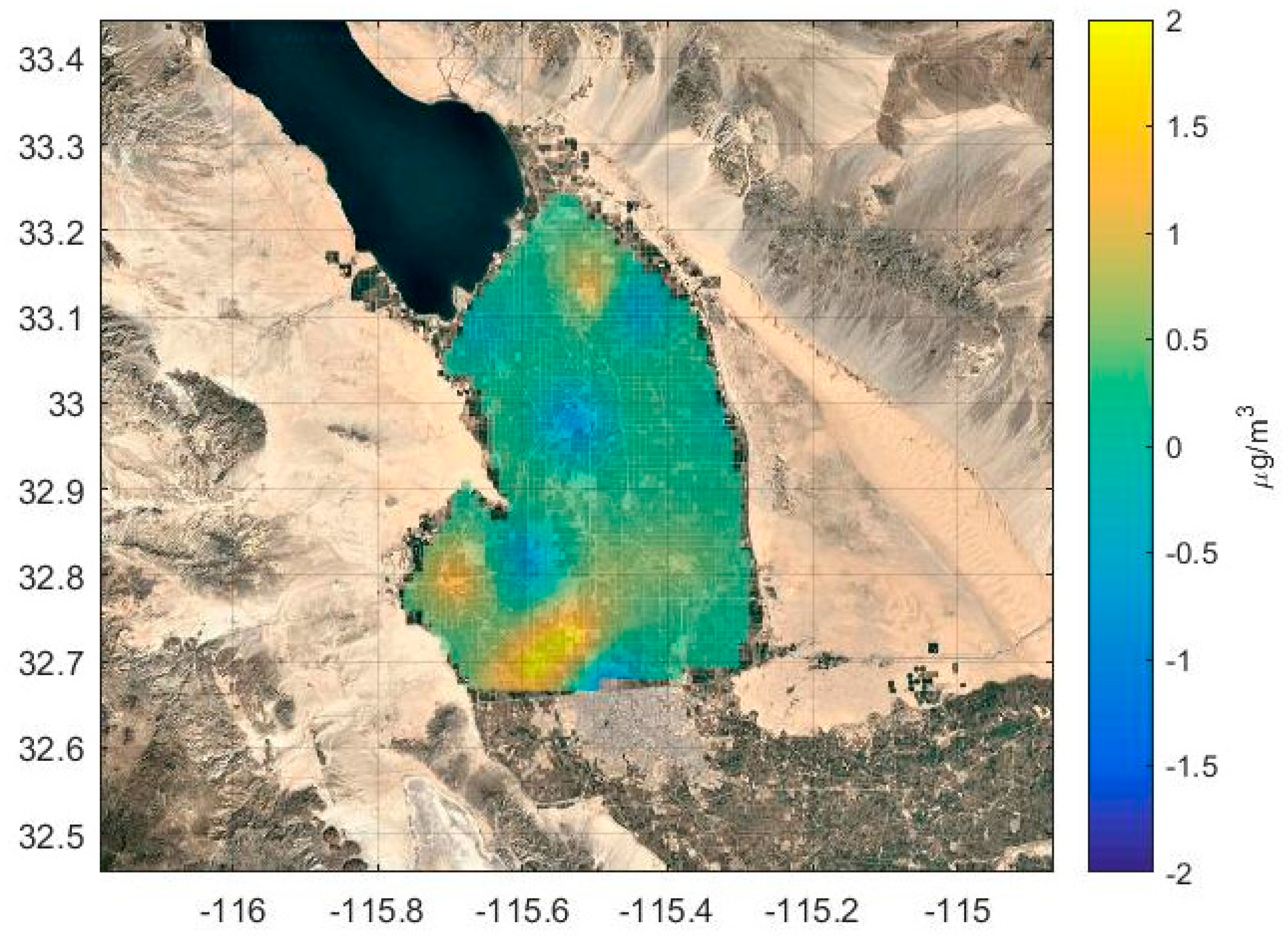
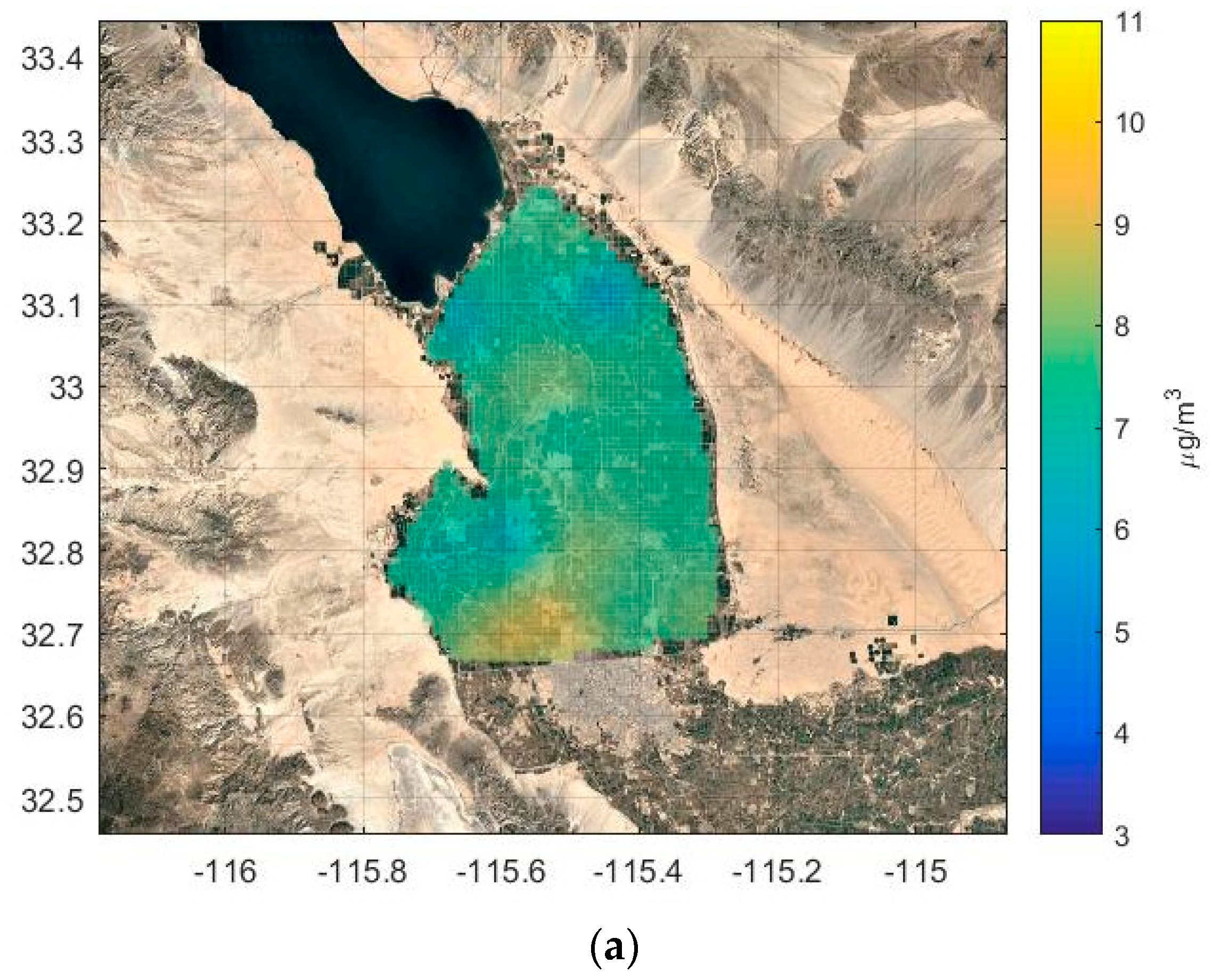
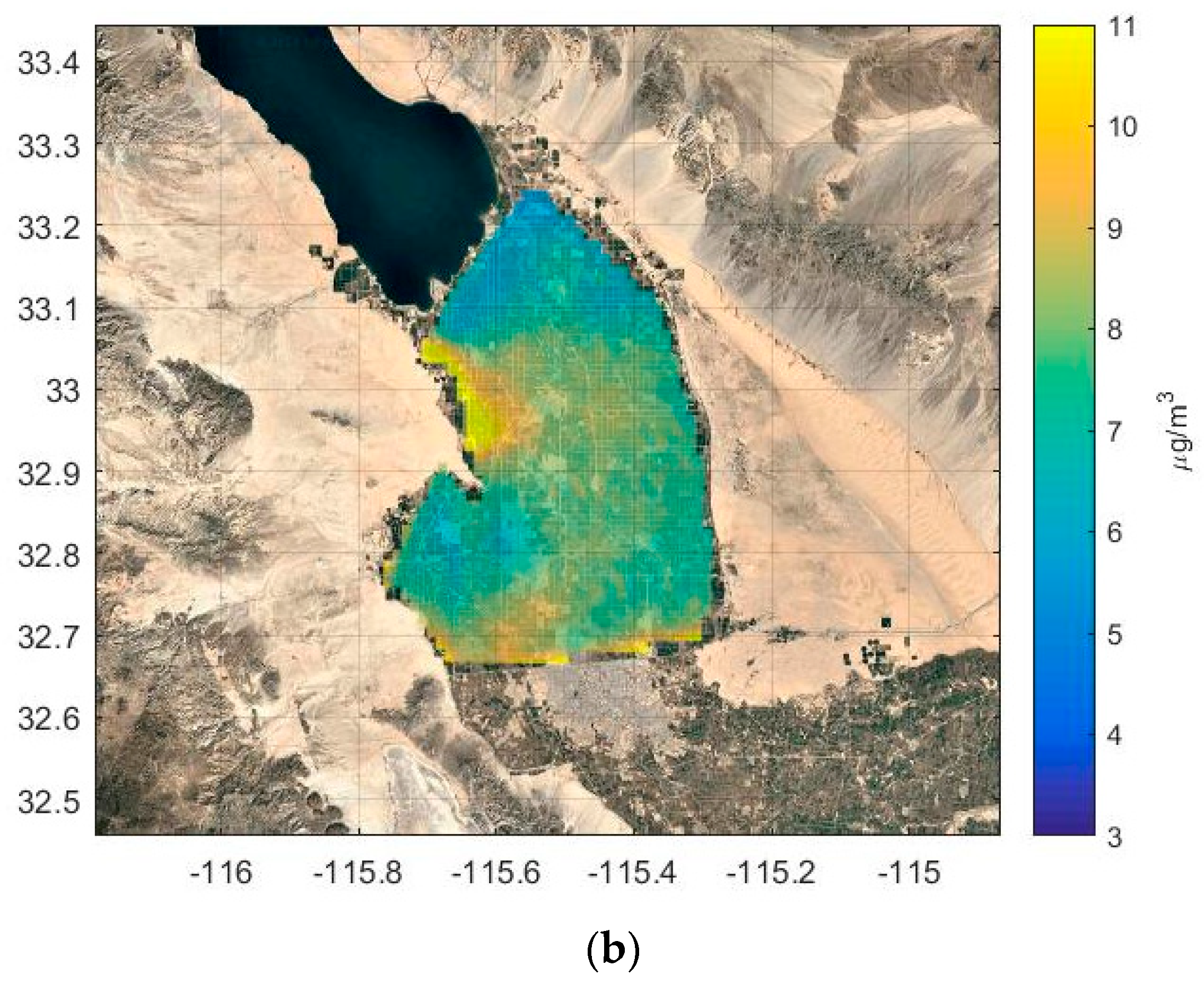
3.3. Using Residual Kriging to Improve Concentration Maps
- Use the dispersion model with fitted emissions to estimate concentrations at monitoring stations and calculate residuals between model estimates and observations.
- Use kriging to construct a field of residuals over a grid at a specified spatial resolution over the study domain.
- Estimate concentrations using the dispersion model with fitted emissions over the grid points of the study domain.
- Add the residuals computed from step 2 to the model estimates from step 3 to create concentration maps.
4. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brook, R.D.; Newby, D.E.; Rajagopalan, S. The global threat of outdoor ambient air pollution to cardiovascular health: Time for intervention. JAMA Cardiol. 2017, 2, 353–354. [Google Scholar] [CrossRef] [PubMed]
- Khreis, H.; Kelly, C.; Tate, J.; Parslow, R.; Lucas, K.; Nieuwenhuijsen, M. Exposure to traffic-related air pollution and risk of development of childhood asthma: A systematic review and meta-analysis. Environ. Int. 2017, 100, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Pope, C.A., III. Lung Cancer, Cardiopulmonary Mortality, and Long-term Exposure to Fine Particulate Air Pollution. JAMA J. Am. Med. Assoc. 2002. [Google Scholar] [CrossRef]
- Hagler, G.S.W.; Solomon, P.A.; Hunt, S.W. New technology for low-cost, real-time air monitoring. In EM Air Waste Manag. Assoc. Mag. Environ. Manag.; Air Waste Manag. Assoc.: Pittsburgh, PA, USA, 2014. [Google Scholar]
- Wang, Y.; Li, J.; Jing, H.; Zhang, Q.; Jiang, J.; Biswas, P. Laboratory evaluation and calibration of three low-cost particle sensors for particulate matter measurement. Aerosol Sci. Technol. 2015, 49, 1063–1077. [Google Scholar] [CrossRef]
- Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.J.; McLeod, M.W.; Hodgson, T.F.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atmos. Environ. 2013, 70, 186–203. [Google Scholar] [CrossRef]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.W.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The changing paradigm of air pollution monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef]
- White, R.M.; Paprotny, I.; Doering, F.; Cascio, W.E.; Solomon, P.A.; Gundel, L.A. Sensors and ‘apps’ for community-based: Atmospheric monitoring. In EM Air Waste Manag. Assoc. Mag. Environ. Manag.; Air Waste Manag. Assoc.: Pittsburgh, PA, USA, 2012; pp. 36–40. [Google Scholar]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef]
- Jiao, W.; Hagler, G.; Williams, R.; Sharpe, R.; Brown, R.; Garver, D.; Judge, R.; Caudill, M.; Rickard, J.; Davis, M. Community Air Sensor Network (CAIRSENSE) project: Evaluation of low-cost sensor performance in a suburban environment in the southeastern United States. Atmos. Meas. Tech. 2016, 9, 5281–5292. [Google Scholar] [CrossRef]
- Yi, W.Y.; Lo, K.M.; Mak, T.; Leung, K.S.; Leung, Y.; Meng, M.L. A survey of wireless sensor network based air pollution monitoring systems. Sensors 2015, 15, 31392–31427. [Google Scholar] [CrossRef]
- Johnston, S.J.; Basford, P.J.; Bulot, F.M.J.; Apetroaie-Cristea, M.; Easton, N.H.C.; Davenport, C.; Foster, G.L.; Loxham, M.; Morris, A.K.R.; Cox, S.J. City scale particulate matter monitoring using LoRaWAN based air quality IoT devices. Sensors 2019, 19, 209. [Google Scholar] [CrossRef]
- Fazio, E.; Bonacquisti, V.; Di Michele, M.; Frasca, F.; Chianese, A.; Siani, A. CleAir Monitoring System for Particulate Matter: A Case in the Napoleonic Museum in Rome. Sensors 2017, 17, 2076. [Google Scholar] [CrossRef] [PubMed]
- Marques, G.; Roque Ferreira, C.; Pitarma, R. A system based on the Internet of Things for real-time particle monitoring in buildings. Int. J. Environ. Res. Public Health 2018, 15, 821. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Levy, J.I.; Wolff, S.K.; Evans, J.S.; Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Risk Anal. Int. J. 2002, 42, 895–904. [Google Scholar] [CrossRef]
- Ryan, P.H.; LeMasters, G.K. A review of land-use regression models for characterizing intraurban air pollution exposure. Inhal. Toxicol. 2007, 19, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Li, X.; Chen, Z.; Zeng, G.; León, T.; Liang, J.; Huang, G.; Gao, Z.; Jiao, S.; He, X. Land use regression models coupled with meteorology to model spatial and temporal variability of NO2 and PM10 in Changsha, China. Atmos. Environ. 2015, 116, 272–280. [Google Scholar] [CrossRef]
- Chen, H.; Goldberg, M.S.; Crouse, D.L.; Burnett, R.T.; Jerrett, M.; Villeneuve, P.J.; Wheeler, A.J.; Labrèche, F.; Ross, N.A. Back-extrapolation of estimates of exposure from current land-use regression models. Atmos. Environ. 2010, 44, 4346–4354. [Google Scholar] [CrossRef]
- Hoogh, K.; De Korek, M.; Vienneau, D.; Keuken, M.; Kukkonen, J.; Nieuwenhuijsen, M.J.; Badaloni, C.; Beelen, R.; Bolignano, A.; Cesaroni, G.; et al. Comparing land use regression and dispersion modelling to assess residential exposure to ambient air pollution for epidemiological studies. Environ. Int. 2014, 73, 382–392. [Google Scholar] [CrossRef]
- Wong, M.; Bejarano, E.; Carvlin, G.; Fellows, K.; King, G.; Lugo, H.; Jerrett, M.; Meltzer, D.; Northcross, A.; Olmedo, L. Combining Community Engagement and Scientific Approaches in Next-Generation Monitor Siting: The Case of the Imperial County Community Air Network. Int. J. Environ. Res. Public Health 2018, 15, 523. [Google Scholar] [CrossRef]
- Pournazeri, S.; Tan, S.; Schulte, N.; Jing, Q.; Venkatram, A. A computationally efficient model for estimating background concentrations of NOx, NO2, and O3. Environ. Model. Softw. 2014, 52. [Google Scholar] [CrossRef]
- Venkatram, A. On the Use of Kriging in the Spatial-Analysis of Acid Precipitation Data. Atmos. Environ. 1988, 22, 1963–1975. [Google Scholar] [CrossRef]
- Schneider, P.; Castell, N.; Vogt, M.; Dauge, F.R.; Lahoz, W.A.; Bartonova, A. Mapping urban air quality in near real-time using observations from low-cost sensors and model information. Environ. Int. 2017, 106, 234–247. [Google Scholar] [CrossRef]
- CARB. Clean Air Act Section 179B Technical Demonstration Imperial County PM2.5 Nonattainment Area. 2018. Available online: https://www.arb.ca.gov/planning/sip/planarea/imperial/final179bwoe.pdf (accessed on 30 March 2019).
- English, P.B.; Olmedo, L.; Bejarano, E.; Lugo, H.; Murillo, E.; Seto, E.; Wong, M.; King, G.; Wilkie, A.; Meltzer, D. The Imperial County Community Air Monitoring Network: A model for community-based environmental monitoring for public health action. Environ. Health Perspect. 2017, 125, 074501. [Google Scholar] [CrossRef]
- Carvlin, G.N.; Lugo, H.; Olmedo, L.; Bejarano, E.; Wilkie, A.; Meltzer, D.; Wong, M.; King, G.; Northcross, A.; Jerrett, M. Development and field validation of a community-engaged particulate matter air quality monitoring network in Imperial, California, USA. J. Air Waste Manag. Assoc. 2017, 67, 1342–1352. [Google Scholar] [CrossRef]
- Ivan Air Monitoring. Available online: www.ivan-imperial.org/air (accessed on 21 March 2019).
- Snyder, M.G.; Venkatram, A.; Heist, D.K.; Perry, S.G.; Petersen, W.B.; Isakov, V. RLINE: A line source dispersion model for near-surface releases. Atmos. Environ. 2013, 77, 748–756. [Google Scholar] [CrossRef]
- Venkatram, A.; Snyder, M.G.; Heist, D.K.; Perry, S.G.; Petersen, W.B.; Isakov, V. Re-formulation of plume spread for near-surface dispersion. Atmos. Environ. 2013, 77. [Google Scholar] [CrossRef]
- Cimorelli, A.J.; Perry, S.G.; Venkatram, A.; Weil, J.C.; Paine, R.J.; Wilson, R.B.; Lee, R.F.; Peters, W.D.; Brode, R.W. AERMOD: A Dispersion Model for Industrial Source Applications. Part I: General Model Formulation and Boundary Layer Characterization. J. Appl. Meteorol. 2005, 44, 682–693. [Google Scholar] [CrossRef]
- Quintero-NUfiez, M.; Sweedler, A. Air quality evaluation in the Mexicali and Imperial Valleys as an element for an Outreach Program. In Imperial-Mexicali Valleys: Development and Environment of the US-Mexican Border Region; San Diego State University Press: San Diego, CA, USA, 2004; p. 263. [Google Scholar]
- Venkatram, A. Computing and displaying model performance statistics. Atmos. Environ. 2008, 42, 6862–6868. [Google Scholar] [CrossRef]
- Matheron, G. The Theory of Regionalized Variables and Its Application; Cahiers du Centre de morphologie mathematique; Centre de morphologie mathematique, École national supérieure des mines: Paris, France, 1971. [Google Scholar]
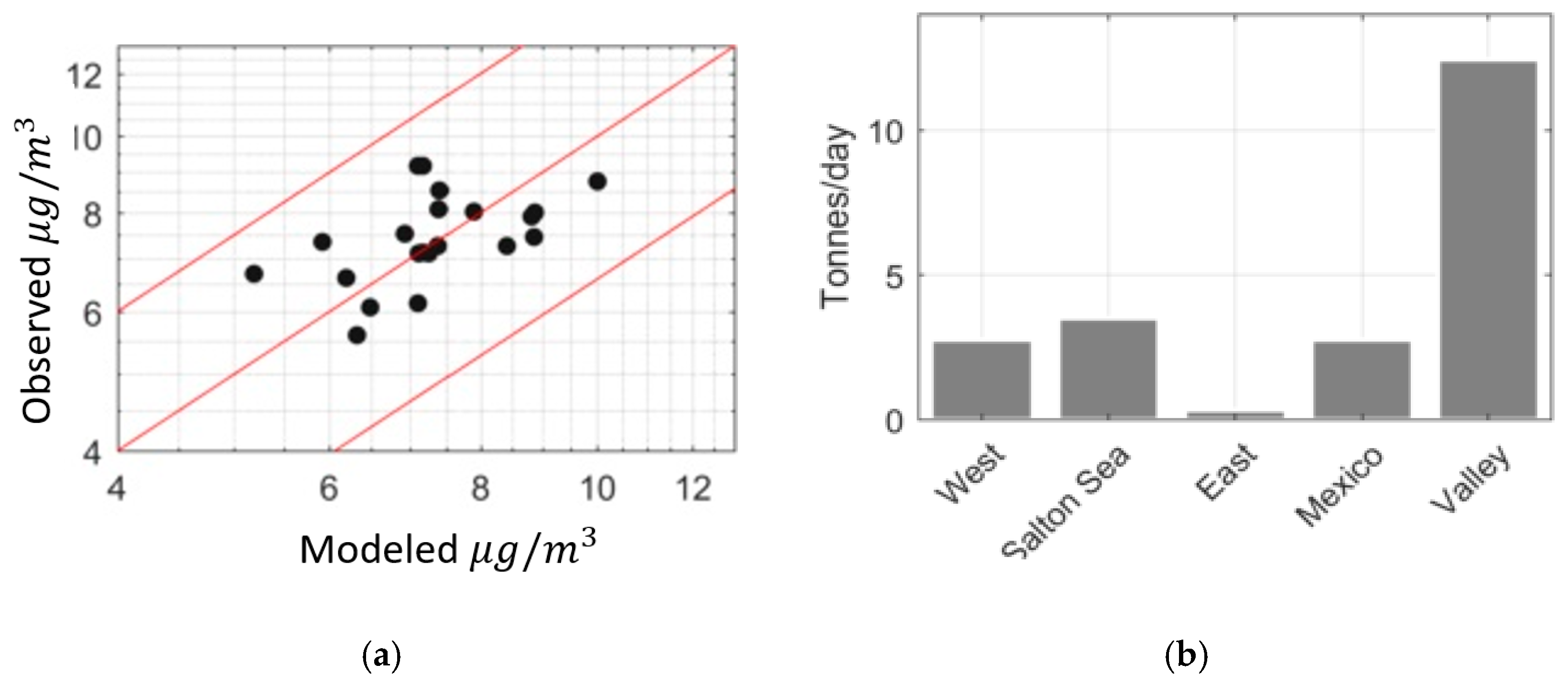
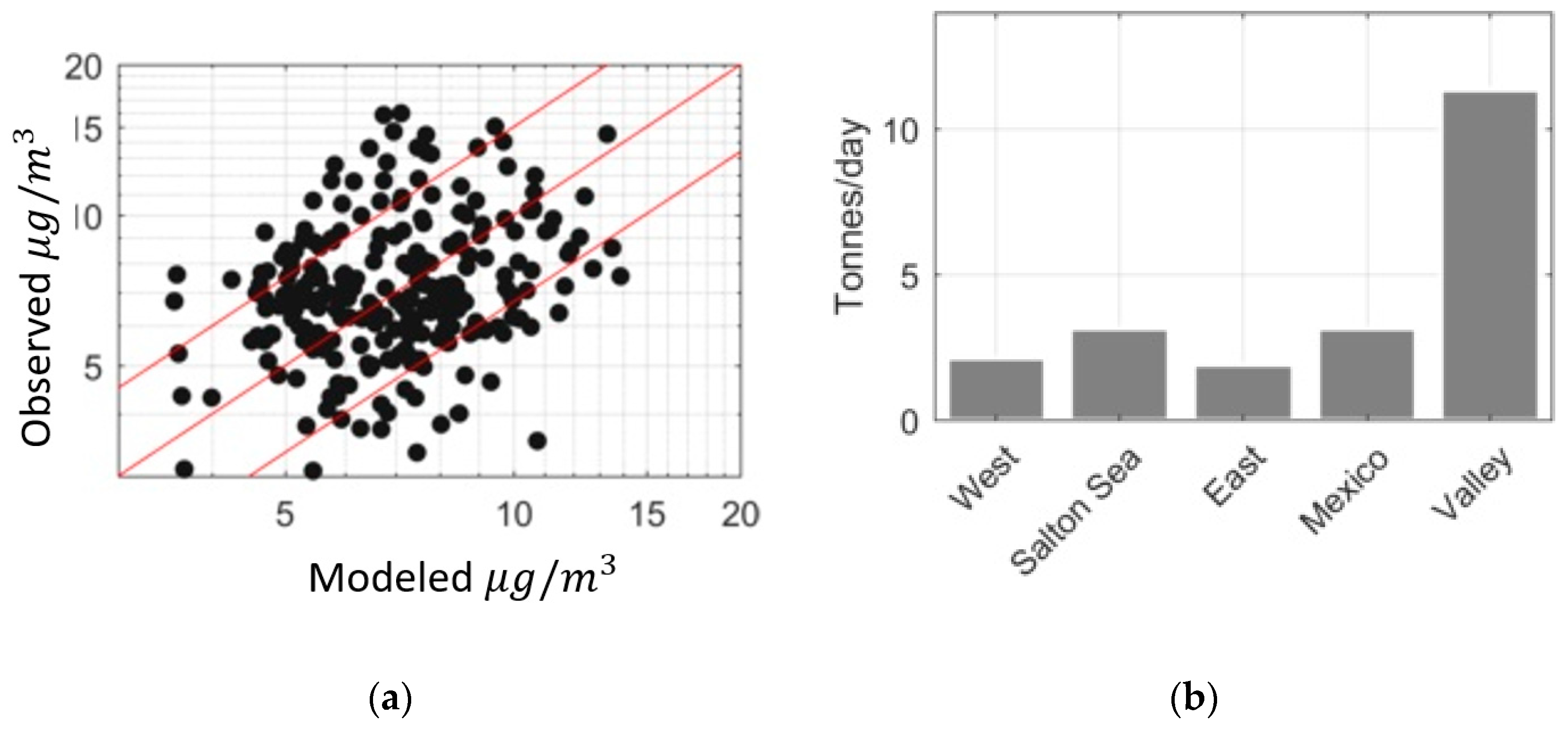
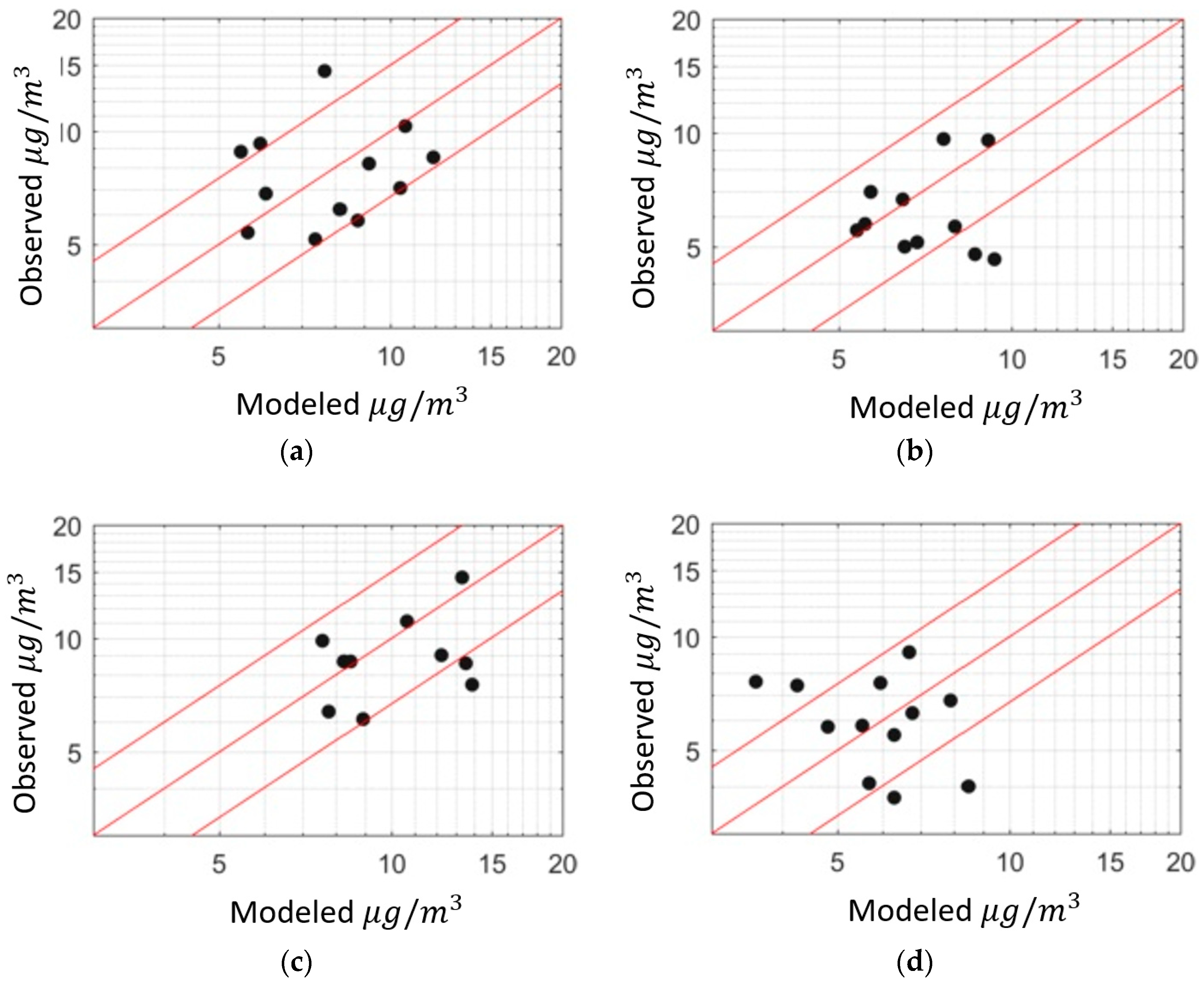
| Source | Emission Rates (Tons/Day) | 95% Confidence Interval (Tons/Day) | 95% Confidence Interval Range (Normalized to the Best Value) |
|---|---|---|---|
| West Desert | 2.8 | 2.0–3.7 | 0.6 |
| Salton Sea | 3.5 | 1.5–5.8 | 1.2 |
| East Desert | 0.3 | 0.0–2.5 | 8.3 |
| Mexico | 2.8 | 1.6–4.1 | 0.9 |
| Valley | 12.4 | 9.0–15.3 | 0.5 |
| Source | Emission Rates (Tons/Day) | 95% Confidence Interval (Tons/Day) | 95% Confidence Interval Range (Normalized by the Best Value) |
|---|---|---|---|
| West Desert | 2.1 | 1.5–2.8 | 0.6 |
| Salton Sea | 3.2 | 1.7–4.9 | 1.0 |
| East Desert | 1.9 | 0.6–3.3 | 1.4 |
| Mexico | 3.2 | 2.1–4.3 | 0.7 |
| Valley | 11.4 | 9.0–13.9 | 0.4 |
| Month | Emission Rate (Tons per Day) | Coefficient of Determination () | ||||
|---|---|---|---|---|---|---|
| West Desert | Salton Sea | East Desert | Mexico | Valley | ||
| January | 2.8 | 1.1 | 0 | 1.9 | 7.9 | 0.55 |
| February | 2.8 | 5.1 | 0 | 4.5 | 10.2 | 0.13 |
| March | 2.5 | 5.2 | 0 | 4.0 | 4.4 | 0.12 |
| April | 3.6 | 4.4 | 3.7 | 3.1 | 11.2 | 0.13 |
| May | 5.4 | 7.8 | 0.9 | 2.8 | 12.5 | 0.55 |
| June | 4.1 | 9.5 | 1.5 | 4.9 | 15.1 | 0.26 |
| July | 3.4 | 1.4 | 1.8 | 3.4 | 10.6 | 0.29 |
| August | 3.4 | 8.7 | 1.0 | 3.1 | 4.3 | 0.34 |
| September | 1.9 | 2.7 | 7.6 | 1.2 | 6.8 | 0.35 |
| October | 2.6 | 2.7 | 1.6 | 4.5 | 11.2 | 0.47 |
| November | 1.4 | 1.2 | 2.8 | 4.4 | 8.8 | 0.18 |
| December | 2.3 | 2.6 | 0 | 10.5 | 27.0 | 0.28 |
| Average | 3.0 | 4.3 | 1.7 | 4.0 | 10.8 | |
| Standard Derivative | 1.0 | 2.8 | 2.1 | 2.2 | 5.7 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahangar, F.E.; Freedman, F.R.; Venkatram, A. Using Low-Cost Air Quality Sensor Networks to Improve the Spatial and Temporal Resolution of Concentration Maps. Int. J. Environ. Res. Public Health 2019, 16, 1252. https://doi.org/10.3390/ijerph16071252
Ahangar FE, Freedman FR, Venkatram A. Using Low-Cost Air Quality Sensor Networks to Improve the Spatial and Temporal Resolution of Concentration Maps. International Journal of Environmental Research and Public Health. 2019; 16(7):1252. https://doi.org/10.3390/ijerph16071252
Chicago/Turabian StyleAhangar, Faraz Enayati, Frank R. Freedman, and Akula Venkatram. 2019. "Using Low-Cost Air Quality Sensor Networks to Improve the Spatial and Temporal Resolution of Concentration Maps" International Journal of Environmental Research and Public Health 16, no. 7: 1252. https://doi.org/10.3390/ijerph16071252
APA StyleAhangar, F. E., Freedman, F. R., & Venkatram, A. (2019). Using Low-Cost Air Quality Sensor Networks to Improve the Spatial and Temporal Resolution of Concentration Maps. International Journal of Environmental Research and Public Health, 16(7), 1252. https://doi.org/10.3390/ijerph16071252





