The Spatial and Heterogeneity Impacts of Population Urbanization on Fine Particulate (PM2.5) in the Yangtze River Economic Belt, China
Abstract
1. Introduction
2. Study area and Method
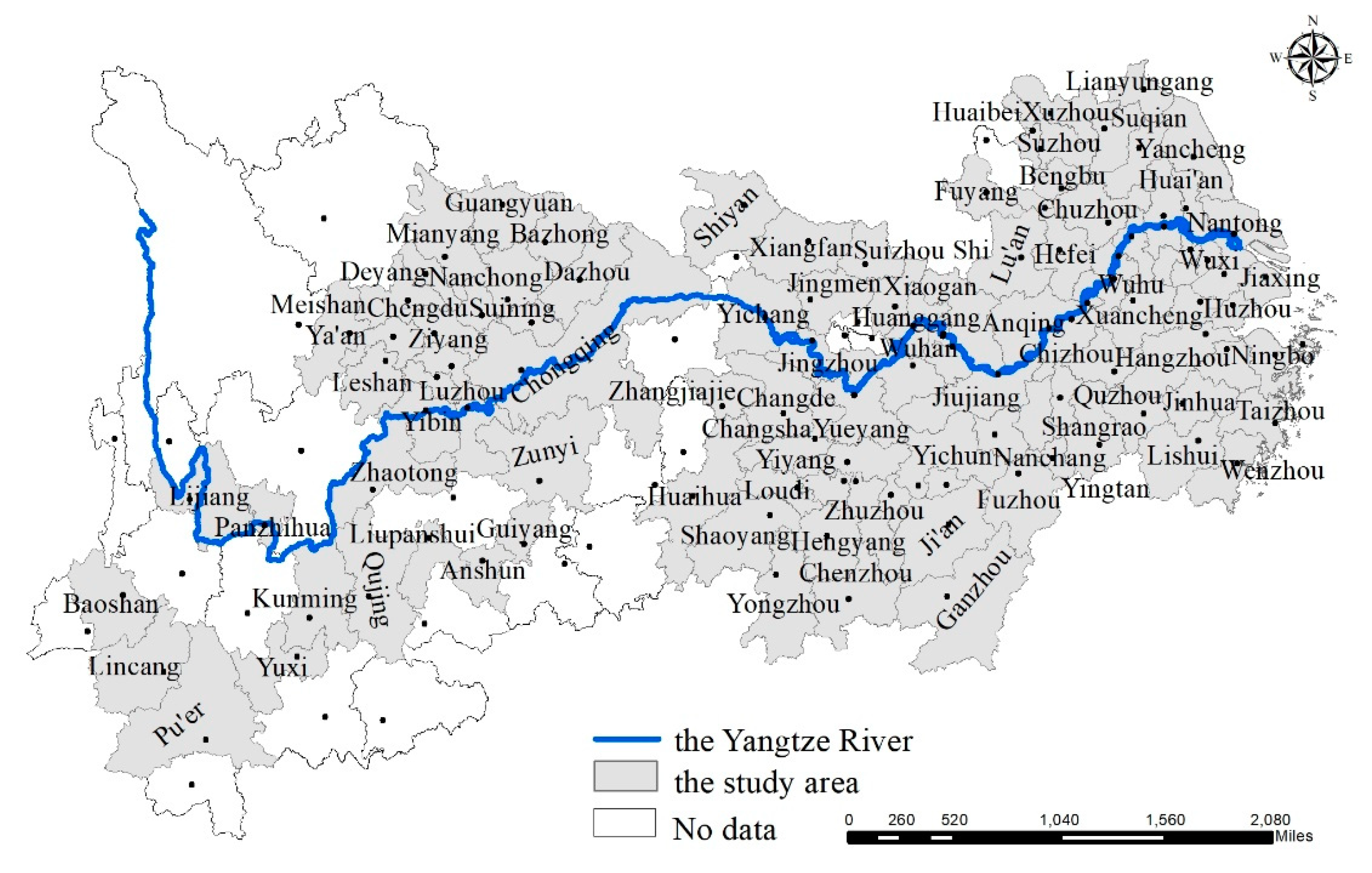
2.1. Study Area
2.2. Empirical Method
2.2.1. STIRPAT Model
2.2.2. Model Specification
2.2.3. Dynamic Spatial Econometric Model
3. Results
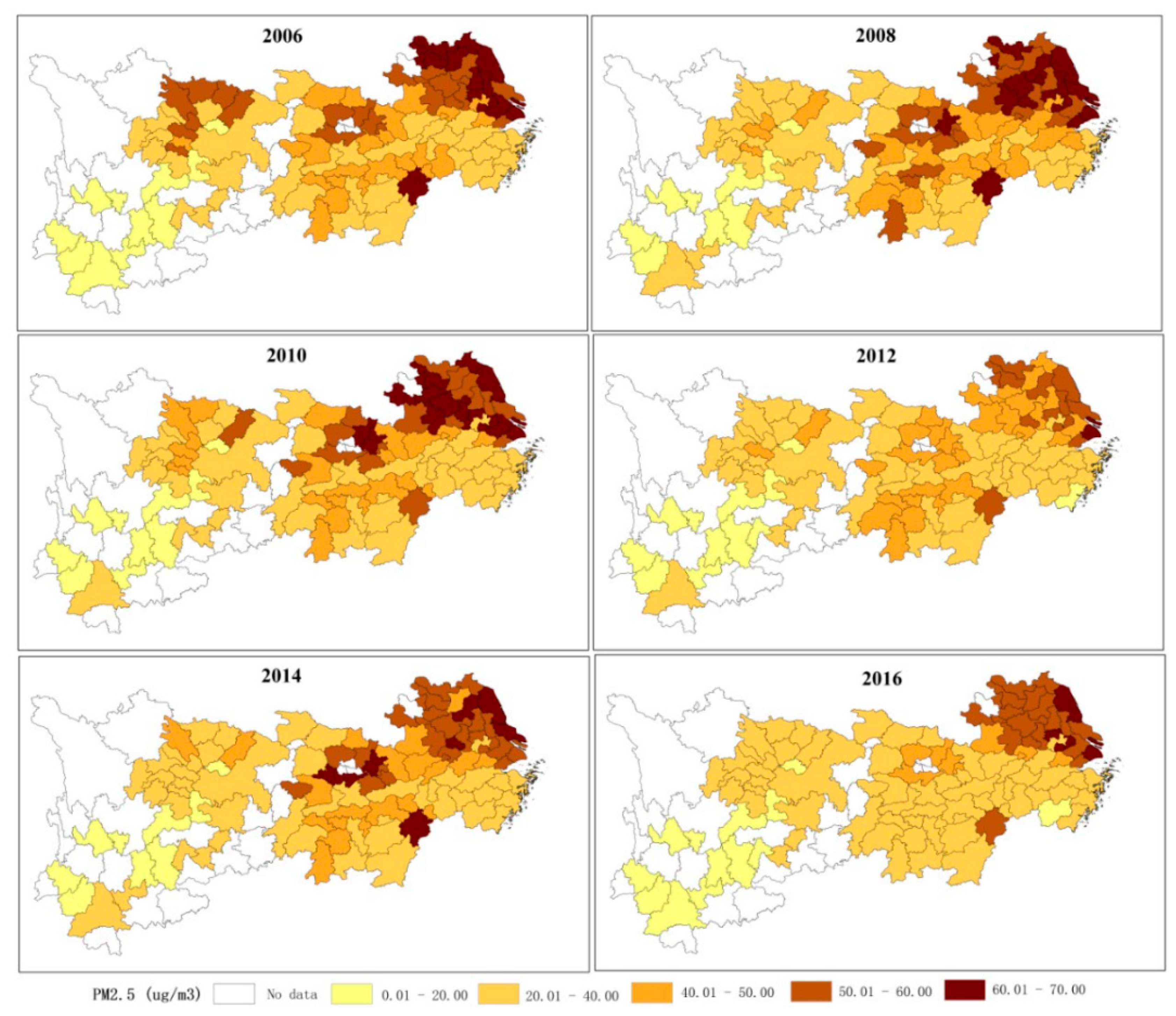
3.1. Spatial Distribution of PM2.5
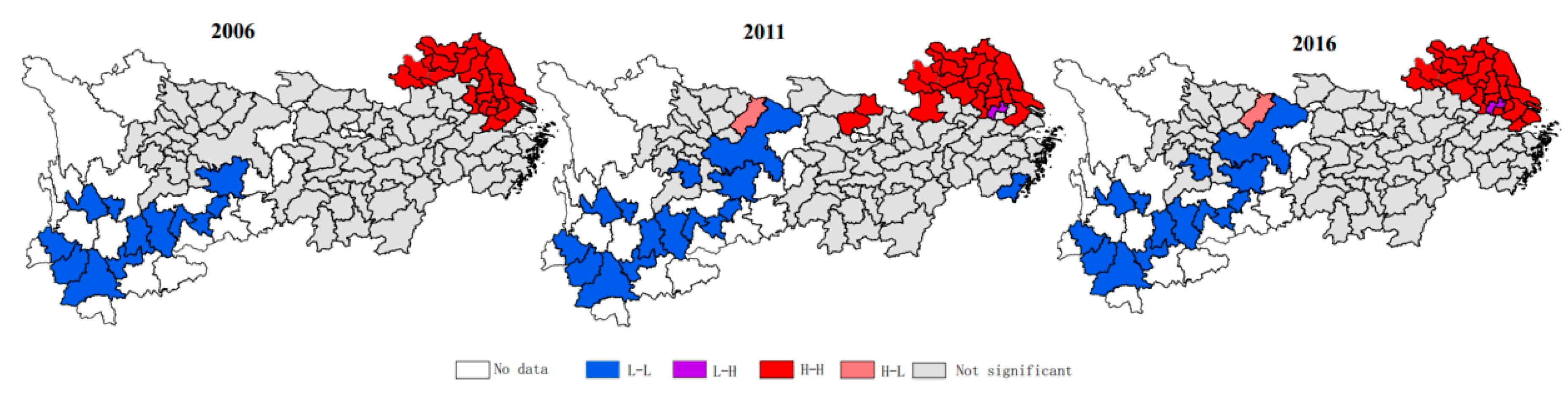
3.2. Spatial Autocorrelation Test
3.3. Full Sample Results
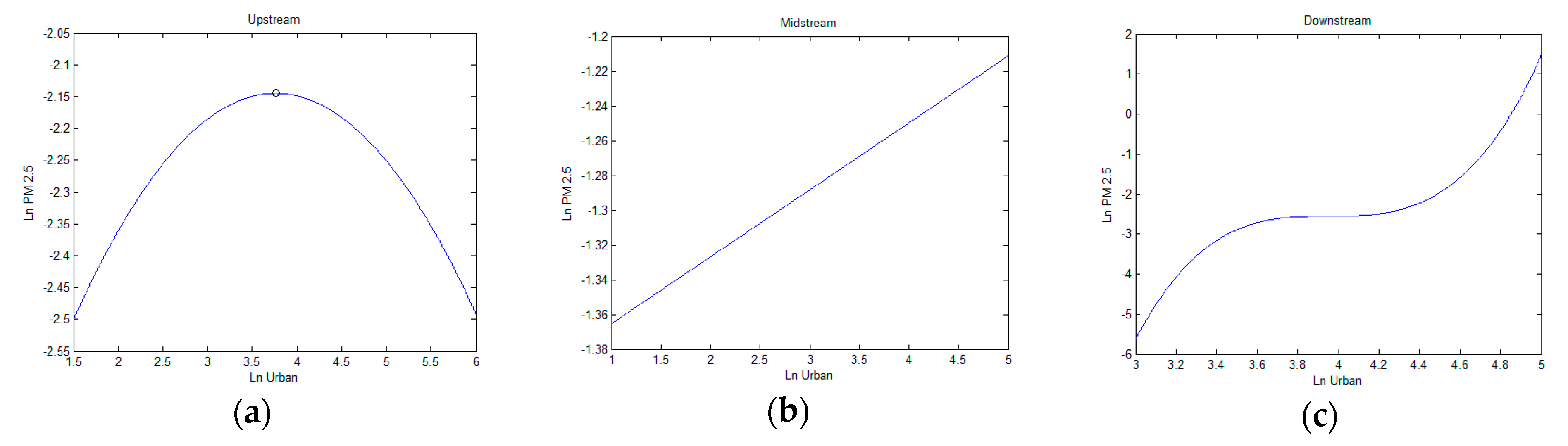
3.4. The Heterogeneous Effects of Upstream, Midstream, and Downstream Cities
3.5. The Heterogeneous Effects of Cities on Different Urbanization Levels
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.J.; Yi, W.C.; Li, B.W. Evaluation of urban resource and environmental efficiency in china based on the DEA model. J. Resour. Ecol. 2014, 5, 11–19. [Google Scholar]
- Luo, J.; Du, P.; Samat, A.; Xia, J.; Che, M.; Xue, Z. Spatiotemporal pattern of PM2.5 concentrations in Mainland China and analysis of its influencing factors using geographically weighted regression. Sci Rep. 2017, 7, 40607. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.Z.; Zhuang, G.S.; Huang, K.; Liu, T.N.; Deng, C.; Xu, J.; Lin, Y.F.; Guo, Z.G.; Chen, Y.; Fu, J.S.; et al. Probing the severe haze pollution in three typical regions of China: Characteristics, sources and regional impacts. Atmos. Environ. 2015, 120, 76–88. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chen, D.K. Air pollution, government regulations and high-quality economic development. Econ. Res. J. 2018, 53, 20–34. (In Chinese) [Google Scholar]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North American Free Trade Agreement; Woking Paper No. 3914; National Bureau of Economic Research: Cambridge, MA, USA, 1991. [Google Scholar]
- Hao, Y.; Peng, H.; Temulun, T.; Liu, L.Q.; Lu, Z.N.; Chen, H. How harmful is air pollution to economic development? New evidence from PM2.5 concentrations of Chinese cities. J. Clean. Prod. 2018, 172, 743–757. [Google Scholar] [CrossRef]
- Guan, D.B.; Su, X.; Zhang, Q.; Peters, G.P.; Liu, Z.; Lei, Y.; He, K.B. The socioeconomic drivers of China’s primary PM2.5 emissions. Environ. Res. Lett. 2014, 9, 024010. [Google Scholar] [CrossRef]
- Gang, L.; Fu, J.J.; Dong, J.; Hu, W.S.; Dong, D.L.; Huang, Y.H.; Zhao, M.D. Spatio-temporal variation of PM2.5 concentrations and their relationship with geographic and socioeconomic factors in China. Int. J. Environ. Res. Public Health 2014, 11, 173–186. [Google Scholar]
- Ji, X.; Yao, Y.X.; Long, X.L. What causes PM2.5 pollution? Cross-economy empirical analysis from socioeconomic perspective. Energy Policy 2018, 119, 458–472. [Google Scholar] [CrossRef]
- Xu, S.C.; Miao, Y.M.; Gao, C.; Long, R.Y.; Chen, H.; Zhao, B.; Wang, S.X. Regional differences in impacts of economic growth and urbanization on air pollutants in China based on provincial panel estimation. J. Clean. Prod. 2019, 208, 340–352. [Google Scholar] [CrossRef]
- Lee, S.H.; Oh, D.W. Economic growth and the environment in China: Empirical evidence using prefecture level data. China Econ. Rev. 2015, 36, 73–85. [Google Scholar] [CrossRef]
- Liu, T.T.; Ma, Z.Y.; Wan, N.Q.; Liu, Z.G. Analysis and prediction on the environmental Kuznets curve in Ningxia. Areal Res. Dev. 2011, 30, 62–66. (In Chinese) [Google Scholar]
- Friedl, B.; Getzner, M. Determinants of CO2 emissions in a small open economy. Ecol. Econ. 2003, 45, 133–148. [Google Scholar] [CrossRef]
- Day, K.; Grafton, R.Q. Growth and the environment in Canada: An empirical analysis. Can. J. Agric. Econ. 2010, 51, 197–216. [Google Scholar] [CrossRef]
- Ji, X.; Chen, B. Assessing the energy-saving effect of urbanization in China based on stochastic impacts by regression on population, affluence and technology (STIRPAT) model. J. Clean. Prod. 2015, 24, 206–209. [Google Scholar] [CrossRef]
- Sun, C.; Luo, Y.; Li, J. Urban traffic infrastructure investment and air pollution: Evidence from the 83 cities in China. J. Clean. Prod. 2017, 172, 488–496. [Google Scholar] [CrossRef]
- Han, L.J.; Zhou, W.Q.; Li, W.F.; Qian, Y.G. Urbanization strategy and environmental changes: An insight with relationship between population change and fine particulate pollution. Sci. Total Environ. 2018, 642, 789–799. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.G.; Gu, J.; Wang, H.W.; Wu, Z.Z. Uncovering the culprits of air pollution: Evidence from China’s economic sectors and regional heterogeneities. J. Clean. Prod. 2018, 171, 1481–1493. [Google Scholar] [CrossRef]
- Wei, F.S.; Teng, E.J.; Wu, G.P.; Hu, W.; Wilson, W.E.; Chapman, R.S.; Pau, J.C.; Zhang, J. Concentrations and elemental components of PM2.5, PM10 in ambient air in four large Chinese cities. Environ. Monit. China 2001, 17, 1–6. (In Chinese) [Google Scholar]
- Du, Y.Y.; Sun, T.S.; Peng, J.; Fang, K.; Liu, Y.X.; Yang, Y.; Wang, Y.L. Direct and spillover effects of urbanization on PM2.5 concentrations in China’s top three urban agglomerations. J. Clean. Prod. 2018, 190, 72–83. [Google Scholar]
- Wu, J.S.; Zheng, H.Q.; Zhe, F.; Xie, W.D.; Song, J. Study on the relationship between urbanization and fine particulate matter (PM2.5) concentration and its implication in China. J. Clean. Prod. 2018, 182, 872–882. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Yi, W.C.; Li, B.W. The impact of urbanization on carbon emission: Empirical evidence in Beijing. Energy Proc. 2015, 75, 2963–2968. [Google Scholar] [CrossRef]
- Lin, S.; Wang, S.; Marinova, D.; Zhao, D.; Hong, J. Impacts of urbanization and real economic development on CO2 emissions in non-high income countries: Empirical research based on the extended STIRPAT model. J. Clean. Prod. 2017, 166, 952–966. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Kwan, M.P.; Yang, H.; Chuai, X. The effect of urbanization on carbon dioxide emissions efficiency in the Yangtze river delta, China. J. Clean. Prod. 2018, 188, 38–48. [Google Scholar] [CrossRef]
- Zhan, D.; Kwan, M.P.; Zhang, W.; Yu, X.; Meng, B.; Liu, Q. The driving factors of air quality index in China. J. Clean. Prod. 2018, 197, 1342–1351. [Google Scholar] [CrossRef]
- Han, L.; Zhou, W.; Li, W.; Li, L. Impact of urbanization level on urban air quality: A case of fine particles (PM2.5) in Chinese cities. Environ. Pollut. 2014, 194, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.B.; Fang, C.L. Spatial-temporal characteristics and determinants of PM2.5 in the Bohai Rim urban agglomeration. Chemosphere 2016, 148, 148–162. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Tang, Q.; Gong, D.Y.; Zhang, Z. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, C.; Wang, Z.; Feng, K.; Hubacek, K. The characteristics and drivers of fine particulate matter (PM2.5) distribution in China. J. Clean. Prod. 2017, 142, 1800–1809. [Google Scholar] [CrossRef]
- The Outline of Yangtze River Economic Belt Development ProgramPlan. Available online: http://www.gov.cn/xinwen/2016-09/12/content_5107501.htm (accessed on 30 January 2019).
- Ehrlich, P.R.; Holdren, J.P. Impact of population growth. Science 1971, 171, 1212–1217. [Google Scholar] [CrossRef] [PubMed]
- Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Wang, M.; Che, Y.; Yang, K.; Wang, M.; Xiong, L.; Huang, Y. A local-scale low-carbon plan based on the STIRPAT model and the scenario method: The case of Minhang District, Shanghai, China. Energy Policy 2011, 39, 6981–6990. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Li, N. Analysis on influence factors of China’s CO2 emissions based on Path–STIRPAT model. Energy Policy 2011, 39, 6906–6911. [Google Scholar] [CrossRef]
- Diao, B.; Ding, L.; Su, P.; Cheng, J. The spatial-temporal characteristics and influential factors of NOx emissions in China: A spatial econometric analysis. Int. J. Environ. Res. Public Health 2018, 15, 1405. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Zheng, T.; Tong, L. An empirical test of the environmental Kuznets curve in China: A panel cointegration approach. China Econ. Rev. 2008, 19, 381–392. [Google Scholar]
- Selden, T.M.; Song, D. Neoclassical growth, the J curve for abatement, and the inverted U curve for pollution. J. Environ. Econ. Manag. 1995, 29, 162–168. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.A.; Sayer, M.; Winker, D.M. Global Annual PM2.5 Grids from MODIS, MISR and SeaWiFS Aerosol Optical Depth (AOD) with GWR, 1998–2016; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2018. [Google Scholar]
- Shao, S.; Yang, L.; Gan, C.; Cao, J.; Geng, Y.; Guan, D. Using an extended LMDI model to explore techno-economic drivers of energy-related industrial CO2 emission changes: A case study for Shanghai (China). Renew. Sustain. Energy Rev. 2016, 55, 516–536. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Wang, Q.; Su, B.; Zhou, P.; Yao, L.X. Industrial energy conservation and emission reduction performance in China: A city-level nonparametric analysis. Appl. Energy 2016, 166, 201–209. [Google Scholar] [CrossRef]
- China’s National Bureau of Statistics (CNBS). Chinese Urban Statistical Yearbook 2007–2017; Chinese Statistics Press: Beijing, China, 2008–2018. Available online: http://www.stats.gov.cn/tjsj/ndsj/ (accessed on 22 March 2019).
- Elhorst, J.P. Dynamic spatial panels: Models, Methods and Inferences. J. Geogr. Syst. 2012, 14, 5–18. [Google Scholar] [CrossRef]
- Peng, J.; Chen, S.; Lü, H.; Liu, Y.; Wu, J. Spatiotemporal patterns of remotely sensed PM2. 5 concentration in China from 1999 to 2011. Remote Sens. Environ. 2016, 174, 109–121. [Google Scholar] [CrossRef]
- Lottmann, F. Spatial dependencies in German matching functions. Reg. Sci Urban Econ. 2012, 42, 27–41. [Google Scholar] [CrossRef]
- Bai, C.E.; Ma, H.; Pan, W. Spatial spillover and regional economic growth in China. China Econ. Rev. 2012, 23, 982–990. [Google Scholar] [CrossRef]
- Jin, G.; Deng, X.; Zhao, X.; Guo, B.; Yang, J. Spatiotemporal patterns in urbanization efficiency within the Yangtze River Economic Belt between 2005 and 2014. J. Geogr. Sci. 2018, 28, 1113–1126. [Google Scholar] [CrossRef]
- Hausman, J.A. Specification tests in econometrics. Econom. J. Econom. Soc. 1978, 1251–1271. [Google Scholar] [CrossRef]
- Blundell, R.; Bond, S. Initial conditions and moment restrictions in dynamic panel data models. J. Econom. 1998, 87, 115–143. [Google Scholar] [CrossRef]
- Arellano, M.; Bover, O. Another look at the instrumental variable estimation of error-components models. J. Econom. 1995, 68, 29–51. [Google Scholar] [CrossRef]
- Wang, X.; Tian, G.; Yang, D.; Zhang, W.; Lu, D.; Liu, Z. Responses of PM2.5 pollution to urbanization in China. Energy Policy 2018, 123, 602–610. [Google Scholar] [CrossRef]
- Xu, S.C.; He, Z.X.; Long, R.Y.; Shen, W.X.; Ji, S.B.; Chen, Q.B. Impacts of economic growth and urbanization on CO2 emissions: Regional differences in China based on panel estimation. Reg. Environ. Chang. 2016, 16, 777–787. [Google Scholar] [CrossRef]

| Variable | Type of Variables | Units of Measurement | Mean | Standard Deviation | Min | Max |
|---|---|---|---|---|---|---|
| PM2.5 | Dependent variable | μg/m3 | 40.15 | 14.883 | 2.41 | 74.04 |
| Urban | Explanatory variable | % | 48.45 | 13.535 | 14.58 | 91.24 |
| Control variable | person/km2 | 898.58 | 632.360 | 53.16 | 3934.35 | |
| Control variable | Yuan | 49,110.74 | 34,216.63 | 4490 | 43,9321 | |
| Control variable | % | 0.17 | 0.05 | 0.05 | 0.36 | |
| Control variable | % | 50.55 | 10.50 | 15.89 | 79.14 |
| Year | Moran’s I | Standard Deviation | p-Value |
|---|---|---|---|
| 2006 | 0.609 | 0.0624 | 0.001 |
| 2007 | 0.721 | 0.0631 | 0.001 |
| 2008 | 0.698 | 0.0651 | 0.001 |
| 2009 | 0.706 | 0.0617 | 0.001 |
| 2010 | 0.657 | 0.0664 | 0.001 |
| 2011 | 0.661 | 0.0637 | 0.001 |
| 2012 | 0.622 | 0.0644 | 0.001 |
| 2013 | 0.663 | 0.0658 | 0.001 |
| 2014 | 0.670 | 0.0640 | 0.001 |
| 2015 | 0.778 | 0.0635 | 0.001 |
| 2016 | 0.743 | 0.0627 | 0.001 |
| Determinants | Fixed Effect Model | System GMM | Spatial Panel Model | Dynamic Spatial Model |
|---|---|---|---|---|
| 0.798 *** | 0.356 *** | |||
| (0.029) | (0.012) | |||
| 0.833 *** | 0.797 *** | |||
| (0.031) | (0.019) | |||
| 3.992 | −10.473 * | 0.361 | 5.231 * | |
| (2.691) | (5.495) | (1.877) | (2.934) | |
| −1.137 | 2.873 * | −0.124 | −1.406 * | |
| (0.760) | (1.545) | (0.527) | (0.799) | |
| 0.104 | −0.263 * | 0.013 | 0.124 ** | |
| (0.071) | (0.143) | (0.049) | (0.072) | |
| 0.010 | 0.098 ** | −0.011 | 0.120 *** | |
| (0.015) | (0.042) | (0.010) | (0.019) | |
| −0.087 *** | −0.024 *** | −0.018 * | 0.013 ** | |
| (0.012) | (0.021) | (0.010) | (0.007) | |
| −0.015 | −0.017 | −0.003 | −0.019 * | |
| (0.014) | (0.034) | (0.010) | (0.012) | |
| 0.151 *** | 0.392 *** | 0.054 * | 0.053 *** | |
| (0.014) | (0.074) | (0.030) | (0.014) | |
| Constant | −0.622 | 11.536* | −8.086 ** | |
| (3.176) | (6.503) | (3.579) | ||
| Observations | 1188 | 1080 | 1188 | 1080 |
| R-squared | 0.231 | 0.251 | 0.9456 |
| Variables | Regional Heterogeneity | ||||
|---|---|---|---|---|---|
| Upstream | Midstream | Downstream | |||
| 0.545 *** | 0.148 *** | 0.149 *** | 0.164 *** | 0.146 *** | |
| (0.037) | (0.007) | (0.007) | (0.009) | (0.036) | |
| 0.996 *** | 1.093 *** | 1.097 *** | 1.051 *** | 1.273 *** | |
| (0.038) | (0.010) | (0.008) | (0.008) | (0.021) | |
| 0.522 ** | 0.130 | 0.289 *** | 0.039 *** | 164.259 *** | |
| (0.235) | (0.089) | (0.022) | (0.005) | (63.064) | |
| −0.069 * | 0.009 | −0.023 *** | −41.521 *** | ||
| (0.036) | (0.017) | (0.002) | (15.772) | ||
| 0.003 | −0.002 ** | 3.499 *** | |||
| (0.002) | (0.001) | (1.313) | |||
| 0.171 *** | −0.001 | −0.001 | −0.001 | −0.011 | |
| (0.028) | (0.001) | (0.001) | (0.002) | (0.007) | |
| 0.107 *** | 0.006 *** | 0.007 *** | 0.009 *** | 0.008 | |
| (0.018) | (0.002) | (0.001) | (0.002) | (0.010) | |
| −0.024* | 0.018 *** | 0.019 *** | 0.020 *** | −0.005 | |
| (0.015) | (0.003) | (0.002) | (0.002) | (0.011) | |
| −0.493 *** | 0.071 *** | 0.064 *** | 0.093 *** | 0.221 *** | |
| (0.068) | (0.011) | (0.010) | (0.010) | (0.073) | |
| Constant | −3.128 *** | −1.761 *** | −2.006 *** | −1.404 *** | −219.2 *** |
| (0.564) | (0.162) | (0.068) | (0.076) | (83.73) | |
| Observations | 310 | 520 | 520 | 520 | 250 |
| AR(1) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| AR(2) | 0.558 | 0.009 | 0.009 | 0.316 | 0.079 |
| Sargan | 1.000 | 0.870 | 0.832 | 0.873 | 1.000 |
| Trajectory | Inversed U | — | — | Line | Line |
| Inflection point | 43% | ||||
| Variables | Urbanization Heterogeneity | |||
|---|---|---|---|---|
| Low Urbanization Level | Medium Urbanization Level | High Urbanization Level | ||
| 0.585 *** | 0.412 *** | 0.190 *** | 0.189 *** | |
| (0.043) | (0.021) | (0.017) | (0.017) | |
| 0.535 *** | 0.766 *** | 1.191 *** | 1.198 *** | |
| (0.080) | (0.025) | (0.021) | (0.023) | |
| −63.703 *** | −81.670 *** | 45.997 | −3.488 ** | |
| (21.886) | (26.471) | (32.127) | (1.570) | |
| 18.806 *** | 22.383 *** | −11.637 | 0.448 ** | |
| (6.454) | (7.133) | (7.915) | (0.194) | |
| −1.842 *** | −2.040 *** | 0.983 | ||
| (0.631) | (0.640) | (0.650) | ||
| 0.0594 * | 0.017 *** | 0.004 | 0.001 | |
| (0.033) | (0.006) | (0.006) | (0.006) | |
| −0.021 | 0.017 *** | 0.007 ** | 0.006 ** | |
| (0.022) | (0.005) | (0.003) | (0.003) | |
| −0.021 * | 0.013 ** | 0.016 *** | 0.016 *** | |
| (0.011) | (0.0062) | (0.004) | (0.004) | |
| −0.050 | 0.115 *** | 0.149 *** | 0.147 *** | |
| (0.071) | (0.029) | (0.047) | (0.045) | |
| Constant | 71.151 *** | 97.662 *** | −62.866 | 4.620 |
| (24.639) | (32.798) | (43.379) | (3.094) | |
| Observations | 320 | 350 | 410 | 410 |
| Sargan test | 1.000 | 0.999 | 0.995 | 0.996 |
| AR(1) | 0.001 | 0.000 | 0.000 | 0.000 |
| AR(2) | 0.352 | 0.707 | 0.846 | 0.854 |
| Trajectory | Inverted N | Inverted N | — | U |
| Inflection point | 24%, 38% | 33%, 46% | — | 49% |
| Year | Low Urbanization Level | Medium Urbanization Level | High Urbanization Level | |||||
|---|---|---|---|---|---|---|---|---|
| <24 | 24–38 | >38 | <33 | 33–46 | >46 | <49 | >49 | |
| 2006 | 7 | 25 | 0 | 11 | 24 | 0 | 17 | 24 |
| 2007 | 4 | 28 | 0 | 2 | 33 | 0 | 13 | 28 |
| 2008 | 1 | 31 | 0 | 0 | 34 | 1 | 5 | 36 |
| 2009 | 1 | 30 | 1 | 0 | 29 | 6 | 2 | 39 |
| 2010 | 1 | 29 | 2 | 0 | 26 | 9 | 0 | 41 |
| 2011 | 1 | 24 | 7 | 0 | 22 | 13 | 0 | 41 |
| 2012 | 0 | 18 | 14 | 0 | 16 | 19 | 0 | 41 |
| 2013 | 0 | 14 | 18 | 0 | 14 | 21 | 0 | 41 |
| 2014 | 0 | 10 | 22 | 0 | 8 | 27 | 0 | 41 |
| 2015 | 0 | 7 | 25 | 0 | 3 | 32 | 0 | 41 |
| 2016 | 0 | 4 | 28 | 0 | 0 | 35 | 0 | 41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Deng, H.; Chong, Z. The Spatial and Heterogeneity Impacts of Population Urbanization on Fine Particulate (PM2.5) in the Yangtze River Economic Belt, China. Int. J. Environ. Res. Public Health 2019, 16, 1058. https://doi.org/10.3390/ijerph16061058
Xie W, Deng H, Chong Z. The Spatial and Heterogeneity Impacts of Population Urbanization on Fine Particulate (PM2.5) in the Yangtze River Economic Belt, China. International Journal of Environmental Research and Public Health. 2019; 16(6):1058. https://doi.org/10.3390/ijerph16061058
Chicago/Turabian StyleXie, Weiwei, Hongbing Deng, and Zhaohui Chong. 2019. "The Spatial and Heterogeneity Impacts of Population Urbanization on Fine Particulate (PM2.5) in the Yangtze River Economic Belt, China" International Journal of Environmental Research and Public Health 16, no. 6: 1058. https://doi.org/10.3390/ijerph16061058
APA StyleXie, W., Deng, H., & Chong, Z. (2019). The Spatial and Heterogeneity Impacts of Population Urbanization on Fine Particulate (PM2.5) in the Yangtze River Economic Belt, China. International Journal of Environmental Research and Public Health, 16(6), 1058. https://doi.org/10.3390/ijerph16061058





