Classification of Fatigued and Drunk Driving Based on Decision Tree Methods: A Simulator Study
Abstract
:1. Introduction
2. Literature Review
2.1. Fatigue Driving
2.2. Drunk Driving
2.3. Driving Simulator Study
3. Materials and Methods
3.1. Participants
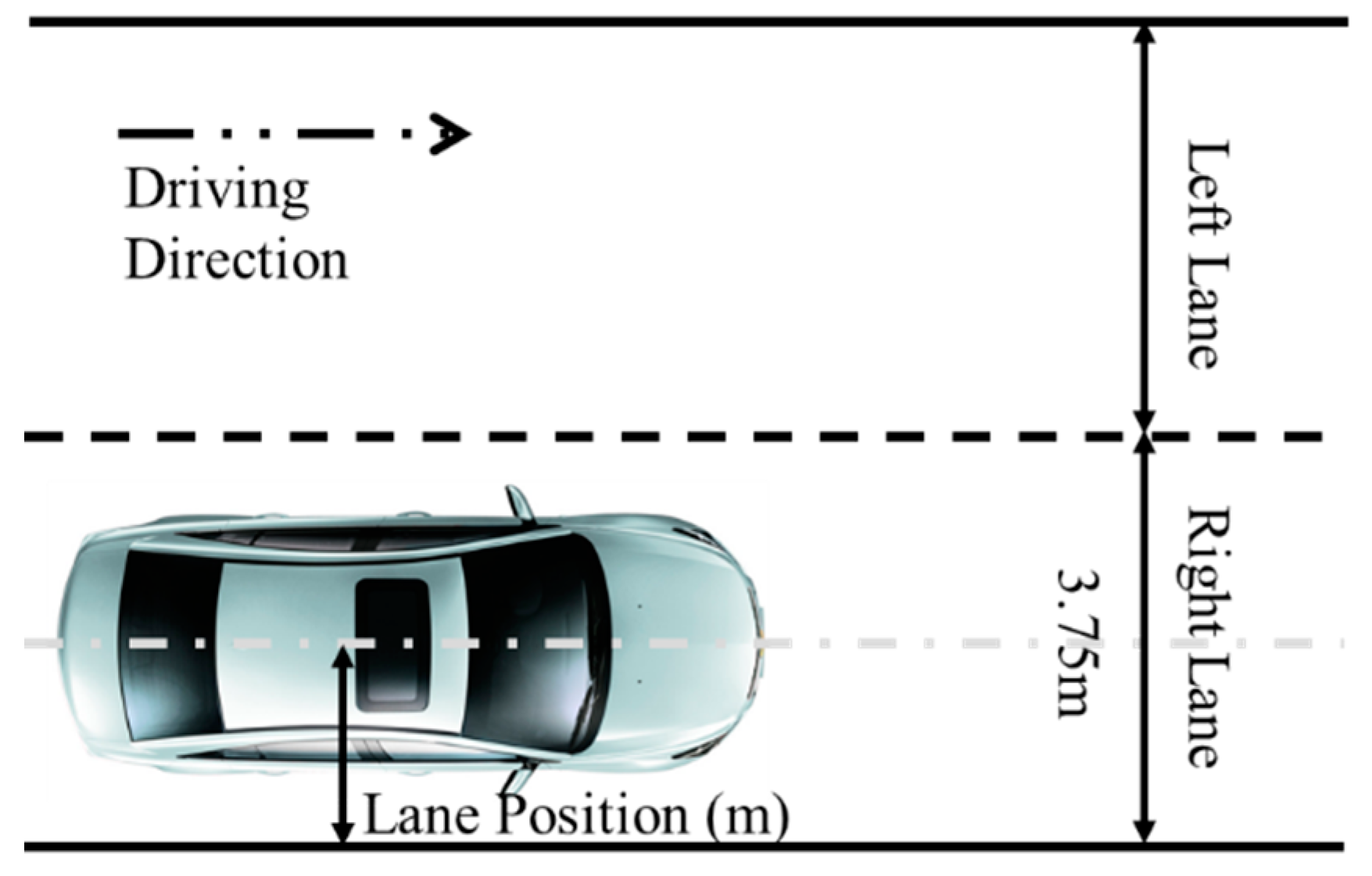
3.2. Apparatus
3.2.1. Equipment
3.2.2. Driving Scenario
3.3. Experimental Design and Procedure
3.4. Data Collection and Analysis
3.5. Introduction of Previous Research
3.6. Decision Trees
- Each tree is composed of a maximum of five depth levels.
- There must be a minimum number of five cases in a child node and a minimum number of 10 cases for the parent node.
- Use “Gini” as the impurity measure.
- The minimum change in improvement is 0.0001.
4. Results and Discussion
Decision Tree
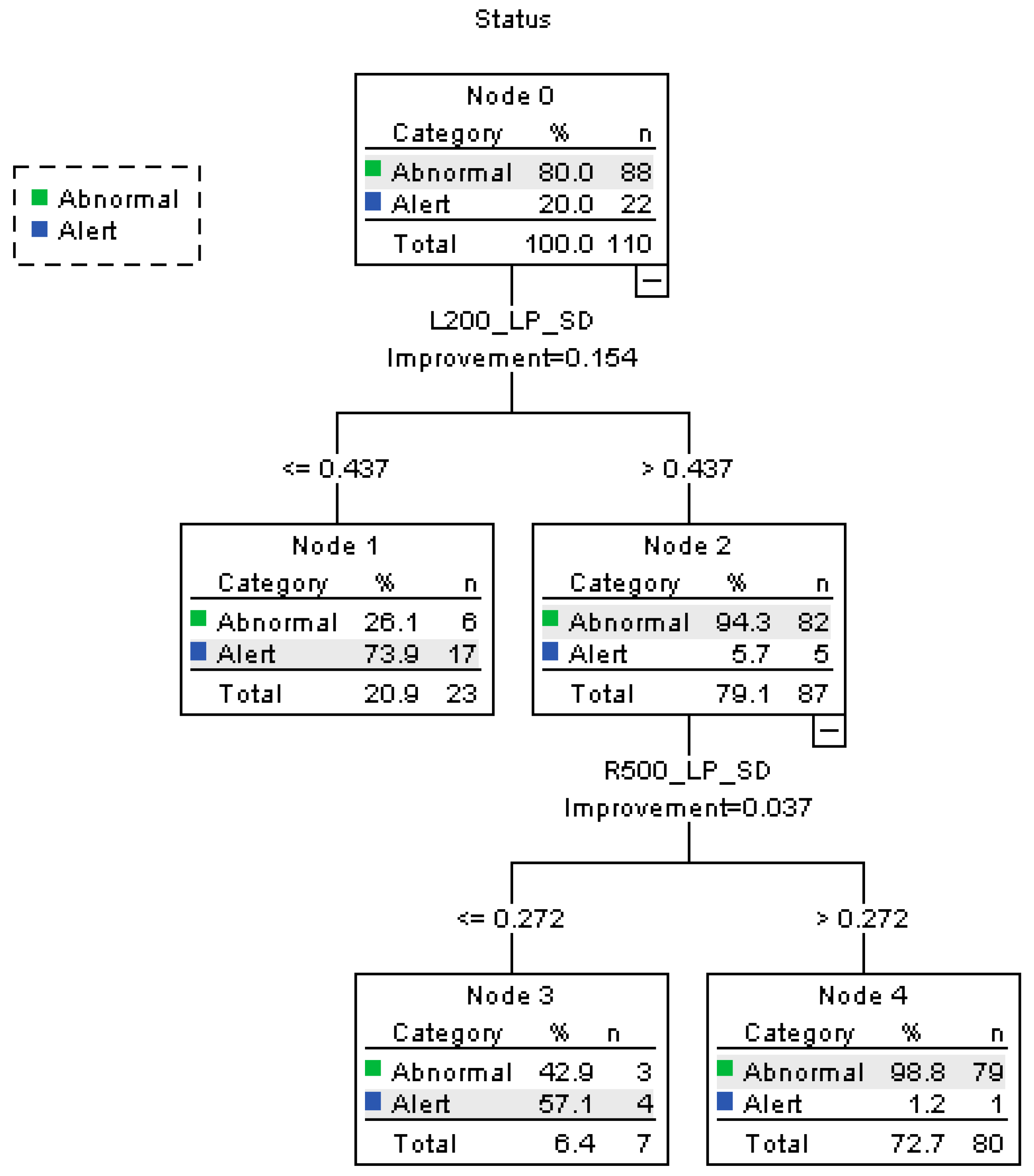
- (1)
- On the curve to the left with a radius of 200 m, when L200_LP_SD ≤ 0.437, 20.9% of the participants fall into “alert” category. The rest 79.1% are under the “abnormal” state.
- (2)
- When L200_LP_SD is larger than 0.437, 94.3% of the participants under abnormal state are correctly classified.
- (3)
- On a curve to the right with a radius of 500 m, when R500_LP_SD > 0.272, 72.7% of the participants are classified as “abnormal”. The percent correct of the abnormal state is 98.8%.
- (4)
- As a conclusion, the accuracy rate of the alert state is 95.5% and abnormal state 89.8%. The overall accuracy rate is 90.9%, the precision is 98.75%, and the recall is 89.77%. The risk estimate of resubstitution is 0.091 and the risk estimate of cross-validation is 0.164.
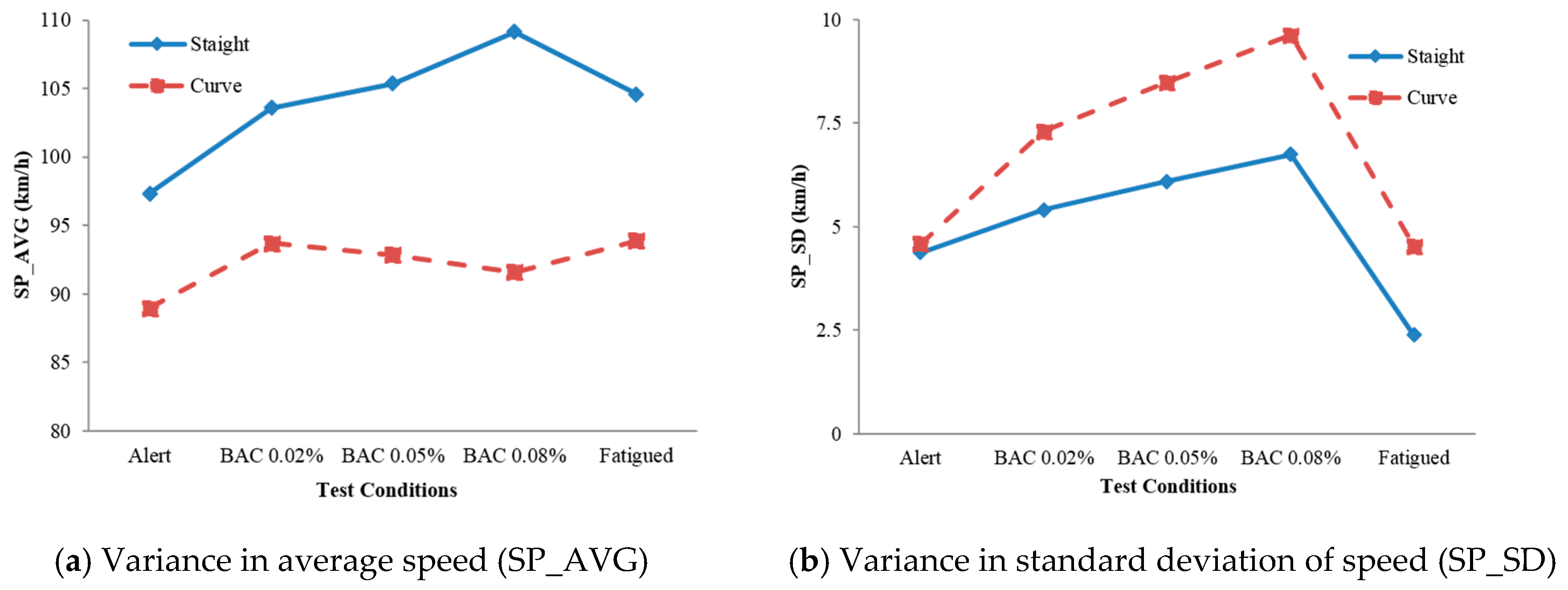
- (1)
- On a curve to the right with a radius of 200 m, when SP_SD > 6.146, 50% of the participants are classified as drunk driving, and none of them are fatigued.
- (2)
- When R200_SP_SD ≤ 6.146, the other 50% of the participant also are considered as “drunk”. Then on a curve to the left with a radius of 500 m, where L500_LP_AVG ≤ 2.082, 18.2% of the drivers are classified as performing fatigued driving. The accuracy rate is 87.5%. When L500_LP_AVG > 2.082, 31.8% of the participants are judged as having drunk alcohol.
- (3)
- When L200_LP_SD ≤ 0.555, 8% of the participants are reclassified as “fatigued”. When L200_LP_SD > 0.555, the other participants are distinguished as “drunk driving”;
- (4)
- As a conclusion, the accuracy rate of fatigued state is 90.9%, and the drinking state 95.5%. The overall accuracy rate is 94.4%, the precision is 96.92%, and the recall is 95.45%.The risk estimate of resubstitution is 0.057 and the risk estimate of cross-validation is 0.250.
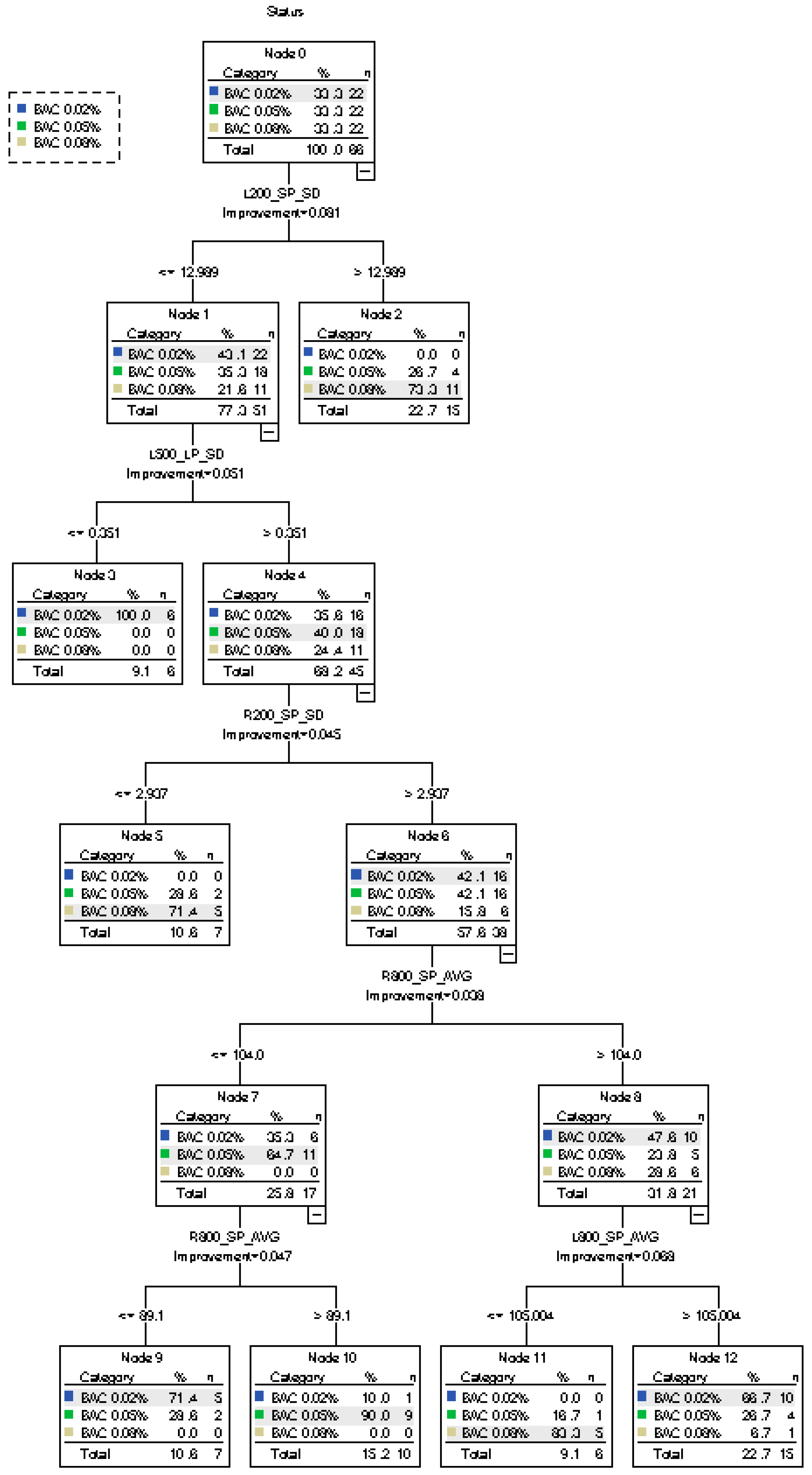
- (1)
- When L200_SP_SD ≤12.989, 77.3% of the participants are classified to level BAC 0.02%. The rest (22.7%) are classified to level BAC 0.08% since L200_SP_SD >12.989.
- (2)
- When L500_LP_SD ≤0.351, 9.1% of the participants are classified as BAC 0.02%, accurately. Here, 68.2% of the participants are classified as BAC 0.05%. When R200_SP_SD ≤2.937, 10.6% of the participants are classified as BAC 0.08%.
- (3)
- Further classification is performed for BAC 0.02%, BAC 0.05%, and BAC 0.08%, according to R800_SP_AVG and L800_SP_AVG
- (4)
- As a conclusion, the accuracy rates of BAC 0.02% and BAC 0.08% are 95.5%, and the accuracy rate of BAC 0.05% is 40.9%. Since this classification has three categories, the accuracy, precision, and recall of each category are calculated, and the overall evaluation indexes are determined by the mean value of each category. The overall accuracy rate is 77.3%, the precision is 61.32%, and the recall is 80%. The risk estimate of resubstitution is 0.227 and the risk estimate of cross-validation is 0.606.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Williamson, A.; Lombardi, D.A.; Folkard, S.; Stutts, J.; Courtney, T.K.; Connor, J.L. The Link Between Fatigue and Safety. Accid. Anal. Prev. 2011, 43, 498–515. [Google Scholar] [CrossRef]
- Qi, J.Y. Study on Driving Fatigue Based on Ergonomics. Adv. Mater. Res. 2013, 706, 2119–2123. [Google Scholar] [CrossRef]
- Williams, A.F. Alcohol-impaired Driving and Its Consequences in the United States: The Past 25 Years. J. Saf. Res. 2006, 37, 123–138. [Google Scholar] [CrossRef]
- Nordbakke, S.; Sagberg, F. Sleepy at the Wheel: Knowledge, Symptoms, and Behavior among Car Drivers. Transp. Res. Part F 2007, 10, 1–10. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Alcohol and Health; WHO: Geneva, Switzerland, 2011; ISBN 9789241564151. [Google Scholar]
- Akerstedt, T.; Peters, B.; Anund, A.; Kecklund, G. Impaired Alertness and Performance Driving Home from the Night Shift: A Driving Simulator Study. J. Sleep Res. 2001, 14, 17–20. [Google Scholar] [CrossRef]
- Eskandarian, A.; Sayed, R.; Delaigue, P.; Blum, J.; Mortazavi, A. Advanced Driver Fatigue Research; DTMC75-03-H-00001; U.S. Department of Transportation: Washington, DC, USA, 2007.
- NHTSA. Drowsy Driving; DOT HS 811 449; National Highway Traffic Safety Administration: Washington, DC, USA, 2011.
- Fillmore, M.T.; Blackburn, J.S.; Harrison, E.L.R. Acute Disinhibiting Effects of Alcohol as a Factor in Risky Driving Behavior. Drug Alcohol Depend. 2008, 95, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Arnedt, J.T.; Wilde, G.J.S.; Munt, P.W.; MacLean, A.W. How Do Prolonged Wakefulness and Alcohol Compare in the Decrements They Produce on a Simulated Driving Task? Accid. Anal. Prev. 2001, 33, 337–344. [Google Scholar] [CrossRef]
- Thiffault, P.; Bergeron, J. Monotony of Road Environment and Driver Fatigue: A Simulator Study. Accid. Anal. Prev. 2003, 35, 381–391. [Google Scholar] [CrossRef]
- Chen, F.; Chen, S. Injury severities of truck drivers in single- and multi-vehicle accidents on rural highways. Accid. Anal. Prev. 2011, 43, 1677–1688. [Google Scholar] [CrossRef]
- Chen, F.; Chen, S.; Ma, X. Analysis of hourly crash likelihood using unbalanced panel data mixed logit model and real-time driving environmental big data. J. Saf. Res. 2018, 65, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Shinar, D. Traffic Safety and Human Behavior; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Desmond, P.A.; Matthews, G. Implications of Task Induced Fatigue Effects for In-Vehicle Countermeasures to Driver Fatigue. Accid. Anal. Prev. 1997, 29, 513–523. [Google Scholar] [CrossRef]
- Dawson, D.; Reid, K. Fatigue, Alcohol and Performance Impairment. Nature 1997, 388, 23. [Google Scholar] [CrossRef]
- Du, H.J.; Zhao, X.H.; Zhang, G.H.; Rong, J. Effects of Alcohol and Fatigue on Driving Performance in Different Roadway Geometries. Transp. Res. Rec. J. Transp. Res. Board 2016, 2584, 88–96. [Google Scholar] [CrossRef]
- Ma, X.; Chen, S.; Chen, F. Multivariate space-time modeling of crash frequencies by injury severity levels. Anal. Methods Accid. Res. 2017, 15, 29–40. [Google Scholar] [CrossRef]
- Hernandezgress, N.; Esteve, D. Multisensory Fusion and Neural Networks Methodology: Application to the Active Security in Driving Behavior. In Proceedings of the 2nd World Congress on Intelligent Transport Systems, Tokyo, Japan, 9–11 November 1995; pp. 1146–1151. [Google Scholar]
- Tsironis, L.; Mavropoulos, H.; Moustakis, V.; Kontogiannis, T. Mining Aberrant Driving Behavior Characteristics. Trans. Inf. Sci. Appl. 2005, 2, 1743–1750. [Google Scholar]
- Kumagai, T.; Akamatsu, M. Prediction of Human Driving Behavior Using Dynamic Bayesian Networks. IEICE Trans. Inf. Syst. 2006, 89, 857–860. [Google Scholar] [CrossRef]
- Berry, M.; Linoff, G. Data Mining Techniques; Wiley: Indianapolis, IN, USA, 2004. [Google Scholar]
- Breiman, J.; Friedman, R.; Olshen, A.; Stone, C. Classification and Regression Trees; Chapman & Hall: New York, NY, USA, 1984. [Google Scholar]
- Miller, T. Data and Text Mining: A Business and Applications Approach; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Lal, S.K.; Craig, A. A critical review of the psychophysiology of driver fatigue. Biol. Psychol. 2001, 55, 173–194. [Google Scholar] [CrossRef]
- Jap, B.T.; Lal, S.; Fischer, P.; Bekiaris, E. Using EEG spectral components to assess algorithms for detecting fatigue. Expert Syst. Appl. 2009, 36, 2352–2359. [Google Scholar] [CrossRef]
- Patel, M.; Lal, S.K.; Kavanagh, D.; Rossiter, P. Applying neural network analysis on heart rate variability data to assess driver fatigue. Expert Syst. Appl. 2011, 38, 7235–7242. [Google Scholar] [CrossRef]
- Katsis, C.D.; Ntouvas, N.E.; Bafas, C.G.; Fotiadis, D.I. Assessment of muscle fatigue during driving using surface EMG. In Proceedings of the IASTED International Conference on Biomedical Engineering, Innsbruck, Austria, 16–18 February 2004. [Google Scholar]
- Ji, Q.; Zhu, Z.; Lan, P. Real-time nonintrusive monitoring and prediction of driver fatigue. IEEE Trans. Veh. Technol. 2004, 53, 1052–1068. [Google Scholar] [CrossRef]
- Friedrichs, F.; Yang, B. Drowsiness monitoring by steering and lane data based features under real driving conditions. In Proceedings of the 2010 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010; pp. 209–213. [Google Scholar]
- Krajewski, J.; Sommer, D.; Trutschel, U.; Edwards, D.; Golz, M. Steering wheel behavior based estimation of fatigue. In Proceedings of the 2009 Driving Assessment Conference, Big Sky, MT, USA, 22–25 June 2009. [Google Scholar]
- Pierce, D.R.; West, J.R. Blood alcohol concentration: A critical factor for producing fetal alcohol effects. Alcohol 1986, 3, 269–272. [Google Scholar] [CrossRef]
- O’Connor, S.; Morzorati, S.; Christian, J.; Li, T.K. Clamping breath alcohol concentration reduces experimental variance: Application to the study of acute tolerance to alcohol and alcohol elimination rate. Alcohol. Clin. Exp. Res. 1998, 22, 202–210. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ho, C.H. The effects of different breath alcohol concentration and post alcohol upon driver’s driving performance. In Proceedings of the 2007 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2–4 December 2007; pp. 505–509. [Google Scholar]
- Hammoud, R.I.; Wilhelm, A.; Malawey, P.; Witt, G.J. Efficient real-time algorithms for eye state and head pose tracking in advanced driver support systems. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; p. 1181. [Google Scholar]
- Zhao, X.; Zhang, X.; Rong, J.; Ma, J. Identifying method of drunk driving based on driving behavior. Int. J. Comput. Intell. Syst. 2011, 4, 361–369. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Rong, J. Study of the effects of alcohol on drivers and driving performance on straight road. Math. Probl. Eng. 2014, 607652. [Google Scholar] [CrossRef]
- Dai, J.; Teng, J.; Bai, X.; Shen, Z.; Xuan, D. Mobile phone based drunk driving detection. In Proceedings of the 2010 4th International Conference on Pervasive Computing Technologies for Healthcare, Munich, Germany, 22–25 March 2010; pp. 1–8. [Google Scholar]
- Bella, F.; Calvi, A.; D’Amico, F. Analysis of driver speeds under night driving conditions using a driving simulator. J. Saf. Res. 2014, 49, 45–52. [Google Scholar] [CrossRef]
- Casutt, G.; Martin, M.; Keller, M.; Jancke, L. The relation between performance in on-road driving, cognitive screening and driving simulator in older healthy drivers. Transp. Res. Part F 2014, 22, 232–244. [Google Scholar] [CrossRef]
- Tuokko, H.; Myers, A.; Jouk, A.; Marshall, S.; Man-Son Hing, M.; Porter, M.M.; Bedard, M.; Gelinas, J.; Korner-Bitensky, N.; Mazer, B.; et al. Associations between age, gender, psychosocial and health characteristics in the Candrive II study cohort. Accid. Anal. Prev. 2015, 61, 267–271. [Google Scholar] [CrossRef]
- Jurecki, R. An Analysis of Collision Avoidance Maneuvers in emergency traffic situations. Arch. Automot. Eng. 2016, 72, 73–93. [Google Scholar]
- Dulebenets, M.A.; Pasha, J.; Abioye, O.F.; Kavoosi, M.; Ozguven, E.E.; Moses, R.; Boot, W.R.; Sando, T. Exact and heuristic solution algorithms for efficient emergency evacuation in areas with vulnerable populations. Int. J. Disaster Risk Reduct. 2019, 101114. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Abioye, O.F.; Ozguven, E.E.; Moses, R.; Boot, W.R.; Sando, T. Development of statistical models for improving efficiency of emergency evacuation in areas with vulnerable population. Reliab. Eng. Syst. Saf. 2019, 182, 233–249. [Google Scholar] [CrossRef]
- Man-Son-Hing, M.; Marshall, S.C.; Molnar, F.J.; Wilson, K.G. Systematic review of driving risk and the efficacy of compensatory strategies in persons with dementia. J. Am. Geriatr. Soc. 2007, 55, 878–884. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhao, X.; Rong, J.; Zhang, Y. How eco-driving training course influences driver behavior and comprehensibility: A driving simulator study. Cogn. Technol. Work 2017, 19, 731–742. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, X.; Du, H.; Zhang, Y.; Rong, J. Classification of Distracted Driving Based on Visual Features and Behavior Data using a Random Forest Method. Transp. Res. Rec. 2018, 2672, 210–221. [Google Scholar] [CrossRef]
- Yan, X.; Abdel-Aty, M.; Radwan, E.; Wang, X.; Chilakapati, P. Validating a driving simulator using surrogate safety measures. Accid. Anal. Prev. 2008, 40, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Zador, P.L. Alcohol-related Relative Risk of Fatal Driver Injuries in Relation to Driver Age and Sex. J. Stud. Alcohol 1991, 52, 302–310. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Zhao, X.H.; Rong, J.; Ma, J.M. Experimental Research on the Effectiveness of Speed Reduction Markings Based on Driving Simulation: A Case Study. Accid. Anal. Prev. 2013, 60, 211–218. [Google Scholar] [CrossRef]
- Watson, P.E. Total Body Water and Blood Alcohol Levels: Updating the Fundamentals. Hum. Metab. Alcohol 1989, 1, 41–58. [Google Scholar]
- Zhang, X.J.; Zhao, X.H.; Du, H.J.; Ma, J.M.; Rong, J. Effect of Different Breath Alcohol Concentrations on Driving Performance in Horizontal Curves. Accid. Anal. Prev. 2014, 72, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Yazici, M.A.; Demiroluk, S.; Ozbay, K.; Carnegie, J.A. Use of Feature Selection and Variable Ranking in Classification and Regression Tree Evacuee Decision Model; Transportation Research Board: Washington, DC, USA, 2012. [Google Scholar]




| Performance Measure | Main | Interaction | ||||
|---|---|---|---|---|---|---|
| S | D | R | S D | S R | S D R | |
| SP_AVG | 0.000 * | 0.019 * | 0.000 * | 0.828 | 0.048 * | 0.806 |
| LP_AVG | 0.000 * | 0.000 * | 0.248 | 0.001 * | 0.746 | 0.404 |
| SP_SD | 0.000 * | 0.224 | 0.247 | 0.148 | 0.001 * | 0.004 * |
| LP_SD | 0.000 * | 0.089 | 0.003 * | 0.095 | 0.175 | 0.183 |
| Observed | Predicted Percent Correct (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Roadway Geometry | A | B | C | D | E | F | G | H | I | X |
| Overall 1 | Straight 2 | Curve 3 | L200 4 | L500 | L800 | R200 | R500 | R800 | Combined 5 | |
| Alert | 68.2 | 27.3 | 86.4 | 86.4 | 90.9 | 77.3 | 90.9 | 68.2 | 54.5 | 86.4 |
| Fatigue | 31.8 | 68.2 | 59.1 | 50.0 | 36.4 | 22.7 | 59.1 | 81.8 | 72.7 | 90.9 |
| BAC 0.02% | 86.4 | 63.6 | 45.5 | 90.9 | 68.2 | 9.1 | 68.2 | 31.8 | 0.0 | 50.0 |
| BAC 0.05% | 36.4 | 0.0 | 81.8 | 0.0 | 50.0 | 77.3 | 36.4 | 72.7 | 68.2 | 54.5 |
| BAC 0.08% | 31.8 | 77.3 | 27.3 | 45.5 | 18.2 | 72.7 | 72.7 | 45.5 | 50.0 | 63.6 |
| Overall Percentage | 50.9 | 47.3 | 60.0 | 54.5 | 52.7 | 51.8 | 65.5 | 60.0 | 49.1 | 69.1 |
| Method | Estimate | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Roadway Geometry | A | B | C | D | E | F | G | H | I | X |
| Overall | Straight | Curve | L200 | L500 | L800 | R200 | R500 | R800 | Combined | |
| Resubstitution | 0.491 | 0.527 | 0.400 | 0.455 | 0.473 | 0.482 | 0.345 | 0.400 | 0.509 | 0.309 |
| Cross-Validation | 0.736 | 0.645 | 0.700 | 0.609 | 0.691 | 0.755 | 0.682 | 0.682 | 0.709 | 0.764 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Zhao, X.; Du, H.; Zhang, Y.; Zhang, G.; Rong, J. Classification of Fatigued and Drunk Driving Based on Decision Tree Methods: A Simulator Study. Int. J. Environ. Res. Public Health 2019, 16, 1935. https://doi.org/10.3390/ijerph16111935
Yao Y, Zhao X, Du H, Zhang Y, Zhang G, Rong J. Classification of Fatigued and Drunk Driving Based on Decision Tree Methods: A Simulator Study. International Journal of Environmental Research and Public Health. 2019; 16(11):1935. https://doi.org/10.3390/ijerph16111935
Chicago/Turabian StyleYao, Ying, Xiaohua Zhao, Hongji Du, Yunlong Zhang, Guohui Zhang, and Jian Rong. 2019. "Classification of Fatigued and Drunk Driving Based on Decision Tree Methods: A Simulator Study" International Journal of Environmental Research and Public Health 16, no. 11: 1935. https://doi.org/10.3390/ijerph16111935
APA StyleYao, Y., Zhao, X., Du, H., Zhang, Y., Zhang, G., & Rong, J. (2019). Classification of Fatigued and Drunk Driving Based on Decision Tree Methods: A Simulator Study. International Journal of Environmental Research and Public Health, 16(11), 1935. https://doi.org/10.3390/ijerph16111935






