Evaluating the Accessibility of Healthcare Facilities Using an Integrated Catchment Area Approach
Abstract
1. Introduction
2. Method
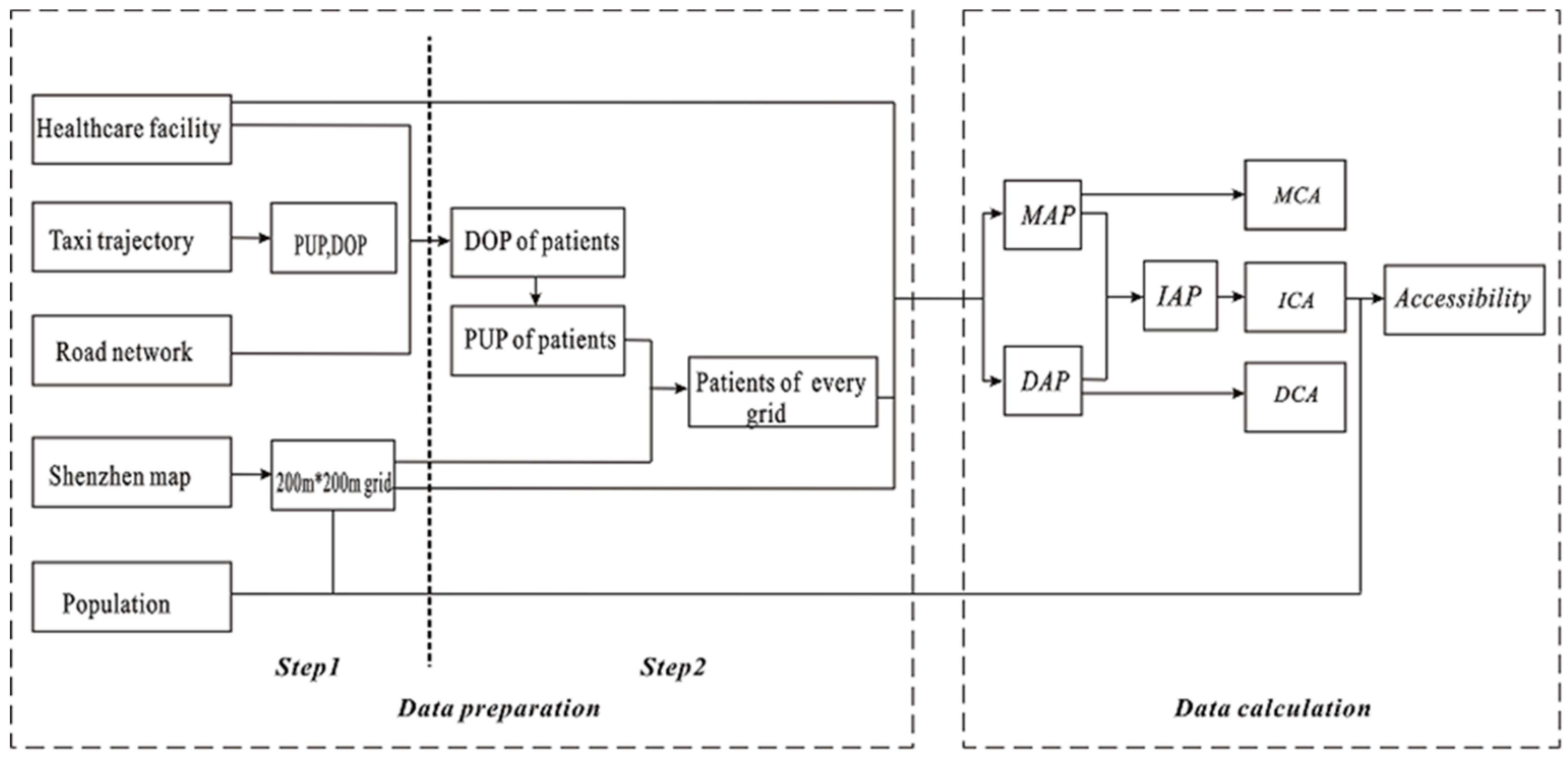
2.1. Conceptual Framework
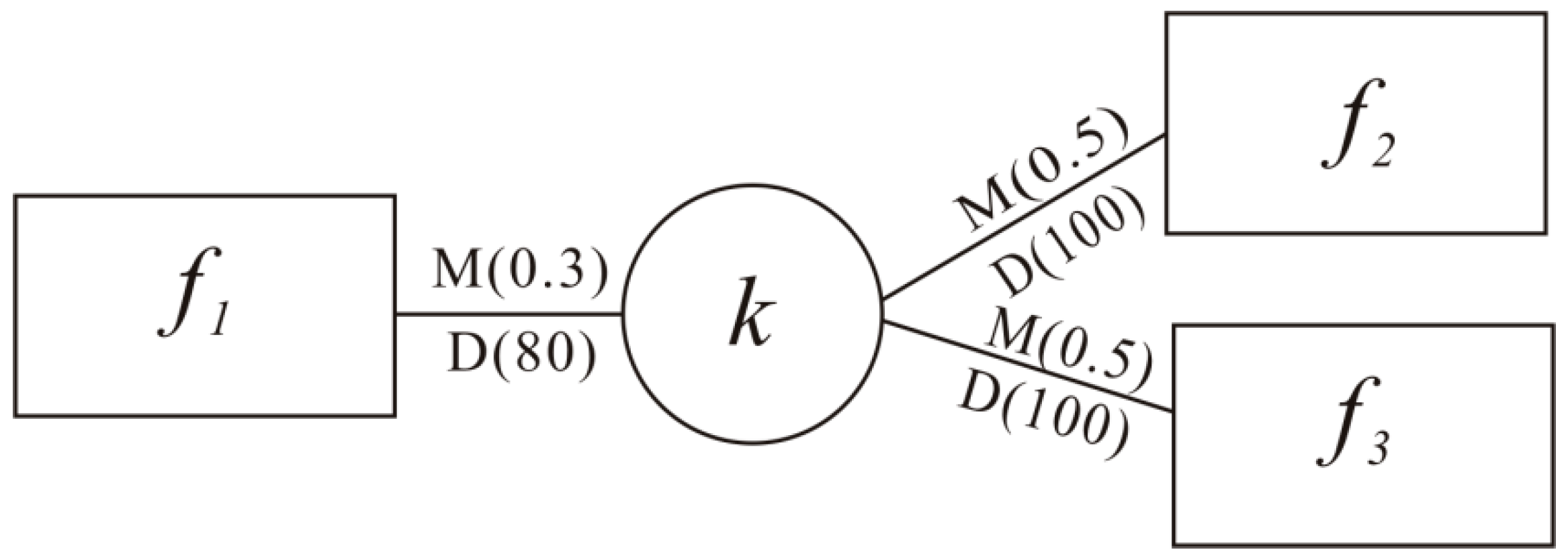
2.2. The Access Probability Indexes
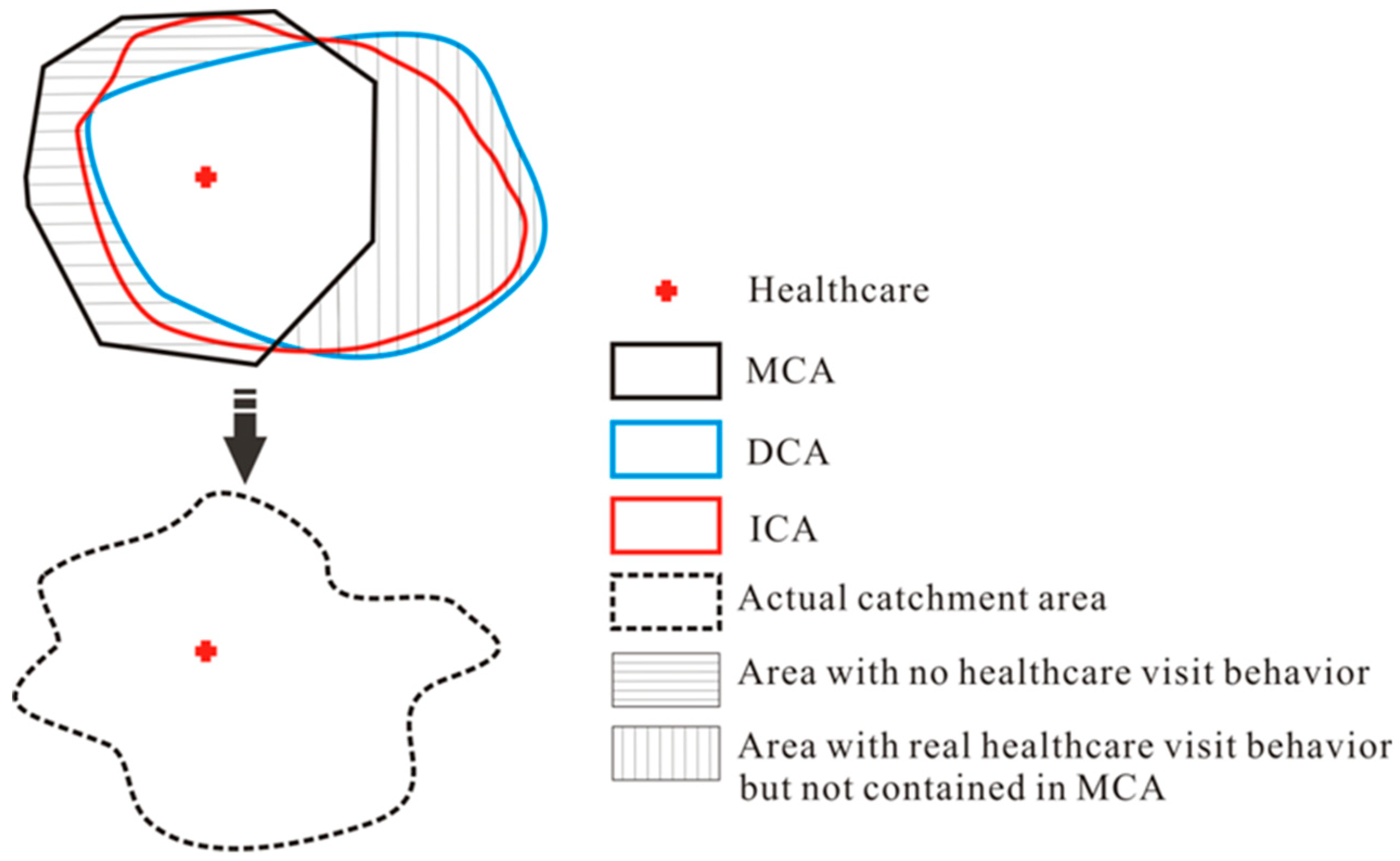
2.3. The Integrated Catchment Area
2.4. Accessibility Measurement Based on ICA
3. Case Study
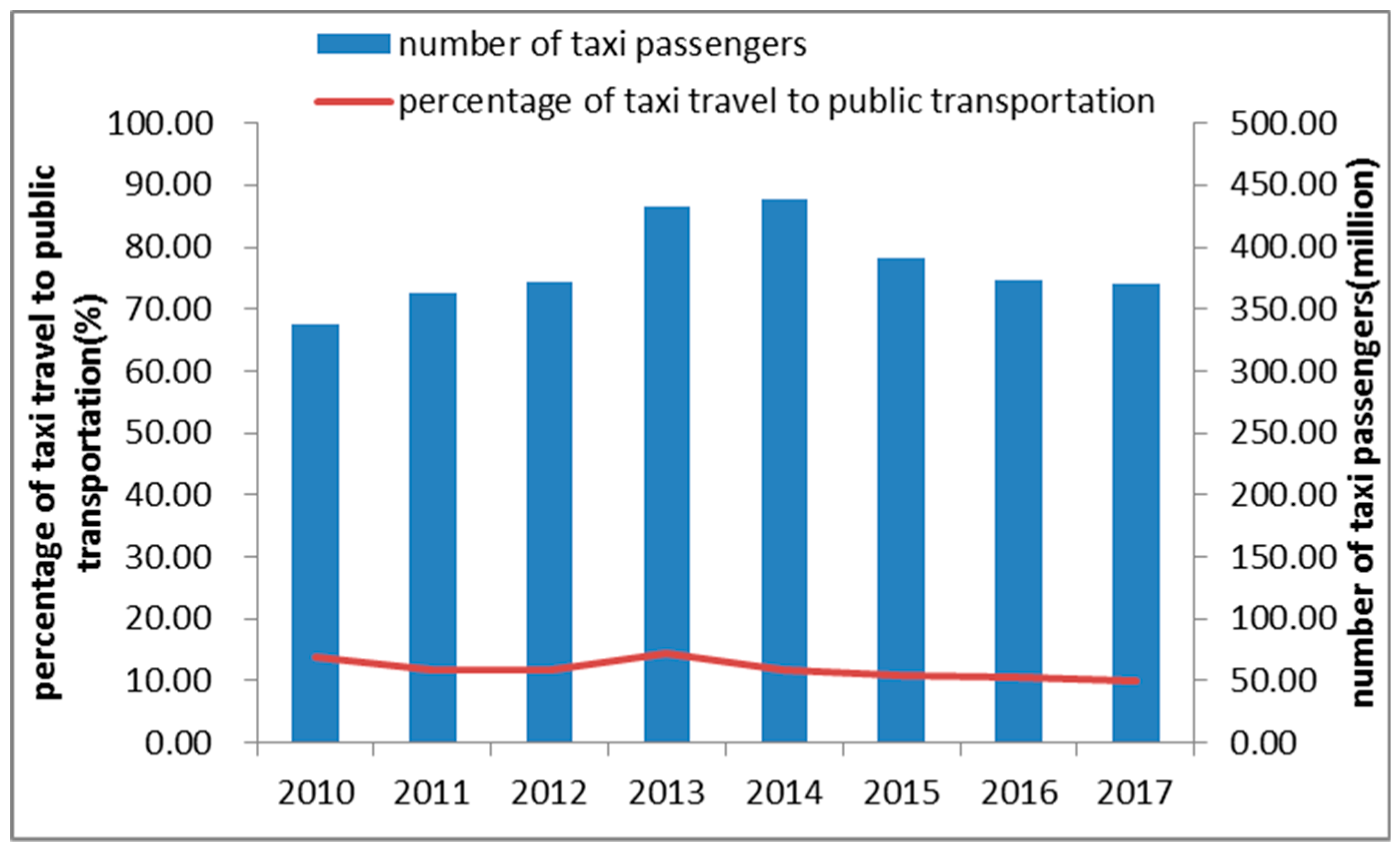
3.1. Study Area
3.2. Data Processing
4. Results and Discussion
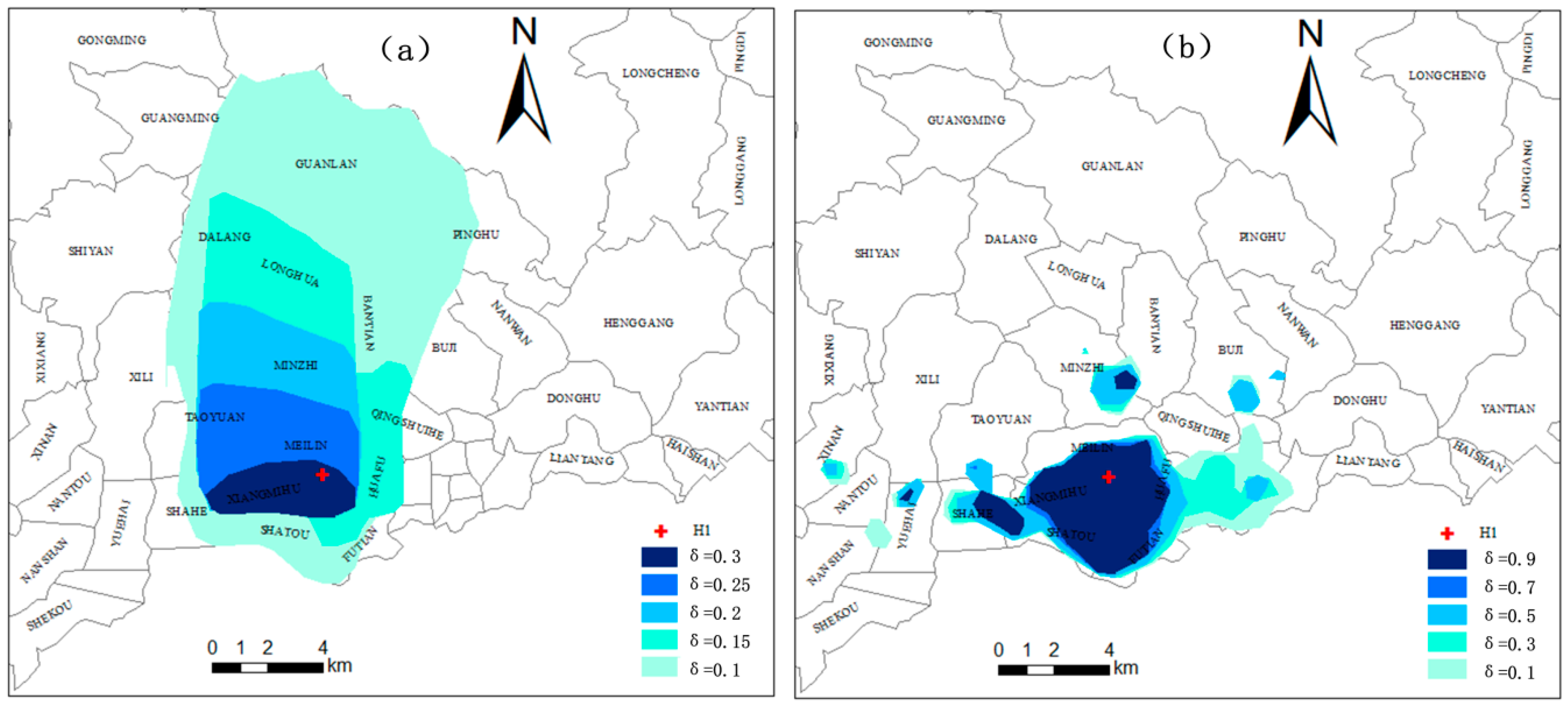
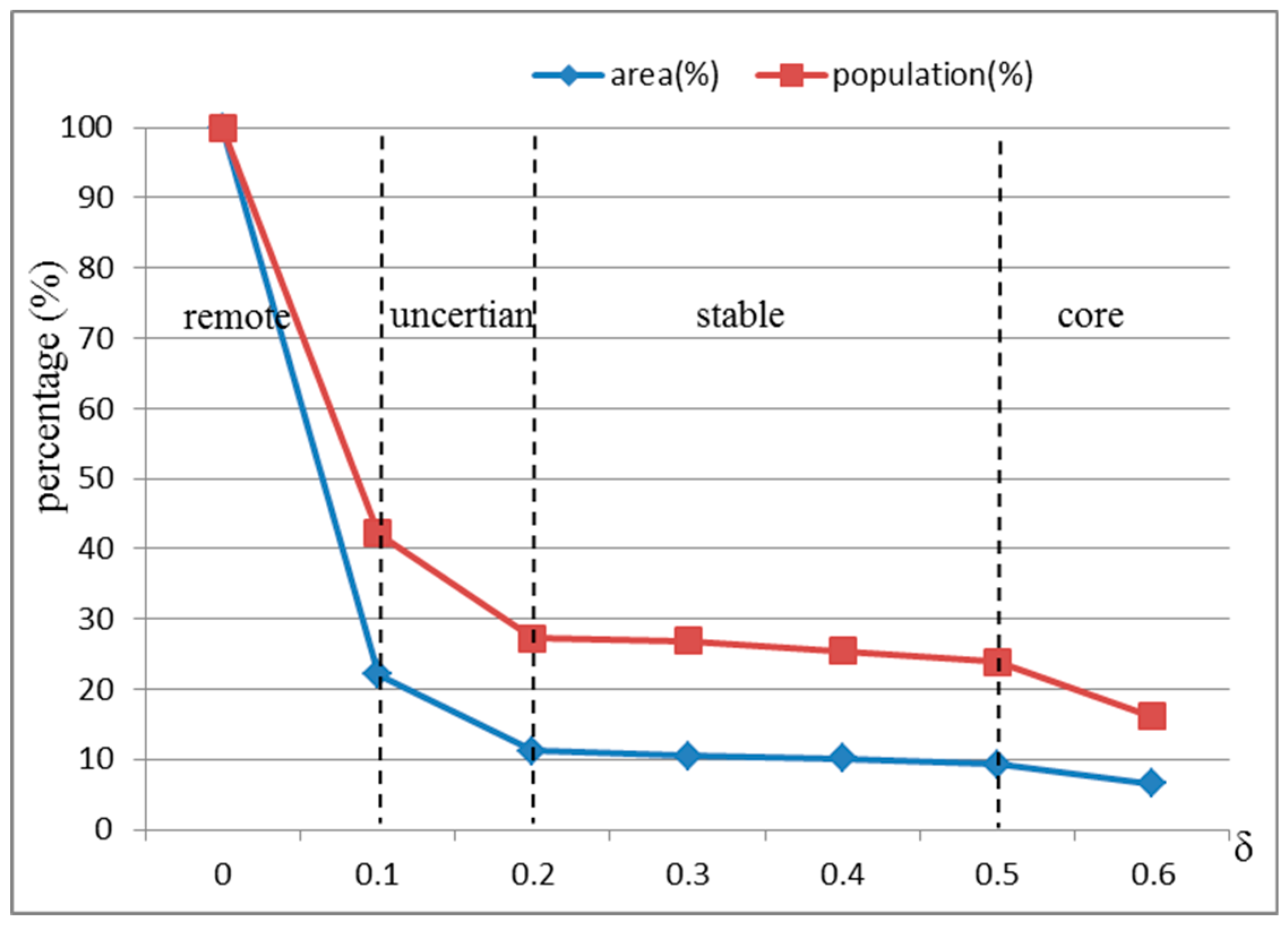
4.1. Analysis of the Access Probability Threshold
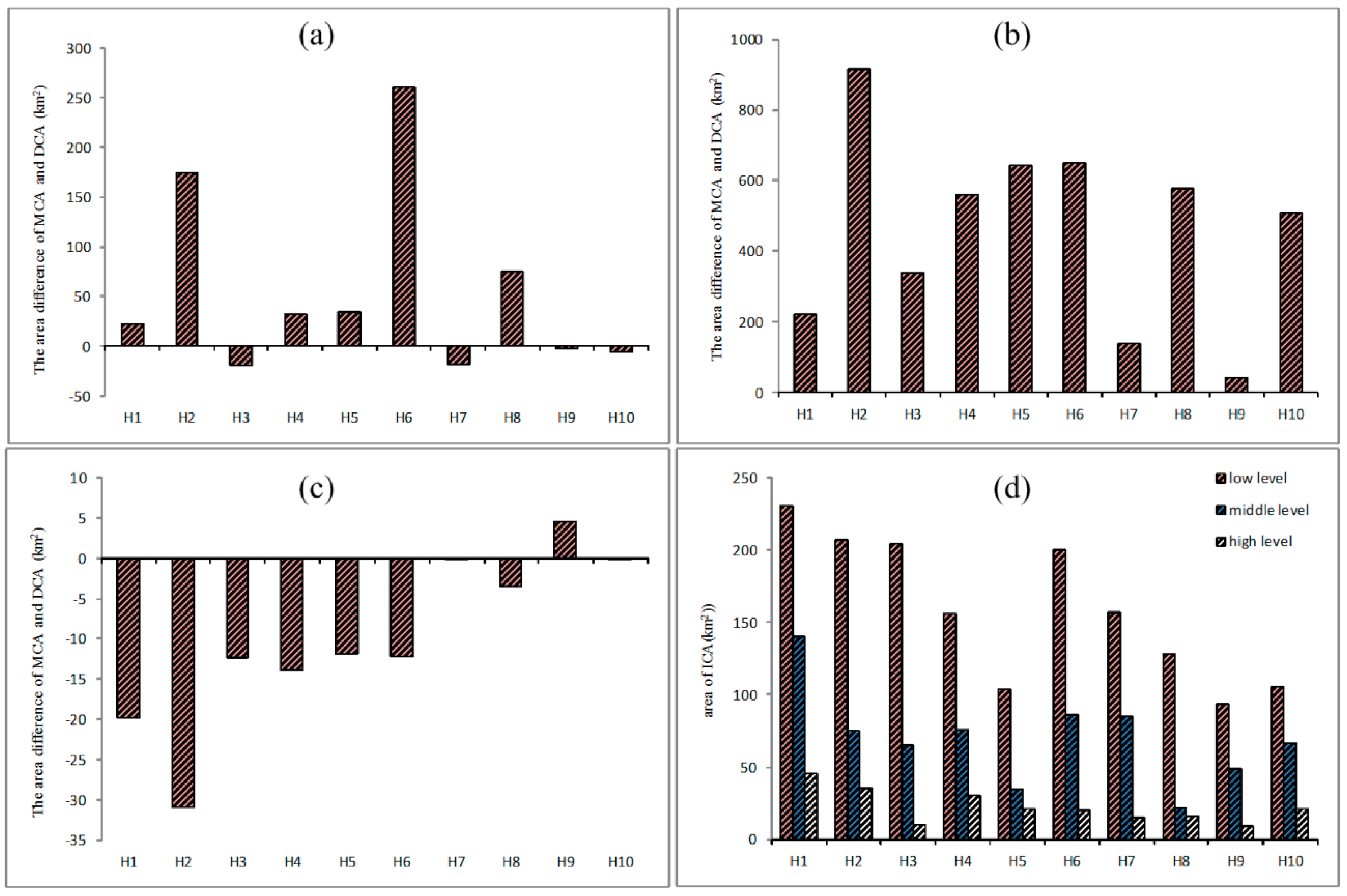
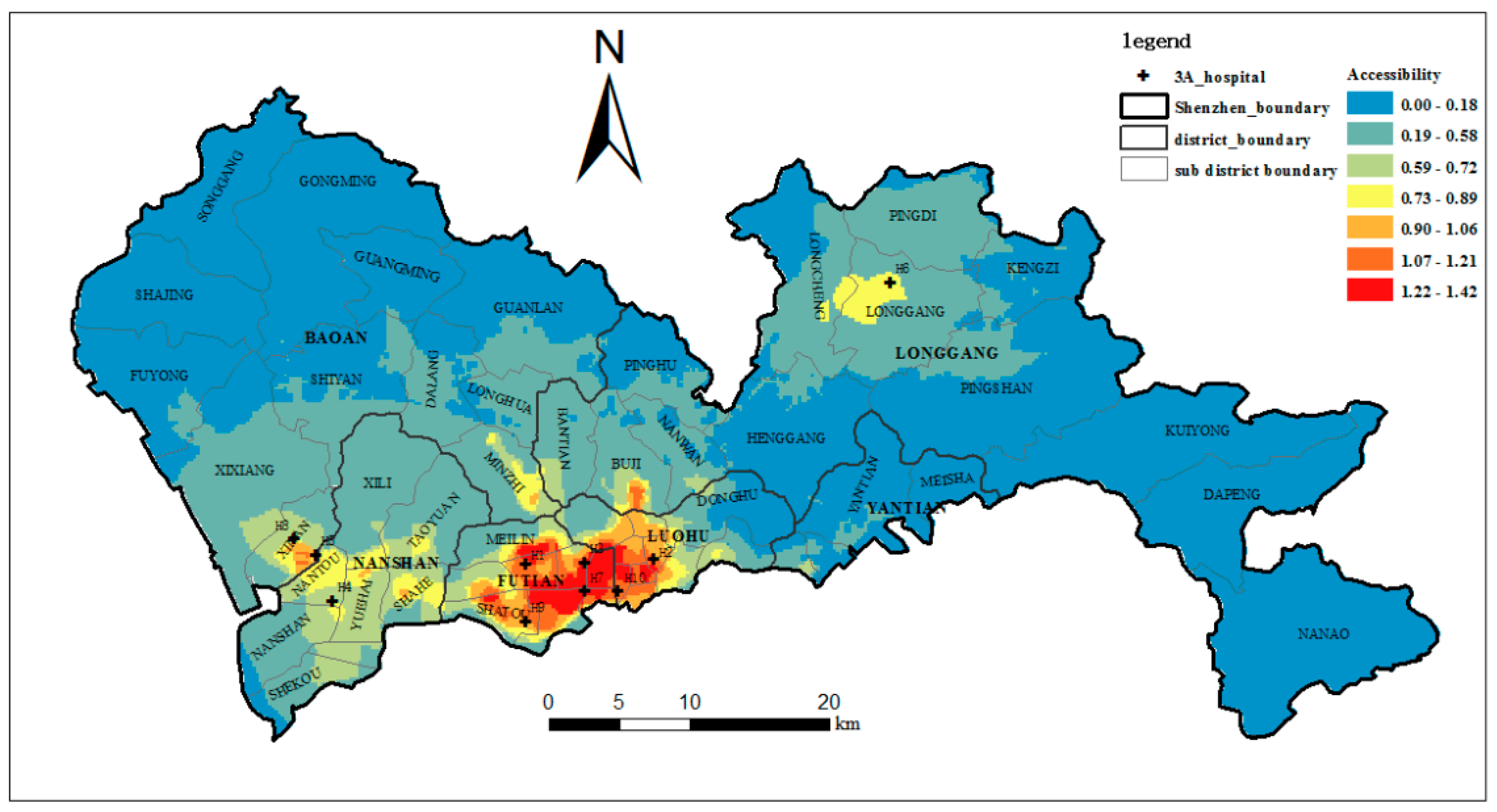
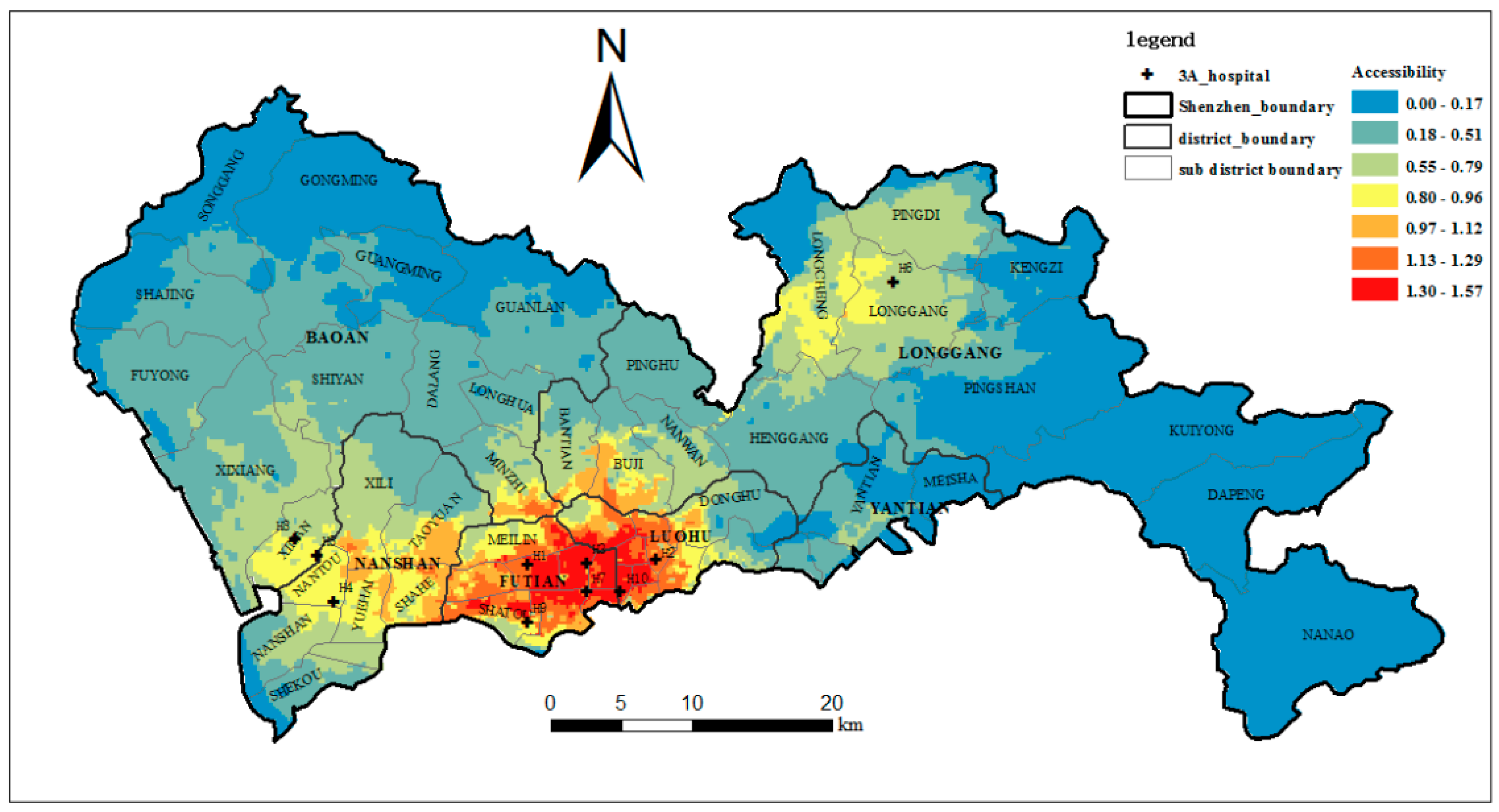
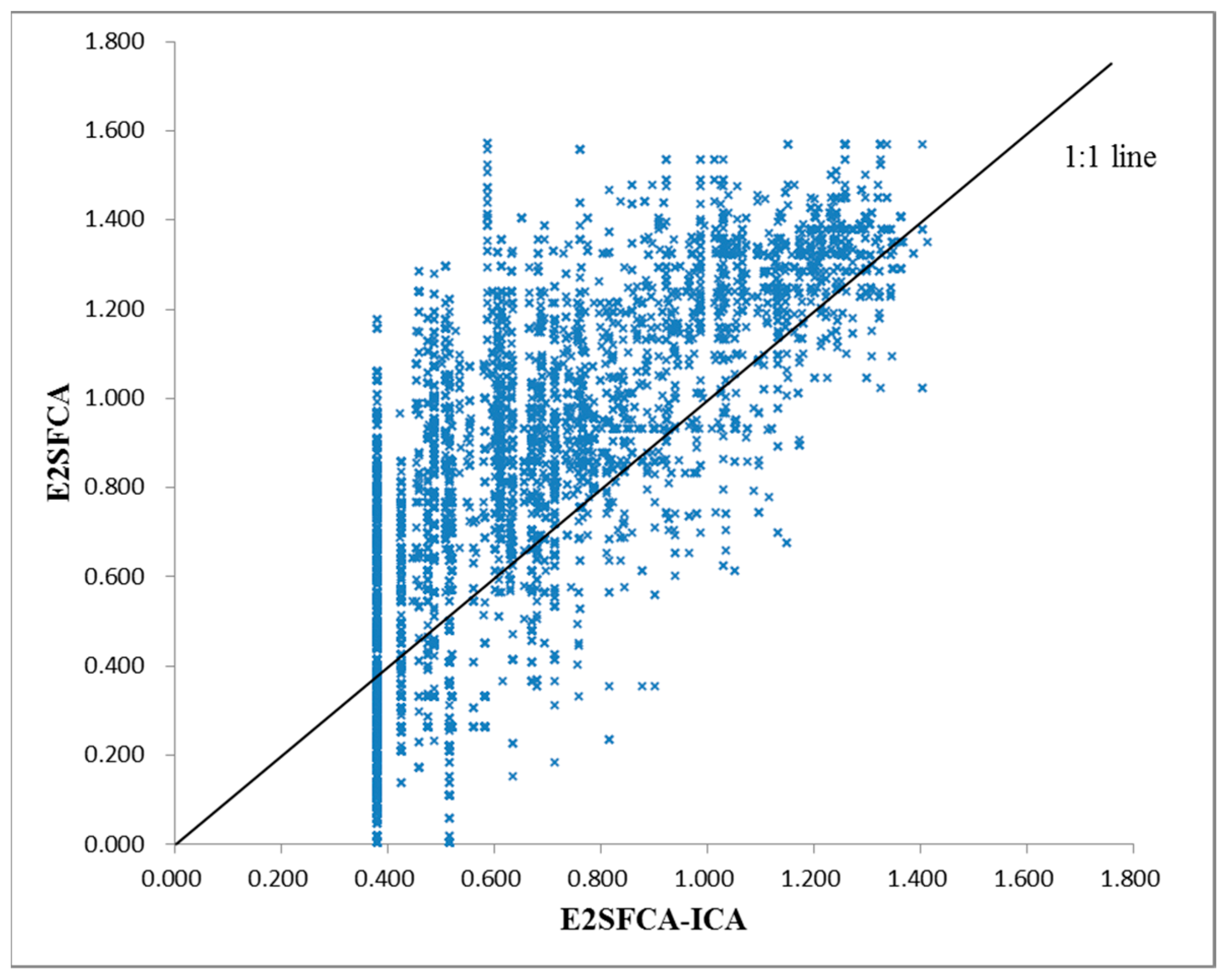
4.2. Analysis of the Differences among MCA, DCA, and ICA
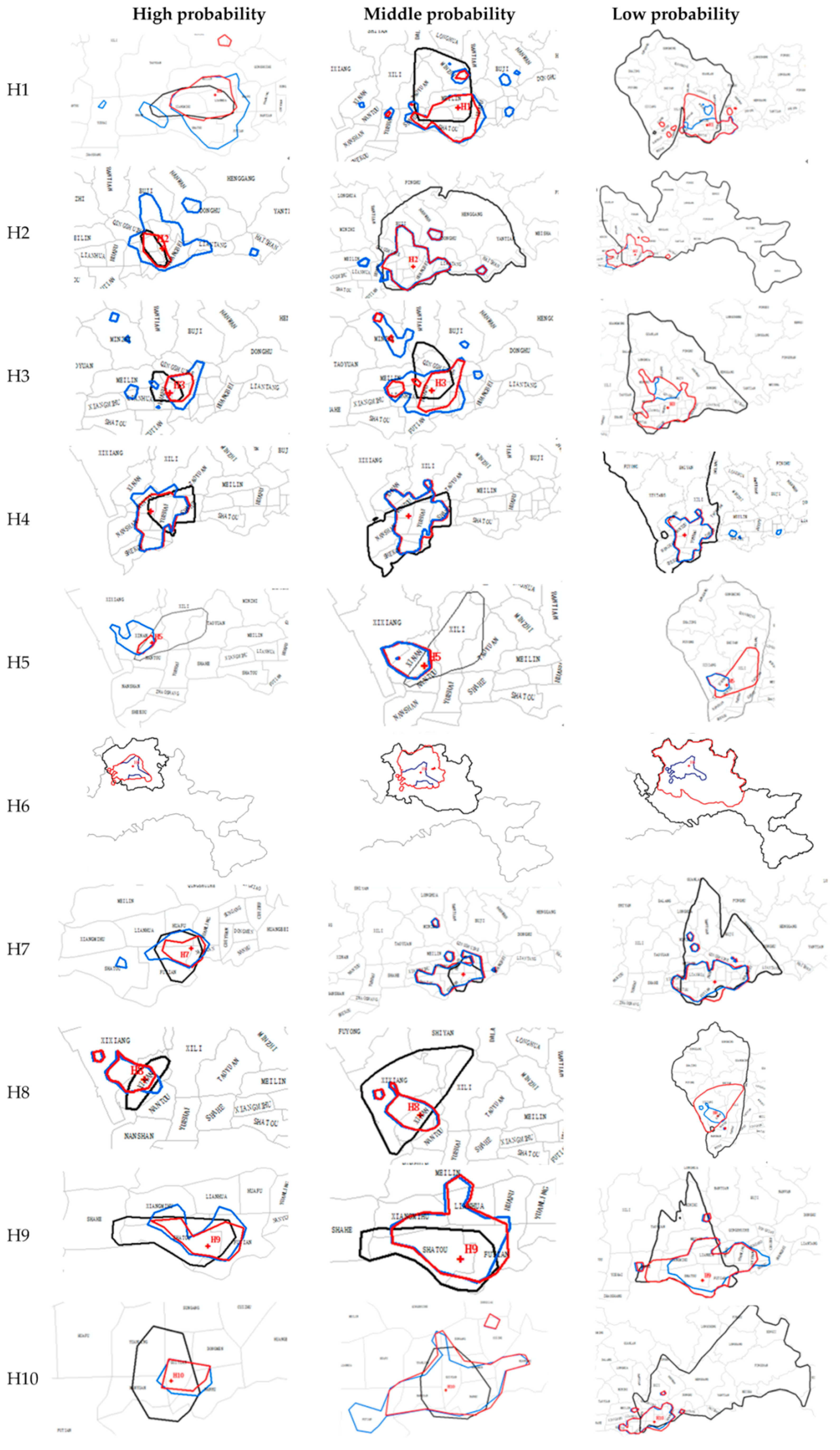
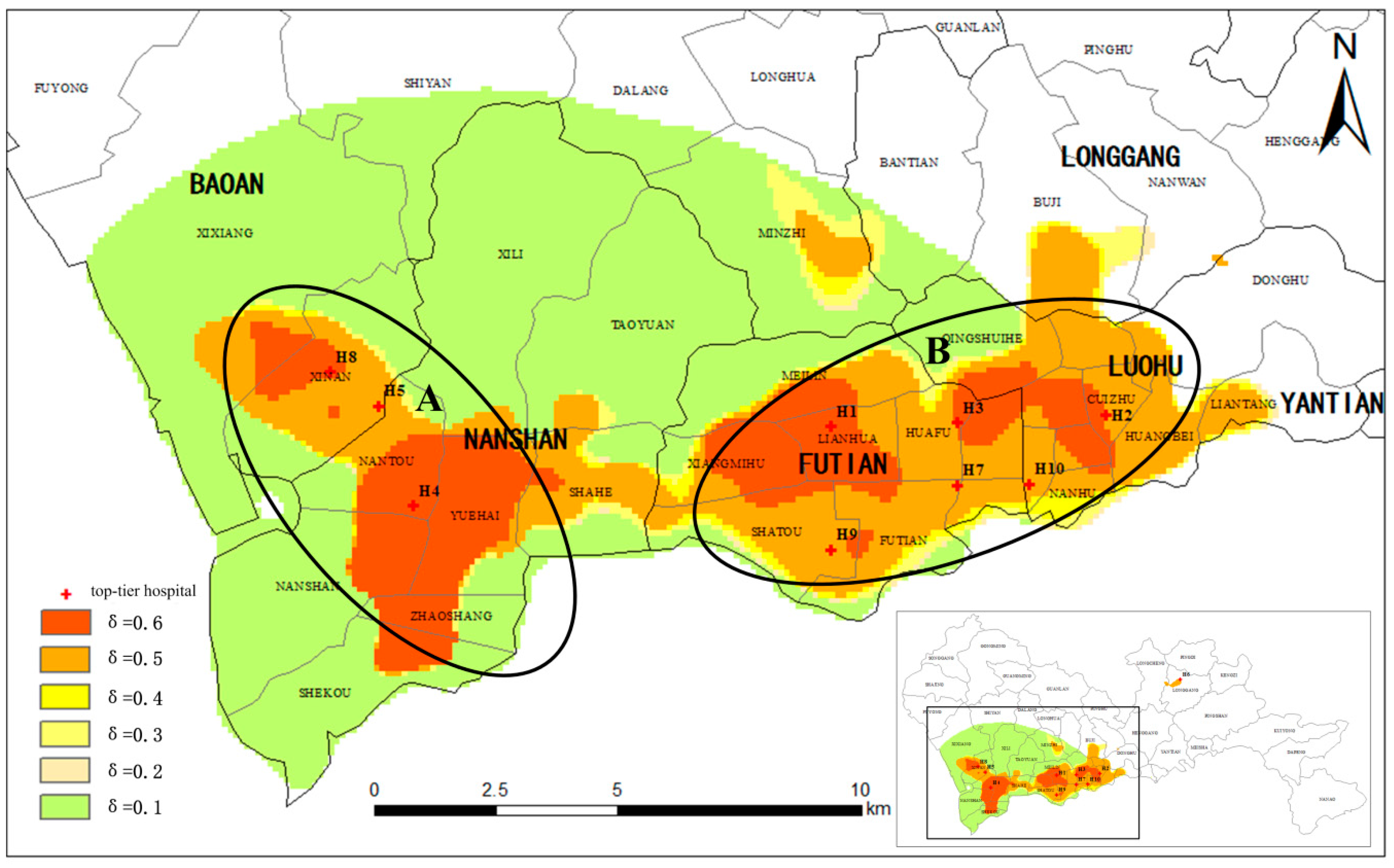
4.3. Analysis of the Characteristics of the ICA
4.4. The Accessibility of the Top-Tier Hospitals
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hansen, W.G. How Accessibility Shapes Land Use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Kwan, M.-P. Space-time and integral measures of individual accessibility: A comparative analysis using a point-based framework. Geogr. Anal. 1998, 30, 191–216. [Google Scholar] [CrossRef]
- Kwan, M.-P. Gender and individual access to urban opportunities: A study using space-time measures. Prof. Geogr. 1999, 51, 210–227. [Google Scholar] [CrossRef]
- Luo, W.; Wang, F. Measures of spatial accessibility to health care in a GIS environment: Synthesis and a case study in the Chicago region. Environ. Plan. B Plan. Des. 2003, 30, 865–884. [Google Scholar] [CrossRef]
- Kwan, M.-P.; Weber, J. Scale and accessibility: Implications for the analysis of land use-travel interaction. Appl. Geogr. 2008, 28, 110–123. [Google Scholar] [CrossRef]
- Wang, H.D.; Yue, Y.; Li, Y.G.; Huang, L. Spatial Correlation Analysis of Attractiveness of Commercial Facilities. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1102–1106. [Google Scholar]
- Dussault, G.; Franceschini, M.C. Not enough there, too many here: Understanding geographical imbalances in the distribution of the health workforce. Hum. Resour. Health 2006, 4, 12. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [Google Scholar] [CrossRef]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary care in rural areas: Improving the effectiveness of the two-step floating catchment area method. Appl. Geogr. 2009, 29, 533–541. [Google Scholar] [CrossRef]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place 2009, 15, 1100–1107. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Dong, S.; Zhao, Y.; Hu, H.; Li, Z. Assessing potential spatial accessibility of health services in rural China: A case study of Donghai county. Int. J. Equity Health 2013, 12, 35. [Google Scholar] [CrossRef] [PubMed]
- Wan, N.; Zhan, F.B.; Zou, B.; Chow, E. A relative spatial access assessment approach for analyzing potential spatial access to colorectal cancer services in Texas. Appl. Geogr. 2012, 32, 291–299. [Google Scholar] [CrossRef]
- Delamater, P.L. Spatial accessibility in suboptimally configured health care systems: A modified two-step floating catchment area (M2SFCA) metric. Health Place 2013, 24, 30–43. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R. Spatial accessibility of primary health care utilising the two step floating catchment area method: An assessment of recent improvements. Int. J. Health Geogr. 2012, 11, 50. [Google Scholar] [CrossRef] [PubMed]
- Guagliardo, M.F. Spatial accessibility of primary care: Concepts, methods and challenges. Int. J. Health Geogr. 2004, 3, 3. [Google Scholar] [CrossRef] [PubMed]
- Dai, D. Racial/ethnic and socioeconomic disparities in urban green space accessibility: Where to intervene? Landsc. Urban Plan. 2011, 102, 234–244. [Google Scholar] [CrossRef]
- Delmelle, E.M.; Cassell, C.H.; Dony, C.; Radcliff, E.; Tanner, J.P.; Siffel, C.; Kirby, R.S. Modeling travel impedance to medical care for children with birth defects using geographic information systems. Birth Defects Res. Part A Clin. Mol. Teratol. 2013, 97, 673–684. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Luo, W. Assessing spatial and nonspatial factors for healthcare access: Towards an integrated approach to defining health professional shortage areas. Health Place 2005, 11, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, J.C.; D’Arcy, C.; Holman, J.; Pritchard, D.A. The influence of attractiveness factors and distance to general practice surgeries by level of social disadvantage and global access in Perth, Western Australia. Soc. Sci. Med. 2003, 56, 387–403. [Google Scholar] [CrossRef]
- Dony, C.C.; Delmelle, E.M.; Delmelle, E.C. Re-conceptualizing accessibility to parks in multi-modal cities: A variable-width floating catchment area (vfca) method. Landsc. Urban Plan. 2015, 143, 90–99. [Google Scholar] [CrossRef]
- Casas, I.; Delmelle, E.; Delmelle, E.C. Potential versus revealed access to care during a dengue fever outbreak. J. Transp. Health 2016, 4, 18–29. [Google Scholar] [CrossRef]
- Yang, G.; Song, C.; Shu, H.; Zhang, J.; Pei, T.; Zhou, C. Assessing patient bypass behavior using taxi trip origin-destination (OD) data. ISPRS Int. J. Geo-Inf. 2016, 5, 157. [Google Scholar] [CrossRef]
- Wang, F.H. Measurement, optimization, and impact of health care accessibility: A methodological review. Ann. Assoc. Am. Geogr. 2012, 102, 1104–1112. [Google Scholar] [CrossRef] [PubMed]
- Zinszer, K.; Charland, K.; Kigozi, R.; Dorsey, G.; Kamya, M.R.; Buckeridge, D.L. Determining health-care facility catchment areas in Uganda using data on malaria-related visits. Bull. World Health Organ. 2014, 92, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Shortt, N.K.; Moore, A.; Coombes, M.; Wymer, C. Defining regions for locality health care planning: A multidimensional approach. Soc. Sci. Med. 2005, 60, 2715–2727. [Google Scholar] [CrossRef] [PubMed]
- Lovett, A.; Haynes, R.; Sünnenberg, G.; Gale, S. Car travel time and accessibility by bus to general practitioner services: A study using patient registers and GIS. Soc. Sci. Med. 2002, 55, 97–111. [Google Scholar] [CrossRef]
- Parker, E.B.; Campbell, J.L. Measuring access to primary medical care: Some examples of the use of geographical information systems. Health Place 1998, 4, 183–193. [Google Scholar] [CrossRef]
- Kwan, M.-P. The uncertain geographic context problem. Ann. Assoc. Am. Geogr. 2012, 102, 958–968. [Google Scholar] [CrossRef]
- Shen, Y.; Kwan, M.P.; Chai, Y. Investigating commuting flexibility with GPS data and 3D geovisualization: A case study of Beijing, China. J. Transp. Geogr. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- González, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Lazer, D.; Pentland, A.; Adamic, L.; Aral, S.; Barabasi, A.L.; Brewer, D.; Christakis, N.; Contractor, N.; Fowler, J.; Gutmann, M. Life in the network: The coming age of computational social science. Science 2009, 323, 721–723. [Google Scholar] [CrossRef] [PubMed]
- Beijing Statistical Yearbook. Available online: http://www.bjstats.gov.cn/tjsj/ (accessed on 23 July 2018).
- Shanghai Urban Transportation Administrative Dept. Available online: http://www.shygc.net/pageHome.do?page=init (accessed on 23 July 2018).
- Guangzhou Statistical Yearbook. Available online: www.gzstats.gov.cn (accessed on 23 July 2018).
- Shenzhen Transportation Commission. Available online: http://www.sztb.gov.cn/ (accessed on 23 July 2018).
- Li, L.; Wang, S.; Li, M.; Tan, J. Comparison of travel mode choice between taxi and subway regarding traveling convenience. Tsinghua Sci. Technol. 2018, 2, 135–144. [Google Scholar] [CrossRef]
- Didi Media Research Institute & CBNData. 2016 Intelligent Travel Big Data Report. 2017. Available online: http://www.imxdata.com/archives/20017 (accessed on 12 April 2017).
- Ingram, D.R. The concept of accessibility: A search for an operational form. Reg. Stud. J. Reg. Stud. Assoc. 1971, 5, 101–107. [Google Scholar] [CrossRef]
- Zhou, Y.; Fang, Z.; Thill, J.C.; Li, Q.; Li, Y. Functionally critical locations in an urban transportation network: Identification and space-time analysis using taxi trajectories. Comput. Environ. Urban Syst. 2015, 52, 34–47. [Google Scholar] [CrossRef]
- Joseph, A.E.; Bantock, P.R. Measuring potential physical accessibility to general practitioners in rural areas: A method and case study. Soc. Sci. Med. 1982, 16, 85–90. [Google Scholar] [CrossRef]
- Kwan, M.-P. Beyond space (as we knew it): Toward temporally integrated geographies of segregation, health, and accessibility. Ann. Assoc. Am. Geogr. 2013, 103, 1078–1086. [Google Scholar] [CrossRef]
- Alford-Teaster, J.; Lange, J.M.; Hubbard, R.A.; Lee, C.I.; Haas, J.S.; Shi, X.; Carlos, H.A.; Henderson, L.; Hill, D.; Tosteson, A.N.A.; et al. Is the closest facility the one actually used? An assessment of travel time estimation based on mammography facilities. Int. J. Health Geogr. 2016, 15, 8. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.L.; Zhou, S.H.; Yan, X.P. Endpoint Attractive Factors of Medical Facilities’ Accessibility: Based on GPS Floating Car Data in Guangzhou. Sci. Geogr. Sin. 2014, 34, 580–586. [Google Scholar]
- Chen, B.Y.; Yuan, H.; Li, Q.; Wang, D.; Shaw, S.L.; Chen, H.P.; Lam, W.H. Measuring place-based accessibility under travel time uncertainty. Int. J. Geogr. Inf. Sci. 2016, 31, 783–804. [Google Scholar] [CrossRef]
- Didi Media Research Institute & CBNData. 2016 Smart Travel Data and Medical Reports. Available online: http://www.sohu.com/a/79676781_355066 (accessed on 12 June 2017).
- Yang, L.; Kwan, M.-P.; Pan, X.; Wan, B.; Zhou, S. Scalable space-time trajectory cube for path-finding: A study using big taxi trajectory data. Transp. Res. Part B 2017, 101, 1–27. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J. Assessing the disparity in spatial access to hospital care in ethnic minority region in sichuan province, china. BMC Health Serv. Res. 2016, 16, 399. [Google Scholar] [CrossRef] [PubMed]
- Vadrevu, L.; Kanjilal, B. Measuring spatial equity and access to maternal health services using enhanced two step floating catchment area method (e2sfca)—A case study of the Indian sundarbans. Int. J. Equity Health 2016, 15, 87. [Google Scholar] [CrossRef] [PubMed]
- Dewulf, B.; Neutens, T.; Weerdt, Y.D.; Weghe, N.V.D. Accessibility to primary health care in Belgium: An evaluation of policies awarding financial assistance in shortage areas. BMC Fam. Pract. 2013, 14, 122. [Google Scholar] [CrossRef] [PubMed]
- Wan, N.; Zou, B.; Sternberg, T. A three-step floating catchment area method for analyzing spatial access to health services. Int. J. Geogr. Inf. Sci. 2012, 6, 1073–1089. [Google Scholar] [CrossRef]
- Ursulica, T.E. The relationship between health care needs and accessibility to health care services in Botosani County-Romania. Procedia Environ. Sci. 2016, 32, 300–310. [Google Scholar] [CrossRef]
- Luo, W.; Whippo, T. Variable catchment sizes for the two-step floating catchment area (2SFCA) method. Health Place 2012, 18, 789–795. [Google Scholar] [CrossRef] [PubMed]
- Ren, F.; Tong, D.; Kwan, M.-P. Space-time measures of demand for service: Bridging location modeling and accessibility studies through a time-geographic framework. Geografiska Annaler B 2014, 96, 329–344. [Google Scholar] [CrossRef]
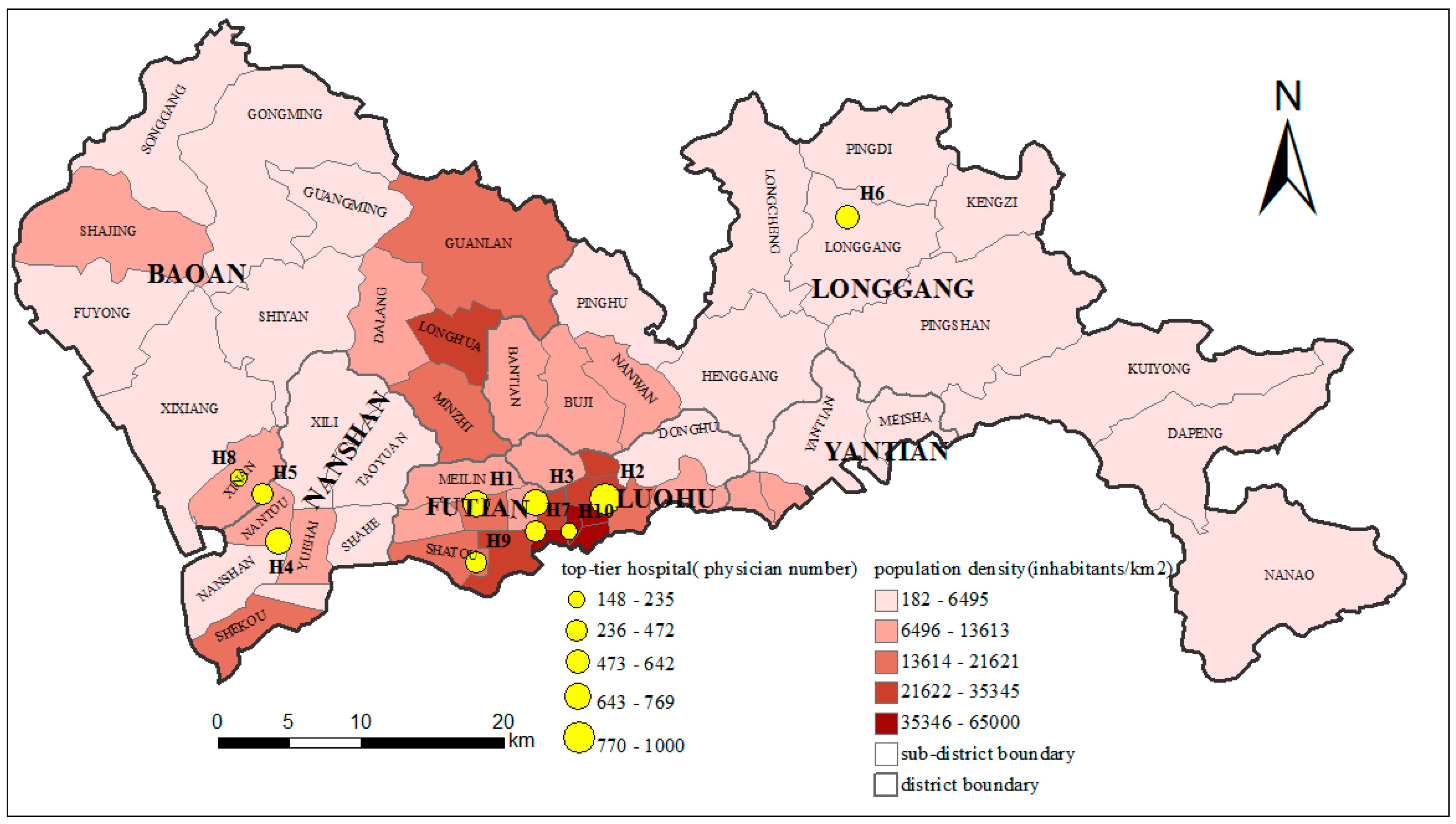
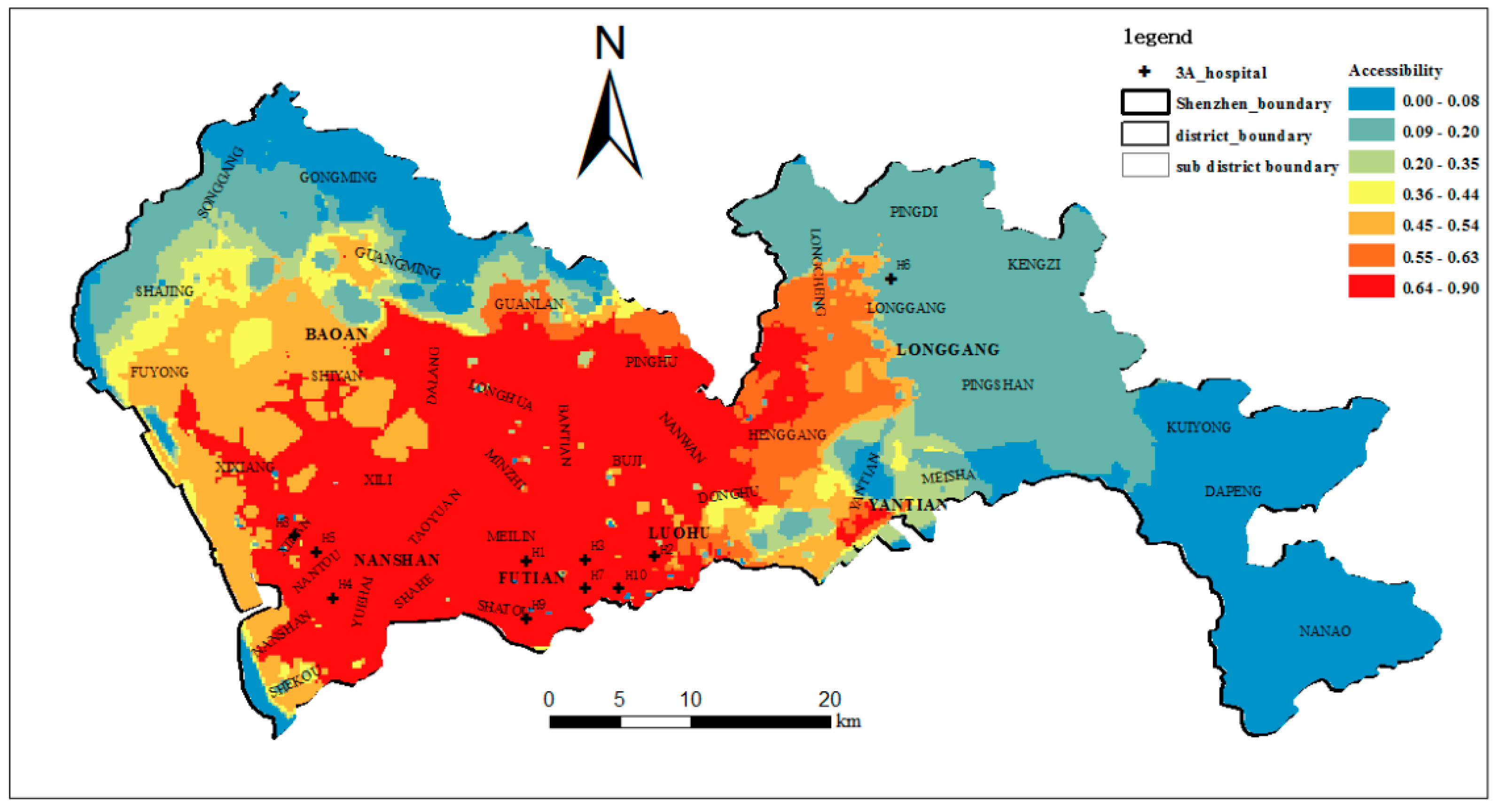
| Hospital Name | Abbreviation |
|---|---|
| Peking University Shenzhen Hospital | H1 |
| Shenzhen People’s Hospital | H2 |
| The Second People’s Hospital of Shenzhen | H3 |
| The SIXTH people’s Hospital of Shenzhen | H4 |
| The Eighth People’s Hospital of Shenzhen | H5 |
| The Ninth People’s Hospital of Shenzhen | H6 |
| Shenzhen Traditional Chinese Medicine Hospital | H7 |
| The Second Traditional Chinese Medicine Hospital of Shenzhen | H8 |
| Shenzhen Maternity & Child Healthcare Hospital | H9 |
| Shenzhen Pingle Orthopedic Hospital | H10 |
| MinValue | MaxValue | Std. | High Level | Middle Level | Low Level | |
|---|---|---|---|---|---|---|
| MAP | 0.000085 | 0.314345 | 0.038918 | 0.3 | 0.2 | 0.1 |
| DAP | 0 | 1 | 0.053472 | 0.9 | 0.5 | 0.1 |
| IAP | 0.000042 | 0.656681 | 0.036113 | 0.5 | 0.3 | 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Kwan, M.-P.; Yang, L.; Zhou, S.; Zuo, Z.; Wan, B. Evaluating the Accessibility of Healthcare Facilities Using an Integrated Catchment Area Approach. Int. J. Environ. Res. Public Health 2018, 15, 2051. https://doi.org/10.3390/ijerph15092051
Pan X, Kwan M-P, Yang L, Zhou S, Zuo Z, Wan B. Evaluating the Accessibility of Healthcare Facilities Using an Integrated Catchment Area Approach. International Journal of Environmental Research and Public Health. 2018; 15(9):2051. https://doi.org/10.3390/ijerph15092051
Chicago/Turabian StylePan, Xiaofang, Mei-Po Kwan, Lin Yang, Shunping Zhou, Zejun Zuo, and Bo Wan. 2018. "Evaluating the Accessibility of Healthcare Facilities Using an Integrated Catchment Area Approach" International Journal of Environmental Research and Public Health 15, no. 9: 2051. https://doi.org/10.3390/ijerph15092051
APA StylePan, X., Kwan, M.-P., Yang, L., Zhou, S., Zuo, Z., & Wan, B. (2018). Evaluating the Accessibility of Healthcare Facilities Using an Integrated Catchment Area Approach. International Journal of Environmental Research and Public Health, 15(9), 2051. https://doi.org/10.3390/ijerph15092051






