A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US
Abstract
1. Introduction
2. Data and Methods
2.1. Data Collection
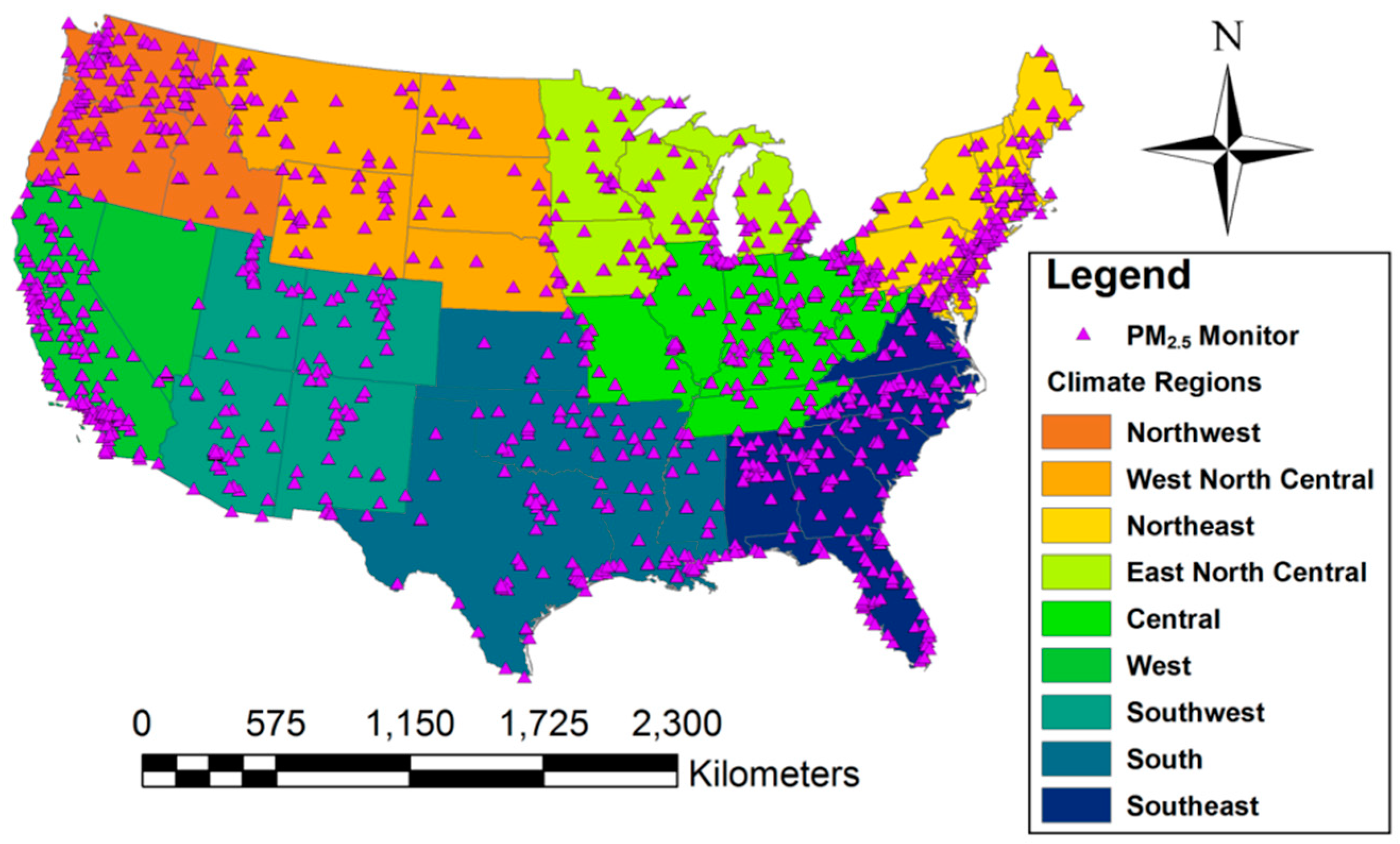
2.2. Climate Regions and Temporal Domains
2.3. National Bayesian Downscaling Model
2.4. Model Fitting and Prediction
3. Results
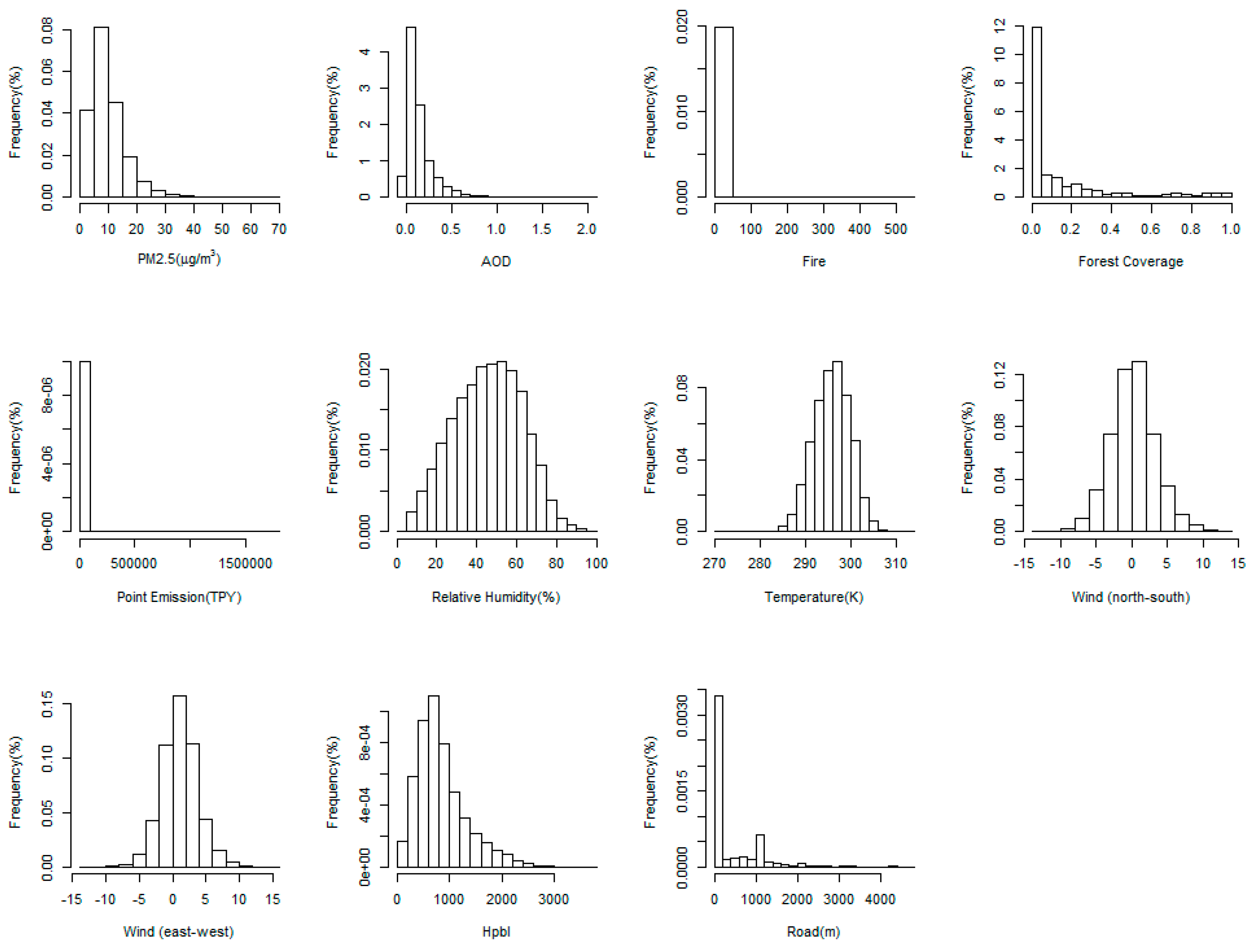
3.1. Data Description and Summary
3.2. Regional and Temporal Varying Geographical Associations
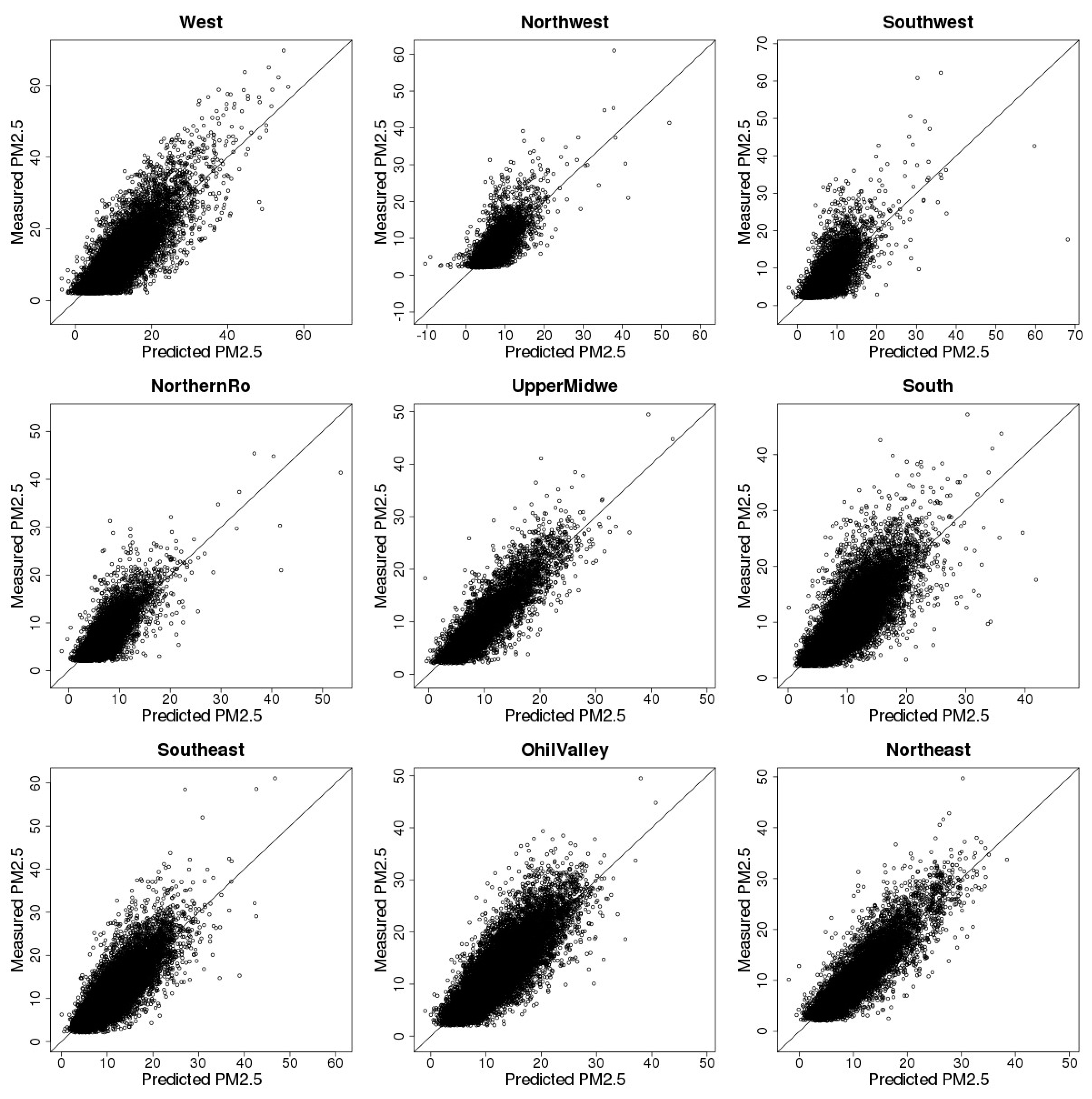
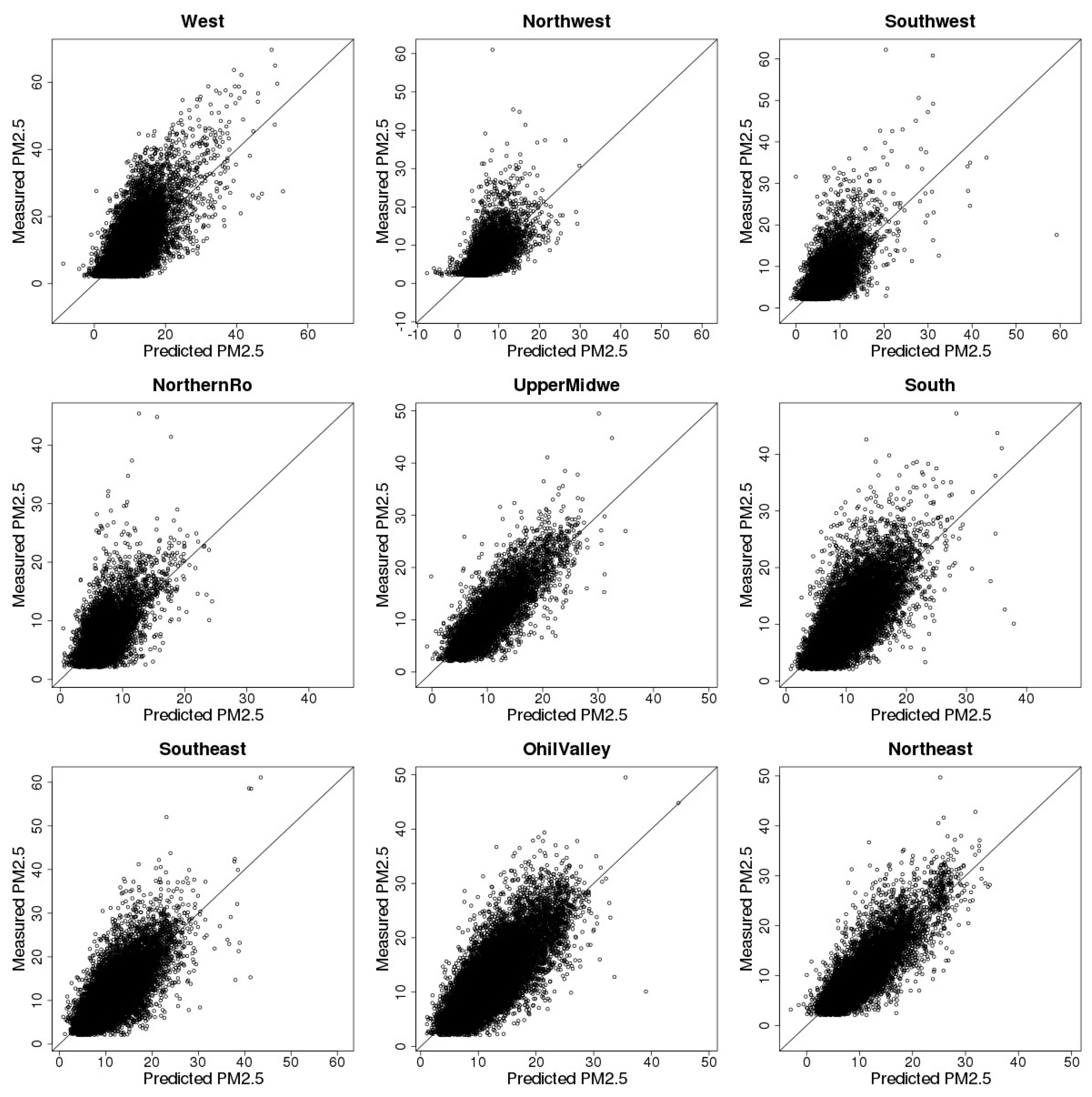
3.3. Model Cross-Validation
3.4. Model Prediction
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pope, C.A., III; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef] [PubMed]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From air Pollution to Global Change; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Anderson, T.; Charlson, R.J.; Winker, D.M.; Ogren, J.A.; Holmen, K. Mesoscale variations of tropospheric aerosols. J. Atmos. Sci. 2003, 60, 119–136. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, A.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the eastern united states using satellite remote sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes Jr, M.G.; Estes, S.M.; Quattrochi, D.A.; Puttaswamy, S.J.; et al. Estimating ground-level PM2.5 concentrations in the Southeastern United States using MAIAC AOD retrievals and a two-stage model. Remote Sens. Environ. 2014, 140, 220–232. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Liu, Y. 10-year spatial and temporal trends of PM2.5 concentrations in the southeastern US estimated using high-resolution satellite data. Atmos. Chem. Phys. 2014, 14, 6301–6314. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Christopher, S.A.; Wang, J.; Gehrig, R.; Lee, Y.; Kumar, N. Satellite remote sensing of particulate matter and air quality assessment over global cities. Atmos. Environ. 2006, 40, 5880–5892. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004–2013. Environ. Health Perspect. 2015, 124, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.H.; Hu, X.; Liu, Y. Calibrating MODIS aerosol optical depth for predicting daily PM2.5 concentrations via statistical downscaling. J. expo. Sci. Environ. Epidemiol. 2014, 24, 398–404. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Gao, X.; Martin, R. Exact prior-free probabilistic inference on the heritability coefficient in a linear mixed model. Electron. J. Stat. 2014, 8, 3062–3076. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes Jr, M.G.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Liu, Y. Improving satellite-driven PM2.5 models with Moderate Resolution Imaging Spectroradiometer fire counts in the southeastern U.S. J. Geophys. Res. Atmos. 2014, 119, 11375–11386. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
- Lee, H.J.; Coull, B.A.; Bell, M.L.; Koutrakis, P. Use of satellite-based aerosol optical depth and spatial clustering to predict ambient PM2.5 concentrations. Environ. Res. 2012, 118, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Kloog, I.; Koutrakis, P.; Coull, B.A.; Lee, H.J.; Schwartz, J. Assessing temporally and spatially resolved PM2.5 exposures for epidemiological studies using satellite aerosol optical depth measurements. Atmos. Environ. 2011, 45, 6267–6275. [Google Scholar] [CrossRef]
- Di, Q.; Koutrakis, P.; Schwartz, J. A hybrid prediction model for PM2.5 mass and components using a chemical transport model and land use regression. Atmos. Environ. 2016, 131, 390–399. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef] [PubMed]
- Thomas, K.; Walter, J.K. Regional and National Monthly, Seasonal, and Annual Temperature Weighted by Area, 1895–1983; National Climatic Data Center: Asheville, NC, USA, 1984. [Google Scholar]
- Andrieu, C.; De Freitas, N.; Doucet, A.; Jordan, M.I. An introduction to MCMC for machine learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Zhang, L.; Liang, J.; Zeng, M.; Liu, X. Graph construction based on re-weighted sparse representation for semi-supervised learning. J. Inf. Comput. Sci. 2013, 10, 375–383. [Google Scholar]
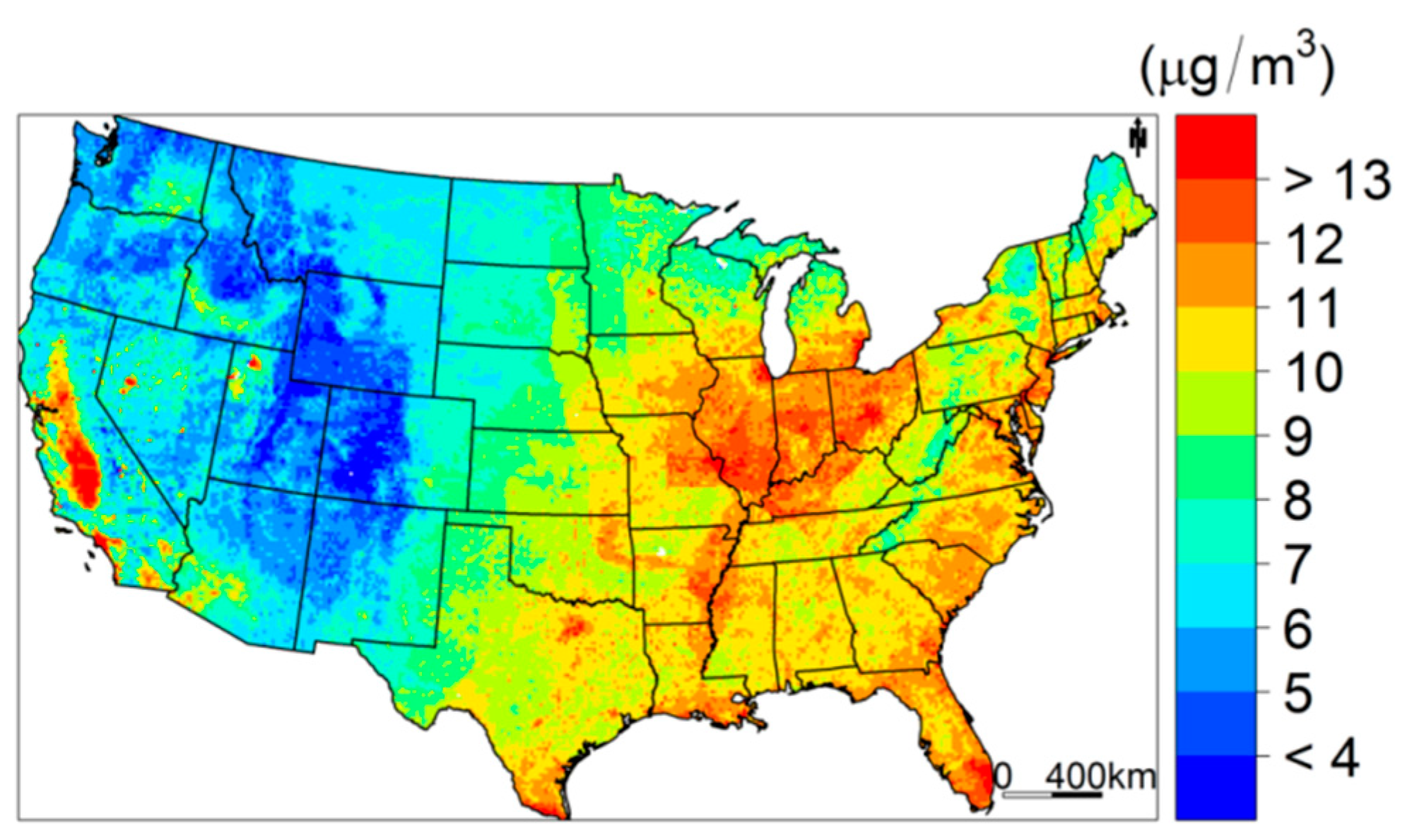
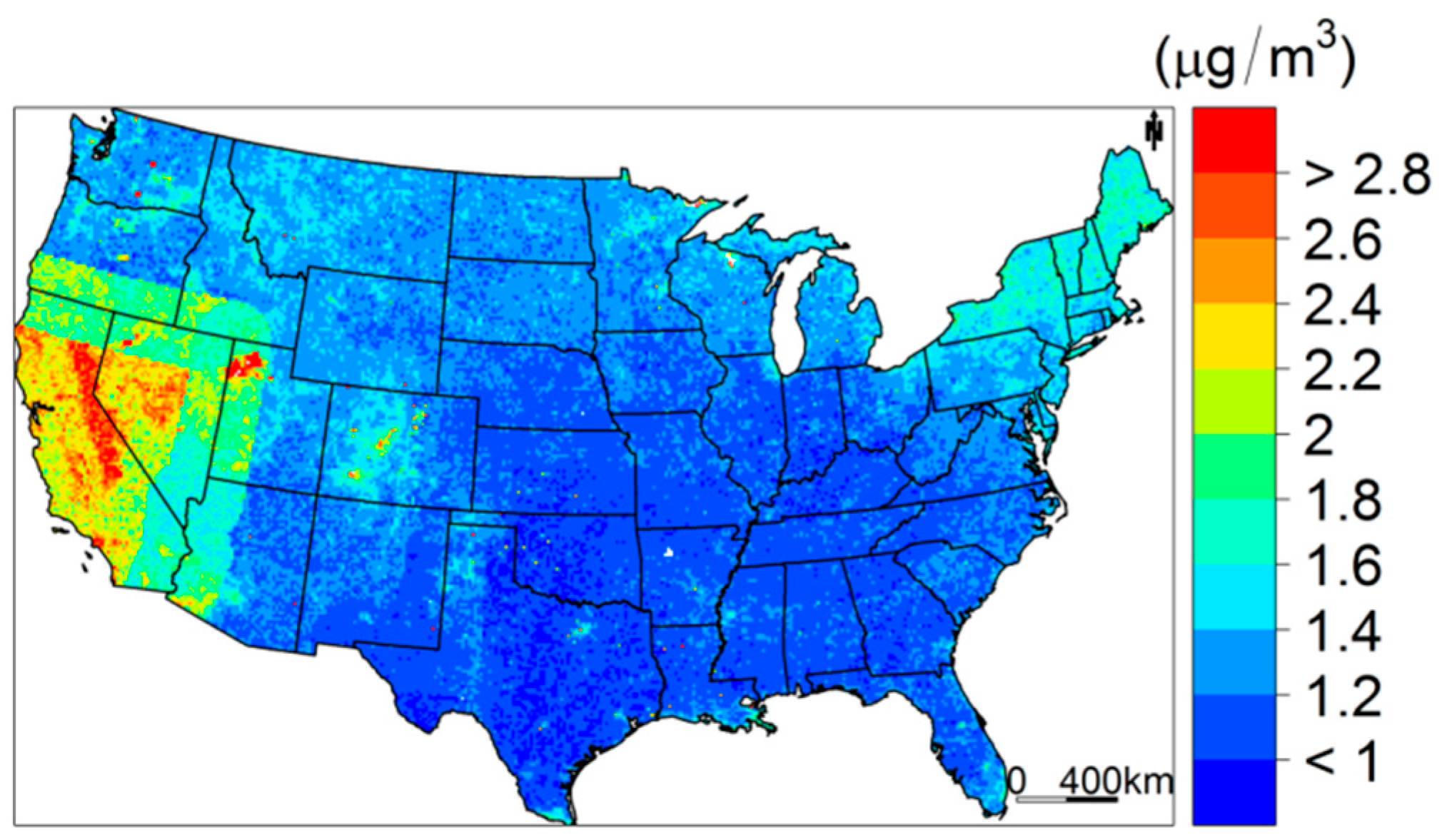
| Regions | PM2.5 (SD) | AOD (SD) |
|---|---|---|
| West | 10.72 (7.17) | 0.10 (0.12) |
| Northwest | 6.23 (4.05) | 0.12 (0.11) |
| Southwest | 7.40 (4.75) | 0.10 (0.11) |
| Northern Rockies and Plains | 7.40 (4.11) | 0.12 (0.13) |
| Upper Midwest | 10.33 (5.87) | 0.18 (0.17) |
| South | 10.17 (5.09) | 0.13 (0.15) |
| Southeast | 10.83 (5.34) | 0.15 (0.17) |
| Ohio Valley | 11.29 (5.79) | 0.17 (0.17) |
| Northeast | 10.68 (6.10) | 0.19 (0.19) |
| Regions | Number of Records | Number of Days | Number of Monitors | Coverage |
|---|---|---|---|---|
| West | 17,096 | 356 | 159 | 30% |
| Northwest | 9486 | 295 | 170 | 19% |
| Southwest | 9567 | 363 | 138 | 19% |
| Northern Rockies and Plains | 7463 | 328 | 150 | 15% |
| Upper Midwest | 6208 | 304 | 145 | 14% |
| South | 15,899 | 364 | 189 | 23% |
| Southeast | 17,525 | 361 | 257 | 19% |
| Ohio Valley | 18,642 | 354 | 361 | 15% |
| Northeast | 8913 | 302 | 238 | 12% |
| Region | Temporal | AOD | Fire | Forest | Emission | RH | TMP | Vgrd | Ugrd | Hpbl | Road | AOD * TMP | R2 | Slope |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| West | 1 | 21.2 (5.9) | −0.7 (0.3) | 0.6 (0.2) | 2.5 (0.2) | 2.4 (0.4) | 1.2 (0.2) | −0.2 (0.1) | 9.8 (3.4) | 0.65 | 0.88 | |||
| 2 | 4.1 (1) | −0.8 (0.3) | 0.4 (0.1) | 0.7 (0.1) | 2.7 (0.2) | −0.1 (0.1) | 0.77 | 0.94 | ||||||
| 3 | 31.2 (5.2) | 0.2 (0.1) | −1.9 (0.3) | 0.8 (0.3) | 0.6 (0.1) | 1.4 (0.1) | −0.4 (0.1) | −0.7 (0.1) | −8.5 (2.5) | 0.72 | 0.91 | |||
| Northwest | 1 | −1.5 (0.5) | −0.7 (0.3) | −1.9 (0.5) | 0.57 | 0.84 | ||||||||
| 2 | 5.4 (1.1) | 0.1 (0) | −0.2 (0.1) | 0.4 (0.1) | 1.5 (0.2) | 4.4 (1) | 0.62 | 0.92 | ||||||
| 3 | 25.4 (3.8) | 0.4 (0.1) | −0.4 (0.2) | 1.2 (0.4) | −0.4 (0.1) | 14.7 (2.1) | 0.69 | 0.9 | ||||||
| Southwest | 1 | 10.6 (5) | 0.3 (0.1) | −0.7 (0.2) | 0.5 (0.2) | 2.4 (0.3) | 0.5 (0.1) | −11 (2.8) | 0.69 | 0.89 | ||||
| 2 | 5.5 (1.8) | −0.3 (0.1) | 0.4 (0.2) | 3.5 (0.3) | 0.3 (0.1) | 0.6 (0.1) | 0.6 | 0.88 | ||||||
| 3 | 18.8 (4.5) | −0.5 (0.2) | 0.7 (0.2) | −0.2 (0.1) | −0.3 (0.1) | 0.68 | 0.9 | |||||||
| Northern Rockies and Plains | 1 | 0.4 (0.1) | 1.2 (0.3) | 0.7 (0.2) | 0.82 | 0.95 | ||||||||
| 2 | 4.4 (1.5) | 0.3 (0.1) | 0.3 (0.1) | 2.4 (0.2) | 0.4 (0.1) | 3.1 (1) | 0.67 | 0.92 | ||||||
| 3 | 11.1 (2.1) | 0.3 (0.1) | 2.1 (0.2) | −0.6 (0.1) | −0.4 (0.1) | 0.73 | 0.92 | |||||||
| Upper Midwest | 1 | 0.5 (0.3) | 1.3 (0.2) | −0.4 (0.2) | 0.79 | 0.95 | ||||||||
| 2 | 4.4 (1.7) | 0.3 (0.1) | −0.6 (0.2) | 0.9 (0.1) | 2.7 (0.3) | 1 (0.1) | −0.3 (0.1) | 3.7 (1) | 0.82 | 0.95 | ||||
| 3 | 9.5 (3) | 0.4 (0.1) | −0.6 (0.2) | 0.3 (0.1) | 2.5 (0.2) | 0.4 (0.1) | −0.3 (0.1) | −0.2 (0.1) | 0.85 | 0.96 | ||||
| South | 1 | 13.1 (2.2) | 0.5 (0) | −0.3 (0.1) | 1.4 (0.2) | 0.3 (0.1) | −0.2 (0.1) | 0.59 | 0.91 | |||||
| 2 | 0.2 (0.1) | 0.5 (0.1) | 4.2 (0.3) | −0.2 (0.1) | 0.2 (0.1) | 0.3 (0.1) | 4.5 (1.1) | 0.67 | 0.94 | |||||
| 3 | 14.7 (1.9) | 0.3 (0) | −0.7 (0.1) | −0.2 (0.1) | 1 (0.2) | 0.3 (0.1) | −0.4 (0.1) | −0.4 (0.1) | 0.3 (0.1) | 0.65 | 0.93 | |||
| Southeast | 1 | 15.1 (1.9) | 0.3 (0) | −0.3 (0.1) | −0.3 (0.1) | 0.8 (0.2) | 0.5 (0.1) | 4.6 (0.9) | 0.68 | 0.94 | ||||
| 2 | 4.6 (1.6) | 0.1 (0) | 1.7 (0.2) | 7 (0.4) | −0.6 (0.1) | 0.2 (0.1) | 6.1 (1.1) | 0.74 | 0.95 | |||||
| 3 | 11.1 (1.4) | 0.3 (0) | −0.6 (0.1) | −0.7 (0.1) | 0.8 (0.2) | 0.7 (0.1) | −0.3 (0.1) | 6.9 (1.1) | 0.69 | 0.94 | ||||
| Ohio Valley | 1 | 21.2 (2.9) | 0.7 (0) | −0.5 (0.1) | 0.4 (0.1) | 0.7 (0.2) | 0.7 (0.1) | −0.3 (0.1) | 5.5 (1) | 0.68 | 0.94 | |||
| 2 | 5.7 (1.3) | 2.2 (0.1) | 5.5 (0.3) | 0.3 (0.1) | 0.2 (0.1) | 2.9 (0.7) | 0.74 | 0.95 | ||||||
| 3 | 14.4 (5.2) | 0.3 (0.1) | −0.8 (0.1) | 1.7(0.2) | 0.5 (0) | −0.3 (0) | −0.3 (0.1) | 3.3(1.3) | 0.77 | 0.95 | ||||
| Northeast | 1 | 10.6 (2.8) | 0.4 (0.1) | 0.9 (0.1) | −0.4 (0.1) | 0.8 | 0.95 | |||||||
| 2 | −0.2 (0.1) | 1.2 (0.2) | 6.4 (0.4) | −0.4 (0.1) | 8.5 (1.1) | 0.84 | 0.96 | |||||||
| 3 | 31 (2.5) | 1.5 (0.2) | −0.8 (0.2) | 1.8 (0.2) | 1.4 (0.4) | 27.5 (2) | 0.8 | 0.95 |
| Regions | R2 | Intercept | Slope |
|---|---|---|---|
| West | 0.69 | 0.04 | 0.99 |
| Northwest | 0.60 | 0.35 | 0.95 |
| Southwest | 0.54 | 0.40 | 0.94 |
| Northern Rockies and Plains | 0.60 | 0.29 | 0.95 |
| Upper Midwest | 0.76 | −0.04 | 0.99 |
| South | 0.59 | 0.27 | 0.97 |
| Southeast | 0.69 | 0.19 | 0.98 |
| Ohio Valley | 0.71 | 0.07 | 0.99 |
| Northeast | 0.78 | 0.07 | 0.99 |
| Regions | R2 | Intercept | Slope |
|---|---|---|---|
| West | 0.46 | 0.36 | 1.02 |
| Northwest | 0.39 | 1.01 | 0.83 |
| Southwest | 0.40 | 0.96 | 0.87 |
| Northern Rockies and Plains | 0.37 | 0.94 | 0.90 |
| Upper Midwest | 0.69 | −0.01 | 0.99 |
| South | 0.50 | 0.38 | 0.96 |
| Southeast | 0.58 | 0.77 | 0.92 |
| Ohio Valley | 0.65 | 0.18 | 0.97 |
| Northeast | 0.70 | 0.33 | 0.97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hu, X.; Chang, H.H.; Waller, L.A.; Belle, J.H.; Liu, Y. A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US. Int. J. Environ. Res. Public Health 2018, 15, 1999. https://doi.org/10.3390/ijerph15091999
Wang Y, Hu X, Chang HH, Waller LA, Belle JH, Liu Y. A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US. International Journal of Environmental Research and Public Health. 2018; 15(9):1999. https://doi.org/10.3390/ijerph15091999
Chicago/Turabian StyleWang, Yikai, Xuefei Hu, Howard H. Chang, Lance A. Waller, Jessica H. Belle, and Yang Liu. 2018. "A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US" International Journal of Environmental Research and Public Health 15, no. 9: 1999. https://doi.org/10.3390/ijerph15091999
APA StyleWang, Y., Hu, X., Chang, H. H., Waller, L. A., Belle, J. H., & Liu, Y. (2018). A Bayesian Downscaler Model to Estimate Daily PM2.5 Levels in the Conterminous US. International Journal of Environmental Research and Public Health, 15(9), 1999. https://doi.org/10.3390/ijerph15091999






