Wave2Vec: Vectorizing Electroencephalography Bio-Signal for Prediction of Brain Disease
Abstract
1. Introduction
2. Encoding-Based Wave2Vec Time Series Classifier
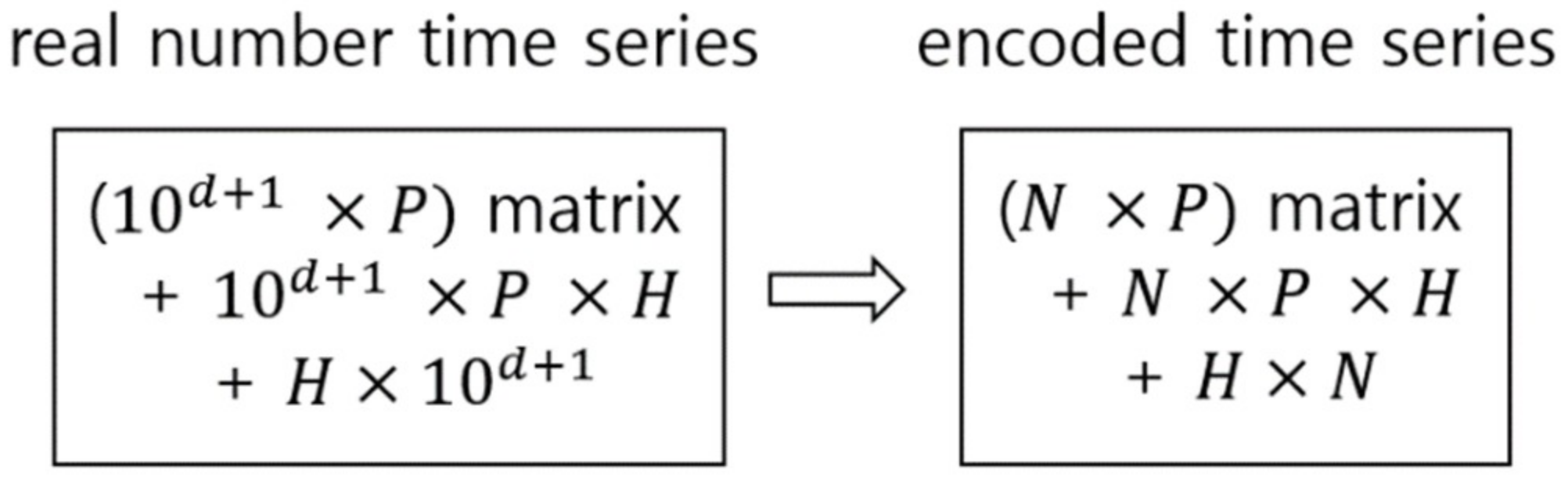
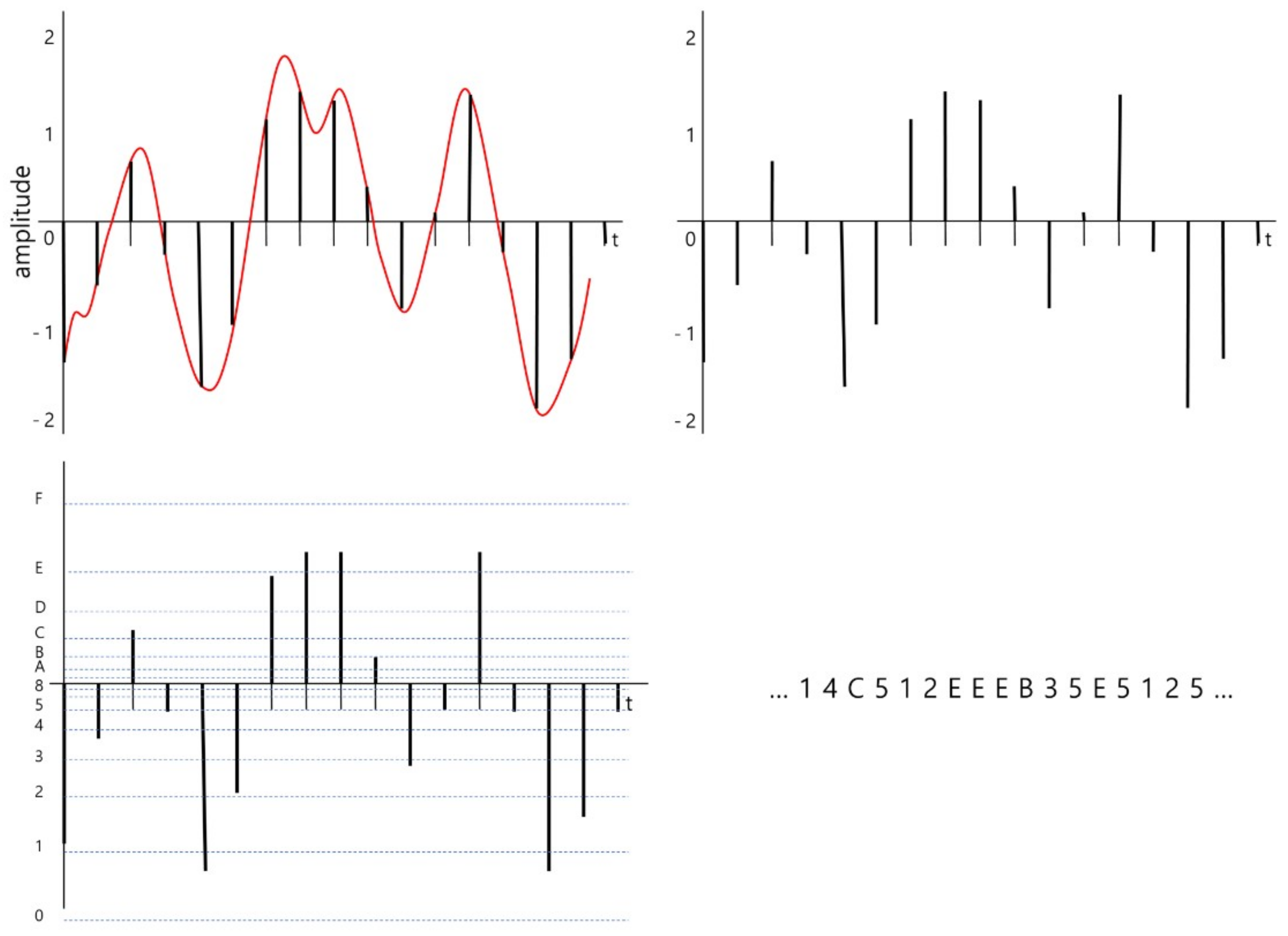
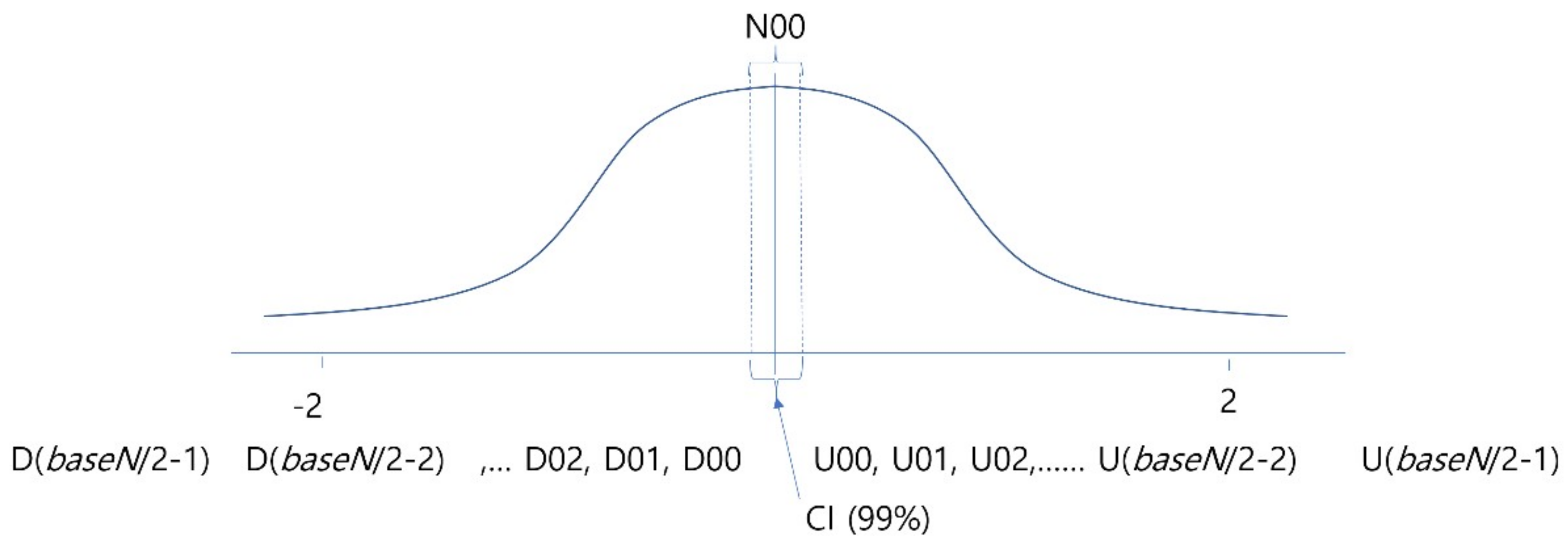
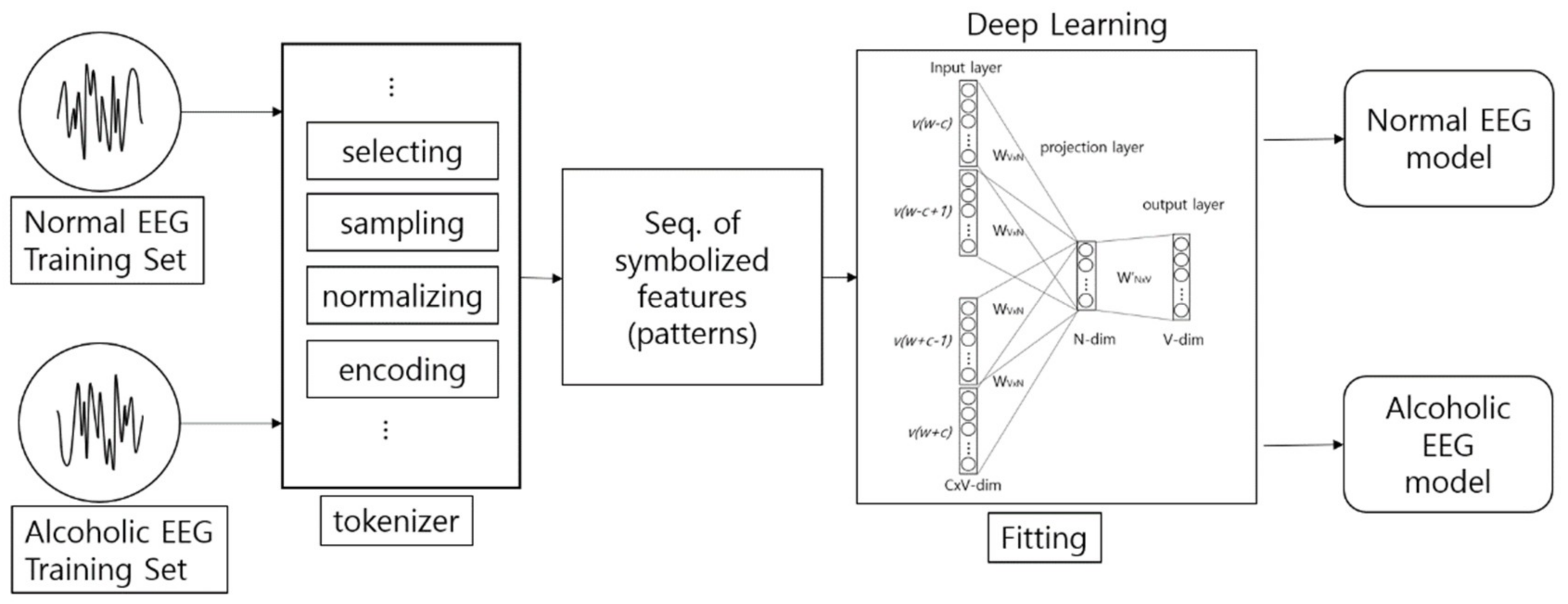
2.1. Signal Encoding
2.2. Sequence Classification
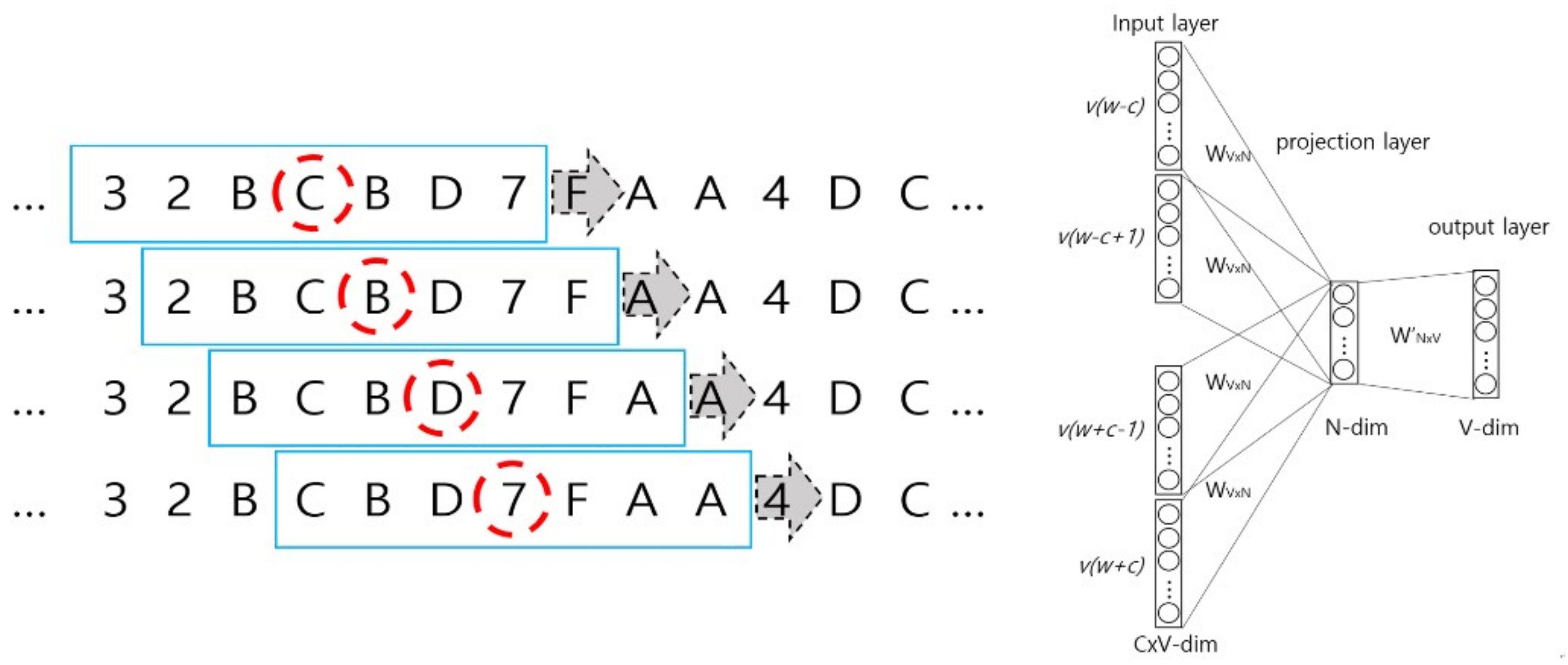
2.3. Wave Embedding and Wave Vector
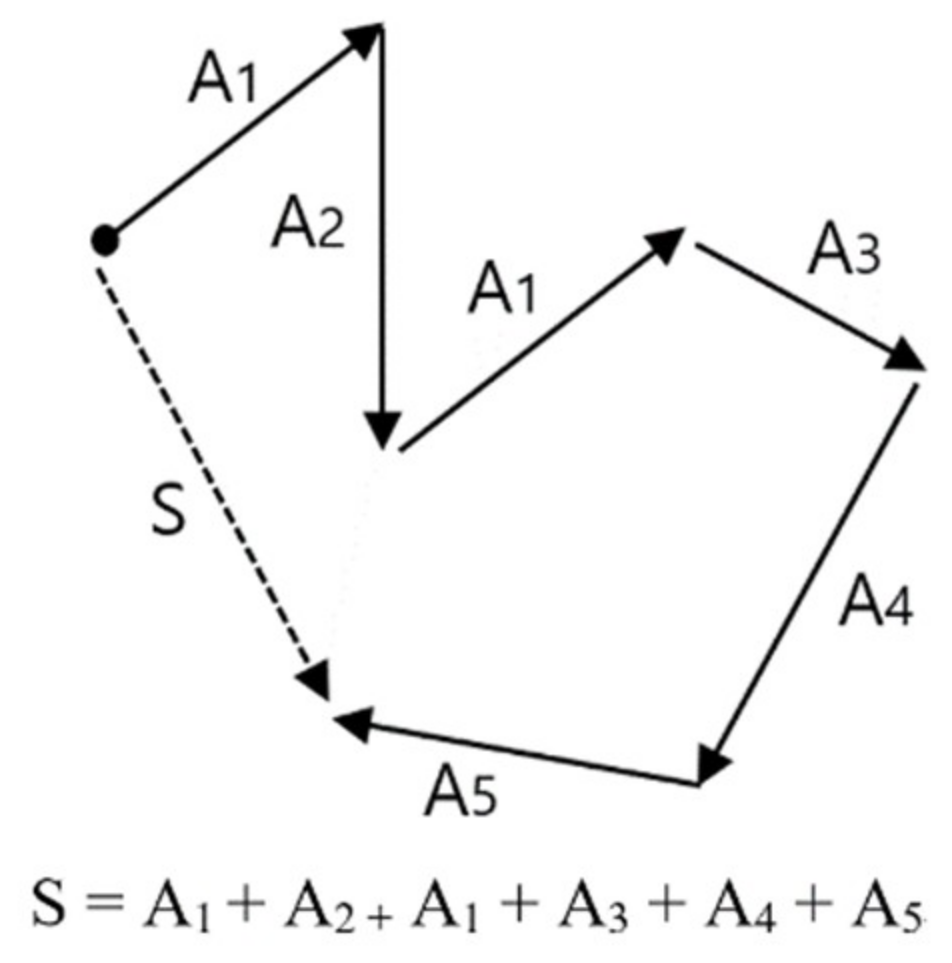
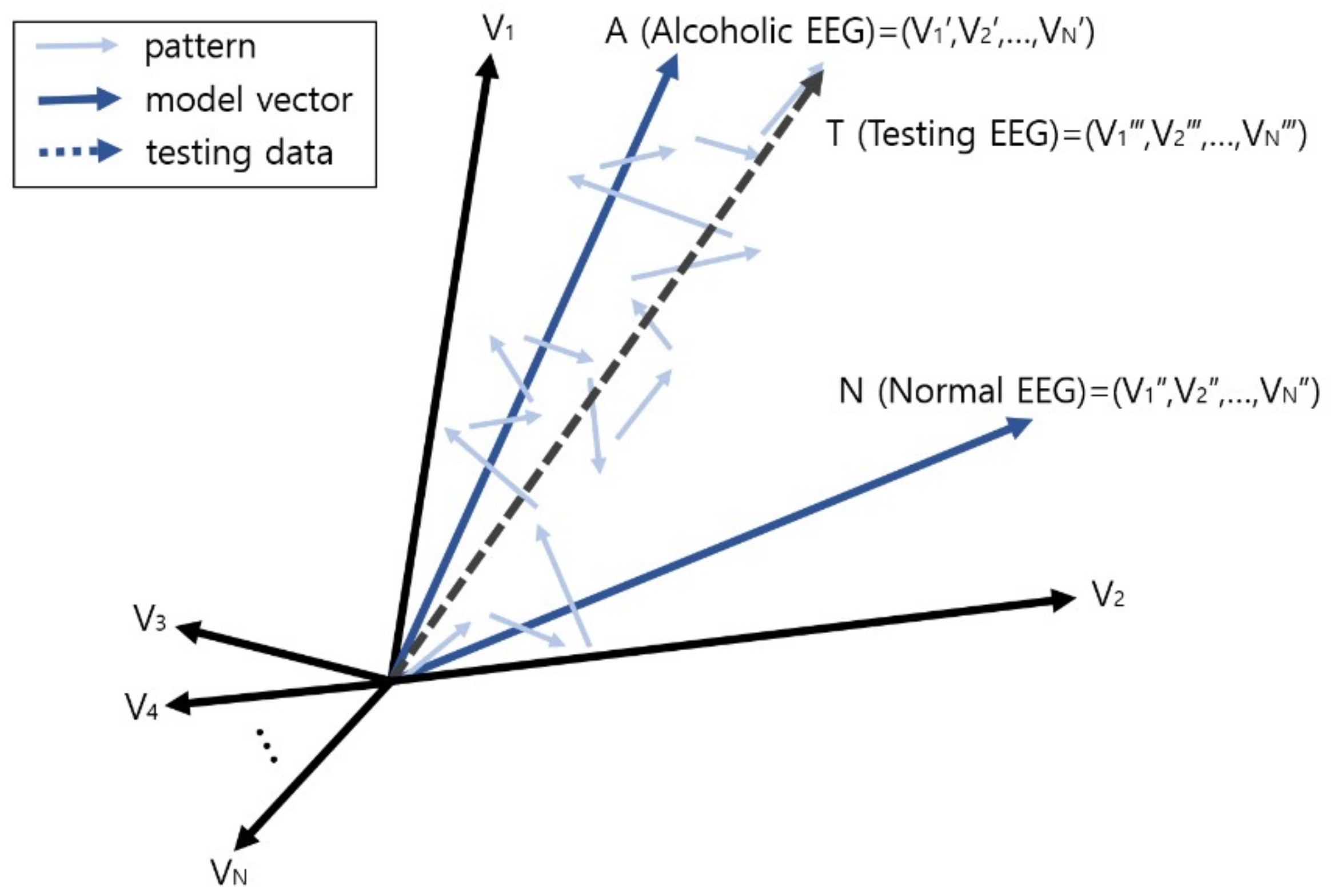
2.4. Vector Operation for Prediction and Diagnosis
3. Experiments and Results
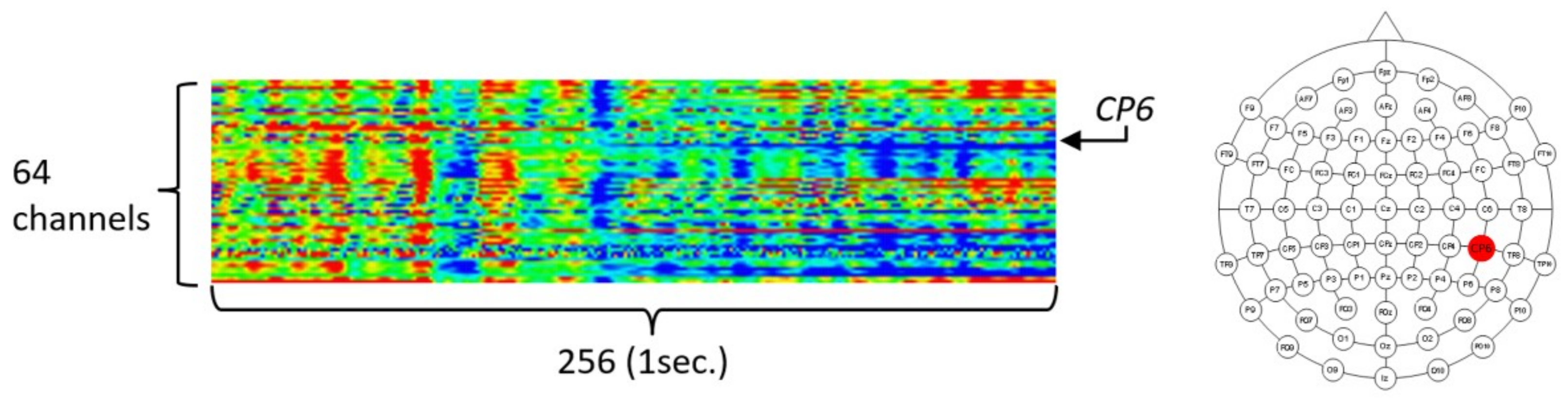
3.1. Data Description
3.2. Experimental Setting
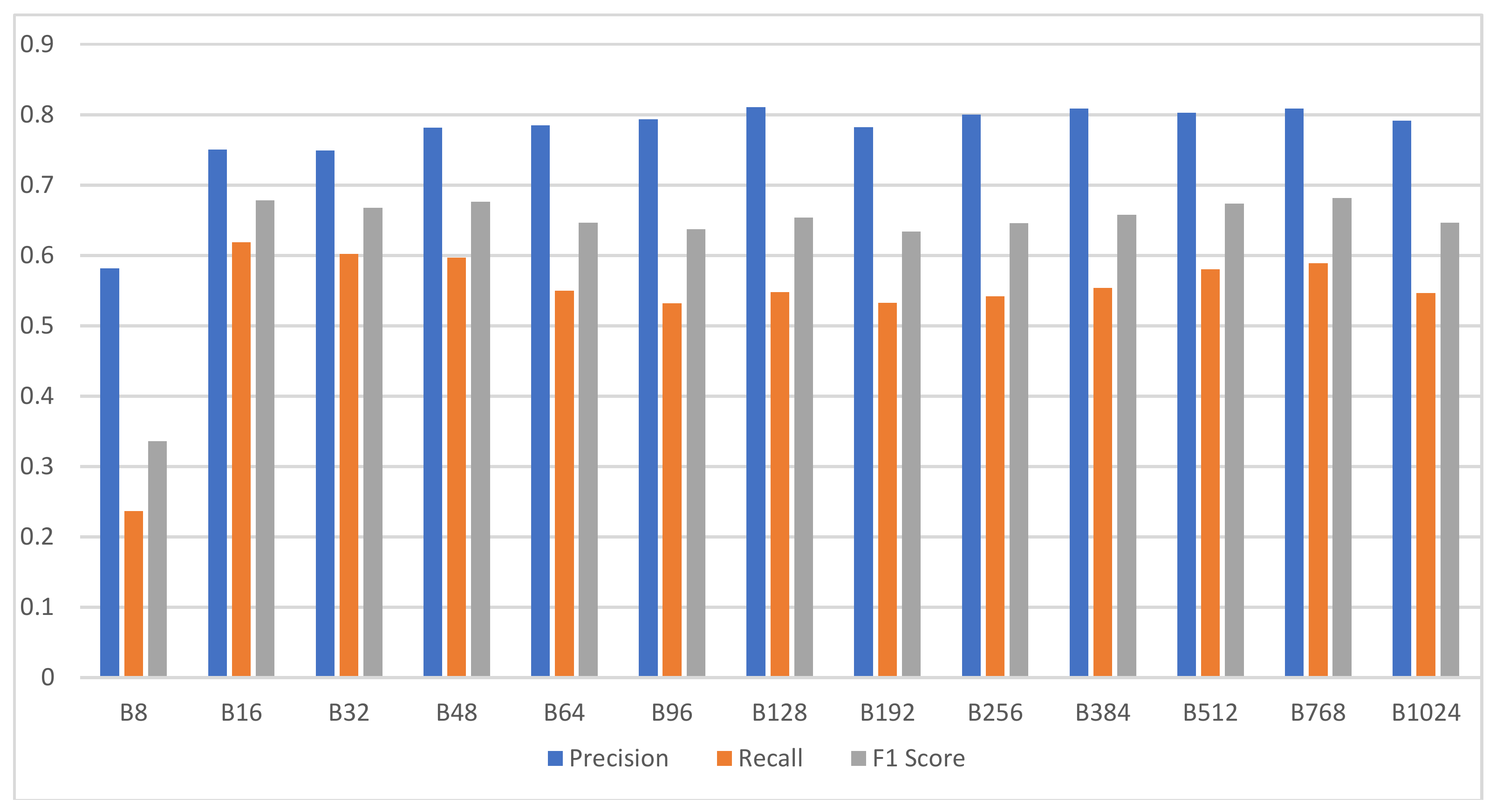
3.3. Experiment 1: Searching for the Optimal Degree of Quantization
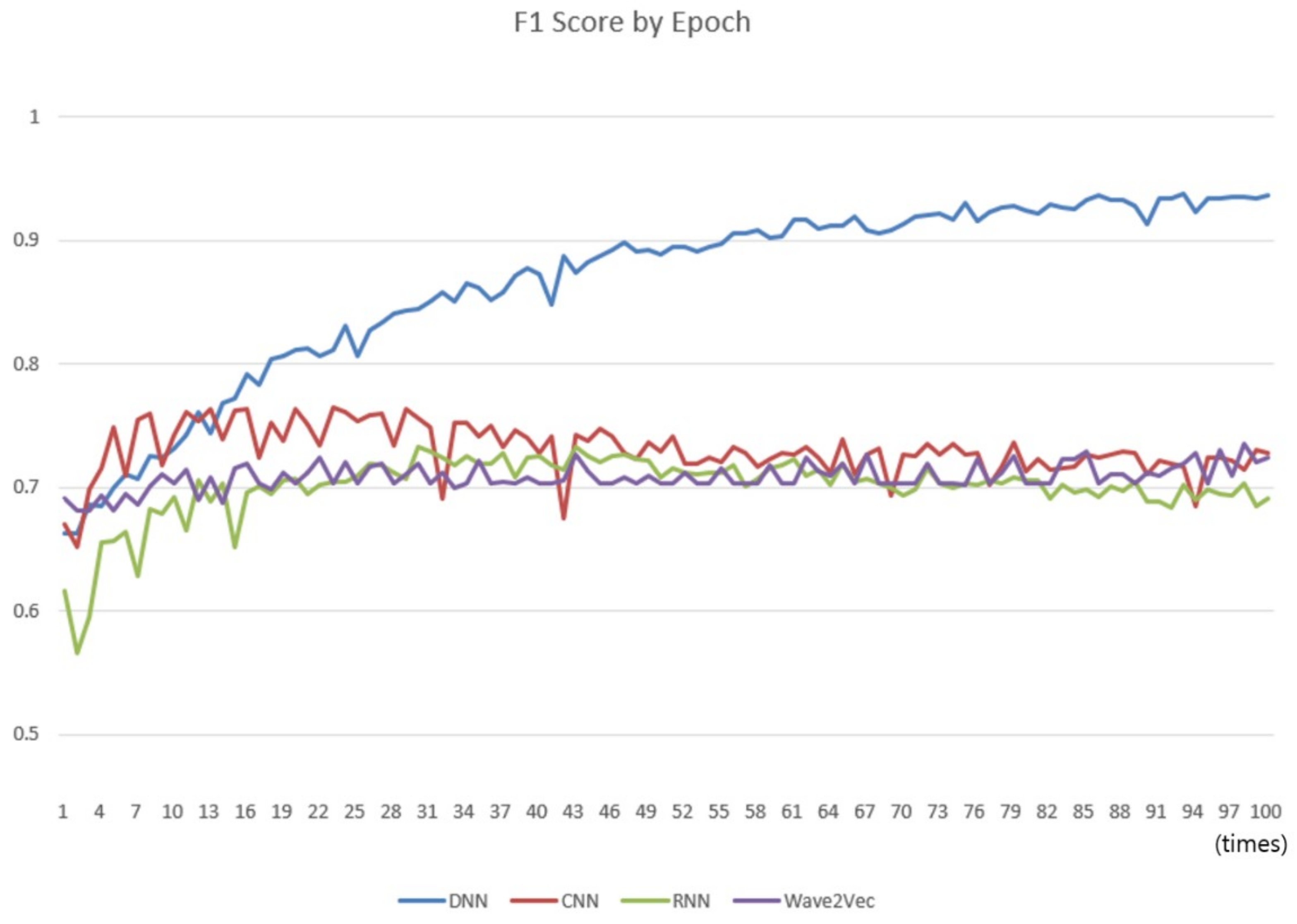
3.4. Experiment 2: Comparison with Other Deep Learning Classifiers
3.5. Experiment 3: Recognition and Identification of Effective Patterns through Model Visualization
4. Discussion
- The current proposed models did not employ any disease-specific context knowledge for enhancing analysis performance. The model is a general-purpose time series classifier, and its main goals are solving specific issues in analyzing bio-signal with conventional deep learning models, such as removing black boxes, reducing complexity, and recognizing and identifying important patterns. For real application to prediction or diagnosis of brain disease, such as dementia or alcoholism, more complicated knowledge and logic of the targeted disease, such as the relationship between the disease and the geometric information of EEG sensing spots, connections between sensing spots on the scalp, and democratic knowledge of the testing person, should be melted at the tokenizing phase.
- The analysis performance of the model, in terms of accuracy, is similar to those of conventional deep learning models and inferior to that of the deep neural network (DNN) if overfitting is ignored.
- Overfitting should be removed. As the number of epochs increases, the DNN tends to converge to a perfect status, which is overfitting. The process for data augmentation and the method of regularization, such as parameter tweaking, need to be studied.
- Unlike conventional deep learning models, the performance of the current approach is not affected directly, or affected inefficiently, by increasing the number of iterations of whole data training. This is caused by replacing large portions of the deep learning process for feature selection and classification with vector operations to reduce the number of black boxes and improve readability.
- A hybrid model, which includes both conventional deep learning modules and the proposed Wave2vec modules, should be considered because the most important values of classifiers, such as accuracy, transparency, readability, visibility, and high speed, will vary depending on the application areas.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, R.; Willis, J.; Gearry, R.; Skidmore, P.; Fleming, E.; Frampton, C.; Carr, A. Inadequate vitamin C status in prediabetes and type 2 diabetes mellitus: Associations with glycaemic control, obesity, and smoking. Nutrients 2017, 9, 997. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Chun, H.-W.; Kim, S.; Coh, B.-Y.; Kwon, O.-J.; Moon, Y.-H. Longitudinal Study-Based Dementia Prediction for Public Health. Int. J. Environ. Res. Public Health 2017, 14, 983. [Google Scholar] [CrossRef] [PubMed]
- Strichartz, R.S. A Guide to Distribution Theory and Fourier Transforms; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Cohen, M.X. Analyzing Neural Time Series Data: Theory and Practice; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Schomer, D.L.; Da Silva, F.L. Niedermeyer’s Electroencephalography: Basic Principles, Clinical Applications, and Related Fields; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2012. [Google Scholar]
- An, X.; Kuang, D.; Guo, X.; Zhao, Y.; He, L. A deep learning method for classification of EEG data based on motor imagery. In Proceedings of the International Conference on Intelligent Computing, Taiyuan, China, 3–6 August 2014; Springer: Cham, Switzerland, 2014; pp. 203–210. [Google Scholar]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2016, 14, 016003. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Wu, Y. Convolutional Deep Belief Networks for Feature Extraction of EEG Signal. In Proceedings of the Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2850–2853. [Google Scholar]
- Hussein, R.; Palangi, H.; Ward, R.; Wang, Z.J. Epileptic Seizure Detection: A Deep Learning Approach. arXiv, 2018; arXiv:1803.09848. [Google Scholar]
- Marcus, G. Deep Learning: A Critical Appraisal. arXiv, 2018; arXiv:1801.00631. [Google Scholar]
- Kivipelto, M.; Ngandu, T.; Laatikainen, T.; Winblad, B.; Soininen, H.; Tuomilehto, J. Risk score for the prediction of dementia risk in 20 years among middle aged people: A longitudinal, population-based study. Lancet Neurol. 2006, 5, 735–741. [Google Scholar] [CrossRef]
- Colon, I.; Cutter, H.S.; Jones, W.C. Prediction of alcoholism from alcohol availability, alcohol consumption and demographic data. J. Stud. Alcohol. 1982, 43, 1199–1213. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Pei, J.; Keogh, E. A brief survey on sequence classification. ACM Sigkdd Explor. Newsl. 2010, 12, 40–48. [Google Scholar] [CrossRef]
- Lesh, N.; Zaki, M.J.; Ogihara, M. Mining features for sequence classification. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999. [Google Scholar]
- Zhang, Y.; Yang, S.; Liu, Y.; Han, B.; Zhou, F. Integration of 24 Feature Types to Accurately Detect and Predict Seizures Using Scalp EEG Signals. Sensors 2018, 18, 5. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Xun, G.; Suo, Q.; Jia, K.; Zhang, A. Wave2vec: Learning deep representations for biosignals. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; Available online: http://icdm2017.bigke.org/ (accessed on 3 January 2018).
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv, 2013; arXiv:1301.3781. [Google Scholar]
- Sun, R.; Alexandre, F. Connectionist-Symbolic Integration: From Unified to Hybrid Approaches; Psychology Press: London, UK, 2013. [Google Scholar]
- Hall, L.O.; Romaniuk, S.G. A Hybrid Connectionist, Symbolic Learning System. In Proceedings of the AAAI, Boston, MA, USA, 29 July–3 August 1990; pp. 783–788. [Google Scholar]
- Moreno, P.J.; Stern, R.M. Sources of degradation of speech recognition in the telephone network. In Proceedings of the 1994 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP-94), Adelaide, Australia, 19–22 April 1994. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wechsler, H. Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition. IEEE. Trans. Image Process. 2002, 11, 467–476. [Google Scholar] [PubMed]
- Rabiner, L.R.; Gold, B. Theory and Application of Digital Signal Processing; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1975; 777p. [Google Scholar]
- Mogul, J.C.; Douglis, F.; Feldmann, A.; Krishnamurthy, B. Potential benefits of delta encoding and data compression for HTTP. ACM SIGCOMM Comput. Commun. Rev. 1997, 27, 181–194. [Google Scholar] [CrossRef]
- Mladenic, D.; Grobelnik, M. Word sequences as features in text-learning. In Proceedings of the 17th Electrotechnical and Computer Science Conference, Ljubljana, Slovenia, 24–26 September 1998. [Google Scholar]
- Sharma, A.; Dey, S. An artificial neural network based approach for sentiment analysis of opinionated text. In Proceedings of the 2012 ACM Research in Applied Computation Symposium, San Antonio, TX, USA, 23–26 October 2012; pp. 37–42. [Google Scholar]
- Zhou, C.; Cule, B.; Goethals, B. Pattern based sequence classification. IEEE Trans. Knowl. Data Eng. 2016, 28, 1285–1298. [Google Scholar] [CrossRef]
- Kim, S.; Yeo, W.; Lee, J.; Kim, K.-H. Linguistic Feature Learning for Technological Information Detection. In Proceedings of the International Conference on Convergence Content (ICCC2012), Saga University, Saga, Japan, 28–31 May 2012. [Google Scholar]
- Salton, G.; McGill, M. Introduction to Modern Information; American Association for Artificial Intelligence Retrieval: Philadelphia, PA, USA, 1983. [Google Scholar]
- Kuang, S.; Davison, B.D. Learning Word Embeddings with Chi-Square Weights for Healthcare Tweet Classification. Appl. Sci. 2017, 7, 846. [Google Scholar] [CrossRef]
- Begleiter, H. EEG Database Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/EEG+Database (accessed on 3 January 2018).
- Zhang, X.L.; Begleiter, H.; Porjesz, B.; Litke, A. Electrophysiological evidence of memory impairment in alcoholic patients. Biol. Psychiatry 1997, 42, 1157–1171. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y.; Wen, P.P.; Wang, S. Analysis of alcoholic EEG signals based on horizontal visibility graph entropy. Brain Inform. 2014, 1, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Keras: Deep Learning Library for Theano and Tensorflow; Data Science Central: Mountain View, CA, USA, 2015. [Google Scholar]
- DeepLearning4j. Deep Learning for Java. Available online: https://deeplearning4j.org/ (accessed on 14 August 2018).
- Wikipedia. Accuracy Paradox. Available online: https://en.wikipedia.org/wiki/Accuracy_paradox (accessed on 14 August 2018).
- Akosa, J. Predictive Accuracy: A Misleading Performance Measure for Highly Imbalanced Data. In Proceedings of the SAS Global Forum, Orlando, FL, USA, 2–5 April 2017. [Google Scholar]
- Buza, K.A.; Koller, J. Classification of electroencephalograph data: A hubness-aware approach. Acta Polytech. Hung. 2016, 13, 27–46. [Google Scholar]
- Wilkinson, L.; Friendly, M. The history of the cluster heat map. Am. Stat. 2009, 63, 179–184. [Google Scholar] [CrossRef]

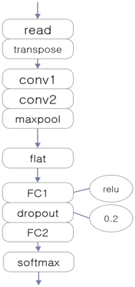
| CNN-Based EEG Classifier | RNN (LSTM)-Based EEG Classifier | DNN-Based EEG Classifier |
|---|---|---|
 | 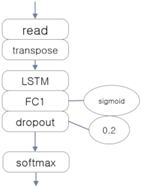 | 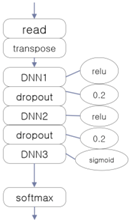 |
| Training Time (Seconds per Epoch) | Testing Time (Seconds per Instance) | |||||
|---|---|---|---|---|---|---|
| Loading | Encoding | Learning | Loading | Encoding | Classifying | |
| Wave2vec | 5.650 | 2.250 | 23.020 | 0.005 | 0.000 | 0.059 |
| CNN | 5.650 | - | 194.030 | 0.005 | - | 0.390 |
| RNN | 5.650 | - | 323.130 | 0.005 | - | 0.574 |
| DNN | 5.650 | - | 206.394 | 0.005 | - | 0.480 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Kim, J.; Chun, H.-W. Wave2Vec: Vectorizing Electroencephalography Bio-Signal for Prediction of Brain Disease. Int. J. Environ. Res. Public Health 2018, 15, 1750. https://doi.org/10.3390/ijerph15081750
Kim S, Kim J, Chun H-W. Wave2Vec: Vectorizing Electroencephalography Bio-Signal for Prediction of Brain Disease. International Journal of Environmental Research and Public Health. 2018; 15(8):1750. https://doi.org/10.3390/ijerph15081750
Chicago/Turabian StyleKim, Seonho, Jungjoon Kim, and Hong-Woo Chun. 2018. "Wave2Vec: Vectorizing Electroencephalography Bio-Signal for Prediction of Brain Disease" International Journal of Environmental Research and Public Health 15, no. 8: 1750. https://doi.org/10.3390/ijerph15081750
APA StyleKim, S., Kim, J., & Chun, H.-W. (2018). Wave2Vec: Vectorizing Electroencephalography Bio-Signal for Prediction of Brain Disease. International Journal of Environmental Research and Public Health, 15(8), 1750. https://doi.org/10.3390/ijerph15081750




