A Novel Multiattribute Decision-Making Method Based on Point–Choquet Aggregation Operators and Its Application in Supporting the Hierarchical Medical Treatment System in China
Abstract
:1. Introduction
2. Preliminaries
2.1. Picture Fuzzy Sets
2.2. Choquet Integral Operator
- (1)
- (boundary conditions),
- (2)
- and, then(monotonicity).
- (1)
- If = 0, then -fuzzy measure reduces to , which is defined as an additive measure.In this situation, if all the elements in X are independent, we get
- (2)
- If all the elements in X are finite, thenwhere , for , and
- (3)
- If , then -fuzzy measure reduces to , which is defined as a super-additive measure.
- (4)
- If , then -fuzzy measure reduces to , which is defined as a sub-additive measure.
3. Some Point Operations for Picture Fuzzy Numbers and Their Properties
- (1)
- From , we get
- (2)
- Then
4. Picture Fuzzy Point–Choquet Integral Aggregation Operators and Their Properties
4.1. Picture Fuzzy Point–Choquet Averaging Operator
- (1)
- Ifthen the series of PFPCA operators are all reduced to the series of picture fuzzy point averaging (PFPWA) operators. In particular, ifthen PFPCA operators is reduced to a picture fuzzy averaging (PFA) operator, which is defined as:
- (2)
- Ifandfor allwhereis the number of the elements in set A,, then the PFPCA operator is reduced to a picture fuzzy order-weighted averaging (PFOWA) operator defined by Garg [13].
- (3)
- Ifthen the series of PFPCA operators are all reduced to the series of picture fuzzy weighted averaging (PFWA) operators defined by Garg [13].
4.2. Picture Fuzzy Point–Choquet Geometric Operator
4.3. Generalized Picture Fuzzy Point–Choquet Averaging Operator
4.4. Generalized Picture Fuzzy Point–Choquet Geometric Ooperator
5. A New Method to Multiattribute Decision-Making with Picture Fuzzy Information
6. Applications in Supporting the Hierarchical Medical Treatment System with the Proposed Approach
6.1. Decision-Making Process
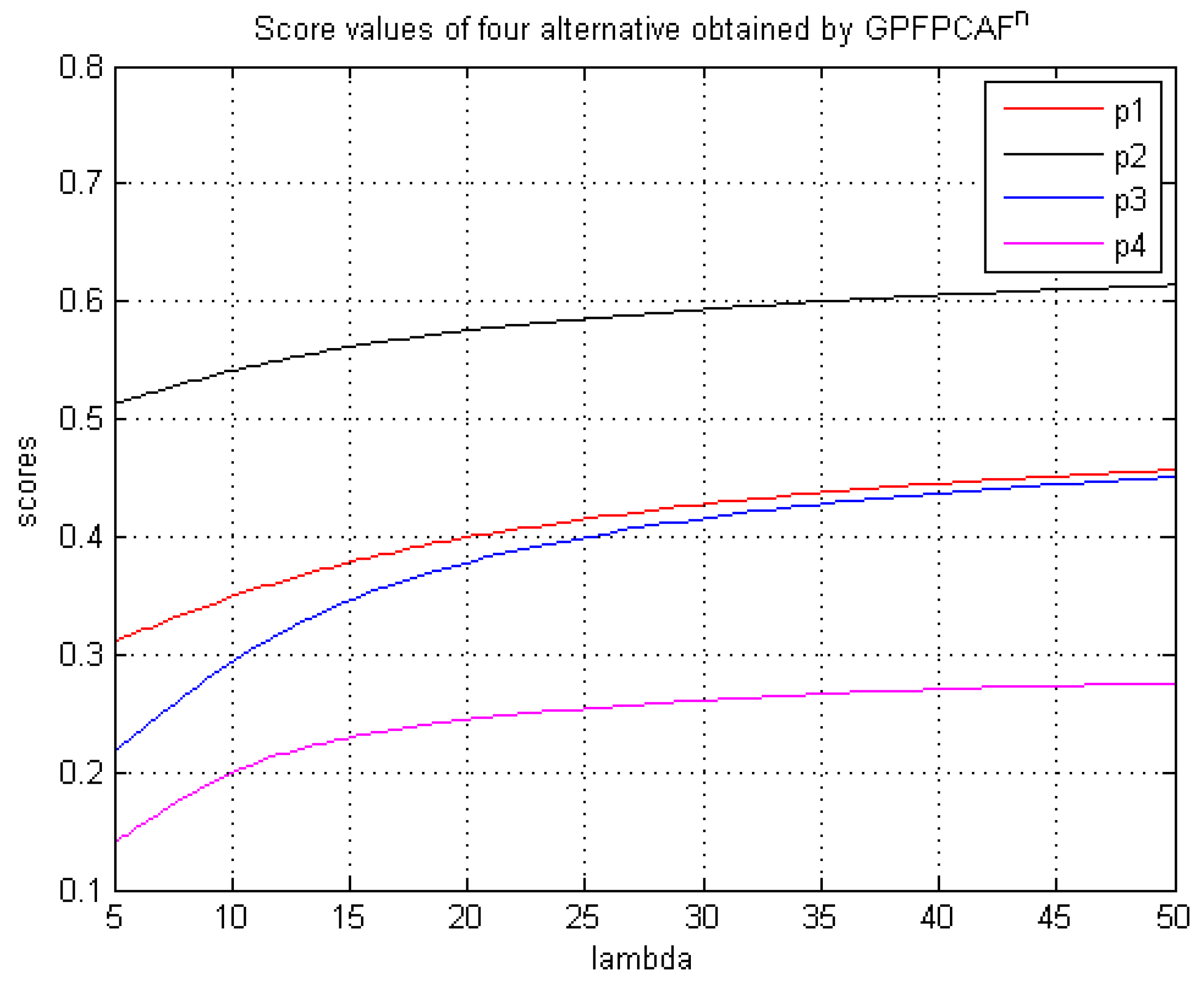
6.2. The Influence of the Parameter Vector λ on the Final Result
6.3. Comparative Analysis
6.3.1. Validity Test
6.3.2. The Advantages of the Proposed Method
- (1)
- (2)
- It should also be noted that the methods introduced in [12,13] are only based on the original information, and thus cannot control the certainty degree, while the new proposed methods can redistribute the membership or non-membership in PFNs according to different principles and thus can get more intensive information from the original PFS.
- (3)
- From Table 6, it can be concluded that aggregation operators introduced in [12,13] cannot consider correlations among arguments, but the proposed aggregation operators can efficiently take the various interactions among the decision criteria into account. Furthermore, when changing the parameter λ, different scores are acquired shown as in Table 3, which makes decision making more flexible and can meet the needs of different types of decision makers.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 2
Appendix B. Proof of Theorem 6
References
- Tang, M.; Liao, H.C.; Li, Z.M.; Xu, Z.S. Nature disaster risk evaluation with a group decision making method based on incomplete hesitant fuzzy linguistic preference relations. Int. J. Environ. Res. Public Health 2018, 15, 751. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.W.; Zhang, J.L.; Zhao, S.P.; Liang, C.Y. Tackling complex emergency response solutions evaluation problems in sustainable development by fuzzy group decision making approaches with considering decision hesitancy and prioritization among assessing criteria. Int. J. Environ. Res. Public Health 2017, 14, 1165. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhou, J.W. Linguistic multi-attribute group decision making with risk preferences and its use in low-carbon tourism destination selection. Int. J. Environ. Res. Public Health. 2017, 14, 1078. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, P.; Mondal, S.; Boral, S.; Banerjee, A.; Chakraborty, S. A novel hybrid method for non-traditional machining process selection using factor relationship and Multi-Attributive Border Approximation Method. Facta Univ. Ser. Mech. Eng. J. 2017, 15, 439–456. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamučar, D. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar]
- Vasiljević, M.; Fazlollahtabar, H.; Stević, Ž.; Vesković, S. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Projection models for multiple attribute decision making with picture fuzzy information. Int. J. Mach. Learn. Cybern. 2018, 9, 713–719. [Google Scholar] [CrossRef]
- Wei, G.W. Picture 2-tuple linguistic Bonferroni mean operators and their application to multiple attribute decision making. Int. J. Fuzzy Syst. 2016, 19, 1–14. [Google Scholar] [CrossRef]
- Wei, G.W. Picture uncertain linguistic Bonferroni mean operators and their application to multiple attribute decision making. Kybernetes 2017, 46, 1777–1800. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, X.; Tu, H. Some geometric aggregation operators based on picture fuzzy sets and their application in multiple attribute decision making. Indian J. Pure Appl. Math. 2017, 37, 477–492. [Google Scholar]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multi-criteria decision-making. Arab. J. Sci. Eng. 2017, 42, 1–16. [Google Scholar] [CrossRef]
- Abbas, M.; Nilashi, M.; Kazimieras, E.; Rahmah, S.; Zare, H.; Mohd, N. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. 2018, 17, 391–466. [Google Scholar]
- He, Y.D.; Chen, H.Y.; He, Z.; Zhou, L.G. Multi-attribute decision making based on neutral averaging operators for intuitionistic fuzzy information. Appl. Soft Comput. 2015, 27, 64–76. [Google Scholar] [CrossRef]
- Choquet, G. On a class of set-functions. Bull. Am. Math. Soc. 1954, 60, 64. [Google Scholar]
- Zhou, L.G.; Chen, H.Y. Continuous generalized OWA operator and its application to decision making. Fuzzy Sets Syst. 2011, 168, 18–34. [Google Scholar] [CrossRef]
- Meng, F.Y.; Zhang, Q. Induced continuous Choquet integral operators and their application to group decision making. Comput. Ind. Eng. 2014, 68, 42–53. [Google Scholar] [CrossRef]
- Xu, Z.S. Choquet integrals of weighted intuitionistic fuzzy information. Inf. Sci. 2010, 180, 726–736. [Google Scholar] [CrossRef]
- Yager, R.R. On Using the Shapley Value to Approximate the Choquet Integral in Cases of Uncertain Arguments. IEEE Trans. Fuzzy Syst. 2018, 26, 1303–1310. [Google Scholar] [CrossRef]
- Liu, B.; Fu, M.; Zhang, S.; Xue, B.; Zhou, Q.; Zhang, S. An interval-valued 2-tuple linguistic group decision-making model based on the Choquet integral operator. Int. J. Syst. Sci. 2018, 49, 407–424. [Google Scholar] [CrossRef]
- Wen, X.Q.; Yan, M.C.; Xian, J.Y.; Yue, R.; Peng, A.H. Supplier selection in supplier chain management using Choquet integral-based linguistic operators under fuzzy heterogeneous environment. Fuzzy Optim. Decis. Mak. 2016, 15, 307–330. [Google Scholar] [CrossRef]
- Qu, G.H.; Li, Y.J.; Qu, W.H.; Li, C.H. Some new Shapley dual hesitant fuzzy Choquet aggregattion operators and their applications to multiple attribute group decision making-based TOPSIS. J. Int. Fuzzy Syst. 2017, 33, 2463–2483. [Google Scholar]
- Joshi, D.; Kumar, S. Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 183–191. [Google Scholar] [CrossRef]
- Peng, X.D.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Physica-Verlag: Heidelberg, Germany; New York, NY, USA, 1999. [Google Scholar]
- Liu, H.W.; Wang, G.J. Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 2007, 179, 220–233. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Generalized point operators for aggregating intuitionistic fuzzy information. Int. J. Intell. Syst. 2010, 25, 1061–1080. [Google Scholar] [CrossRef]
- Xia, M.M. Point operators for intuitionistic multiplicative information. J. Intell. Fuzzy Syst. 2016, 28, 615–620. [Google Scholar]
- Peng, X.D.; Yang, Y. Fundamental properties of Pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 2016, 147, 415–446. [Google Scholar] [CrossRef]
- Peng, X.D.; Yuan, H.Y. Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 2016, 31, 444–487. [Google Scholar] [CrossRef]
- Xing, Y.P.; Zhang, R.T.; Xia, M.M.; Wang, J. Generalized point aggregation operators for dual hesitant fuzzy information. J. Intell. Fuzzy Syst. 2017, 33, 515–527. [Google Scholar] [CrossRef]
- Grabisch, M. Fuzzy integral in multi-criteria decision making. Fuzzy Sets Syst. 1995, 69, 279–298. [Google Scholar] [CrossRef]
- Guan, W.J.; Zheng, X.Y.; Chung, K.F.; Zhong, N.F. Impact of air pollution on the burden of chronic respiratory diseases in China: time for urgent action. Lancet 2016, 388, 1939–1951. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Y.; Zeng, Y.; Gao, G.F.; Liang, X.; Zhou, M.; Wan, X.; Yu, S.; Jiang, Y.; Naghavi, M.; et al. Rapid health transition in China,1990–2010: findings from the Global Burden of Disease Study 2010. Lancet. 2013, 381, 1987–2015. [Google Scholar] [CrossRef]
- Wang, X.; Triantaphyllou, E. Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega 2008, 36, 45–63. [Google Scholar] [CrossRef]
- Zeng, S. Pythagorean fuzzy multi-attribute group decision making with probabilistic information and OWA approach. Int. J. Intell. Syst. 2017, 32, 1136–1150. [Google Scholar] [CrossRef]
- Xiong, S.H.; Chen, Z.S.; Chin, K.S. A novel MAGDM approach with proportional hesitant fuzzy sets. Int. J. Comput. Intell. Syst. 2018, 11, 256–271. [Google Scholar] [CrossRef]
- Zhai, Y.L.; Xu, Z.S.; Liao, H.C. Measures of probabilistic interval-valued intuitionistic hesitant fuzzy sets and the application in reducing excessive medical examinations. IEEE Trans. Fuzzy Syst. 2018, 26, 1651–1671. [Google Scholar] [CrossRef]
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| x1 | (0.6, 0.1, 0.2) | (0.5, 0.3, 0.1) | (0.5, 0.1, 0.3) | (0.2, 0.3, 0.4) |
| x2 | (0.4, 0.4, 0.1) | (0.6, 0.3, 0.1) | (0.5, 0.2, 0.2) | (0.7, 0.1, 0.2) |
| x3 | (0.2, 0.2, 0.3) | (0.6, 0.2, 0.1) | (0.4, 0.1, 0.3) | (0.4, 0.3, 0.3) |
| x4 | (0.6, 0.1, 0.3) | (0.1, 0.2, 0.6) | (0.1, 0.3, 0.5) | (0.2, 0.3, 0.2) |
| x1 | 0.3 | 0.186 | 0.354 | 0.16 |
| x2 | 0.3 | 0.186 | 0.177 | 0.337 |
| x3 | 0.3 | 0.186 | 0.177 | 0.337 |
| x4 | 0.4 | 0.186 | 0.174 | 0.246 |
| Parameters | Ranking Results | |
|---|---|---|
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| x1 | (0.5, 0.1,0.1) | (0.4, 0.3,0.2) | (0.4, 0.1, 0.4) | (0.1, 0.3, 0.5) |
| x2 | (0.4, 0.4, 0.1) | (0.6, 0.3, 0.1) | (0.5, 0.2, 0.2) | (0.7, 0.1, 0.2) |
| x3 | (0.1, 0.2, 0.4) | (0.5, 0.2, 0.2) | (0.3, 0.1, 0.2) | (0.3, 0.3, 0.4) |
| x4 | (0.5, 0.1, 0.4) | (0.1, 0.2, 0.7) | (0.1, 0.3, 0.6) | (0.1, 0.3, 0.3) |
| Approaches | Score Value of Xi (i = 1, 2, 3, 4) | Ranking |
|---|---|---|
| Approach based on the PFWA operator [13] | ||
| Approach based on the PFHA operator [13] | ||
| Approach based on the PFWG operator [12] | ||
| Approach based on the PFHG operator [12] | ||
| Approach based on the PFEWA operator [13] | ||
operator (in this paper) | ||
operator (in this paper) | ||
operator (in this paper) | ||
operator (in this paper) |
| Aggregation Operators | Whether It Can Consider Correlations among Arguments | Whether It Can Control the Certainty of PFNs | Flexible (Whether There Is a Parameter to Reflect Preferences) |
|---|---|---|---|
| PFWA [13] | No | No | No |
| PFOWA [13] | No | No | No |
| PFHA [13] | No | No | No |
| PFWG [12] | No | No | No |
| PFOWG [12] | No | No | No |
| PFHG [12] | No | No | No |
| PFEWA [13] | No | No | No |
| PFHA [13] | No | No | No |
| PFPCA | Yes | Yes | Yes |
| PFPCG | Yes | Yes | Yes |
| GPFPCA | Yes | Yes | Yes |
| GPFPCG | Yes | Yes | Yes |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Xing, Y.; Wang, J.; Shang, X.; Zhu, X. A Novel Multiattribute Decision-Making Method Based on Point–Choquet Aggregation Operators and Its Application in Supporting the Hierarchical Medical Treatment System in China. Int. J. Environ. Res. Public Health 2018, 15, 1718. https://doi.org/10.3390/ijerph15081718
Zhang R, Xing Y, Wang J, Shang X, Zhu X. A Novel Multiattribute Decision-Making Method Based on Point–Choquet Aggregation Operators and Its Application in Supporting the Hierarchical Medical Treatment System in China. International Journal of Environmental Research and Public Health. 2018; 15(8):1718. https://doi.org/10.3390/ijerph15081718
Chicago/Turabian StyleZhang, Runtong, Yuping Xing, Jun Wang, Xiaopu Shang, and Xiaomin Zhu. 2018. "A Novel Multiattribute Decision-Making Method Based on Point–Choquet Aggregation Operators and Its Application in Supporting the Hierarchical Medical Treatment System in China" International Journal of Environmental Research and Public Health 15, no. 8: 1718. https://doi.org/10.3390/ijerph15081718
APA StyleZhang, R., Xing, Y., Wang, J., Shang, X., & Zhu, X. (2018). A Novel Multiattribute Decision-Making Method Based on Point–Choquet Aggregation Operators and Its Application in Supporting the Hierarchical Medical Treatment System in China. International Journal of Environmental Research and Public Health, 15(8), 1718. https://doi.org/10.3390/ijerph15081718





