Using a Counting Process Method to Impute Censored Follow-Up Time Data
Abstract
1. Introduction
2. Materials and Methods
3. Results
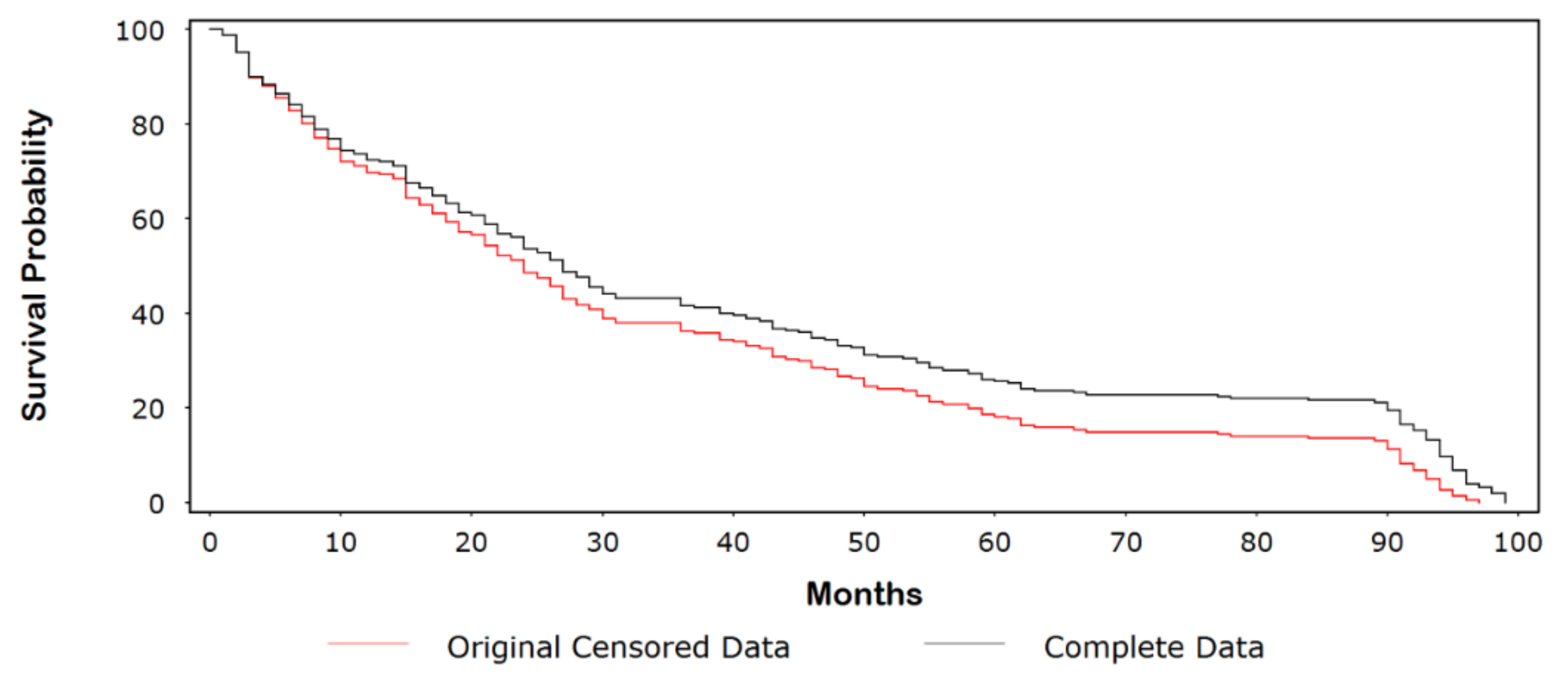
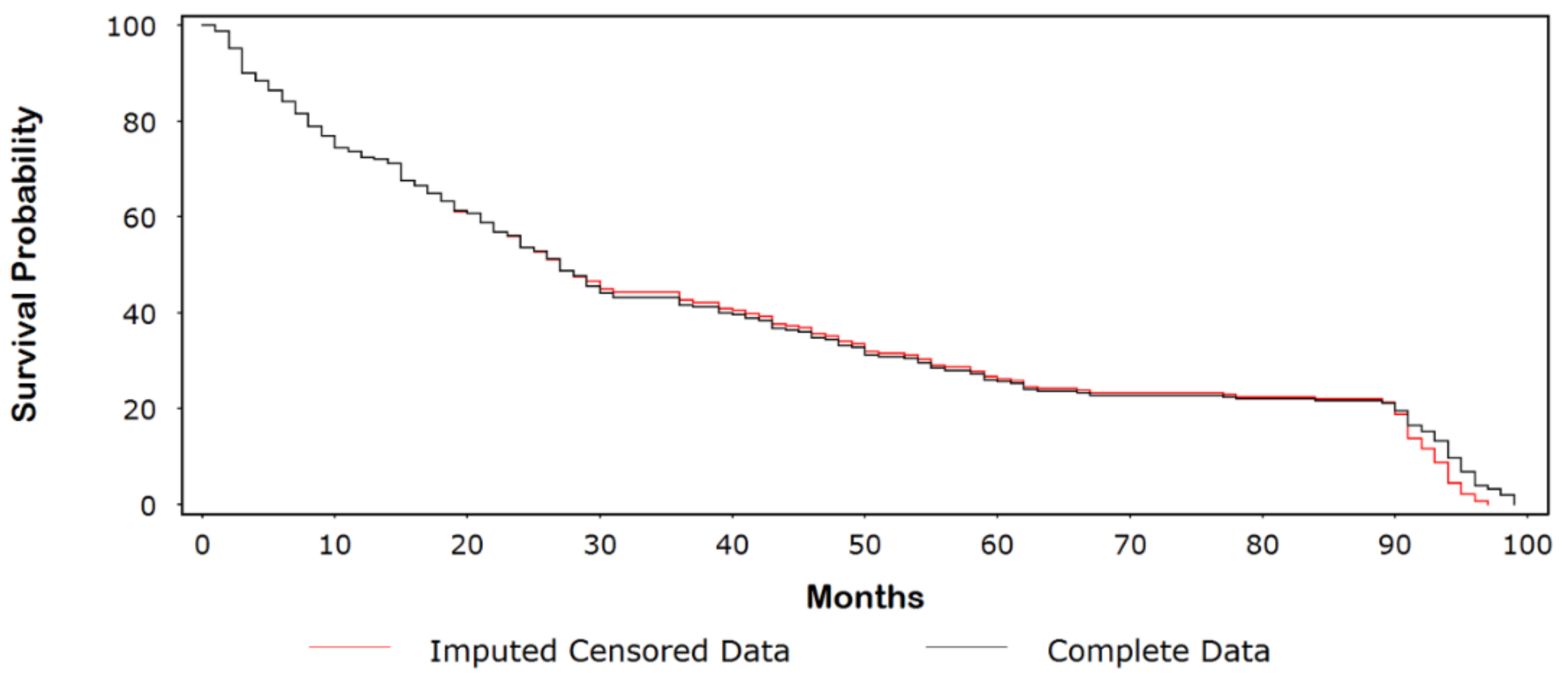
3.1. Kaplan-Meier (Product-Limit) Example
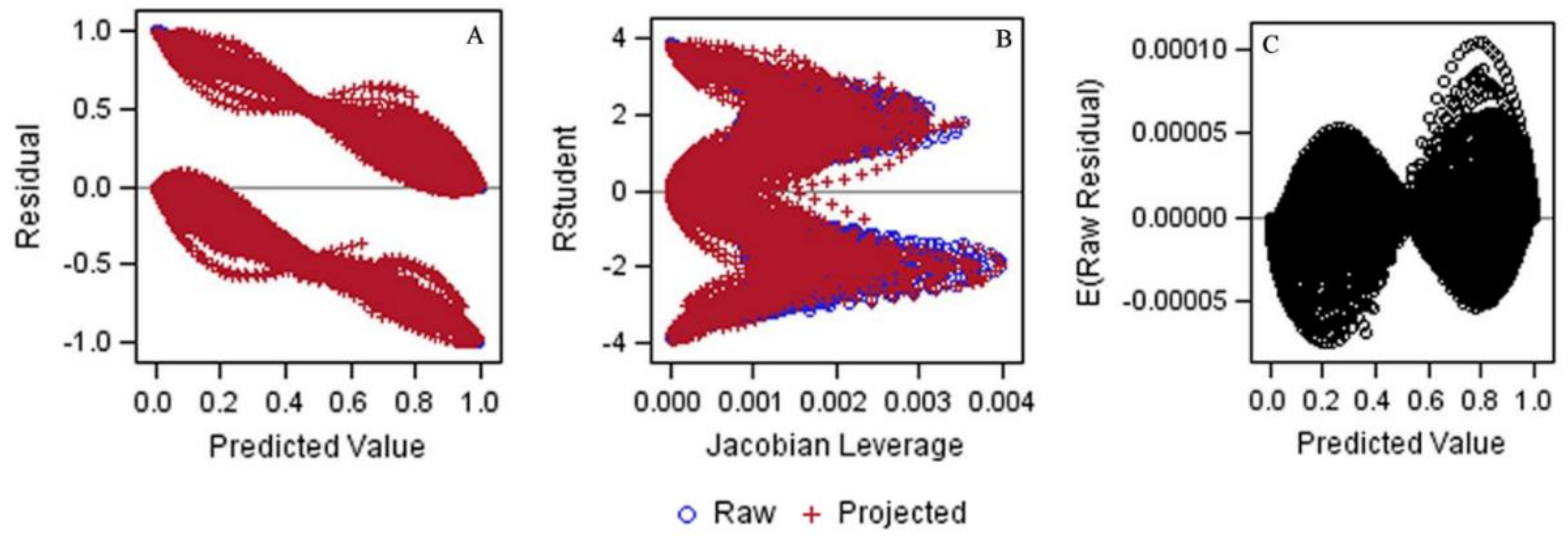
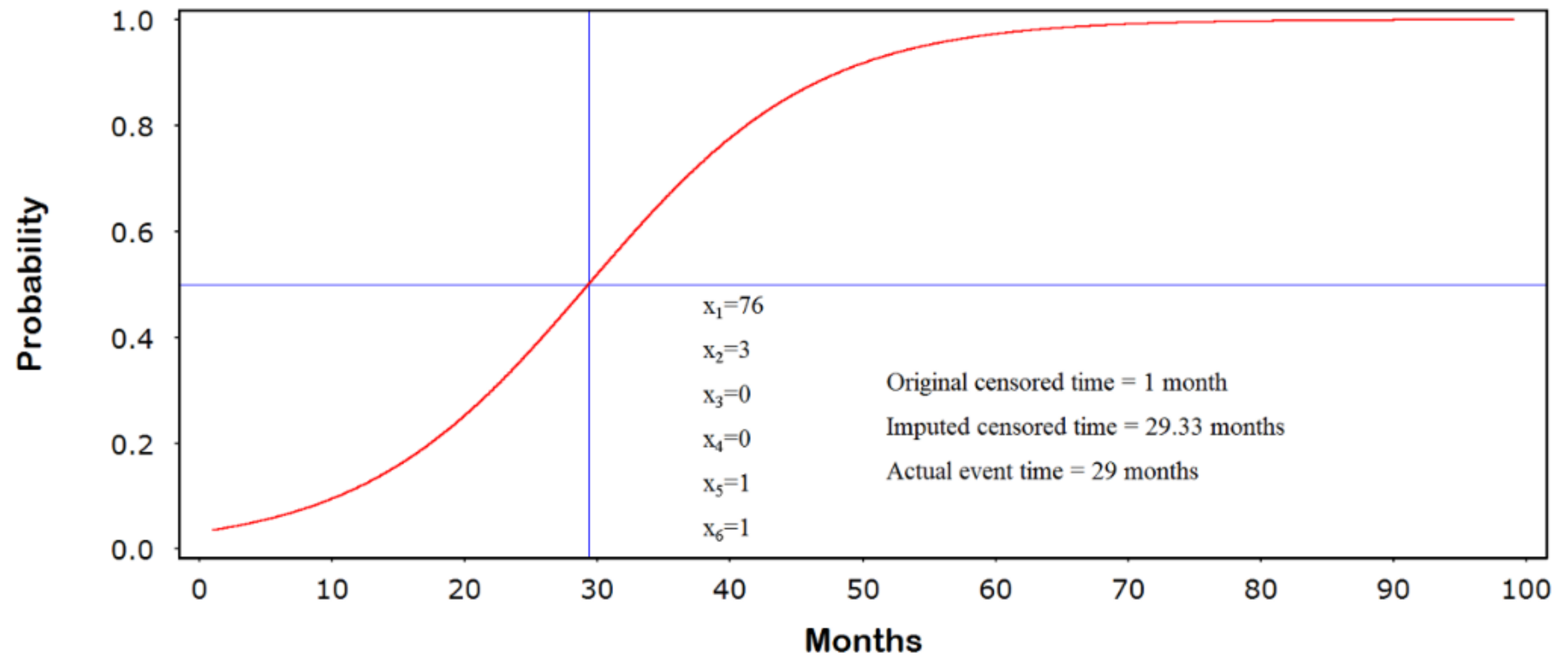
3.2. Generating the Jump-Point Plot
3.3. SAS Code
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| A | B | C | D | E | F | G | H | I | J | K | A | B | C | D | E | F | G | H | I | J | K | A | B | C | D | E | F | G | H | I | J | K |
| 1 | 93 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | -- | 1 | 36 | 96 | 4 | 1 | 0 | 1 | 1 | 6 | 6 | -- | 1 | 71 | 99 | 3 | 0 | 0 | 1 | 1 | 14 | 14 | -- | 1 |
| 2 | 90 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | -- | 1 | 37 | 93 | 3 | 1 | 0 | 1 | 1 | 6 | 6 | -- | 1 | 72 | 83 | 2 | 1 | 1 | 1 | 1 | 14 | 14 | -- | 1 |
| 3 | 89 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | -- | 1 | 38 | 94 | 3 | 1 | 0 | 0 | 1 | 6 | 6 | -- | 1 | 73 | 85 | 4 | 1 | 1 | 0 | 1 | 15 | 15 | -- | 1 |
| 4 | 89 | 4 | 1 | 0 | 1 | 1 | 2 | 2 | -- | 1 | 39 | 93 | 3 | 1 | 1 | 1 | 1 | 6 | 6 | -- | 1 | 74 | 83 | 3 | 1 | 1 | 0 | 1 | 15 | 15 | -- | 1 |
| 5 | 86 | 3 | 1 | 1 | 1 | 0 | 2 | 2 | -- | 1 | 40 | 97 | 3 | 1 | 1 | 1 | 1 | 6 | 6 | -- | 1 | 75 | 81 | 3 | 1 | 0 | 1 | 1 | 15 | 15 | -- | 1 |
| 6 | 86 | 3 | 1 | 0 | 1 | 1 | 2 | 2 | -- | 1 | 41 | 97 | 3 | 1 | 0 | 1 | 1 | 7 | 7 | -- | 1 | 76 | 98 | 1 | 1 | 0 | 0 | 1 | 15 | 15 | -- | 1 |
| 7 | 95 | 4 | 1 | 1 | 1 | 1 | 2 | 2 | -- | 1 | 42 | 97 | 2 | 1 | 0 | 1 | 1 | 7 | 7 | -- | 1 | 77 | 94 | 3 | 1 | 0 | 0 | 1 | 15 | 15 | -- | 1 |
| 8 | 90 | 3 | 1 | 1 | 1 | 1 | 2 | 2 | -- | 1 | 43 | 86 | 3 | 1 | 1 | 1 | 1 | 7 | 7 | -- | 1 | 78 | 93 | 4 | 1 | 0 | 0 | 0 | 15 | 15 | -- | 1 |
| 9 | 86 | 3 | 0 | 1 | 1 | 1 | 2 | 2 | -- | 1 | 44 | 85 | 3 | 1 | 0 | 1 | 1 | 7 | 7 | -- | 1 | 79 | 90 | 2 | 1 | 0 | 1 | 1 | 15 | 15 | -- | 1 |
| 10 | 84 | 4 | 1 | 0 | 0 | 1 | 2 | 2 | -- | 1 | 45 | 91 | 3 | 1 | 0 | 1 | 1 | 7 | 7 | -- | 1 | 80 | 88 | 3 | 1 | 0 | 1 | 1 | 15 | 15 | -- | 1 |
| 11 | 82 | 4 | 1 | 0 | 1 | 1 | 2 | 2 | -- | 1 | 46 | 94 | 3 | 1 | 1 | 1 | 1 | 7 | 7 | -- | 1 | 81 | 82 | 3 | 1 | 0 | 1 | 1 | 15 | 15 | -- | 1 |
| 12 | 91 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | -- | 1 | 47 | 86 | 3 | 1 | 0 | 1 | 1 | 8 | 8 | -- | 1 | 82 | 85 | 4 | 1 | 1 | 0 | 0 | 16 | 16 | -- | 1 |
| 13 | 96 | 4 | 1 | 0 | 0 | 1 | 3 | 3 | -- | 1 | 48 | 86 | 4 | 1 | 0 | 1 | 1 | 8 | 8 | -- | 1 | 83 | 88 | 2 | 1 | 0 | 0 | 0 | 16 | 16 | -- | 1 |
| 14 | 95 | 3 | 1 | 0 | 1 | 1 | 3 | 3 | -- | 1 | 49 | 83 | 1 | 1 | 1 | 0 | 1 | 8 | 8 | -- | 1 | 84 | 82 | 3 | 1 | 0 | 1 | 0 | 16 | 16 | -- | 1 |
| 15 | 89 | 2 | 1 | 1 | 1 | 1 | 3 | 3 | -- | 1 | 50 | 96 | 3 | 1 | 1 | 1 | 1 | 8 | 8 | -- | 1 | 85 | 84 | 4 | 1 | 1 | 0 | 0 | 17 | 17 | -- | 1 |
| 16 | 88 | 4 | 1 | 0 | 1 | 0 | 3 | 3 | -- | 1 | 51 | 94 | 4 | 1 | 0 | 0 | 1 | 8 | 8 | -- | 1 | 86 | 90 | 2 | 1 | 1 | 0 | 1 | 17 | 17 | -- | 1 |
| 17 | 91 | 3 | 1 | 1 | 0 | 1 | 3 | 3 | -- | 1 | 52 | 91 | 3 | 1 | 1 | 1 | 1 | 8 | 8 | -- | 1 | 87 | 93 | 3 | 1 | 0 | 1 | 0 | 17 | 17 | -- | 1 |
| 18 | 91 | 3 | 1 | 1 | 1 | 1 | 3 | 3 | -- | 1 | 53 | 99 | 3 | 1 | 1 | 1 | 1 | 8 | 8 | -- | 1 | 88 | 90 | 4 | 1 | 1 | 1 | 1 | 17 | 17 | -- | 1 |
| 19 | 90 | 4 | 1 | 1 | 1 | 1 | 3 | 3 | -- | 1 | 54 | 93 | 4 | 1 | 1 | 0 | 0 | 9 | 9 | -- | 1 | 89 | 88 | 3 | 0 | 0 | 1 | 0 | 18 | 18 | -- | 1 |
| 20 | 98 | 4 | 1 | 0 | 1 | 1 | 3 | 3 | -- | 1 | 55 | 92 | 2 | 1 | 1 | 0 | 1 | 9 | 9 | -- | 1 | 90 | 97 | 3 | 1 | 1 | 1 | 1 | 18 | 18 | -- | 1 |
| 21 | 94 | 3 | 1 | 1 | 1 | 1 | 3 | 3 | -- | 1 | 56 | 98 | 2 | 1 | 0 | 1 | 1 | 9 | 9 | -- | 1 | 91 | 94 | 4 | 1 | 1 | 0 | 0 | 18 | 18 | -- | 1 |
| 22 | 96 | 3 | 1 | 0 | 1 | 1 | 3 | 3 | -- | 1 | 57 | 83 | 4 | 1 | 1 | 0 | 1 | 9 | 9 | -- | 1 | 92 | 85 | 2 | 1 | 0 | 1 | 1 | 18 | 18 | -- | 1 |
| 23 | 88 | 3 | 1 | 0 | 1 | 1 | 3 | 3 | -- | 1 | 58 | 48 | 3 | 1 | 0 | 1 | 1 | 9 | 9 | -- | 1 | 93 | 84 | 4 | 1 | 0 | 1 | 1 | 19 | 19 | -- | 1 |
| 24 | 95 | 3 | 0 | 1 | 1 | 1 | 3 | 3 | -- | 1 | 59 | 87 | 2 | 1 | 1 | 1 | 1 | 10 | 10 | -- | 1 | 94 | 83 | 2 | 1 | 1 | 1 | 1 | 19 | 19 | -- | 1 |
| 25 | 83 | 3 | 1 | 0 | 1 | 1 | 3 | 3 | -- | 1 | 60 | 83 | 4 | 1 | 1 | 0 | 1 | 10 | 10 | -- | 1 | 95 | 99 | 4 | 1 | 0 | 0 | 1 | 19 | 19 | -- | 1 |
| 26 | 88 | 3 | 1 | 0 | 1 | 1 | 4 | 4 | -- | 1 | 61 | 83 | 3 | 1 | 0 | 0 | 0 | 10 | 10 | -- | 1 | 96 | 93 | 3 | 1 | 1 | 0 | 1 | 19 | 19 | -- | 1 |
| 27 | 95 | 4 | 1 | 1 | 1 | 1 | 4 | 4 | -- | 1 | 62 | 88 | 4 | 0 | 1 | 1 | 1 | 10 | 10 | -- | 1 | 97 | 83 | 2 | 1 | 0 | 0 | 0 | 19 | 19 | -- | 1 |
| 28 | 95 | 2 | 1 | 1 | 0 | 1 | 4 | 4 | -- | 1 | 63 | 97 | 2 | 1 | 0 | 1 | 1 | 10 | 10 | -- | 1 | 98 | 81 | 3 | 0 | 0 | 1 | 1 | 20 | 20 | -- | 1 |
| 29 | 92 | 3 | 1 | 1 | 0 | 0 | 4 | 4 | -- | 1 | 64 | 87 | 3 | 1 | 1 | 1 | 1 | 10 | 10 | -- | 1 | 99 | 87 | 3 | 1 | 1 | 0 | 1 | 21 | 21 | -- | 1 |
| 30 | 96 | 4 | 1 | 0 | 1 | 1 | 5 | 5 | -- | 1 | 65 | 89 | 4 | 1 | 1 | 1 | 1 | 11 | 11 | -- | 1 | 100 | 85 | 4 | 1 | 1 | 1 | 1 | 21 | 21 | -- | 1 |
| 31 | 96 | 3 | 1 | 0 | 1 | 0 | 5 | 5 | -- | 1 | 66 | 89 | 2 | 1 | 1 | 1 | 1 | 11 | 11 | -- | 1 | 101 | 85 | 3 | 1 | 1 | 0 | 1 | 21 | 21 | -- | 1 |
| 32 | 90 | 3 | 1 | 1 | 0 | 1 | 5 | 5 | -- | 1 | 67 | 84 | 2 | 0 | 0 | 0 | 1 | 12 | 12 | -- | 1 | 102 | 82 | 3 | 1 | 0 | 0 | 1 | 21 | 21 | -- | 1 |
| 33 | 89 | 4 | 1 | 1 | 1 | 1 | 5 | 5 | -- | 1 | 68 | 94 | 4 | 1 | 0 | 0 | 1 | 12 | 12 | -- | 1 | 103 | 80 | 3 | 1 | 1 | 1 | 1 | 21 | 21 | -- | 1 |
| 34 | 87 | 3 | 1 | 0 | 1 | 1 | 5 | 5 | -- | 1 | 69 | 97 | 3 | 1 | 1 | 0 | 1 | 12 | 12 | -- | 1 | 104 | 81 | 2 | 1 | 1 | 1 | 1 | 22 | 22 | -- | 1 |
| 35 | 97 | 2 | 1 | 1 | 1 | 1 | 6 | 6 | -- | 1 | 70 | 96 | 2 | 1 | 1 | 0 | 1 | 13 | 13 | -- | 1 | 105 | 80 | 4 | 1 | 0 | 0 | 1 | 22 | 22 | -- | 1 |
| A | B | C | D | E | F | G | H | I | J | K | A | B | C | D | E | F | G | H | I | J | K | A | B | C | D | E | F | G | H | I | J | K |
| 106 | 91 | 3 | 0 | 1 | 0 | 1 | 22 | 22 | -- | 1 | 141 | 78 | 2 | 0 | 0 | 0 | 0 | 31 | 31 | -- | 1 | 176 | 74 | 4 | 1 | 0 | 0 | 1 | 54 | 54 | -- | 1 |
| 107 | 75 | 3 | 1 | 0 | 1 | 0 | 22 | 22 | -- | 1 | 142 | 64 | 4 | 1 | 0 | 0 | 0 | 31 | 31 | -- | 1 | 177 | 52 | 1 | 0 | 0 | 0 | 1 | 55 | 55 | -- | 1 |
| 108 | 72 | 4 | 0 | 0 | 1 | 1 | 22 | 22 | -- | 1 | 143 | 69 | 3 | 1 | 0 | 1 | 1 | 36 | 36 | -- | 1 | 178 | 69 | 3 | 1 | 0 | 0 | 0 | 55 | 55 | -- | 1 |
| 109 | 83 | 3 | 1 | 1 | 0 | 0 | 23 | 23 | -- | 1 | 144 | 68 | 2 | 1 | 0 | 0 | 0 | 36 | 36 | -- | 1 | 179 | 41 | 3 | 0 | 0 | 1 | 1 | 55 | 55 | -- | 1 |
| 110 | 79 | 3 | 1 | 1 | 1 | 1 | 23 | 23 | -- | 1 | 145 | 62 | 2 | 1 | 0 | 0 | 0 | 36 | 36 | -- | 1 | 180 | 64 | 3 | 1 | 0 | 0 | 1 | 56 | 56 | -- | 1 |
| 111 | 79 | 4 | 1 | 0 | 0 | 1 | 24 | 24 | -- | 1 | 146 | 58 | 3 | 1 | 0 | 1 | 1 | 36 | 36 | -- | 1 | 181 | 64 | 2 | 1 | 0 | 1 | 1 | 58 | 58 | -- | 1 |
| 112 | 78 | 3 | 1 | 1 | 0 | 1 | 24 | 24 | -- | 1 | 147 | 69 | 4 | 1 | 0 | 0 | 1 | 37 | 37 | -- | 1 | 182 | 58 | 3 | 1 | 0 | 1 | 1 | 58 | 58 | -- | 1 |
| 113 | 75 | 4 | 1 | 0 | 0 | 1 | 24 | 24 | -- | 1 | 148 | 68 | 3 | 0 | 0 | 0 | 1 | 39 | 39 | -- | 1 | 183 | 53 | 2 | 0 | 1 | 1 | 1 | 59 | 59 | -- | 1 |
| 114 | 84 | 3 | 1 | 0 | 0 | 1 | 24 | 24 | -- | 1 | 149 | 65 | 3 | 1 | 0 | 0 | 1 | 39 | 39 | -- | 1 | 184 | 53 | 3 | 1 | 0 | 0 | 1 | 59 | 59 | -- | 1 |
| 115 | 78 | 2 | 1 | 1 | 1 | 1 | 24 | 24 | -- | 1 | 150 | 65 | 3 | 1 | 1 | 0 | 0 | 39 | 39 | -- | 1 | 185 | 58 | 1 | 0 | 0 | 0 | 0 | 59 | 59 | -- | 1 |
| 116 | 78 | 2 | 1 | 0 | 1 | 1 | 24 | 24 | -- | 1 | 151 | 68 | 3 | 1 | 1 | 1 | 0 | 40 | 40 | -- | 1 | 186 | 54 | 3 | 1 | 0 | 0 | 1 | 60 | 60 | -- | 1 |
| 117 | 79 | 3 | 1 | 0 | 0 | 1 | 25 | 25 | -- | 1 | 152 | 68 | 4 | 1 | 0 | 1 | 1 | 41 | 41 | -- | 1 | 187 | 54 | 2 | 0 | 0 | 1 | 1 | 61 | 61 | -- | 1 |
| 118 | 73 | 3 | 1 | 1 | 1 | 1 | 25 | 25 | -- | 1 | 153 | 63 | 3 | 1 | 1 | 0 | 1 | 41 | 41 | -- | 1 | 188 | 67 | 3 | 1 | 1 | 0 | 0 | 62 | 62 | -- | 1 |
| 119 | 73 | 4 | 1 | 0 | 0 | 1 | 26 | 26 | -- | 1 | 154 | 62 | 3 | 0 | 0 | 1 | 0 | 42 | 42 | -- | 1 | 189 | 66 | 2 | 1 | 0 | 0 | 1 | 62 | 62 | -- | 1 |
| 120 | 72 | 2 | 1 | 0 | 0 | 0 | 26 | 26 | -- | 1 | 155 | 68 | 1 | 1 | 0 | 1 | 1 | 43 | 43 | -- | 1 | 190 | 53 | 2 | 0 | 0 | 0 | 0 | 62 | 62 | -- | 1 |
| 121 | 75 | 2 | 1 | 0 | 0 | 0 | 26 | 26 | -- | 1 | 156 | 68 | 2 | 0 | 0 | 0 | 0 | 43 | 43 | -- | 1 | 191 | 56 | 3 | 1 | 1 | 1 | 1 | 63 | 63 | -- | 1 |
| 122 | 69 | 3 | 1 | 1 | 1 | 0 | 26 | 26 | -- | 1 | 157 | 69 | 2 | 0 | 0 | 1 | 1 | 43 | 43 | -- | 1 | 192 | 53 | 2 | 1 | 0 | 0 | 1 | 66 | 66 | -- | 1 |
| 123 | 89 | 2 | 1 | 0 | 0 | 1 | 27 | 27 | -- | 1 | 158 | 62 | 3 | 1 | 0 | 1 | 1 | 43 | 43 | -- | 1 | 193 | 49 | 3 | 1 | 1 | 1 | 1 | 67 | 67 | -- | 1 |
| 124 | 78 | 3 | 1 | 0 | 0 | 0 | 27 | 27 | -- | 1 | 159 | 67 | 3 | 0 | 1 | 1 | 1 | 44 | 44 | -- | 1 | 194 | 69 | 2 | 1 | 0 | 1 | 1 | 77 | 77 | -- | 1 |
| 125 | 78 | 4 | 1 | 1 | 1 | 1 | 27 | 27 | -- | 1 | 160 | 68 | 2 | 1 | 0 | 1 | 1 | 45 | 45 | -- | 1 | 195 | 69 | 2 | 0 | 1 | 0 | 0 | 78 | 78 | -- | 1 |
| 126 | 72 | 3 | 1 | 1 | 0 | 1 | 27 | 27 | -- | 1 | 161 | 64 | 3 | 1 | 0 | 0 | 1 | 46 | 46 | -- | 1 | 196 | 54 | 2 | 1 | 0 | 1 | 1 | 84 | 84 | -- | 1 |
| 127 | 63 | 2 | 1 | 0 | 1 | 1 | 27 | 27 | -- | 1 | 162 | 62 | 2 | 1 | 1 | 0 | 0 | 46 | 46 | -- | 1 | 197 | 49 | 2 | 1 | 0 | 0 | 1 | 89 | 89 | -- | 1 |
| 128 | 62 | 4 | 1 | 1 | 0 | 1 | 27 | 27 | -- | 1 | 163 | 64 | 3 | 0 | 0 | 0 | 0 | 46 | 46 | -- | 1 | 198 | 40 | 3 | 0 | 1 | 1 | 1 | 90 | 90 | -- | 1 |
| 129 | 79 | 3 | 1 | 0 | 0 | 1 | 28 | 28 | -- | 1 | 164 | 61 | 3 | 0 | 0 | 1 | 1 | 47 | 47 | -- | 1 | 199 | 40 | 3 | 1 | 1 | 0 | 0 | 90 | 90 | -- | 1 |
| 130 | 73 | 3 | 1 | 0 | 1 | 0 | 28 | 28 | -- | 1 | 165 | 58 | 4 | 1 | 1 | 0 | 0 | 48 | 48 | -- | 1 | 200 | 40 | 2 | 1 | 0 | 1 | 1 | 90 | 90 | -- | 1 |
| 131 | 73 | 2 | 1 | 0 | 0 | 0 | 28 | 28 | -- | 1 | 166 | 52 | 3 | 0 | 0 | 0 | 1 | 48 | 48 | -- | 1 | 201 | 45 | 2 | 1 | 1 | 1 | 1 | 90 | 90 | -- | 1 |
| 132 | 76 | 3 | 0 | 0 | 1 | 1 | 29 | 1 | 29.33 | 0 | 167 | 51 | 2 | 1 | 0 | 0 | 1 | 48 | 48 | -- | 1 | 202 | 46 | 3 | 1 | 1 | 1 | 1 | 91 | 2 | 73.22 | 0 |
| 133 | 79 | 4 | 1 | 0 | 0 | 1 | 29 | 4 | 18.88 | 0 | 168 | 51 | 2 | 1 | 0 | 1 | 1 | 49 | 49 | -- | 1 | 203 | 47 | 2 | 0 | 0 | 0 | 1 | 91 | 91 | -- | 1 |
| 134 | 84 | 4 | 1 | 0 | 0 | 1 | 29 | 29 | -- | 1 | 169 | 53 | 3 | 1 | 0 | 0 | 1 | 50 | 50 | -- | 1 | 204 | 46 | 2 | 1 | 0 | 0 | 1 | 91 | 91 | -- | 1 |
| 135 | 82 | 2 | 0 | 0 | 0 | 1 | 29 | 29 | -- | 1 | 170 | 81 | 3 | 0 | 0 | 0 | 1 | 50 | 50 | -- | 1 | 205 | 49 | 1 | 1 | 0 | 1 | 1 | 91 | 91 | -- | 1 |
| 136 | 78 | 2 | 1 | 0 | 1 | 1 | 29 | 3 | 26.73 | 0 | 171 | 77 | 3 | 1 | 1 | 0 | 0 | 50 | 50 | -- | 1 | 206 | 50 | 1 | 0 | 1 | 0 | 1 | 91 | 91 | -- | 1 |
| 137 | 78 | 3 | 0 | 0 | 0 | 1 | 30 | 30 | -- | 1 | 172 | 44 | 3 | 1 | 0 | 1 | 1 | 50 | 50 | -- | 1 | 207 | 47 | 2 | 1 | 1 | 1 | 1 | 91 | 91 | -- | 1 |
| 138 | 73 | 4 | 0 | 0 | 0 | 1 | 30 | 30 | -- | 1 | 173 | 68 | 3 | 1 | 0 | 0 | 1 | 51 | 51 | -- | 1 | 208 | 41 | 2 | 1 | 0 | 1 | 0 | 91 | 91 | -- | 1 |
| 139 | 60 | 3 | 1 | 0 | 0 | 0 | 30 | 30 | -- | 1 | 174 | 72 | 3 | 0 | 1 | 0 | 0 | 53 | 53 | -- | 1 | 209 | 46 | 2 | 0 | 1 | 0 | 0 | 91 | 91 | -- | 1 |
| 140 | 71 | 2 | 1 | 1 | 0 | 0 | 30 | 30 | -- | 1 | 175 | 87 | 3 | 0 | 1 | 1 | 1 | 54 | 54 | -- | 1 | 210 | 46 | 2 | 0 | 0 | 1 | 1 | 92 | 92 | -- | 1 |
| A | B | C | D | E | F | G | H | I | J | K | A | B | C | D | E | F | G | H | I | J | K | |||||||||||
| 211 | 49 | 3 | 1 | 0 | 1 | 1 | 92 | 92 | -- | 1 | 246 | 47 | 1 | 0 | 0 | 1 | 1 | 99 | 3 | 85.42 | 0 | |||||||||||
| 212 | 52 | 2 | 1 | 0 | 1 | 1 | 92 | 92 | -- | 1 | 247 | 43 | 2 | 0 | 0 | 1 | 1 | 99 | 10 | 86.12 | 0 | |||||||||||
| 213 | 47 | 2 | 0 | 0 | 1 | 1 | 93 | 4 | 79.90 | 0 | 248 | 42 | 1 | 1 | 0 | 1 | 1 | 99 | 5 | 88.18 | 0 | |||||||||||
| 214 | 48 | 2 | 1 | 0 | 0 | 0 | 93 | 93 | -- | 1 | 249 | 42 | 1 | 1 | 0 | 0 | 0 | 99 | 2 | 90.24 | 0 | |||||||||||
| 215 | 44 | 2 | 1 | 1 | 0 | 1 | 93 | 93 | -- | 1 | 250 | 46 | 1 | 0 | 0 | 0 | 1 | 99 | 4 | 91.71 | 0 | |||||||||||
| 216 | 50 | 3 | 1 | 0 | 0 | 1 | 93 | 93 | -- | 1 | ||||||||||||||||||||||
| 217 | 40 | 1 | 0 | 0 | 0 | 1 | 93 | 93 | -- | 1 | ||||||||||||||||||||||
| 218 | 40 | 3 | 1 | 0 | 1 | 1 | 94 | 2 | 80.26 | 0 | ||||||||||||||||||||||
| 219 | 56 | 2 | 1 | 1 | 0 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 220 | 51 | 2 | 1 | 0 | 1 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 221 | 48 | 2 | 0 | 0 | 0 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 222 | 51 | 1 | 0 | 0 | 1 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 223 | 51 | 2 | 1 | 1 | 1 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 224 | 52 | 1 | 1 | 1 | 1 | 1 | 94 | 94 | -- | 1 | ||||||||||||||||||||||
| 225 | 48 | 2 | 0 | 1 | 0 | 1 | 94 | 6 | 85.36 | 0 | ||||||||||||||||||||||
| 226 | 42 | 2 | 1 | 0 | 0 | 1 | 94 | 1 | 87.41 | 0 | ||||||||||||||||||||||
| 227 | 49 | 1 | 0 | 0 | 1 | 1 | 95 | 95 | -- | 1 | ||||||||||||||||||||||
| 228 | 49 | 2 | 1 | 1 | 1 | 1 | 95 | 95 | -- | 1 | ||||||||||||||||||||||
| 229 | 51 | 2 | 1 | 0 | 1 | 1 | 95 | 2 | 68.68 | 0 | ||||||||||||||||||||||
| 230 | 51 | 3 | 0 | 0 | 1 | 1 | 95 | 95 | -- | 1 | ||||||||||||||||||||||
| 231 | 45 | 1 | 1 | 0 | 0 | 0 | 95 | 8 | 85.58 | 0 | ||||||||||||||||||||||
| 232 | 45 | 1 | 1 | 1 | 0 | 1 | 95 | 4 | 90.53 | 0 | ||||||||||||||||||||||
| 233 | 43 | 2 | 0 | 0 | 0 | 0 | 95 | 2 | 88.18 | 0 | ||||||||||||||||||||||
| 234 | 47 | 1 | 1 | 1 | 0 | 1 | 96 | 3 | 87.43 | 0 | ||||||||||||||||||||||
| 235 | 42 | 1 | 1 | 0 | 1 | 1 | 96 | 96 | -- | 1 | ||||||||||||||||||||||
| 236 | 46 | 3 | 0 | 0 | 1 | 1 | 96 | 1 | 75.95 | 0 | ||||||||||||||||||||||
| 237 | 47 | 2 | 1 | 1 | 1 | 1 | 96 | 96 | -- | 1 | ||||||||||||||||||||||
| 238 | 45 | 2 | 0 | 0 | 1 | 1 | 96 | 4 | 83.01 | 0 | ||||||||||||||||||||||
| 239 | 46 | 1 | 1 | 1 | 1 | 1 | 96 | 7 | 84.24 | 0 | ||||||||||||||||||||||
| 240 | 46 | 2 | 0 | 1 | 0 | 1 | 96 | 1 | 88.47 | 0 | ||||||||||||||||||||||
| 241 | 46 | 1 | 1 | 0 | 0 | 1 | 97 | 7 | 86.70 | 0 | ||||||||||||||||||||||
| 242 | 46 | 2 | 1 | 1 | 1 | 1 | 97 | 97 | -- | 1 | ||||||||||||||||||||||
| 243 | 46 | 3 | 0 | 1 | 1 | 1 | 98 | 4 | 78.22 | 0 | ||||||||||||||||||||||
| 244 | 46 | 2 | 0 | 0 | 1 | 1 | 98 | 5 | 81.46 | 0 | ||||||||||||||||||||||
References
- Lagakos, S.W. General right censoring and its impact on the analysis of survival data. Biometrics 1979, 35, 139–156. [Google Scholar] [CrossRef] [PubMed]
- Leung, K.M.; Elashoff, R.M.; Afifi, A.A. Censoring issues in survival analysis. Annu. Rev. Public Health 1997, 18, 83–104. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Heitjan, D.F. Nonignorable censoring in randomized clinical trials. Clin. Trials 2005, 2, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Shih, W. Problems in dealing with missing data and informative censoring in clinical trials. Curr. Control Trials Cardiovasc. Med. 2002, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Miettinen, O.S. Survival analysis: Up from Kaplan-Meier-Greenwood. Eur. J. Epidemiol. 2008, 23, 585–592. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.C.; Bailey, K.R. Estimation and comparison of changes in the presence of informative right censoring: Conditional linear model. Biometrics 1989, 45, 939–955. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, P.; Pramesh, C.S. Censoring in survival analysis: Potential for bias. Perspect. Clin. Res. 2012, 3, 40. [Google Scholar] [CrossRef] [PubMed]
- Collett, D. Modelling Survival Data in Medical Research, 3rd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Laurent, R.T.S.; Cook, R.D. Leverages and superleverages in nonlinear regression. J. Am. Stat. Assoc. 1992, 87, 985–990. [Google Scholar] [CrossRef]
- Laurent, R.T.S.; Cook, R.D. Leverages, local influence, and curvature in nonlinear regression. Biometrika 1993, 80, 99–106. [Google Scholar] [CrossRef]
- Pregibon, D. Logistic regression diagnostic. Ann. Stat. 1981, 9, 705–724. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Hosmer, T.; Cessie, S.L.; Lemeshow, S. A comparison of goodness-of-fit tests for the logistic regression model. Stat. Med. 1997, 16, 965–980. [Google Scholar] [CrossRef]
- Williams, D. Probability with Martingales; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Crowder, M.J.; Kimber, A.C.; Smith, R.L.; Sweeting, T.J. Statistical Analysis of Reliability Data; Chapman & Hall: London, UK, 1991. [Google Scholar]
- White, H. Maximum likelihood estimation of misspecified models. Econometrica 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Freedman, D.A. On The So-Called “Huber Sandwich Estimator” and “Robust Standard Errors”. Am. Stat. 2006, 60, 299–302. [Google Scholar] [CrossRef]
- Huber, P.J. The Behavior of Maximum Likelihood Estimates under Nonstandard Conditions. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, NC, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; Volume I; University of California Press: Berkeley, CA USA, 1967; pp. 221–333. [Google Scholar]
- Stukel, T.A. Generalized logistic models. J. Am. Stat. Assoc. 1988, 83, 426–431. [Google Scholar] [CrossRef]
- Diggle, P.; Kenward, M.G. Informative drop-out in longitudinal data analysis. J. R. Stat. Soc. Ser. C Appl. Stat. 1994, 43, 49–93. [Google Scholar] [CrossRef]
- Plante, J.F. About an adaptively weighted Kaplan-Meier estimate. Lifetime Data Anal. 2009, 15, 295–315. [Google Scholar] [CrossRef] [PubMed]
- Hogan, J.W.; Laird, N.M. Model-based approaches to analysing incomplete longitudinal and failure time data. Stat. Med. 1997, 16, 259–272. [Google Scholar] [CrossRef]
- Wu, M.C.; Albert, P.S.; Wu, B.U. Adjusting for drop-out in clinical trials with repeated measures: Design and analysis issues. Stat. Med. 2001, 20, 93–108. [Google Scholar] [CrossRef]
- Wei, L.; Shih, W.J. Partial imputation approach to analysis of repeated measurements with dependent drop-outs. Stat. Med. 2001, 20, 1197–1214. [Google Scholar] [CrossRef] [PubMed]
- Little, R.J.A. Modeling the drop-out mechanism in repeated-measures studies. J. Am. Stat. Assoc. 1995, 90, 1112–1121. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efird, J.T.; Jindal, C. Using a Counting Process Method to Impute Censored Follow-Up Time Data. Int. J. Environ. Res. Public Health 2018, 15, 690. https://doi.org/10.3390/ijerph15040690
Efird JT, Jindal C. Using a Counting Process Method to Impute Censored Follow-Up Time Data. International Journal of Environmental Research and Public Health. 2018; 15(4):690. https://doi.org/10.3390/ijerph15040690
Chicago/Turabian StyleEfird, Jimmy T., and Charulata Jindal. 2018. "Using a Counting Process Method to Impute Censored Follow-Up Time Data" International Journal of Environmental Research and Public Health 15, no. 4: 690. https://doi.org/10.3390/ijerph15040690
APA StyleEfird, J. T., & Jindal, C. (2018). Using a Counting Process Method to Impute Censored Follow-Up Time Data. International Journal of Environmental Research and Public Health, 15(4), 690. https://doi.org/10.3390/ijerph15040690






