Quick Estimation Model for the Concentration of Indoor Airborne Culturable Bacteria: An Application of Machine Learning
Abstract
1. Introduction
2. Modeling Methods
3. Results and Discussion
3.1. Statistical Analysis
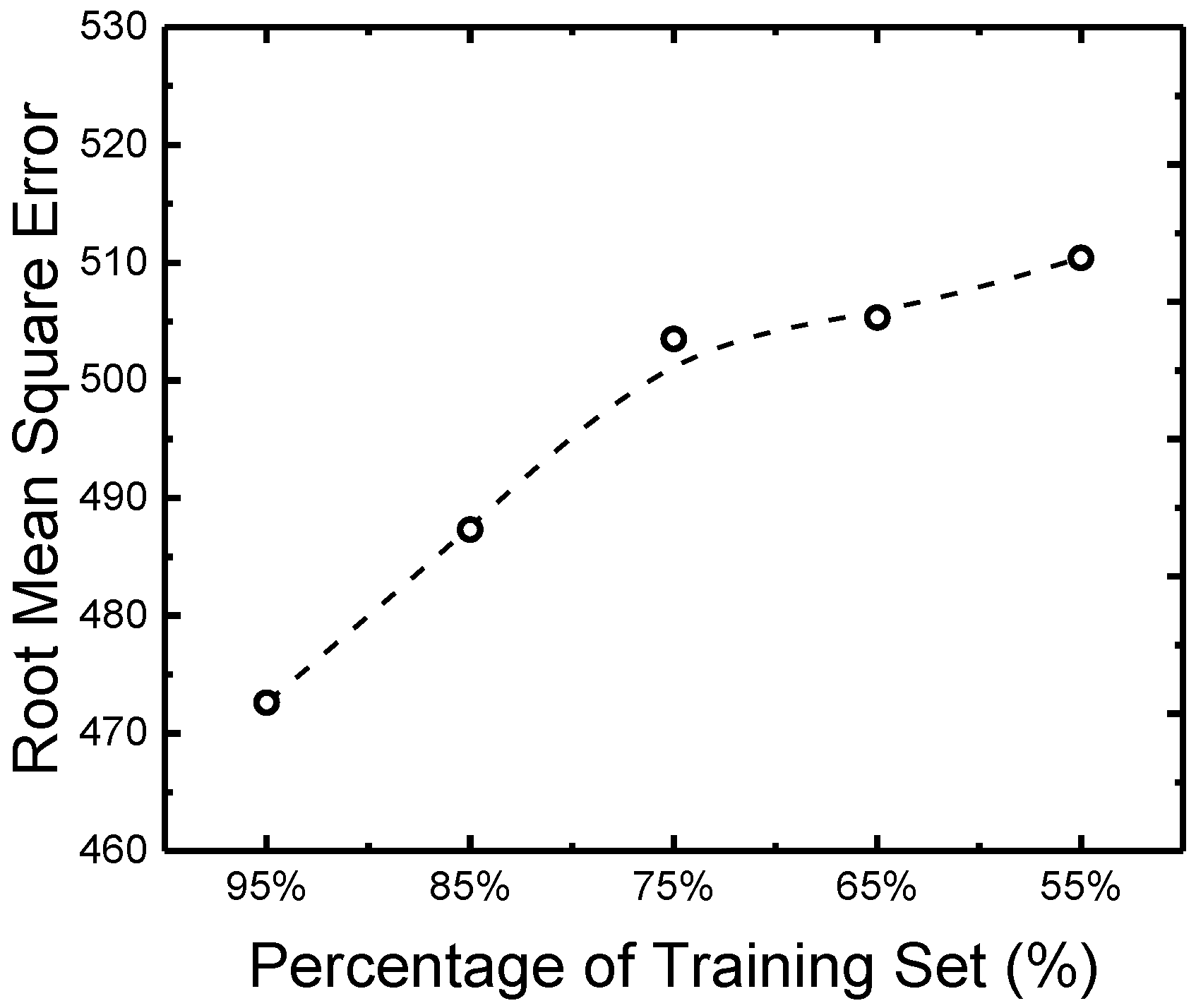
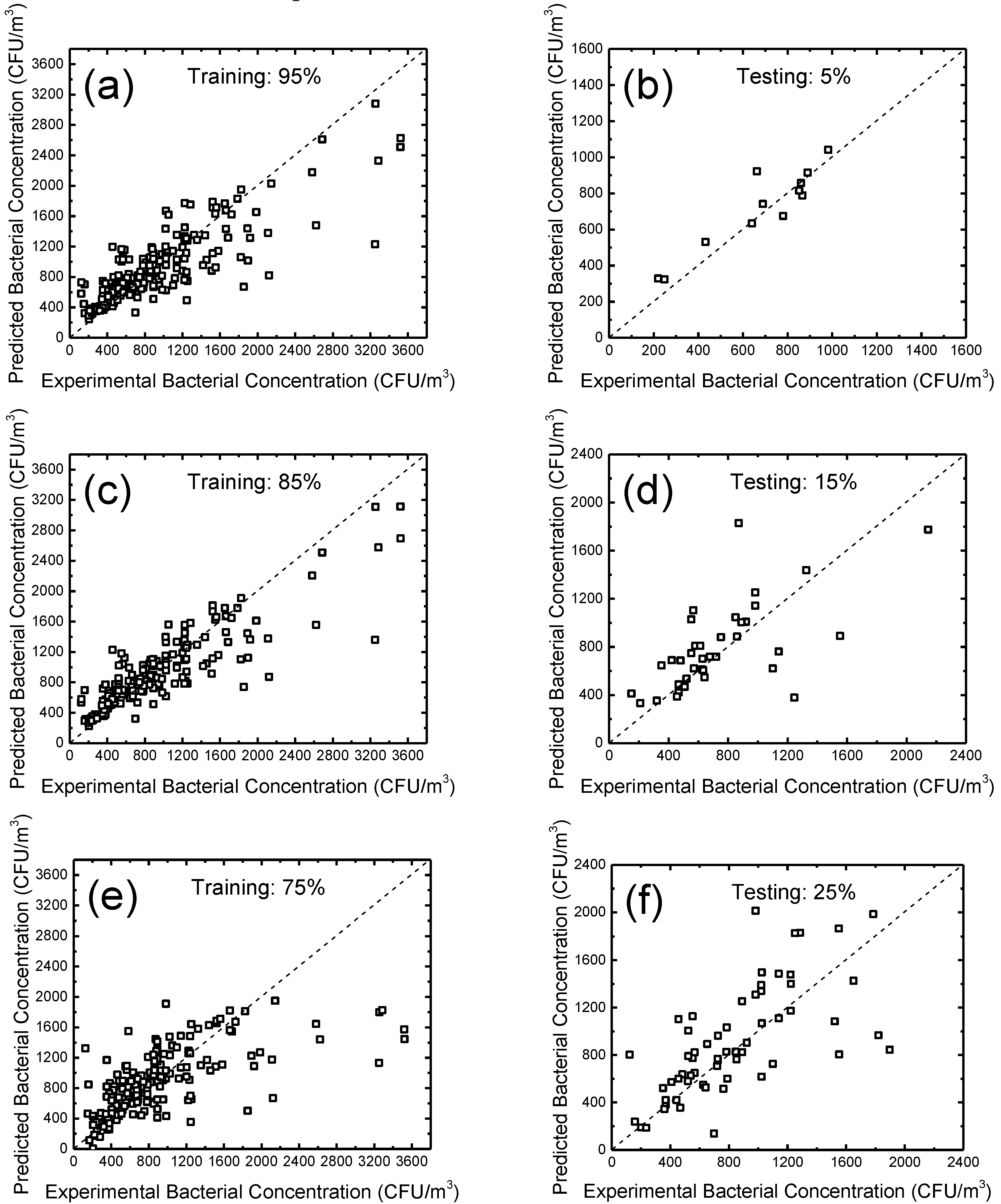
3.2. Machine Learning-Based Prediction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prussin, A.J.; Garcia, E.B.; Marr, L.C. Total concentrations of virus and bacteria in indoor and outdoor air. Environ. Sci. Technol. Lett. 2015, 2, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Mentese, S.; Mirici, N.A.; Otkun, M.T.; Bakar, C.; Palaz, E.; Tasdibi, D.; Cevizci, S.; Cotuker, O. Association between respiratory health and indoor air pollution exposure in Canakkale, Turkey. Build. Environ. 2015, 93, 72–83. [Google Scholar] [CrossRef]
- Bragoszewska, E.; Mainka, A.; Pastuszka, J.S. Bacterial and fungal aerosols in rural nursery schools in Southern Poland. Atmosphere (Basel) 2016, 7. [Google Scholar] [CrossRef]
- Hospodsky, D.; Qian, J.; Nazaroff, W.W.; Yamamoto, N.; Bibby, K.; Rismani-Yazdi, H.; Peccia, J. Human occupancy as a source of indoor airborne bacteria. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Spendlove, J.C.; Fannin, K.F. Source, significance, and control of indoor microbial aerosols: Human health aspects. Public Health Rep. 1983, 98, 229–244. [Google Scholar] [PubMed]
- Husman, T. Health effects of indoor-air microorganisms. Scand. J. Work Environ. Health 1996, 22, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Daisey, J.M.; Angell, W.J.; Apte, M.G. Indoor air quality, ventilation and health symptoms in schools: An analysis of existing information. Indoor Air 2003, 13, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, A.; Hu, Z.; Sun, H. Study on the potential relationships between indoor culturable fungi, particle load and children respiratory health in Xi’an, China. Build. Environ. 2014. [Google Scholar] [CrossRef]
- Lanthier-Veilleux, M.; Baron, G.; Généreux, M. Respiratory diseases in university students associated with exposure to residential dampness or mold. Int. J. Environ. Res. Public Health 2016, 13, 1154. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Jiang, W.; Wang, B.; Fang, J.; Lang, J.; Tian, G.; Jiang, J.; Zhu, T.F. Inhalable microorganisms in Beijing’s PM2.5 and PM10 pollutants during a severe smog event. Environ. Sci. Technol. 2014, 48, 1499–1507. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhu, Z.; Zhu, Y.; Xu, W.; Li, H. Investigation of dust loading and culturable microorganisms of HVAC systems in 24 office buildings in Beijing. Energy Build. 2015, 103, 166–174. [Google Scholar] [CrossRef]
- Pham, T.D.; Lee, B.K. Feasibility of silver doped TiO2 glass fiber photocatalyst under visible irradiation as an indoor air germicide. Int. J. Environ. Res. Public Health 2014, 11, 3271–3288. [Google Scholar] [CrossRef] [PubMed]
- Rogawansamy, S.; Gaskin, S.; Taylor, M.; Pisaniello, D. An evaluation of antifungal agents for the treatment of fungal contamination in indoor air environments. Int. J. Environ. Res. Public Health 2015, 12, 6319–6332. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Eddy Patuwo, B.; Y. Hu, M. Forecasting with artificial neural networks. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Panteliou, S.; Dentsoras, A. Artificial neural networks used for the performance prediction of a thermosiphon solar water heater. Renew. Energy 1999, 18, 87–99. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Zhang, X.; Jin, G.; Cheng, K. Novel method for measuring the heat collection rate and heat loss coefficient of water-in-glass evacuated tube solar water heaters based on artificial neural networks and support vector machine. Energies 2015, 8, 8814–8834. [Google Scholar] [CrossRef]
- Hile, R.; Cova, T.J.; Aubrecht, C.; Kainz, W. Exploratory testing of an artificial neural network classification for enhancement of the social vulnerability index. ISPRS Int. J. Geo-Inf. 2015, 4, 1774–1790. [Google Scholar] [CrossRef]
- Zanardi, M.M.; Sarotti, A.M. GIAO C-H COSY Simulations merged with artificial neural networks pattern recognition analysis. Pushing the structural validation a step forward. J. Org. Chem. 2015, 80, 9371–9378. [Google Scholar] [CrossRef] [PubMed]
- Perea, J.D.; Langner, S.; Salvador, M.; Kontos, J.; Jarvas, G.; Winkler, F.; Machui, F.; Görling, A.; Dallos, A.; Ameri, T.; et al. Combined computational approach based on density functional theory and artificial neural networks for predicting the solubility parameters of fullerenes. J. Phys. Chem. B 2016, 120, 4431–4438. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Tang, X.; Wang, R.; Lin, F.; Liu, Z.; Cheng, K. Comparative study on theoretical and machine learning methods for acquiring compressed liquid densities of 1,1,1,2,3,3,3-heptafluoropropane (r227ea) via song and mason equation, support vector machine, and artificial neural networks. Appl. Sci. 2016, 6, 25. [Google Scholar] [CrossRef]
- Chen, F.; Li, H.; Xu, Z.; Hou, S.; Yang, D. User-friendly optimization approach of fed-batch fermentation conditions for the production of iturin A using artificial neural networks and support vector machine. Electron. J. Biotechnol. 2015, 18, 273–280. [Google Scholar] [CrossRef]
- Khan, J.; Wei, J.S.; Ringnér, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Hsu, K.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Liu, K.; Yu, H.; Cheng, K. Design of high-performance water-in-glass evacuated tube solar water heaters by a high-throughput screening based on machine learning: A combined modeling and experimental study. Sol. Energy 2017, 142, 61–67. [Google Scholar] [CrossRef]
- Sanaye, S.; Asgari, H. Thermal modeling of gas engine driven air to water heat pump systems in heating mode using genetic algorithm and Artificial Neural Network methods. Int. J. Refrig. 2013, 36, 2262–2277. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Su, S. Solar irradiance short-term prediction model based on BP neural network. Energy Procedia 2011, 12, 488–494. [Google Scholar] [CrossRef]
- Wang, J.Z.; Wang, J.J.; Zhang, Z.G.; Guo, S.P. Forecasting stock indices with back propagation neural network. Expert Syst. Appl. 2011, 38, 14346–14355. [Google Scholar] [CrossRef]
- Peng, H.; Ling, X. Optimal design approach for the plate-fin heat exchangers using neural networks cooperated with genetic algorithms. Appl. Therm. Eng. 2008, 28, 642–650. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.; Siew, C.; Ã, G.H.; Zhu, Q.; Siew, C.; Huang, G.-B.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, H.; Tang, X.; Zhang, X.; Lin, F.; Cheng, K. Extreme learning machine: A new alternative for measuring heat collection rate and heat loss coefficient of water-in-glass evacuated tube solar water heaters. SpringerPlus 2016. [Google Scholar] [CrossRef] [PubMed]
- Kalogirou, S. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. Neural Netw. IEEE Trans. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Liu, Z.; Zhu, X.; Liu, Y.; Wang, Q. The effect of air-conditioning parameters and deposition dust on microbial growth in supply air ducts. Energy Build. 2010, 42, 449–454. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Arundel, A.V.; Sterling, E.M.; Biggin, J.H.; Sterling, T.D. Indirect health effects of relative humidity in indoor environments. Environ. Health Perspect. 1986, 65, 351–361. [Google Scholar] [CrossRef] [PubMed]
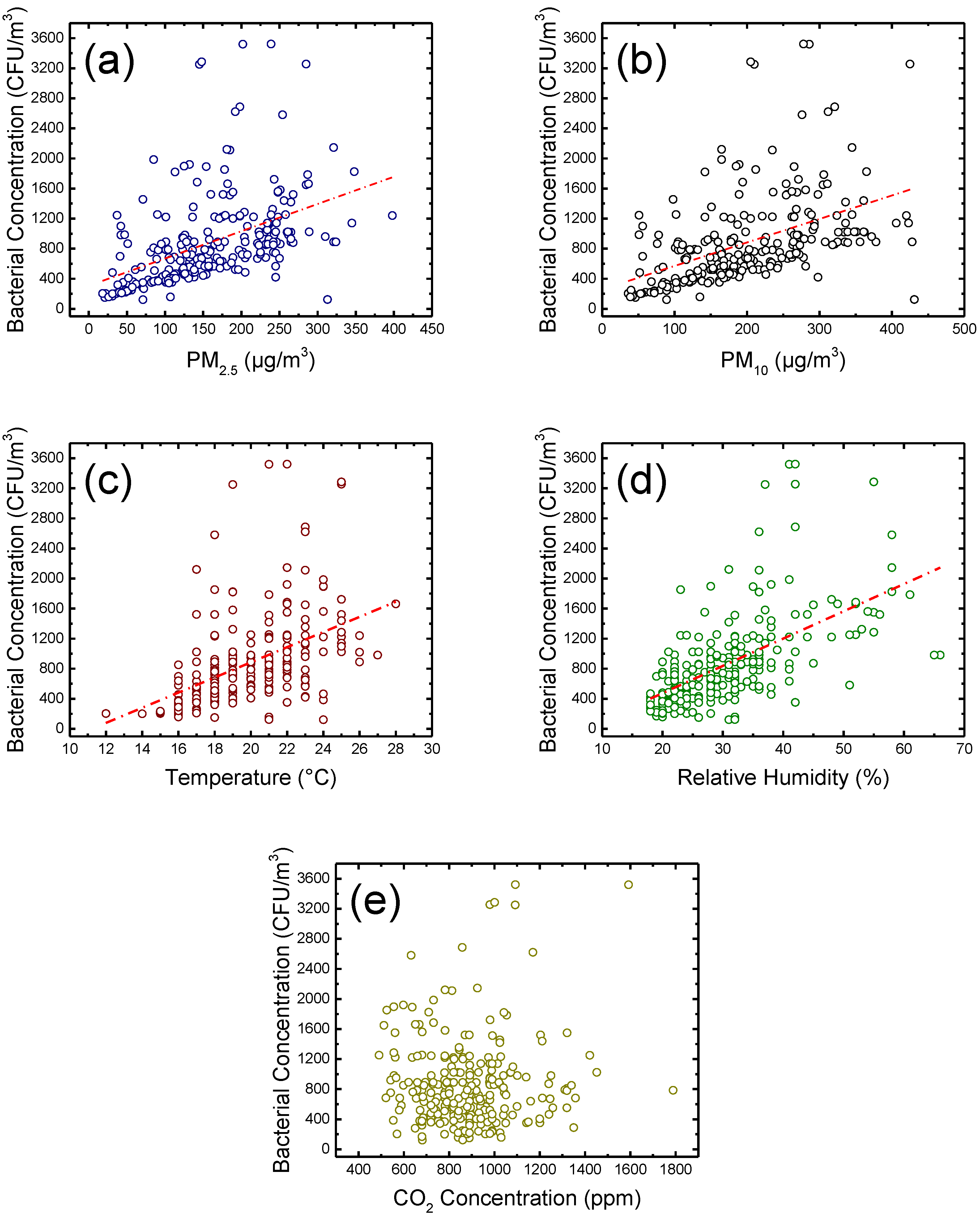

| Item | Indoor PM2.5 (μg/m3) | Indoor PM10 (μg/m3) | Temperature (°C) | Relative Humidity (%) | CO2 Concentration (ppm) | Bacterial Concentration (CFU/m3) |
|---|---|---|---|---|---|---|
| Maximum | 398 | 431 | 28 | 66 | 1789 | 3522 |
| Minimum | 18 | 36 | 12 | 18 | 491 | 122 |
| Range | 380 | 395 | 16 | 48 | 1298 | 3400 |
| Average | 157 | 198 | 20 | 31 | 881 | 877.3 |
| Standard Deviation | 76 | 91 | 3 | 10 | 204 | 596.6 |
| Model | Average RMS Error (Testing) | Maximum RMS Error (Testing) | Minimum RMS Error (Testing) | Range |
|---|---|---|---|---|
| Linear Regression | 488.51 | 742.40 | 183.63 | 558.77 |
| GRNN | 412.69 | 630.87 | 243.59 | 387.28 |
| MLFN-2 | 501.51 | 842.10 | 191.61 | 650.49 |
| MLFN-3 | 567.56 | 936.49 | 261.92 | 674.57 |
| MLFN-4 | 551.14 | 762.22 | 238.96 | 523.26 |
| MLFN-5 | 537.75 | 905.98 | 221.88 | 684.09 |
| MLFN-6 | 618.37 | 1168.41 | 169.72 | 998.69 |
| MLFN-7 | 613.02 | 1232.63 | 137.23 | 1095.40 |
| MLFN-8 | 554.64 | 852.59 | 239.91 | 612.68 |
| MLFN-9 | 617.65 | 873.16 | 198.35 | 674.81 |
| MLFN-10 | 646.42 | 924.84 | 255.50 | 669.34 |
| MLFN-11 | 614.87 | 1015.63 | 218.95 | 796.68 |
| MLFN-12 | 644.37 | 1313.63 | 223.55 | 1090.08 |
| MLFN-13 | 675.69 | 1033.43 | 279.78 | 753.65 |
| MLFN-14 | 746.24 | 1304.57 | 321.40 | 983.17 |
| MLFN-15 | 716.42 | 1761.50 | 250.64 | 1510.86 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, H.; Cao, G. Quick Estimation Model for the Concentration of Indoor Airborne Culturable Bacteria: An Application of Machine Learning. Int. J. Environ. Res. Public Health 2017, 14, 857. https://doi.org/10.3390/ijerph14080857
Liu Z, Li H, Cao G. Quick Estimation Model for the Concentration of Indoor Airborne Culturable Bacteria: An Application of Machine Learning. International Journal of Environmental Research and Public Health. 2017; 14(8):857. https://doi.org/10.3390/ijerph14080857
Chicago/Turabian StyleLiu, Zhijian, Hao Li, and Guoqing Cao. 2017. "Quick Estimation Model for the Concentration of Indoor Airborne Culturable Bacteria: An Application of Machine Learning" International Journal of Environmental Research and Public Health 14, no. 8: 857. https://doi.org/10.3390/ijerph14080857
APA StyleLiu, Z., Li, H., & Cao, G. (2017). Quick Estimation Model for the Concentration of Indoor Airborne Culturable Bacteria: An Application of Machine Learning. International Journal of Environmental Research and Public Health, 14(8), 857. https://doi.org/10.3390/ijerph14080857





