Developing and Validating an Age-Independent Equation Using Multi-Frequency Bioelectrical Impedance Analysis for Estimation of Appendicular Skeletal Muscle Mass and Establishing a Cutoff for Sarcopenia
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Multi-Frequency Bioelectrical Impedance Analysis
2.3. Dual-Energy X-ray Absorptiometry
2.4. Statistical Analysis
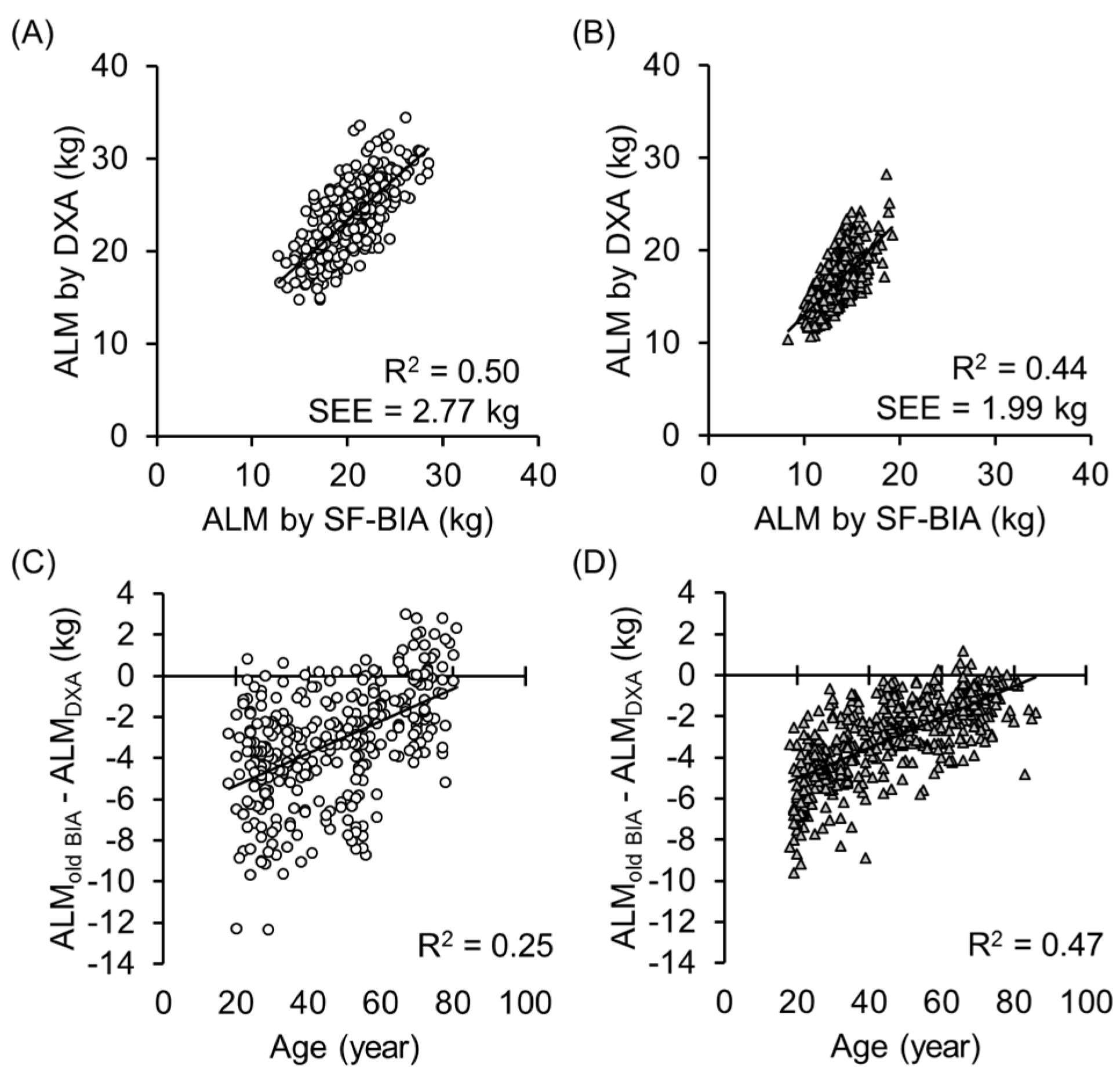
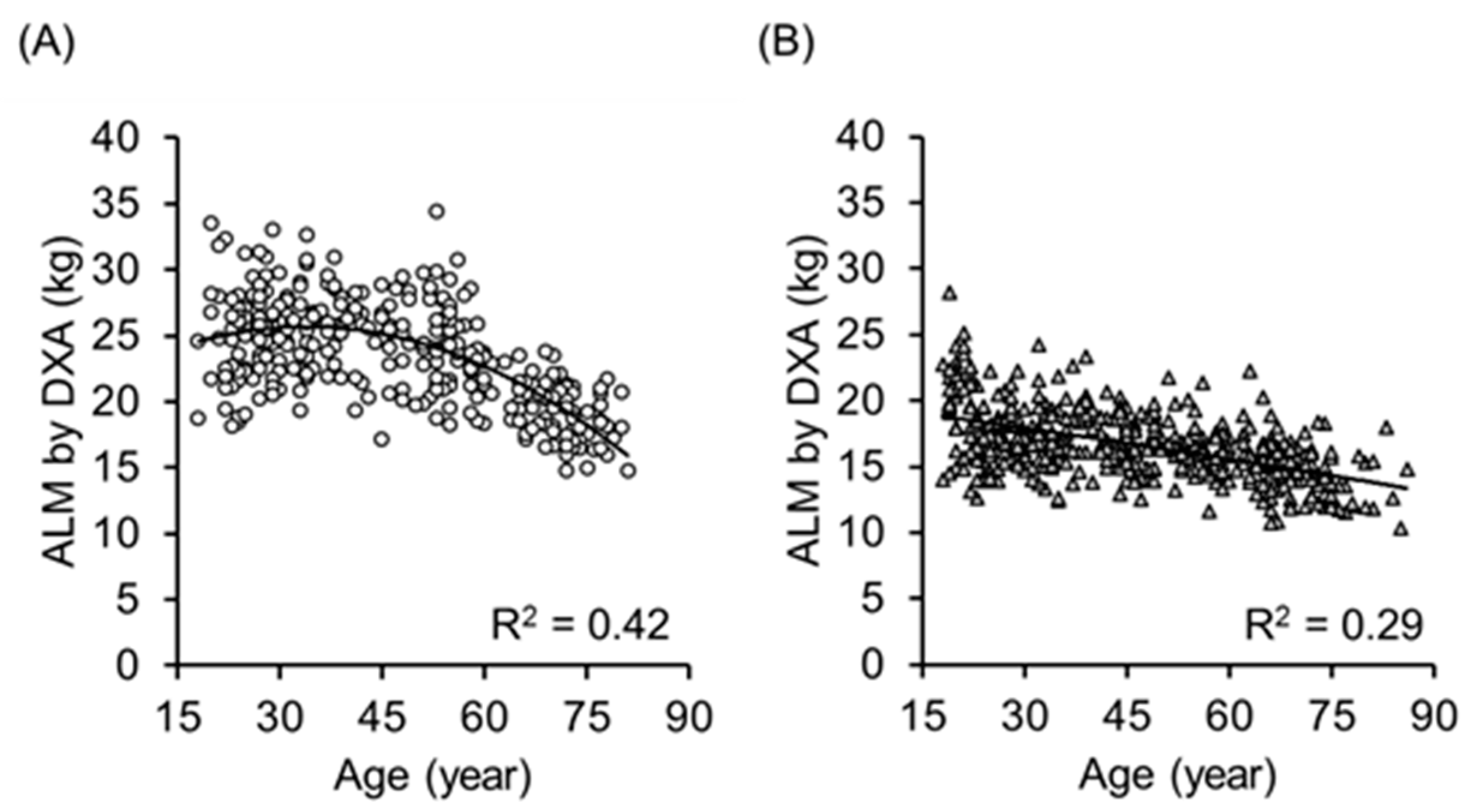
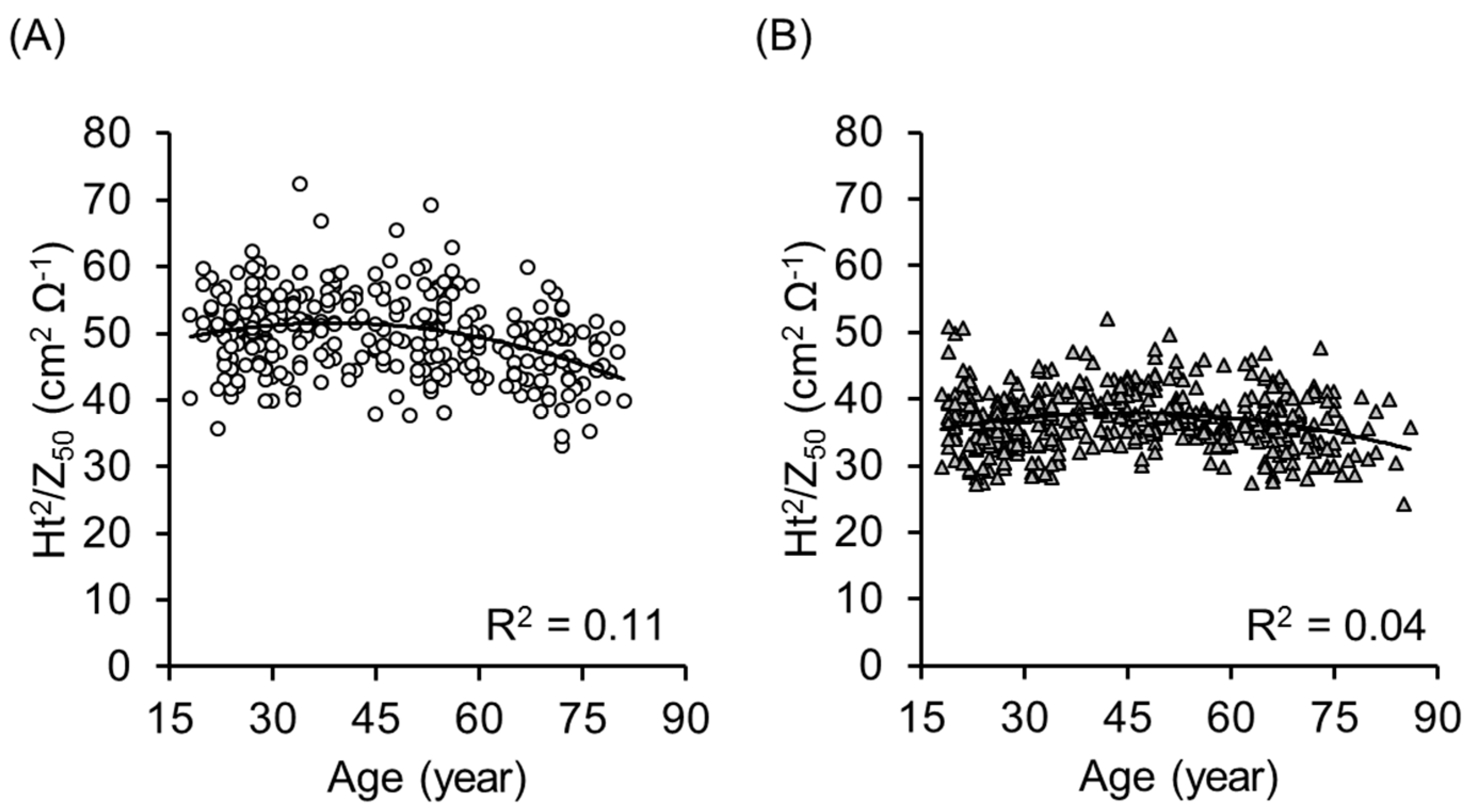
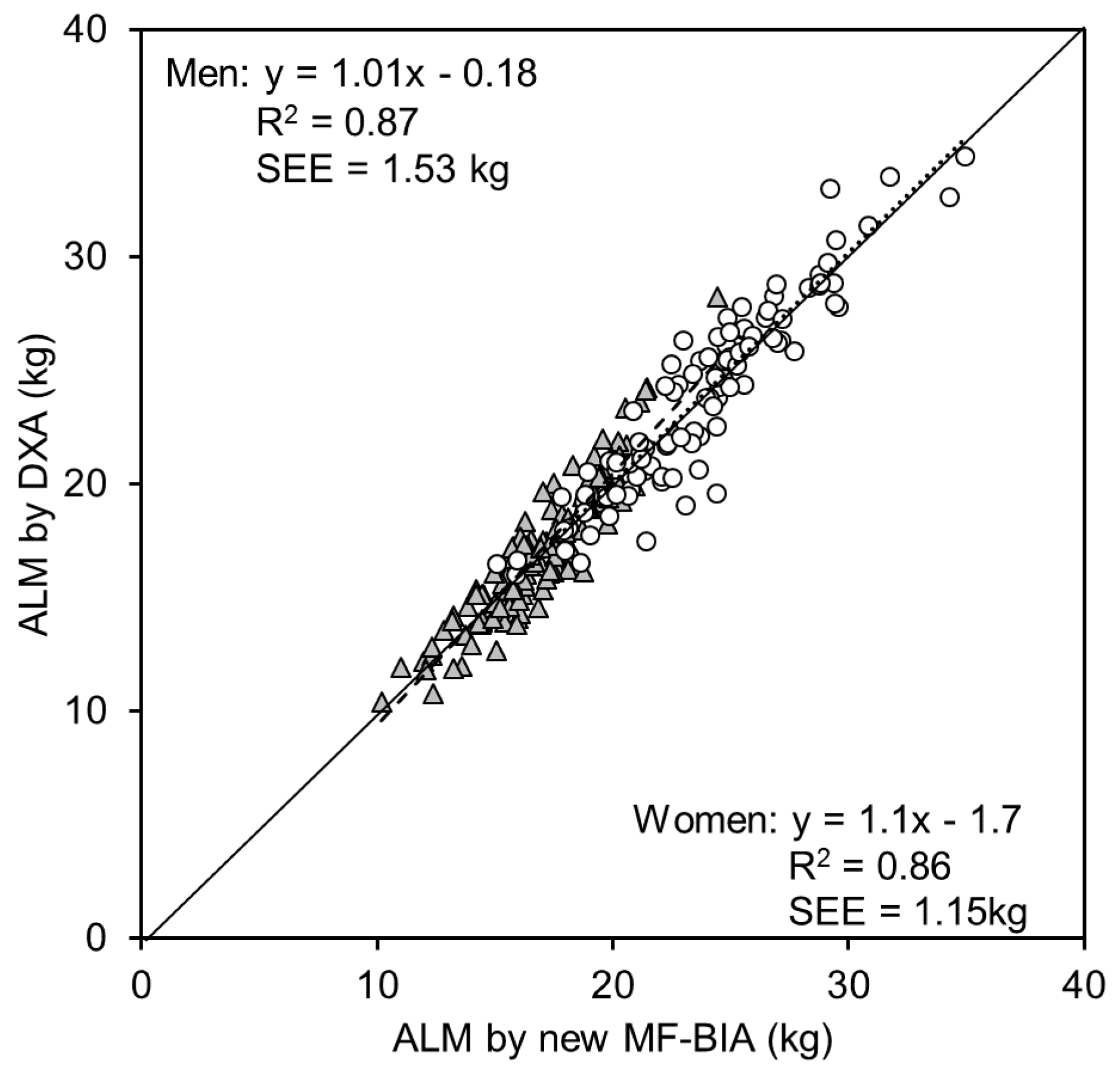
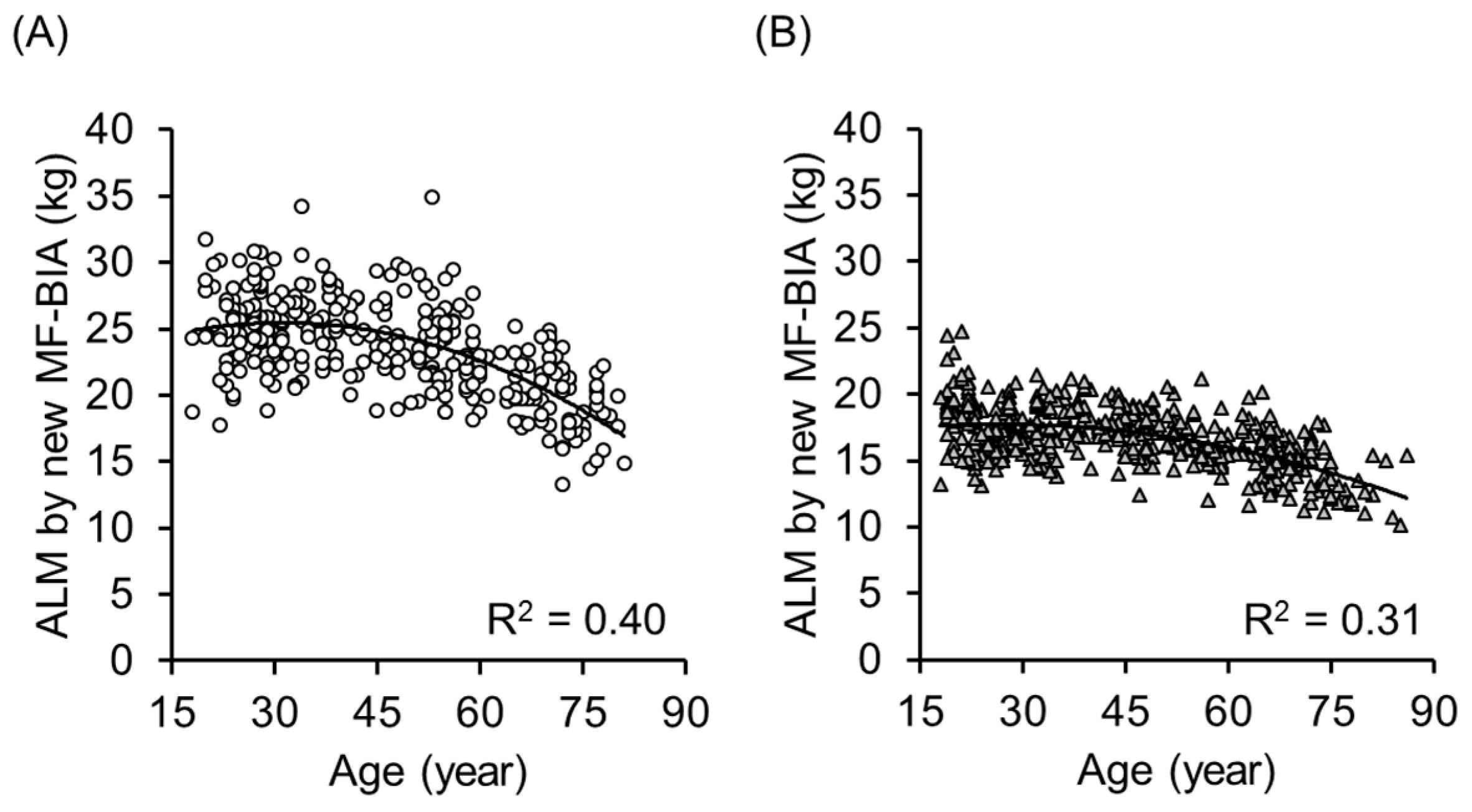
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Health Organization. World Report on Ageing and Health; World Health Organization: Genava, Switzerland, 2015. [Google Scholar]
- Cabinet Office Japan. Annual Report on the Aging Society; Cabinet Office Japan: Tokyo, Japan, 2016. [Google Scholar]
- Yamada, Y.; Nanri, H.; Watanabe, Y.; Yoshida, T.; Yokoyama, K.; Itoi, A.; Date, H.; Yamaguchi, M.; Miyake, M.; Yamagata, E.; et al. Prevalence of frailty assessed by fried and kihon checklist indexes in a prospective cohort study: Design and demographics of the Kyoto-Kameoka longitudinal study. J. Am. Med. Dir. Assoc. 2017. [Google Scholar] [CrossRef] [PubMed]
- Janssen, I.; Ross, R. Linking age-related changes in skeletal muscle mass and composition with metabolism and disease. J. Nutr. Health Aging 2005, 9, 408–419. [Google Scholar] [PubMed]
- Janssen, I.; Heymsfield, S.B.; Wang, Z.M.; Ross, R. Skeletal muscle mass and distribution in 468 men and women aged 18–88 yr. J. Appl. Physiol. 2000, 89, 81–88. [Google Scholar] [PubMed]
- Cruz-Jentoft, A.J.; Landi, F.; Schneider, S.M.; Zúñiga, C.; Arai, H.; Boirie, Y.; Chen, L.K.; Fielding, R.A.; Martin, F.C.; Michel, J.P.; et al. Prevalence of and interventions for sarcopenia in ageing adults: A systematic review. Report of the International Sarcopenia Initiative (EWGSOP and IWGS). Age Ageing 2014, 43, 748–759. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Jentoft, A.J.; Baeyens, J.P.; Bauer, J.M.; Boirie, Y.; Cederholm, T.; Landi, F.; Martin, F.C.; Michel, J.P.; Rolland, Y.; Schneider, S.M.; et al. Sarcopenia: European consensus on definition and diagnosis: Report of the European Working Group on Sarcopenia in older people. Age Ageing 2010, 39, 412–423. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.K.; Liu, L.K.; Woo, J.; Assantachai, P.; Auyeung, T.W.; Bahyah, K.S.; Chou, M.Y.; Chen, L.Y.; Hsu, P.S.; Krairit, O.; et al. Sarcopenia in Asia: Consensus report of the Asian Working Group for Sarcopenia. J. Am. Med. Dir. Assoc. 2014, 15, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Fielding, R.A.; Vellas, B.; Evans, W.J.; Bhasin, S.; Morley, J.E.; Newman, A.B.; van Kan, G.A.; Andrieu, S.; Bauer, J.; Breuille, D.; et al. Sarcopenia: An undiagnosed condition in older adults. Current consensus definition: Prevalence, etiology, and consequences. International working group on Sarcopenia. J. Am. Med. Dir. Assoc. 2011, 12, 249–256. [Google Scholar] [CrossRef]
- Yamada, Y.; Masuo, Y.; Yokoyama, K.; Hashii, Y; Ando, S.; Okayama, Y.; Morimoto, T.; Kimura, M.; Oda, S. Proximal electrode placement improves the estimation of body composition in obese and lean elderly during segmental bioelectrical impedance analysis. Eur. J. Appl. Physiol. 2009, 107, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.C. Segmental bioelectrical impedance analysis: An update. Curr. Opin. Clin. Nutr. Metab. Care 2012, 15, 424–429. [Google Scholar] [CrossRef] [PubMed]
- Thomas, B.J.; Ward, L.C.; Cornish, B.H. Bioimpedance spectrometry in the determination of body water compartments: Accuracy and clinical significance. Appl. Radiat. Isot. 1998, 49, 447–455. [Google Scholar] [CrossRef]
- Pietrobelli, A.; Tato, L. Body composition measurements: From the past to the future. Acta Paediatr. Suppl. 2005, 94, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Organ, L.W.; Bradham, G.B.; Gore, D.T.; Lozier, S.L. Segmental bioelectrical-impedance analysis—Theory and application of a new technique. J. Appl. Physiol. 1994, 77, 98–112. [Google Scholar] [PubMed]
- Miyatani, M.; Kanehisa, H.; Masuo, Y.; Ito, M.; Fukunaga, T. Validity of estimating limb muscle volume by bioelectrical impedance. J. Appl. Physiol. 2001, 91, 386–394. [Google Scholar] [PubMed]
- Lukaski, H.C. Applications of bioelectrical impedance analysis: A critical review. Basic Life Sci. 1990, 55, 365–374. [Google Scholar] [PubMed]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef] [PubMed]
- Kushner, R.F.; Schoeller, D.A. Estimation of total body water by bioelectrical impedance analysis. Am. J. Clin. Nutr. 1986, 44, 417–424. [Google Scholar] [PubMed]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Kuhlmann, M.K.; Kaysen, G.A.; Sarkar, S.; Kaitwatcharachai, C.; Khilnani, R.; Stevens, L.; Leonard, E.F.; Wang, J.; Heymsfield, S.; et al. Segment-specific resistivity improves body fluid volume estimates from bioimpedance spectroscopy in hemodialysis patients. J. Appl. Physiol. 2006, 100, 717–724. [Google Scholar] [CrossRef] [PubMed]
- Kaysen, G.A.; Zhu, F.; Sarkar, S.; Heymsfield, S.B.; Wong, J.; Kaitwatcharachai, C.; Kuhlmann, M.K.; Levin, N.W. Estimation of total-body and limb muscle mass in hemodialysis patients by using multifrequency bioimpedance spectroscopy. Am. J. Clin. Nutr. 2005, 82, 988–995. [Google Scholar] [PubMed]
- Piccoli, A.; Pillon, L.; Dumler, F. Impedance vector distribution by sex, race, body mass index, and age in the United States: Standard reference intervals as bivariate Z scores. Nutrition 2002, 18, 153–167. [Google Scholar] [CrossRef]
- De Lorenzo, A.; Andreoli, A.; Matthie, J.; Withers, P. Predicting body cell mass with bioimpedance by using theoretical methods: A technological review. J. Appl. Physiol. 1997, 96, 161–166. [Google Scholar]
- De Lorenzo, A.; Andreoli, A. Segmental bioelectrical impedance analysis. Curr. Opin. Clin. Nutr. Metab. Care 2003, 6, 551–555. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Heymsfield, S.B. Bioelectrical impedance analysis for diagnosing sarcopenia and cachexia: What are we really estimating? J. Cachexia Sarcopenia Muscle 2017, 8, 187–189. [Google Scholar] [CrossRef] [PubMed]
- Bosy-Westphal, A.; Jensen, B.; Braun, W.; Pourhassan, M.; Gallagher, D.; Müller, M.J. Quantification of whole-body and segmental skeletal muscle mass using phase-sensitive 8-electrode medical bioelectrical impedance devices. Eur. J. Clin. Nutr. 2017. [Google Scholar] [CrossRef] [PubMed]
- Bosy-Westphal, A.; Schautz, B.; Later, W.; Kehayias, J.J.; Gallagher, D.; Müller, M.J. What makes a BIA equation unique? Validity of eight-electrode multifrequency BIA to estimate body composition in a healthy adult population. Eur. J. Clin. Nutr. 2013, 67, S14–S21. [Google Scholar] [CrossRef] [PubMed]
- Ohta, M.; Midorikawa, T.; Hikihara, Y.; Masuo, Y.; Sakamoto, S.; Torii, S.; Kawakami, Y.; Fukunaga, T.; Kanehisa, H. Validity of segmental bioelectrical impedance analysis for estimating fat-free mass in children including overweight individuals. Appl. Physiol. Nutr. Metab. 2017, 42, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, N.I.; Hanawa, S.; Murakami, H.; Cao, Z.B.; Tanimoto, M.; Sanada, K.; Miyachi, M. Accuracy of segmental bioelectrical impedance analysis for predicting body composition in pre-and postmenopausal women. J. Clin. Densitom. 2015, 18, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Janssen, I.; Heymsfield, S.B.; Baumgartner, R.N.; Ross, R. Estimation of skeletal muscle mass by bioelectrical impedance analysis. J. Appl. Physiol. 2000, 89, 465–471. [Google Scholar] [PubMed]
- Mingrone, G.; Bertuzzi, A.; Capristo, E.; Greco, A.V.; Manco, M.; Pietrobelli, A.; Salinari, S.; Heymsfield, S.B. Unreliable use of standard muscle hydration value in obesity. Am. J. Physiol. Endocrinol. Metab. 2001, 280, E365–E371. [Google Scholar] [PubMed]
- Yamada, Y.; Schoeller, D.A.; Nakamura, E.; Morimoto, T.; Kimura, M.; Oda, S. Extracellular water may mask actual muscle atrophy during aging. J. Gerontol. Biol. Sci. Med. Sci. 2010, 65, 510–516. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Ikenaga, M.; Takeda, N.; Morimura, K.; Miyoshi, N.; Kiyonaga, A.; Kimura, M.; Higaki, Y.; Tanaka, H. Estimation of thigh muscle cross-sectional area by single-and multi-frequency segmental bioelectrical impedance analysis in elderly. J. Appl. Physiol. 2014, 116, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Matsuda, K.; Björkman, M.P.; Kimura, M. Application of segmental bioelectrical impedance spectroscopy to the assessment of skeletal muscle cell mass in elderly men. Geriatr. Gerontol. Int. 2014, 14, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Skourou, C.; Rohr, A.; Hoopes, P.J.; Paulsen, K.D. In vivo EIS characterization of tumour tissue properties is dominated by excess extracellular fluid. Phys. Med. Biol. 2007, 52, 347–363. [Google Scholar] [CrossRef] [PubMed]
- Rutkove, S.B. Electrical impedance myography: Background, current state, and future directions. Muscle Nerve 2009, 40, 936–946. [Google Scholar] [CrossRef] [PubMed]
- Pichonnaz, C.; Bassin, J.P.; Currat, D.; Martin, E.; Jolles, B.M. Bioimpedance for oedema evaluation after total knee arthroplasty. Physiother. Res. Int. 2013, 18, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, D.; Shimada, H.; Park, H.; Anan, Y.; Ito, T.; Harada, A.; Suzuki, T. Development of an equation for estimating appendicular skeletal muscle mass in Japanese older adults using bioelectrical impedance analysis. Geriatr. Gerontol. Int. 2014, 14, 851–857. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Yoshida, T.; Yokoyama, K.; Watanabe, Y.; Miyake, M.; Yamagata, E.; Yamada, M.; Kimura, M.; Kyoto-Kameoka Study. The extracellular to intracellular water ratio in upper legs is negatively associated with skeletal muscle strength and gait speed in older people. J. Gerontol. Biol. Sci. Med. Sci. 2017, 72, 293–298. [Google Scholar] [CrossRef]
- Yamada, Y.; Watanabe, Y.; Ikenaga, M.; Yokoyama, K.; Yoshida, T.; Morimoto, T.; Kimura, M. Comparison of single-or multifrequency bioelectrical impedance analysis and spectroscopy for assessment of appendicular skeletal muscle in the elderly. J. Appl. Physiol. 2013, 115, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Buehring, B.; Krueger, D.; Anderson, R.M.; Schoeller, D.A.; Binkley, N. Electrical properties assessed by bioelectrical impedance spectroscopy as biomarkers of age-related loss of skeletal muscle quantity and quality. J. Gerontol. Biol. Sci. Med. Sci. 2017. [Google Scholar] [CrossRef]
- Janssen, I.; Heymsfield, S.B.; Ross, R. Low relative skeletal muscle mass (Sarcopenia) in older persons is associated with functional impairment and physical disability. J. Am. Geriatr. Soc. 2002, 50, 889–896. [Google Scholar] [CrossRef] [PubMed]
- Sergi, G.; De Rui, M.; Stubbs, B.; Veronese, N.; Manzato, E. Measurement of lean body mass using bioelectrical impedance analysis: A consideration of the pros and cons. Aging Clin. Exp. Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Shinkai, S.; Murayama, H.; Mori, S. Comparison of segmental multifrequency bioelectrical impedance analysis with dual-energy X-ray absorptiometry for the assessment of body composition in a community-dwelling older population. Geriatr. Gerontol. Int. 2015, 15, 1013–1022. [Google Scholar] [CrossRef] [PubMed]
- Shiose, K.; Yamada, Y.; Motonaga, K.; Sagayama, H.; Higaki, Y.; Tanaka, H.; Takahashi, H. Segmental extracellular and intracellular water distribution and muscle glycogen after 72-h carbohydrate loading using spectroscopic techniques. J. Appl. Physiol. 2016, 121, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Sanaada, K.; Miyachi, M.; Tanimoto, M.; Yamamoto, K.; Murakami, H.; Okumura, S.; Gando, Y.; Suzuki, K.; Tabata, I.; Higuchi, M. A cross-sectional study of sarcopenia in Japanese men and women: Reference values and association with cardiovascular risk factors. Eur. J. Appl. Physiol. 2010, 110, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Tanimoto, Y.; Watanabe, M.; Sun, W.; Sugiura, Y.; Tsuda, Y.; Kimura, M.; Hayashida, I.; Kusabiraki, T.; Kono, K. Association between sarcopenia and higher-level functional capacity in daily living in community-dwelling elderly subjects in Japan. Arch. Gerontol. Geriatr. 2012, 55, e9–e13. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Nishiguchi, S.; Fukutani, N.; Tanigawa, T.; Yukutake, T.; Kayama, H.; Aoyama, T.; Arai, H. Prevalence of sarcopenia in community-dwelling Japanese older adults. J. Am. Med. Dir. Assoc. 2013, 14, 911–915. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Yamada, Y.; Arai, H. Comparability of two representative devices for bioelectrical impedance data acquisition. Geriatr. Gerontol. Int. 2016, 16, 1087–1088. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, Y.; Yamada, Y.; Fukumoto, Y.; Ishihara, T.; Yokoyama, K.; Yoshida, T.; Miyake, M.; Yamagata, E.; Kimura, M. Echo intensity obtained from ultrasonography images reflecting muscle strength in elderly men. Clin. Interv. Aging 2013, 8, 993–998. [Google Scholar] [CrossRef] [PubMed]
- Kent-Braun, J.A.; Ng, A.V.; Young, K. Skeletal muscle contractile and noncontractile components in young and older women and men. J. Appl. Physiol. 2000, 88, 662–668. [Google Scholar] [PubMed]
- Goodpaster, B.H.; Carlson, C.L.; Visser, M.; Kelley, D.E.; Scherzinger, A.; Harris, T.B.; Stamm, E.; Newman, A.B. Attenuation of skeletal muscle and strength in the elderly: The Health ABC Study. J. Appl. Physiol. 2001, 90, 2157–2165. [Google Scholar] [PubMed]
- Galban, C.J.; Maderwald, S.; Stock, F.; Ladd, M.E. Age-related changes in skeletal muscle as detected by diffusion tensor magnetic resonance imaging. J. Gerontol. Biol. Sci. Med. Sci. 2007, 62, 453–458. [Google Scholar] [CrossRef]
- Fukumoto, Y.; Ikezoe, T.; Yamada, Y.; Tsukagoshi, R.; Nakamura, M.; Mori, N.; Kimura, M.; Ichihashi, N. Skeletal muscle quality assessed from echo intensity is associated with muscle strength of middle-aged and elderly persons. Eur. J. Appl. Physiol. 2012, 112, 1519–1525. [Google Scholar] [CrossRef] [PubMed]
- Heymsfield, S.B.; Gonzalez, M.C.; Lu, J.; Jia, G.; Zheng, J. Skeletal muscle mass and quality: Evolution of modern measurement concepts in the context of sarcopenia. Proc. Nutr. Soc. 2015, 74, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Ticinesi, A.; Meschi, T.; Narici, M.V.; Lauretani, F.; Maggio, M. Muscle ultrasound and Sarcopenia in older individuals: A clinical perspective. J. Am. Med. Dir. Assoc. 2017, 18, 290–300. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, W.K.; Williams, J.; Atherton, P.; Larvin, M.; Lund, J.; Narici, M. Sarcopenia, dynapenia, and the impact of advancing age on human skeletal muscle size and strength; a quantitative review. Front. Physiol. 2012, 3, 260. [Google Scholar] [CrossRef] [PubMed]
- Prado, C.M.; Siervo, M.; Mire, E.; Heymsfield, S.B.; Stephan, B.C.; Broyles, S.; Smith, S.R.; Wells, J.C.; Katzmarzyk, P.T. A population-based approach to define body-composition phenotypes. Am. J. Clin. Nutr. 2014, 99, 1369–1377. [Google Scholar] [CrossRef] [PubMed]

| Equation Developing Group (222 Men) | Validation Group (97 Men) | |||||
| Mean ± SD | MAX | MIN | Mean ± SD | MAX | MIN | |
| Age | 46 ± 17 | 81 | 18 | 49 ± 18 | 78 | 18 |
| Ht | 167.5 ± 6.8 | 181.9 | 147.1 | 167.0 ± 7.6 | 184.6 | 150.0 |
| Wt | 64.8 ± 9.5 | 93.3 | 45.4 | 67.0 ± 10.4 | 99.0 | 47.3 |
| BMI | 23.1 ± 2.8 | 31.5 | 16.2 | 24.0 ± 3.1 | 31.1 | 17.6 |
| ALMDXA | 23.5 ± 3.8 | 32.3 | 14.8 | 23.8 ± 4.2 | 34.5 | 16.0 |
| Z5 | 655.2 ± 64.8 | 837.2 | 498.7 | 636.4 ± 62.5 | 811.1 | 499.4 |
| Z50 | 573.6 ± 58.0 | 735.6 | 437.2 | 557.0 ± 56.5 | 719.7 | 442.1 |
| Z250 | 508.6 ± 52.6 | 657.2 | 388.6 | 494.5 ± 50.3 | 641.4 | 391.3 |
| Ht2/Z50 | 49.5 ± 5.8 | 66.9 | 33.1 | 50.6 ± 6.5 | 72.4 | 34.5 |
| Z250/Z5 | 0.776 ± 0.020 | 0.838 | 0.724 | 0.777 ± 0.020 | 0.830 | 0.736 |
| 1/Z50 | 0.00176 ± 0.00018 | 0.00229 | 0.00136 | 0.00181 ± 0.00018 | 0.00226 | 0.00139 |
| Equation Developing Group (301 Women) | Validation Group (136 Women) | |||||
| Mean ± SD | MAX | MIN | Mean ± SD | MAX | MIN | |
| Age | 47 ± 18 | 86 | 18 | 44 ± 18 | 85 | 18 |
| Ht | 154.7 ± 6.7 | 172.4 | 137.3 | 155.2 ± 7.1 | 170.2 | 138.3 |
| Wt | 54.0 ± 7.3 | 83.6 | 38.3 | 54.1 ± 8.3 | 80.4 | 32.5 |
| BMI | 22.6 ± 3.1 | 33.7 | 16.6 | 22.4 ± 3.0 | 32.9 | 16.0 |
| ALMDXA | 16.5 ± 2.5 | 24.2 | 10.8 | 17.0 ± 3.1 | 28.2 | 10.4 |
| Z5 | 730.8 ± 81.2 | 965.4 | 536.9 | 736.7 ± 79.9 | 995.7 | 508.5 |
| Z50 | 657.9 ± 73.0 | 885.1 | 484.3 | 661.1 ± 72.6 | 901.1 | 464.6 |
| Z250 | 591.0 ± 65.7 | 799.5 | 438.7 | 592.7 ± 66.0 | 815.0 | 420.1 |
| Ht2/Z50 | 36.8 ± 4.2 | 49.8 | 27.1 | 36.9 ± 5.2 | 52.1 | 24.3 |
| Z250/Z5 | 0.809 ± 0.018 | 0.861 | 0.746 | 0.805 ± 0.020 | 0.851 | 0.742 |
| 1/Z50 | 0.00154 ± 0.00017 | 0.00206 | 0.00113 | 0.00153 ± 0.00017 | 0.00215 | 0.00111 |
| Men (n = 222) | Coefficients | Sig. | Collinearity VIF | ||
| Unstandardized | Standardized | ||||
| B | Beta | ||||
| 1 | Ht2/Z50 | 0.5153 | 0.797 | <0.001 | |
| (Constant) | −1.941 | 0.1401 | |||
| R2 = 0.635, SEE = 2.27 kg | |||||
| 2 | Ht2/Z50 | 0.4396 | 0.680 | <0.001 | 1.138 |
| Z250/Z5 | −62.84 | −0.337 | <0.001 | 1.138 | |
| (Constant) | 50.58 | <0.001 | |||
| R2 = 0.735, SEE = 1.94 kg | |||||
| 3 | Ht2/Z50 | 0.6947 | 1.075 | <0.001 | 2.473 |
| Z250/Z5 | −55.24 | −0.296 | <0.001 | 1.152 | |
| 1/Z50 | −10941 | −0.513 | <0.001 | 2.254 | |
| (Constant) | 51.33 | <0.001 | |||
| R2 = 0.851, SEE = 1.46 kg | |||||
| Women (n = 301) | B | Beta | VIF | ||
| 1 | Ht2/Z50 | 0.3797 | 0.644 | <0.001 | |
| (Constant) | 2.567 | 0.008 | |||
| R2 = 0.415, SEE = 1.88 kg | |||||
| 2 | Ht2/Z50 | 0.3346 | 0.568 | <0.001 | 1.043 |
| Z250/Z5 | −50.68 | −0.378 | <0.001 | 1.043 | |
| (Constant) | 45.22 | <0.001 | |||
| R2 = 0.552, SEE = 1.65 kg | |||||
| 3 | Ht2/Z50 | 0.6144 | 1.042 | <0.001 | 2.14 |
| Z250/Z5 | −36.61 | −0.273 | <0.001 | 1.096 | |
| 1/Z50 | −9332 | −0.649 | <0.001 | 2.053 | |
| (Constant) | 37.91 | <0.001 | |||
| R2 = 0.757, SEE = 1.22 kg | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, Y.; Nishizawa, M.; Uchiyama, T.; Kasahara, Y.; Shindo, M.; Miyachi, M.; Tanaka, S. Developing and Validating an Age-Independent Equation Using Multi-Frequency Bioelectrical Impedance Analysis for Estimation of Appendicular Skeletal Muscle Mass and Establishing a Cutoff for Sarcopenia. Int. J. Environ. Res. Public Health 2017, 14, 809. https://doi.org/10.3390/ijerph14070809
Yamada Y, Nishizawa M, Uchiyama T, Kasahara Y, Shindo M, Miyachi M, Tanaka S. Developing and Validating an Age-Independent Equation Using Multi-Frequency Bioelectrical Impedance Analysis for Estimation of Appendicular Skeletal Muscle Mass and Establishing a Cutoff for Sarcopenia. International Journal of Environmental Research and Public Health. 2017; 14(7):809. https://doi.org/10.3390/ijerph14070809
Chicago/Turabian StyleYamada, Yosuke, Miyuki Nishizawa, Tomoka Uchiyama, Yasuhiro Kasahara, Mikio Shindo, Motohiko Miyachi, and Shigeho Tanaka. 2017. "Developing and Validating an Age-Independent Equation Using Multi-Frequency Bioelectrical Impedance Analysis for Estimation of Appendicular Skeletal Muscle Mass and Establishing a Cutoff for Sarcopenia" International Journal of Environmental Research and Public Health 14, no. 7: 809. https://doi.org/10.3390/ijerph14070809
APA StyleYamada, Y., Nishizawa, M., Uchiyama, T., Kasahara, Y., Shindo, M., Miyachi, M., & Tanaka, S. (2017). Developing and Validating an Age-Independent Equation Using Multi-Frequency Bioelectrical Impedance Analysis for Estimation of Appendicular Skeletal Muscle Mass and Establishing a Cutoff for Sarcopenia. International Journal of Environmental Research and Public Health, 14(7), 809. https://doi.org/10.3390/ijerph14070809






