1. Introduction
The continuous degradation of urban air quality is closely related to intensive worldwide urbanization. It is estimated that in coming decades almost 70% of the world’s population will live in urban areas [
1]. A rapid pace of urbanization is associated with an increase of pollutant concentrations, originating from industrial and traffic emissions. This increase in source emissions in combination with extreme climate or weather events requires the development and application of state-of-the-art numerical simulation tools, which will be able to better understand local environmental conditions to support the development of sustainable environmental solutions for urban areas [
2,
3]. Sustainable solutions for urban areas usually include a minimization of air and water pollution, as well as a reduction of energy and water use. To achieve the required reductions in air and water pollution, various scenarios including local meteorological, climate, geographical and emission conditions need to be taken into account in numerical simulations. In the present study, to provide detailed information of air pollution in urban areas generated by traffic emissions, we apply our recently developed computer simulation code that merges computational environmental fluid mechanics with computational atmospheric chemistry. Both parts of this code are based on solving a discretized system of full transport equations for conservation of mass, momentum and reactive species (pollutants). This computational framework represents an approach, which integrates computational fluid dynamics and computational reaction dynamics. Discretization of transport equations is based on a finite-volume method for general non-orthogonal geometries. One of the crucial aspects of the development of such advanced numerical simulation tools is their detailed testing and validation against available experimental studies such as [
4,
5,
6,
7] wherein we demonstrated the capabilities of the modeling approach presented here. Note that resolving a simulation in such detail (including buildings, vegetation, and terrain) as an integral part of the Computational Fluid Dynamics/Computational Reaction Dynamics approach is significantly more accurate in predicting local flow patterns, turbulence intensity and distributions of the passive or reactive scalars than other simplified methods discussed in the literature. The simplified models include the DEGADIS and SLAB models for dense gas dispersion [
8], the BM model [
9], AERMOD and CALPUFF models supported by the US’ EPA [
10], ADMS model developed by Cambridge Environment Research Consultants [
11], etc. The majority of these models are based on a relatively simple standard or slightly extended Gaussian approach for predictions of pollutant dispersion.
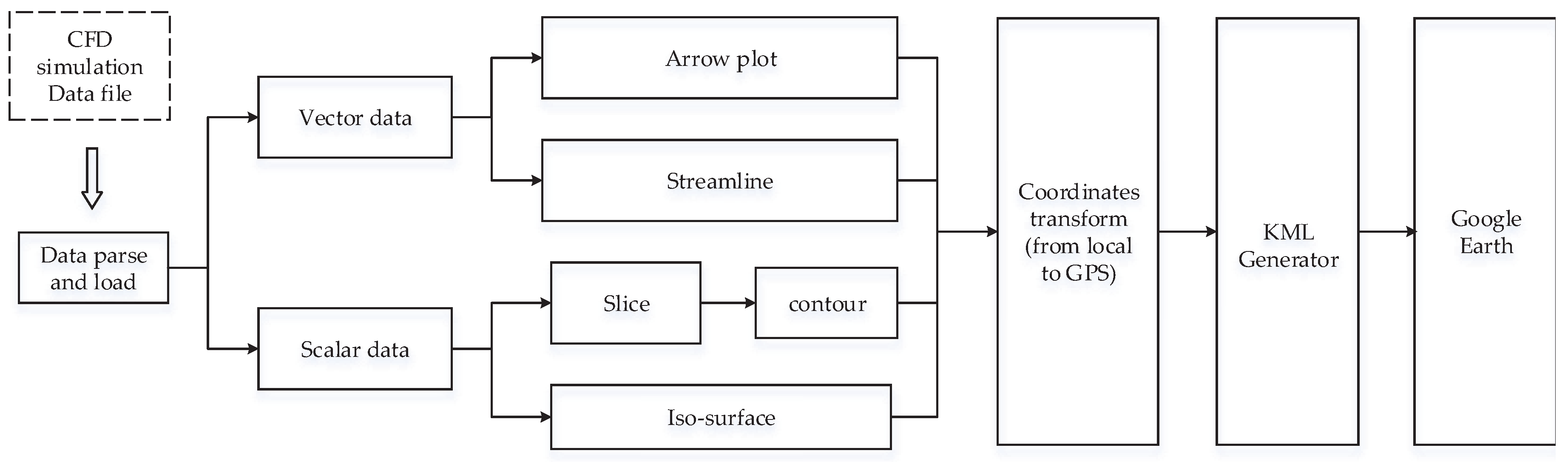
In addition to accurate predictions, it is also crucial to have advanced visualization tools for interpretation and extraction of detailed information from the simulation results obtained. In the past, we have used various stand-alone advanced visualization tools such as ParaView, Tecplot, Advanced Visual System, Visit, etc. Despite numerous features that are commonly used to show and analyze CFD datasets, in all these applications we are missing a photo-realistic representation of simulated cases. Furthermore, to be able to use these above-mentioned stand-alone visualization tools, users need to have rather advanced technical or engineering skills. In the present study, we propose to circumvent some of these limitations by developing a novel visualization method that is based on the Google Earth. Our goal is to have a relatively simple, cost- and user-friendly visualization tool, which will make possible to generate a photo-realistic environment for analysis of generic CFD/CRD datasets.
Google Earth, provided by Google Inc. (Mountain View, CA, USA), is free of charge and is the most popular virtual globe software. In addition to the standard use as a geo-browser for exploring spatially referenced data, it can also be applied to serve as a visualization platform for various scientific disciplines. In recent years, some scientific types of visualizations based on Google Earth have been reported, including leaking gas diffusion [
12,
13], meteorological satellite data [
14], seismic tomographic data [
15], meteorological data [
16], structure of the earth’s lithosphere [
17], remote sensing data [
18], hurricane disasters [
19] and land use land cover dataset [
20].
Some of the core elements of Google Earth/Sketchup/Maps based visualizations that are similar to the present study were shown in [
12,
13,
16]. In [
12], a relatively simple Gaussian dispersion models (i.e., “plume” and “puff” variants) were used to predict spreading of the unexpected gas (carbon monoxide) leak accident. The results were visualized as the 2D projections of the pollution regions in Google Maps. In [
13] a different approach was followed—the Google Sketchup was used to extract the coordinates of buildings, which are then used for CFD simulations (based on a commercial Fluent software) of a gas leakage (methane) within the Sun Yat-sen University East campus. The entire post-processing was performed within the Fluent. Finally, in [
16], authors used Google Maps/Earth to visualize the data originating from meteorological models. The primary focus was on the wind (generated by 3DWF weather forecasting model) visualization in complex terrains, but without providing any details behind algorithms for conversion of data and their visualization.
The present work extends previously mentioned studies in the sense that it provides ways to convert and to visualize results of integrated CFD/CRD approach (which include velocity fields, pressure, turbulence parameters as well as the reactive scalar distributions) used to predict levels of the local pollution within complex urban areas in the Google Earth. Moreover, we also report on the most important steps in constructing the integrated algorithm as well as on details in generating various geometrical elements used for visualization of the data. This is especially important for the code/algorithm developers who want to adopt the presented approach for their needs.
Finally, capabilities of developed tools will be demonstrated in a case of photochemical smog formation for a selected neighborhood in the city of Rotterdam (The Netherlands).
3. Results and Discussion
In this section, we demonstrate an application of the above-described algorithms to show results of an integrated CFD and CRD approach in simulating flow, turbulence, and dispersion of reactive pollutants in a real scale urban area, and how generated results are finally visualized in the Google Earth. Here we present data calculated in [
22] for traffic pollution and ozone distribution in one neighborhood of the city of Rotterdam (The Netherlands,
Figure 5). The region of interest covers a zone of 1 × 1 km located in the “Oude Noorden” neighborhood with three main traffic arteries: Bergselaan, Schieweg and Bergweg streets (which are shown in red color—where the source emissions of NO and NO
2 are defined). The GPS coordinates of the left bottom corner of the simulated domain are (51.928640, 4.461468, 0) (in decimal degrees), where the “0” indicates the ground level in the
z-direction. The buildings of selected neighborhood are generated from the digital elevation map (DEM) dataset obtained from the city officials.
The environmental chemistry is simulated by applying the GRS model, which includes photovoltaic chemical reactions involving NO, NO
2, O
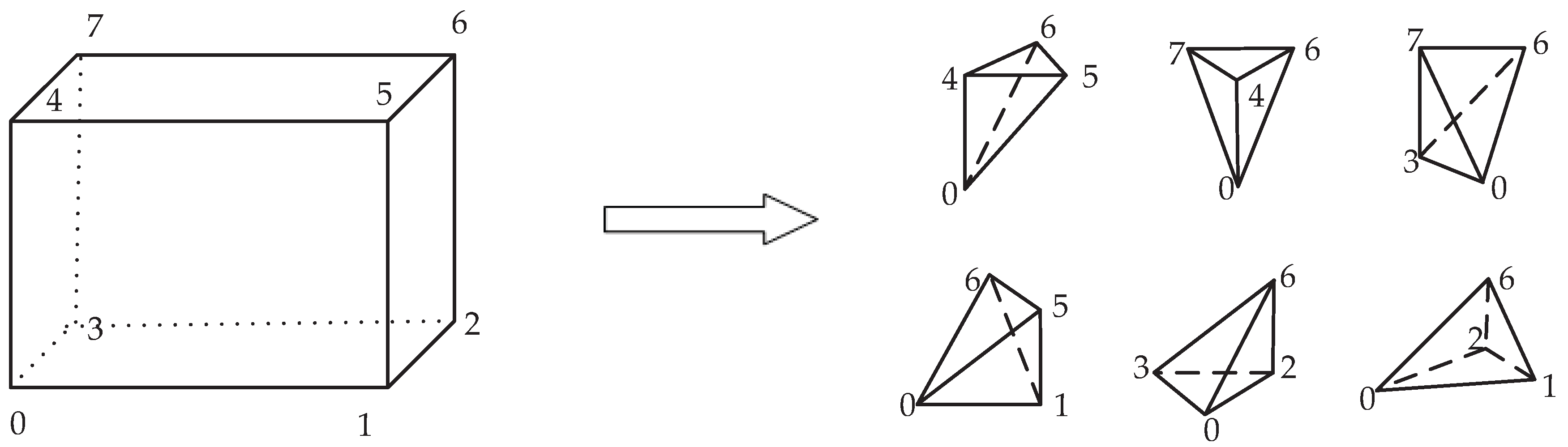
3 and Reactive Organic Compounds (ROC). The environmental fluid mechanics is simulated by applying a RANS approach to obtain velocity, pressure and turbulence variables (turbulence kinetic energy and its dissipation rate). The locally refined hexagonal numerical mesh is used with typical control volume sizes of 3.5 × 3.5 × 0.25 m in the proximity of buildings, up to 40 × 40 × 40 m for regions above the urban canopy, in the
x-,
y- and
z-coordinate directions, respectively. Note that the
z-direction indicates the vertical coordinate. Approximately 5.4 × 10
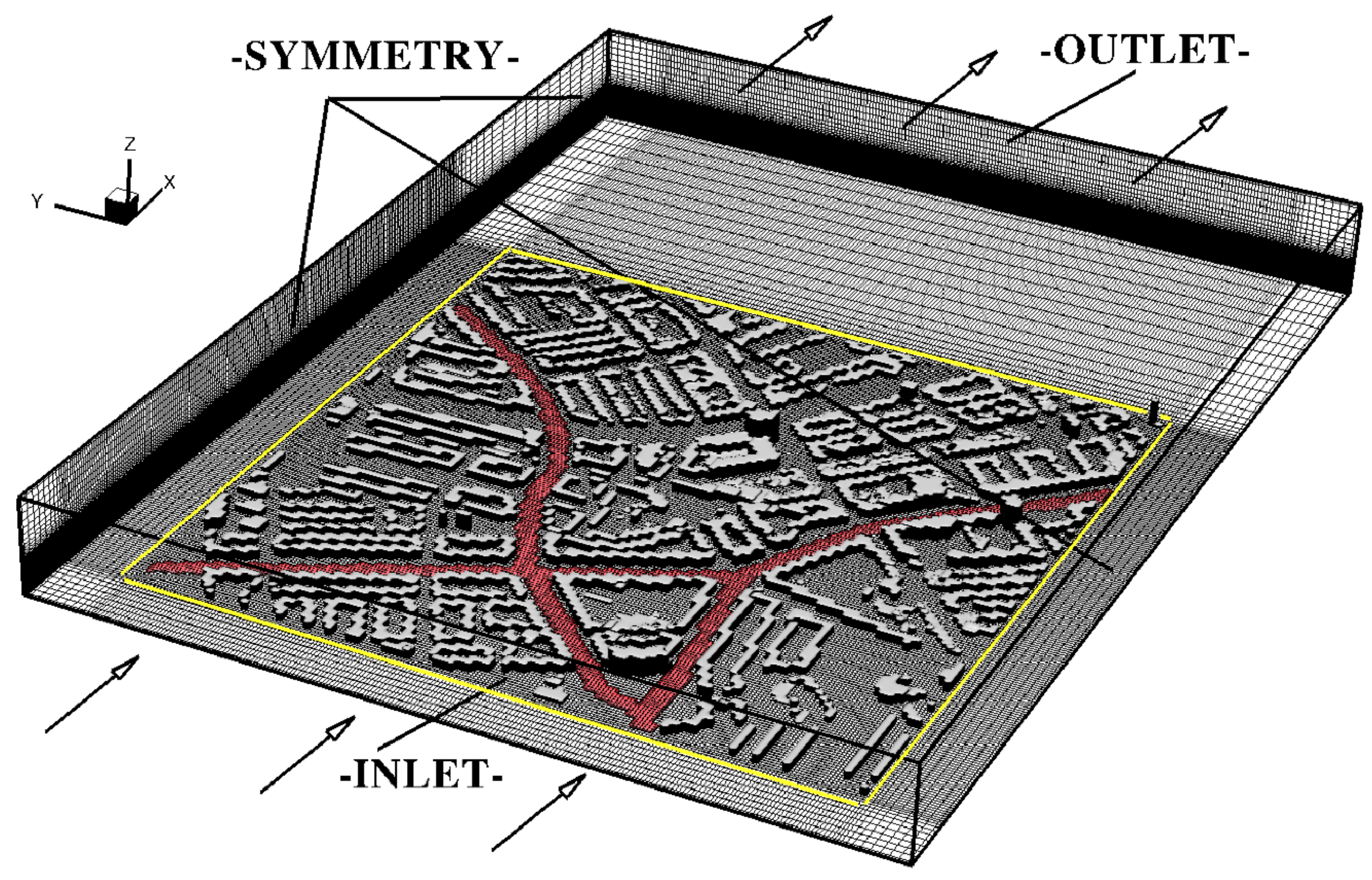
6 control volumes are used for the entire simulation domain, and about 1800 obstacles are used to represent the buildings. The simulated CFD domain with imposed boundary conditions and numerical mesh used is depicted in
Figure 6. At the inlet, approaching wind profile and intensity of the turbulence kinetic energy and its dissipation rate are defined from available meteorological measurements. The simulated scenario includes a light breeze wind conditions (~2 m/s) blowing from the West, which was based on the wind-rose map for that area for the selected time period. The symmetry boundary conditions are applied to the side and top boundaries.
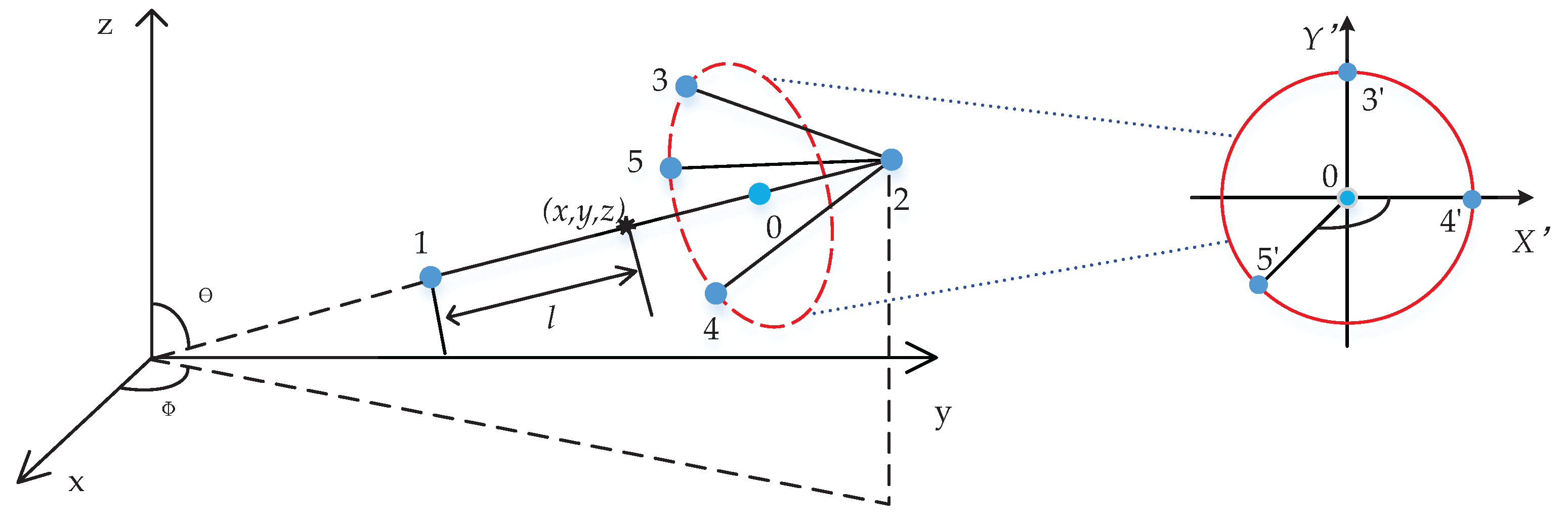
First, we demonstrate how the local wind patterns can be visualized. This information can be used to evaluate locations where the wind intensity at the pedestrian level exhibits some critical threshold values (so-called “pedestrian wind comfort”). Simulations can reveal places where the wind along the street can reach too high values. Furthermore, some mitigation scenarios can also be considered. For example, what are the effects of planted trees along the street and how the type and placing of trees can be optimized? The velocity field in the selected
z-plane with the height of
z = 1 m and
y-plane where
y = 454 m is shown in
Figure 7. The top panel shows the wind field in the whole domain, whereas the bottom panel is a zoom-in showing the local wind distribution in more detail. Colors are used to denote the wind speed compared to a threshold value. The street-canyon effects (i.e., local acceleration of the wind due to blockage effects of buildings—indicated by red vectors), the local wind recirculation as well as the low wind intensity regions (indicated by blue vectors) can be easily observed. Similar information can be extracted even without showing the 3D velocity vectors. This is achieved by plotting the streamlines or streamlets, which are straightforward and intuitive ways to interpret a local wind distribution. In
Figure 8, the top panel denotes streamlines with 50 seeds located in the line where
x = 0 m and
z = 0.75 m.
The bottom panel denotes the streamlets calculated with first seeds located in the z-plane where z = 1.8 m. For both panels, nine colors (in gradations from blue to red) are used, and they denote different velocity ranges with the threshold values 0.3, 0.6, 0.9, 1.2, 1.5, 1.8, 2.1 and 3 m/s, respectively. Now, locations with a sudden velocity increase can be easily mapped. Note that we selected just one plane for demonstration purposes, but streamlines or streamlets can be easily plotted for any arbitrary pre-selected planes.
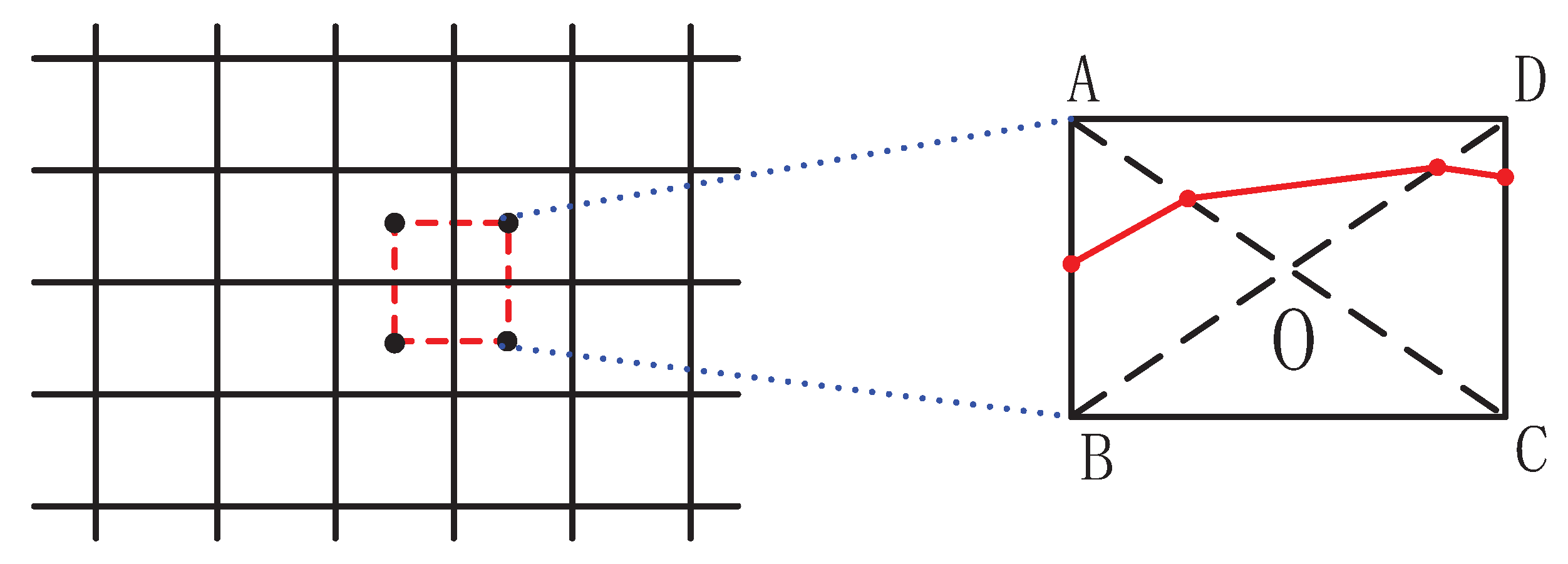
Next, we focus on visualizations of the pollution distribution within the simulated neighborhood. Here, due to the scalar nature of variables (concentrations of chemical species), we use isolines and isosurfaces to identify their spatial distributions. The isolines are primarily useful to map concentrations of chemical species in pre-selected planes. In contrast to that, isosurfaces are used to estimate fronts of pollution spreading. With a combination of these two approaches, a detailed analysis of the local levels of pollution can be performed (e.g., to identify the most critical pollution spots).
As an example, the isolines of the NO
2 and O
3 are shown in
z = 2 m plane,
Figure 9. It can be seen that the maximum concentrations of the NO
2 are observed in the proximity of the roads, which is expected since the NO
2 is a direct product of traffic emission (
Figure 9a). It is also important to see that the local concentrations of NO
2 vary significantly along different sides of streets due to the imposed wind conditions. In contrast to the NO
2, the ozone O
3 levels show a significantly different behavior (
Figure 9b). This is the result of the complex convection-turbulent diffusion-chemical reaction mechanisms, which are simulated within the CFD/CRD model. This additionally stresses a potential of such advanced mathematical models to map various pollution scenarios based on different meteorological (wind intensity and direction) and traffic (low, moderate or high intensity) conditions.
The isosurfaces of NO
2 (with levels of 0.5 ppm and 0.1 ppm, respectively) and O
3 (with levels of 0.15 ppm and 0.1 ppm, respectively) are shown in
Figure 10. Note that this way of presenting of results can be very useful to identify regions with increased risks for population suffering from the chronic respiratory diseases (e.g., asthma, chronic obstructive pulmonary disease (COPD), etc.) by a simple pre-specification of critical concentration thresholds for individual chemical species (e.g., NO
2, NO, O
3, SO
x, particulate meter, etc.). In present work, in addition to isolines and isotherms, we also propose a simple method to visualize the local concentrations as discrete volume objects, as demonstrated in
Figure 11. Here, size and color of the object define the concentration level at pre-defined locations. This method is simple for understanding and can be easily interpreted as a kind of the virtual probes/sensors at given locations. The pre-defined critical concentration thresholds can be re-scaled to provide an easy navigation through the data. For example, the red objects indicate increased and potentially harmful levels, the yellow objects indicate intermediate pollution levels, and finally, the blue objects indicate safe concentrations. This concept was used in showing the distributions of O
3 (
Figure 11a,b) and of NO
2 (
Figure 11c,d). Please note that the density of the virtual probes/monitors distribution can be easily adjusted for specific regions (e.g., along streets or in the proximity of particular buildings or crossroads, parks, hospitals, schools, etc.).
4. Conclusions
In the present study, we have developed an efficient tool, which enables Google Earth visualization of results obtained by CFD simulation of environmental flow and turbulent dispersion of reactive scalars in urban areas. The most common ways of representing 3D vector and scalar variables are included in this tool (3D vectors and their projections at specified planes, streamlines, isolines or isosurfaces of scalar variables). In contrast to the standard stand-alone visualization packages for displaying the CFD data, the Google Earth provides a photo-realistic description (that includes numerous geographic information system (GIS) features such as the 3D terrain, buildings, vegetation, roads, water surfaces, soil, etc.) of the simulated domain, making the interpretation of the visualized datasets relatively easy and intuitive. Besides, the Google Earth provides an easy interface to record animations with fly-through effects of the selected datasets (an example of such animation is attached as the
Supplementary File/Video).
To demonstrate some capabilities of the newly developed CFD/CRD to Google Earth dataset conversion and visualization algorithms, we analyzed the flow and turbulent dispersion of reactive scalars (photochemical smog generation) for a neighborhood in the city of Rotterdam, The Netherlands. Here, the surface pollutant sources and incoming wind conditions were specified to match realistic traffic emissions and typical meteorological situations. Maps of the local velocity field at different heights were generated. On top of that, isolines and isosurfaces of the reactive scalars were shown. Furthermore, the discrete volume objects were used as a kind of the virtual probes/monitors/sensors making it possible to quantify the local pollution thresholds in a straightforward and efficient way. Finally, the fly-by animations (attached as
supplementary material video) along the streets under study provided insights in depth into the local levels of pollution. Furthermore, apart from the 3D buildings natively provided by the Google Earth, the manually created geometry models of the simulation domain can also be imported (as shown in
Figure 5). It means that the presented tool can also be used in the areas where the 3D obstacles (or buildings) utilized in the model do not exist in the Google Earth.
Note that due to simplicity of the requested structure of the input data (spatial coordinates of the control volume nodes and values of vector and scalar components at the control volume centers) here presented tool can also be used for any other visualizations of the CFD/CRD model of environmental flow and pollution dispersion in a city-scale or neighborhood scale. Finally, we conclude that the presented approach of CFD/CRD conversion and visualization in the Google Earth proved to be a numerically efficient and user-friendly way of displaying results.