WHO Environmental Noise Guidelines for the European Region: A Systematic Review on Environmental Noise and Annoyance
Abstract
:1. Introduction
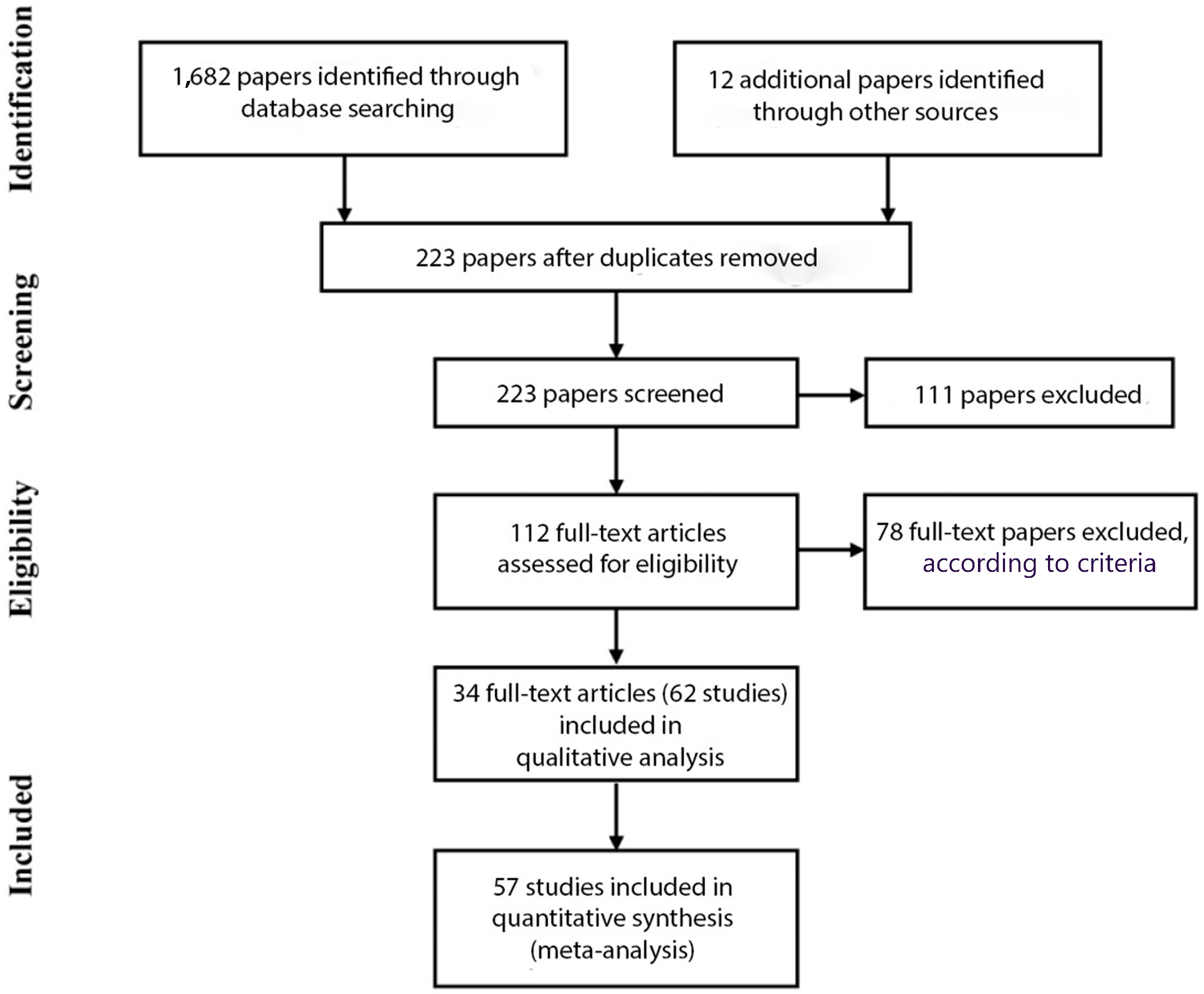
2. Materials and Methods
2.1. Defining the Effect Variable: Annoyance
- (1)
- an often repeated disturbance due to noise (repeated disturbance of intended activities, e.g., communicating with other persons, listening to music or watching TV, reading, working, sleeping), and often combined with behavioral responses in order to minimize disturbances;
- (2)
- an emotional/attitudinal response (anger about the exposure and negative evaluation of the noise source); and
- (3)
- a cognitive response (e.g., the distressful insight that one cannot do much against this unwanted situation).
2.2. Search and Selection of Studies
- (1)
- Study type: cross-sectional or longitudinal surveys, using an explicit protocol for selecting respondents.
- (2)
- Participants: Studies including members of the general population (mainly residents of noise-exposed areas).
- (3)
- Exposure type: Long-term outside noise levels which are either expressed in LAeq,24h, Ldn, Lden or its components (Lday, Levening, Lnight and the duration in hours of night—see Supplementary Materials S37 for definitions of these terms), or can be easily converted from similar acoustic variables AND:
- The level is based on a reliable calculation procedure, using the actual traffic volume, composition, and speed per 24 h per road/railway/airport as input, or the type and sound power of an industrial installation, OR
- is based on measurements for a minimum of one week by qualified staff, and adjusted for data under point (a) as well as meteorological conditions when necessary.
- (4)
- Outcome measure: The base of the outcome measure is the individual annoyance response made during a standardized survey. The annoyance question and the response format either follow the recommendations given by ICBEN [8] and/or ISO TS 156666 [9] directly, or are very close to them. The paper (or the authors on request) gives at least one original table, formula, or graph which can be used for an ERR.
- (5)
- Confounders: Papers containing a potential second risk factor besides noise (e.g., vibrations in case of railway noise close to the tracks) are included and got special remarks in the list of included papers.
- (6)
- Language: Papers in English, French, Dutch, and German were included as long as they met the selection criteria. These languages were selected according to the language understanding of the present authors.
2.3. Data Extraction
2.4. Effect-Size Measures
- Pearson correlations for LAeq vs. annoyance raw scores. Correlation coefficients using the (partially restricted) range of reported noise exposure levels for a specific source in 1 dB steps and the full range of the noise annoyance scale for each study are taken as effect-size measures for our formal meta-analysis. The noise level ranges vary between noise sources and studies (see Tables 1, 3 and 5. Although correlations as such do not indicate a causal relationship, it is plausible that a statistical association between (external) transportation noise levels—related to the past 12 months—and annoyance judgments due to transportation noise—related to the same 12 months—indicates an effect of noise on annoyance—and not the other way round. Correlation coefficients between noise levels and annoyance raw scores contain the most complete information about the effect of environmental noise levels on noise annoyance, as observed in surveys, although they are rarely used for health impact assessments. Pearson correlations restrict this information to linear relations, but it has been shown in the past that raw annoyance scale variables usually show a linear relation to LAeq-variables, and the inclusion of non-linear terms does not improve the correlation—at least with such large samples as used here. Here, mainly LAeq,24h or Lden are used as exposure variables, and raw scores on the 11-point numeric or 5-point verbal ICBEN scale as response variables.
- Increase of percent HA with increase of LAeq levels, based on observed data. The %HA-increase was determined in terms of odds ratios (OR). The OR denotes the ratio of two odds. Here, each of these odds represents the proportion of highly annoyed participants divided by the proportion of those not highly annoyed at a certain exposure level. Thus, the OR referring to a %HA-increase by an increase of exposure levels is defined as the ratio of the odds for each of the two exposure levels. The increase of the event rate (such as %HA) for an increase of 5 or 10 dB LAeq is sometimes used in noise effect reports [15,16,17], because this metric indicates the increase of a severe noise effect (%HA) with a certain increase of noise exposure. Although the use of this metric is quite popular in political contexts, we should keep in mind that the size of the “increase effect” is heavily dependent on three parameters: (a) the definition of “highly annoyed” (see above); (b) the noise level range considered for the dB-difference, together with the form of the exposure-response relation; and (c) the data source (e.g., observed data vs. calculated ERF). Provided that the standard definition of HA is used, it is often seen that the %HA-curves show a nonlinear relation to equivalent noise levels, taking the form of a “J” (as is the case in the well-known %HA curves in Miedema and Oudshoorn [4]). In such cases, it can be expected that the %HA-difference between two noise levels at the lower end of the exposure scale is lower than the respective difference at medium or higher noise levels. There may be other forms of ERRs and especially in case of a small range of noise levels which are not comparable between studies, the 10-dB-difference approach may produce misleading results. With respect to (c) we should keep in mind that calculated ERFs for %HA use a wide range of noise levels and data from the whole set of respondents together with assumptions about the S-form of the ERR, and %HA can be calculated in small steps on the decibel scale. On the other hand, observed data for certain noise levels (e.g., 50 and 60 dB) often imply using small groups of respondents (often N < 100) around these levels (e.g., from 47.5 to 52.4 dB in the case of a “50 dB group”), leading to “real” subsamples of small size. We use the OR based on the %HA at 50 and 60 dB for transportation noise and the OR based on the %HA at 42.5 and 47.5 dB for low level noise source types, e.g., wind turbines.
- Increase of %HA with increase of LAeq levels, based on modelled data. We used equation/parameter values (e.g., B or exp(B) for logistic regression) for the model, specified for type of ERR (e.g., linear regression, logistic regression: binary, polynomial fit, etc.). Such parameters partially use the full information contained in the ERR and partly restricted information (e.g., in the case of logistic regression). Generally, a modelled ERF may overcome restrictions due to small samples in certain noise level groups. They can be used to calculate predicted annoyance values for specified noise levels as well as for determining the change in annoyance between specified noise level differences. This change could be expressed as an OR. The slope parameter B from logistic regressions represents a logarithmized OR (ln(OR)) and can be used to estimate the effect of a 10 dB difference; these estimated ORs can be compared to the ORs based on the observed %HA at each of the two levels. Furthermore, the regression equations from the studies can be used for estimating aggregated ERR.
2.5. Publication Bias Assessment
2.6. Quality of Evidence Assessment
3. Results
3.1. Aircraft Noise Effects on Annoyance
3.1.1. Studies Selected
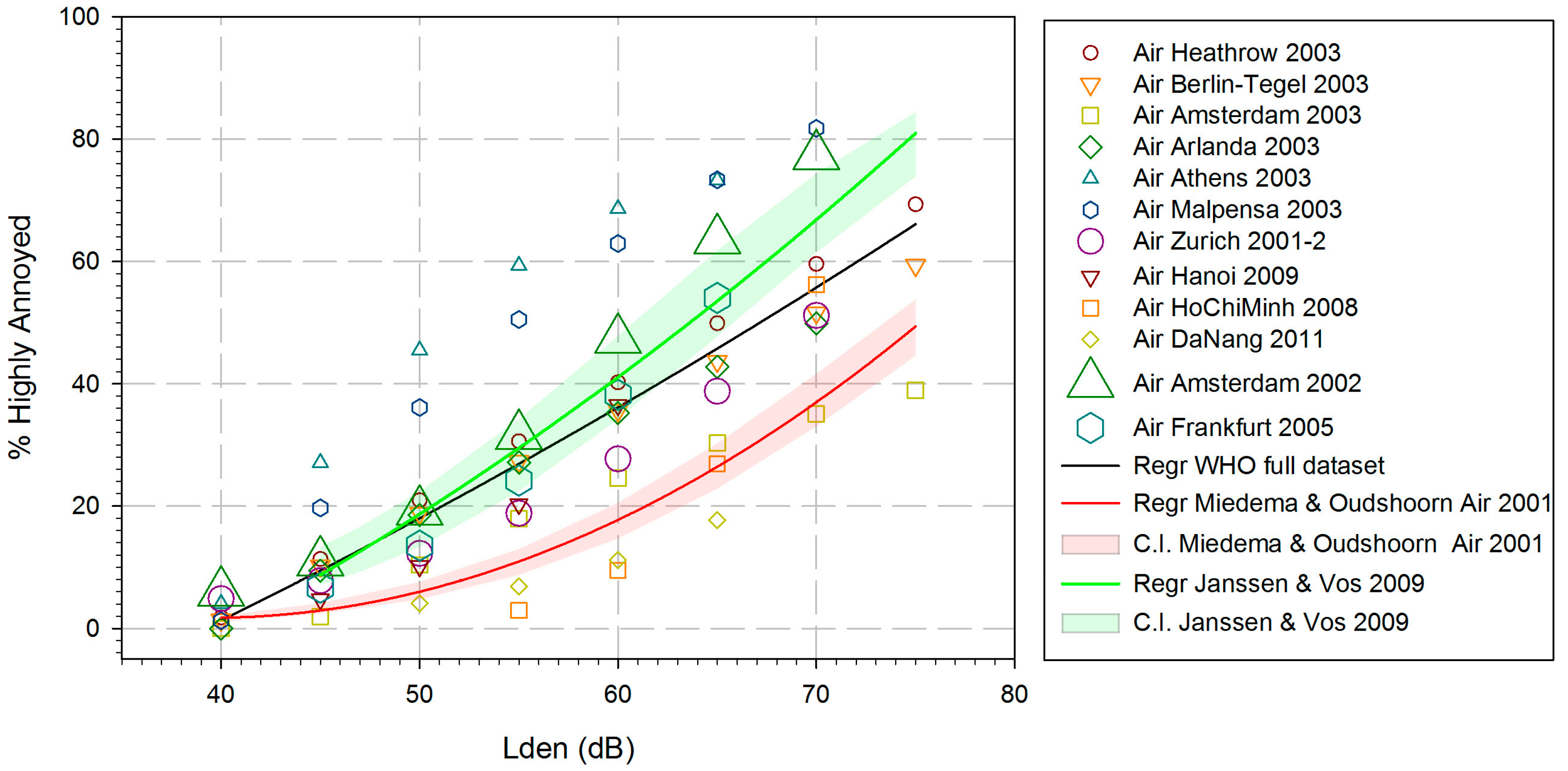
3.1.2. Aircraft Noise Effects (1): ERRs in the Full Dataset
3.1.3. Grading the Quality of Evidence for the ERR of %HA by Aircraft Noise
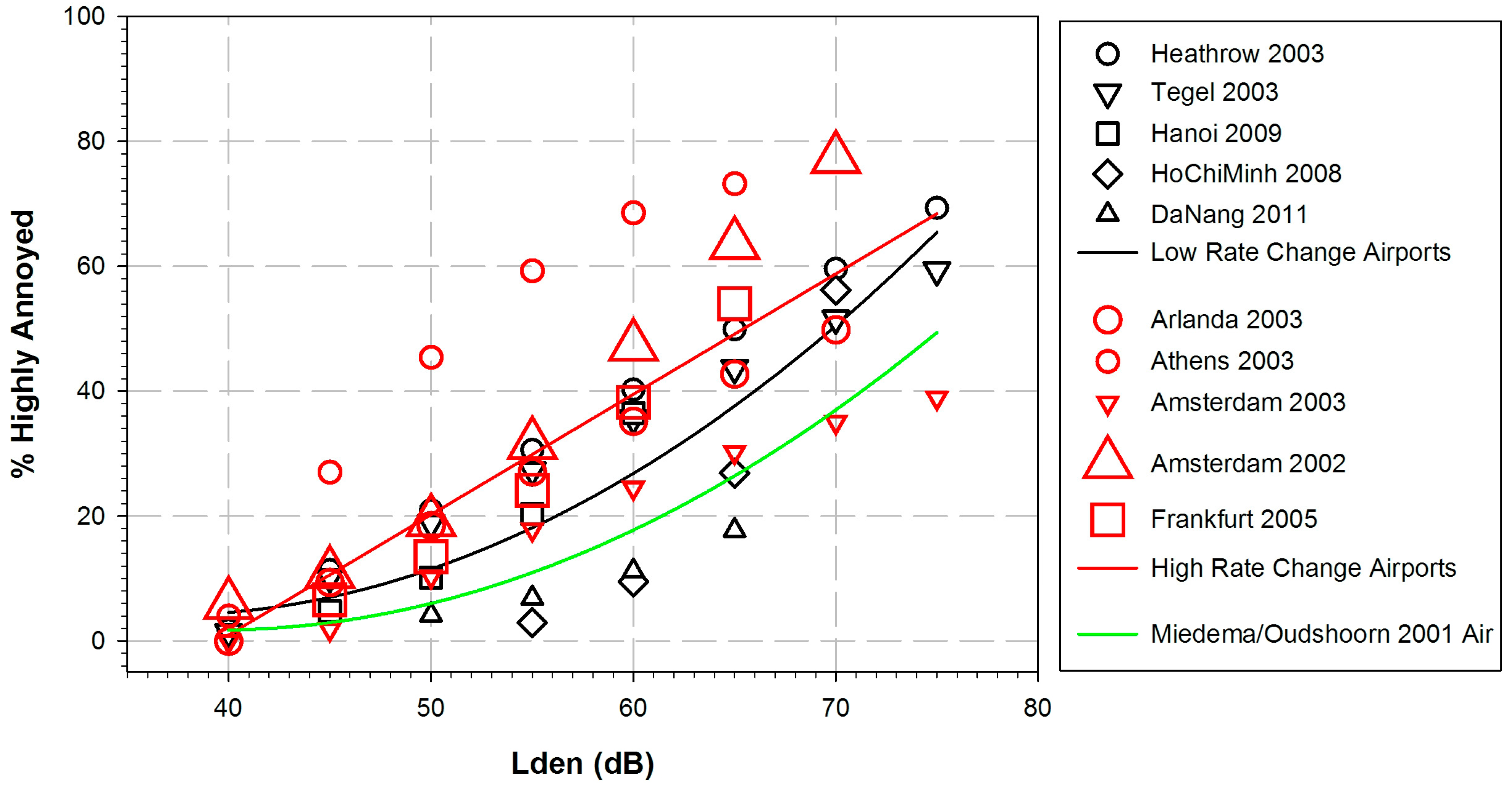
3.1.4. Aircraft Noise Effects (2): ERRs in High-Rate and Low-Rate Airport Change Situations
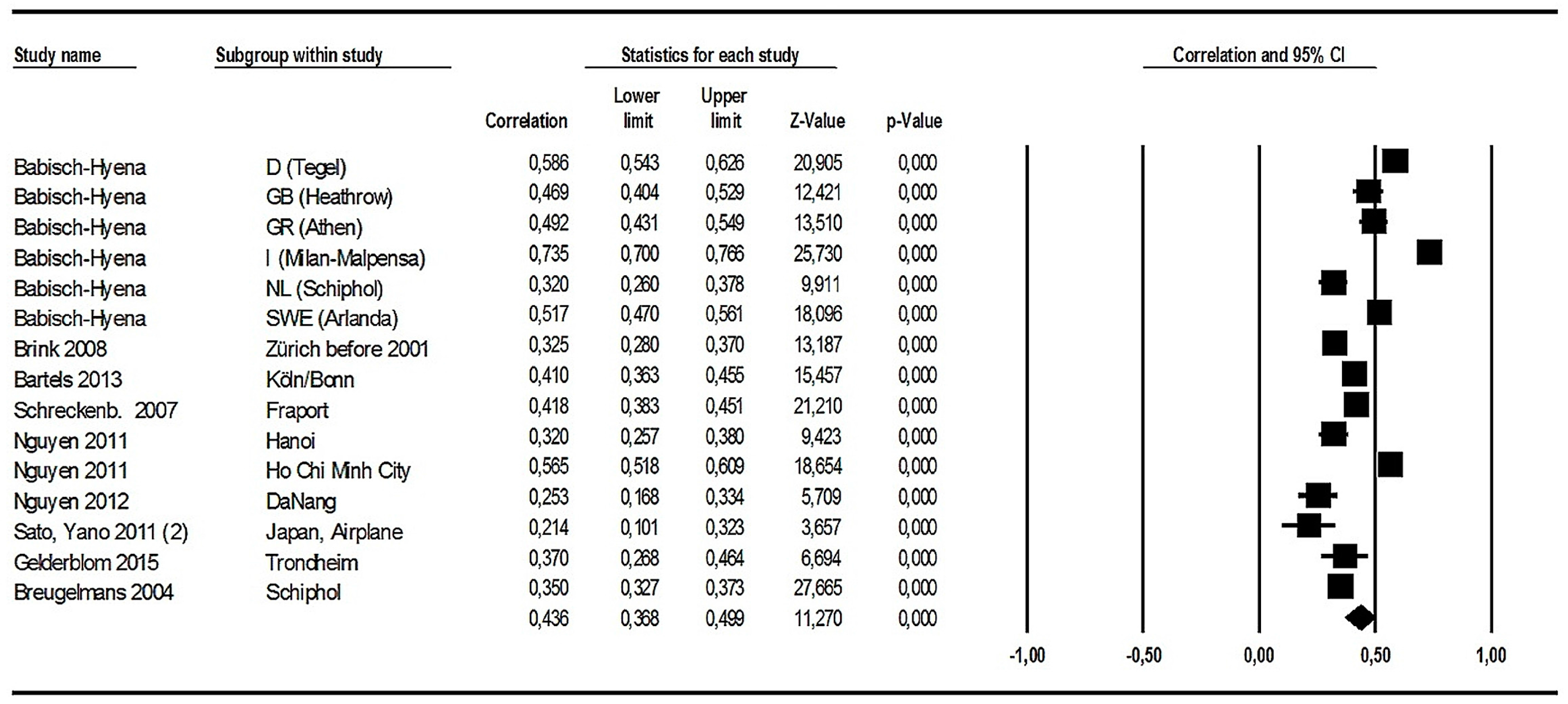
3.1.5. Aircraft Noise Effects (3): Correlations between Noise Levels and Annoyance Raw Scores
Meta-Analyses in the Full Dataset
Grading the Quality of Evidence for the Correlation between Aircraft Noise Levels and Annoyance
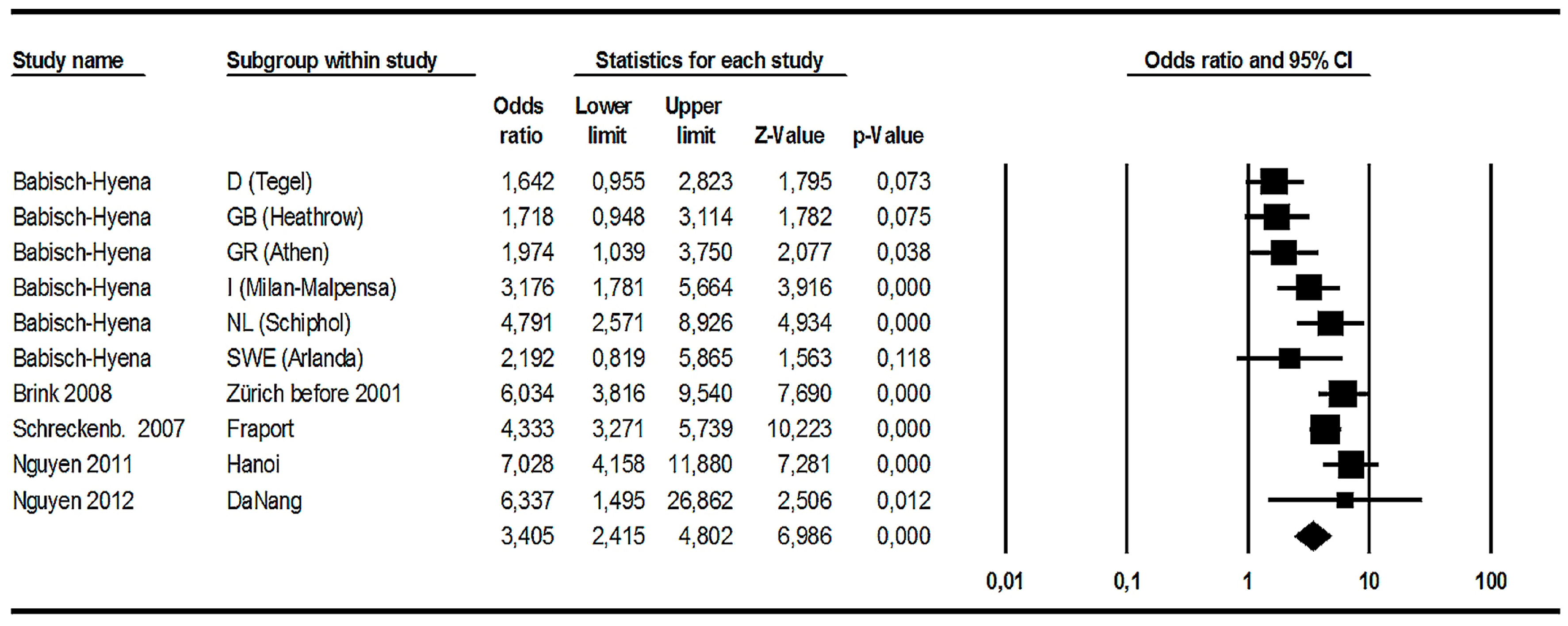
3.1.6. Aircraft Noise Effects (4): ORs Referring to the %HA Increase per 10 dB Level Increase
Meta-Analysis Based on Original Grouped Data
Meta-Analysis Based on Modelled Data
Grading the Evidence Based on ORs Representing the %HA Increase by a 10 dB Lden-Increase of Aircraft Noise
3.1.7. The Influence of Co-Determinants in Aircraft Noise Studies
3.1.8. Summary of the Analyses Related to Aircraft Noise Effects on Annoyance
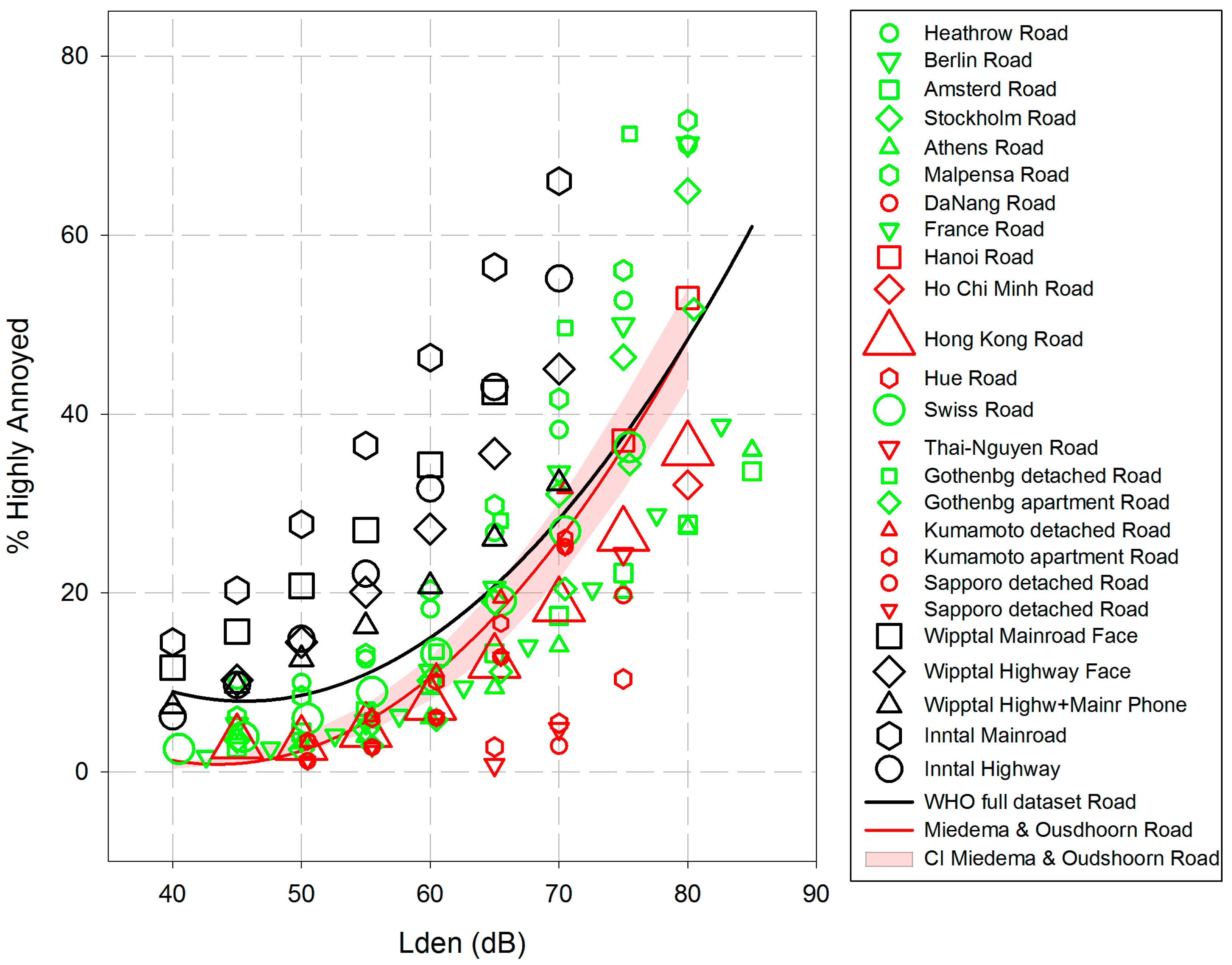
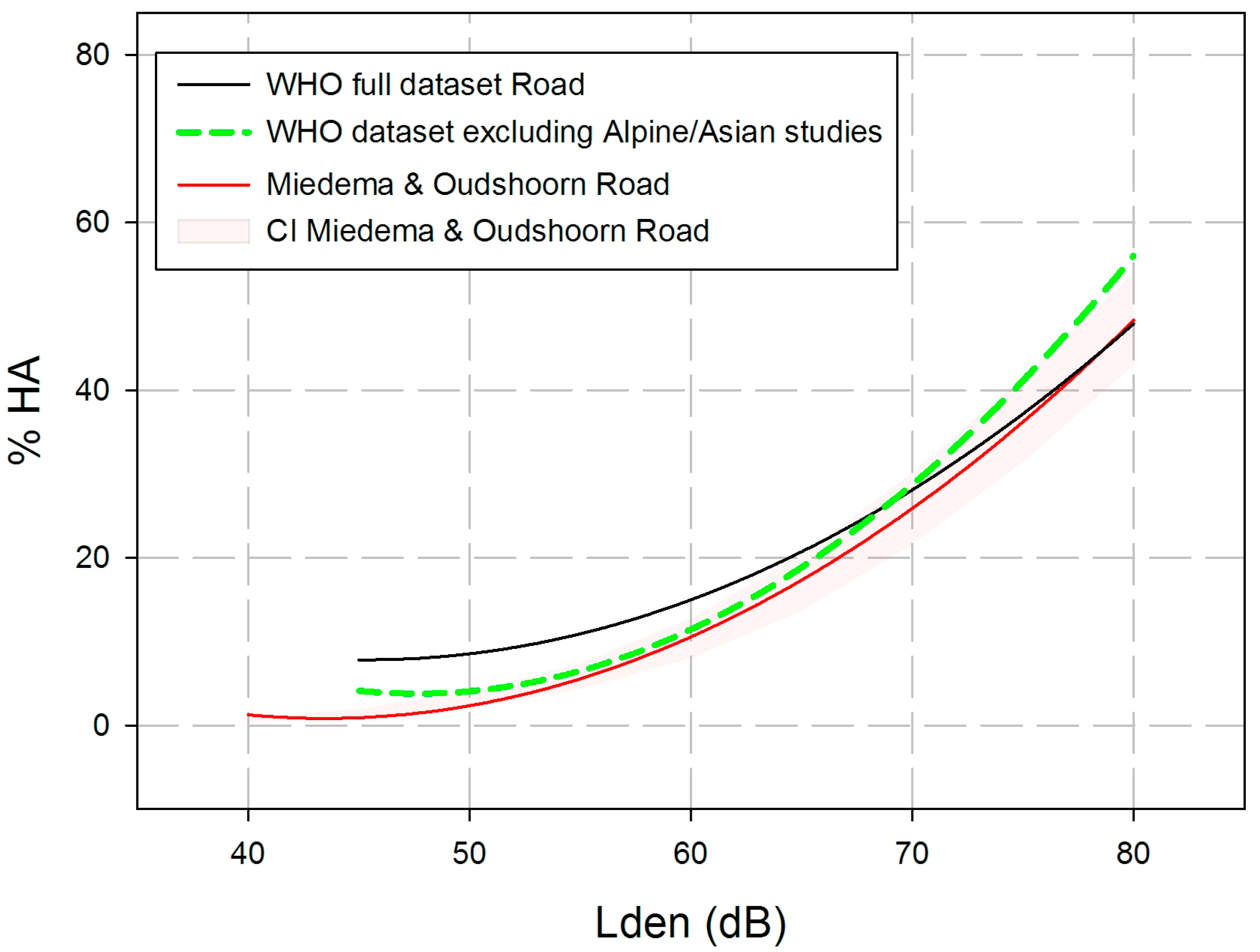
3.2. Road Traffic Noise Effects on Annoyance
- (1)
- Some of the Asian studies show a restricted range of road traffic noise levels. We tested the hypothesis that a restricted level range will decrease correlations between noise levels and annoyance raw scores, but could not find a statistically significant difference between “high-range” and “low-range” level studies.
- (2)
- The full data set includes five studies from Alpine valleys in Austria. With respect to acoustics, valleys are different from flat areas due to the so-called amphitheater effect, i.e., the propagation of sound to the valley slopes, including back-and-forth reflections of sounds produced in the valley. In the past, it has been shown that annoyance responses are usually higher in Alpine areas than in non-Alpine areas at similar levels of LAeq [38]. In addition, three of the five Alpine studies used ≥60% of the scale as a criterion for being highly annoyed (see Table 3), and some of the Alpine research sites are subject to long lasting discussions about heavy transalpine road and rail traffic due to the European integration. Especially with respect to road traffic, a large increase of goods traffic has been reported [38]. All of these factors may have contributed to increased annoyance at comparable exposure levels.
- (3)
- The full data set includes the large Hong Kong study as well as nine additional studies from Asia, where many participants are living in air conditioned homes. This co-determinant factor may have contributed to a lower degree of annoyance, compared to the other studies included.
3.2.1. Road Traffic Noise Effects (1): ERRs
Data Analysis for ERRs
Grading the Quality of Evidence for the ERR of %HA by Road Traffic Noise in the Full WHO Dataset
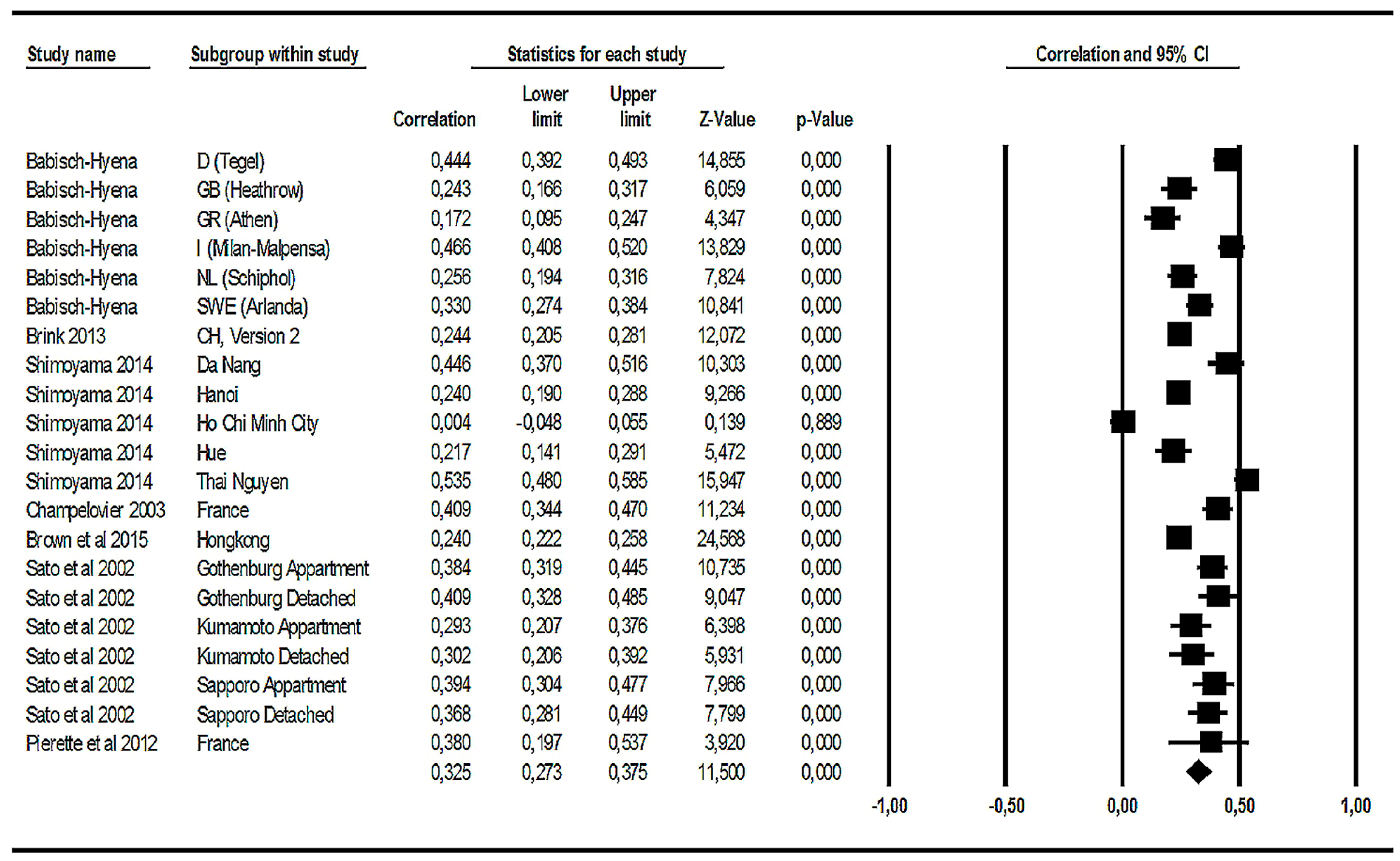
3.2.2. Road Traffic Noise Effects (2): Correlations between Noise Levels and Annoyance Raw Scores
Meta-Analysis in the Dataset
Grading the Evidence Based on Correlations between Road Traffic Noise Levels and Annoyance Raw Scores
3.2.3. Road Traffic Noise Effects (3): ORs Referring to the %HA Increase per 10 dB Level Increase
Meta-Analysis Based on Observed Data
Meta-Analysis Based on Modelled Data
Grading the Evidence of ORs Representing the %HA-Increase per 10 dB Level Increase of Road Traffic Noise
The Influence of Co-Determinants in Road Traffic Noise Studies
3.2.4. Summary of the Analyses Related to Road Traffic Noise Effects on Annoyance
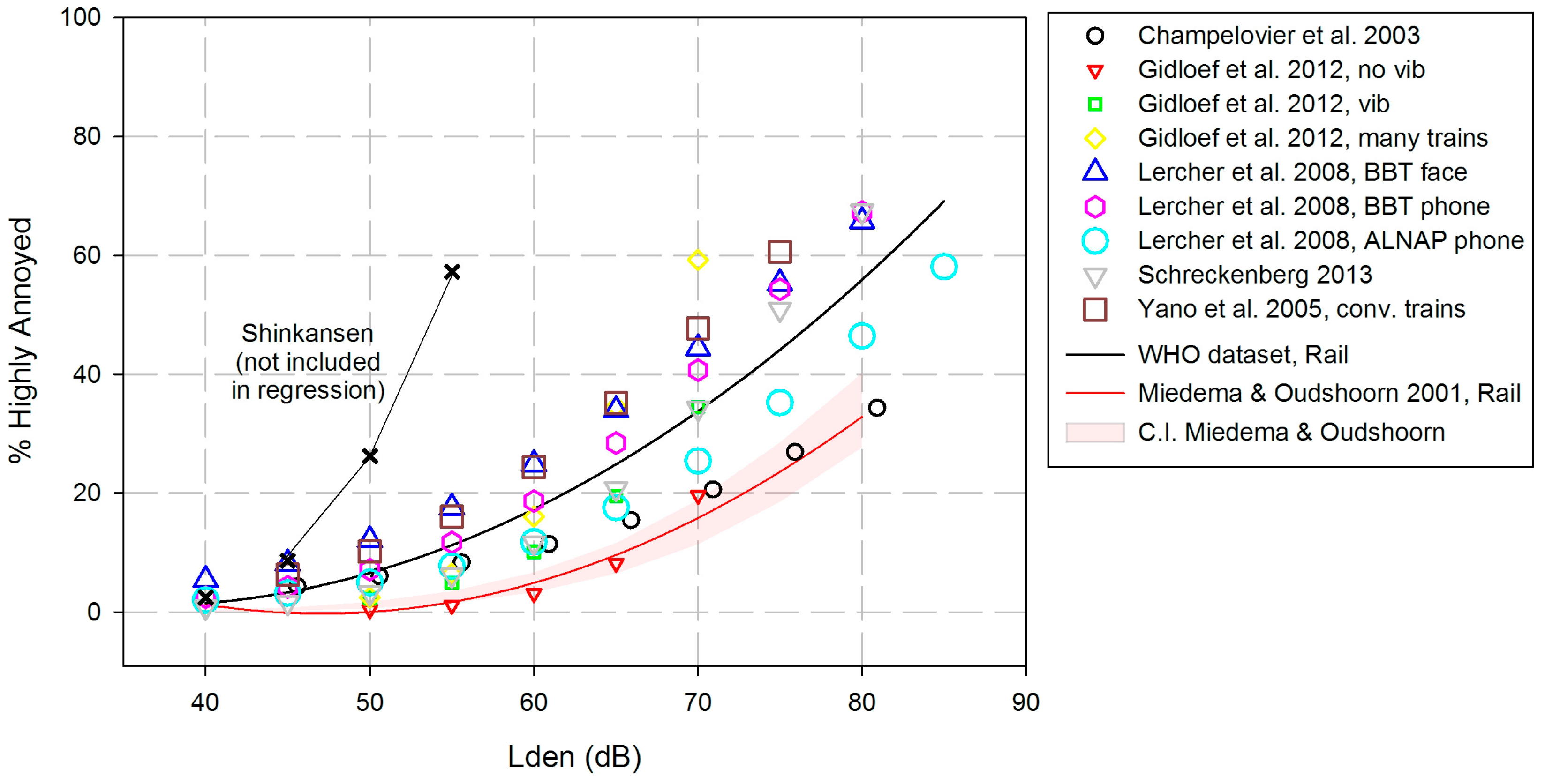
3.3. Railway Noise Effects on Annoyance
3.3.1. Railway Noise Effects (1): ERRs
Data Analysis
- (1)
- The number of studies is rather small in both data sets—each includes nine studies; the older ones contain two tramway studies, the newer ones only long-distance lines in a variety of situations (see next paragraph).
- (2)
- The reasons presented in Section 3.2 relating to the exclusion of the Alpine and Asian studies from a common road traffic noise exposure-response curve should be applied here, too: four of the nine rail studies took place in valleys and are subject to an “amphitheater effect”, and the Japanese study includes respondents mostly living in air-conditioned houses. (In this case, it should be mentioned that Japanese houses often are built close to the railway tracks, and are prone to vibrations). In addition, the four studies performed in valleys underwent long-lasting public discussion about the possible effects of railway noise. However, excluding five of nine studies from the full set of eleven studies would not allow for providing any exposure-response curve at all. Therefore, we refrained from additional exposure-response analyses in subsets of data.
- (3)
- The definition of HA differs between the two datasets: While the EU standard curves use a cut-off at 72% of the response scale, five of the present studies define HA by the upper two scale points of the 5-point scale, i.e., HA: ≥60% of the response scale.
Grading the Quality of Evidence for the ERR of %HA by Railway Traffic Noise
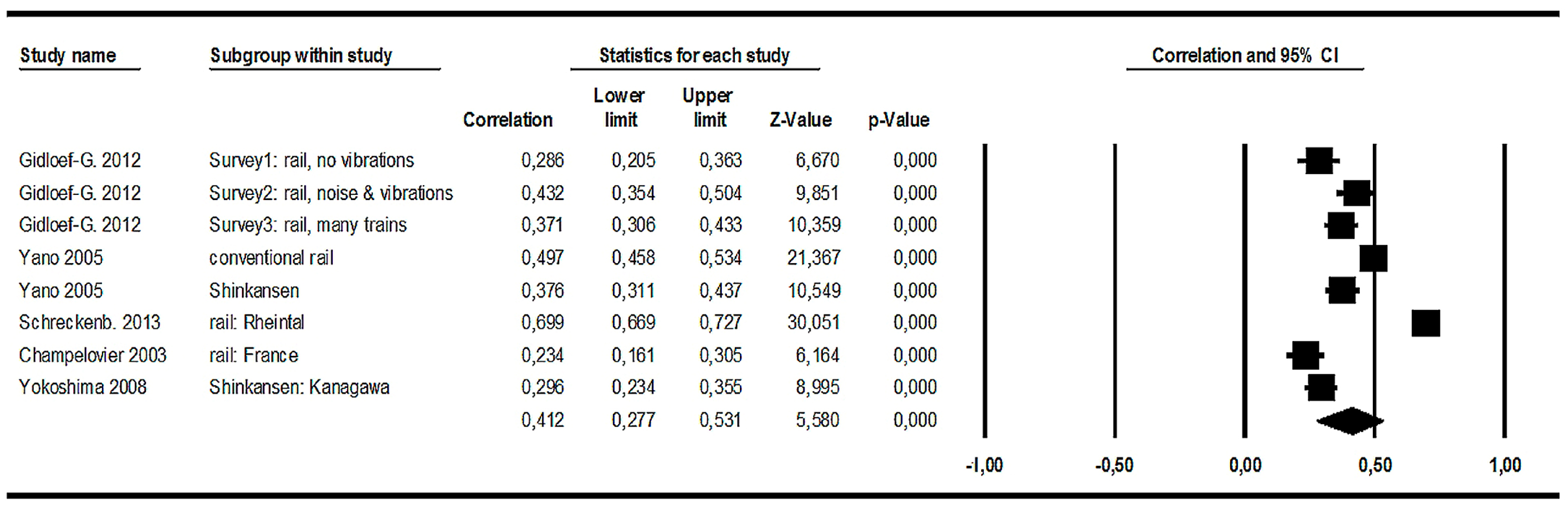
3.3.2. Railway Noise Effects (2): Correlations between Noise Levels and Annoyance Raw Scores
Meta-Analysis in the Full Dataset
Grading the Evidence Based on Railway Noise Correlations between Noise Levels and Annoyance Raw Scores
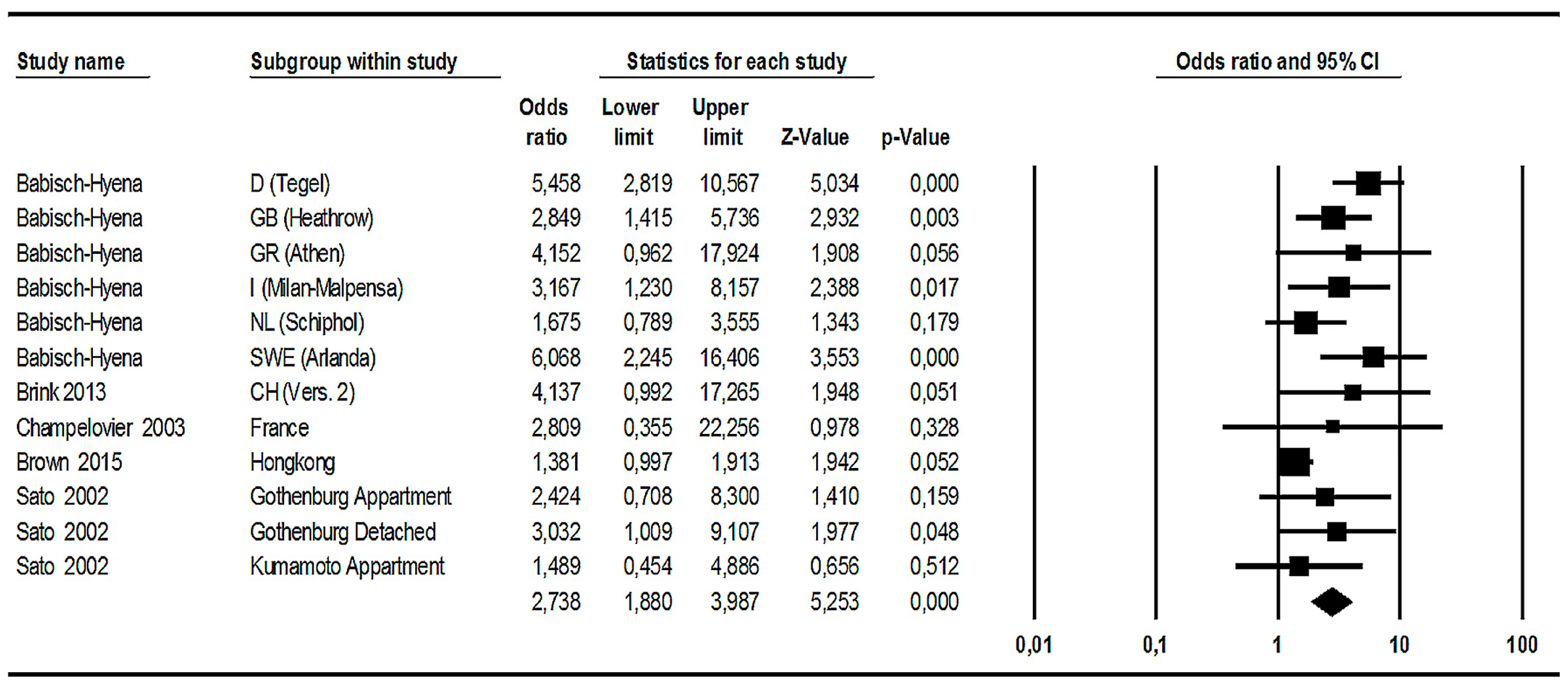
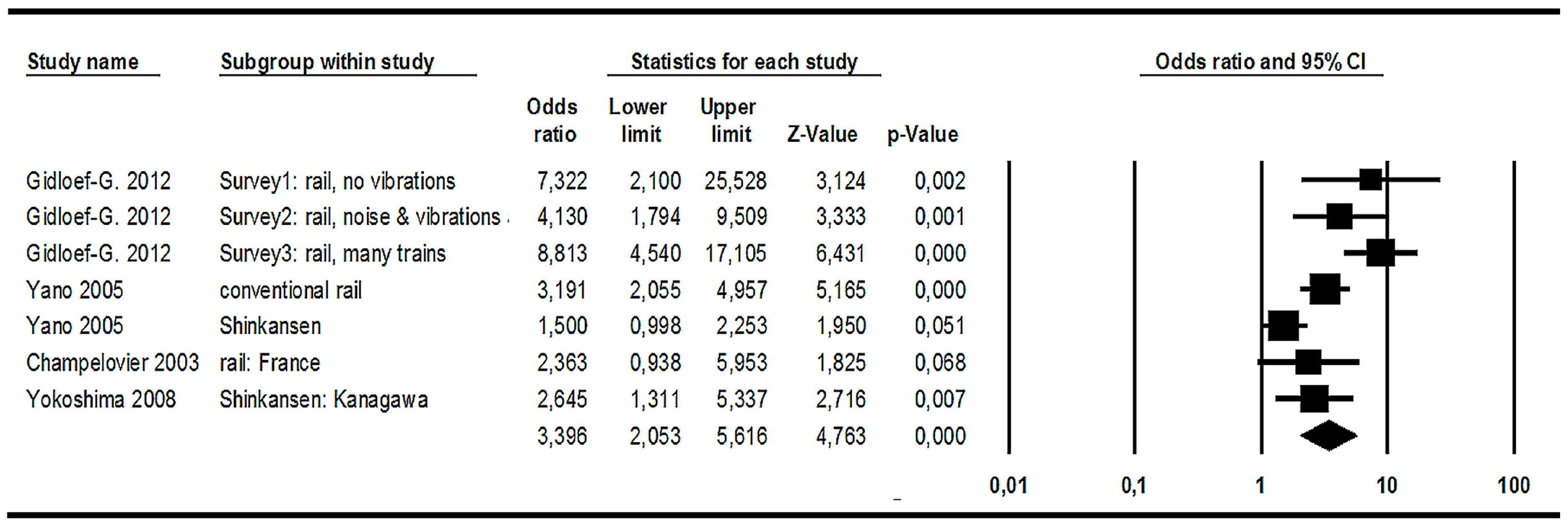
3.3.3. Railway Noise Effects (3): ORs Referring to the Increase of %HA per 10 dB Level Increase
Meta-Analysis Based on Observed Data
Meta-Analysis of Railway Noise ORs, Based on Modelled Data
Grading the Evidence of ORs Representing the %HA Increase per 10 dB Level Increase of Railway Noise
3.3.4. The Influence of Co-Determinants in Railway Noise Annoyance Studies
3.3.5. Summary of the Analyses Related to Railway Noise Effects on Annoyance
3.4. Wind Turbine Noise Effects on Annoyance
3.5. Combined Noise Effects
3.6. Effects of Noise from Stationary Sources
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guski, R.; Felscher-Suhr, U.; Schuemer, R. The concept of noise annoyance: How international experts see it. J. Sound Vib. 1999, 223, 513–527. [Google Scholar] [CrossRef]
- World Health Organization. Burden of Disease from Environmental Noise. Quantification of Healthy Life Years Lost in Europe; WHO: Bonn, Germany, 2011. [Google Scholar]
- Miedema, H.M.E.; Vos, H. Exposure-response relationships for transportation noise. J. Acoust. Soc. Am. 1998, 104, 3432–3445. [Google Scholar] [CrossRef] [PubMed]
- Miedema, H.M.E.; Oudshoorn, C.G. Annoyance from transportation noise: Relationships with exposure Metrics DNL and DENL and their confidence intervals. Environ. Health Perspect. 2001, 109, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Janssen, S.A.; Vos, H.; Van Kempen, E.E.M.M.; Breugelmans, O.R.P.; Miedema, H.M.E. Trends in annoyance by aircraft noise. In Proceedings of the International Congress on Noise as a Public Health Problem, Foxwoods, CT, USA, 21–25 July 2008. [Google Scholar]
- Heroux, M.-E.; Babisch, W.; Belojevic, G.; Brink, M.; Janssen, S.; Lercher, P.; Paviotti, M.; Pershagen, G.; Persson-Waye, K.; Preis, A.; et al. WHO Environmental Noise Guidelines for the European Region—What Is New? 1. Policy Context and Methodology Used for Guideline Development. Paper Presented at the Inter-Noise 2016, Hamburg, Germany, 21–24 August 2016. (Unpublished). [Google Scholar]
- Stallen, P.J. A theoretical framework for environmental noise annoyance. Noise Health 1999, 1, 69–80. [Google Scholar] [PubMed]
- Fields, J.M.; De Jong, R.G.; Gjestland, T.; Flindell, I.H.; Job, R.F.S.; Kurra, S.; Lercher, P.V.M.; Yano, T.; Guski, R.; Felscher-Suhr, U.; et al. Standardized noise reaction questions for community noise surveys: Research and a recommendation. J. Sound Vib. 2001, 242, 641–679. [Google Scholar] [CrossRef]
- International Standards Organization. ISO TS 15666: Acoustics—Assessment of Noise Annoyance by Means of Social and Socio-Acoustic Surveys; ISO: Geneva, Switzerland, 2003. [Google Scholar]
- Schultz, T.J. Synthesis of social surveys on noise annoyance. J. Acoust. Soc. Am. 1978, 64, 377–405. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.A.; Van Kamp, I. WHO Environmental Noise Guidelines for the European Region. A systematic review of transport noise interventions and their impacts on health. Int. J. Environ. Res. Public Health 2017, 14, 873. [Google Scholar] [CrossRef] [PubMed]
- Fields, J.M.; De Jong, R.G.; Brown, A.L.; Flindell, I.H.; Gjestland, T.; Job, R.F.S.; Kurra, S.; Lercher, P.; Schuemer-Kohrs, A.; Vallet, M.; et al. Guidelines for reporting core information from community noise reaction surveys. J. Sound Vib. 1997, 206, 685–695. [Google Scholar] [CrossRef]
- Borenstein, M.; Hedges, L.; Higgins, J.; Rothstein, H. CMA—Comprehensive Meta-Analysis V3—Manual, 2015. Available online: http://www.meta-analysis.com/index.php (accessed on 28 November 2017).
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Group, T.P. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef]
- Babisch, W. Updated exposure-response relationship between road traffic noise and coronary heart diseases: A meta-analysis. Noise Health 2014, 16, 1–9. [Google Scholar] [PubMed]
- MVA Consultancy. ANASE: Attitudes to Noise from Aviation Sources in England. In Final Report; Queen’s Printer and Controller of HMSO: Woking/Norwich, UK, 2007. [Google Scholar]
- Vienneau, D.; Schindler, C.; Perez, L.; Probst-Hensch, N.; Röösli, M. The relationship between transportation noise exposure and ischemic heart disease: A meta-analysis. Environ. Res. 2015, 138, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Finegold, L.S.; Harris, C.S.; von Gierke, H.E. Community annoyance and sleep disturbance: Updated criteria for assessing the impacts of general transportation noise on people. Noise Control Eng. J. 1994, 42, 25–30. [Google Scholar] [CrossRef]
- Van Gerven, P.W.M.; Vos, H.; Van Boxtel, M.; Janssen, S.; Miedema, H. Annoyance from environmental noise across the lifespan. J. Acoust. Soc. Am. 2009, 126, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Janssen, S.A.; Vos, H. A Comparison of Recent Surveys to Aircraft Noise Exposure-Response Relationships. In TNO Report; The Netherlands Organisation for Applied Scientific Research: The Hague, The Netherlands, 2009; 14p. [Google Scholar]
- Guyatt, G.H.; Oxman, A.D.; Vist, G.E.; Kunz, R.; Falck-Ytter, Y.; Alonso-Coello, P.; Schünemann, H.J. GRADE: An emerging consensus on rating quality of evidence and strength of recommendations. BMJ 2008, 336, 924. [Google Scholar] [CrossRef] [PubMed]
- Guyatt, G.H.; Oxman, A.D.; Kunz, R.; Vist, G.E.; Falck-Ytter, Y.; Schünemann, H.J. What is “quality of evidence” and why is it important to clinicians? BMJ 2008, 336, 995–998. [Google Scholar] [CrossRef] [PubMed]
- Janssen, S.A.; Guski, R. Aircraft noise annoyance. In Evidence Review on Aircraft Noise and Health; Stansfeld, S.A., Berglund, B., Kephalopoulos, S., Paviotti, M., Eds.; Bonn (D) Directorate General Joint Research Center and Directorate General for Environment, European Union: Brussels, Belgium, 2017; in press. [Google Scholar]
- Gjestland, T.; Gelderblom, F.B.; Fidell, S.A.; Berry, B. Temporal trends in aircraft noise annoyance. Paper Presented at the Inter-Noise 2015, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Schreckenberg, D.; Faulbaum, F.; Guski, R.; Ninke, L.; Peschel, C.; Spilski, J.; Wothge, J. Wirkungen von Verkehrslärm auf die Belästigung und Lebensqualität. In NORAH (Noise Related Annoyance Cognition and Health): Verkehrslärmwirkungen im Flughafenumfeld; Umwelthaus gGmbH: Kelsterbach, Germany, 2015; Available online: http://www.norah-studie.de (accessed on 29 November 2017).
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.T.; Rothstein, H. Introduction to Meta-Analysis; Wiley: Chichester, UK, 2009. [Google Scholar]
- Job, R.F.S. Community response to noise: A review of factors influencing the relationship between noise exposure and reaction. J. Acoust. Soc. Am. 1988, 83, 991–1001. [Google Scholar] [CrossRef]
- Berglund, B.; Lindvall, T.; Schwela, D.H. (Eds.) Guidelines for Community Noise; World Health Organization (WHO): Geneva, Switzerland, 1999. [Google Scholar]
- Huss, A.; Spoerri, A.; Egger, M.; Röösli, M. for-the-Swiss-National-Cohort-Study-Group. Aircraft Noise, Air Pollution, and Mortality from Myocardial Infarction. Epidemiology 2010, 21, 829–836. [Google Scholar] [CrossRef] [PubMed]
- Fleiss, J.L.; Berlin, J.A. Effect Sizes for Dichotomous Data. In The Handbook of Research Synthesis and Meta-Analysis, 2nd ed.; Cooper, H., Hedges, L.V., Valentine, J.C., Eds.; Russell Sage Foundation: New York, NY, USA, 2009; pp. 237–253. [Google Scholar]
- Sweeting, M.J.; Sutton, A.J.; Lambert, P.C. What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Stat. Med. 2004, 23, 1351–1375. [Google Scholar] [CrossRef] [PubMed]
- Miedema, H.M.E.; Vos, H. Demographic and attitudinal factors that modify annoyance from transportation noise. J. Acoust. Soc. Am. 1999, 105, 3336–3344. [Google Scholar] [CrossRef]
- Guski, R. Personal and social variables as co-determinants of noise annoyance. Noise Health 1999, 1, 45–56. [Google Scholar] [PubMed]
- Flindell, I.H.; Stallen, P.J. Non-acoustical factors in environmental noise. Noise Health 1999, 3, 11–16. [Google Scholar]
- Vos, J. On the Relevance of Nonacoustic Factors Influencing the Annoyance Caused by Environmental Sounds—A Literature Study. Paper Presented at the Inter-Noise 2010, Lisbon, Portugal, 13–16 June 2010. [Google Scholar]
- Van Kempen, E.; Van Kamp, I. Annoyance from Air Traffic Noise. Possible Trends in Exposure-Response relationships. In RIVM Report 01/2005; RIVM: Bilthoven, The Netherlands, 2005. [Google Scholar]
- Janssen, S.A.; Vos, H.; Van Kempen, E.; Breugelmans, O.; Miedema, H.M.E. Trends in aircraft noise annoyance: The role of study and sample characteristics. J. Acoust. Soc. Am. 2011, 129, 1953–1962. [Google Scholar] [CrossRef] [PubMed]
- Lercher, P.; de Greve, B.; Botteldooren, D.; Rüdisser, J. A comparison of regional noise-annoyance-curves in alpine areas with the European standard curves. In Proceedings of the 9th International Conference on Noise as a Public Health Problem (ICBEN 2008), Foxwoods, CT, USA, 21–25 July 2008. [Google Scholar]
- Brink, M. Conversion of transportation noise exposure metrics Leq24h, LDay, LEvening, Ldn, and Lden to LNight. In Working Paper; Federal Office for the Environment: Bern, Switzerland, 2015. [Google Scholar]
- Schmidt, F.L.; Hunter, J.E. Methods of Meta-Analysis. Correcting Error and Bias in Research Findings, 3rd ed.; Sage: Los Angeles, CA, USA, 2015. [Google Scholar]
- Janssen, S.A.; Vos, H.; Eisses, A.R.; Pedersen, E. A comparison between exposure-response relationships for wind turbine annoyance and annoyance due to other noise sources. J. Acoust. Soc. Am. 2011, 130, 3746–3753. [Google Scholar] [CrossRef] [PubMed]
- Kuwano, S.; Yano, T.; Kageyama, T.; Sueoka, S.; Tachibanae, H. Social survey on wind turbine noise in Japan. Noise Control Eng. J. 2014, 62, 503–520. [Google Scholar] [CrossRef]
- Miedema, H.M.E.; Vos, H. Noise annoyance from stationary sources: Relationships with exposure metric day evening night level (DENL) and their confidence intervals. J. Acoust. Soc. Am. 2004, 116, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Brink, M. Annoyance Assessment in Postal Surveys Using the 5-point and 11-point ICBEN Scales: Effects of Sale and Question Arrangement. In Proceedings of the 42nd International Congress and Exposition on Noise Control Engineering 2013 (INTER-NOISE 2013): Noise Control for Quality of Life, Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Brink, M.; Wunderli, J.-M. A field study of the exposure-annoyance relationship of military shooting noise. J. Acoust. Soc. Am. 2010, 127, 2301–2311. [Google Scholar] [CrossRef] [PubMed]
| Publication (See Supplementary Materials S3 for References) | Location | Year Data | Sample Type | Type of Survey | Sample Size (n) | Response Rate (RR) | Age/Age Range | Noise Level Descriptors | Noise Level Range | Annoyance Scale | Remarks | Study Quality Rating |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Babisch et al. 2009 | Amsterdam Schiphol, The Netherlands | 2003–2005 | Stratified. | face-to-face interview | 898 | 46% | 45–70 years | LAeq,24h | 36–72 * | ICBEN 11-p num. | New runway opened 2003 | 23 |
| Persons (living for at least 5 years near the airport) selected at random from registers | LAeq,16h | 38–74 | Annoyance during the day and during the night were assessed separately in the HYENA study. Only annoyance during the day is used here. | |||||||||
| Lden | 40–75 | |||||||||||
| Ldn | 39–77 | HA ≥ 73% | ||||||||||
| Babisch et al. 2009 | Athens Elephterios Venizelos, Greece | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interview | 635 | 56% | 45–70 years | LAeq,24h | 36–64 | ICBEN 11-p num. | Airport opened 2001 | 23 |
| LAeq,16h | 37–66 | Annoyance during the day. | ||||||||||
| Lden | 40–66 | |||||||||||
| Ldn | 39–64 | HA ≥ 73% | ||||||||||
| Babisch et al. 2009 | Berlin Tegel, Germany | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interview | 972 | “not less than 30% in Germany…” | 45–70 years | LAeq,24h | 30–73 | ICBEN 11-p num. | 23 | |
| LAeq,16h | 32–74 | Annoyance during the day. | ||||||||||
| Lden | 32–76 | |||||||||||
| Ldn | 31–74 | HA ≥ 73% | ||||||||||
| Babisch et al. 2009 | London Heathrow, UK | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interview | 600 | “not less than 30% in… the UK” | 45–70 years | LAeq,24h | 29–74 | ICBEN 11-p num. | 23 | |
| LAeq,16h | 31–76 | Annoyance during the day. | ||||||||||
| Lden | 34–78 | |||||||||||
| Ldn | 32–77 | HA ≥ 73% | ||||||||||
| Babisch et al. 2009 | Milano Malpensa, Italy | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interview | 753 | “not less than 30% in… Italy” | 45–70 years | LAeq,24h | 22–68 | ICBEN 11-p num. | Airport expanded 1998. Long lasting public discussion about expansion | 23 |
| LAeq,16h | 24–70 | Annoyance during the day. | ||||||||||
| Lden | 22–70 | |||||||||||
| Ldn | 22–68 | HA ≥ 73% | ||||||||||
| Babisch et al. 2009 | Stockholm Arlanda + Brömma, Sweden | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interview | 1003 | 78% | 45–70 years | LAeq,24h | 11–64 | ICBEN 11-p num. | New runway 2003 | 23 |
| LAeq,16h | 13–66 | Annoyance during the day. | ||||||||||
| Lden | 12–68 | |||||||||||
| Ldn | 11–67 | HA ≥ 73% | ||||||||||
| Bartels et al. 2013 | Cologne/Bonn, Germany | 2010 | Random within 3 exposure classes (40, 50, 55 Ldn) | Phone interview | 1262 | More than 4000 numbers dialed; 9.2% not valid; 34.1% persons interested to take part | 18–95 years | LAeq,24h | 40–55 | ICBEN 5-p verbal (general + night) | Night-time air traffic | 20 |
| CATI | LAeq,6–22h | 40–55 | ||||||||||
| LAeq,22–6h | 40–55 | HA ≥ 60% | ||||||||||
| Ldn | 46–61 | |||||||||||
| Breugelmans et al. 2004 | Amsterdam Schiphol, The Netherlands | 2002 | Stratified; | Written questionnaire; mailed | 5873 | 46.10% | Age: ≥18 years | Lden | 33–72 | ICBEN 11-p num. | New runway 2003 | 23 |
| Randomly selected within strata | ||||||||||||
| HA ≥ 73% | ||||||||||||
| Brink et al. 2008 | Zurich, Switzerland | 2001 | Random within 20 km from airport | Written questionnaire; mailed | 1816 | 54% | 18–98 years | LAeq,24h | 22–69 | ICBEN 11-p num. | Change of flights in October 2001. Only data before change are used here | 23 |
| LAeq,16h | 35–70 | |||||||||||
| Lden | 35–70 | HA ≥ 73% | ||||||||||
| Ldn | 36–70 | |||||||||||
| Gelderblom et al. 2014 | Trondheim, Norway | 2014 | Random within 55 dB Ldn contour | phone | 300 | 16–92 | LAeq,24h | 36–65 | ICBEN 11-p num. | Only Trondheim (civil airport) is used here | 21 | |
| LAeq,16h | 37–66 | |||||||||||
| Lden | 40–68 | HA ≥ 73% | ||||||||||
| Ldn | 39–68 | |||||||||||
| Nguyen et al. 2011 | Ho Chi Minh Tan Son Nhat, Vietnam | 2008 | 8 sites under flight path + 2 control sites. | Face-to-face | 880 | 87% | Age: >18 years | LAeq,24h | 49–66 | ICBEN 5-p verbal + 11-p num. | Only data for aircraft noise are used here. | 16 |
| Convenience sample; selection with regard to age (>18 years) and gender | Lday | 50–67 | ||||||||||
| Lden | 53–71 | HA ≥ 73% | ||||||||||
| Ldn | 53–70 | (for the 11p scale) | ||||||||||
| Nguyen et al. 2011 | Hanoi Noi Bai, Vietnam | 2009 | 7 sites under flight path + 2 control sites. | Face-to-face | 824 | 84% | Age: >18 years | LAeq,24h | 44–57 | ICBEN 5-p verbal + 11-p num. | Only data for aircraft noise are used here. | 16 |
| Convenience sample (see above) | Lday | 46–58 | ||||||||||
| Lden | 48–61 | HA ≥ 73% | ||||||||||
| Ldn | 48–61 | |||||||||||
| Nguyen et al. 2012 | Da Nang, Vietnam | 2011 | 6 sites around the airport | Face-to-face | 528 | 84% | LAeq,24h | 49–60 | ICBEN 5-p verbal + 11-p num. | 17 | ||
| Lday | 51–62 | HA ≥ 73% | ||||||||||
| Lden | 52–64 | |||||||||||
| Ldn | 51–63 | |||||||||||
| Sato & Yano 2011 | Sapporo Okadama, Japan | 2008 | 5 sites around the airport. | Postal | 291 | 76% | Age: >18 years | LAeq,24h | 28–40 | ICBEN 5-p verbal + 11-p num. | Only data for airplane noise are used | 16 |
| Respondents (age >18 years) selected on a one-person-per-family basis. | Lden | 28–40 | ||||||||||
| Ldn | 28–40 | HA ≥ 73% (for the 11p-scale) | ||||||||||
| Schreckenberg + Meis 2007 | Frankfurt/M, Germany | 2005 | Stratified; random | Face-to-face | 2312 | 61% | Age: 17–93 years; (M = 52.7; s = 18.4) | LAeq,24h | 40–62 | ICBEN 5-p verbal + 11-p num. | Long lasting public discussion about airport expansion. New runway opened 2011 | 24 |
| LAeq,16h | 41–63 | |||||||||||
| Lden | 43–66 | HA ≥ 73% (for the 11 p-scale) | ||||||||||
| Ldn | 42–65 |
| Study | Subgroup | Midpoints of the Two Exposure Classes | HA Rate in the Upper dB Class | Number of Respondents in the Upper dB Class | HA Rate in the Lower dB Class | Number of Respondents in the Lower dB Class |
|---|---|---|---|---|---|---|
| Babisch-Hyena | GB (Heathrow) | 63 vs. 53 | 0.424 | 170 | 0.300 | 70 |
| Babisch-Hyena | D (Tegel) | 63 vs. 53 | 0.398 | 171 | 0.287 | 94 |
| Babisch-Hyena | NL (Schiphol) | 63 vs. 53 | 0.259 | 286 | 0.068 | 191 |
| Babisch-Hyena | SWE (Arlanda) | 63 vs 53 | 0.271 | 48 | 0.145 | 55 |
| Babisch-Hyena | GR (Athens) | 63 vs. 53 | 0.690 | 58 | 0.530 | 151 |
| Babisch-Hyena | I (Milan Malpensa) | 63 vs. 53 | 0.703 | 101 | 0.427 | 103 |
| Brink 2008 | Zurich before 2001 | 60 vs. 50 | 0.327 | 199 | 0.074 | 457 |
| Schreckenberg & Meis 2007 | Fraport | 60 vs. 50 | 0.413 | 611 | 0.139 | 603 |
| Nguyen 2011 | Hanoi | 60 vs. 50 | 0.395 | 190 | 0.085 | 259 |
| Nguyen 2012 | Da Nang | 60 vs. 50 | 0.163 | 257 | 0.030 | 67 |
| Gelderblom 2015 * | Trondheim | 60 vs. 50 | 0.038 | 52 | 0 | 76 |
| Publication (See Supplementary Materials S3 for References) | Location | Year Data | Sample Type | Type of Survey | Sample Size (n) | Response Rate (RR) | Age/Age Range | Noise Level Descriptors | Noise Level Range | Annoyance Scale | Remarks | Study Quality Rating |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Babisch et al. 2009 | Amsterdam Schiphol, The Netherlands | 2003–2005 | Stratified. Persons (living for at least 5 years near the airport) selected at random from registers. | face-to-face interviews | 898 | 46% | 45–70 years | LAeq,24h | 36–74 * | ICBEN 11-p numeric. Annoyance during the day and during the night were assessed separately in the HYENA study. Used here: only the annoyance during the day. HA ≥ 73%. | 23 | |
| LAeq,16h | 37–75 | |||||||||||
| Lden | 39–77 | |||||||||||
| Ldn | 39–77 | |||||||||||
| Babisch et al. 2009 | Athens Elephterios Venizelos, Greece | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interviews | 635 | 56% | 45–70 years | LAeq,24h | 10–69 * | ICBEN 11-p numeric. Annoyance during the day. HA ≥ 73% | 23 | |
| LAeq,16h | 10–70 | |||||||||||
| Lden | 16–72 | |||||||||||
| Ldn | 16–71 | |||||||||||
| Babisch et al. 2009 | Berlin Tegel, Germany | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interviews | 972 | “not less than 30% in Germany …” | 45–70 years | LAeq,24h | 45–73 * | ICBEN 11-p numeric. Annoyance during the day. HA ≥ 73% | 23 | |
| LAeq,16h | 46–74 | |||||||||||
| Lden | 45–77 | |||||||||||
| Ldn | 46–76 | |||||||||||
| Babisch et al. 2009 | London Heathrow, UK | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interviews | 600 | “not less than 30% in … the UK” | 45–70 years | LAeq,24h | 40–75 * | ICBEN 11-p numeric. Annoyance during the day. HA ≥ 73% | 23 | |
| LAeq,16h | 41–76 | |||||||||||
| Lden | 42–77 | |||||||||||
| Ldn | 42–76 | |||||||||||
| Babisch et al. 2009 | Milano Malpensa, Italy | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interviews | 753 | “not less than 30% in … Italy” | 45–70 years | LAeq,24h | 25–77 * | ICBEN 11-p numeric. Annoyance during the day. HA ≥ 73% | 23 | |
| LAeq,16h | 26–78 | |||||||||||
| Lden | 25–79 | |||||||||||
| Ldn | 22–78 | |||||||||||
| Babisch et al. 2009 | Stockholm Arlanda + Brömma, Sweden | 2003–2005 | Stratified; random (see the first entry above) | face-to-face interviews | 1003 | 78% | 45–70 years | LAeq,24h | 25–71 * | ICBEN 11-p numeric. Annoyance during the day. HA ≥ 73% | 23 | |
| LAeq,16h | 26–72 | |||||||||||
| Lden | 28–74 | |||||||||||
| Ldn | 27–73 | |||||||||||
| Brink 2013 | German speaking Switzerland | 2012–2013 | Stratified; random | Written questionnaire, mailed | 2386 | LAeq,24h | 42–75 | ICBEN 5-p & 11-p | Data pooled from two different waves of the same survey. The results from one wave were not part of the Brink 2013 paper. | 20 | ||
| LAeq,16h | 44–77 | |||||||||||
| Ldn | 44–78 | |||||||||||
| HA ≥ 73% (for the 11p scale) | ||||||||||||
| Brown et al. 2015 | Hong Kong, China | 2009–2010 | Random | Face-to-face Interviews conducted by the Census department; routine thematic household survey | 10,077 | 76% | Age: ≥18 years | Lden | 30–80 (Most analyses used only the range of 42 to 77 dB) | ICBEN 11-p numeric | High road traffic intensity. | 22 |
| HA ≥ 73% | ||||||||||||
| Champelovier et al. 2003 | France 61 sites all over France | 1997–1998 | Convenience sample | Face-to-face interviews | 701 in total; a subsample with n = 673 used here | Age: ≥18 years | LAeq,24h | 41–78 | 4-p verbal scale (inside) & 11p scale. | Only road data used | 19 | |
| LAeq,16h | 42–80 | |||||||||||
| Lden | 43–81 | HA ≥ 73% (for 11p) | ||||||||||
| Ldn | 42–81 | |||||||||||
| Heimann/Lercher 2007; Lercher et al. 2008 | Inn valley, Austria | 2006 | Stratified random sampling; (Strata = distance to source) | Computer-assisted telephone interviewing | 1641 | 35% | 25–75 years | Lden | ICBEN 5-p verbal | Alpine areas, Main road. The Inn valley is part of a route for heavy goods traffic over the Brenner. Long lasting public discussion about road traffic noise. | 22 | |
| HA ≥ 60% | ||||||||||||
| Heimann/Lercher 2007; Lercher et al. 2008 | Inn valley, Austria | 2006 | Stratified random sampling; (Strata = distance to source) | Computer-assisted telephone interviewing | 1641 | 35% | 25–75 years | Lden | ICBEN 5-p verbal | Alpine areas, Highway. The Inn valley is part of a route for heavy goods traffic over the Brenner. Long lasting public discussion about road traffic noise. | 22 | |
| HA ≥ 60% | ||||||||||||
| Pierrette et al. 2012 | Near Lyon, France | ? | Residents living near an industrial site and surrounded by two roads | Face-to-face interviews | 99 | Mean age: 45.9 years (s = 17.9) | Lden | 43–70 | ICBEN 5-p & 11-p | Only road data used. | 20 | |
| Med.Univ. Innsbruck/Lercher 2008 | Wipp valley, Austria | 2004 | Stratified (distance) | Face to face | 1991 | 80% | 17–85 years | Lden | ICBEN 11-p numeric | Alpine areas, Main road The Wipp valley is part of a route for heavy goods traffic over the Brenner. Long lasting public discussion about road traffic noise. | 22 | |
| HA ≥ 73% | ||||||||||||
| Med.Univ. Innsbruck Lercher/2008 | Wipp valley, Austria | 2004 | Stratified (distance) | Face to face interviews | 1762 | 80% | 17–85 years | Lden | ICBEN 11-p numeric | Alpine areas; Highway The Wipp valley is part of a route for heavy goods traffic over the Brenner. Long lasting public discussion about road traffic noise. | 22 | |
| HA ≥ 73% | ||||||||||||
| Med.Univ. Innsbruck Lercher/2008 | Wipp valley, Austria | 2004 | Stratified (distance) | Phone | 1327 | 62% | 17–85 years | Lden | ICBEN 5-p verbal | Alpine areas. Motorway + main road (others below 40 dB(A)) The Wipp valley is part of a route for heavy goods traffic over the Brenner. Long lasting public discussion about road traffic noise. | 22 | |
| HA ≥ 60% | ||||||||||||
| Sato et al. 2002 | Gothenburg, Sweden, detached | 1996 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; by mail | 436 | 73.3% | 18–75 years | LAeq,24h | 46.2–73.6 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 50.1–76.9 | HA ≥ 75% | ||||||||||
| Sato et al. 2002 | Gothenburg, Sweden, Apartments | 1996 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; by mail | 706 | 66.4% | 18–75 years | LAeq,24h | 48.5–82.3 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 51.8–86.2 | |||||||||||
| HA ≥ 75%’ | ||||||||||||
| Sato et al. 2002 | Kumamoto, Japan, detached | 1996 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; distribute-collect method | 378 | 76.1% | 20–75 years | LAeq,24h | 49.3–73.7 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 52.4–76.8 | |||||||||||
| HA ≥ 75% | ||||||||||||
| Sato et al. 2002 | Kumamoto, Japan, Apartments | 1996 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; distribute-collect method | 458 | 64.6% | 20–75 years | LAeq,24h | 51.3–73.5 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 54.4–78.7 | |||||||||||
| HA ≥ 75% | ||||||||||||
| Sato et al. 2002 | Sapporo, Japan, detached | 1997–1998 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; distribute-collect method | 411 | 63.5% | 20–75 years | LAeq,24h | 53.3–73.6 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 57.5–77.5 | |||||||||||
| HA ≥ 75% | ||||||||||||
| Sato et al. 2002 | Sapporo, Japan, Apartment | 1997–1998 | 11–15 residential areas. Respondents randomly selected on a one person-per-family basis | Written questionnaire; distribute-collect method | 369 | 52.0% | 20–75 years | LAeq,24h | 52.1–70.7 | 4-p verbal scale plus “notice filter” | 14 | |
| Ldn | 56.3–75.8 | |||||||||||
| HA ≥ 75% | ||||||||||||
| Shimoyama et al. 2014 ** | Hanoi, Vietnam | 2005 | 8 sites. One Member from each household in the selected sites. | Face-to-face. | 1503 | 50% | Age: >18 years (Most of the respondents were in their 20s) | LAeq,24h | 64.5–76.5 | ICBEN 5-p & 11-p | Motorbikes are the most dominant traffic constituent. | 11 |
| HA ≥ 73% (for the 11p scale) | ||||||||||||
| Lden | 69.5–81.2 | |||||||||||
| Shimoyama et al. 2014 ** | Ho Chi Minh City, Vietnam | 2007 | 8 sites. One Member from each household in the selected sites. | Face-to-face | 1471 | 61% | Age: >18 years | LAeq,24h | 70.3–78.5 | ICBEN 5-p & 11-p | Motorbikes are the most dominant traffic constituent | 11 |
| Lden | 74.9–83.1 | |||||||||||
| HA ≥ 73% | ||||||||||||
| Shimoyama et al. 2014 ** | Da Nang, Vietnam | 2011 | 6 sites. | Face-to-face | 492 | 82% | Age: >18 years | LAeq,24h | 63.3–72.1 | ICBEN 5-p & 11-p | 11 | |
| Lden | 66.4–75.8 | HA ≥ 73% | ||||||||||
| Shimoyama et al. 2014 ** | Hue, Vietnam | 2012 | 7 sites | Face-to-face | 688 | 98% | Age: >18 years | LAeq,24h | 58.0–75.6 | ICBEN 5-p & 11-p | 11 | |
| Lden | 60.9–79.6 | HA ≥ 73% | ||||||||||
| Shimoyama et al. 2014 ** | Thai Nguyen, Vietnam | 2013 | 10 sites | Face-to-face | 813 | 81% | Age: >18 years | LAeq,24h | 57.8–73.7 | ICBEN 5-p & 11-p | 11 | |
| Lden | 60.9–77.9 | HA ≥ 73% |
| Study (See Supplementary Materials S3 for References) | Subgroup | Midpoints of the Two Exposure Classes | Exposure Descriptor | HA Rate in the Upper dB Class | Number of Respondents in the Upper dB Class | HA Rate in the Lower dB Class | Number of Respondents in the Lower dB Class |
|---|---|---|---|---|---|---|---|
| Babisch-Hyena | D (Tegel) | 60 vs. 50 | Lden | 0.288 | 156 | 0.069 | 189 |
| Babisch-Hyena | GB (Heathrow) | 60 vs. 50 | Lden | 0.224 | 98 | 0.092 | 174 |
| Babisch-Hyena | GR (Athens) | 60 vs. 50 | Lden | 0.154 | 26 | 0.042 | 95 |
| Babisch-Hyena | I (Milano Malpensa) | 60 vs. 50 | Lden | 0.209 | 115 | 0.077 | 78 |
| Babisch-Hyena | NL (Schiphol) | 60 vs. 50 | Lden | 0.115 | 139 | 0.072 | 195 |
| Babisch-Hyena | SWE (Arlanda) | 60 vs. 50 | Lden | 0.125 | 72 | 0.023 | 341 |
| Brink 2013 | CH, Vers. 2 | 60 vs. 50 | Ldn | 0.129 | 652 | 0.035 | 58 |
| Champelovier 2003 | France | 60 vs. 50 | Lden | 0.081 | 161 | 0.030 | 33 |
| Brown 2015 | Hong Kong | 60 vs. 50 | Lden | 0.060 | 3037 | 0.044 | 1089 |
| Sato 2002 | Gothenburg Apartment | 65 vs. 55 | Ldn | 0.134 | 217 | 0.060 | 50 |
| Sato 2002 | Gothenburg Detached | 65 vs. 55 | Ldn | 0.252 | 143 | 0.100 | 40 |
| Sato 2002 | Kumamoto Apartment | 65 vs. 55 | Ldn | 0.146 | 89 | 0.103 | 39 |
| Sato 2002 | Sapporo Detached | 70 vs. 60 | Ldn | 0.243 | 189 | 0.094 | 32 |
| Sato 2002 | Sapporo Apartment | 70 vs. 60 | Ldn | 0.332 | 187 | 0.030 | 33 |
| Sato 2002 | Kumamoto Detached | 70 vs. 60 | Ldn | 0.268 | 112 | 0.114 | 70 |
| Shimoyama 2014 | Hanoi | 80 vs. 70 | Lden | 0.523 | 704 | 0.290 | 31 |
| Shimoyama 2014 | Ho Chi Minh City | 80 vs. 70 | Lden | 0.406 | 1423 | 0 | |
| Shimoyama 2014 | Da Nang | 80 vs. 70 | Lden | 0 | 0.0402 | 199 | |
| Shimoyama 2014 | Hue | 70 vs. 60 | Lden | 0.0616 | 292 | 0.0213 | 47 |
| Shimoyama 2014 | Thai Nguyen | 80 vs. 60 | Lden | 0.4667 | 90 | 0.0154 | 65 |
| Publication (See Supplementary Materials S3 for References) | Location | Year Data | Sample Type | Type of Survey | Sample Size (n) | Response Rate (RR) | Age/Age Range | Noise Level Descriptors | Noise Level Range | Annoyance Scale | Remarks | Study Quality Rating |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Champelovier et al. 2003 | 61 sites all over France | 1997–1998 | Convenience sample | Face-to-face interviews | 701 in total; a subsample with n = 673 used here | Age: ≥18 years | LAeq,24h | 38–79 | 4-p verbal scale (inside) & 11p scale. | Only rail data used. Noise from TGV and from conventional trains | 19 | |
| LAeq,16h | 36–79 | HA ≥ 73% (for 11p) | ||||||||||
| Lden | 43–85 | |||||||||||
| Ldn | 43–84 | |||||||||||
| Gidlöf-Gunnarsson et al. 2012 | Area with 2 different study sites in Sweden | 2007–2008 | Stratified | Postal; questionnaire sent by mail | 521 | 53% (Total RR for the three Swedish studies) | Age: 18–75 years | LAeq,24h | 41–65 | ICBEN 5-p & 11-p | No vibrations. 124 trains/24 h (44 freight trains) | 20 |
| Lden | 48–72 | HA ≥ 60% | ||||||||||
| Gidlöf-Gunnarsson et al. 2012 | Area with 2 different study sites in Sweden | 2007–2008 | Stratified | Postal; questionnaire sent by mail | 459 | 53% (Total RR for the three Swedish studies) | Age: 18–75 years | LAeq,24h | 41–64 | ICBEN 5-p & 11-p | Noise + vibration. 206 or 179 trains resp./24 h (48 or 22 freight trains resp./24 h) | 21 |
| Lden | 48–71 | HA ≥ 60% | ||||||||||
| Gidlöf-Gunnarsson et al. 2012 | Area with one study site in Sweden | 2007–2008 | Stratified | Postal; questionnaire sent by mail | 715 | 53% (Total RR for the three Swedish studies) | Age: 18–75 years | LAeq,24h | 45–66 | ICBEN 5-p & 11-p | Many trains: 481 trains/24 h (15 freight trains) | 21 |
| Lden | 49–70 | HA ≥ 60% | ||||||||||
| Lercher et al. 2008 | Wipp valley, Austria | 2004 | Stratified; random (Strata = distance to source) | Face-to-face interviews | 2017 in total; a subsample with n = 1449 used here | 80% | 17–85 years | Lden | ICBEN 11-p | Alpine areas; only rail data used. High proportion of freight trains. Public discussion about rail traffic noise | 22 | |
| HA ≥ 73% | ||||||||||||
| Lercher et al. 2008 | Wipp valley, Austria | 2004 | Stratified; random | Phone-interviews | 2002 in total, a subsample with n = 1081 used here | 62% | 17–85 years | Lden | ICBEN 5-p HA ≥ 60% | Alpine areas; only rail data used. High proportion of freight trains. Public discussion about rail traffic noise | 22 | |
| Lercher et al. 2008 Heimann/ Lercher 2007 | Inn valley, Austria | 2006 | Stratified; random | Phone-interviews | 1643 | 35% | 25–75 years. | Lden | ICBEN 5-p | Alpine areas; only rail data used. Noise barriers were erected before interviews. High proportion of freight trains. Public discussion about rail traffic noise | 22 | |
| HA ≥ 60% | ||||||||||||
| Schreckenberg 2013 | Railway Rhine valley, Germany | 2010 | random sampling in 2 areas | Phone-interviews | 1211 Respondents. (Main sample: n = 1005; supplemental sample: n = 206). | Main sample: response rate: 41%. Supplemental sample: response rate: 58%. | 16–95 years | LAeq,24h | 37–86 | ICBEN 5-p | Long lasting public discussion about railway noise. High proportion of freight trains; many freight trains during the night. | 24 |
| Lden | 44–93 | HA ≥ 60% | ||||||||||
| Yano et al. 2005 | Fukuoka Prefecture, Japan | 2002 | All Detached houses in railway vicinity | Written questionnaire; distribute- collect method | 1612 | 64% | LAeq,24h | 24–78 | ICBEN 5-p + 11-p. | Conventional trains. 52–381 trains per day. | 14 | |
| Lden | 30–82 | The 11-p-scale used here with HA ≥ 73% | ||||||||||
| Ldn | 30–82 | |||||||||||
| Yano et al. 2005 | Fukuoka Prefecture, Japan | 2003 | Detached houses in railway vicinity; one person per family; random selection | Written questionnaire; distribute-collect method | 724 | 66% | 20–75 years | LAeq,24h | 32–50 | ICBEN 5-p + 11-p. | Shinkansen trains + vibration. 180 trains per day. | 14 |
| Lden | 36–54 | The 11-p-scale used here with HA ≥ 73% | ||||||||||
| Ldn | 35–53 | |||||||||||
| Yokoshima et al. 2008 | Kanagawa, Japan (Data from Kanagawa and Fukuoka; but only data from Kanagawa used here; see Yano et al. 2005 for Shinkansen in Fukuoka) | 2001–2002 | Detached houses in railway vicinity | Distribution-by-mail: Questionnaires distributed at 98 survey sites | 872 respondents. (114 from 986 excluded because of aircraft noise). | 55% | Age: ≥18 years | LAeq,24h | 28–61 | ICBEN 5-p | Shinkansen trains. 287 and 180 trains per day, resp. | 13 |
| Ldn | 31–64 | HA ≥ 73% (after weighting of the category “4” by 0.4) used here |
| Study (See Supplementary Materials S3 for References) | Subgroup | Type of Rail | Midpoints of the Two Exposure Classes | HA Rate in the Upper dB Class | Number of Respondents in the Upper dB Class | HA Rate in the Lower dB Class | Number of Respondents in the Lower dB Class |
|---|---|---|---|---|---|---|---|
| Gidloef-G. 2012 | Survey1: rail, no vibrations | conventional | 60 vs. 50 | 0.130 | 48 | 0.020 | 230 |
| Gidloef-G. 2012 | Survey2: rail, noise & vibrations | conventional | 60 vs. 50 | 0.290 | 45 | 0.090 | 167 |
| Gidloef-G. 2012 | Survey3: rail, many trains | conventional | 60 vs. 50 | 0.360 | 128 | 0.060 | 220 |
| Yano 2005 | conventional rail | conventional | 60 vs. 50 | 0.353 | 292 | 0.146 | 226 |
| Yano 2005 | Shinkansen | Shinkansen | 60 vs. 50 | 0.338 | 160 | 0.254 | 346 |
| Champelovier 2003 | rail: France | Conv. + TGV | 60 vs. 50 | 0.157 | 178 | 0.073 | 82 |
| Yokoshima 2008 | Shinkansen: Kanagawa | Shinkansen | 60 vs. 50 | 0.483 | 36 | 0.261 | 305 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guski, R.; Schreckenberg, D.; Schuemer, R. WHO Environmental Noise Guidelines for the European Region: A Systematic Review on Environmental Noise and Annoyance. Int. J. Environ. Res. Public Health 2017, 14, 1539. https://doi.org/10.3390/ijerph14121539
Guski R, Schreckenberg D, Schuemer R. WHO Environmental Noise Guidelines for the European Region: A Systematic Review on Environmental Noise and Annoyance. International Journal of Environmental Research and Public Health. 2017; 14(12):1539. https://doi.org/10.3390/ijerph14121539
Chicago/Turabian StyleGuski, Rainer, Dirk Schreckenberg, and Rudolf Schuemer. 2017. "WHO Environmental Noise Guidelines for the European Region: A Systematic Review on Environmental Noise and Annoyance" International Journal of Environmental Research and Public Health 14, no. 12: 1539. https://doi.org/10.3390/ijerph14121539
APA StyleGuski, R., Schreckenberg, D., & Schuemer, R. (2017). WHO Environmental Noise Guidelines for the European Region: A Systematic Review on Environmental Noise and Annoyance. International Journal of Environmental Research and Public Health, 14(12), 1539. https://doi.org/10.3390/ijerph14121539





