An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields
Abstract
:1. Introduction
2. Induced Electric Fields within Biological Cells in Mitosis
3. Subcellular Electrical Conduction and Electrostatics
3.1. Protein Conduction
3.2. Electrostatic Interactions Involving Charges and Dipoles of Tubulin
3.3. MT Conductivity
4. Collective Effects in the Membrane and Cytoplasm
4.1. Membrane Depolymerization Effects
4.2. Ion Channel Conduction Effects
4.3. Electric Field Effects on Cytoplasmic Ions
5. AC Electric Field Effects on Subcellular Structures
5.1. Electric Field Effects on MTs
5.2. Tubulin’s C-Termini Dynamics and AC Electric Fields
5.3. Ionic Waves along MTs and AC Electric Fields
5.4. Resonance Effects on MTs
5.5. Ionic Wave Conductivity along Actin Filaments and AC Fields
5.6. Electric Field Effects on DNA
5.7. Electric Field Effects on Motor Proteins
6. Discussion
- Longitudinal waves propagating along the MT surface. In this case each protofilament of a microtubule acts like a cable with its inherent resistance r, so the resistance of an entire microtubule would be R = r/13 since all these cables are in parallel to each other.
- Helical waves propagating around and along each microtubule, there could be three or five such waves propagating simultaneously mimicking the three-start or five-start geometry of a microtubule. The effective resistance of such cables would be the individual resistance divided by the number of cables in parallel.
- Radial waves propagating perpendicularly to the microtubule surface.
- Interfere with ion flows in the cleavage area of dividing cells.
- Interfere with motor protein motion and MAP-MT interactions.
- May to a lesser degree affect ion channel dynamics.
- May in general affect the net charge of the cytoplasm.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DC | direct current |
| AC | alternating current |
| TTFields | Tumor Treating Fields |
| GBM | glioblastoma multiforme |
| EM | electromagnetic |
| MT | microtubule |
| DEP | dielectrophoretic |
| AF | actin filament |
| TT | C-terminal tail |
| MAP | microtubule associated protein |
| MD | molecular dynamics |
References
- Cifra, M.; Fields, J.Z.; Farhadi, A. Electromagnetic cellular interactions. Prog. Biophys. Mol. Biol. 2011, 105, 223–246. [Google Scholar] [CrossRef] [PubMed]
- Kirson, E.D.; Gurvich, Z.; Schneiderman, R.; Dekel, E.; Itzhaki, A.; Wasserman, Y.; Schatzberger, R.; Palti, Y. Disruption of cancer cell replication by alternating electric fields. Cancer Res. 2004, 64, 3288–3295. [Google Scholar] [CrossRef] [PubMed]
- Kirson, E.D.; Dbalý, V.; Tovarys, F.; Vymazal, J.; Soustiel, J.F.; Itzhaki, A.; Mordechovich, D.; Steinberg-Shapira, S.; Gurvich, Z.; Schneiderman, R.; et al. Alternating electric fields arrest cell proliferation in animal tumor models and human brain tumors. Proc. Natl. Acad. Sci. USA 2007, 104, 10152–10157. [Google Scholar] [CrossRef] [PubMed]
- Davies, A.M.; Weinberg, U.; Palti, Y. Tumor treating fields: A new frontier in cancer therapy. Ann. N. Y. Acad. Sci. 2013, 1291, 86–95. [Google Scholar] [CrossRef] [PubMed]
- Stupp, R.; Wong, E.T.; Kanner, A.A.; Steinberg, D.; Engelhard, H.; Heidecke, V.; Kirson, E.D.; Taillibert, S.; Liebermann, F.; Dbalý, V.; et al. NovoTTF-100A versus physician’s choice chemotherapy in recurrent glioblastoma: A randomised phase III trial of a novel treatment modality. Eur. J. Cancer 2012, 48, 2192–2202. [Google Scholar] [CrossRef] [PubMed]
- Kirson, E.D.; Giladi, M.; Gurvich, Z.; Itzhaki, A.; Mordechovich, D.; Schneiderman, R.S.; Wasserman, Y.; Ryffel, B.; Goldsher, D.; Palti, Y. Alternating electric fields (TTFields) inhibit metastatic spread of solid tumors to the lungs. Clin. Exp. Metastasis 2009, 26, 633–640. [Google Scholar] [CrossRef] [PubMed]
- Stupp, R.; Taillibert, S.; Kanner, A.A.; Kesari, S.; Steinberg, D.M.; Toms, S.A.; Taylor, L.P.; Lieberman, F.; Silvani, A.; Fink, K.L.; et al. Maintenance therapy with tumor-treating fields plus temozolomide vs. temozolomide alone for glioblastoma: A randomized clinical trial. JAMA 2015, 314, 2535–2543. [Google Scholar] [CrossRef] [PubMed]
- Kirson, E.D.; Schneiderman, R.S.; Dbalý, V.; Tovaryš, F.; Vymazal, J.; Itzhaki, A.; Mordechovich, D.; Gurvich, Z.; Shmueli, E.; Goldsher, D.; et al. Chemotherapeutic treatment efficacy and sensitivity are increased by adjuvant alternating electric fields (TTFields). BMC Med. Phys. 2009, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Berg, H.; Günther, B.; Hilger, I.; Radeva, M.; Traitcheva, N.; Wollweber, L. Bioelectromagnetic field effects on cancer cells and mice tumors. Electromagn. Biol. Med. 2010, 29, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Funk, R.H.W.; Monsees, T.; Ozkucur, N. Electromagnetic effects—From cell biology to medicine. Prog. Histochem. Cytochem. 2009, 43, 177–264. [Google Scholar] [CrossRef] [PubMed]
- Dyshlovoi, V.D.; Panchuk, A.S.; Kachura, V.S. Effect of electromagnetic field of industrial frequency on the growth pattern and mitotic activity of cultured human fibroblastoid cells. Cytol. Genet. 1981, 15, 9–12. [Google Scholar]
- Robertson, D.; Miller, M.W.; Cox, C.; Davis, H.T. Inhibition and recovery of growth processes in roots of Pisum sativum L. exposed to 60-Hz electric fields. Bioelectromagnetics 1981, 2, 329–340. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, L.F.; Nuccitelli, R. Electrical controls of development. Annu. Rev. Biophys. Bioeng. 1977, 6, 446–476. [Google Scholar] [CrossRef] [PubMed]
- Tuszyński, J.A.; Hameroff, S.; Satarić, M.V.; Trpisová, B.; Nip, M.L.A. Ferroelectric behavior in microtubule dipole lattices: Implications for information processing, signaling and assembly/disassembly. J. Theor. Biol. 1995, 174, 371–380. [Google Scholar] [CrossRef]
- Gagliardi, L.J. Electrostatic force in prometaphase, metaphase, and anaphase-A chromosome motions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2002, 66, 011901. [Google Scholar] [CrossRef] [PubMed]
- Gagliardi, L.J. Microscale electrostatics in mitosis. J. Electrostat. 2002, 54, 219–232. [Google Scholar] [CrossRef]
- Pohl, H.A. Dielectrophoresis; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Cooper, M. Coherent polarization waves in cell division and cancer. Collect. Phenom. 1981, 3, 273–288. [Google Scholar]
- Pohl, H.A.; Braden, T.; Robinson, S.; Piclardi, J.; Pohl, D.G. Life cycle alterations of the micro-dielectrophoretic effects of cell. J. Biol. Phys. 1981, 9, 133–154. [Google Scholar] [CrossRef]
- Pohl, H.A. Oscillating fields about growing cells. Int. J. Quantum Chem. 1980, 18, 411–431. [Google Scholar] [CrossRef]
- Jelínek, F.; Pokorný, J.; Saroch, J.; Trkal, V.; Hasek, J.; Palán, B. Microelectronic sensors for measurement of electromagnetic fields of living cells and experimental results. Bioelectrochem. Bioenerg. 1999, 48, 261–266. [Google Scholar] [CrossRef]
- Gagliardi, L.J. Electrostatic force generation in chromosome motions during mitosis. J. Electrostat. 2005, 63, 309–327. [Google Scholar] [CrossRef]
- Tuszynski, J.A.; Dixon, J.M. Biomedical applications of introductory physics. Eur. J. Phys. 2002, 23, 591. [Google Scholar] [CrossRef]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Grosse, C.; Schwan, H.P. Cellular membrane potentials induced by alternating fields. Biophys. J. 1992, 63, 1632–1642. [Google Scholar] [CrossRef]
- Kotnik, T.; Bobanović, F.; Miklavčič, D. Sensitivity of transmembrane voltage induced by applied fields—A theoretical analysis. Bioelectrochem. Bioenergy 1997, 43, 285–291. [Google Scholar] [CrossRef]
- Bernhardt, J.; Pauly, H. On the generation of potential differences across the membranes of ellipsoidal cells in an alternating electrical field. Biophysik 1973, 10, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Gimsa, J.; Wachner, D. A polarization model overcoming the geometric restrictions of the laplace solution for spheroidal cells: Obtaining new equations for field-induced forces and transmembrane potential. Biophys. J. 1999, 77, 1316–1326. [Google Scholar] [CrossRef]
- Gimsa, J.; Wachner, D. Analytical description of the transmembrane voltage induced on arbitrarily oriented ellipsoidal and cylindrical cells. Biophys. J. 2001, 81, 1888–1896. [Google Scholar] [CrossRef]
- Kotnik, T.; Miklavčič, D. Second-order model of membrane electric field induced by alternating external electric fields. IEEE Trans. Biomed. Eng. 2000, 47, 1074–1081. [Google Scholar] [CrossRef] [PubMed]
- Kotnik, T.; Miklavčič, D. Theoretical evaluation of voltage inducement on internal membranes of biological cells exposed to electric fields. Biophys. J. 2006, 90, 480–491. [Google Scholar] [CrossRef] [PubMed]
- Gowrishankar, T.R.; Weaver, J.C. An approach to electrical modeling of single and multiple cells. Proc. Natl. Acad. Sci. USA 2003, 100, 3203–3208. [Google Scholar] [CrossRef] [PubMed]
- Stewart, D.A.; Gowrishankar, T.R.; Smith, K.C.; Weaver, J.C. Cylindrical cell membranes in uniform applied electric fields: Validation of a transport lattice method. IEEE Trans. Biomed. Eng. 2005, 52, 1643–1653. [Google Scholar] [CrossRef] [PubMed]
- Pavlin, M.; Miklavčič, D. The effective conductivity and the induced transmembrane potential in dense cell system exposed to DC and AC electric fields. IEEE Trans. Plasma Sci. 2009, 37, 99–106. [Google Scholar] [CrossRef]
- Hobbie, R.K.; Roth, B.J. Intermediate Physics for Medicine and Biology, 4th ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- King, R.W.P.; Wu, T.T. Electric field induced in cells in the human body when this is exposed to low-frequency electric fields. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 1998, 58, 2363–2369. [Google Scholar] [CrossRef]
- Wenger, C.; Giladi, M.; Bomzon, Z.; Salvador, R.; Basser, P.J.; Miranda, P.C. Modeling Tumor Treating Fields (TTFields) application in single cells during metaphase and telophase. In In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 6892–6895.
- Boucrot, E.; Kirchhausen, T. Mammalian cells change volume during mitosis. PLoS ONE 2008, 3, e1477. [Google Scholar] [CrossRef] [PubMed]
- Habela, C.W.; Sontheimer, H. Cytoplasmic volume condensation is an integral part of mitosis. Cell Cycle 2007, 6, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Vajrala, V.; Claycomb, J.R.; Sanabria, H.; Miller, J.H. Effects of oscillatory electric fields on internal membranes: An analytical model. Biophys. J. 2008, 94, 2043–2052. [Google Scholar] [CrossRef] [PubMed]
- Giladi, M.; Porat, Y.; Blatt, A.; Wasserman, Y.; Kirson, E.D.; Dekel, E.; Palti, Y. Microbial growth inhibition by alternating electric fields. Antimicrob. Agents Chemother. 2008, 52, 3517–3522. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Morgan, H.; Green, N. Analytical solutions of AC electrokinetics in interdigitated electrode arrays: Electric field, dielectrophoretic and traveling-wave dielectrophoretic forces. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 046610. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.B. Basic theory of dielectrophoresis and electrorotation. IEEE Eng. Med. Biol. Mag. 2003, 22, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Markx, G.H. The use of electric fields in tissue engineering: A review. Organogenesis 2008, 4, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Giladi, M.; Schneiderman, R.S.; Porat, Y.; Munster, M.; Itzhaki, A.; Mordechovich, D.; Cahal, S.; Kirson, E.D.; Weinberg, U.; Palti, Y. Mitotic disruption and reduced clonogenicity of pancreatic cancer cells in vitro and in vivo by tumor treating fields. Pancreatology 2014, 14, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Tyner, K.M.; Kopelman, R.; Philbert, M.A. “Nanosized voltmeter” enables cellular-wide electric field mapping. Biophys. J. 2007, 93, 1163–1174. [Google Scholar] [CrossRef] [PubMed]
- Qvist, J.; Persson, E.; Mattea, C.; Halle, B. Time scales of water dynamics at biological interfaces: Peptides, proteins and cells. Faraday Discuss. 2009, 141, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Tuszynski, J.A. Molecular and Cellular Biophysics; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Szent-Györgyi, A. The study of energy-levels in biochemistry. Nature 1941, 148, 157–159. [Google Scholar] [CrossRef]
- Szent-Györgyi, A. Bioenergetics; Academic Press: New York, NY, USA, 1957. [Google Scholar]
- Gascoyne, P.R.C.; Pethig, R.; Szent-Györgyi, A. Water structure-dependent charge transport in proteins. Proc. Natl. Acad. Sci. USA 1981, 78, 261–265. [Google Scholar] [CrossRef] [PubMed]
- Szent-Györgyi, A. Biolectronics and cancer. J. Bioenerg. 1973, 4, 533–562. [Google Scholar] [CrossRef] [PubMed]
- Szent-Györgyi, A. Electronic biology and its relation to cancer. Life Sci. 1974, 15, 863–875. [Google Scholar] [CrossRef]
- Craddock, T.J.; Tuszyński, J.A.; Priel, A.; Freedman, H. Microtubule ionic conduction and its implications for higher cognitive functions. J. Integr. Neurosci. 2010, 9, 103–122. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.; Ghosh, S.; Ghosh, B.; Aswani, K.; Hirata, K.; Fujita, D.; Bandyopadhyay, A. Atomic water channel controlling remarkable properties of a single brain microtubule: Correlating single protein to its supramolecular assembly. Biosens. Bioelectron. 2013, 47, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Levin, M. Bioelectromagnetics in morphogenesis. Bioelectromagnetics 2003, 24, 295–315. [Google Scholar] [CrossRef] [PubMed]
- McCaig, C.D.; Rajnicek, A.M.; Song, B.; Zhao, M. Controlling cell behavior electrically: Current views and future potential. Physiol. Rev. 2005, 85, 943–978. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Fels, D.; Cifra, M. Non-chemical and non-contact cell-to-cell communication: A short review. Am. J. Transl. Res. 2013, 5, 586–593. [Google Scholar] [PubMed]
- Zheng, J.M.; Chin, W.C.; Khijniak, E.; Khijniak, E.J.; Pollack, G.H. Surfaces and interfacial water: Evidence that hydrophilic surfaces have long-range impact. Adv. Colloid Interface Sci. 2006, 127, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Priel, A.; Ramos, A.J.; Tuszynski, J.A.; Cantiello, H.F. A biopolymer transistor: Electrical amplification by microtubules. Biophys. J. 2006, 90, 4639–4643. [Google Scholar] [CrossRef] [PubMed]
- Sekulić, D.L.; Satarić, B.M.; Tuszyński, J.A.; Satarić, M.V. Nonlinear ionic pulses along microtubules. Eur. Phys. J. E Soft Matter 2011, 34, 49. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Zhang, C.T.; Maggiora, G.M. Solitary wave dynamics as a mechanism for explaining the internal motion during microtubule growth. Biopolymers 1994, 34, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Kučera, O.; Havelka, D. Mechano-electrical vibrations of microtubules—Link to subcellular morphology. Biosystems 2012, 109, 346–355. [Google Scholar] [CrossRef] [PubMed]
- Havelka, D.; Kučera, O.; Deriu, M.A.; Cifra, M. Electro-acoustic behavior of the mitotic spindle: A semi-classical coarse-grained model. PLoS ONE 2014, 9, e86501. [Google Scholar] [CrossRef] [PubMed]
- Preto, J.; Pettini, M.; Tuszyński, J.A. Possible role of electrodynamic interactions in long-distance biomolecular recognition. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91, 052710. [Google Scholar] [CrossRef] [PubMed]
- Cifra, M.; Havelka, D.; Deriu, M.A. Electric field generated by longitudinal axial microtubule vibration modes with high spatial resolution microtubule model. J. Phys. Conf. Ser. 2011, 329, 012013. [Google Scholar] [CrossRef]
- Cifra, M.; Pokorný, J.; Havelka, D.; Kučera, O. Electric field generated by axial longitudinal vibration modes of microtubule. Biosystems 2010, 100, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Tuszyński, J.A.; Brown, J.A.; Crawford, E.; Carpenter, E.J.; Nip, M.L.; Dixon, J.M.; Satarić, M.V. Molecular dynamics simulations of tubulin structure and calculations of electrostatic properties of microtubules. Math. Comput. Model. 2005, 41, 1055–1070. [Google Scholar] [CrossRef]
- Carpenter, E.J.; Huzil, J.T.; Ludueña, R.F.; Tuszyński, J.A. Homology modeling of tubulin: Influence predictions for microtubule’s biophysical properties. Eur. Biophys. J. 2006, 36, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Tuszynski, J.A.; Carpenter, E.J.; Huzil, J.T.; Malinski, W.; Luchko, T.; Luduena, R.F. The evolution of the structure of tubulin and its potential consequences for the role and function of microtubules in cells and embryos. Int. J. Dev. Biol. 2006, 50, 341–358. [Google Scholar] [CrossRef] [PubMed]
- Vassilev, P.M.; Dronzine, T.; Vassileva, M.P.; Georgiev, G.A. Parallel arrays of microtubules formed in electric and magnetic fields. Biosci. Rep. 1982, 2, 1025–1029. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.A.; Dixon, J.M.; Cantiello, H.F.; Priel, A.; Tuszyński, J.A. Electronic and ionic conductivities of microtubules and actin filaments, their consequences for cell signaling and applications to bioelectronics. In Nano and Molecular Electronics Handbook; Lyshevski, S.E., Ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Priel, A.; Tuszyński, J. A nonlinear cable-like model of amplified ionic wave propagation along microtubules. Eur. Lett. 2008, 83, 68004. [Google Scholar] [CrossRef]
- Friesen, D.E.; Craddock, T.J.A.; Kalra, A.P.; Tuszynski, J.A. Biological wires, communication systems, and implications for disease. Biosystems 2015, 127, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Stracke, R.; Böhm, K.J.; Wollweber, L.; Tuszynski, J.A.; Unger, E. Analysis of the migration behaviour of single microtubules in electric fields. Biochem. Biophys. Res. Commun. 2002, 293, 602–609. [Google Scholar] [CrossRef]
- Sahu, S.; Ghosh, S.; Hirata, K.; Fujita, D.; Bandyopadhyay, A. Multi-level memory-switching properties of a single brain microtubule. Appl. Phys. Lett. 2013, 102, 123701. [Google Scholar] [CrossRef]
- Minoura, I.; Muto, E. Dielectric measurement of individual microtubules using the electroorientation method. Biophys. J. 2006, 90, 3739–3748. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.A.; Tuszynski, J.A. A review of the ferroelectric model of microtubules. Ferroelectrics 1999, 220, 141–155. [Google Scholar] [CrossRef]
- Uppalapati, M.; Huang, Y.-M.; Jackson, T.N.; Hancock, W.O. Microtubule alignment and manipulation using AC electrokinetics. Small 2008, 4, 1371–1381. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.S.; Astumian, R.D.; Tsong, T.Y. Activation of Na+ and K+ pumping modes of (Na, K)-ATPase by an oscillating electric field. J. Biol. Chem. 1990, 265, 7260–7267. [Google Scholar] [PubMed]
- Tsong, T.Y.; Astumian, R.D. 863—Absorption and conversion of electric field energy by membrane bound ATPases. Bioelectrochem. Bioenergy 1986, 15, 457–476. [Google Scholar] [CrossRef]
- Tsong, T.Y. Electrical modulation of membrane proteins: Enforced conformational oscillations and biological energy and signal transductions. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 83–106. [Google Scholar] [CrossRef] [PubMed]
- White, J.A.; Rubinstein, J.T.; Kay, A.R. Channel noise in neurons. Trends Neurosci. 2000, 23, 131–137. [Google Scholar] [CrossRef]
- Roux, B.; Schulten, K. Computational studies of membrane channels. Structure 2004, 12, 1343–1351. [Google Scholar] [CrossRef] [PubMed]
- Bernèche, S.; Roux, B. Energetics of ion conduction through the K+ channel. Nature 2001, 414, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Kuyucak, S.; Andersen, O.S.; Chung, S.-H. Models of permeation in ion channels. Rep. Prog. Phys. 2001, 64, 1427–1472. [Google Scholar] [CrossRef]
- Guidoni, L.; Carloni, P. Potassium permeation through the KcsA channel: A density functional study. Biochim. Biophys. Acta 2002, 1563, 1–6. [Google Scholar] [CrossRef]
- Shrivastava, I.H.; Tieleman, D.P.; Biggin, P.C.; Sansom, M.S.P. K+ versus Na+ ions in a K channels selectivity filter: A simulation study. Biophys. J. 2002, 83, 633–645. [Google Scholar] [CrossRef]
- Bernèche, S.; Roux, B. A gate in the selectivity filter of potassium channels. Structure 2005, 13, 591–600. [Google Scholar] [CrossRef] [PubMed]
- Mastro, A.M.; Babich, M.A.; Taylor, W.D.; Keith, A.D. Diffusion of a small molecule in the cytoplasm of mammalian cells. Proc. Natl. Acad. Sci. USA 1984, 81, 3414–3418. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: Berlin, Germany, 1985. [Google Scholar]
- Preto, J.; Floriani, E.; Nardecchia, I.; Ferrier, P.; Pettini, M. Experimental assessment of the contribution of electrodynamic interactions to long-distance recruitment of biomolecular partners: Theoretical basis. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 85, 041904. [Google Scholar] [CrossRef] [PubMed]
- Brics, M.; Kaupuzs, J.; Mahnke, R. How to solve Fokker-Planck equation treating mixed eigenvalue spectrum? Condens. Matter Phys. 2013, 16, 1–13. [Google Scholar] [CrossRef]
- Alexandrov, B.S.; Gelev, V.; Bishop, A.R.; Usheva, A.; Rasmussen, K. DNA breathing dynamics in the presence of a terahertz field. Phys. Lett. A 2010, 374, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Isozaki, N.; Ando, S.; Nakahara, T.; Shintaku, H.; Kotera, H.; Meyhöfer, E.; Yokokawa, R. Control of microtubule trajectory within an electric field by altering surface charge density. Sci. Rep. 2015, 5, 7669. [Google Scholar] [CrossRef] [PubMed]
- Van den Heuvel, M.G.L.; de Graaff, M.P.; Lemay, S.G.; Dekker, C. Electrophoresis of individual microtubules in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 7770–7775. [Google Scholar] [CrossRef] [PubMed]
- Priel, A.; Tuszyński, J.A.; Woolf, N.J. Transitions in microtubule C-termini conformations as a possible dendritic signaling phenomenon. Eur. Biophys. J. 2005, 35, 40–52. [Google Scholar] [CrossRef] [PubMed]
- Manning, G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978, 11, 179–246. [Google Scholar] [CrossRef] [PubMed]
- Le Bret, M.; Zimm, B. Distribution of counterions around a cylindrical polyelectrolyte and Manning’s condensation theory. Biopolymers 1984, 23, 287–312. [Google Scholar] [CrossRef]
- Satarić, M.V.; Ilić, D.I.; Ralević, N.; Tuszynski, J.A. A nonlinear model of ionic wave propagation along microtubules. Eur. Biophys. J. 2009, 38, 637–647. [Google Scholar] [CrossRef] [PubMed]
- Ussing, H.H.; Thorn, N.A. Transport Mechanisms in Epithelia; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Porat-Shilom, N.; Chen, Y.; Tora, M.; Shitara, A.; Masedunskas, A.; Weigert, R. In vivo tissue-wide synchronization of mitochondrial metabolic oscillations. Cell Rep. 2014, 9, 514–524. [Google Scholar] [CrossRef] [PubMed]
- Cosic, I.; Lazar, K.; Cosic, D. Prediction of Tubulin resonant frequencies using the Resonant Recognition Model (RRM). IEEE Trans Nanobiosci. 2014, 14, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Cosic, I.; Cosic, D.; Lazar, K. Is it possible to predict electromagnetic resonances in proteins, DNA and RNA? EPJ Nonlinear Biomed. Phys. 2015, 3, 5. [Google Scholar] [CrossRef]
- Ayoub, A.T.; Craddock, T.J.; Klobukowski, M.; Tuszyński, J. Analysis of the strength of interfacial hydrogen bonds between tubulin dimers using quantum theory of atoms in molecules. Biophys. J. 2014, 107, 740–750. [Google Scholar] [CrossRef] [PubMed]
- Pizzi, R.; Strini, G.; Fiorentini, S.; Pappalardo, V.; Pregnolato, M. Evidences of new biophysical propeties of microtubules. In Artificial Networks; Kwon, S.J., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Kobayashi, S.; Asai, H.; Oosawa, F. Electric birefringence of actin. Biochim. Biophys. Acta Spec. Sect. Biophys. Subj. 1964, 88, 528–540. [Google Scholar] [CrossRef]
- Cantiello, H.F.; Patenaude, C.; Zaner, K. Osmotically induced electrical signals from actin filaments. Biophys. J. 1991, 59, 1284–1289. [Google Scholar] [CrossRef]
- Lin, E.C.; Cantiello, H.F. A novel method to study the electrodynamic behavior of actin filaments. Evidence for cable-like properties of actin. Biophys. J. 1993, 65, 1371–1378. [Google Scholar] [CrossRef]
- Lonngren, K.E. Observations of solitons on nonlinear dispersive transmission lines. In Solitons in Action; Lonngren, K.E., Scott, A., Eds.; Academic Press: New York, NY, USA, 1978; pp. 127–152. [Google Scholar]
- Oosawa, F. Polyelectrolytes; Marcel Dekker, Inc.: New York, NY, USA, 1971. [Google Scholar]
- Tuszyński, J.A.; Portet, S.; Dixon, J.M.; Luxford, C.; Cantiello, H.F. Ionic wave propagation along actin filaments. Biophys. J. 2004, 86, 1890–1903. [Google Scholar] [CrossRef]
- Arsenault, M.E.; Zhao, H.; Purohit, P.K.; Goldman, Y.E.; Bau, H.H. Confinement and manipulation of actin filaments by electric fields. Biophys. J. 2007, 93, L42–L44. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.R.; Thatte, H.S.; Lee, R.C.; Golan, D.E. Reorganization of microfilament structure induced by AC electric fields. FASEB J. 1996, 10, 1552–1558. [Google Scholar] [PubMed]
- Anderson, C.F.; Record, M.T.J. Ion distributions around DNA and other cylindrical polyions: Theoretical descriptions and physical implications. Annu. Rev. Biophys. Bioeng. Chem. 1990, 19, 4232–4265. [Google Scholar] [CrossRef] [PubMed]
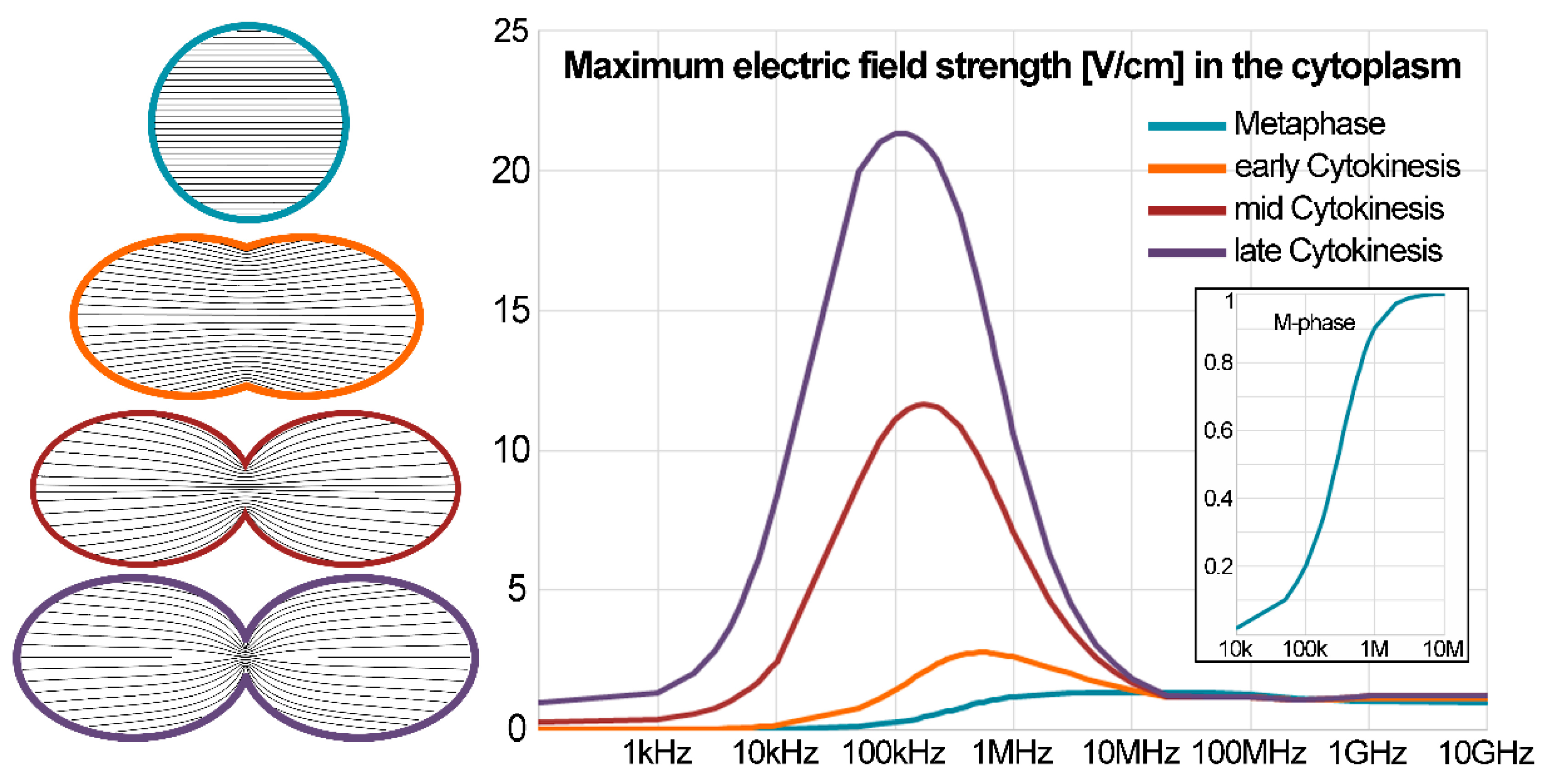
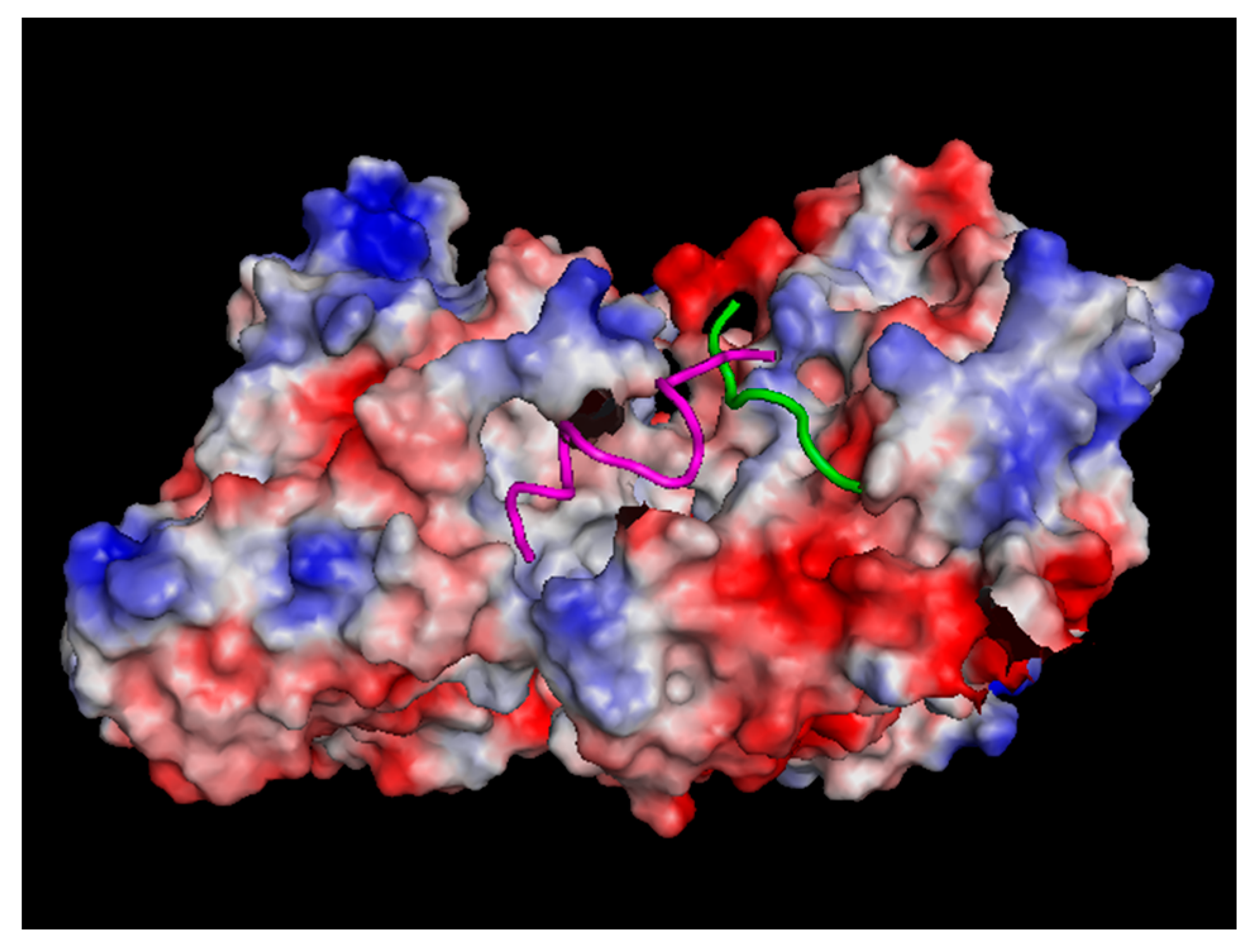
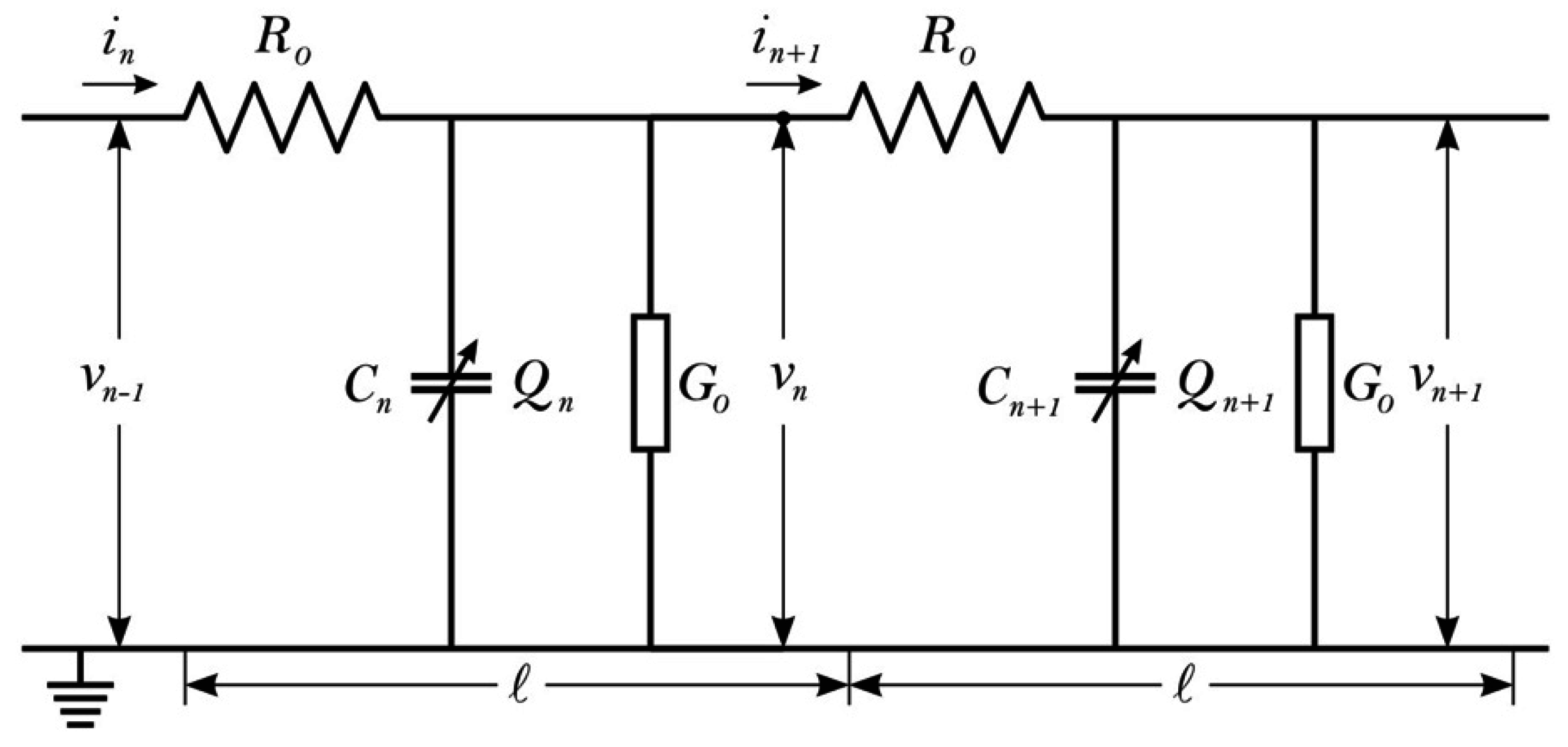
| Ions | Concentration mM | Non-Ionic Constituents | Concentration mg/mL |
|---|---|---|---|
| K+ | 140 | protein | 200–300 |
| Na+ | 10 | actin | 2–8 |
| Cl− | 10 | tubulin (electrolyte) | 4 |
| Ca2+ | 10−4 | pH | ~7.2 |
| Mg2+ | 0.5 | Specific tissues may differ | Specific tissues may differ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuszynski, J.A.; Wenger, C.; Friesen, D.E.; Preto, J. An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields. Int. J. Environ. Res. Public Health 2016, 13, 1128. https://doi.org/10.3390/ijerph13111128
Tuszynski JA, Wenger C, Friesen DE, Preto J. An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields. International Journal of Environmental Research and Public Health. 2016; 13(11):1128. https://doi.org/10.3390/ijerph13111128
Chicago/Turabian StyleTuszynski, Jack A., Cornelia Wenger, Douglas E. Friesen, and Jordane Preto. 2016. "An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields" International Journal of Environmental Research and Public Health 13, no. 11: 1128. https://doi.org/10.3390/ijerph13111128
APA StyleTuszynski, J. A., Wenger, C., Friesen, D. E., & Preto, J. (2016). An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields. International Journal of Environmental Research and Public Health, 13(11), 1128. https://doi.org/10.3390/ijerph13111128







