Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Condition
2.2. Sampling and Processing
| Vegetation Types | Vegetation Coverage (%) | Tree Age (Year) | Elevation (m) | Slope (°) | Aspect ‡ | |
|---|---|---|---|---|---|---|
| Mixed forest | QRM site † | 90.3 | 7 | 326 | 10–15 | sunny |
| PPM site | 89.4 | 7 | 344 | 15–25 | half-sunny | |
| Pure forest | PTP site | 78.8 | 7 | 346 | 15–25 | sunny |
| JRL site | 80.7 | 6 | 316 | 10–15 | sunny | |
| Comparison | ABG site | 35.2 | − | 340 | 15–25 | sunny |
2.3. Monofractal Method
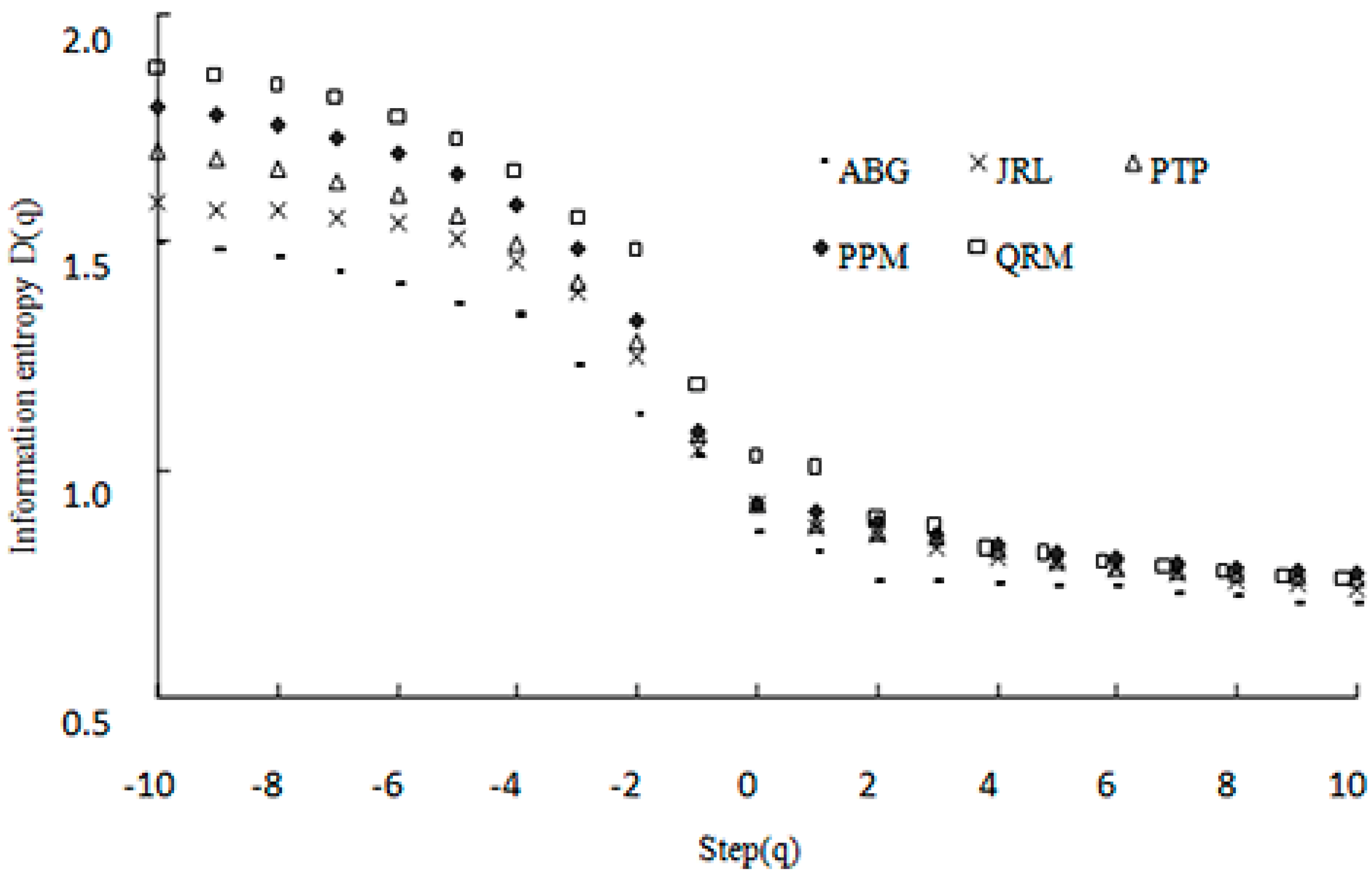
2.4. Multifractal Method
2.5. The Fractal Dimensions of the Soil WRC
2.6. Statistical Data Analyses
3. Results and Discussions
3.1. Soil PSD and Its Fractal Dimension under Different Vegetation Types
| Vegetation Type | Sand Volume Content (%) | Silt Volume Content (%) | Clay Volume Content (%) | ||||
|---|---|---|---|---|---|---|---|
| Very Coarse Sand | Coarse Sand | Sand | Fine Sand | Very Fine Sand | |||
| QRM † | 0.019 ± 0.004 a | 8.54 ± 0.58 a,* | 20.61 ± 1.84 a | 18.35 ± 1.07 a | 8.35 ± 0.74 a | 39.06 ± 3.18 a | 4.90 ± 0.51 a |
| PPM | 0.020 ± 0.005 a | 4.39 ± 0.37 b | 16.43 ± 1.09 b | 25.63 ± 2.16 b | 10.86 ± 0.82 b | 38.02 ± 3.02 a | 4.65 ± 0.48 a |
| PTP | 5.82 ± 0.52 b | 26.40 ± 2.12 c | 22.16 ± 1.98 c | 12.40 ± 0.96 c | 5.16 ± 0.47 c | 25.68 ± 2.35 b | 2.38 ± 0.32 b |
| JRL | 8.63 ± 0.65 c | 14.28 ± 1.21 d | 24.11 ± 2.05 d | 20.96 ± 1.78 d | 7.60 ± 0.59 d | 22.00 ± 1.89 c | 2.12 ± 0.25 b |
| ABG | 8.97 ± 0.62 c | 24.40 ± 2.02 e | 26.95 ± 2.35 e | 18.11 ± 1.02 e | 5.00 ± 0.38 e | 16.40 ± 1.14 d | 1.08 ± 0.12 c |
| Vegetation Type | D † | D0 | D1 | D1/D0 | D′ | R2 |
|---|---|---|---|---|---|---|
| QRM † | 2.5576 ± 0.48 a,* | 0.9317 ± 0.09 a | 0.9104 ± 0.07 a | 0.9824 ± 0.10 a | 2.6165 ± 0.50 a | 0.9111 |
| PPM | 2.5462 ± 0.43 a | 0.9241 ± 0.09 a | 0.9057 ± 0.06 a | 0.9773 ± 0.10 a | 2.5913 ± 0.47 a | 0.8477 |
| PTP | 2.4563 ± 0.37 b | 0.9212 ± 0.08 a | 0.8799 ± 0.05 b | 0.9495 ± 0.09 b | 2.5341 ± 0.42 b | 0.8253 |
| JRL | 2.4331 ± 0.35 b | 0.9205 ± 0.08 a | 0.8761 ± 0.05 b | 0.9454 ± 0.09 b | 2.5110 ± 0.40 b | 0.8511 |
| ABG | 2.3288 ± 0.0.32 c | 0.9142 ± 0.07 b | 0.8542 ± 0.05 c | 0.9244 ± 0.08 c | 2.4491 ± 0.36 c | 0.8618 |
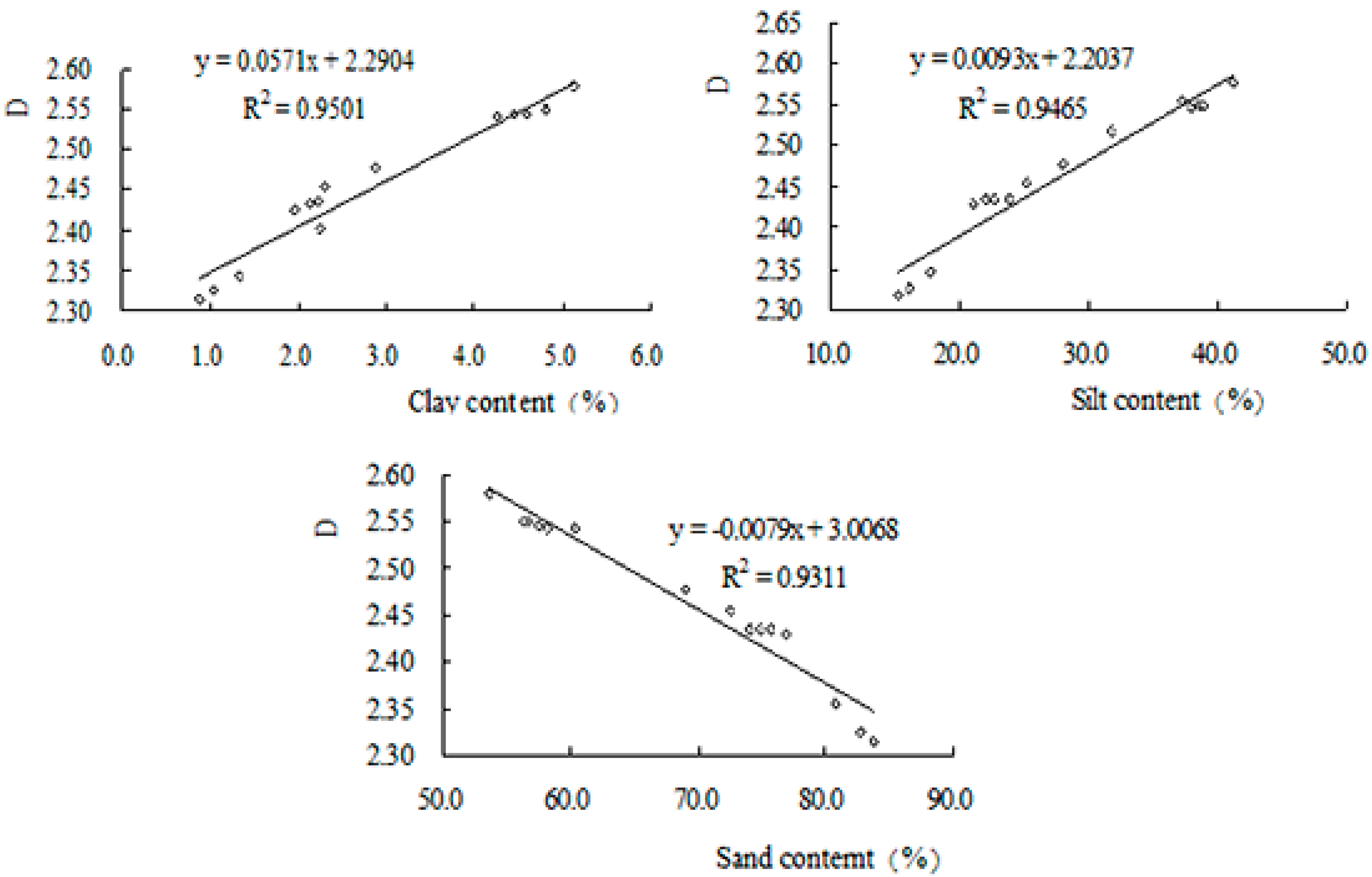
| Parameter Types | Clay | Slit | Sand | D † | D0 | D1 | D1/D0 |
|---|---|---|---|---|---|---|---|
| Slit † | 0.935 * | ||||||
| Sand | −0.950 * | −0.999 ** | |||||
| D | 0.944 * | 0.957 * | −0.963 ** | ||||
| D0 | 0.663 | 0.685 | −0.687 | 0.849 | |||
| D1 | 0.978 ** | 0.984 ** | −0.990 ** | 0.962 ** | 0.682 | ||
| D1/D0 | 0.969 ** | 0.971 ** | −0.978 ** | 0.914 * | 0.568 | 0.989 ** | |
| D′ | 0.942 * | 0.992 ** | −0.993 ** | 0.986 ** | 0.769 | 0.982 ** | 0.952 * |
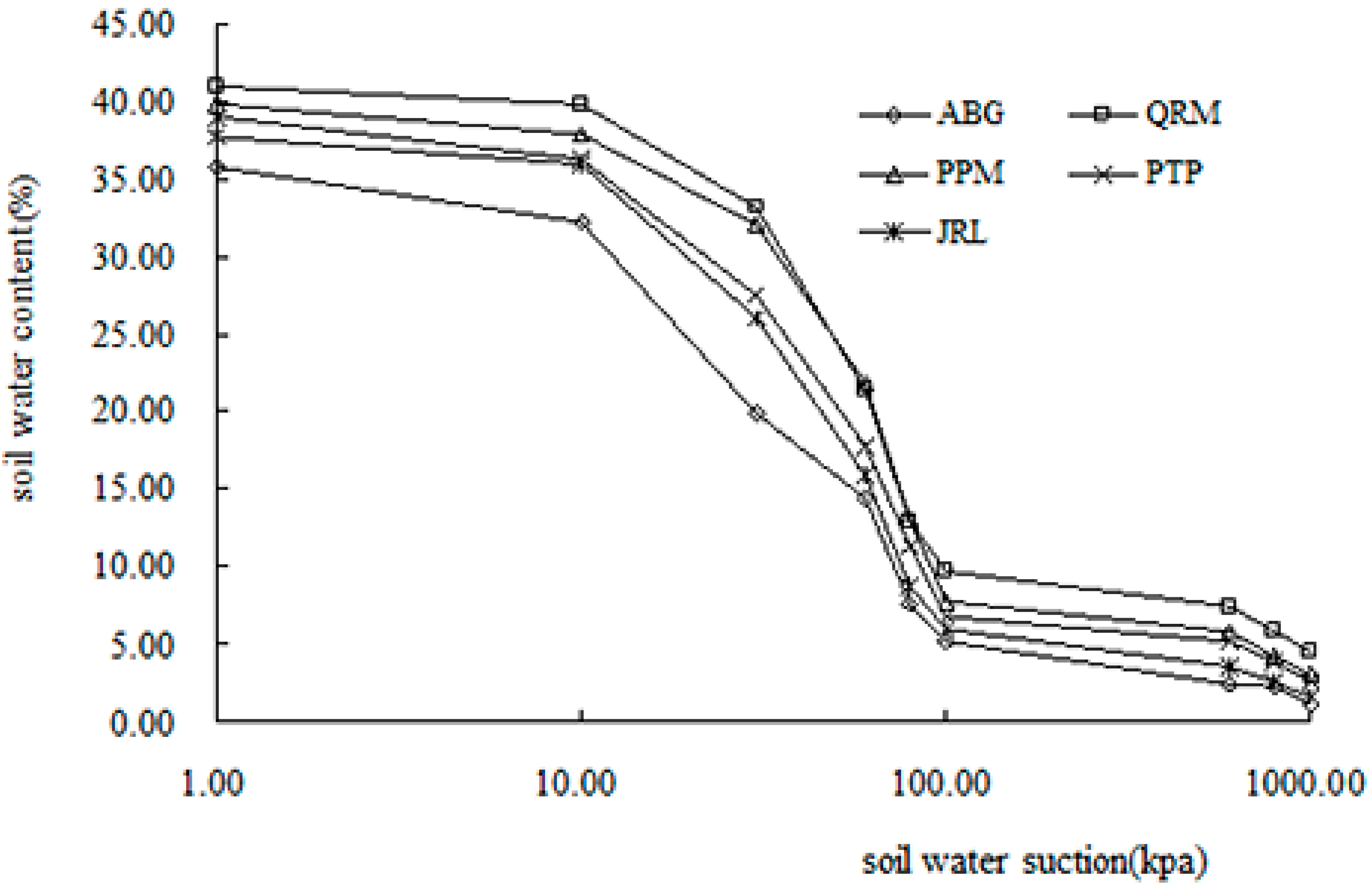
3.2. Soil WRC and Its Fractal Dimension under Different Vegetation Types
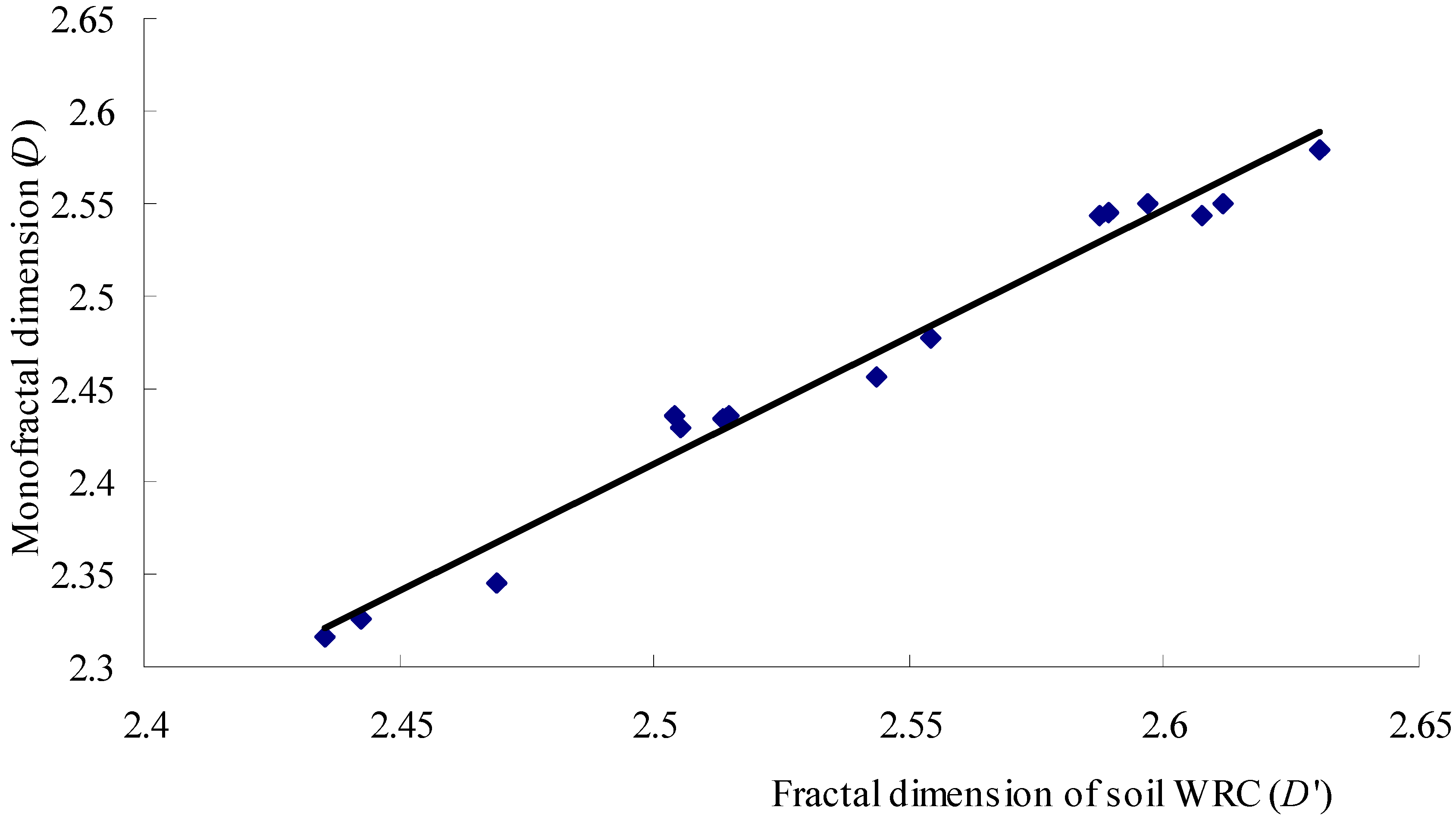
3.3. Correlation Analysis between D′ and D of the Soil PSD
4. Conclusions
- (1)
- The fractal parameters of soil PSDs and soil WRCs under different vegetation types were significantly different (p < 0.05), and all analyses showed that QRM > PPM > PTP > JRL > ABG. The soil fractal dimensions of mixed forests (QRM and PPM) were higher than that in pure forests (PTP and JRL), and the soil fractal dimensions of woodlands (QRM, PPM, PTP and JRL) were significantly higher than in ABG (p < 0.05). These results indicated that the woodland vegetation types had obvious effects on improving the soil structure, preventing the loss of soil, and increasing the soil fractal dimensions. These results also indicated that fractal dimensions could adequately describe the influences of different vegetation types on the soil particle composition and the soil PSD. Furthermore, fractal dimensions served as an important index for soil improvement and development. Therefore, it was necessary to construct different ecological forest types for preventing soil erosion and improving soil structure, especially for the construction and management of mixed forests in a study area.
- (2)
- The D of the soil PSD was positively correlated with the fractal dimension of the soil WRC. Therefore, the relationship between the fractal dimension of the soil PSD and WRC could be used to describe the corresponding soil WRC.
- (3)
- The fractal parameters of the soil PSD and WRC were closely related to the soil structure and were used as quantitative indices to reflect changes in the physical properties of the soil. Thus, the fractal parameters of the soil PSD and WRC could also act as an index and theoretical basis for the construction of environmental construction projects (such as Return Farmland to Forests Project) and the evaluation of forest ecological service function in the study area.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Giménez, D.; Perfect, E.; Rawls, W.J.; Pachepsky, Y. Fractal models for predicting soil hydraulic properties: A review. Eng. Geol. 1997, 48, 161–183. [Google Scholar] [CrossRef]
- Rieu, M.; Sposito, G. Fractal fragmentation, soil porosity and soil water properties: I. Theory. Soil Sci. Soc. Am. J. 1991, 55, 1231–1238. [Google Scholar] [CrossRef]
- Smolander, A.; Heiskanen, J. Soil N and C transformations in two forest clear-cuts during three years after mounding and inverting. Can. J. Soil Sci. 2007, 87, 251–258. [Google Scholar] [CrossRef]
- Hu, Y.F.; Liu, J.Y.; Zhuang, D.F. Fractal dimension of soil particle size distribution under different land use/land coverage. J. Soil 2005, 42, 336–339. [Google Scholar]
- Tyler, S.W.; Wheatcraft, S.W. Application of fractal mathematics to soil water retention. Soil Sci. Soc. Am. J. 1989, 53, 987–996. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Bittelli, M.; Campbell, G.S.; Flury, M. Characterization of particle-size distribution in soils with a fragmentation model. Soil. Sci. Soc. Am. J. 1999, 63, 782–788. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, Y.Q.; Xia, Y.P. Soil fractal features of typical forest stands in Jinyun mountain of Chongqing city. Sci. Soil Water Conserv. 2006, 4, 39–46. [Google Scholar]
- Gao, P.; Yang, H.L.; Wang, H.W. Characteristics of soil particles fractal dimension under different forest stands of the ecological restoration area in Dahei Mountain area. Sci. Soil Water Conserv. 2009, 7, 52–57. [Google Scholar]
- Tripathi, S.K. Application of fractal theory in assessing soil aggregates in Indian tropical ecosystems. J. For. Res. 2012, 23, 355–364. [Google Scholar] [CrossRef]
- Montero, E. Rényi dimensions analysis of soil particle-size distributions. Ecol. Model. 2005, 182, 305–315. [Google Scholar] [CrossRef]
- Grout, H.; Tarquis, A.M.; Wiesner, M.R. Multifractal analysis of particle size distributions in soil. Environ. Sci. Technol. 1998, 32, 1176–1182. [Google Scholar] [CrossRef]
- Posadas, A.N.D.; Giménez, D.; Quiroz, R.; Protz, R. Multifractal characterization of soil pore systems. Soil Sci. Soc. Am. J. 2003, 67, 1361–1369. [Google Scholar] [CrossRef]
- Wang, X.D.; Fan, J.R.; Chai, Z.X.; Liu, S.Z. Fractal study on bending of gully head in the Yuanmou Basin on lower reaches of the Jinsha River. J. Soil Water Conserv. 2001, 15, 65–67. [Google Scholar]
- Wang, Z.; Zhou, Y.C.; Yu, N. Feasibility research on estimating the soil water retention curve of brown earth with fractal method. J. Shenyang Agric. Univ. 2005, 36, 570–574. [Google Scholar]
- Ghanbarian-Alavijeh, B.; Hunt, A.G. Estimation of soil-water retention from particle-size distribution: Fractal approaches. Soil Sci. 2012, 177, 321–326. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E. Hydraulic conductivity limited equilibration: Effect on water retention characteristics. Vadose Zone J. 2005, 4, 145–150. [Google Scholar] [CrossRef]
- Yang, J.H.; Hu, J.M.; Luo, M.D. Functions and benefits of soil conservation of different forest types in sandstone mountains in central south Shandong. J. Soil Water Conserv. 2011, 25, 64–68. [Google Scholar]
- Wan, N.F.; Ji, X.Y.; Gu, X.J. Ecological engineering of ground cover vegetation promotes biocontrol services in peach orchards. Ecol. Eng. 2014, 64, 62–65. [Google Scholar] [CrossRef]
- China flora editorial board, Chinese Acadmy of Sciences (CAS). Flora of China. China Science and Technology Press: Beijing, China, 2004; pp. 214–220. [Google Scholar]
- Wang, B.; Lu, S.W.; Li, H.J.; Niu, X. Observation Methodology for Long-Term Forest Ecosystem Research; State Forestry Administration: Beijing, China, 2011; pp. 133–162. [Google Scholar]
- Institute of Soil Sciences, Chinese Acadmy of Sciences (ISSCAS). Physical and Chemical Analysis Methods of Soils; Shanghai Science Technology Press: Shanghai, China, 1978; pp. 7–59. [Google Scholar]
- Cheng, D.B.; Cai, C.F.; Peng, Y.P. Estimating soil water retention curve based on fractal dimension of soil particle size distribution of purple soil. J. Soil 2009, 46, 30–35. [Google Scholar]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar]
- Ghanbarian-Alavijeh, B.; Daigle, H. Fractal dimension of soil fragment mass-size distribution: A critical analysis. Geoderma 2015, 245–246, 98–103. [Google Scholar] [CrossRef]
- Miranda, J.G.V.; Montero, E.; Alves, M.C. Multifractal characterization of saprolite particle-size distributions after topsoil removal. Geoderma 2006, 134, 373–385. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour Res. 1990, 26, 1047–1056. [Google Scholar] [CrossRef]
- Zhang, B.H. Study on aggragate formation and stability mechanism of forests Soil in typical region of upper reaches of the Yangtze River in China. J. Liaocheng Univ. China 2007, 20, 12–17. [Google Scholar]
- Ghanbarian-Alavijeh, B.; Millan, H. The relationship between surface fractal dimension and soil water content at permanent wilting point. Geoderma 2009, 151, 224–232. [Google Scholar] [CrossRef]
- Huang, G.H.; Zhang, R.D. Evaluation of soil water retention curve with the pore-solid fractal model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Gao, P.; Wang, B.; Liu, Y. Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China. Int. J. Environ. Res. Public Health 2015, 12, 15379-15389. https://doi.org/10.3390/ijerph121214978
Niu X, Gao P, Wang B, Liu Y. Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China. International Journal of Environmental Research and Public Health. 2015; 12(12):15379-15389. https://doi.org/10.3390/ijerph121214978
Chicago/Turabian StyleNiu, Xiang, Peng Gao, Bing Wang, and Yu Liu. 2015. "Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China" International Journal of Environmental Research and Public Health 12, no. 12: 15379-15389. https://doi.org/10.3390/ijerph121214978
APA StyleNiu, X., Gao, P., Wang, B., & Liu, Y. (2015). Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China. International Journal of Environmental Research and Public Health, 12(12), 15379-15389. https://doi.org/10.3390/ijerph121214978





