Metrics, Dose, and Dose Concept: The Need for a Proper Dose Concept in the Risk Assessment of Nanoparticles
Abstract
:1. Introduction
- (1)
- The deposited dose, which is the total deposited NP surface area (SA) per tissue mass or volume (m2/kg, or m2/m3 or m−1). This SA of the NP has the potential to induce biological effects. Moreover, we consider agglomerated NPs as well.
- (2)
- The equivalent dose, whereby the deposited NP dose is weighted by factors quantifying the effects of several other physico-chemical properties of the NPs, such as the specific surface area, surface texture, electron band gap interval at the NP surface, surface charge (zeta-potential), NP morphology (shape, surface roughness, length-to-width ratio (aspect ratio)), and the dissolution rate.
2. Dose Assessment for Ionizing Radiation
2.1. Exposure to Ionizing Radiation
2.2. Absorbed Dose of Ionizing Radiation
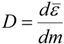
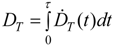
| Dose quantities | Radiation | NP |
|---|---|---|
| Absorbed/deposited dose (D): | The absorbed dose (D) is the mean energy dε imparted to matter of mass dm by ionising radiation, J·kg−1 or Gy: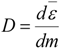 | The deposited dose of NP (DNP) is the total deposited surface area (SA) of NP per mass of living matter dm, m2/kg: |
| Dose rate: | The mean absorbed radiation dose rate in T at time t: ḊT(t) | The mean absorbed NP dose rate in T at time t: ḊNP,T(t) |
| Committed tissue dose: | The quantity of radiation absorbed per unit time: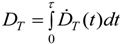 | The quantity of absorbed NP dose (uptake) per unit time: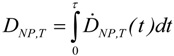 |
| Equivalent dose: | The mean absorbed dose from radiation R in a tissue or organ T, multiplied by the radiation weighting factor wR, J·kg−1 or Sv: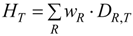 | Absorbed dose weighted by NP property(material) dependent reactivity weighting factor(s) wPC,i (i = 1, 2, ….) for different physico-chemical properties or functional “behaviors” of NP: |
| Effective dose: | The tissue-weighted sum of the equivalent doses in all specified tissues and organs of the body, J·kg−1 or Sv: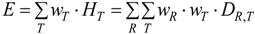 | The tissue-weighted sum of the equivalent doses in all specified tissues and organs of the body: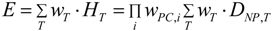 |
2.3. Equivalent Dose of Ionizing Radiation
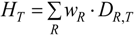
2.4. Effective Dose of Ionizing Radiation
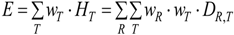
3. Dose Assessment for NPs
3.1. Exposure to NPs
3.2. Dosimetry for NPs
3.2.1. Deposited Dose of NP
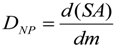
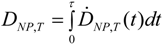
3.2.2. Equivalent Dose of NP and Weighting Factors
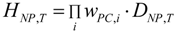
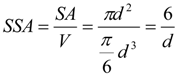
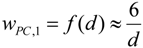
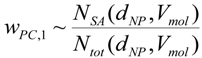
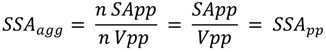
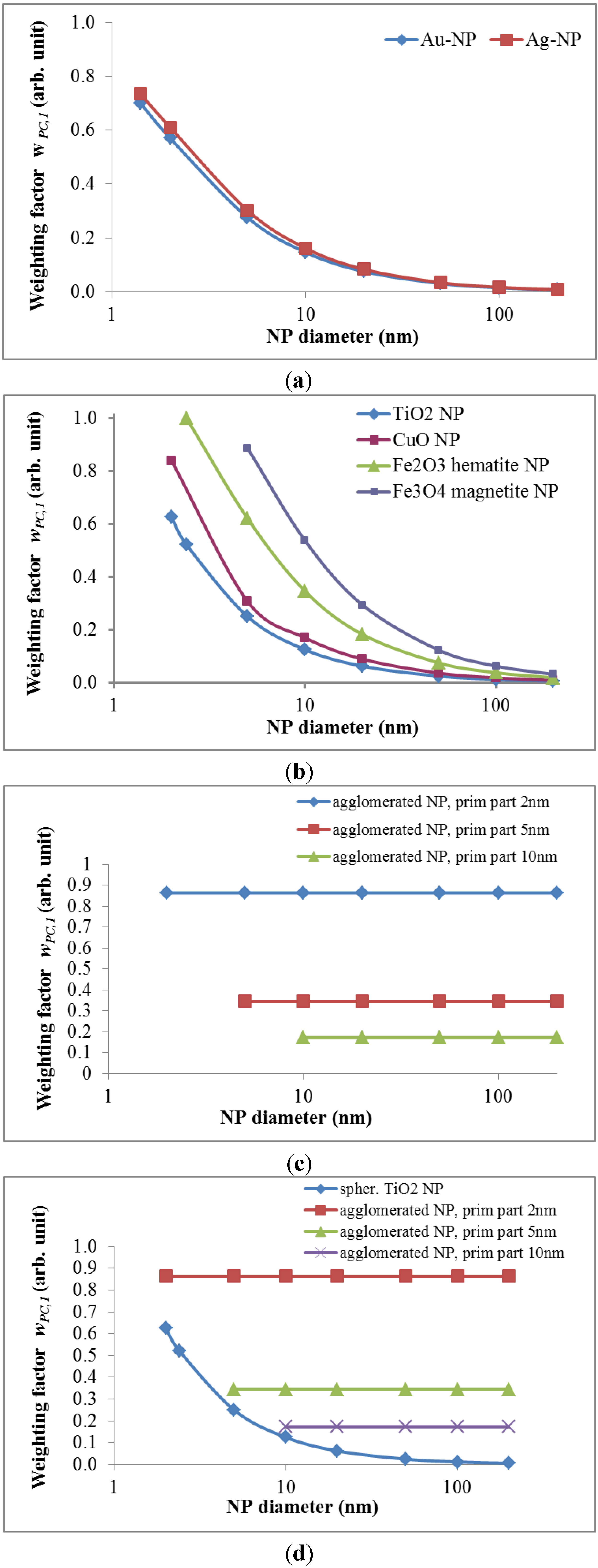
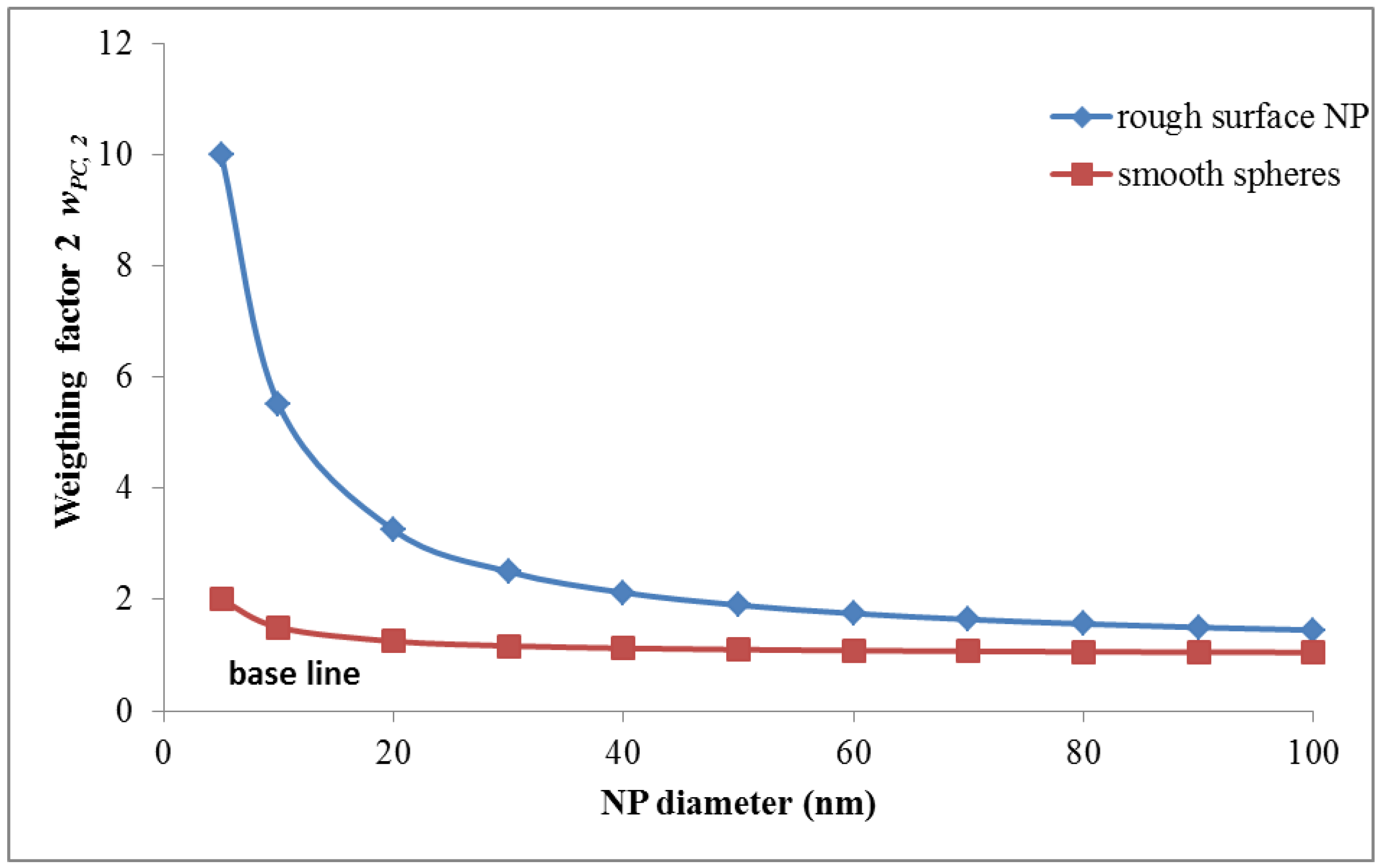
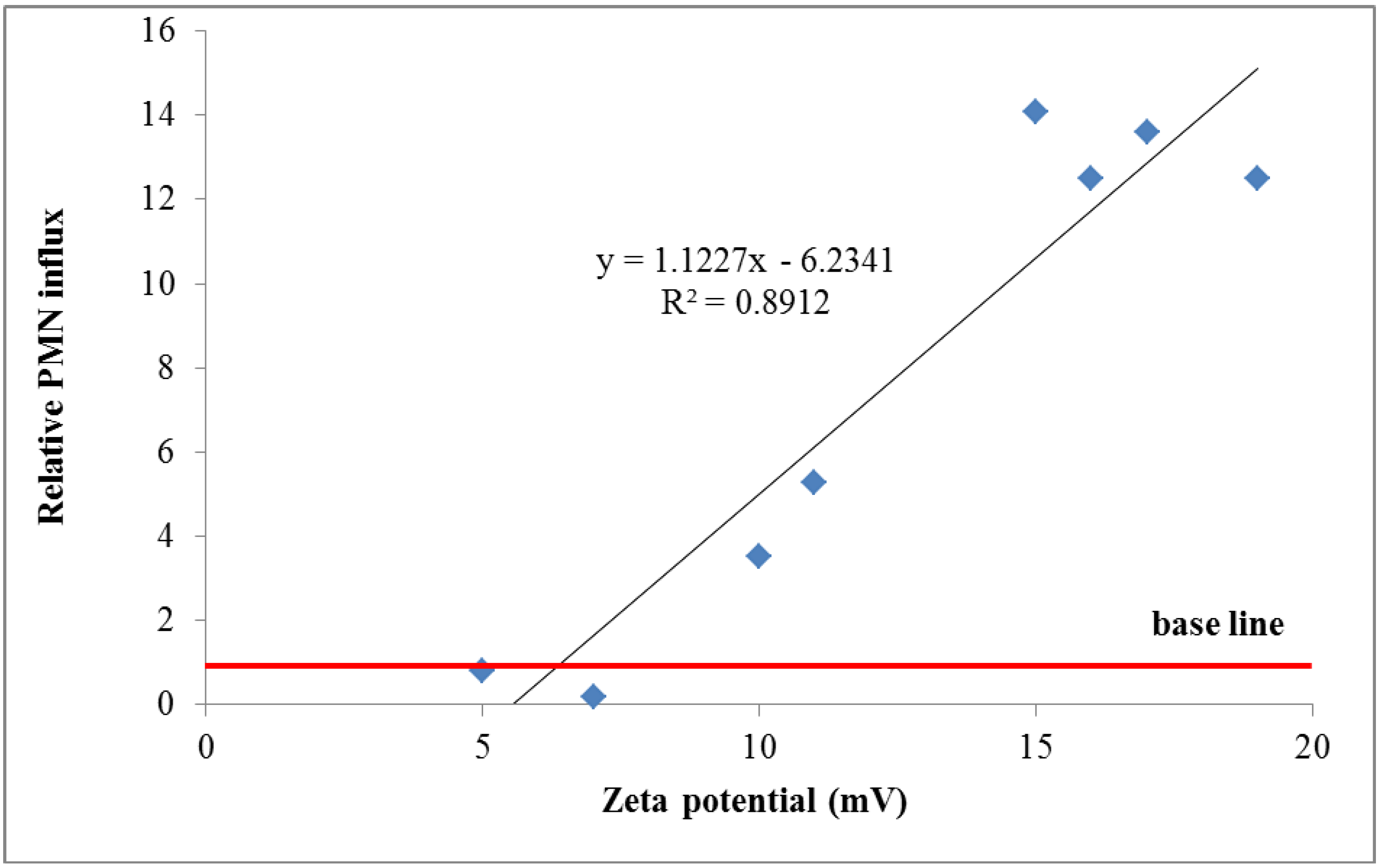
wPC,4 = 500 for NNI at frustrated phagocytosis
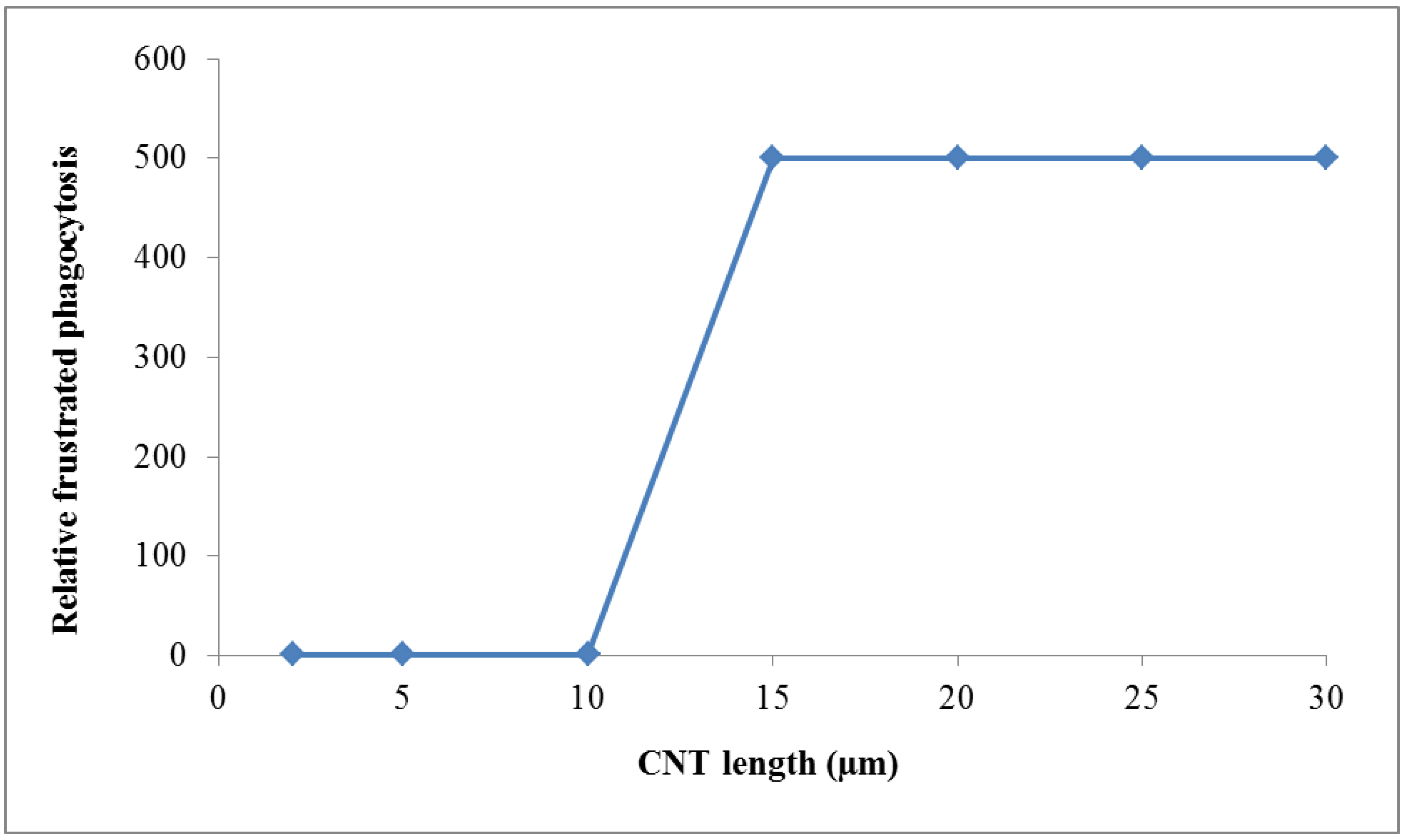
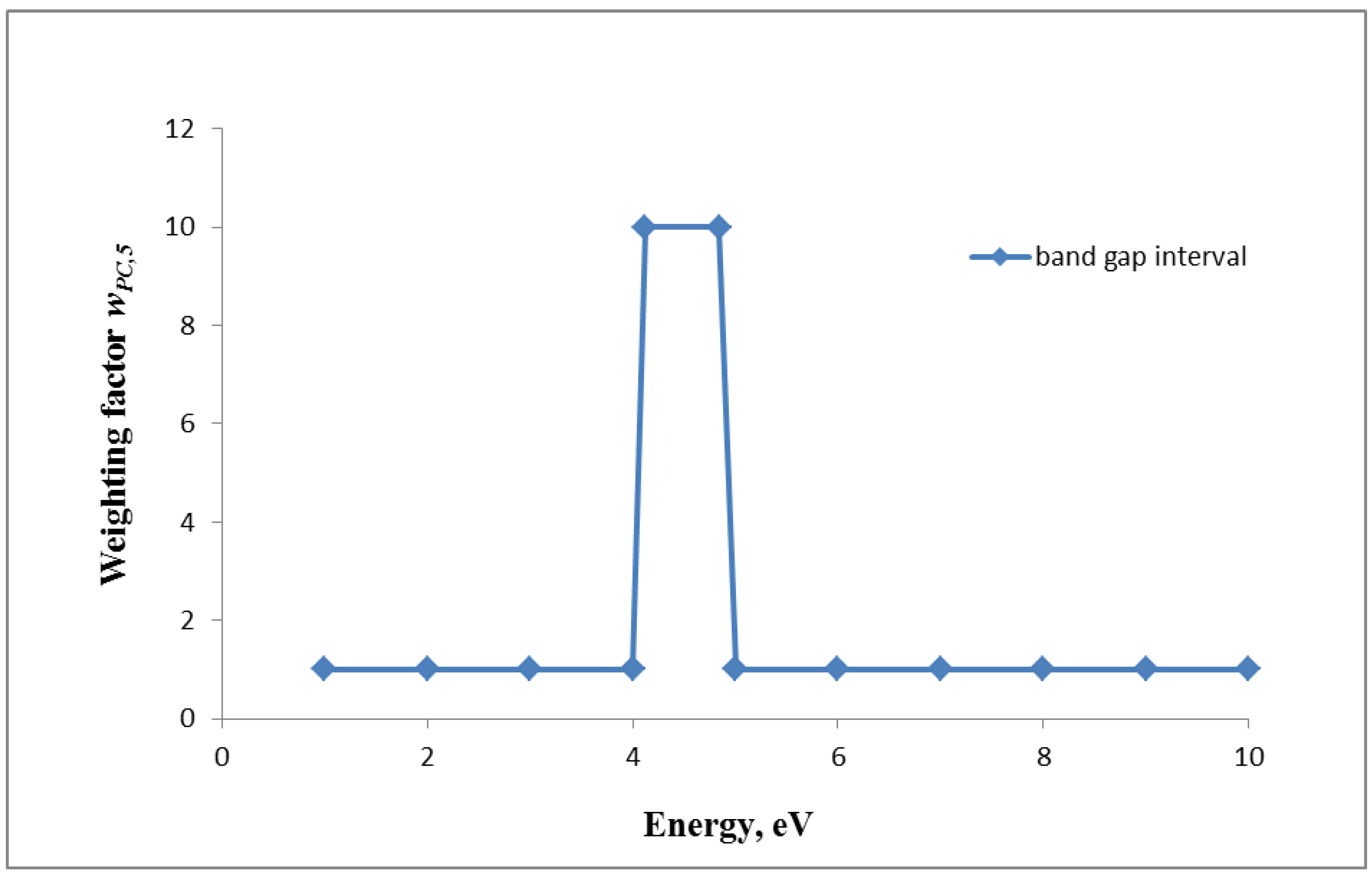
wPC,5 = 1 for NP atoms/molecules outside the above band gap interval
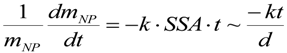
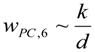

3.2.3. Consequences for Equivalent Dose of NP
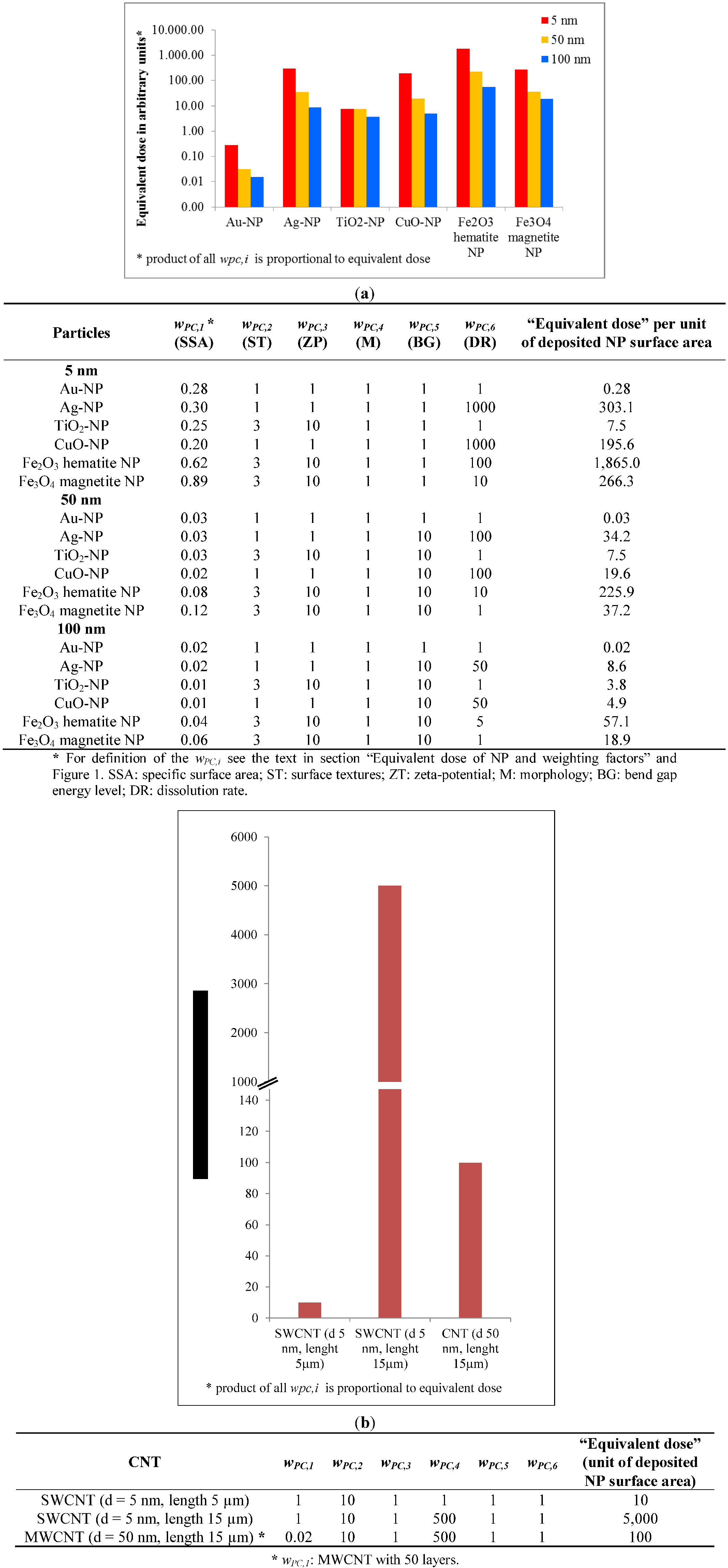
3.2.4. Effective Dose
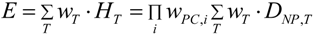
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hullmann, A. Who is winning the global nanorace? Nat. Nanotechnol. 2006, 1, 81–83. [Google Scholar] [CrossRef]
- Borm, P.J.; Robbins, D.; Haubold, S.; Kuhlbusch, T.; Fissan, H.; Donaldson, K.; Schins, R.; Stone, V.; Kreyling, W.; Lademann, J.; et al. The potential risks of nanomaterials: A review carried out for ecetoc. Part. Fibre Toxicol. 2006, 3. [Google Scholar] [CrossRef]
- Oberdorster, G.; Oberdorster, E.; Oberdorster, J. Nanotoxicology: An emerging discipline evolving from studies of ultrafine particles. Environ. Health Perspect. 2005, 113, 823–839. [Google Scholar] [CrossRef]
- Balasubramanian, S.K.; Poh, K.W.; Ong, C.N.; Kreyling, W.G.; Ong, W.Y.; Yu, L.E. The effect of primary particle size on biodistribution of inhaled gold nano-agglomerates. Biomaterials 2013, 34, 5439–5452. [Google Scholar] [CrossRef]
- Bergin, I.L.; Witzmann, F.A. Nanoparticle toxicity by the gastrointestinal route: Evidence and knowledge gaps. Int. J. Biomed. Nanosci. Nanotechnol. 2013, 3, 163–210. [Google Scholar] [CrossRef]
- Benfenati, E.; Pardoe, S.; Martin, T.; Gonella Diaza, R.; Lombardo, A.; Manganaro, A.; Gissi, A. Using toxicological evidence from QSAR models in practice. Altex 2013, 30, 19–40. [Google Scholar] [CrossRef]
- Burello, E.; Worth, A.P. A rule for designing safer nanomaterials: Do not interfere with the cellular redox equilibrium. Nanotoxicology 2013, 2013. [Google Scholar] [CrossRef]
- Aranda, A.; Sequedo, L.; Tolosa, L.; Quintas, G.; Burello, E.; Castell, J.V.; Gombau, L. Dichloro-dihydro-fluorescein diacetate (DCFH-DA) assay: A quantitative method for oxidative stress assessment of nanoparticle-treated cells. Toxicol. In Vitro 2013, 27, 954–963. [Google Scholar] [CrossRef]
- Burello, E.; Worth, A.P. A theoretical framework for predicting the oxidative stress potential of oxide nanoparticles. Nanotoxicology 2011, 5, 228–235. [Google Scholar] [CrossRef]
- Burello, E.; Worth, A. Computational nanotoxicology: Predicting toxicity of nanoparticles. Nat. Nanotechnol. 2011, 6, 138–139. [Google Scholar] [CrossRef]
- Dusinska, M.; Dusinska, M.; Fjellsbo, L.; Magdolenova, Z.; Rinna, A.; Runden Pran, E.; Bartonova, A.; Heimstad, E.; Harju, M.; Tran, L.; et al. Testing strategies for the safety of nanoparticles used in medical applications. Nanomedicine (Lond.) 2009, 4, 605–607. [Google Scholar] [CrossRef]
- Burello, E.; Worth, A.P. Qsar modeling of nanomaterials. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2011, 3, 298–306. [Google Scholar] [CrossRef]
- Nel, A.; Xia, T.; Meng, H.; Wang, X.; Lin, S.; Ji, Z.; Zhang, H. Nanomaterial toxicity testing in the 21st century: Use of a predictive toxicological approach and high-throughput screening. Acc. Chem. Res. 2013, 46, 607–621. [Google Scholar] [CrossRef]
- Nel, A.E.; Madler, L.; Velegol, D.; Xia, T.; Hoek, E.M.; Somasundaran, P.; Klaessig, F.; Castranova, V.; Thompson, M. Understanding biophysicochemical interactions at the nano-bio interface. Nat. Mater. 2009, 8, 543–557. [Google Scholar] [CrossRef]
- Puzyn, T.; Rasulev, B.; Gajewicz, A.; Hu, X.; Dasari, T.P.; Michalkova, A.; Hwang, H.M.; Toropov, A.; Leszczynska, D.; Leszczynski, J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 2011, 6, 175–178. [Google Scholar] [CrossRef]
- Gajewicz, A.; Rasulev, B.; Dinadayalane, T.C.; Urbaszek, P.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Advancing risk assessment of engineered nanomaterials: Application of computational approaches. Adv. Drug Deliv. Rev. 2012, 64, 1663–1693. [Google Scholar] [CrossRef]
- Winkler, D.A.; Mombelli, E.; Pietroiusti, A.; Tran, L.; Worth, A.; Fadeel, B.; McCall, M.J. Applying quantitative structure-activity relationship approaches to nanotoxicology: Current status and future potential. Toxicology 2013, 313, 15–23. [Google Scholar] [CrossRef]
- Engineered Nanoparticles: Review of Health and Environmental Safety (ENRHES). Available online: http://ihcp.jrc.ec.europa.eu/whats-new/enhres-final-report (accessed on 11 April 2014).
- Castranova, V. Overview of current toxicological knowledge of engineered nanoparticles. J. Occup. Environ. Med. 2011, 53, S14–S17. [Google Scholar] [CrossRef]
- Borm, P.J.; Kelly, F.; Kunzli, N.; Schins, R.P.; Donaldson, K. Oxidant generation by particulate matter: From biologically effective dose to a promising, novel metric. Occup. Environ. Med. 2007, 64, 73–74. [Google Scholar]
- Nel, A.; Xia, T.; Madler, L.; Li, N. Toxic potential of materials at the nanolevel. Science 2006, 311, 622–627. [Google Scholar] [CrossRef]
- International Commission on Radiological Protection. Human respiratory tract model for radiological protection. Ann. ICRP 1994, 24, 1–482. [Google Scholar]
- International Commission on Radiological Protection. Human alimentary tract model for radiological protection. ICRP Publication 100. Ann. ICRP 2006, 36, 25–327. [Google Scholar]
- International Commission on Radiological Protection. Recommendations of the international commission on radiological protection. ICRP Publication 60. Ann. ICRP 1991, 21, 1–3. [Google Scholar]
- International Commission on Radiological Protection. The 2007 recommendations of the international commission on radiological protection. ICRP. Publication 103. Ann. ICRP 2007, 37, 1–332. [Google Scholar]
- International Commission on Radiological Protection. Recommendations of the International Commission on Radiological Protection. ICRP Publication 26; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Boxall, A.B.; Chaudrhry, Q.; Sinclair, C.; Jones, A.; Aitken, R.; Jefferson, B.; Watts, C. Current and Future Predicted Environmental Exposure to Engineered Nanoparticles; Central Science Laboratory: New York, NY, USA, 2008. [Google Scholar]
- Mueller, N.C.; Nowack, B. Exposure modeling of engineered nanoparticles in the environment. Environ. Sci. Technol. 2008, 42, 4447–4453. [Google Scholar] [CrossRef]
- Oberdorster, G. Safety assessment for nanotechnology and nanomedicine: Concepts of nanotoxicology. J. Intern. Med. 2010, 267, 89–105. [Google Scholar] [CrossRef]
- Hinds, W.C. Adhesion of Particles. In Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Hinds, W.C. Particle Size Statistics. In Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Cho, W.S.; Duffin, R.; Thielbeer, F.; Bradley, M.; Megson, I.L.; Macnee, W.; Poland, C.A.; Tran, C.L.; Donaldson, K. Zeta potential and solubility to toxic ions as mechanisms of lung inflammation caused by metal/metal oxide nanoparticles. Toxicol. Sci. 2012, 126, 469–477. [Google Scholar] [CrossRef]
- Donaldson, K.; Schinwald, A.; Murphy, F.; Cho, W.S.; Duffin, R.; Tran, L.; Poland, C. The biologically effective dose in inhalation nanotoxicology. Acc. Chem. Res. 2013, 46, 723–732. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, Z.; Xia, T.; Meng, H.; Low-Kam, C.; Liu, R.; Pokhrel, S.; Lin, S.; Wang, X.; Liao, Y.P.; et al. Use of metal oxide nanoparticle band gap to develop a predictive paradigm for oxidative stress and acute pulmonary inflammation. ACS Nano 2012, 6, 4349–4368. [Google Scholar] [CrossRef]
- Mercer, T.T. On the role of particle size in the dissolution of lung burdens. Health Phys. 1967, 13, 1211–1221. [Google Scholar] [CrossRef]
- Moss, O.R.; Kanapilly, G.M. Dissolution of Inhaled. In Generation of Aerosols and Facilities for Exposure Experiments; Willeke, K., Ed.; Ann Arbor Science Publishers Inc.: Ann Arbor, MI, USA, 1980; pp. 105–124. [Google Scholar]
- Kreyling, W.G. Aerosol particle parameters maintaining lung clearance by intracellular dissolution and translocation. J. Aerosol Sci. 1990, 21, 371–374. [Google Scholar] [CrossRef]
- Kreyling, W.G.; Godleski, J.J.; Kariya, S.T.; Rose, R.M.; Brain, J.D. In vitro dissolution of uniform cobalt oxide particles by human and canine alveolar macrophages. Am. J. Respir. Cell Mol. Biol. 1990, 2, 413–422. [Google Scholar] [CrossRef]
- Park, M.V.; Lankveld, D.P.; van Loveren, H.; de Jong, W.H. The status of in vitro toxicity studies in the risk assessment of nanomaterials. Nanomedicine (Lond.) 2009, 4, 669–685. [Google Scholar] [CrossRef]
- Sohaebuddin, S.K.; Thevenot, P.T.; Baker, D.; Eaton, J.W.; Tang, L. Nanomaterial cytotoxicity is composition, size, and cell type dependent. Particle Fibre Toxicol. 2010, 7. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Simkó, M.; Nosske, D.; Kreyling, W.G. Metrics, Dose, and Dose Concept: The Need for a Proper Dose Concept in the Risk Assessment of Nanoparticles. Int. J. Environ. Res. Public Health 2014, 11, 4026-4048. https://doi.org/10.3390/ijerph110404026
Simkó M, Nosske D, Kreyling WG. Metrics, Dose, and Dose Concept: The Need for a Proper Dose Concept in the Risk Assessment of Nanoparticles. International Journal of Environmental Research and Public Health. 2014; 11(4):4026-4048. https://doi.org/10.3390/ijerph110404026
Chicago/Turabian StyleSimkó, Myrtill, Dietmar Nosske, and Wolfgang G. Kreyling. 2014. "Metrics, Dose, and Dose Concept: The Need for a Proper Dose Concept in the Risk Assessment of Nanoparticles" International Journal of Environmental Research and Public Health 11, no. 4: 4026-4048. https://doi.org/10.3390/ijerph110404026
APA StyleSimkó, M., Nosske, D., & Kreyling, W. G. (2014). Metrics, Dose, and Dose Concept: The Need for a Proper Dose Concept in the Risk Assessment of Nanoparticles. International Journal of Environmental Research and Public Health, 11(4), 4026-4048. https://doi.org/10.3390/ijerph110404026




