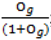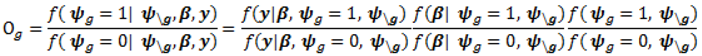Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach
Abstract
:1. Introduction
2. Methods
2.1. Esophageal Cancer Incidence Data in the Caspian Region of Iran
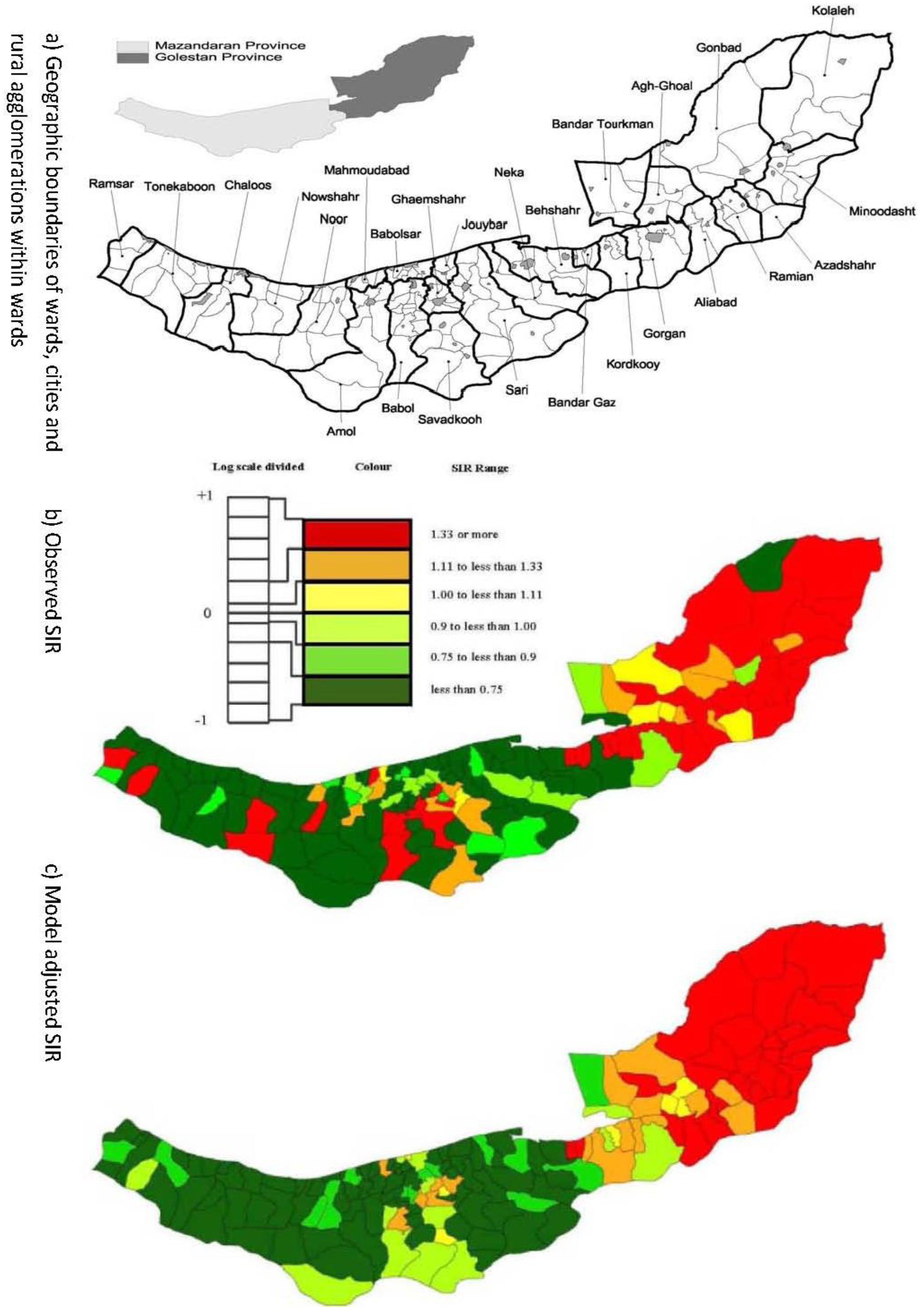
2.2. Model & Data Structure
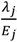 ).
).2.3. Distributions for Disease Counts



2.4. Hierarchical Models for Relative Risks
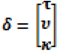 .
.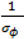 ) , describing the spatial variation in the heterogeneity component so that geographically close areas tend to present similar risks. One way of expressing this spatial structure is via Markov random fields models where the distribution of each ϕi given all the other elements {ϕ1, …, ϕi – 1, ϕi + 1, …, ϕJ} depends only on its neighbourhood [17]. A commonly used form for the conditional distribution of each ϕi is the Gaussian:
) , describing the spatial variation in the heterogeneity component so that geographically close areas tend to present similar risks. One way of expressing this spatial structure is via Markov random fields models where the distribution of each ϕi given all the other elements {ϕ1, …, ϕi – 1, ϕi + 1, …, ϕJ} depends only on its neighbourhood [17]. A commonly used form for the conditional distribution of each ϕi is the Gaussian:

2.5. Specification of Priors
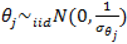 describing the non-spatial heterogeneity. The hyperparameters σθ, σϕ and δ are defined below.
describing the non-spatial heterogeneity. The hyperparameters σθ, σϕ and δ are defined below.2.6. Specification of Hyperpriors
2.7. Gibbs Variable Selection, GVS

- (1).
- Sample the parameters included in the model from the posterior:f (βψǀβ\ψ, ψ, y) ∝ (yǀβ,ψ) f (βψǀψ)
- (2).
- Sample the parameters excluded from the model from the pseudoprior:f (β\ψǀβψ, ψ, y) ∝ f(β\ψǀψ)
- (3).
- Sample each variable indicator j from a Bernoulli distribution with success probability
; where Og is given by:

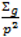 with p = 10 were made as they have also been shown to be adequate [18]. The pseudoprior parameters µG and Sg are only relevant to the behaviour of the MCMC chain and do not affect the posterior distribution [20].
with p = 10 were made as they have also been shown to be adequate [18]. The pseudoprior parameters µG and Sg are only relevant to the behaviour of the MCMC chain and do not affect the posterior distribution [20].
2.7.1. Fully Bayesian Estimation
2.7.2. Comparison of Model Performance
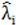 to calculate all the goodness of fit measures discussed in this paper.
to calculate all the goodness of fit measures discussed in this paper.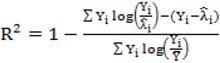 , however since R2 increases as more parameters are added to a model regardless of their contribution pseudo R2 is defined as Pseudo
, however since R2 increases as more parameters are added to a model regardless of their contribution pseudo R2 is defined as Pseudo 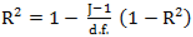 where d.f. for degrees of freedom equal J minus the effective number of free parameters [26].
where d.f. for degrees of freedom equal J minus the effective number of free parameters [26].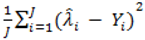 and mean absolute deviance as
and mean absolute deviance as  .
.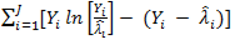 } provides evidence of overdispersion as follows: If the deviance index
} provides evidence of overdispersion as follows: If the deviance index 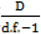 is much greater than 1 this suggests overdispersion. Rules of thumb on the size of the critical threshold vary from 1.2 or 1.3 to as large as 2.0 [30].
is much greater than 1 this suggests overdispersion. Rules of thumb on the size of the critical threshold vary from 1.2 or 1.3 to as large as 2.0 [30].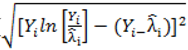 were plotted against the corresponding fitted values. For a satisfactory specification of the variance function this plot should show a running mean that is approximately straight and flat.
were plotted against the corresponding fitted values. For a satisfactory specification of the variance function this plot should show a running mean that is approximately straight and flat.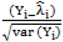 on the horizontal-axis versus the spatial lag of the standardised Pearson residual on the vertical axis. The spatial lag averages the effects of the neighbouring spatial agglomerations. By construction, the slope of the line in the scatterplot is equivalent to the Moran’s I coefficient [31]. If the slope is positive it means that there is positive spatial autocorrelation and a negative slope indicates a “checkerboard” spatial pattern.
on the horizontal-axis versus the spatial lag of the standardised Pearson residual on the vertical axis. The spatial lag averages the effects of the neighbouring spatial agglomerations. By construction, the slope of the line in the scatterplot is equivalent to the Moran’s I coefficient [31]. If the slope is positive it means that there is positive spatial autocorrelation and a negative slope indicates a “checkerboard” spatial pattern.3. Results
3.1. Automatic Bayesian Model Averaging
| Model | Posterior median of regression coefficient β1, (95% credible interval) | Random components | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Distribution | Spatial structure | income | urbanisation | literacy | unrestricted food choice | restricted food choice | σθ | σϕ | 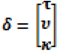 |
| Poisson | IN | −0.22, (−0.60, −0.03) | −0.36, (−0.42, −0.15) | −0.16, (−0.26, −0.08) | 0.12, (0.08, 0.16) | −0.32, (−0.41, −0.09) | 0.78 | - | - |
| Poisson | IN + N | −0.19, (−0.68, 0.02) | −0.36, (−0.51, −0.16) | −0.15, (−0.22, −0.05) | 0.07, (−0.04, 0.16) | −0.24, (−0.38, −0.06) | 0.35 | 0.73 | - |
| Poisson | IN + D | −0.18, (−0.69, 0.07) | −0.35, (−0.51, 0.03) | −0.15, (−0.22, 0.02) | 0.07, (−0.03, 0.16) | −0.23, (−0.38, 0.04) | 0.13 | - |  |
| G-Poisson | IN | −0.24, (−0.61, −0.09) | −0.38, (−0.51, −0.09) | −0.18, (−0.22, −0.05) | 0.11, (0.09, 0.16) | −0.28, (−0.44, −0.11) | 0.56 | - | - |
| G-Poisson | IN + N | −0.19, (−0.69, −0.04) | −0.35, (−0.51, −0.03) | −0.12, (−0.21, −0.03) | 0.07, (−0.02, 0.16) | 0.23, (−0.38, −0.04) | 0.12 | 0.66 | - |
| G-Poisson | IN + D | −0.19, (−0.68, 0.01) | −0.36, (−0.51, −0.07) | −0.15, (−0.22, 0.06) | 0.07, (−0.02, 0.16) | −0.24, (−0.39, −0.07) | 0.17 | - |  |
| NB | IN | −0.23, (−0.59, −0.10) | −0.39, (−0.58, 0.09) | −0.17, (−0.27, −0.7) | 0.17, (0.03, 0.16) | −0.31, (−0.48, −-0.12) | 0.36 | - | - |
| NB | IN + N | −0.17, (−0.68−0.06) | −0.35, (−0.51, 0.11) | −0.11, (−0.21, 0.01) | 0.07, (−0.04, 0.16) | −0.23, (−0.38, 0.02) | 0.12 | 0.74 | - |
| NB | IN + D | −0.20, (−0.68, 0.10) | −0.35, (−0.51, 0.08) | −0.15, (−0.22, 0.08) | 0.07, (−0.01, 0.16) | −0.24, (−0.38, 0.09) | 0.11 | - |  |
| Model distribution | Spatial structure | Subset | Covariates * | f(m|y) ** |
|---|---|---|---|---|
| Poisson | IN | 1 | income, restricted food choice | 0.37 |
| Poisson | IN | 2 | income, restricted food choice, urbanisation | 0.12 |
| Poisson | IN + N | 1 | income, restricted food choice, urbanisation | 0.31 |
| Poisson | IN + N | 2 | income, restricted food choice | 0.15 |
| Poisson | IN + D | 1 | urbanisation | 0.25 |
| Poisson | IN + D | 2 | income | 0.20 |
| G-Poisson | IN + D | 2 | income, urbanisation | 0.18 |
| G-Poisson | IN | 1 | income, restricted food choice | 0.28 |
| G-Poisson | IN | 2 | income, restricted food choice, urbanisation | 0.17 |
| G-Poisson | IN + N | 1 | income, urbanisation, restricted food choice | 0.28 |
| G-Poisson | IN + N | 2 | urbanisation, restricted food choice | 0.13 |
| G-Poisson | IN + D | 1 | restricted food choice | 0.19 |
| G-Poisson | IN + D | 2 | income, urbanisation | 0.18 |
| NB | IN | 1 | income, restricted food choice | 0.21 |
| NB | IN | 2 | restricted food choice, urbanisation | 0.11 |
| NB | IN + N | 1 | income | 0.26 |
| NB | IN + N | 2 | income, restricted food choice | 0.13 |
| NB | IN + D | 1 | income | 0.18 |
| NB | IN + D | 2 | restricted food choice | 0.12 |
| Model | Spatial structure | Subset | Covariates | f(ψg = 1ǀy) * |
|---|---|---|---|---|
| distribution | ||||
| Poisson | IN | 1 | income | 0.67 |
| restricted food choice | 0.42 | |||
| Poisson | IN + N | 1 | income | 0.61 |
| restricted food choice | 0.48 | |||
| urbanisation | 0.37 | |||
| Poisson | IN + D | 1 | urbanisation | 0.40 |
| G-Poisson | IN | 1 | income | 0.57 |
| restricted food choice | 0.33 | |||
| G-Poisson | IN + N | 1 | income | 0.59 |
| urbanisation | 0.43 | |||
| restricted food choice | 0.25 | |||
| G-Poisson | IN + D | 1 | restricted food choice | 0.22 |
| NB | IN | 1 | income | 0.64 |
| restricted food choice | 0.42 | |||
| NB | IN + N | 1 | income | 0.47 |
| NB | IN + D | 1 | income | 0.55 |
3.2. Prediction Performance
| Model | MAD a | MSPE b | Pseudo-R2 | Deviance index c | |
|---|---|---|---|---|---|
| Distribution | Spatial structure | ||||
| Poisson | IN | 4.4 | 30.3 | 0.24 | 3.1 |
| Poisson | IN + N | 3.7 | 16.6 | 0.32 | 2.8 |
| Poisson | IN + D | 2.6 | 13.8 | 0.28 | 2.9 |
| G-Poisson | IN | 3.2 | 14.9 | 0.30 | 2.6 |
| G-Poisson | IN + N | 2.1 | 10.1 | 0.35 | 1.6 |
| G-Poisson | IN + D | 2.3 | 11.6 | 0.33 | 1.7 |
| NB | IN | 3.4 | 15.8 | 0.30 | 2.4 |
| NB | IN + N | 2.2 | 10.3 | 0.33 | 1.7 |
| NB | IN + D | 2.3 | 13.0 | 0.35 | 1.4 |
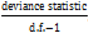
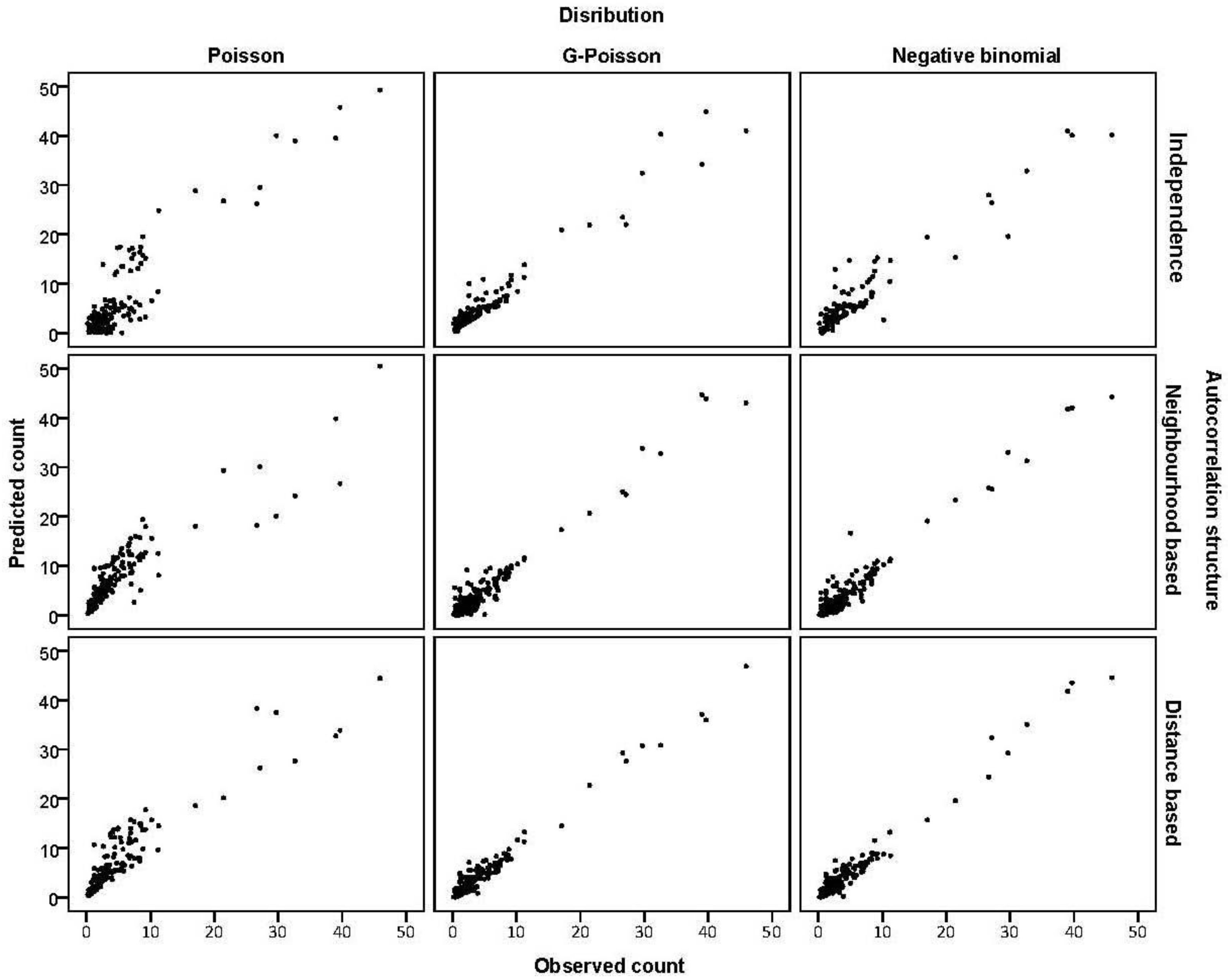
3.3. Assessing Overdispersion
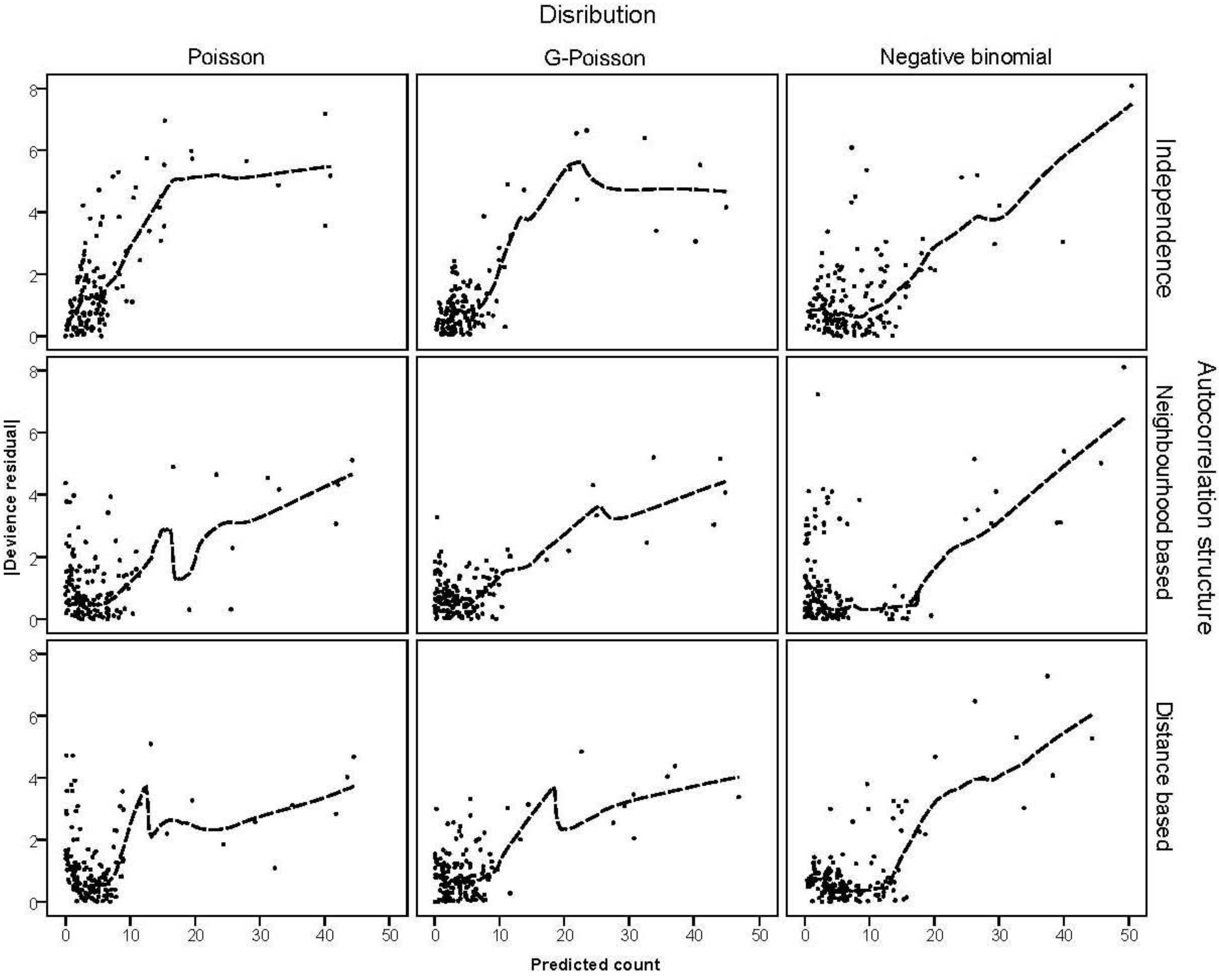
3.4. The Moran Scatterplots
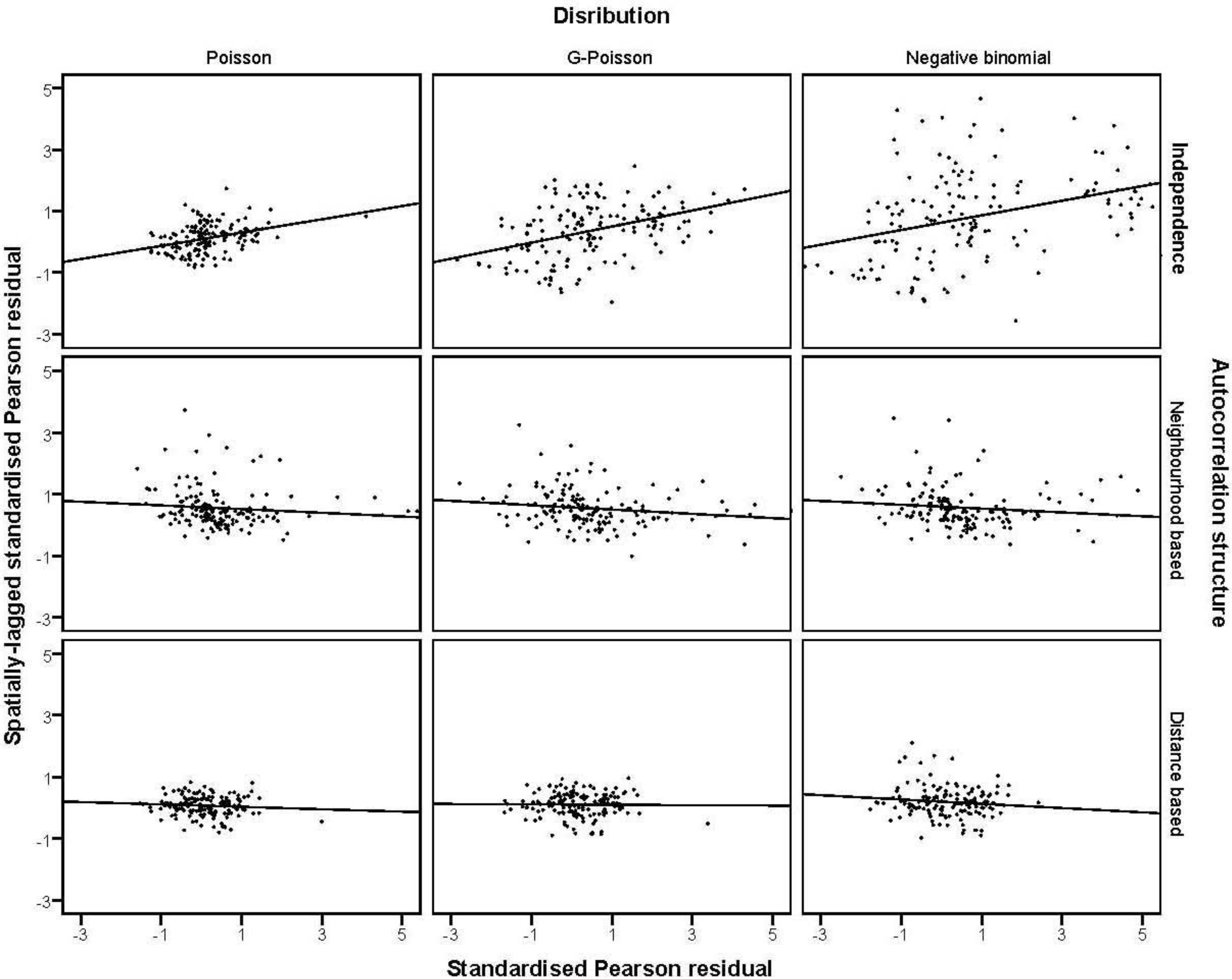
4. Discussion
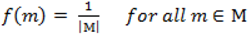 . When using the variable selection indicators ψ, this prior is equivalent to specifying independent Bernoulli prior distribution with inclusion probability equal to
. When using the variable selection indicators ψ, this prior is equivalent to specifying independent Bernoulli prior distribution with inclusion probability equal to 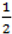 . Although ψ =
. Although ψ = 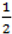 prior may be considered noninformative in the sense that it gives the same weight to all possible models it has been shown that this prior can be considered as informative since it puts more weight on models of size close to k/2 supporting a priori overparameterised and complicated models. This is especially problematic when k is large [37,38]. When meaningful prior information about ψ is unavailable, as is usually the case, perhaps the most reasonable strategy would be a fully Bayes approach that puts weak hyperior distributions on ψ. The potential drawback of this procedure is the computational limitation of visiting only a very small portion of the posterior when k is large yielding unreliable estimates of ψ. We defined the inclusion indicators as ψg ~ Bernoulli(0.5) for three reasons: First, our set of covariates was small (k = 5) and it was very unlikely that this choice of prior affects BMA. Second, to minimise any possible tendency towards overparameterised models we implemented a two stage modelling strategy and eliminated covariates with small inclusion probability at the first stage. Third, MCMC computations for fully Bayesian models potentially impose high computational costs. By choosing conventional empirical Bayesian method we aimed to retain useful features of Bayesian variable selection in a pragmatic way.
prior may be considered noninformative in the sense that it gives the same weight to all possible models it has been shown that this prior can be considered as informative since it puts more weight on models of size close to k/2 supporting a priori overparameterised and complicated models. This is especially problematic when k is large [37,38]. When meaningful prior information about ψ is unavailable, as is usually the case, perhaps the most reasonable strategy would be a fully Bayes approach that puts weak hyperior distributions on ψ. The potential drawback of this procedure is the computational limitation of visiting only a very small portion of the posterior when k is large yielding unreliable estimates of ψ. We defined the inclusion indicators as ψg ~ Bernoulli(0.5) for three reasons: First, our set of covariates was small (k = 5) and it was very unlikely that this choice of prior affects BMA. Second, to minimise any possible tendency towards overparameterised models we implemented a two stage modelling strategy and eliminated covariates with small inclusion probability at the first stage. Third, MCMC computations for fully Bayesian models potentially impose high computational costs. By choosing conventional empirical Bayesian method we aimed to retain useful features of Bayesian variable selection in a pragmatic way.5. Conclusions
Conflicts of Interest
Acknowledgements
References
- Best, N.G.; Ickstadt, K.; Wolpert, R.L. Spatial Poisson regression for health and exposure data measured at disparate resolutions. J. Am. Stat. Assoc. 2000, 95, 1076–1088. [Google Scholar] [CrossRef]
- Wakefield, J. Disease mapping and spatial regression with count data. Biostatistics 2007, 8, 158–183. [Google Scholar] [CrossRef]
- Kelsall, J.; Wakefield, J. Modelling spatial variation in disease risk: A geostatistical approach. J. Am. Stat. Assoc. 2002, 97, 692–701. [Google Scholar] [CrossRef]
- Haining, R.; Law, J.; Griffith, D. Modelling small area counts in the presence of overdispersion and spatial autocorrelation. Comput. Stat. Data Anal. 2009, 53, 2923–2937. [Google Scholar] [CrossRef]
- Pascutto, C.; Wakefield, J.; Best, N.G.; Richardson, S.; Bernardinelli, L.; Staines, A.; Elliott, A. Statistical issues in the analysis of disease mapping data. Stat. Med. 2000, 19, 2493–2519. [Google Scholar] [CrossRef]
- Liang, K.Y.; Zeger, S. Regression analysis for correlated data. Annu. Rev. Public Health 1993, 14, 43–68. [Google Scholar] [CrossRef]
- Joe, H.; Zhu, R. Generalized Poisson distribution: The property of mixture of Poisson and comparison with negative binomial distribution. Biom. J. 2005, 47, 219–229. [Google Scholar] [CrossRef]
- Lord, D.; Washington, S.; Ivan, J. Poisson, Poisson gamma and zero-inflated regression models of motor vehicle crashes: Balancing statistical fit and theory. Accid. Anal. Prev. 2005, 37, 35–46. [Google Scholar] [CrossRef]
- Ntzoufras, I.; Katsis, A.; Karlis, D. Bayesian assessment of the distribution of insurance claim counts using reversible jump MCMC. North Am. Actuar. J. 2005, 9, 90–108. [Google Scholar] [CrossRef]
- Manton, K.G.; Stallard, E. Methods for the analysis of mortality risks across heterogeneous small populations: Estimation of space-time gradients in cancer mortality in North Carolina counties 1970–75. Demography 1981, 18, 217–230. [Google Scholar] [CrossRef]
- Frey, C.; Feuer, E.; Timmel, M. Projection of incidence rates to a larger population using ecologic variables. Stat. Med. 1994, 13, 1755–1770. [Google Scholar] [CrossRef]
- Mohebbi, M.; Nourijelyani, K.; Mahmoudi, M.; Mohammad, K.; Zeraati, H.; Fotouhi, A.; Moghadaszadeh, B. Time of occurrence and age distribution of digestive tract cancers in Northern Iran. Iran. J. Public Health 2008, 37, 8–19. [Google Scholar]
- Mohebbi, M.; Mahmoodi, M.; Wolfe, R.; Nourijelyani, K.; Mohammad, K.; Zeraati, H.; Fotouhi, A. Geographical spread of gastrointestinal tract cancer incidence in the Caspian Sea region of Iran: Spatial analysis of cancer registry data. BMC Cancer 2008, 8, 137. [Google Scholar] [CrossRef]
- Mohebbi, M.; Wolfe, M.; Jolley, D.; Forbes, D.; Mahmoodi, M.; Burton, R. The spatial distribution of esophageal and gastric cancer in Caspian region of Iran: An ecological analysis of diet and socio-economic influences. Int. J. Health Geogr. 2011, 10, 13. [Google Scholar] [CrossRef]
- Richardson, S. Statistical Methods for Geographical Correlation Studies. In Geographical and Environmental Epidemiology; Elliott, P., Cuzick, J., English, D., Stern, R., Eds.; Oxford University Press: Oxford, UK, 1992; pp. 181–204. [Google Scholar]
- Besag, J.; York, J.; Mollie, A. Bayesian image restoration with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–59. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- George, E.; McCulloch, R. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Dellaportas, P.; Forster, J.; Ntzoufras, I. Bayesian Variable Selection Using the Gibbs Sampler. In Generalized Linear Models: A Bayesian Perspective; Dey, D., Ghosh, S., Mallick, B., Eds.; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Ntzoufras, I. Gibbs variable selection using BUGS. J. Stat. Soft. 2002, 7, 1–19. [Google Scholar]
- Feldkircher, M.; Zeugner, S. Benchmark Priors Revisited: On Adaptive Shrinkage and the Supermodel Effect in Bayesian Model Averaging; International Monetary Fund: Washington, DC, USA, 2009. [Google Scholar]
- Hoeting, J.A.; David, M.; Adrian, E.R.; Chris, T.V. Bayesian model averaging: A tutorial (with discussion). Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Dellaportas, P.; Forster, J.; Ntzoufras, I. On Bayesian model and variable selection using MCMC. Stat. Comp. 2002, 12, 27–36. [Google Scholar] [CrossRef]
- Ntzoufras, I. Appendix C: Checking Convergence Using CODA/BOA. In Bayesian Modeling Using WinBUGS; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS—A Bayesian modelling framework: Concepts, structure, and extensibility. Stat. Comp. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Cameron, A.; Windmeijer, F. R2 measures for count data regression models with applications to health-care utilization. J. Bus. Econ. Stat. 1996, 14, 209–220. [Google Scholar]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; Chapman and Hall: London, UK, 1989. [Google Scholar]
- Cliff, A.D.; Ord, J.K. Spatial Processes; Pion: London, UK, 1981. [Google Scholar]
- Xiang, L.; Lee, A.H. Sensitivity of test for overdispersion in Poisson regression. Biom. J. 2005, 47, 167–176. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Advanced Topics in Response Surface Methodology. In Response Surface Methodology: PROCESS and Product Optimization Using Designed Experiments, 3rd ed.; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Ntzoufras, I. Bayesian Model and Variable Evaluation. In Bayesian Modeling Using WinBUGS; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Hegarty, A.C.; Carsin, A.-E.; Comber, H. Geographical analysis of cancer incidence in Ireland: A comparison of two Bayesian spatial models. Cancer Epidemiol. 2010, 34, 373–381. [Google Scholar] [CrossRef]
- Kanga, E.L.; Liu, D.; Cressie, N. Statistical analysis of small-area data based on independence, spatial, non-hierarchical, and hierarchical models. Comput. Stat. Data Anal. 2009, 53, 3016–3032. [Google Scholar] [CrossRef]
- Quddus, M.A. Modelling area-wide count outcomes with spatial correlation and heterogeneity: An analysis of London crash data. Accid. Anal. Prev. 2008, 40, 1486–1497. [Google Scholar] [CrossRef]
- Leroux, B.G.; Lei, X.; Breslow, N. Estimation of Disease Rates in Small Areas: A New Mixed Model for Spatial Dependence. In Statistical Models in Epidemiology the Environment and Clinical Trials; Halloran, M.E., Berry, D.A., Eds.; Springer: New York, NY, USA, 1999; pp. 179–192. [Google Scholar]
- George, E.; Foster, D. Calibration and empirical Bayes variable selection. Biometrika 2000, 87, 731–748. [Google Scholar] [CrossRef]
- Chipman, H. Bayesian variable selection with related predictors. Can. J. Stat. 1996, 24, 17–36. [Google Scholar] [CrossRef]
- Douglas, J.B. Empirical fitting of discrete distributions. Biometrics 1994, 50, 576–579. [Google Scholar] [CrossRef]
- Murphy, M.; Wang, D. Do previous birth interval and maternal education influence infant survival? A Bayesian model averaging analysis of Chinese data. Popul. Stud. 2001, 55, 37–47. [Google Scholar] [CrossRef]
- Duolao, W.; Wenyang, Z.; Ameet, B. Comparison of Bayesian model averaging and stepwise methods for model selection in logistic regression. Stat. Med. 2004, 23, 3451–3467. [Google Scholar] [CrossRef]
- Genell, A.; Nemes, S.; Steineck, G.; Dickman, P. Model selection in medical research: A simulation study comparing Bayesian model averaging and stepwise regression. BMC Med. Res. Methodol. 2010, 10. [Google Scholar] [CrossRef]
- Ley, E.; Steel, M.F.J. On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. J. Appl. Econom. 2009, 24, 651–674. [Google Scholar] [CrossRef]
- Liang, F.; Paulo, R.; German, G.; Clyde, M.A.; Jo, B. Mixtures of g priors for Bayesian variable selection. J. Am. Stat. Assoc. 2008, 103, 401–414. [Google Scholar]
- Eicher, T.S.; Papageorgiou, C. Default priors and predictive performance in Bayesian model averaging, with application to growth determinants. J. Appl. Econom. 2011, 26, 30–55. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mohebbi, M.; Wolfe, R.; Forbes, A. Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach. Int. J. Environ. Res. Public Health 2014, 11, 883-902. https://doi.org/10.3390/ijerph110100883
Mohebbi M, Wolfe R, Forbes A. Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach. International Journal of Environmental Research and Public Health. 2014; 11(1):883-902. https://doi.org/10.3390/ijerph110100883
Chicago/Turabian StyleMohebbi, Mohammadreza, Rory Wolfe, and Andrew Forbes. 2014. "Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach" International Journal of Environmental Research and Public Health 11, no. 1: 883-902. https://doi.org/10.3390/ijerph110100883
APA StyleMohebbi, M., Wolfe, R., & Forbes, A. (2014). Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach. International Journal of Environmental Research and Public Health, 11(1), 883-902. https://doi.org/10.3390/ijerph110100883